Evaluation of Thermal Decomposition Kinetics of Poly (Lactic Acid)/Ethylene Elastomer (EE) Blends
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of PLA/EE Blends
2.3. PLA and PLA Blends Thermal Characterization
2.3.1. Thermal Decomposition Kinetic Approach
2.3.2. Thermodynamic Approach
3. Results and Discussion
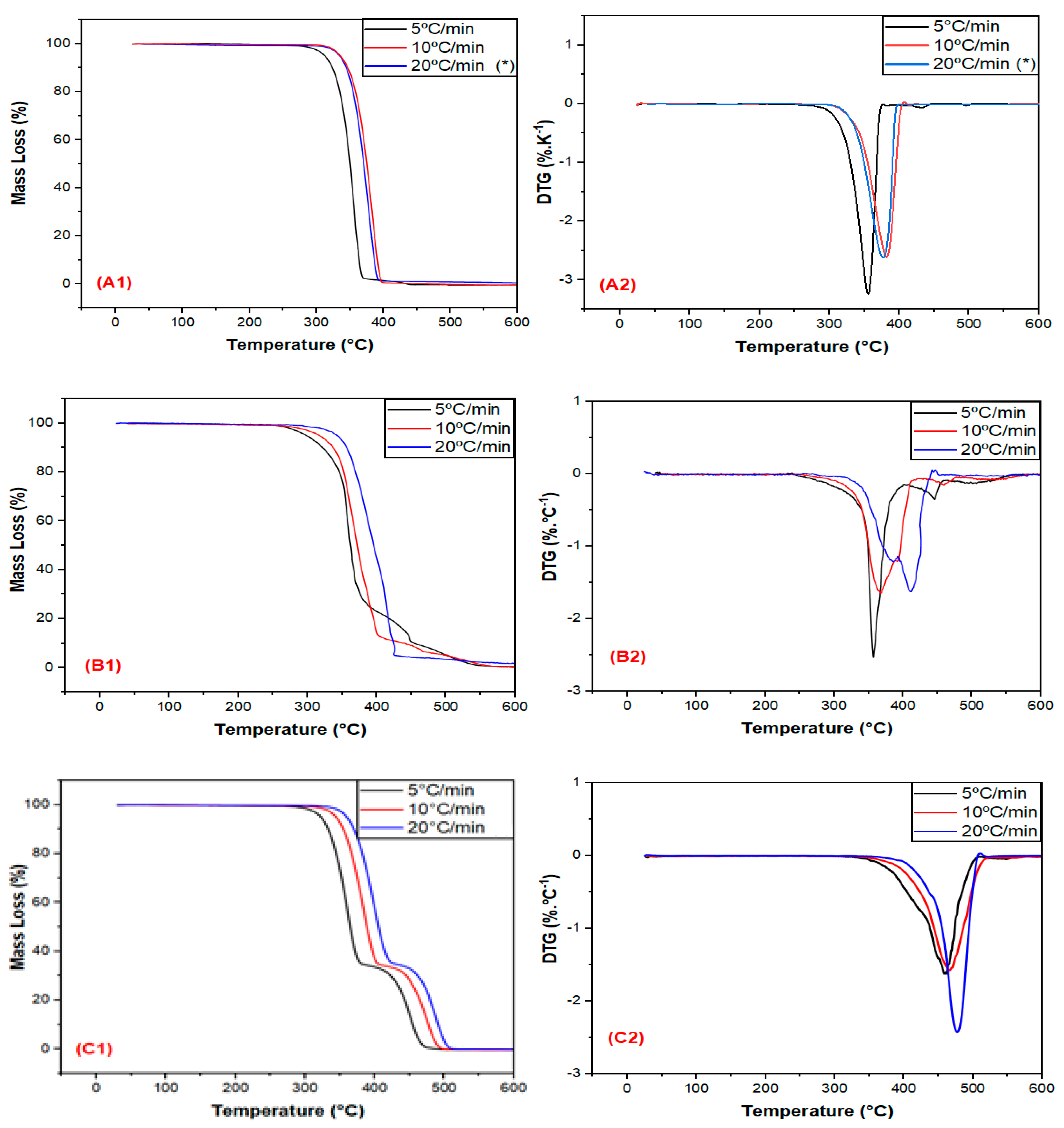
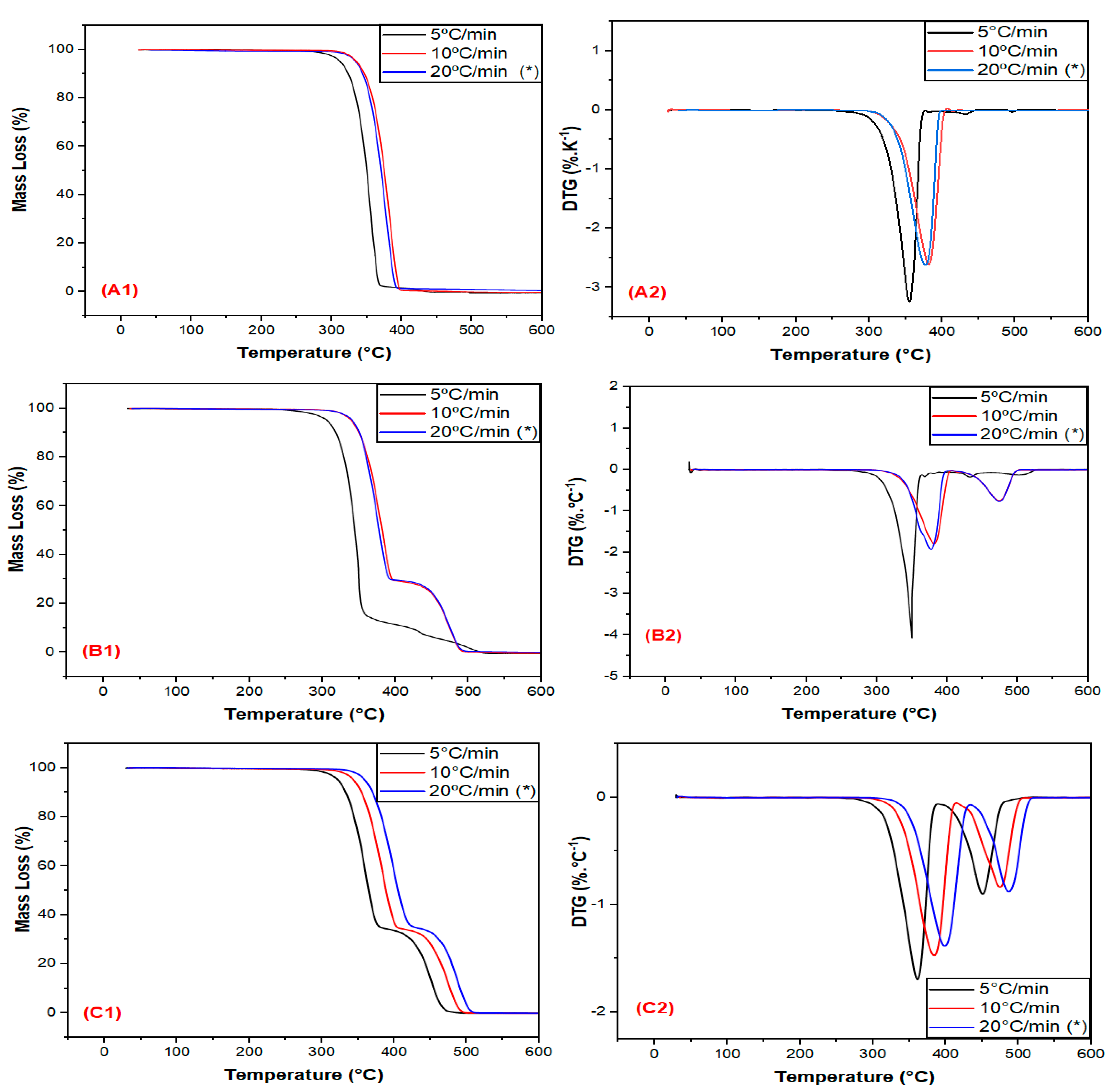
3.1. Thermal Stability Evaluation in a Non-Oxidative Atmosphere
3.2. PLA and PLA/EE Blends Kinetics of Thermal Degradation
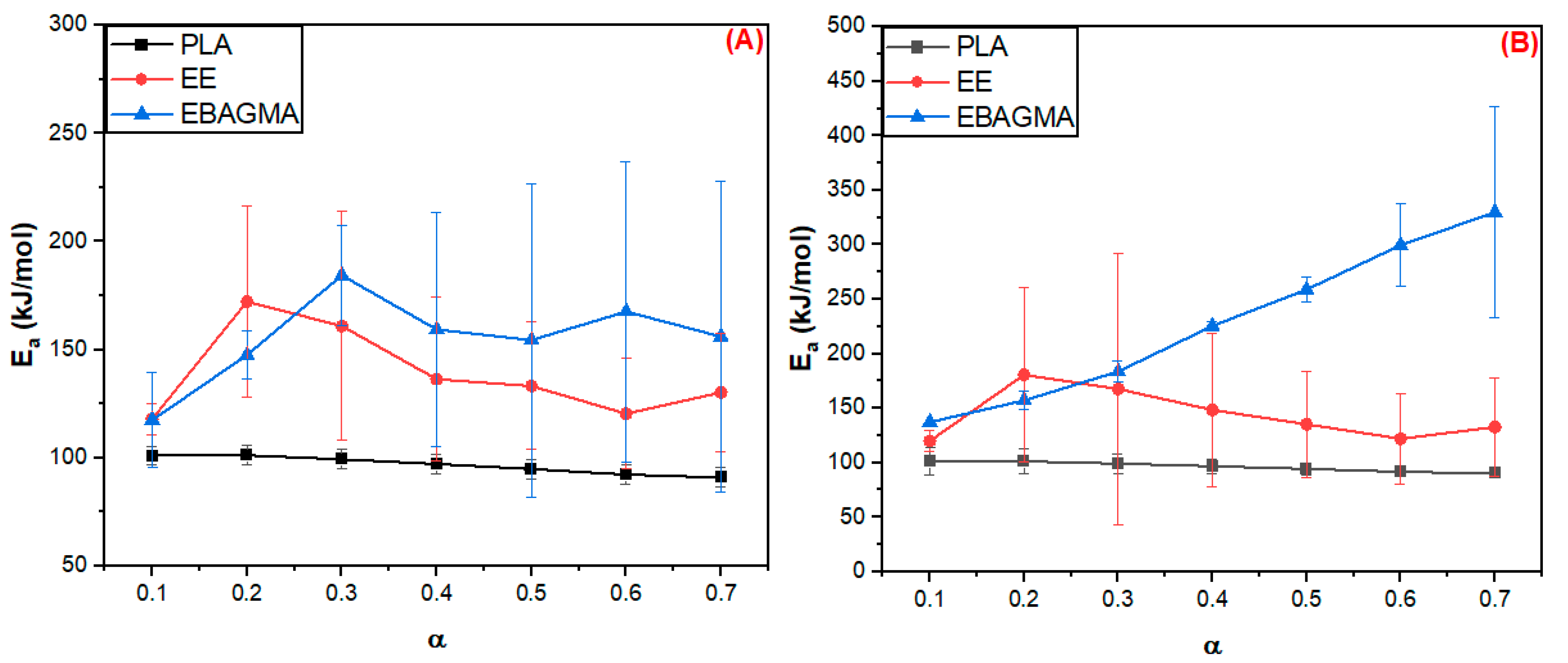
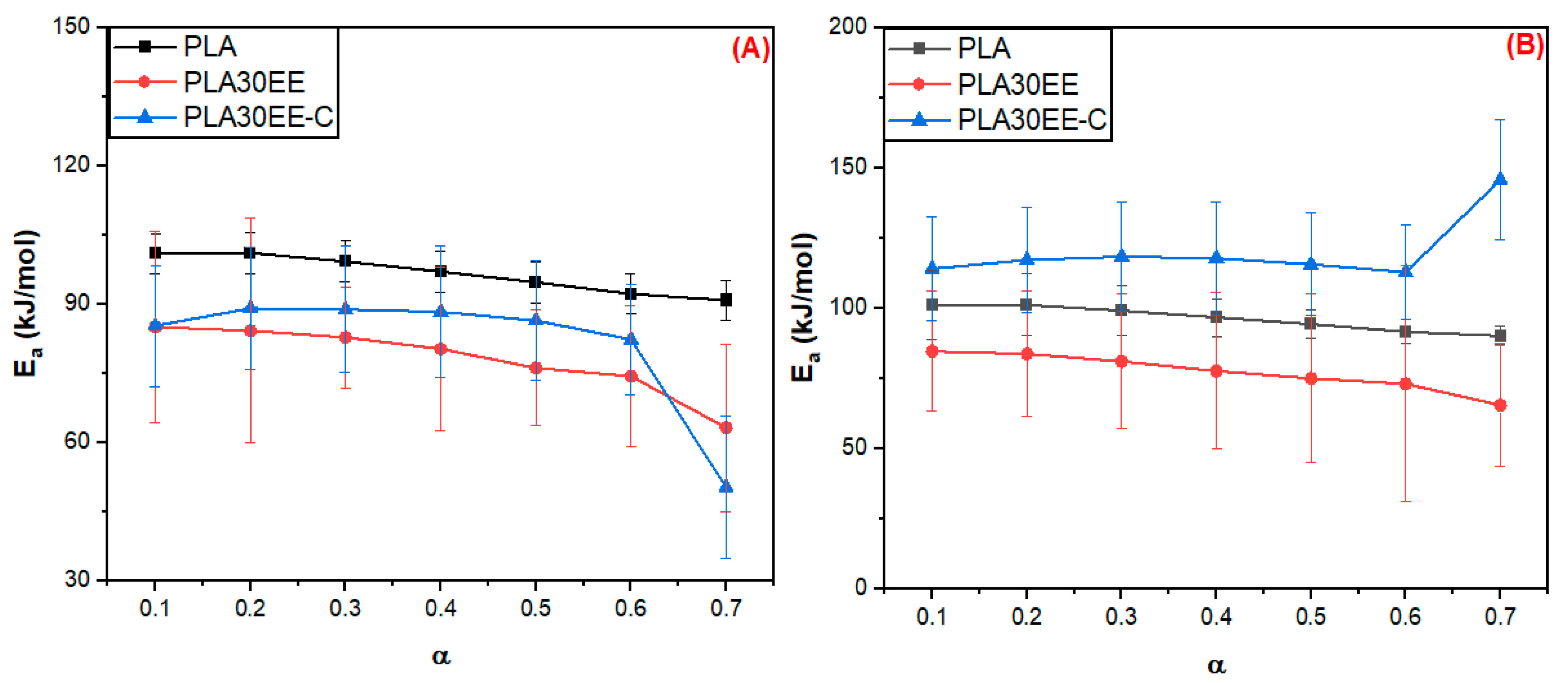
3.2.1. Estimative of Apparent Activation Energy (Ea)
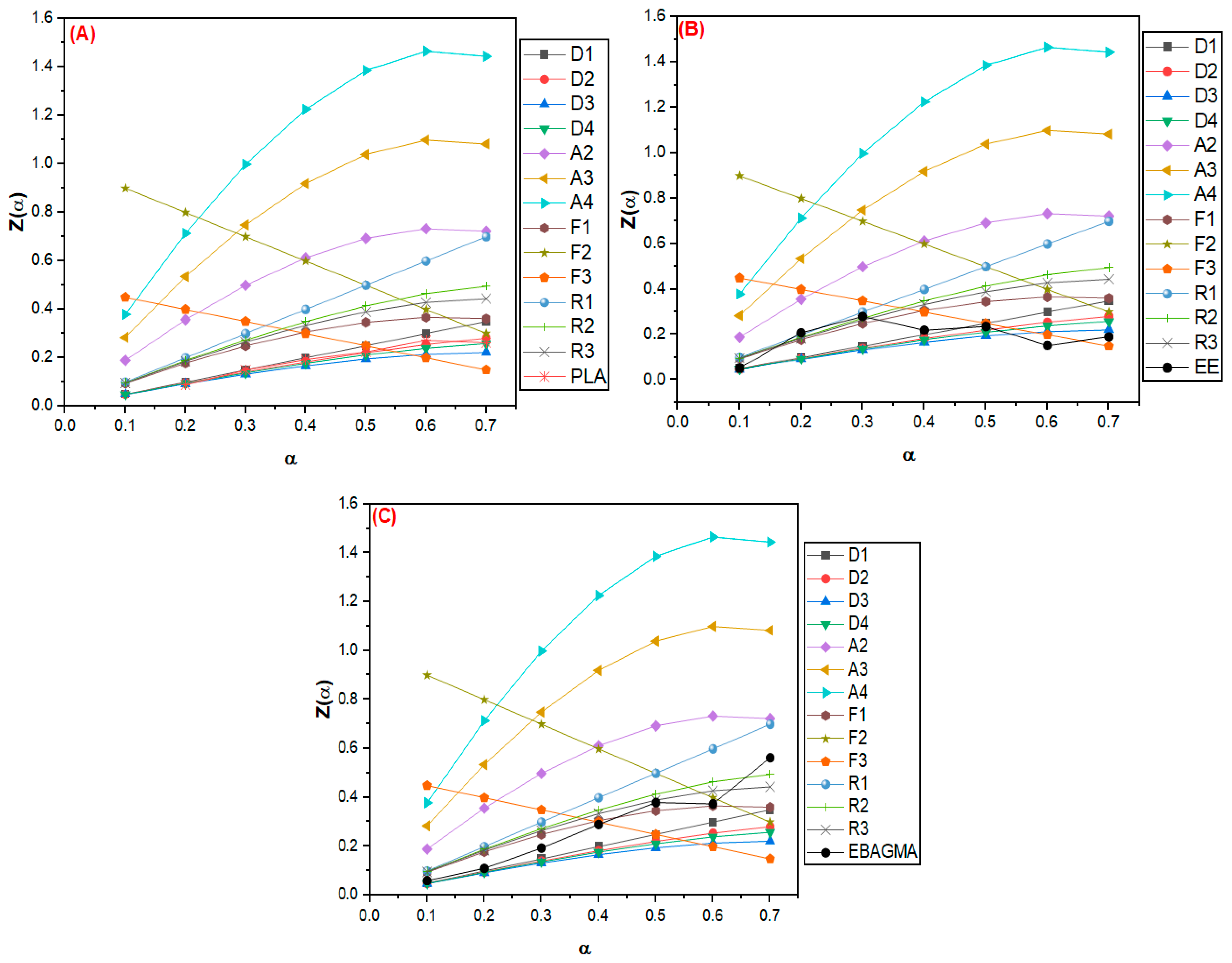
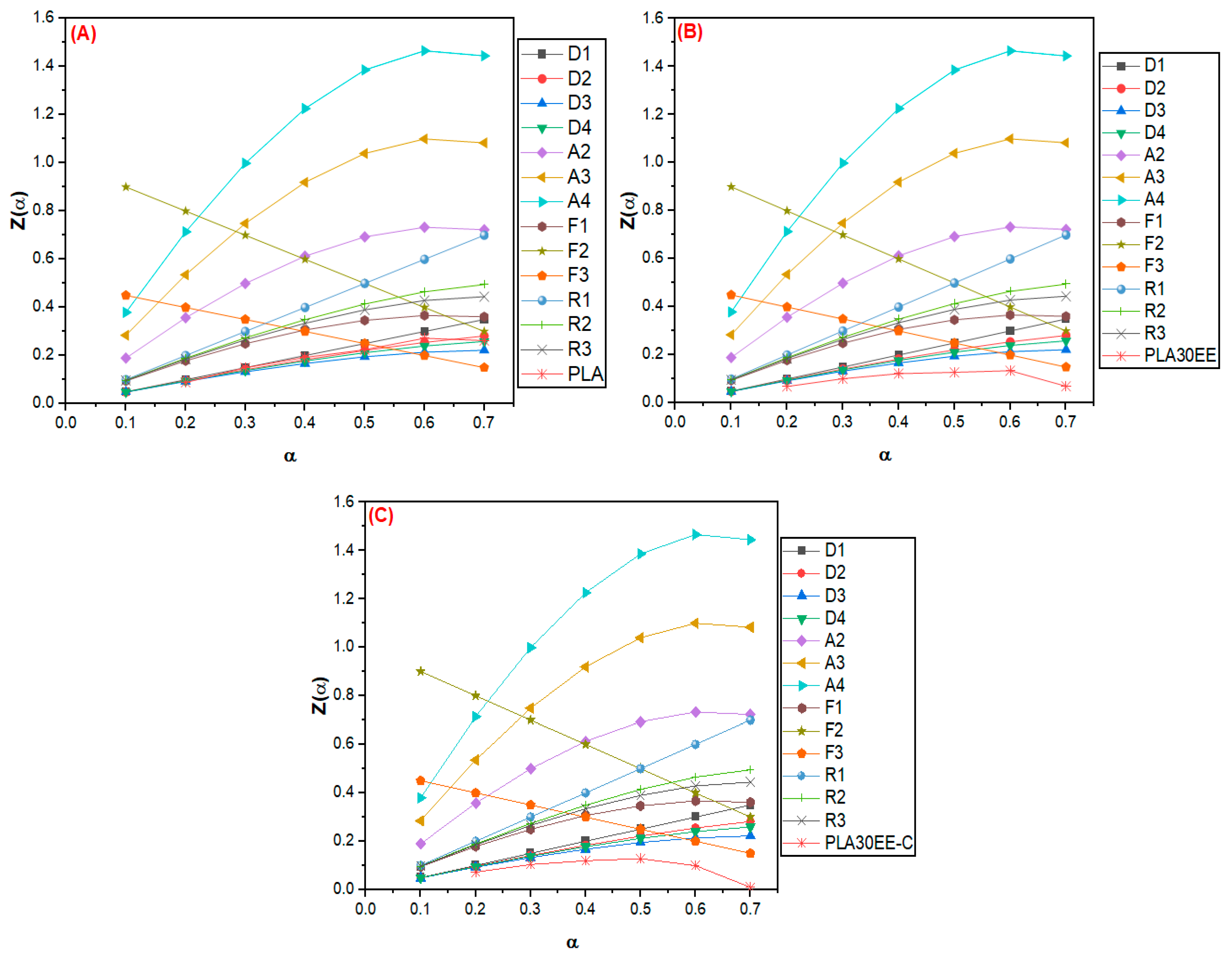
3.2.2. Evaluation of Thermal Degradation Mechanism by the Criado Method
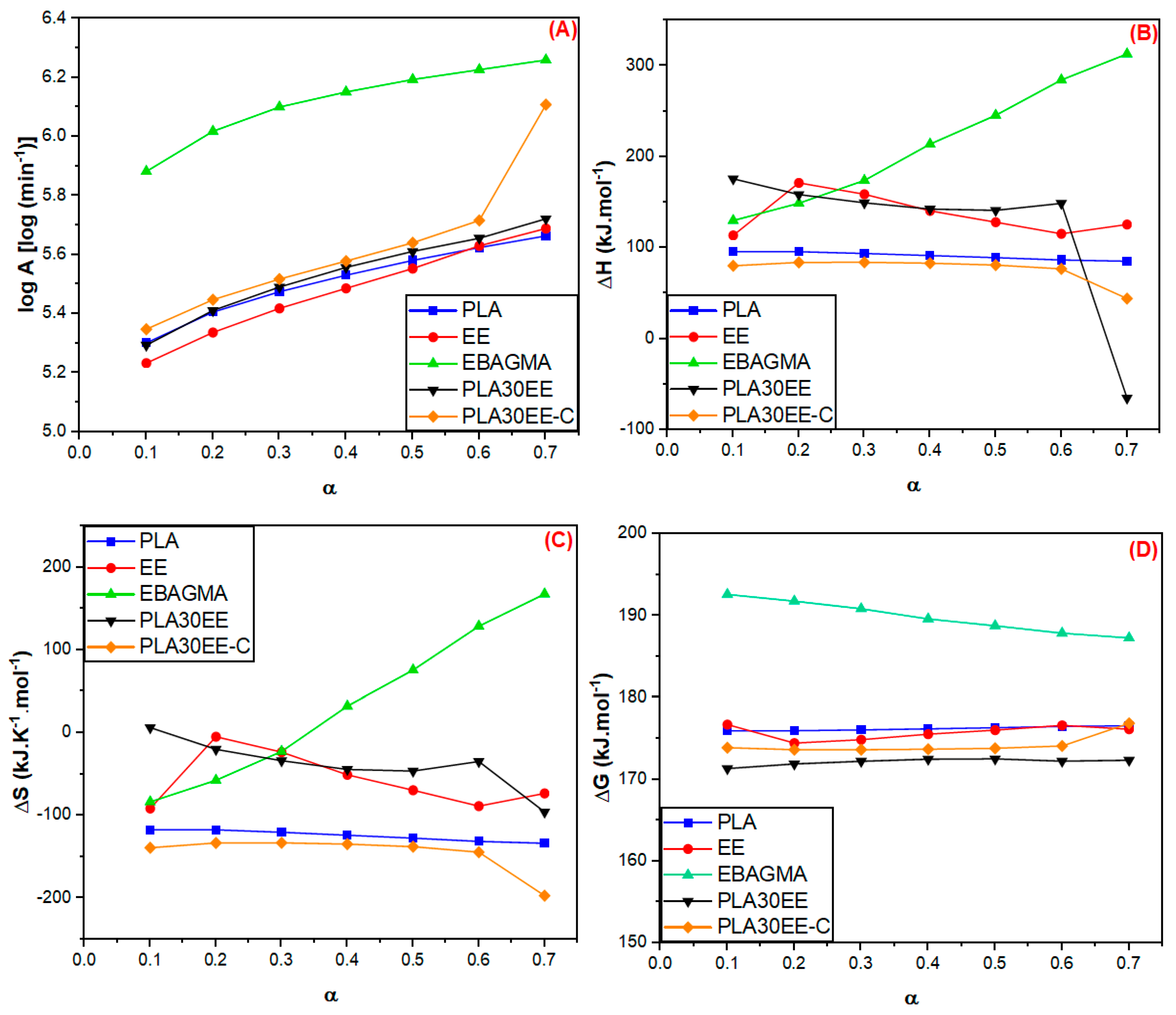
3.3. Thermodynamics Parameters of the PLA and the PLA/EE Blends
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Samir, A.; Ashour, F.H.; Hakim, A.A.A.; Bassyouni, M. Recent advances in biodegradable polymers for sustainable applications. NPJ Mater. Degrad. 2022, 6, 68. [Google Scholar] [CrossRef]
- Karande, R.D.; Abitha, V.K.; Rane, A.V.; Mishra, R.K. Preparation of polylactide from synthesized lactic acid and effect of reaction parameters on conversion. J. Mater. Sci. Eng. Adv. Technol. 2015, 12, 1–37. [Google Scholar] [CrossRef]
- Amin, U.; Khan, M.U.; Majeed, Y.; Rebezov, M.; Khayrullin, M.; Bobkova, E.; Shariati, M.A.; Chung, I.M.; Thiruvengadam, M. Potentials of polysaccharides, lipids and proteins in biodegradable food packaging applications. Int. J. Biol. Macromol. 2021, 183, 2184–2198. [Google Scholar] [CrossRef] [PubMed]
- Briassoulis, D.; Tserotas, P.; Athanasoulia, I.-G. Alternative optimization routes for improving the performance of poly(3-hydroxybutyrate) (PHB) based plastics. J. Clean. Prod. 2021, 318, 128555. [Google Scholar] [CrossRef]
- Eslami, H.; Grady, M.; Mekonnen, T.H. Biobased and compostable trilayer thermoplastic films based on poly(3-hydroxybutyrate-co-3-hydroxyvalerate) (PHBV) and thermoplastic starch (TPS). Int. J. Biol. Macromol. 2022, 220, 385–394. [Google Scholar] [CrossRef] [PubMed]
- Vroman, I.; Tighzert, L. Biodegradable Polymers. Materials 2009, 2, 307–344. [Google Scholar] [CrossRef]
- Cao, Y.; Lai, S.; Wu, W.; Sang, L.; Lin, Y.; Liu, T.; Liang, C.; Liu, W.; Zhao, Y. Design and mechanical evaluation of additively-manufactured graded TPMS lattices with biodegradable polymer composites. J. Mater. Res. Technol. 2023, 23, 2868–2880. [Google Scholar] [CrossRef]
- Barletta, M.; Aversa, C.; Ayyoob, M.; Gisario, A.; Hamad, K.; Mehrpouya, M.; Vahabi, H. Poly(butylene succinate) (PBS): Materials, processing, and industrial applications. Prog. Polym. Sci. 2022, 132, 101579. [Google Scholar] [CrossRef]
- Xiao, X.; Chevali, V.S.; Song, P.; Yu, B.; Yang, Y.; Wang, H. Enhanced toughness of PLLA/PCL blends using poly(d-lactide)-poly(ε-caprolactone)-poly(d-lactide) as compatibilizer. Compos. Commun. 2020, 21, 100385. [Google Scholar] [CrossRef]
- Aversa, C.; Barletta, M.; Cappiello, G.; Gisario, A. Compatibilization strategies and analysis of morphological features of poly(butylene adipate-co-terephthalate) (PBAT)/poly(lactic acid) PLA blends: A state-of-art review. Eur. Polym. J. 2022, 173, 111304. [Google Scholar] [CrossRef]
- Khan, I.; Kumar, N.; Yadav, J.S.; Choudhary, M.; Chauhan, A.; Singh, T. Utilization of waste slate powder in poly(lactic acid) based composite for 3D printer filament. J. Mater. Res. Technol. 2023, 24, 703–714. [Google Scholar] [CrossRef]
- Tábi, T.; Ageyeva, T.; Kovács, J.G. Improving the ductility and heat deflection temperature of injection molded Poly(lactic acid) products: A comprehensive review. Polym. Test. 2021, 101, 107282. [Google Scholar] [CrossRef]
- Arastouei, M.; Khodaei, M.; Atyabi, S.M.; Nodoushan, M.J. Poly lactic acid-akermanite composite scaffolds prepared by fused filament fabrication for bone tissue engineering. J. Mater. Res. Technol. 2020, 9, 14540–14548. [Google Scholar] [CrossRef]
- De Oliveira, P.Z.; Vandenberghe, L.P.d.S.; de Mello, A.F.M.; Soccol, C.R. A concise update on major poly-lactic acid bioprocessing barriers. Bioresour. Technol. Rep. 2022, 18, 101094. [Google Scholar] [CrossRef]
- Tábi, T.; Ageyeva, T.; Kovács, J.G. The influence of nucleating agents, plasticizers, and molding conditions on the properties of injection molded PLA products. Mater. Today Commun. 2022, 32, 103936. [Google Scholar] [CrossRef]
- Zhao, X.; Hu, H.; Wang, X.; Yu, X.; Zhou, W.; Peng, S. Super tough poly(lactic acid) blends: A comprehensive review. RSC Adv. 2020, 10, 13316–13368. [Google Scholar] [CrossRef]
- Bernardes, G.P.; da Rosa Luiz, N.; Santana, R.M.C.; de Camargo Forte, M.M. Rheological behavior and morphological and interfacial properties of PLA/TPE blends. J. Appl. Polym. Sci. 2019, 136, 47962. [Google Scholar] [CrossRef]
- Mazidi, M.M.; Sharifi, H.; Aghjeh, M.K.R.; Zare, L.; Khonakdar, H.A.; Reuter, U. Super-Tough PLA-Based Blends with Excellent Stiffness and Greatly Improved Thermal Resistance via Interphase Engineering. ACS Appl. Mater. Interfaces 2023, 15, 22445–22470. [Google Scholar] [CrossRef]
- Abu Aldam, S.; Dey, M.; Javaid, S.; Ji, Y.; Gupta, S. On the Synthesis and Characterization of Polylactic Acid, Polyhydroxyalkanoate, Cellulose Acetate, and Their Engineered Blends by Solvent Casting. J. Mater. Eng. Perform. 2020, 29, 5542–5556. [Google Scholar] [CrossRef]
- Yong, W.F.; Zhang, H. Recent advances in polymer blend membranes for gas separation and pervaporation. Prog. Mater. Sci. 2021, 116, 100713. [Google Scholar] [CrossRef]
- Moradi, S.; Yeganeh, J.K. Highly toughened poly(lactic acid) (PLA) prepared through melt blending with ethylene-co-vinyl acetate (EVA) copolymer and simultaneous addition of hydrophilic silica nanoparticles and block copolymer compatibilizer. Polym. Test. 2020, 91, 106735. [Google Scholar] [CrossRef]
- Shin, H.; Thanakkasaranee, S.; Sadeghi, K.; Seo, J. Preparation and characterization of ductile PLA/PEG blend films for eco-friendly flexible packaging application. Food Packag. Shelf Life 2022, 34, 100966. [Google Scholar] [CrossRef]
- Aliotta, L.; Gigante, V.; Geerinck, R.; Coltelli, M.-B.; Lazzeri, A. Micromechanical analysis and fracture mechanics of Poly(lactic acid) (PLA)/Polycaprolactone (PCL) binary blends. Polym. Test. 2023, 121, 107984. [Google Scholar] [CrossRef]
- Qi, X.-D.; Yang, J.-H.; Zhang, N.; Huang, T.; Zhou, Z.-W.; Kühnert, I.; Pötschke, P.; Wang, Y. Selective localization of carbon nanotubes and its effect on the structure and properties of polymer blends. Prog. Polym. Sci. 2021, 123, 101471. [Google Scholar] [CrossRef]
- Yang, X.; Wei, F.; Wang, Z.; Li, G.; Yang, S.; Feng, J. High-reactive silica nanosheets as compatibilizers for immiscible PLLA/PBAT polymer blends. Compos. Sci. Technol. 2023, 236, 109979. [Google Scholar] [CrossRef]
- Gaylord, N.G. Compatibilizing Agents: Structure and Function in Polyblends. J. Macromol. Sci. Part A Chem. 1989, 26, 1211–1229. [Google Scholar] [CrossRef]
- Muthuraj, R.; Mekonnen, T. Recent progress in carbon dioxide (CO2) as feedstock for sustainable materials development: Co-polymers and polymer blends. Polymer 2018, 145, 348–373. [Google Scholar] [CrossRef]
- Coltelli, M.-B.; Mallegni, N.; Rizzo, S.; Fiori, S.; Signori, F.; Lazzeri, A. Compatibilization of Poly(Lactic Acid) (PLA)/Plasticized Cellulose Acetate Extruded Blends through the Addition of Reactively Extruded Comb Copolymers. Molecules 2021, 26, 2006. [Google Scholar] [CrossRef]
- Ferri, J.M.; Garcia-Garcia, D.; Rayón, E.; Samper, M.D.; Balart, R. Compatibilization and Characterization of Polylactide and Biopolyethylene Binary Blends by Non-Reactive and Reactive Compatibilization Approaches. Polymers 2020, 12, 1344. [Google Scholar] [CrossRef] [PubMed]
- Lv, S.; Zhang, Y.; Tan, H. Thermal and thermo-oxidative degradation kinetics and characteristics of poly (lactic acid) and its composites. Waste Manag. 2019, 87, 335–344. [Google Scholar] [CrossRef]
- Alhulaybi, Z.; Dubdub, I.; Al-Yaari, M.; Almithn, A.; Al-Naim, A.F.; Aljanubi, H. Pyrolysis Kinetic Study of Polylactic Acid. Polymers 2023, 15, 12. [Google Scholar] [CrossRef] [PubMed]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Das, P.; Tiwari, P. Thermal degradation kinetics of plastics and model selection. Thermochim. Acta 2017, 654, 191–202. [Google Scholar] [CrossRef]
- Palmay, P.; Mora, M.; Barzallo, D.; Bruno, J.C. Determination of Thermodynamic Parameters of Polylactic Acid by Thermogravimetry under Pyrolysis Conditions. Appl. Sci. 2021, 11, 10192. [Google Scholar] [CrossRef]
- Carrasco, F.; Pérez, O.S.; Maspoch, M.L. Kinetics of the Thermal Degradation of Poly(lactic acid) and Polyamide Bioblends. Polymers 2021, 13, 3996. [Google Scholar] [CrossRef]
- Bernardes, G.P.; Luiz, N.d.R.; Santana, R.M.C.; Forte, M.M.d.C. Influence of the morphology and viscoelasticity on the thermomechanical properties of poly(lactic acid)/thermoplastic polyurethane blends compatibilized with ethylene-ester copolymer. J. Appl. Polym. Sci. 2020, 137, 48926. [Google Scholar] [CrossRef]
- Borkotoky, S.S.; Chakraborty, G.; Katiyar, V. Thermal degradation behaviour and crystallization kinetics of poly (lactic acid) and cellulose nanocrystals (CNC) based microcellular composite foams. Int. J. Biol. Macromol. 2018, 118, 1518–1531. [Google Scholar] [CrossRef]
- Mulchandani, N.; Katiyar, V. Generalized kinetics for thermal degradation and melt rheology for poly (lactic acid)/poly (butylene succinate)/functionalized chitosan based reactive nanobiocomposite. Int. J. Biol. Macromol. 2019, 141, 831–842. [Google Scholar] [CrossRef]
- Bernardes, G.P.; Andrade, M.d.P.; Poletto, M. Effect of alkaline treatment on the thermal stability, degradation kinetics, and thermodynamic parameters of pineapple crown fibres. J. Mater. Res. Technol. 2023, 23, 64–76. [Google Scholar] [CrossRef]
- Zeng, C.; Zhang, N.-W.; Feng, S.-Q.; Ren, J. Thermal stability of copolymer derived from l-lactic acid and poly(tetramethylene) glycol through direct polycondensation. J. Therm. Anal. Calorim. 2013, 111, 633–646. [Google Scholar] [CrossRef]
- Manafi, P.; Ghasemi, I.; Karrabi, M.; Azizi, H.; Manafi, M.R.; Ehsaninamin, P. Thermal stability and thermal degradation kinetics (model-free kinetics) of nanocomposites based on poly (lactic acid)/graphene: The influence of functionalization. Polym. Bull. 2015, 72, 1095–1112. [Google Scholar] [CrossRef]
- Teixeira, S.; Eblagon, K.M.; Miranda, F.; Pereira, M.F.R.; Figueiredo, J.L. Towards Controlled Degradation of Poly(lactic) Acid in Technical Applications. C 2021, 7, 42. [Google Scholar] [CrossRef]
- Ruz-Cruz, M.A.; Herrera-Franco, P.J.; Flores-Johnson, E.A.; Moreno-Chulim, M.V.; Galera-Manzano, L.M.; Valadez-González, A. Thermal and mechanical properties of PLA-based multiscale cellulosic biocomposites. J. Mater. Res. Technol. 2022, 18, 485–495. [Google Scholar] [CrossRef]
- Karimpour-Motlagh, N.; Khonakdar, H.A.; Jafari, S.M.A.; Mahjub, A.; Panahi-Sarmad, M.; Kasbi, S.F.; Shojaei, S.; Goodarzi, V.; Arjmand, M. Influence of polypropylene and nanoclay on thermal and thermo-oxidative degradation of poly(lactide acid): TG-FTIR, TG-DSC studies and kinetic analysis. Thermochim. Acta 2020, 691, 178709. [Google Scholar] [CrossRef]
- Hayoune, F.; Chelouche, S.; Trache, D.; Zitouni, S.; Grohens, Y. Thermal decomposition kinetics and lifetime prediction of a PP/PLA blend supplemented with iron stearate during artificial aging. Thermochim. Acta 2020, 690, 178700. [Google Scholar] [CrossRef]
- Abu Hassan, N.A.; Ahmad, S.; Chen, R.S.; Shahdan, D.; Kassim, M.H.M. Tailoring lightweight, mechanical and thermal performance of PLA/recycled HDPE biocomposite foams reinforced with kenaf fibre. Ind. Crop. Prod. 2023, 197, 116632. [Google Scholar] [CrossRef]
- Roy, A.; Panda, S.; Gupta, J.; Singh, R.P.; Kour, P.; Sharma, M.P.; Yadav, K. Effects of interfacial interactions on structural, optical, thermal degradation properties and photocatalytic activity of low-density polyethylene/BaTiO3 nanocomposite. Polymer 2023, 276, 125932. [Google Scholar] [CrossRef]
- Patwary, F.; Mittal, V. Degradable polyethylene nanocomposites with silica, silicate and thermally reduced graphene using oxo-degradable pro-oxidant. Heliyon 2015, 1, e00050. [Google Scholar] [CrossRef]
- Koffi, A.; Mijiyawa, F.; Koffi, D.; Erchiqui, F.; Toubal, L. Mechanical Properties, Wettability and Thermal Degradation of HDPE/Birch Fiber Composite. Polymers 2021, 13, 1459. [Google Scholar] [CrossRef]
- Kaci, M.; Cimmino, S.; Silvestre, C.; Duraccio, D.; Benhamida, A.; Zaidi, L. Ethylene Butyl Acrylate Glycidyl Methacrylate Terpolymer as an Interfacial Agent for Isotactic Poly(propylene)/Wood Flour Composites. Macromol. Mater. Eng. 2006, 291, 869–876. [Google Scholar] [CrossRef]
- Gere, D.; Czigany, T. Future trends of plastic bottle recycling: Compatibilization of PET and PLA. Polym. Test. 2020, 81, 106160. [Google Scholar] [CrossRef]
- Siddiqui, M.N.; Redhwi, H.H.; Achilias, D.S. Simulation of the thermal degradation kinetics of biobased/biodegradable and non-biodegradable polymers using the random chain-scission model. Capabilities and limitations. J. Anal. Appl. Pyrolysis 2022, 168, 105767. [Google Scholar] [CrossRef]
- Hoff, A.; Jacobsson, S.; Pfäffli, P.; Zitting, A.; Frostling, H. Degradation products of the plastics: Polyethylene and styrenecontaining thermoplastics—Analytical, occupational and toxicologic aspects. Scand. J. Work. Environ. Health 1982, 8 (Suppl. S2), 55–58. [Google Scholar]
- Özlem, S.; Hacaloglu, J. Thermal degradation of poly(n-butyl methacrylate), poly(n-butyl acrylate) and poly(t-butyl acrylate). J. Anal. Appl. Pyrolysis 2013, 104, 161–169. [Google Scholar] [CrossRef]
- Hu, Y.-H.; Chen, C.-Y.; Wang, C.-C. Thermal degradation kinetics of poly(n-butyl acrylate) initiated by lactams and thiols. Polym. Degrad. Stab. 2004, 84, 505–514. [Google Scholar] [CrossRef]
- Huang, J.-W.; Kang, C.-C. Unusual Thermal Degradation Behavior of PEGMA in Air at Different Heating Rates. Polym. J. 2004, 36, 574–576. [Google Scholar] [CrossRef][Green Version]
- Lee, S.H.; Jeon, H.-B.; Hwang, G.-H.; Kwon, Y.S.; Lee, J.-S.; Park, G.-T.; Kim, S.-Y.; Kang, H.-E.; Choi, E.-J.; Jang, S.-H.; et al. Effects of Poly(ethylene-co-glycidyl methacrylate) on the Microstructure, Thermal, Rheological, and Mechanical Properties of Thermotropic Liquid Crystalline Polyester Blends. Polymers 2020, 12, 2124. [Google Scholar] [CrossRef]
- Lu, X.; Tang, L.; Wang, L.; Zhao, J.; Li, D.; Wu, Z.; Xiao, P. Morphology and properties of bio-based poly(lactic acid)/high-density polyethylene blends and their glass fiber reinforced composites. Polym. Test. 2016, 54, 90–97. [Google Scholar] [CrossRef]
- Carrasco, F.; Pérez-Maqueda, L.A.; Sánchez-Jiménez, P.E.; Perejón, A.; Santana, O.O.; Maspoch, M.L.L. Enhanced general analytical equation for the kinetics of the thermal degradation of poly(lactic acid) driven by random scission. Polym. Test. 2013, 32, 937–945. [Google Scholar] [CrossRef]
- Sinfrônio, F.S.M.; Santos, J.C.O.; Pereira, L.G.; Souza, A.G.; Conceiçăo, M.M.; Fernandes, V.J., Jr.; Fonseca, V.M. Kinetic of thermal degradation of low-density and high-density polyethylene by non-isothermal thermogravimetry. J. Therm. Anal. Calorim. 2005, 79, 393–399. [Google Scholar] [CrossRef]
- Iyer, K.S.; Balsora, H.K.; Dixit, S.D.; Sharma, A.; Sonar, P.; Doherty, W.O.S.; Chakinala, A.G.; Joshi, J.B. Elucidation of Thermal Degradation Model for Low and High Density Polyethylene by Statistical Parameters. Chem. Sel. 2020, 5, 14153–14160. [Google Scholar] [CrossRef]
- Harris, M.; Potgieter, J.; Ray, S.; Archer, R.; Arif, K.M. Polylactic acid and high-density polyethylene blend: Characterization and application in additive manufacturing. J. Appl. Polym. Sci. 2020, 137, e49602. [Google Scholar] [CrossRef]
- Reddy, J.P.; Misra, M.; Mohanty, A. Injection Moulded Biocomposites from Oat Hull and Polypropylene/Polylactide Blend: Fabrication and Performance Evaluation. Adv. Mech. Eng. 2013, 5, 761840. [Google Scholar] [CrossRef]
- Sobek, S.; Werle, S. Kinetic modelling of waste wood devolatilization during pyrolysis based on thermogravimetric data and solar pyrolysis reactor performance. Fuel 2020, 261, 116459. [Google Scholar] [CrossRef]
- Sharma, A.; Mohanty, B. Thermal degradation of mango (Mangifera indica) wood sawdust in a nitrogen environment: Characterization, kinetics, reaction mechanism, and thermodynamic analysis. RSC Adv. 2021, 11, 13396–13408. [Google Scholar] [CrossRef]
- Shao, Z.; Kumagai, S.; Kameda, T.; Saito, Y.; Yoshioka, T. Effects of heating rate and temperature on product distribution of poly-lactic acid and poly-3-hydroxybutyrate-co-3-hydroxyhexanoate. J. Mater. Cycles Waste Manag. 2023, 25, 650–661. [Google Scholar] [CrossRef]
- Gharsallah, A.; Layachi, A.; Louaer, A.; Satha, H. Thermal degradation kinetics of Opuntia Ficus Indica flour and talc-filled poly (lactic acid) hybrid biocomposites by TGA analysis. J. Compos. Mater. 2021, 55, 3099–3118. [Google Scholar] [CrossRef]
- Aboulkas, A.; El Harfi, K.; El Bouadili, A. Thermal degradation behaviors of polyethylene and polypropylene. Part I: Pyrolysis kinetics and mechanisms. Energy Convers. Manag. 2010, 51, 1363–1369. [Google Scholar] [CrossRef]
- Choudhary, J.; Alawa, B.; Chakma, S. Insight into the kinetics and thermodynamic analyses of co-pyrolysis using advanced isoconversional method and thermogravimetric analysis: A multi-model study of optimization for enhanced fuel properties. Process. Saf. Environ. Prot. 2023, 173, 507–528. [Google Scholar] [CrossRef]
- Poletto, M.; Ornaghi, H.L., Jr.; Zattera, A.J. Thermal decomposition of natural fibers: Kinetics and degradation mechanisms. In Reactions and Mechanisms in Thermal Analysis of Advanced Materials; Tiwari, A., Raj, B., Eds.; Wiley: Hoboken, NJ, USA, 2015; pp. 515–545. [Google Scholar] [CrossRef]
- Vyazovkin, S. Determining preexponential factor in model-free kinetic methods: How and why? Molecules 2021, 26, 3077. [Google Scholar] [CrossRef]
- Kaur, R.; Gera, P.; Jha, M.K.; Bhaskar, T. Pyrolysis kinetics and thermodynamic parameters of castor (Ricinus communis) residue using thermogravimetric analysis. Bioresour. Technol. 2018, 250, 422–428. [Google Scholar] [CrossRef] [PubMed]
- Müsellim, E.; Tahir, M.H.; Ahmad, M.S.; Ceylan, S. Thermokinetic and TG/DSC-FTIR study of pea waste biomass pyrolysis. Appl. Therm. Eng. 2018, 137, 54–61. [Google Scholar] [CrossRef]
| Polymer | Density (g/cm3) | MFI (g/10 min) | Tg (°C) | Tm (°C) | Company |
|---|---|---|---|---|---|
| Poly (lactic acid) (PLA) | 1.24 | 35 a | 60 | 170 | NatureWorks |
| Ethylene elastomer (EE) | 0.87 | 23 b | −45 | 43 | DuPont |
| Ethylene-butyl acrylate-glycidyl methacrylate (EBAGMA) | 0.94 | 12 a | −45 | 74 | DuPont |
| Sample | PLA/EE/EBAGMA (wt. %) |
|---|---|
| PLA | 100/0/0 |
| PLA30EE | 70/30/0 |
| PLA30EE-C | 65/30/5 |
| Model | Z(α) Type Function |
|---|---|
| Theoretical | Z(α) = f(α)g(α) |
| Experimental | Z(α) = (dα/dT)(Ea/R)(exp (Ea/RT))P(x) |
| Parameter | Equation |
|---|---|
| A | A = [β Ea exp (Ea/RTp)]/RTp2 |
| ΔH | ΔH = Ea − RTα |
| ΔG | ΔG = Ea + RTp ln [(kBTp)/(hA) |
| ΔS | ΔS = (ΔH − ΔG)/Tp |
| Sample | Heating Rate (β) (°C/min) | T5% (°C) | T10% (°C) | Tp (°C) |
|---|---|---|---|---|
| PLA | 5 | 312 | 324 | 358 |
| 10 | 335 | 347 | 380 | |
| 20 * | 334 * | 365 | 378 * | |
| EE | 5 | 298 | 322 | 364 |
| 10 | 317 | 337 | 375 | |
| 20 | 407 | 421 | 470 | |
| EBAGMA | 5 | 377 | 396 | 456 |
| 10 | 396 | 415 | 466 | |
| 20 | 405 | 422 | 470 |
| Sample | Heating Rate (β) (°C/min) | T5% (°C) | T10% (°C) | Tp,1 (°C) | Tp,2 (°C) |
|---|---|---|---|---|---|
| PLA | 5 | 312 | 324 | 358 | - |
| 10 | 335 | 347 | 380 | - | |
| 20 | 334 * | 365 | 378 * | - | |
| PLA30EE | 5 | 331 | 341 | 365 | 459 |
| 10 | 340 | 350 | 384 | 473 | |
| 20 | 341 * | 364 | 377 * | 474 * | |
| PLA30EE-C | 5 | 310 | 323 | 360 | 450 |
| 10 | 344 | 355 | 385 | 475 | |
| 20 | 342 * | 370 | 371 * | 466 * |
| Sample | Ea (kJ/mol) | |
|---|---|---|
| FWO Method | Vyazovkin Method | |
| PLA | 4.4 | 4.5 |
| EE | 20.4 | 23.0 |
| EBAGMA | 20.4 | 72.7 |
| PLA30EE | 7.7 | 6.8 |
| PLA30EE-C | 14.0 | 11.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernardes, G.P.; Andrade, M.P.; Poletto, M.; Luiz, N.R.; Santana, R.M.C.; Forte, M.M.d.C. Evaluation of Thermal Decomposition Kinetics of Poly (Lactic Acid)/Ethylene Elastomer (EE) Blends. Polymers 2023, 15, 4324. https://doi.org/10.3390/polym15214324
Bernardes GP, Andrade MP, Poletto M, Luiz NR, Santana RMC, Forte MMdC. Evaluation of Thermal Decomposition Kinetics of Poly (Lactic Acid)/Ethylene Elastomer (EE) Blends. Polymers. 2023; 15(21):4324. https://doi.org/10.3390/polym15214324
Chicago/Turabian StyleBernardes, Giordano P., Matheus P. Andrade, Matheus Poletto, Nathália R. Luiz, Ruth M. C. Santana, and Maria M. de C. Forte. 2023. "Evaluation of Thermal Decomposition Kinetics of Poly (Lactic Acid)/Ethylene Elastomer (EE) Blends" Polymers 15, no. 21: 4324. https://doi.org/10.3390/polym15214324
APA StyleBernardes, G. P., Andrade, M. P., Poletto, M., Luiz, N. R., Santana, R. M. C., & Forte, M. M. d. C. (2023). Evaluation of Thermal Decomposition Kinetics of Poly (Lactic Acid)/Ethylene Elastomer (EE) Blends. Polymers, 15(21), 4324. https://doi.org/10.3390/polym15214324






