Mechanical Performance and Failure Analysis of a 3D-Printed “Continuous Layer–Lattice Layer–Continuous Layer” Sandwich Structure
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material Selection
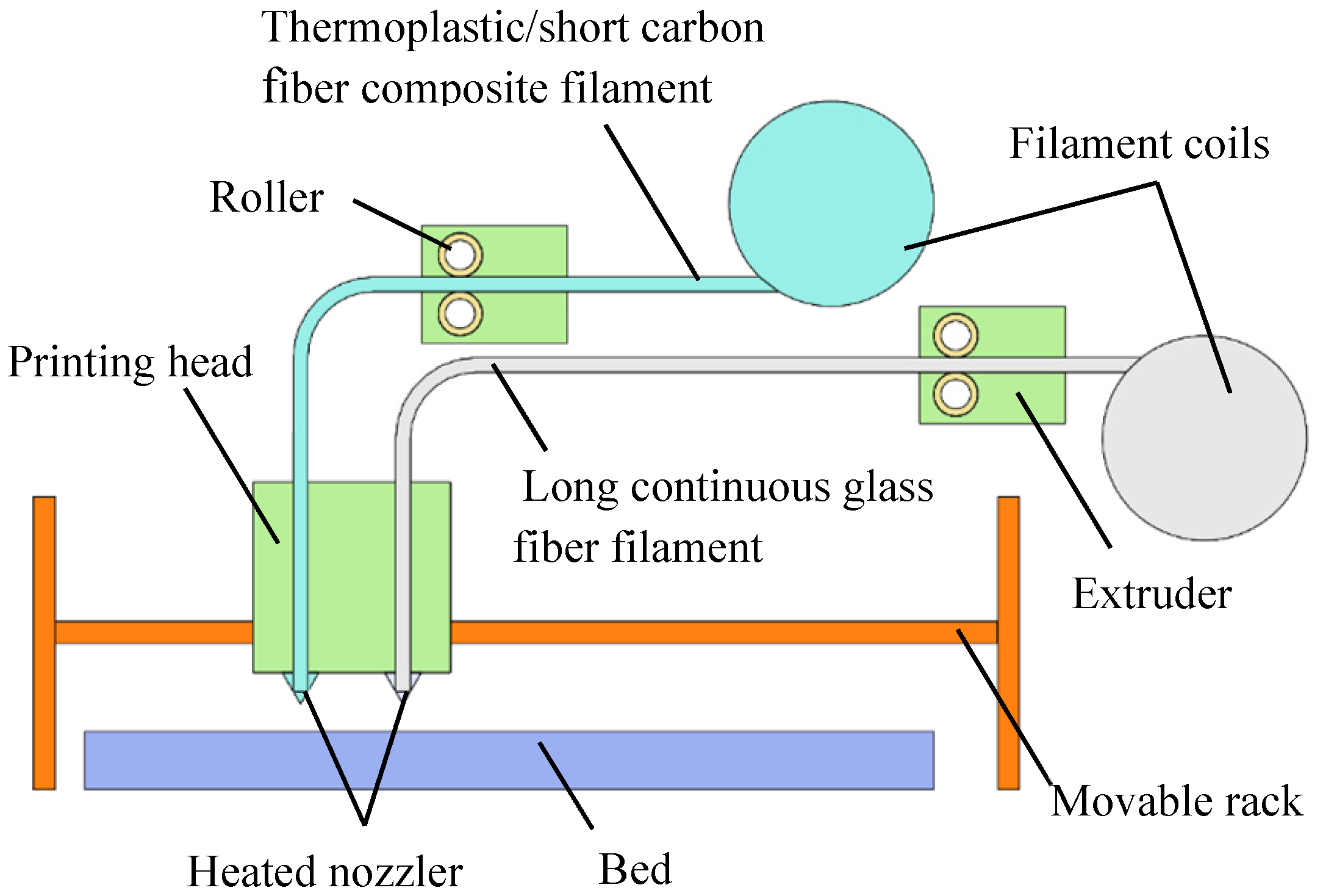
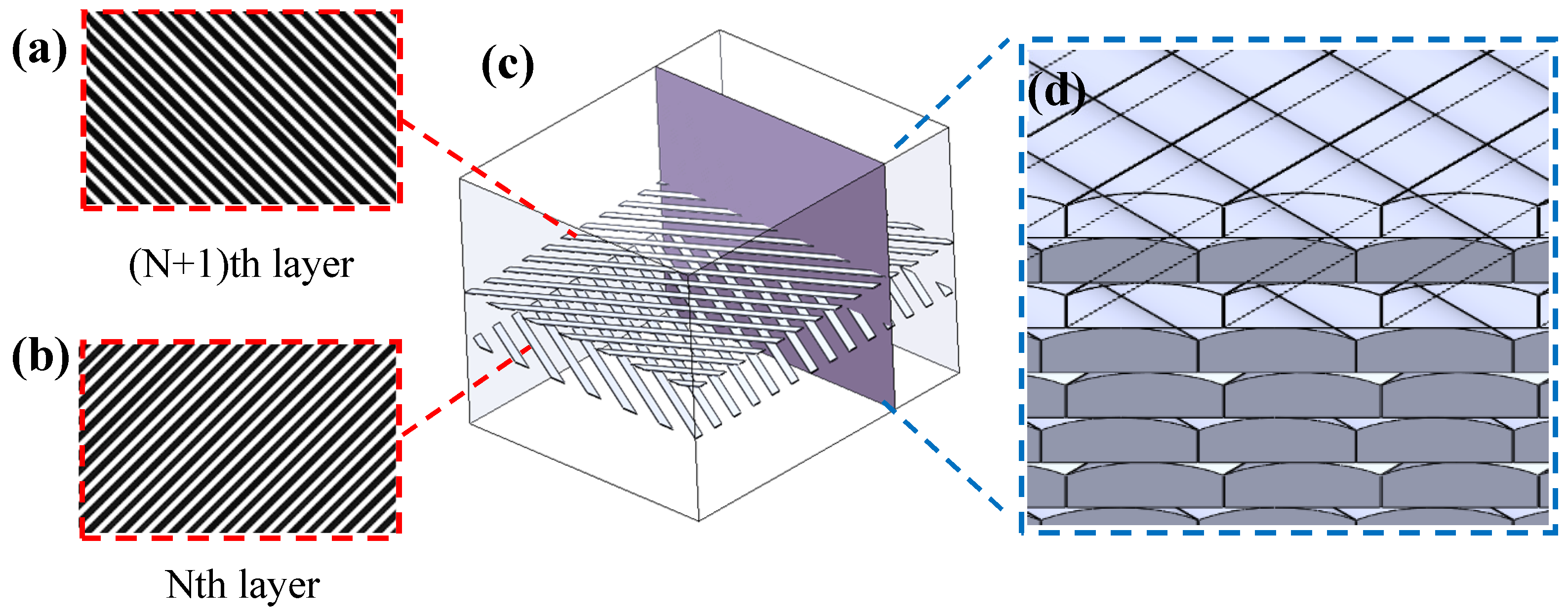
2.2. Sample Preparation
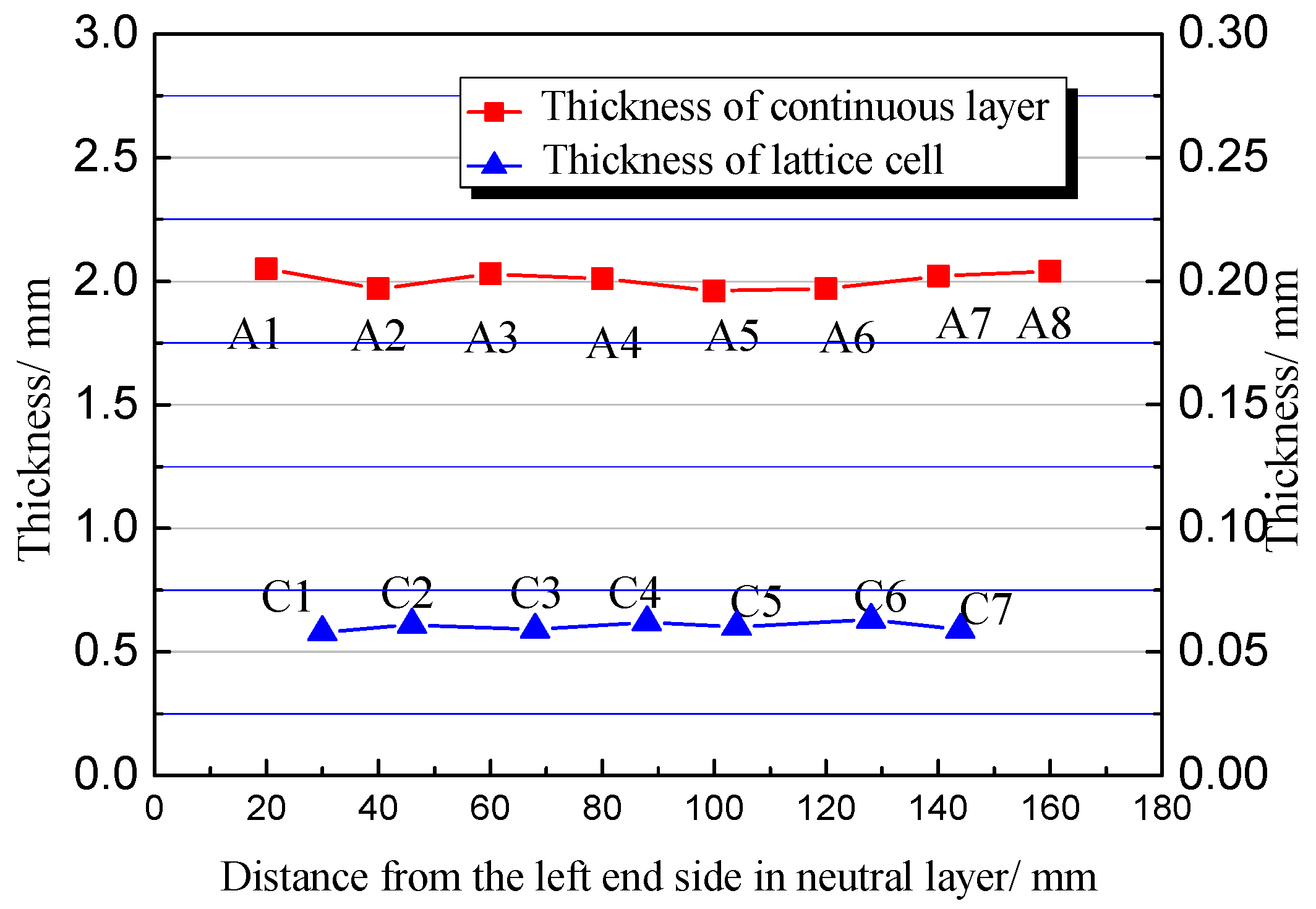
2.3. Accurancy Measurement of Samples
3. Experimental Results
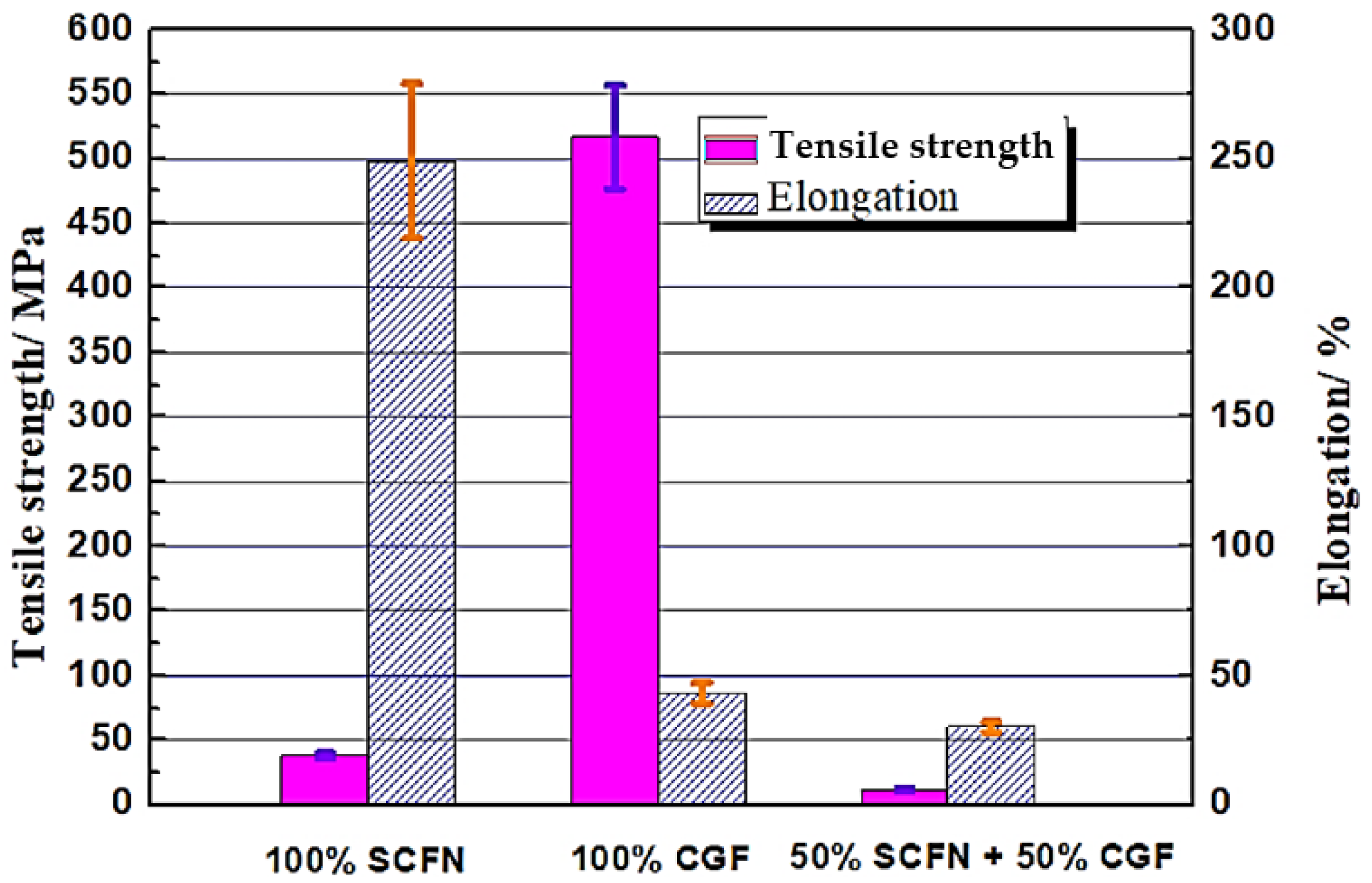
3.1. Analysis of Interface Strength
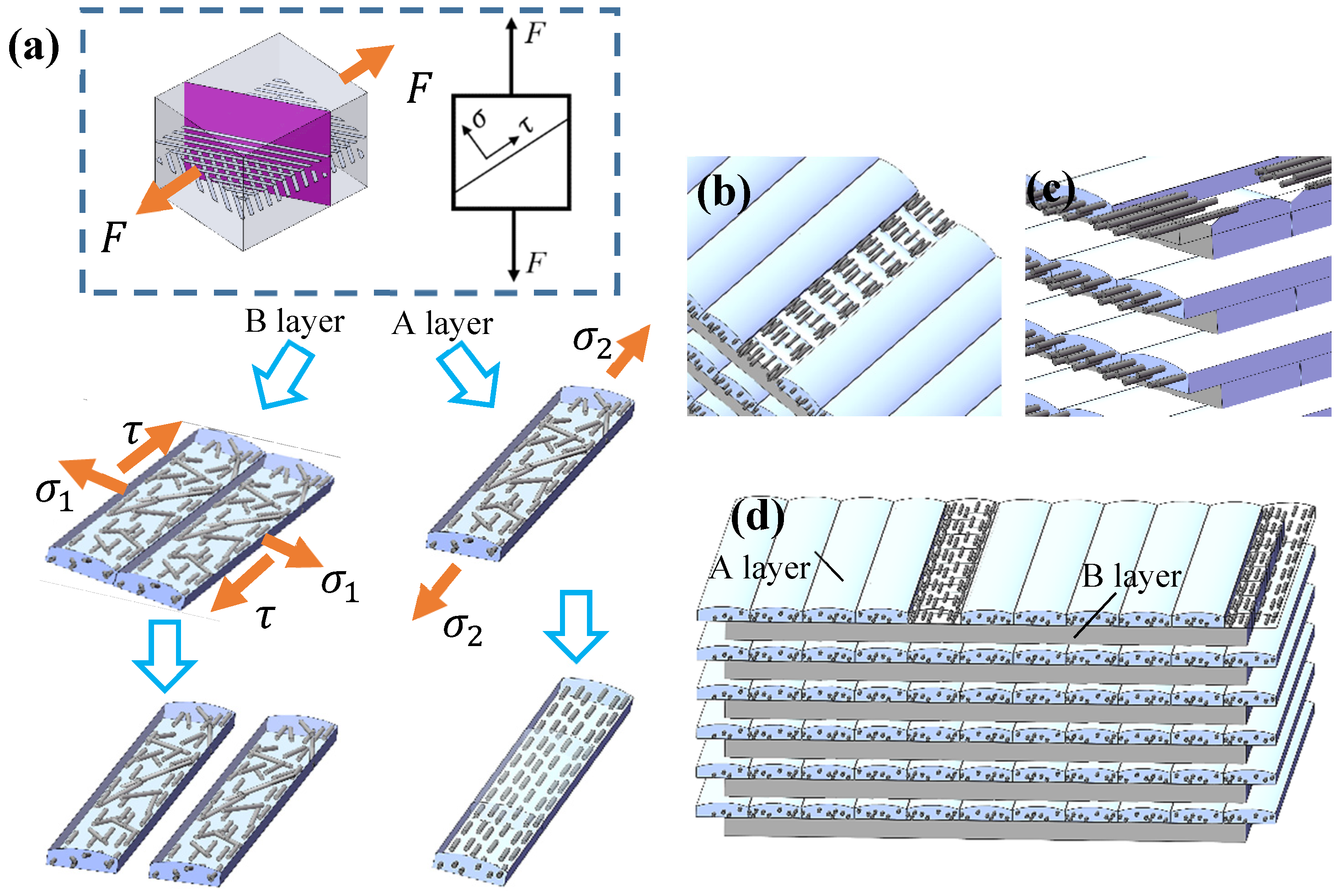
3.2. Failure Analysis of Samples
3.2.1. Failure Analysis of SCF/N Sample
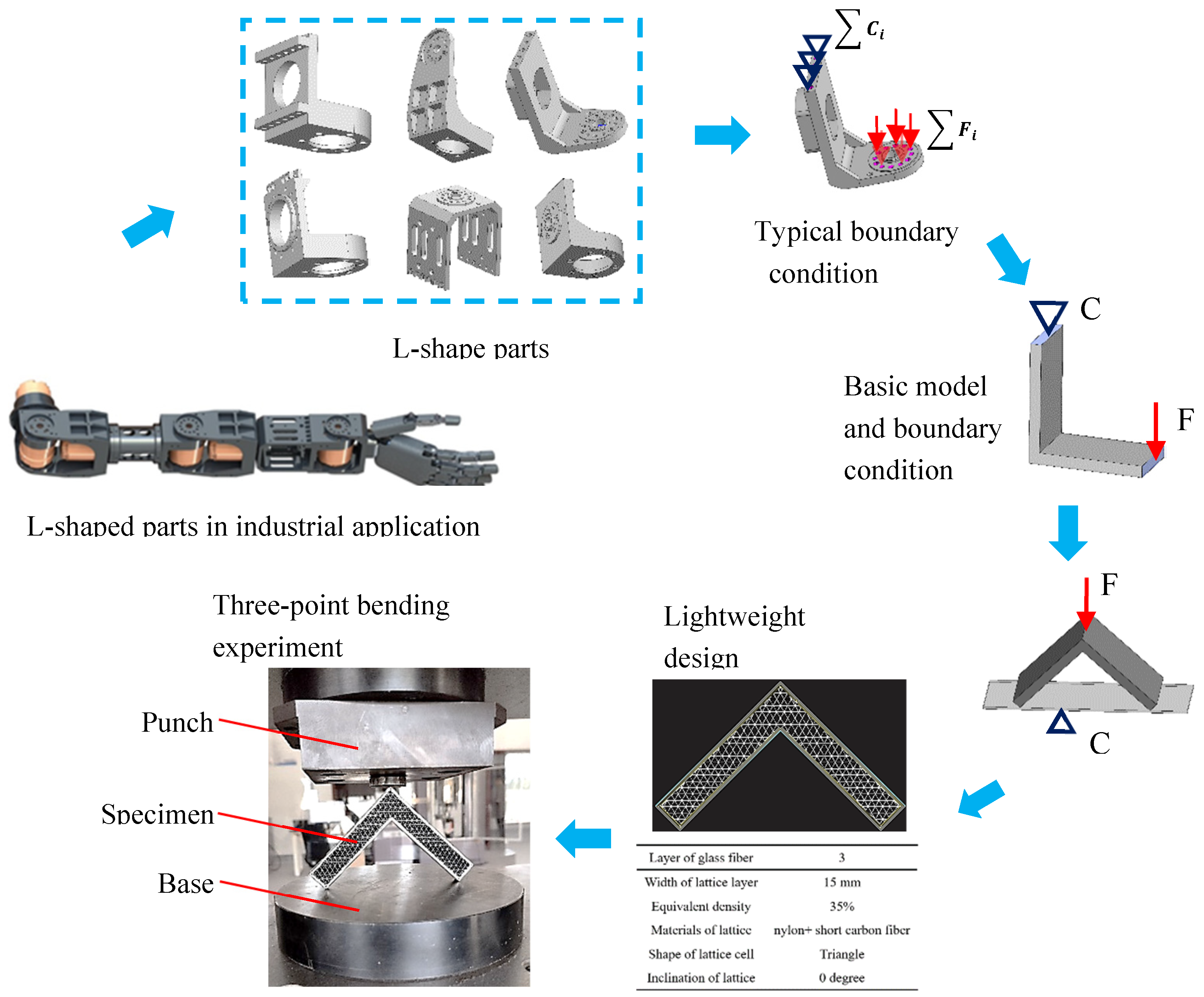
3.3. Performance of L-Shaped Sandwich Structure
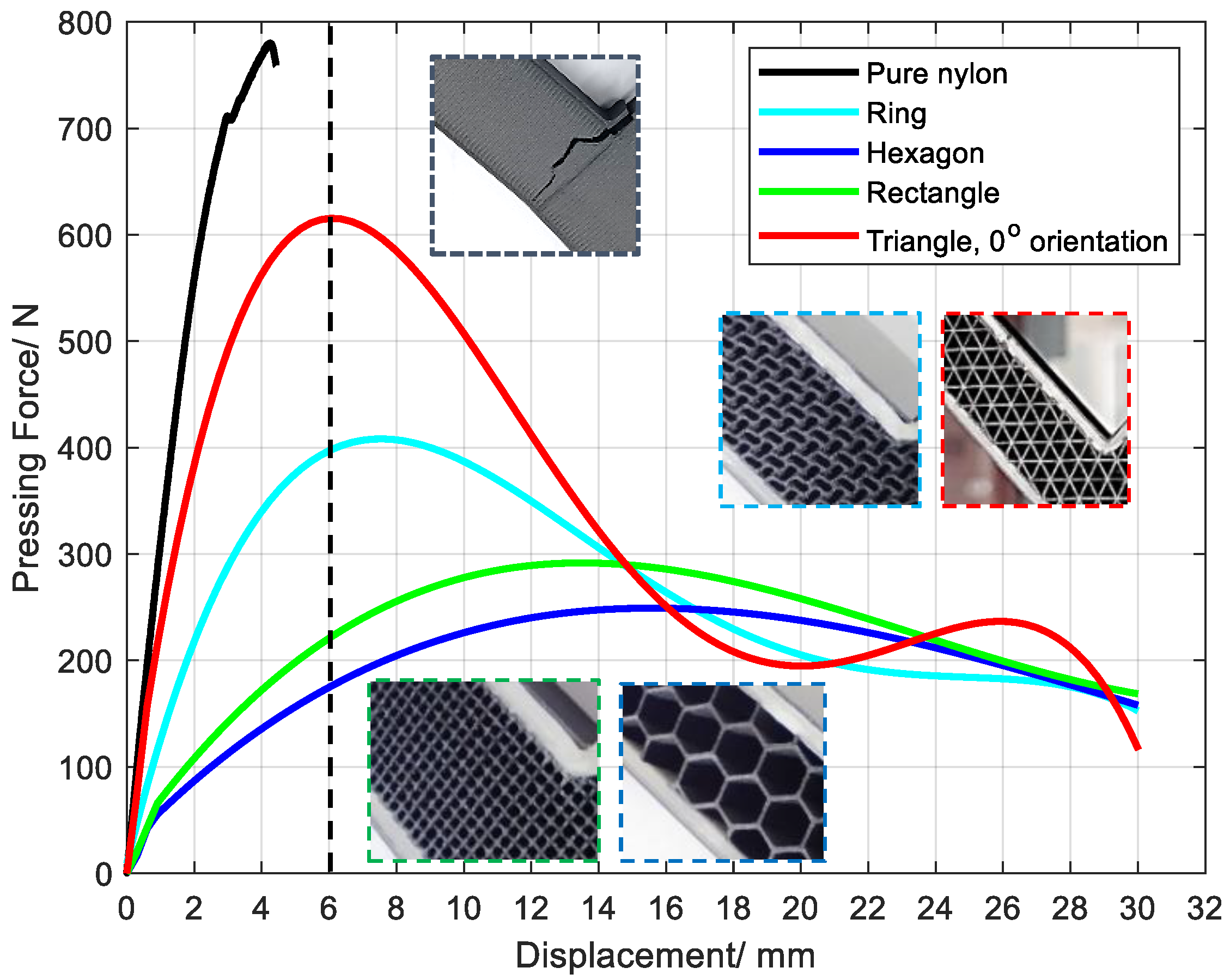
3.4. Effect of Cell Type on Structural Mechanical Properties
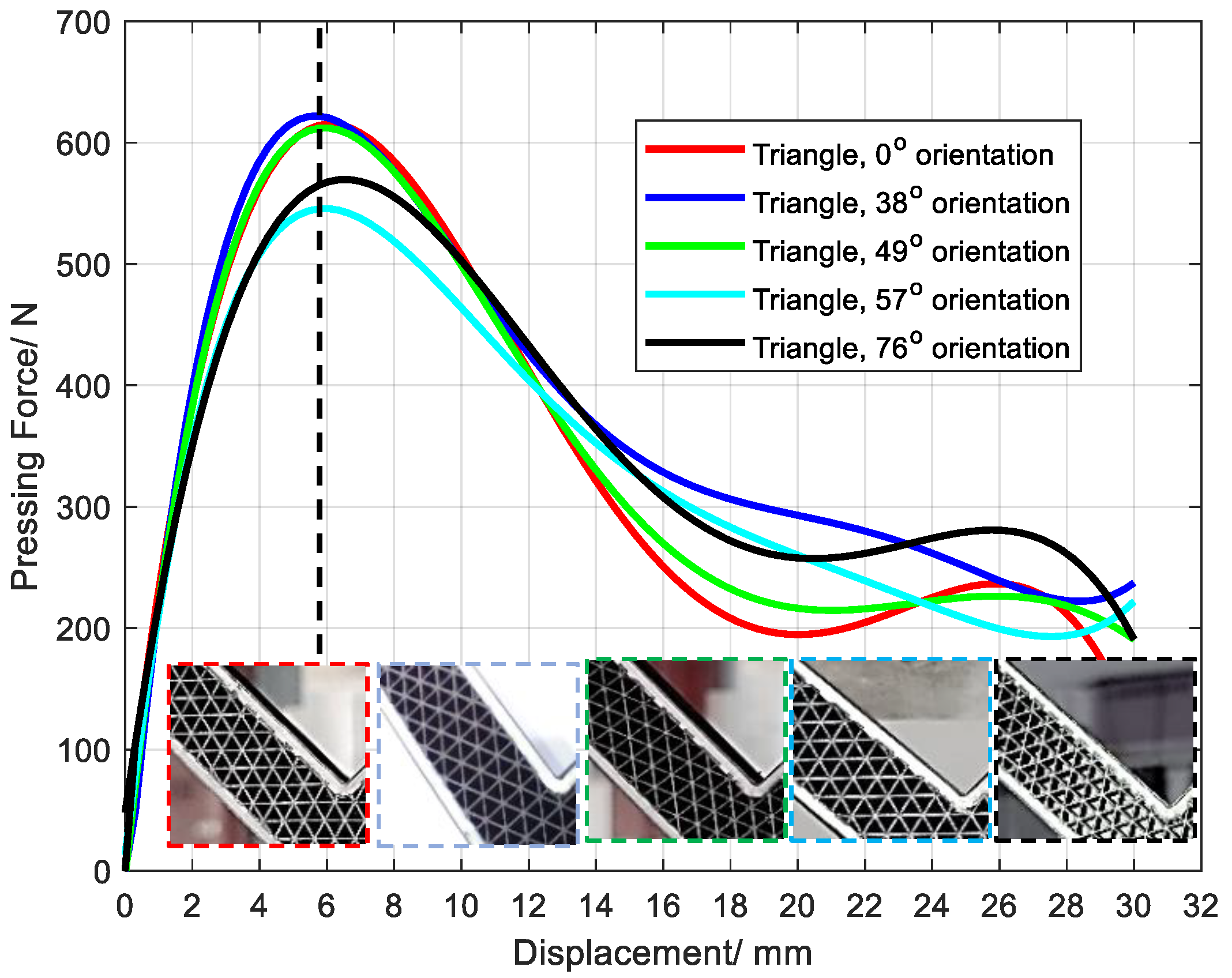
3.5. Effect of Lattice Orientation on Structural Mechanical Properties
4. Conclusions
- (1)
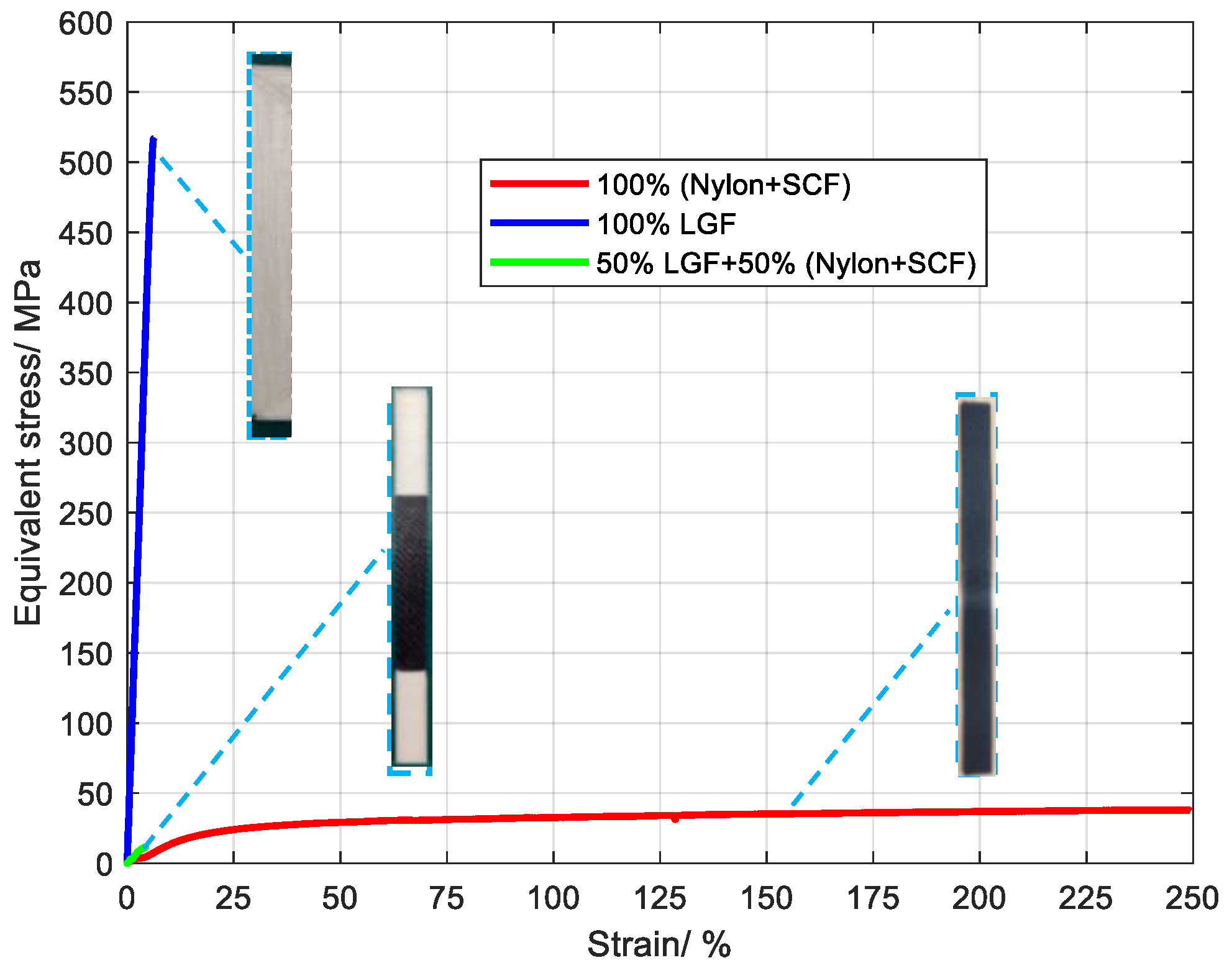
- The mechanical properties and failure modes of carbon fiber reinforced polyamide materials exhibit evident anisotropy in deformation by biaxial tension/compression. The cause is different scanning paths during 3D printing, and the differences cannot be eliminated through the fusion of polyamide, mainly due to temperature variation in processing and the surface tension of hot-melt polyamide.
- (2)
- Two kinds of fracture forms exist simultaneously in the 100% SCF/N under uniaxial tension. One is the shearing off, mainly by the action of shear force. The fracture section is flat and the layer thickness is nearly unchanged. The other is cracks that form under tensile force. The fiber orientation in the layer is approximately parallel to the tensile direction, and the layer thickness is significantly reduced. Parameter δ proposed in Section 3.2.1 could characterize the width shrinkage of this material before fracture.
- (3)
- Fractures along the direction of continuous filament are similar to the “cleavage fracture” in poly-crystal metal, which leads to two parallel disconnected surfaces. These fractures are mainly caused by colloid stripping on the surface of the filament, supplemented by inner tearing of the colloid, and accompanied by fiber shearing in about 10% of the area of the cross-sections.
- (4)
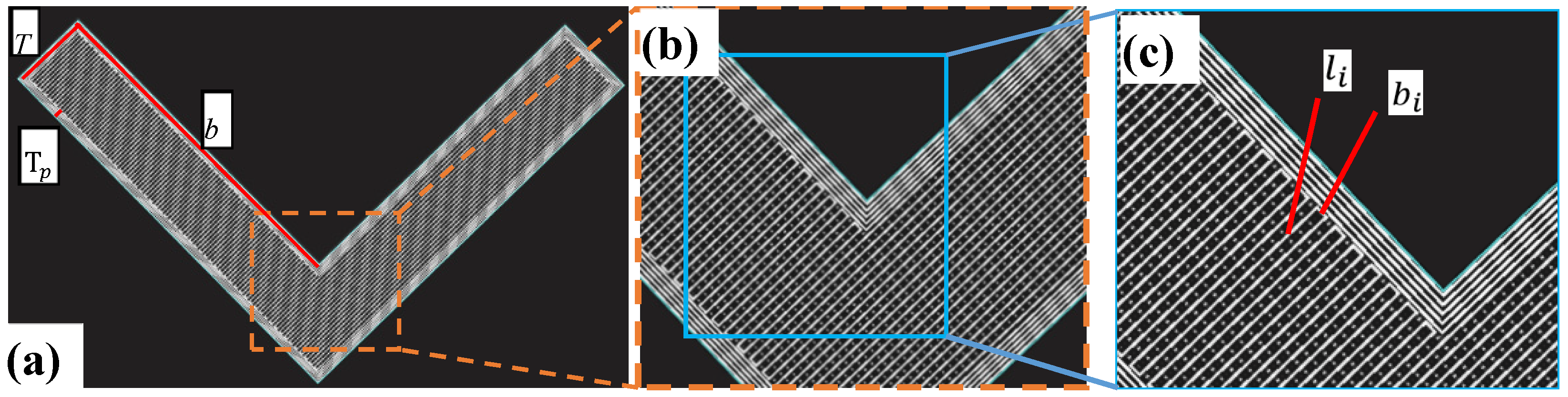
- The concept of shape factor is proposed to evaluate the three-point bending resistance by analyzing the failure characteristics and causes of the L-shaped specimens. The parameters of total lap area, the overlapping position of each lattice layer and the maximum included angle of the lattice cell are the crucial factors.
- (5)
- The bending resistance per unit weight of the L-shaped part was 54.3% larger than that of pure SCF/N, while the weight was decreased by 49%. The bending flexibility before fracture increased by 44%. This lightweight effect has obvious application value in some scenarios in which it is necessary to maintain the appearance, shape and a certain degree of stiffness of the workpiece, while also remaining sufficiently lightweight, such as in the upper arms of robots.
- (6)
- After formula derivation, the bending strength of the L-shaped specimens could not be directly calculated by the formulas. The relationship between compression force and displacement of L-shaped parts is a quartic polynomial. The force–stroke curves of L-shaped specimens with different orientations varies little, and the design of the sandwich structure can significantly reduce the effect of lattice anisotropy, which could provide a method to reduce the anisotropy of composite materials in use.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Du, Z.; Jiang, S.; Zhang, K.; Lu, Z.; Li, B.; Zhang, D. The structural design and superplastic forming/diffusion bonding of Ti2AlNb based alloy for four-layer structure. Mater. Des. 2016, 104, 242–250. [Google Scholar] [CrossRef]
- Farooq, U.; Gu, J.; Mohammed, E.; Muhammad, A.; Cantwell, W. Fuzzy Model Based Bilateral Control Design of Nonlinear Tele-Operation System Using Method of State Convergence. IEEE Access 2016, 4, 4119–4135. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Y.; Li, K.; Yuan, H.; Du, J.; Qin, Q. Dynamic response of sandwich plates with GLARE face-sheets and honeycomb core under metal foam projectile impact: Experimental and numerical investigations. Int. J. Impact Eng. 2022, 164, 104201. [Google Scholar] [CrossRef]
- Upadhyaya, S.; Korgal, A.; Sridhar, B.S.; Kumar, B.K.N. Synthesis and characterization of honeycomb sandwiched composite material for automobile applications. Mater. Today. Proc. 2022, 54, 502–506. [Google Scholar] [CrossRef]
- Liu, Y.; Wensing, P.M.; Orin, D.E.; Zheng, Y.F. Trajectory generation for dynamic walking in a humanoid over uneven terrain using a 3D-actuated Dual-SLIP model. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 374–380. [Google Scholar]
- Hou, Z.; Tian, X.; Zhang, J.; Li, D. 3D printed continuous fibre reinforced composite corrugated structure. Compos. Struct. 2018, 184, 1005–1010. [Google Scholar] [CrossRef]
- Liu, S.; Li, Y.; Li, N. A novel free-hanging 3D printing method for continuous carbon fiber reinforced thermoplastic lattice truss core structures. Mater. Des. 2018, 137, 235–244. [Google Scholar] [CrossRef]
- Luo, M.; Tian, X.; Shang, J.; Zhu, W.; Li, D.; Qin, Y. Impregnation and interlayer bonding behaviours of 3D-printed continuous carbon-fiber-reinforced poly-ether-ether-ketone composites. Compos. Part A 2019, 121, 130–138. [Google Scholar] [CrossRef]
- Shang, J.; Tian, X.; Luo, M.; Zhu, W.; Li, D.; Qin, Y.; Shan, Z. Controllable inter-line bonding performance and fracture patterns of continuous fiber reinforced composites by sinusoidal-path 3D printing. Compos. Sci. Technol. 2020, 192, 108096. [Google Scholar] [CrossRef]
- Kang, S.; Liu, W.; Wang, J.; Song, H.; Yuan, W.; Huang, C. Self-adaptive 3D lattice for curved sandwich structures. Addit. Manuf. 2022, 54, 102761. [Google Scholar] [CrossRef]
- Rajpal, R.; Lijesh, K.P.; Gangadharan, K.V. Parametric studies on bending stiffness and damping ratio of Sandwich structures. Addit. Manuf. 2018, 22, 583–591. [Google Scholar] [CrossRef]
- Pierre, J.; Iervolino, F.; Farahani, R.D.; Piccirelli, N.; Lévesque, M.; Therriault, D. Material extrusion additive manufacturing of multifunctional sandwich panels with load-bearing and acoustic capabilities for aerospace applications. Addit. Manuf. 2023, 61, 103344. [Google Scholar] [CrossRef]
- Serra, T.; Planell, J.A.; Navarro, M. High-resolution PLA-based composite scaffolds via 3-D printing technology. Acta Biomater. 2013, 9, 5521–5530. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Jiang, M.; Zhou, Z.; Gou, J.; Hui, D. 3D printing of polymer matrix composites: A review and prospective. Compos. Part B 2017, 110, 442–458. [Google Scholar] [CrossRef]
- Li, C.; Fei, J.; Zhang, T.; Zhao, S.; Qi, L. Relationship between surface characteristics and properties of fiber-reinforced resin-based composites. Compos. Part B 2023, 249, 110422. [Google Scholar] [CrossRef]
- Wang, Z.; Luan, C.; Liao, G.; Yao, X.; Fu, J. Mechanical and self-monitoring behaviors of 3D printing smart continuous carbon fiber-thermoplastic lattice truss sandwich structure. Compos. Part B 2019, 176, 107215. [Google Scholar] [CrossRef]
- Abdul, B.; Roberet, S.; Jason, G. Single Landmark Based Self-localization of Mobile Robots. In Proceedings of the 3rd Canadian Conference on Computer and Robot Vision, Quebec City, QC, Canada, 7–9 June 2006; pp. 67–74. [Google Scholar]
- Karaş, B.; Smith, P.J.; Fairclough, J.P.A.; Mumtaz, K. Additive manufacturing of high density carbon fibre reinforced polymer composites. Addit. Manuf. 2022, 58, 103044. [Google Scholar] [CrossRef]
- Papon, E.A.; Haque, A. Fracture toughness of additively manufactured carbon fiber reinforced composites. Addit. Manuf. 2019, 26, 41–52. [Google Scholar] [CrossRef]
- Wysmulski, P. Non-linear analysis of the postbuckling behaviour of eccentrically compressed composite channel-section columns. Compos. Struct. 2023, 305, 116446. [Google Scholar] [CrossRef]
- Rozylo, P. Comparison of Failure for Thin-Walled Composite Columns. Materials 2022, 15, 167. [Google Scholar] [CrossRef]
- Dickson, A.N.; Barry, J.N.; McDonnell, K.A.; Dowling, D.P. Fabrication of continuous carbon, glass and Kevlar fibre reinforced polymer composites using additive manufacturing. Addit. Manuf. 2017, 16, 146–152. [Google Scholar] [CrossRef]
- Maskery, I.; Ashcroft, I.A. The deformation and elastic anisotropy of a new gyroid-based honeycomb made by laser sintering. Addit. Manuf. 2020, 36, 101548. [Google Scholar] [CrossRef]
- Georges, H.; Großmann, A.; Mittelstedt, C.; Becker, W. Structural modeling of sandwich panels with additively manufactured strut-based lattice cores. Addit. Manuf. 2022, 55, 102788. [Google Scholar] [CrossRef]
- Moeini, M.; Begon, M.; Lévesque, M. Numerical homogenization of a linearly elastic honeycomb lattice structure and comparison with analytical and experimental results. Mech. Mater. 2022, 167, 104210. [Google Scholar] [CrossRef]
- Milleret, A.; Laitinen, V.; Ullakko, K.; Fenineche, N.; Attallah, M.M. Laser powder bed fusion of (14 M) Ni-Mn-Ga magnetic shape memory alloy lattices. Addit. Manuf. 2022, 60, 103231. [Google Scholar] [CrossRef]
- Zhang, P.; Sun, S.; Duan, J.; Fu, H.; Han, Z.; Geng, H.; Feng, Y. Line width prediction and mechanical properties of 3D printed continuous fiber reinforced polypropylene composites. Addit. Manuf. 2023, 61, 103372. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Frohn-Sörensen, P.; Reuter, J.; Engel, B.; Reinicke, T. Fracture studies of 3D-printed continuous glass fiber reinforced composites. Theor. Appl. Fract. Mech. 2022, 119, 103317. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, Y.; Dai, W.; Long, R. Mechanical properties of 304 austenite stainless steel manufactured by laser metal deposition. Mater. Sci. Eng. A 2019, 758, 60–70. [Google Scholar] [CrossRef]
- Zhang, Z.; Yavas, D.; Liu, Q.; Wu, D. Effect of build orientation and raster pattern on the fracture behavior of carbon fiber reinforced polymer composites fabricated by additive manufacturing. Addit. Manuf. 2021, 47, 102204. [Google Scholar] [CrossRef]
- Katalagarianakis, A.; Van de Voorde, B.; Pien, N.; Polyzos, E.; Duretek, I.; Holzer, C.; Cardon, L.; Bernaerts, K.V.; Van Hemelrijck, D.; Van Vlierberghe, S.; et al. The effect of carbon fiber content on physico-mechanical properties of recycled poly(ethylene terephthalate) composites additively manufactured with fused filament fabrication. Addit. Manuf. 2022, 60, 103246. [Google Scholar] [CrossRef]
- Iragi, M.; Pascual-González, C.; Esnaola, A.; Lopes, C.S.; Aretxabaleta, L. Ply and interlaminar behaviours of 3D printed continuous carbon fibre-reinforced thermoplastic laminates; effects of processing conditions and microstructure. Addit. Manuf. 2019, 30, 100884. [Google Scholar] [CrossRef]
- Nie, D.; Lu, Z.; Zhang, K. Hot V-bending behavior of pre-deformed pure titanium sheet assisted by electrical heating. Int. J. Adv. Manuf. Technol. 2018, 94, 163–174. [Google Scholar] [CrossRef]
- Sieberer, S.; Savandaiah, C.; Leßlhumer, J.; Schagerl, M. Shear property measurement of additively manufactured continuous fibre reinforced plastics by in-plane torsion testing. Addit. Manuf. 2022, 55, 102805. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, H.; Wu, J.; McCarthy, E.D. Fibre flow and void formation in 3D printing of short-fibre reinforced thermoplastic composites: An experimental benchmark exercise. Addit. Manuf. 2021, 37, 101686. [Google Scholar] [CrossRef]
- Lei, H.; Li, C.; Zhang, X.; Wang, P.; Zhou, H.; Zhao, Z.; Fang, D. Deformation behavior of heterogeneous multi-morphology lattice core hybrid structures. Addit. Manuf. 2021, 37, 101674. [Google Scholar] [CrossRef]
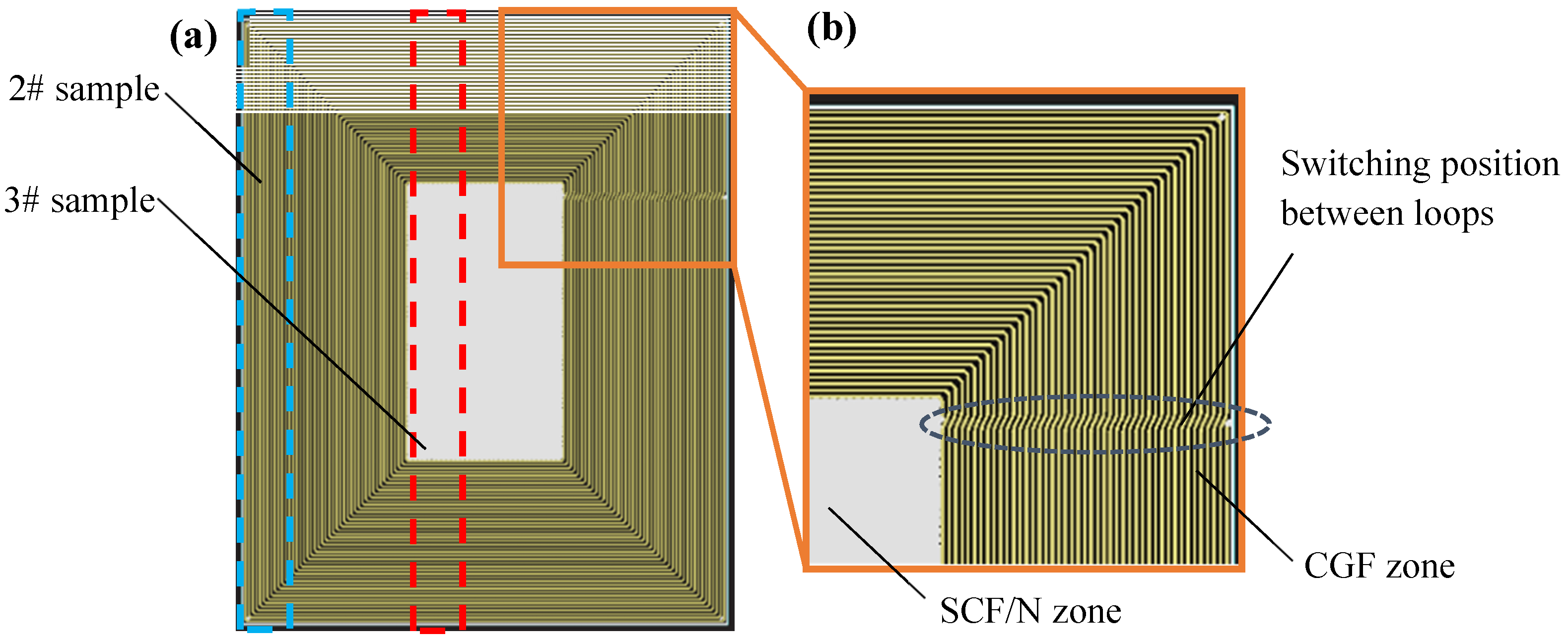







| Sequence Number | Composition of Materials | Layout Design |
|---|---|---|
| 1# | Short carbon fiber + Polyamide (SCF/N) | 45°/135°/45° from the length direction |
| 2# | Continuous glass fiber (CGF) | Parallel to the length direction |
| 3# | 50% CGF + 50% (SCF/N) | CGF on the two ends, SCF/N in the middle |
| Sequence Number | Proportion of Volume in Lattice Layer (%) | Cell Type | Orientation (Degree) | Contour Shape |
|---|---|---|---|---|
| 4# | 35 | Triangle | 0 | L shape |
| 5# | 35 | Rectangle | 0 | L shape |
| 6# | 35 | Hexagon | 0 | L shape |
| 7# | 35 | Gyroid | 0 | L shape |
| Sequence Number | Proportion of Volume in Lattice Layer (%) | Cell Type | Orientation (Degree) | Contour Shape |
|---|---|---|---|---|
| 4# | 35 | Triangle | 0 | L shape |
| 8# | 35 | Triangle | 19 | L shape |
| 9# | 35 | Triangle | 38 | L shape |
| 10# | 35 | Triangle | 57 | L shape |
| 11# | 35 | Triangle | 76 | L shape |
| Ring | Hexagon | Rectangle | 0° Oriented Triangle | 38° Oriented Triangle | 49° Oriented Triangle | 57° Oriented Triangle | 76° Oriented Triangle | |
|---|---|---|---|---|---|---|---|---|
| a | −0.0069 | −0.0004 | −0.0003 | −0.0186 | −0.0155 | −0.0166 | −0.0109 | −0.0144 |
| b | 0.527 | 0.0404 | 0.0529 | 1.2864 | 1.0856 | 1.1709 | 0.7962 | 1.0131 |
| c | −13.8 | −1.9572 | −2.815 | −29.626 | −25.439 | −27.478 | −19.552 | −23.87 |
| d | 129.95 | 36.985 | 49.506 | 235.16 | 209.44 | 222.59 | 168.29 | 198.44 |
| e | 9.1793 | 16.223 | 15.275 | 18.288 | 51.546 | 28.975 | 72.528 | 37.411 |
| 0.967 | 0.998 | 0.9985 | 0.997 | 0.9627 | 0.994 | 0.9734 | 0.9989 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, D.; Kong, L.; Zhang, Y.; Qiu, X.; Fu, Y.; Gu, J. Mechanical Performance and Failure Analysis of a 3D-Printed “Continuous Layer–Lattice Layer–Continuous Layer” Sandwich Structure. Polymers 2023, 15, 4283. https://doi.org/10.3390/polym15214283
Nie D, Kong L, Zhang Y, Qiu X, Fu Y, Gu J. Mechanical Performance and Failure Analysis of a 3D-Printed “Continuous Layer–Lattice Layer–Continuous Layer” Sandwich Structure. Polymers. 2023; 15(21):4283. https://doi.org/10.3390/polym15214283
Chicago/Turabian StyleNie, Daming, Lingyu Kong, Yu Zhang, Xingyu Qiu, Yili Fu, and Jason Gu. 2023. "Mechanical Performance and Failure Analysis of a 3D-Printed “Continuous Layer–Lattice Layer–Continuous Layer” Sandwich Structure" Polymers 15, no. 21: 4283. https://doi.org/10.3390/polym15214283
APA StyleNie, D., Kong, L., Zhang, Y., Qiu, X., Fu, Y., & Gu, J. (2023). Mechanical Performance and Failure Analysis of a 3D-Printed “Continuous Layer–Lattice Layer–Continuous Layer” Sandwich Structure. Polymers, 15(21), 4283. https://doi.org/10.3390/polym15214283





