A Visco-Hyperelastic Constitutive Model to Characterize the Stress-Softening Behavior of Ethylene Propylene Diene Monomer Rubber
Abstract
1. Introduction
2. Construction of Visco-Hyperelastic Constitutive Model
2.1. Hyper-Elastic Constitutive Model
2.1.1. The Yeoh Hyper-Elastic Constitutive Model
2.1.2. The Ogden Hyper-Elastic Constitutive Model
2.2. Pseudo-Elastic Model
Pseudo-Elastic Model for Uniaxial and Equal Biaxial Cases
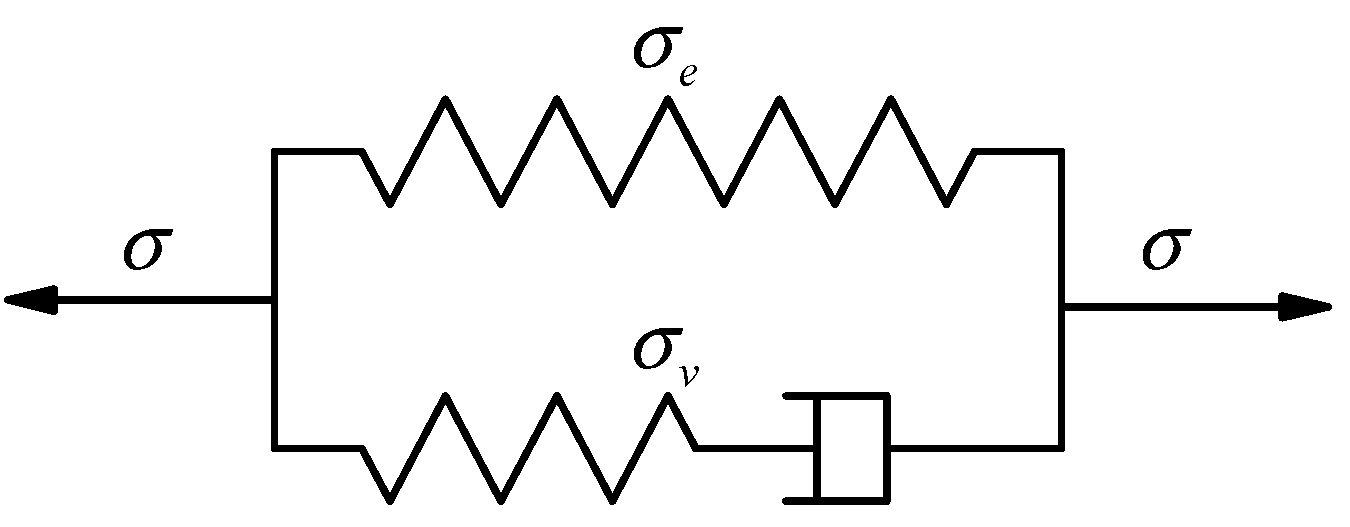
2.3. Constitutive Model of Viscoelastic Unit
2.4. Construction of the Visco-Hyperelastic Constitutive Model
2.4.1. The Visco-Hyperelastic Constitutive Model of Yeoh Type
2.4.2. The Visco-Hyperelastic Constitutive Model of Ogden Type
3. Experimental Procedure
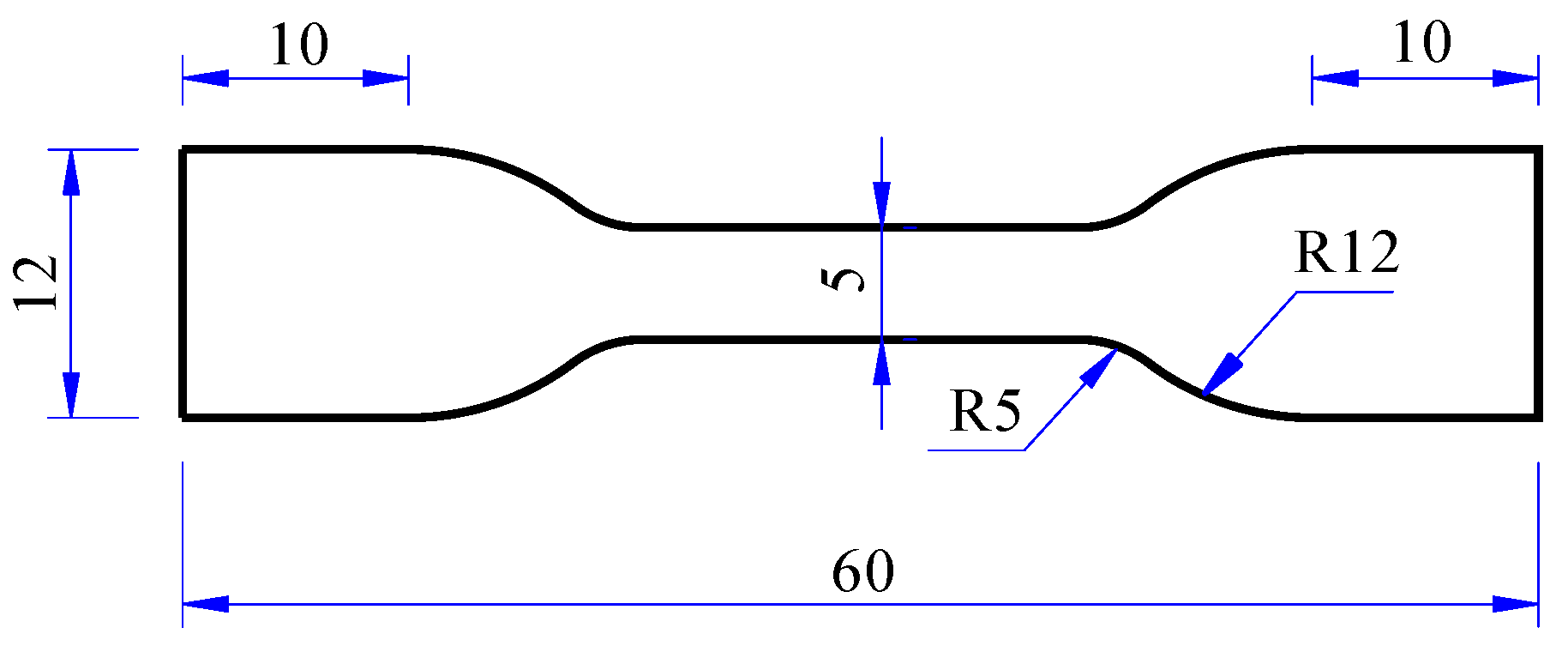
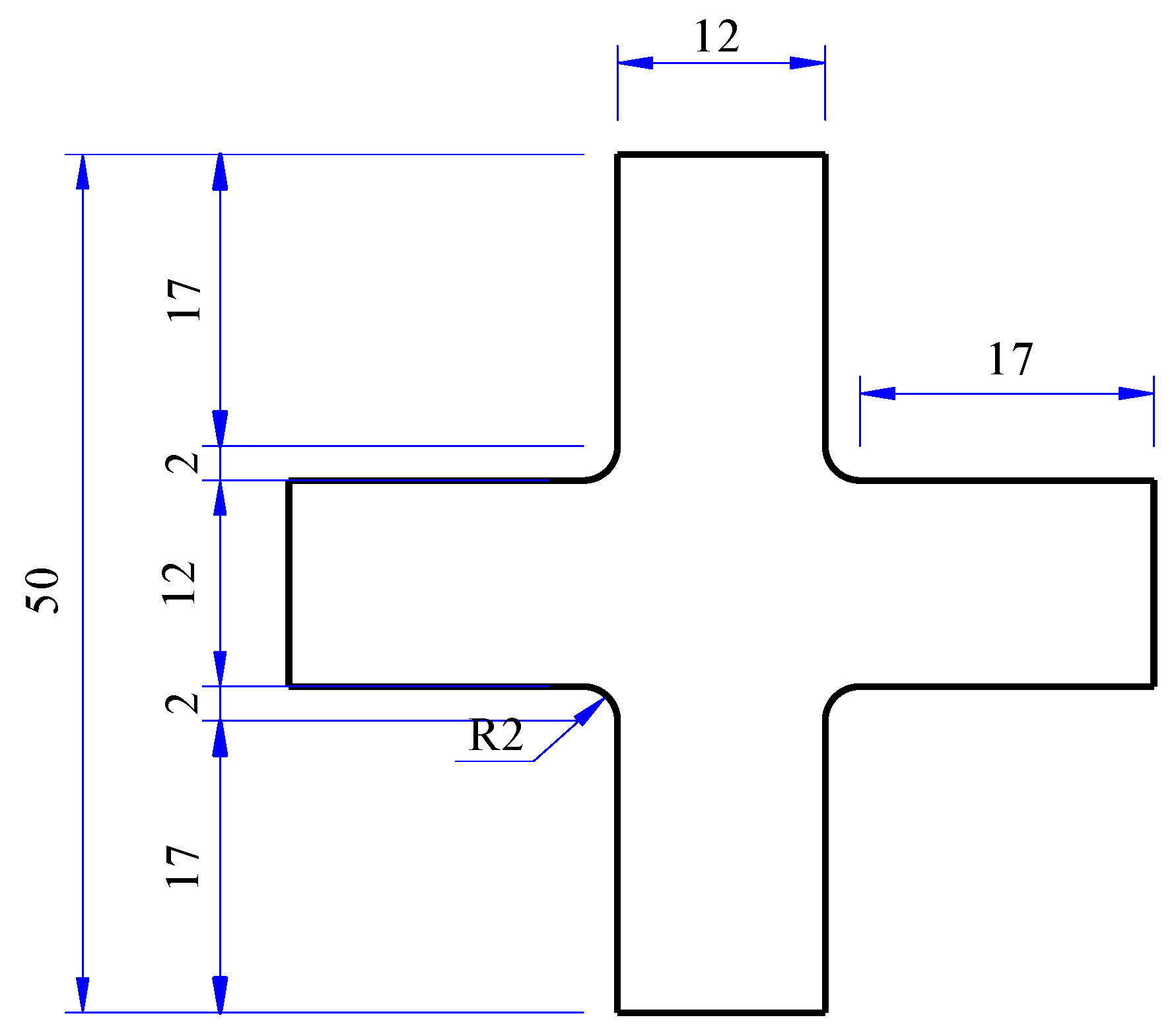
3.1. Test Material
3.2. Test Schemes
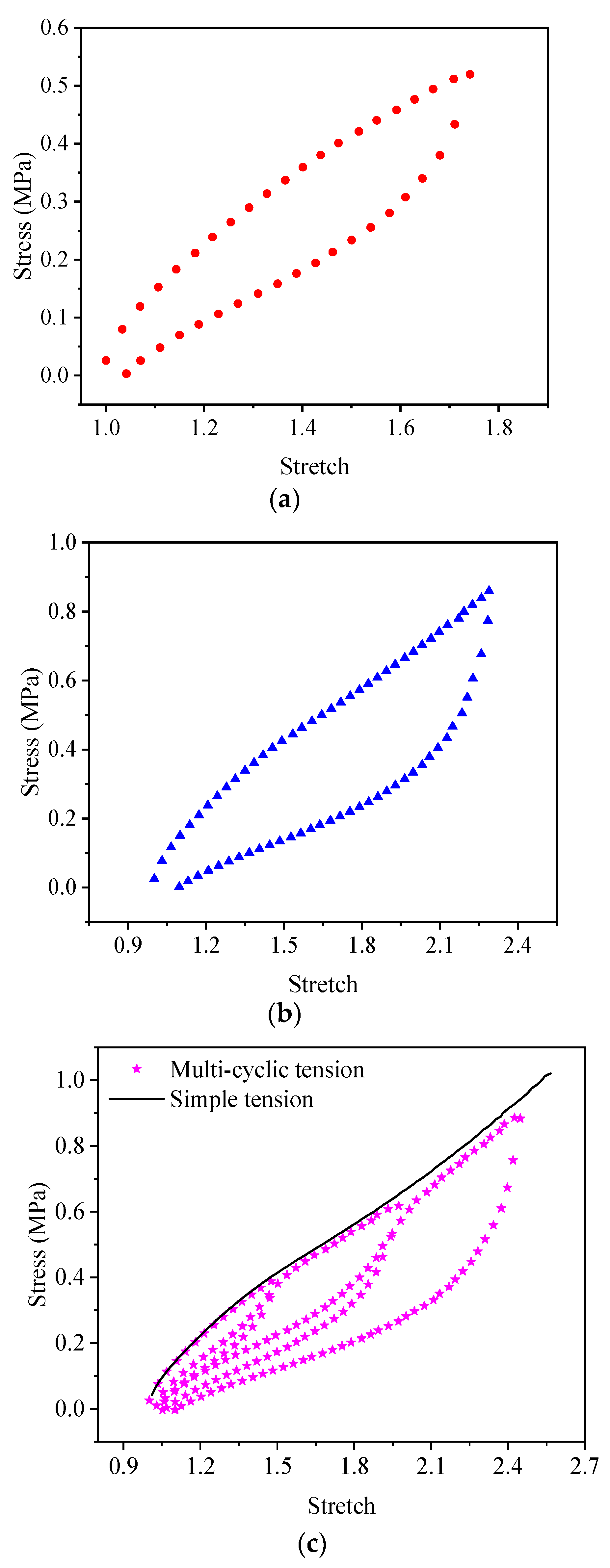
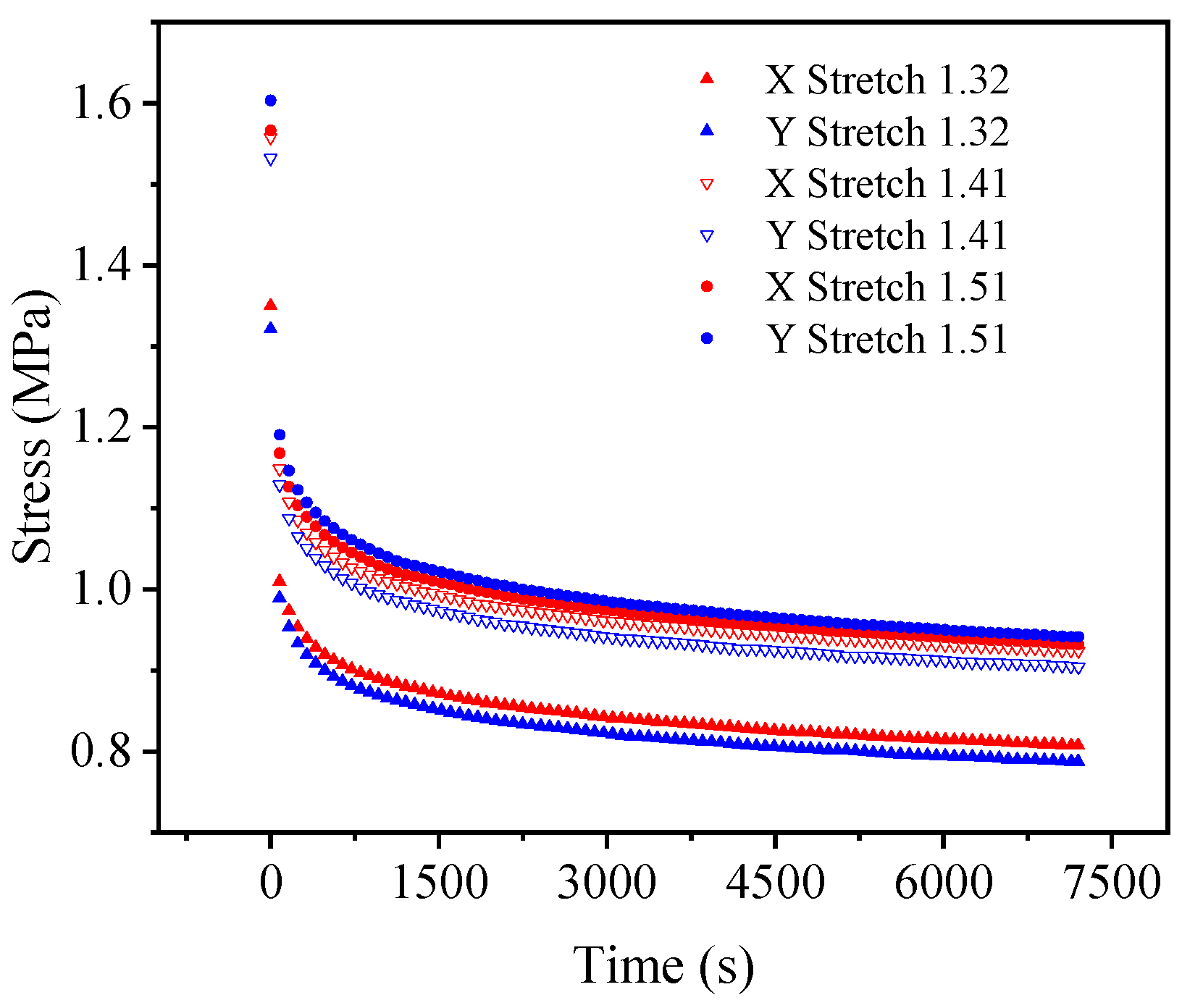
3.3. Test Results
4. Model Fitting and Analysis
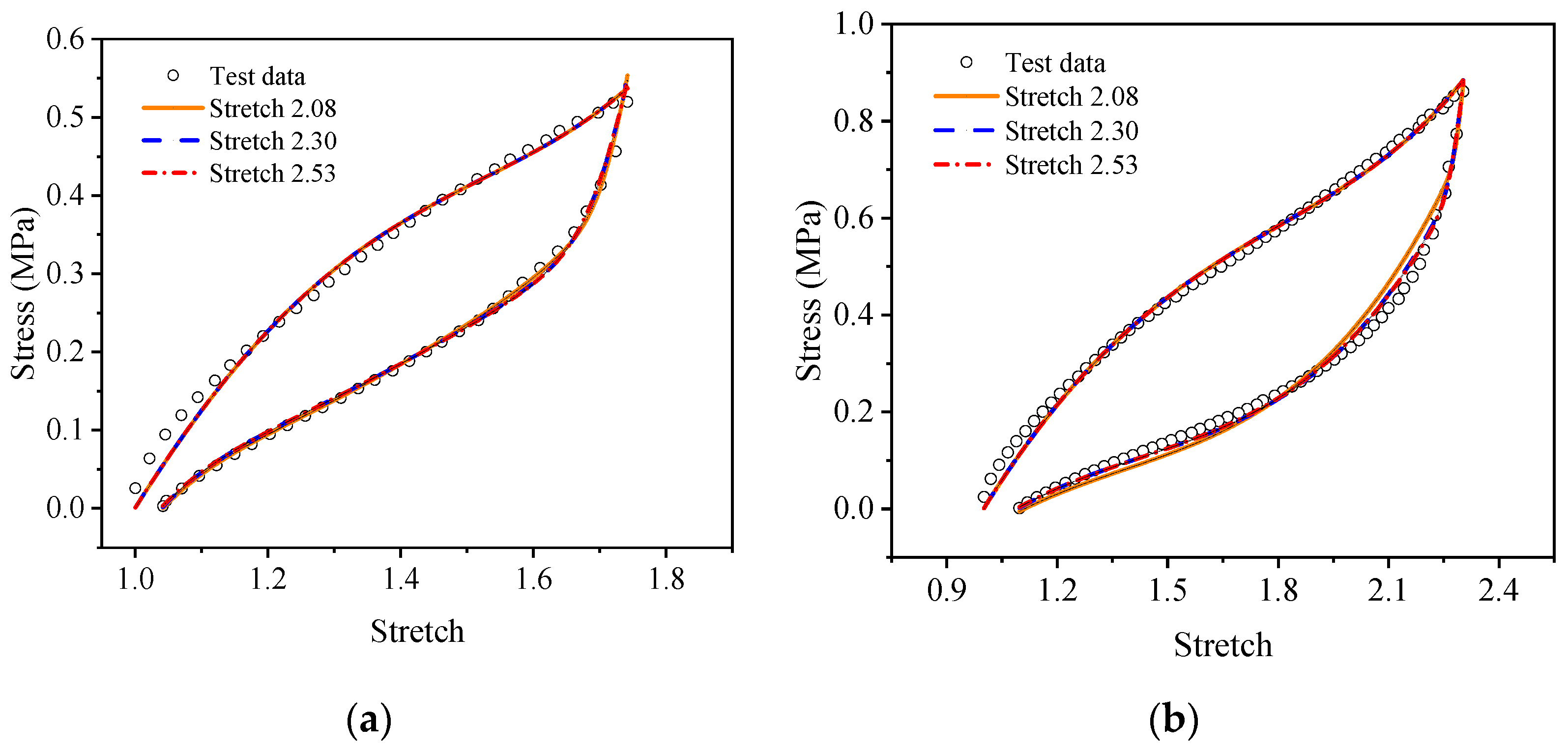
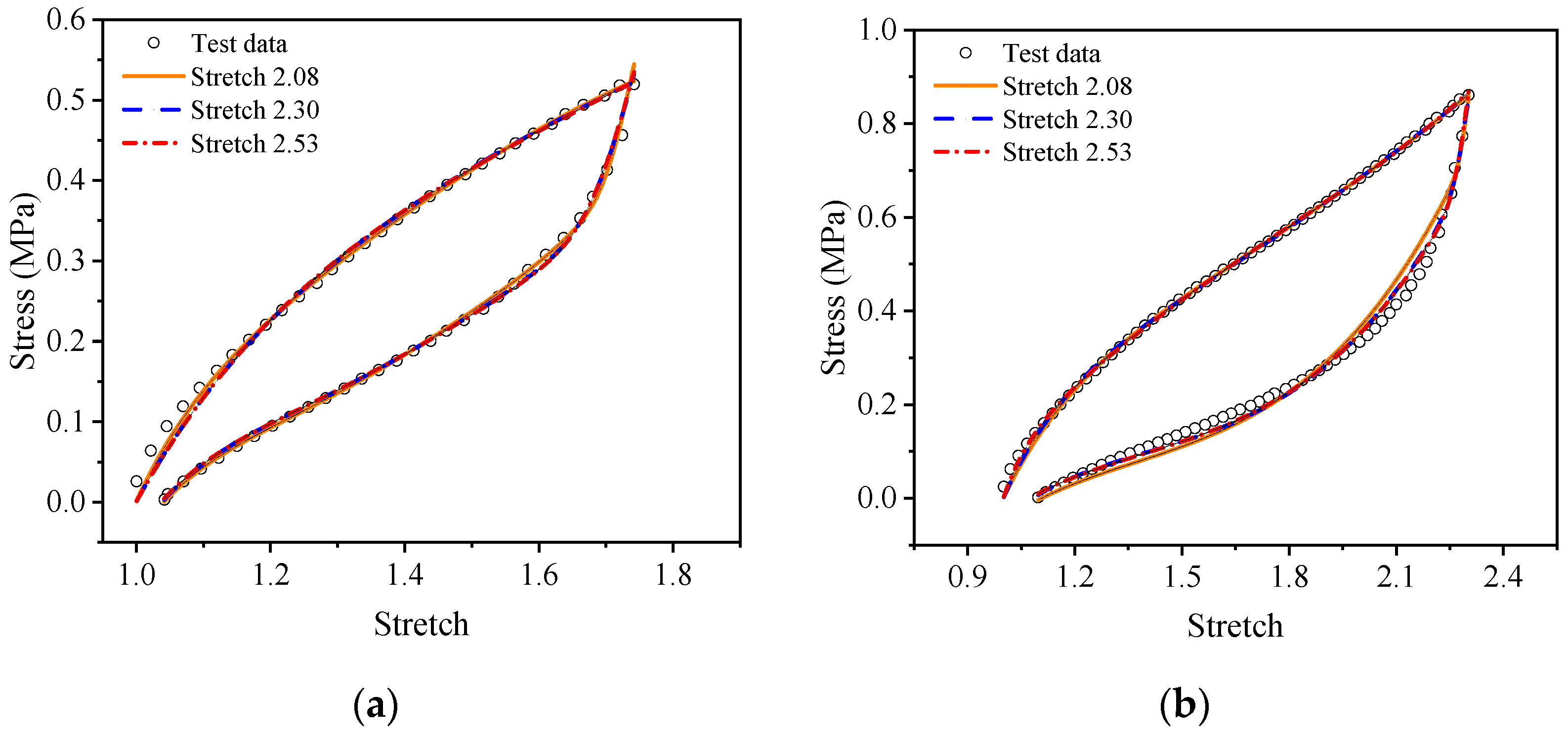
4.1. Determination of Parameters of the Proposed Visco-Hyperelastic Constitutive Model
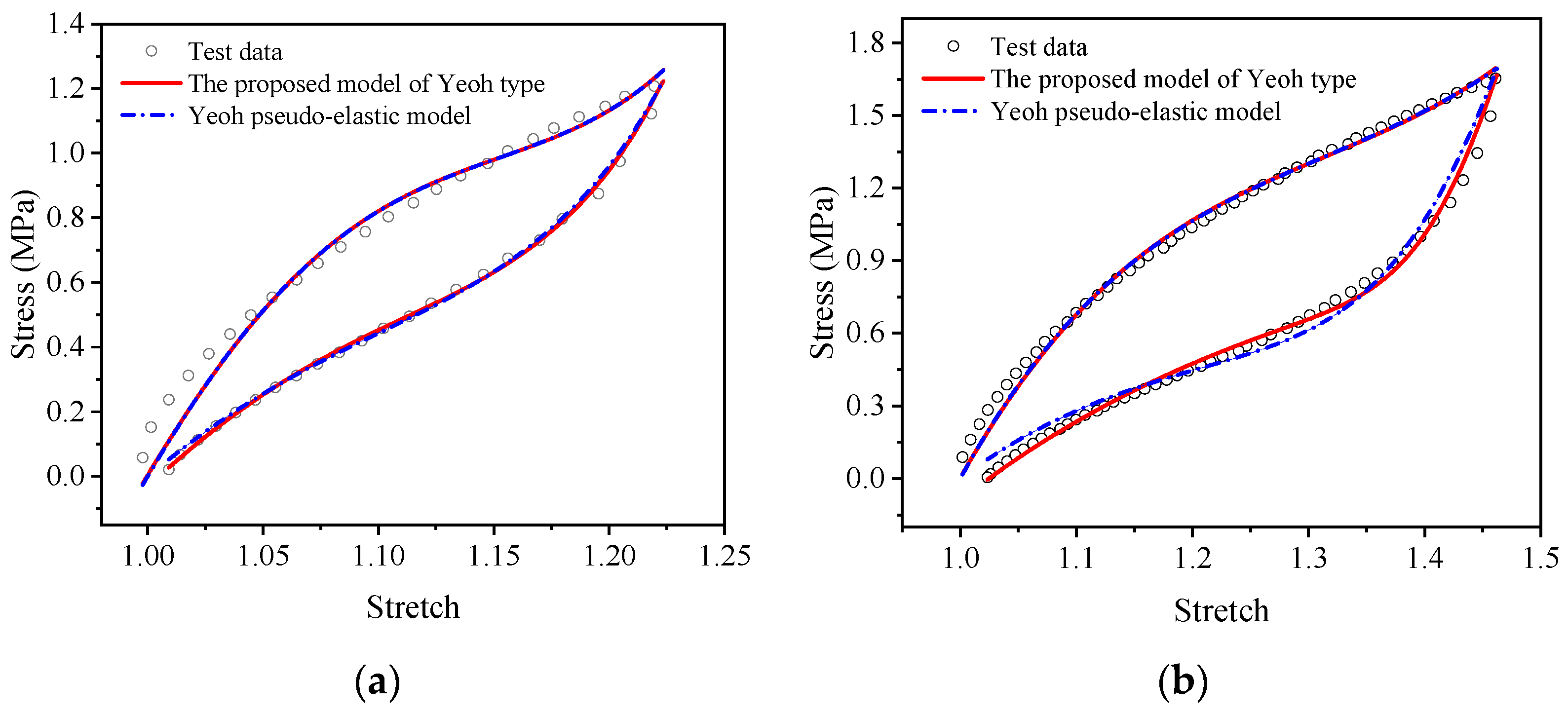
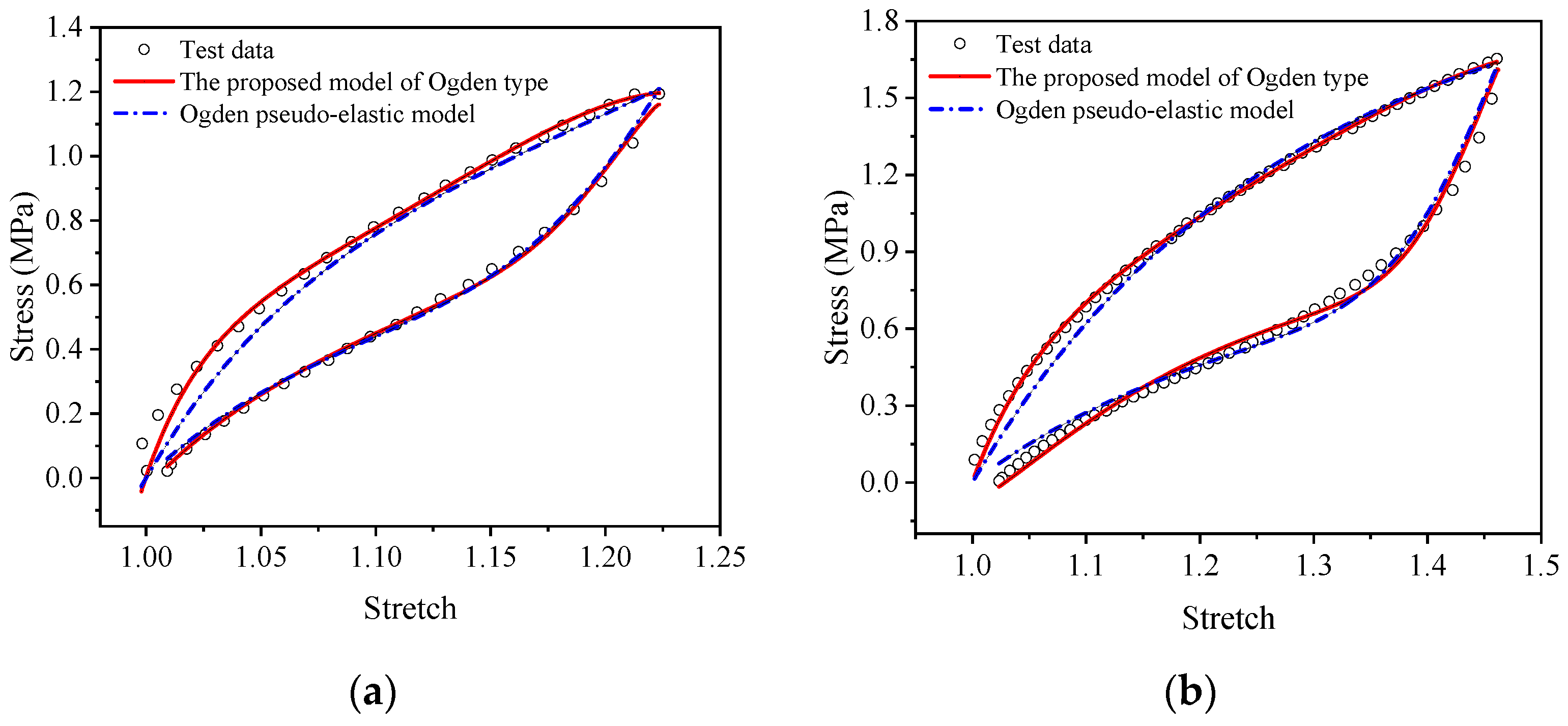
4.2. Validation of the Visco-Hyperelasticity Constitutive Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Findik, F.; Yilmaz, R.; Koksal, T. Investigation of mechanical and physical properties of several industrial rubbers. Mater. Des. 2004, 25, 269–276. [Google Scholar] [CrossRef]
- Yuan, J.; Lv, S.T.; Peng, X.H.; You, L.Y.; Milkos, B.C. Investigation of strength and fatigue life of rubber asphalt mixture. Materials 2020, 13, 3325. [Google Scholar] [CrossRef]
- Wang, Z.N.; Shen, S.L.; Zhou, A.N.; Xu, Y.S. Experimental evaluation of aging characteristics of EPDM as a sealant for undersea shield tunnels. J. Mater. Civil Eng. 2020, 32, 04020182. [Google Scholar] [CrossRef]
- Lu, S.W.; Li, B.H.; Ma, K.M.; Wang, S.; Liu, X.M.; Ma, Z.; Lin, L.Y.; Zhou, G.N.; Zhang, D.X. Flexible MXene/EPDM rubber with excellent thermal conductivity and electromagnetic interference performance. Appl. Phys. A 2020, 126, 1283. [Google Scholar] [CrossRef]
- Qu, H.J.; Wang, L.; Hui, K.; Bian, C.; Li, H.Y.; Guan, Y.W.; Luan, T.; Yan, N. Enhancing thermal insulation of EPDM ablators via constructing alternating planar architectures. Polymers 2022, 14, 1570. [Google Scholar] [CrossRef]
- Mullins, L. Effect of stretching on the properties of rubber. Rubber Chem. Technol. 1948, 21, 281–300. [Google Scholar] [CrossRef]
- Diani, J.; Fayolle, B.; Gilormini, P. A review on the Mullins effect. Eur. Polym. J. 2009, 45, 601–612. [Google Scholar] [CrossRef]
- Candau, N.; Oguz, O.; Peuvrel-Disdier, E.; Bouvard, J.L.; Maspoch, M.L.; Corvec, G.; Pradille, C.; Billon, N. Heat source and voiding signatures of Mullins damage in filled EPDM. Polym. Test. 2020, 91, 106838. [Google Scholar] [CrossRef]
- Li, Z.Y.; Wen, F.X.; Hussain, M.; Song, Y.H.; Zheng, Q. Scaling laws of Mullins effect in nitrile butadiene rubber nanocomposites. Polymers 2020, 193, 122350. [Google Scholar] [CrossRef]
- Morovati, V.; Bahrololoumi, A.; Dargazany, R. Fatigue-induced stress-softening in cross-linked multi-network elastomers: Effect of damage accumulation. Int. J. Plast. 2021, 142, 102993. [Google Scholar] [CrossRef]
- Bahrololoumi, A.; Morovati, V.; Poshtan, E.A.; Dargazany, R. A multi-physics constitutive model to predict hydrolytic aging in quasi-static behaviour of thin cross-linked polymers. Int. J. Plast. 2020, 130, 102676. [Google Scholar] [CrossRef]
- Ricker, A.; Kroger, N.H.; Wriggers, P. Comparison of discontinuous damage models of Mullins-Type. Arch. Appl. Mech. 2021, 91, 4097–4119. [Google Scholar] [CrossRef]
- Pebdani, M.H. Study Mullins effect of polyurethane reinforcement with halloysite nanotube by molecular dynamics simulation. J. Elastom. Plast. 2022, 54, 659–675. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Mooney, M. A theory of large elastic deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Ogden, R.W. Large deformation isotropic elasticity—On the correlation of theory and experiment for incompressible rubberlike solids. Ser. A-Math. Phys. Sci. 1972, 326, 565–584. [Google Scholar] [CrossRef]
- Yeoh, O. Characterization of elastic properties of carbon-black filled rubber vulcanizates. Rubber Chem. Technol. 1990, 63, 792–805. [Google Scholar] [CrossRef]
- Ogden, R.W.; Roxburgh, D.G. A pseudo–elastic model for the Mullins effect in filled rubber. Proc. R. Soc. Lond. A 1999, 455, 2861–2877. [Google Scholar] [CrossRef]
- Xiao, Y.; Jiang, D.J. Constitutive modelling of transformation pattern in hyper-elastic Niti shape memory alloy under cyclic loading. Int. J. Mech. Sci. 2020, 182, 105743. [Google Scholar] [CrossRef]
- Viet, N.V.; Zaki, W.; Umer, R. Analytical Model for a hyper-elastic Timoshenko shape memory alloy beam subjected to a loading–unloading cycle. J. Intell. Mater. Syst. Struct. 2018, 29, 3902–3922. [Google Scholar] [CrossRef]
- Simoes, M.; Martínez-Pañeda, E. Phase field modelling of fracture and fatigue in shape memory alloys. Comput. Method Appl. Mech. 2021, 373, 113504. [Google Scholar] [CrossRef]
- Viet, N.; Zaki, W.; Umer, R.; Xu, Y. Mathematical model for hyper-elastic shape memory alloy springs with large spring index. Int. J. Solids Struct. 2020, 185, 159–169. [Google Scholar] [CrossRef]
- Bernstein, B.; Kearsley, E.A.; Zapas, L.J. A study of stress relaxation with finite strain. Trans. Soc. Rheol. 1963, 7, 391–410. [Google Scholar] [CrossRef]
- Christensen, R.M. A nonlinear theory of viscoelasticity for application to elastomers. J. Appl. Mech. 1980, 47, 762–768. [Google Scholar] [CrossRef]
- Chang, W.V.; Bloch, R.; Tshoegl, N.W. On the theory of the viscoelastic behavior of soft polymers in moderately large deformations. Rheol. Acta 1976, 15, 367–378. [Google Scholar] [CrossRef]
- Gong, C.; Chen, Y.; Li, T.; Liu, T.; Zhang, Z.; Guo, B.H.; Wang, H.Y.; Dai, L.H. Free volume based nonlinear viscoelastic model for polyurea over a wide range of strain rates and temperatures. Mech. Mater. 2021, 152, 103650. [Google Scholar] [CrossRef]
- Sedaghat, M.H.; George, U.Z.; Abouali, O. A nonlinear viscoelastic model of mucociliary clearance. Rheol. Acta 2021, 60, 371–384. [Google Scholar] [CrossRef]
- Chopin, J.; Villey, R.; Yarusso, D.; Barthel, E.; Creton, C.; Ciccotti, M. Nonlinear viscoelastic modeling of adhesive failure for polyacrylate pressure-sensitive adhesives. Macromolecules 2018, 51, 8605–8610. [Google Scholar] [CrossRef]
- Zhao, B.; Hu, J.H.; Chen, W.J.; Chen, J.W.; Jing, Z.L. A nonlinear uniaxial stress-strain constitutive model for viscoelastic membrane materials. Polym. Test. 2020, 90, 1006633. [Google Scholar] [CrossRef]
- Huang, R.Y.; Yu, P.S.; Liu, Y.; Tian, C.L.; Chang, J.Y.; Wang, P.F.; Zhao, J.H. Study on the visco-hyperelastic behavior of poly-siloxane rubber. Chin. J. Theor. Appl. Mech. 2021, 53, 184–193. [Google Scholar]
- Tan, B.D.; Xu, J.S.; Sun, C.X.; Jia, Y.F.; Fan, X.G. A transversely isotropic visco-hyperelastic constitutive model for short fiber reinforced EPDM. Chin. J. Theor. Appl. Mech. 2022, 49, 677–684. [Google Scholar]
- Pearson, I.; Pickering, M. The determination of a highly elastic adhesive’s material properties and their representation in finite element analysis. Finite. Elem. Anal. Des. 2001, 37, 221–230. [Google Scholar]
- Sasso, M.; Palmieri, G.; Chiappini, G.; Amodio, D. Characterization of hyperelastic rubber-like materials by biaxial and uniaxial stretching tests based on optical methods. Polym. Test. 2008, 27, 995–1004. [Google Scholar] [CrossRef]
- Zhou, G.M.; Lu, X.H.; Xv, Z.H. Experimental investigations of biaxial tensile strength of 3-D fine-woven-penetrated carbon/composites. J. Nanjing Univ. Sci. Technol. 2007, 31, 390–393. [Google Scholar]
- Fujikawa, M.; Maeda, N.; Yamabe, J.; Kodama, Y.; Koishi, M. Determining stress–strain in rubber with in-plane biaxial tensile tester. Exp. Mech. 2014, 54, 1639–1649. [Google Scholar] [CrossRef]
- Anani, Y.; Rahimi, G. Modeling of visco-hyperelastic behavior of transversely isotropic functionally graded rubbers. Polym. Eng. Sci. 2016, 10, 343–347. [Google Scholar] [CrossRef]
- Hu, X.L.; Liu, X.; Li, M.; Luo, W.B. Selection strategies of hyper-elastic constitutive models for carbon black filled rubber. Eng. Mech. 2014, 31, 34–42. [Google Scholar]
- Yang, T.Q. Single-integral constitutive relations for nonlinear viscoelasticity. Adv. Mech. 1988, 18, 52–60. [Google Scholar]
- Prony, R. Essai éxperimental et analytique: Sur les lois de la dilatabilité de uides élas tique et sur celles de la force expansive de la vapeur de l’alkool, à diérentes temperatures. J. De L’école Polytech. 1795, 22, 24–76. [Google Scholar]
- GB/T5574-2008; Industrial Rubber Sheet. China Standard Publication: Beijing, China, 2008.
- Pearson, K.X. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1900, 50, 157–175. [Google Scholar] [CrossRef]
- Kar, K.K.; Bhowmick, A.K. Hysteresis loss in filled rubber vulcanizates and its relationship with heat generation. J. Appl. Polym. Sci. 1997, 64, 1541–1555. [Google Scholar] [CrossRef]









| Composition | Proportion |
|---|---|
| EPDM raw rubber | 32% |
| Sulfurization agent | 0.2% |
| Accelerator | 0.8% |
| Surfactant | 1.2% |
| Reinforcing filler | 60.6% |
| Antioxidant | 0.2% |
| Emollient | 5% |
| ST | ET | ||||||
|---|---|---|---|---|---|---|---|
| Displacement (mm) | Speed (mm/s) | Time (s) | Displacement (mm) | Speed (mm/s) | Time (s) | ||
| 2.08 | 33 | 1 | 7200 | 1.32 | 25 | 1 | 7200 |
| 2.30 | 42 | 1 | 7200 | 1.41 | 31 | 1 | 7200 |
| 2.53 | 50 | 1 | 7200 | 1.51 | 38 | 1 | 7200 |
| Test | Load (mm) | Unload (mm) | Speed (mm/s) | |
|---|---|---|---|---|
| ST | A | 0–25 | 25–0 | 0.5 |
| B | 0–45 | 45–0 | 0.5 | |
| C | 0–16 | 16–0 | 0.5 | |
| 0–32 | 32–0 | 0.5 | ||
| 0–50 | 50–0 | 0.5 | ||
| ET | A | 0–20 | 20–0 | 0.5 |
| B | 0–35 | 35–0 | 0.5 | |
| C | 0–13 | 13–0 | 0.5 | |
| 0–26 | 26–0 | 0.5 | ||
| 0–39 | 39–0 | 0.5 | ||
| Test | |||
|---|---|---|---|
| ST | A | 0.0155 | −0.0157 |
| B | 0.0148 | −0.0148 | |
| ET | A | 0.0062 | −0.0063 |
| B | 0.0067 | −0.0070 | |
| Test | |||||||
|---|---|---|---|---|---|---|---|
| ST | 2.08 | 0.1188 | 0.02734 | 0.01911 | 88.58 | 2091.00 | 0.9898 |
| 2.30 | 0.1052 | 0.02548 | 0.01871 | 90.46 | 2172.00 | 0.9906 | |
| 2.53 | 0.1049 | 0.02478 | 0.01894 | 80.67 | 1939.00 | 0.9898 | |
| ET | 1.32 | 0.5642 | 0.1504 | 0.09726 | 81.19 | 2100.00 | 0.9875 |
| 1.41 | 0.5282 | 0.1436 | 0.08825 | 73.28 | 1942.00 | 0.9862 | |
| 1.51 | 0.4490 | 0.1229 | 0.08146 | 74.00 | 2061.00 | 0.9873 |
| Test | Load | Unload | |||||||
|---|---|---|---|---|---|---|---|---|---|
| ST | A | 2.08 | 0.1501 | −0.0811 | 0.02414 | 0.9903 | 1.3790 | 0.0082 | 0.9968 |
| 2.30 | 0.1574 | −0.0750 | 0.02157 | 0.9904 | 1.5110 | 0.0138 | 0.9959 | ||
| 2.53 | 0.1578 | −0.0747 | 0.02152 | 0.9904 | 1.4860 | 0.0147 | 0.9958 | ||
| B | 2.08 | 0.1280 | −0.0338 | 0.0040 | 0.9954 | 1.0980 | 0.0039 | 0.9774 | |
| 2.30 | 0.1372 | −0.0320 | 0.0039 | 0.9956 | 1.2750 | 0.0092 | 0.9932 | ||
| 2.53 | 0.1377 | −0.0318 | 0.0039 | 0.9956 | 1.2300 | 0.0102 | 0.994 | ||
| ET | A | 1.32 | 0.6637 | −0.9669 | 0.8774 | 0.9718 | 1.1360 | 0.0636 | 0.9983 |
| 1.41 | 0.6857 | −0.9590 | 0.8741 | 0.9718 | 1.1990 | 0.0718 | 0.998 | ||
| 1.51 | 0.7327 | −0.9462 | 0.8688 | 0.9717 | 1.3000 | 0.0915 | 0.9977 | ||
| B | 1.32 | 0.3756 | −0.1725 | 0.0430 | 0.9928 | 0.5832 | 0.0451 | 0.9873 | |
| 1.41 | 0.3984 | −0.1673 | 0.0424 | 0.9929 | 0.6599 | 0.0602 | 0.9927 | ||
| 1.51 | 0.4465 | −0.1586 | 0.0412 | 0.9930 | 0.7923 | 0.1063 | 0.9936 | ||
| Test | Load | Unload | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ST | A | 2.08 | 1.7030 | −0.4769 | 0.2257 | −0.2071 | 1.0230 | −0.4958 | 0.9966 | 1.3860 | 0.0078 | 0.9978 |
| 2.30 | −0.0571 | −1.4500 | 3.6400 | −0.3666 | 0.7922 | −0.0554 | 0.9935 | 1.5050 | 0.0140 | 0.9976 | ||
| 2.53 | 2.8320 | −0.4192 | 2.8600 | −12.600 | 0.7373 | 12.2300 | 0.9930 | 1.4750 | 0.0146 | 0.9972 | ||
| B | 2.08 | −3.7080 | 1.2880 | −2.0800 | 0.0137 | −0.3574 | 0.7323 | 0.9988 | 1.0900 | 0.0038 | 0.9768 | |
| 2.30 | −3.7980 | 0.6406 | 1.6240 | 0.6598 | 0.3103 | −0.5153 | 0.9991 | 1.2670 | 0.0093 | 0.9921 | ||
| 2.53 | 0.5773 | −13.2600 | 6.5700 | 0.2631 | 0.7617 | −0.4005 | 0.9995 | 1.2220 | 0.0103 | 0.9930 | ||
| ET | A | 1.32 | 19.2000 | 16.5200 | −9.0790 | 1.5790 | 3.5290 | −2.2560 | 0.9981 | 1.1440 | 0.0600 | 0.9977 |
| 1.41 | −6.8170 | 6.3960 | 3.8820 | −1.0730 | 19.3600 | −15.7300 | 0.9870 | 1.2100 | 0.0683 | 0.9969 | ||
| 1.51 | 13.1900 | 17.1900 | −8.8050 | 0.6069 | 4.6740 | −2.27900 | 0.9879 | 1.3070 | 0.0883 | 0.9958 | ||
| B | 1.32 | −2.8810 | −2.5630 | 5.9070 | −1.7720 | 0.9527 | 1.9290 | 0.9977 | 0.5838 | 0.0416 | 0.9817 | |
| 1.41 | −3.7390 | 5.0350 | 6.4350 | −1.0450 | −1.5490 | 3.9680 | 0.9985 | 0.6642 | 0.0596 | 0.9872 | ||
| 1.51 | 3.8680 | 6.5250 | −3.6940 | −0.5164 | 2.9890 | −1.0080 | 0.9985 | 0.7956 | 0.1053 | 0.9922 | ||
| Test | Parameter | ST | ET | ||
|---|---|---|---|---|---|
| A | B | A | B | ||
| Load | 0.2346 | 0.2200 | 1.0080 | 0.7292 | |
| −0.0488 | −0.0146 | −0.8661 | −0.1041 | ||
| 0.0168 | 0.0027 | 0.8361 | 0.0340 | ||
| 0.9913 | 0.9967 | 0.9712 | 0.9933 | ||
| Unload | 1.8410 | 1.5780 | 1.8690 | 1.6960 | |
| 0.1055 | 0.2115 | 0.2411 | 0.4180 | ||
| 0.9858 | 0.9751 | 0.9972 | 0.9797 | ||
| Test | Parameter | ST | ET | ||
|---|---|---|---|---|---|
| A | B | A | B | ||
| Load | 1.6740 | −1.0110 | 4.2510 | 1.1700 | |
| −1.1940 | 3.4500 | −2.1840 | 1.1940 | ||
| 1.5880 | 3.3720 | 0.8228 | −1.0920 | ||
| 4.9170 | 1.6140 | 3.8200 | −1.6850 | ||
| 0.3152 | 22.1600 | −0.8709 | 3.0400 | ||
| −4.7830 | −23.1100 | −0.9007 | −0.0860 | ||
| 0.9953 | 0.9866 | 0.9656 | 0.9859 | ||
| Unload | 1.5770 | 1.6610 | 2.2410 | 1.7820 | |
| 0.2072 | 0.1407 | 0.1847 | 0.3599 | ||
| 0.9819 | 0.9755 | 0.9957 | 0.9877 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Liu, C.; Zhu, D.; Lin, J. A Visco-Hyperelastic Constitutive Model to Characterize the Stress-Softening Behavior of Ethylene Propylene Diene Monomer Rubber. Polymers 2023, 15, 3388. https://doi.org/10.3390/polym15163388
Liu X, Liu C, Zhu D, Lin J. A Visco-Hyperelastic Constitutive Model to Characterize the Stress-Softening Behavior of Ethylene Propylene Diene Monomer Rubber. Polymers. 2023; 15(16):3388. https://doi.org/10.3390/polym15163388
Chicago/Turabian StyleLiu, Xiu, Chen Liu, Dingxiang Zhu, and Jianguo Lin. 2023. "A Visco-Hyperelastic Constitutive Model to Characterize the Stress-Softening Behavior of Ethylene Propylene Diene Monomer Rubber" Polymers 15, no. 16: 3388. https://doi.org/10.3390/polym15163388
APA StyleLiu, X., Liu, C., Zhu, D., & Lin, J. (2023). A Visco-Hyperelastic Constitutive Model to Characterize the Stress-Softening Behavior of Ethylene Propylene Diene Monomer Rubber. Polymers, 15(16), 3388. https://doi.org/10.3390/polym15163388






