Computational Fluid Dynamics Modeling of Top-Down Digital Light Processing Additive Manufacturing
Abstract
1. Introduction
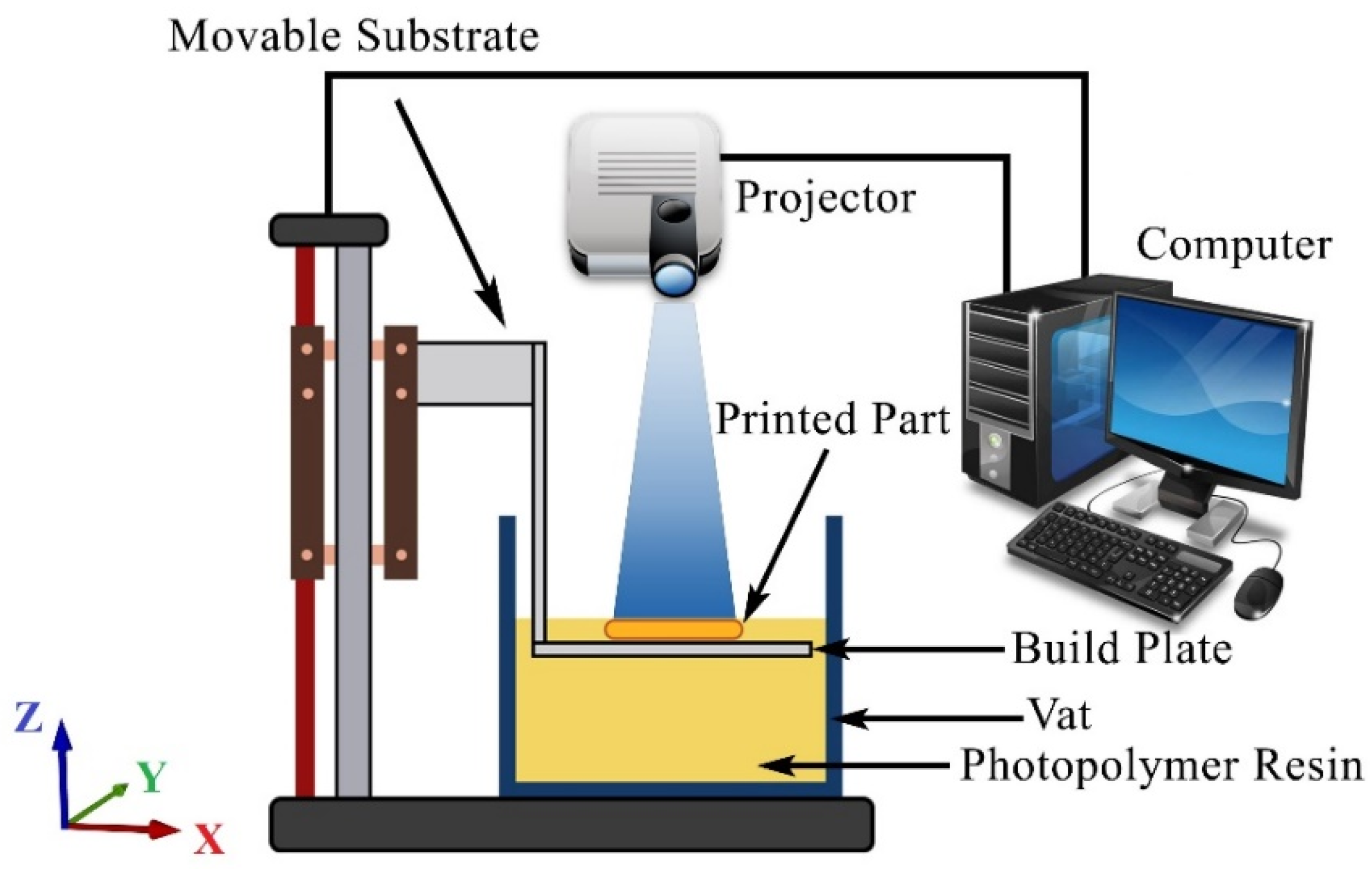
2. Model Description
2.1. Governing Equations
2.2. Numerical Model
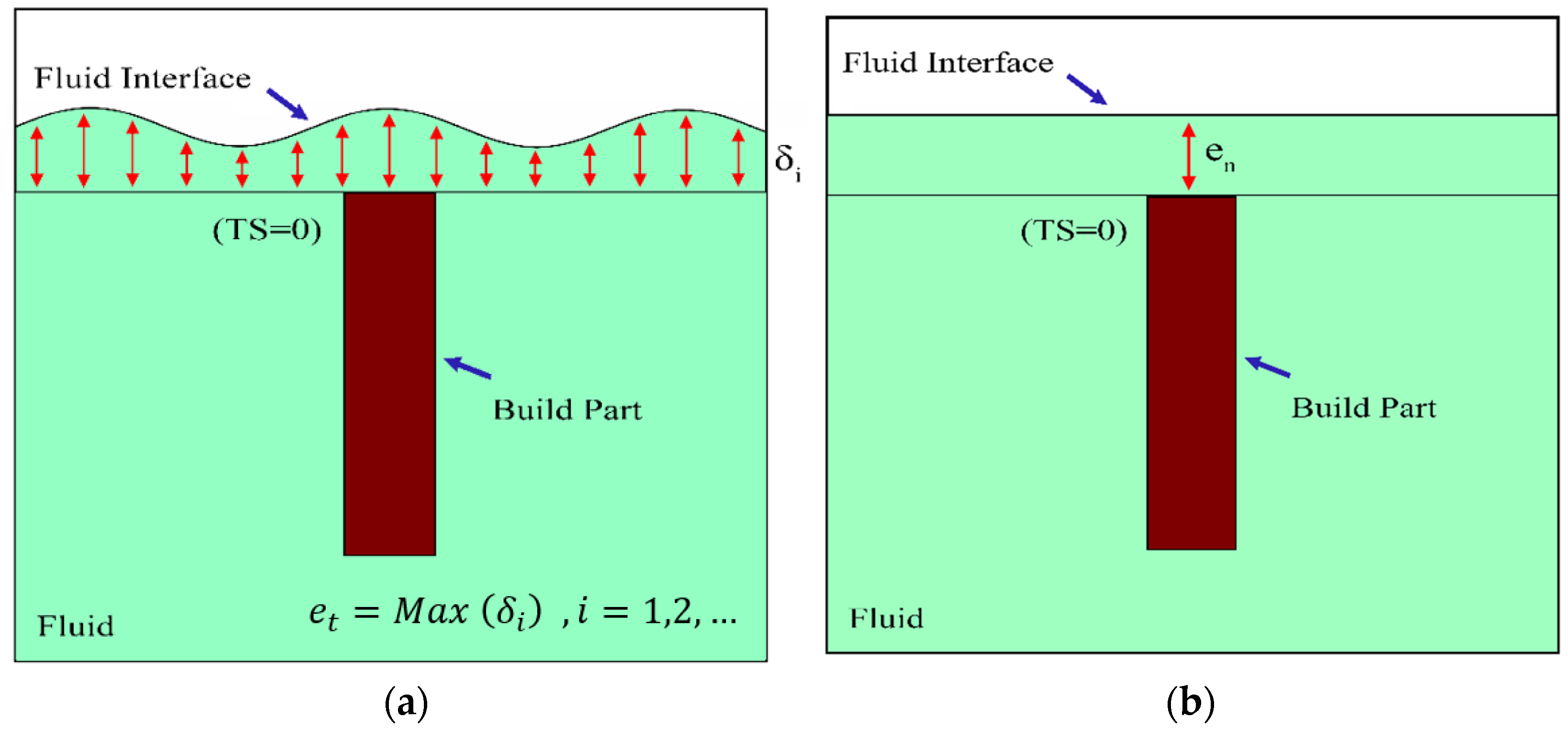
2.3. Post-Processing
3. Results and Discussion
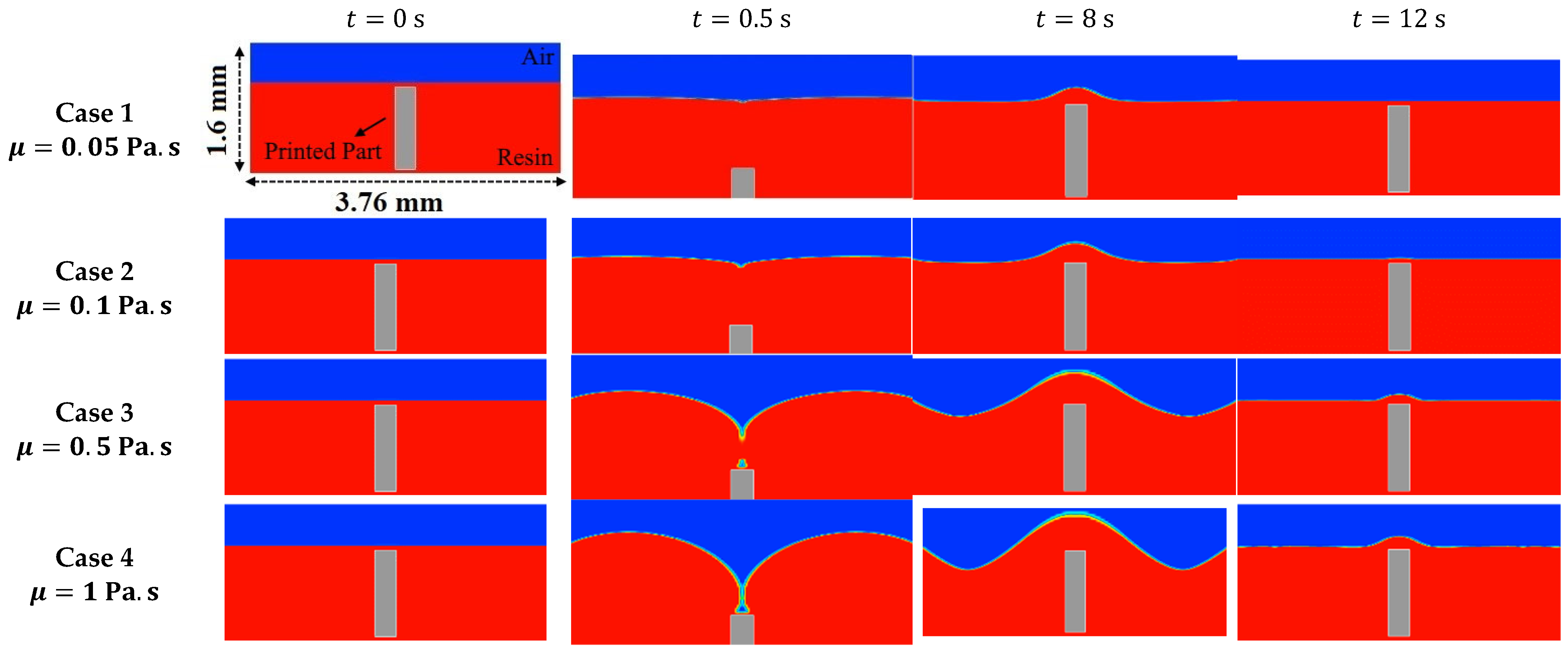
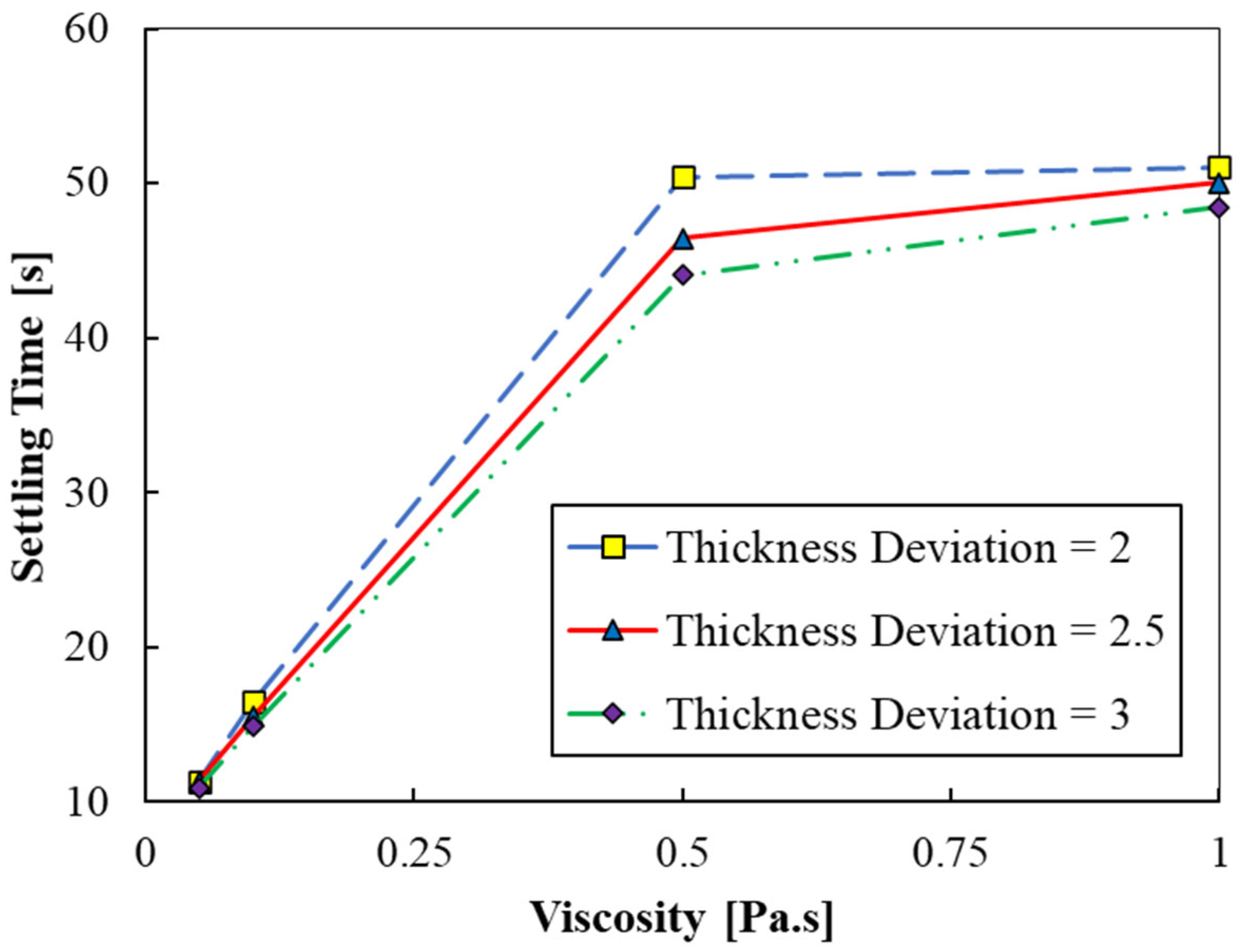
3.1. Fluid Viscosity
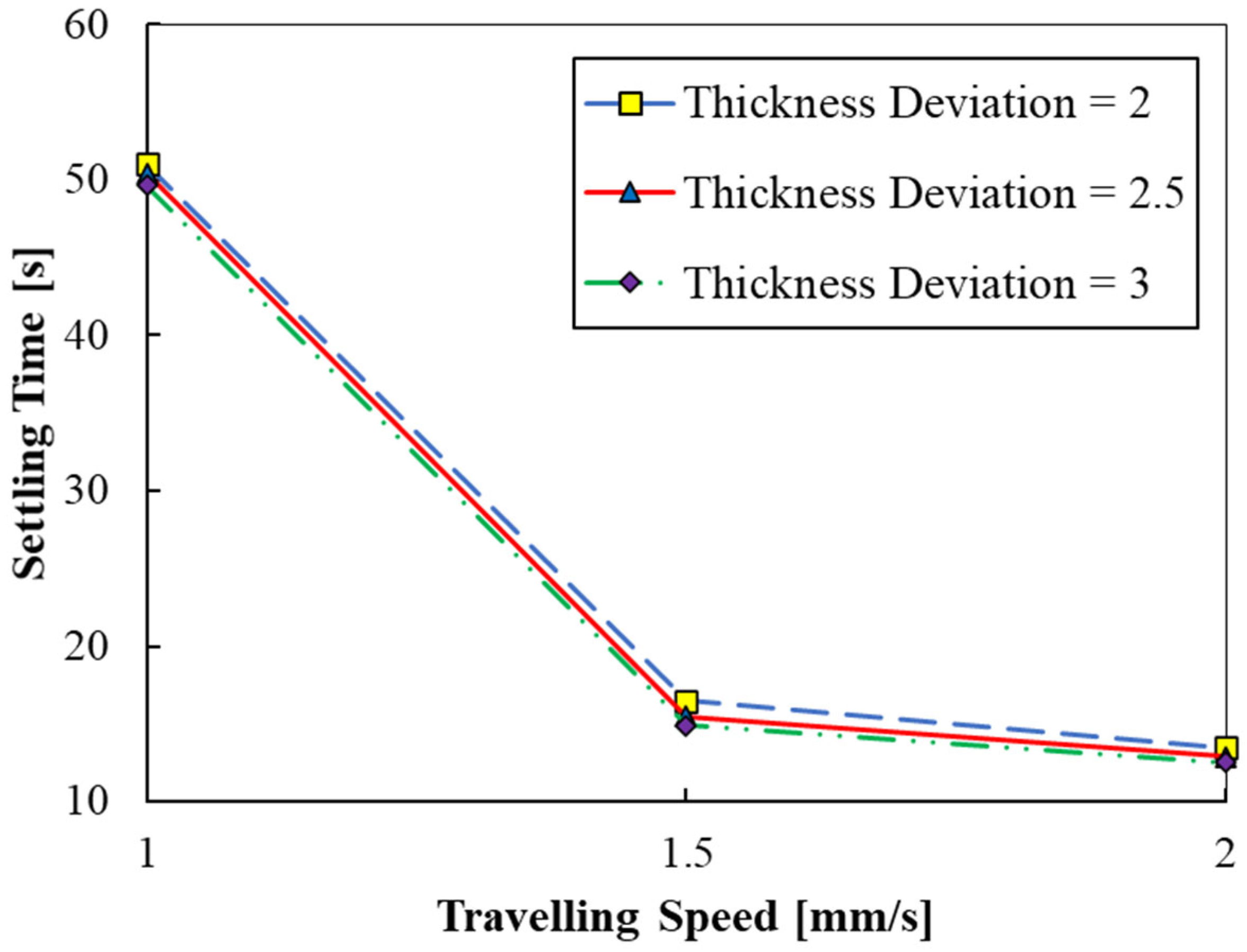
3.2. Traveling Speed
3.3. Travelling Speed Ratio
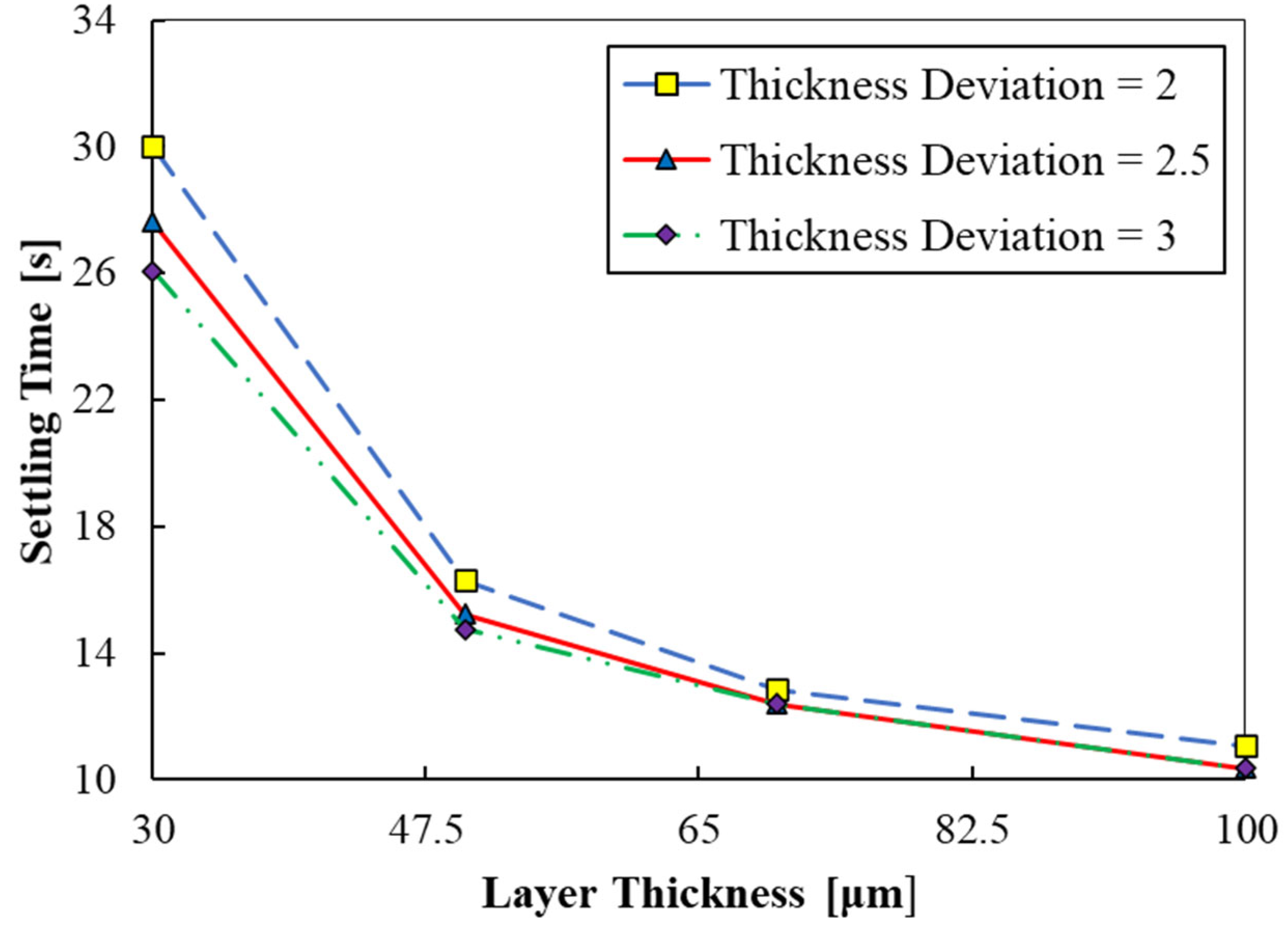
3.4. Print Layer Thickness
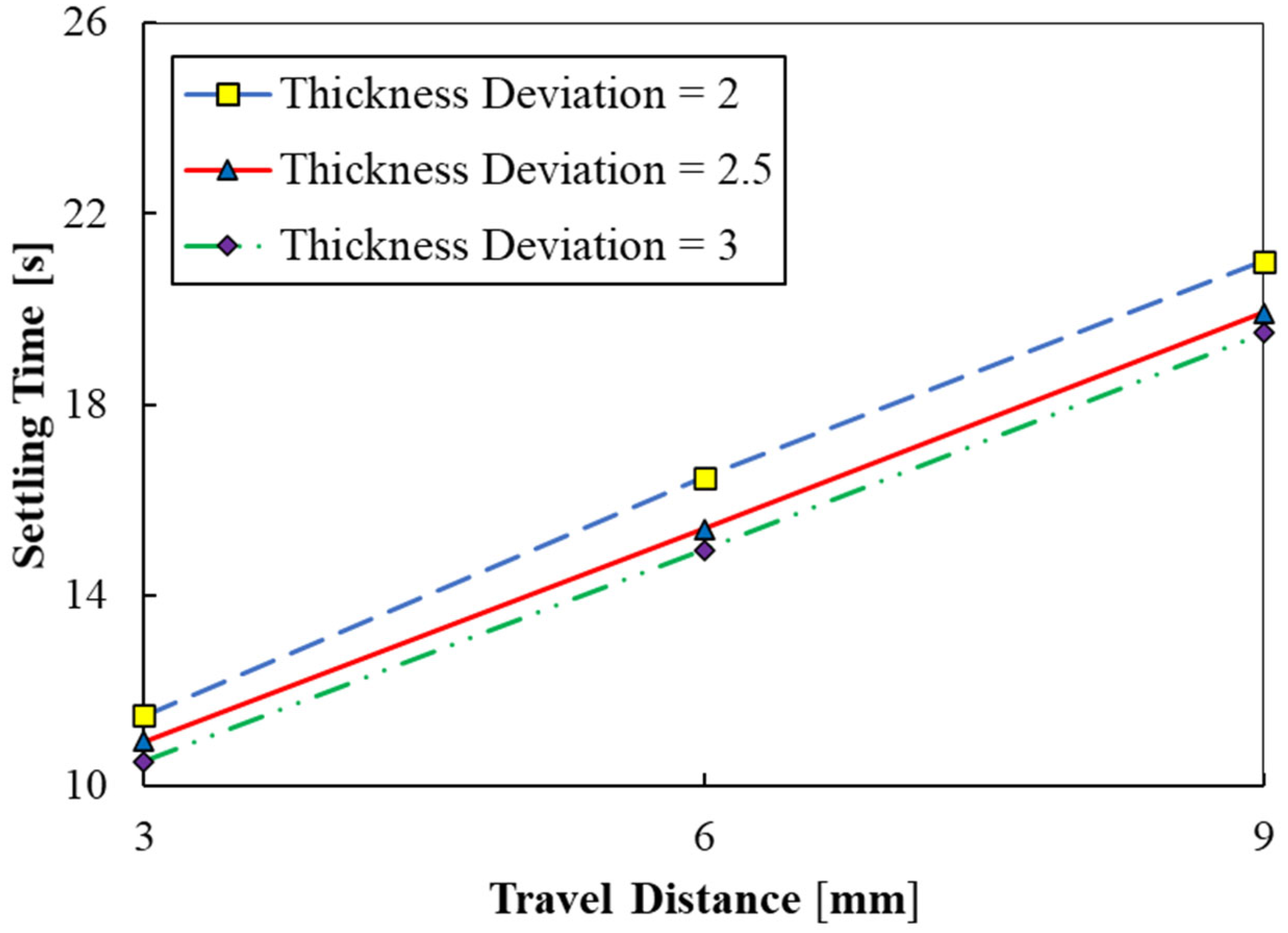
3.5. Travel Distance
4. Conclusions
- By increasing the fluid viscosity from 0.05 to 1 Pa.s, the fluid interface will need more time for reaching a stable state. According to the plotted working curves, stabilizing the fluid interface requires approximately 16.5 s when applying the reference parameters.
- Considering the optimization results, for case 4 with the fluid viscosity of 1 Pa.s, a maximum stability time of 51 was achieved.
- A diminishing trend was found for the stability time by augmentation of the traveling speed from 1 to 2 mm/s, remarkably. Moreover, the maximum stability time of almost 51 s was obtained for thickness deviation of 2 µm and the traveling speed of 1 mm/s.
- A smaller stability time of the fluid interface was obtained by increasing the travelling speed ratio from 0.75 to 1.25. In addition, the minimum and maximum stability times for the travelling speed ratio parameter considering thickness deviation of 2.5 µm were obtained at roughly 15 s and 17 s, respectively.
- A stable situation was obtained for the fluid interface in a shorter time considering high printed layer thickness values.
- According to the results of the travel distance parameter, the minimum and maximum stability times at thickness deviation of 3 µm were achieved at approximately 10.5 s and 19.5 s, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | |
| The thickness of the layer at time | |
| Nominal thickness of the layer | |
| The velocity component in the -direction | |
| Local pressure | |
| Gravitational body forces per mass unit in the -direction | |
| Time | |
| Traveling time | |
| Finishing time | |
| Stability time | |
| Spatial coordinates | |
| Coordinates | |
| Greek symbols | |
| Distance of the fluid interface from the surface of the build part | |
| Thickness deviation | |
| Particular thickness deviation | |
| Fluid viscosity | |
| Abbreviations | |
| AM | Additive manufacturing |
| CFD | Computational fluid dynamics |
| DLP | Digital light processing |
| DMD | Digital micromirror device |
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| FDM | Fused deposition modeling |
| GMRES | Generalized minimum residual |
| LCD | Liquid crystal display |
| SLA | Stereolithography |
| TD | Travelling distance |
| TS | Traveling speed |
| TSR | Traveling speed ratio |
| UV | Ultraviolet |
| VOF | Volume of fluid |
References
- Li, J.; Wu, C.; Chu, P.K.; Gelinsky, M. 3D printing of hydrogels: Rational design strategies and emerging biomedical applications. Mater. Sci. Eng. R. Rep. 2020, 140, 100543. [Google Scholar] [CrossRef]
- Comminal, R.; da Silva, W.R.L.; Andersen, T.J.; Stang, H.; Spangenberg, J. Modelling of 3D concrete printing based on computational fluid dynamics. Cem. Concr. Res. 2020, 138, 106256. [Google Scholar] [CrossRef]
- Lotfi, R.; Eslahi, N.; Koohkhezri, M.; Moghadasi, H. 9-3D printing of graphene polymer composites. In Innovations in Graphene-Based Polymer Composites; Woodhead Publishing: Sawston, UK, 2022; pp. 247–281. [Google Scholar] [CrossRef]
- Van Waeleghem, T.; Marchesini, F.H.; Cardon, L.; D’hooge, D.R. Melt exit flow modelling and experimental validation for fused filament fabrication: From Newtonian to non-Newtonian effects. J. Manuf. Process. 2022, 77, 138–150. [Google Scholar] [CrossRef]
- Zhang, F.; Wei, M.; Viswanathan, V.V.; Swart, B.; Shao, Y.; Wu, G.; Zhou, C. 3D printing technologies for electrochemical energy storage. Nano Energy 2017, 40, 418–431. [Google Scholar] [CrossRef]
- Tian, X.; Jin, J.; Yuan, S.; Chua, C.K.; Tor, S.B.; Zhou, K. Emerging 3D-printed electrochemical energy storage devices: A critical review. Adv. Energy Mater. 2017, 7, 1700127. [Google Scholar] [CrossRef]
- Murr, L.E. Frontiers of 3D printing/additive manufacturing: From human organs to aircraft fabrication. J. Mater. Sci. Technol. 2016, 32, 987–995. [Google Scholar] [CrossRef]
- Nickels, L. AM and aerospace: An ideal combination. Met. Powder Rep. 2015, 70, 300–303. [Google Scholar] [CrossRef]
- Gul, J.Z.; Sajid, M.; Rehman, M.M.; Siddiqui, G.U.; Shah, I.; Kim, K.-H.; Lee, J.-W.; Choi, K.H. 3D printing for soft robotics—A review. Sci. Technol. Adv. Mater. 2018, 19, 243–262. [Google Scholar] [CrossRef] [PubMed]
- Stanton, M.; Trichet-Paredes, C.; Sanchez, S. Applications of three-dimensional (3D) printing for microswimmers and bio-hybrid robotics. Lab Chip 2015, 15, 1634–1637. [Google Scholar] [CrossRef] [PubMed]
- Godoi, F.C.; Prakash, S.; Bhandari, B.R. 3d printing technologies applied for food design: Status and prospects. J. Food Eng. 2016, 179, 44–54. [Google Scholar] [CrossRef]
- Sun, J.; Peng, Z.; Zhou, W.; Fuh, J.Y.; Hong, G.S.; Chiu, A. A review on 3D printing for customized food fabrication. Procedia Manuf. 2015, 1, 308–319. [Google Scholar] [CrossRef]
- Gross, B.; Lockwood, S.Y.; Spence, D.M. Recent advances in analytical chemistry by 3D printing. Anal. Chem. 2017, 89, 57–70. [Google Scholar] [CrossRef] [PubMed]
- Johnson, R.D. Chemical creativity with 3D printing. Nat. Chem. 2012, 4, 338–339. [Google Scholar] [CrossRef] [PubMed]
- Trenfield, S.J.; Awad, A.; Goyanes, A.; Gaisford, S.; Basit, A.W. 3D printing pharmaceuticals: Drug development to frontline care. Trends Pharmacol. Sci. 2018, 39, 440–451. [Google Scholar] [CrossRef] [PubMed]
- Awad, A.; Trenfield, S.J.; Goyanes, A.; Gaisford, S.; Basit, A.W. Reshaping drug development using 3D printing. Drug Discov. Today 2018, 23, 1547–1555. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, U.; Ning, S.; Wang, Y.; Kong, Y.L. Addressing unmet clinical needs with 3D printing technologies. Adv. Healthc. Mater. 2018, 7, 1800417. [Google Scholar] [CrossRef] [PubMed]
- Lerman, M.J.; Lembong, J.; Gillen, G.; Fisher, J.P. 3D printing in cell culture systems and medical applications. Appl. Phys. Rev. 2018, 5, 041109. [Google Scholar] [CrossRef]
- Quan, H.; Zhang, T.; Xu, H.; Luo, S.; Nie, J.; Zhu, X. Photo-curing 3D printing technique and its challenges. Bioact. Mater. 2020, 5, 110–115. [Google Scholar] [CrossRef]
- Kroiher, M. Morphological chimeras of larvae and adults in a hydrozoan—Insights into the control of pattern formation and morphogenesis. Int. J. Dev. Biol. 2002, 44, 861–866. [Google Scholar]
- Gao, S.; Wang, C.; Xing, B.; Shen, M.; Zhao, W.; Zhao, Z. Experimental investigation on bending behaviour of ZrO2 honeycomb sandwich structures prepared by DLP stereolithography. Thin-Walled Struct. 2020, 157, 107099. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.; Shen, Y.; Xiong, Y.; Dong, L.; Zheng, J.; Zhao, S. Fabrication of porous β-TCP/58S bioglass scaffolds via top-down DLP printing with high solid loading ceramic-resin slurry. Mater. Chem. Phys. 2021, 267, 124587. [Google Scholar] [CrossRef]
- Sun, Y.; Li, M.; Jiang, Y.; Xing, B.; Shen, M.; Cao, C.; Wang, C.; Zhao, Z. High-Quality Translucent Alumina Ceramic Through Digital Light Processing Stereolithography Method. Adv. Eng. Mater. 2021, 23, 2001475. [Google Scholar] [CrossRef]
- Ngadiman, N.H.A.; Basri, M.A.B.; Yusof, N.M.; Idris, A.; Fallahiarezoudar, E. Digital Light Processing (DLP) 3D Printing of Polyethylene Glycol (PEG) Biopolymer, Commercially available Ultra-High and Tough (UHT) Resin and Maghemite (γ-Fe2O3) Nanoparticles Mixture for Tissue Engineering Scaffold Application. Adv. Mater. Lett. 2019, 10, 802–806. [Google Scholar] [CrossRef]
- Li, Y.; Huang, S.; Wang, S.; Zhang, X.; Wang, Y.; Lu, B.; Luo, Y.; He, F.; Liu, W.; Wu, S. Research on the effects of surface modification of ceramic powder on cure performance during digital light processing (DLP). Ceram. Int. 2022, 48, 3652–3658. [Google Scholar] [CrossRef]
- Zhao, L.; Jiang, Z.; Zhang, C.; Guo, W.; Jiang, Z.; Gao, X.; Cui, Y.; Shi, X. Theoretical modeling based on stress wave propagation and experimental verification of residual stress in stereolithography printed ZrO2 ceramic suspensions. Ceram. Int. 2021, 47, 26935–26941. [Google Scholar] [CrossRef]
- Borrello, J.; Nasser, P.; Iatridis, J.C.; Costa, K.D. 3D printing a mechanically-tunable acrylate resin on a commercial DLP-SLA printer. Addit. Manuf. 2018, 23, 374–380. [Google Scholar] [CrossRef]
- Yu, Y.; Zou, B.; Wang, X.; Huang, C. Rheological behavior and curing deformation of paste containing 85 wt% Al2O3 ceramic during SLA-3D printing. Ceram. Int. 2022, 48, 24560–24570. [Google Scholar] [CrossRef]
- Korkunova, O.S.; Kholkhoev, B.C.; Burdukovskii, V.F. Photosensitive thiol–ene composition for DLP 3D printing of thermally stable polymer materials. Mendeleev Commun. 2022, 32, 231–233. [Google Scholar] [CrossRef]
- Li, Y.; Mao, Q.; Yin, J.; Wang, Y.; Fu, J.; Huang, Y. Theoretical prediction and experimental validation of the digital light processing (DLP) working curve for photocurable materials. Addit. Manuf. 2021, 37, 101716. [Google Scholar] [CrossRef]
- Kadry, H.; Wadnap, S.; Xu, C.; Ahsan, F. Digital light processing (DLP) 3D-printing technology and photoreactive polymers in fabrication of modified-release tablets. Eur. J. Pharm. Sci. 2019, 135, 60–67. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, X. Experimental and numerical investigations on microstereolithography of ceramics. J. Appl. Phys. 2002, 92, 4796–4802. [Google Scholar] [CrossRef]
- Tarabeux, J.; Pateloup, V.; Michaud, P.; Chartier, T. Development of a numerical simulation model for predicting the curing of ceramic systems in the stereolithography process. J. Eur. Ceram. Soc. 2018, 38, 4089–4098. [Google Scholar] [CrossRef]
- FLOW-3D|We Solve the World’s Toughest CFD Problems. FLOW SCIENCE. Available online: https://www.flow3d.com/ (accessed on 15 June 2021).
- Mollah, M.T.; Comminal, R.; Serdeczny, M.P.; Pedersen, D.B.; Spangenberg, J. Stability and deformations of deposited layers in material extrusion additive manufacturing. Addit. Manuf. 2021, 46, 102193. [Google Scholar] [CrossRef]
- Mollah, M.T.; Comminal, R.; Serdeczny, M.P.; Pedersen, D.B.; Spangenberg, J. Numerical Predictions of Bottom Layer Stability in Material Extrusion Additive Manufacturing. JOM 2022, 74, 1096–1101. [Google Scholar] [CrossRef]
- Serdeczny, M.P.; Comminal, R.; Mollah, M.T.; Pedersen, D.B.; Spangenberg, J. Numerical modeling of the polymer flow through the hot-end in filament-based material extrusion additive manufacturing. Addit. Manuf. 2020, 36, 101454. [Google Scholar] [CrossRef]
- Comminal, R.; da Silva, W.R.L.; Andersen, T.J.; Stang, H.; Spangenberg, J. Influence of processing parameters on the layer geometry in 3D concrete printing: Experiments and modelling. In RILEM International Conference on Concrete and Digital Fabrication; Springer: Berlin/Heidelberg, Germany, 2020; pp. 852–862. [Google Scholar]
- Ashby, S.F.; Manteuffel, T.A.; Saylor, P.E. A taxonomy for conjugate gradient methods. SIAM J. Numer. Anal. 1990, 27, 1542–1568. [Google Scholar] [CrossRef]
- Barrett, R.; Berry, M.; Chan, T.F.; Demmel, J.; Donato, J.; Dongarra, J.; Eijkhout, V.; Pozo, R.; Romine, C.; Van der Vorst, H. Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Saad, Y. Iterative Methods for Sparse Linear Systems; SIAM: Philadelphia, PA, USA, 2003. [Google Scholar]
- Comminal, R.; Spangenberg, J.; Hattel, J.H. Cellwise conservative unsplit advection for the volume of fluid method. J. Comput. Phys. 2015, 283, 582–608. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
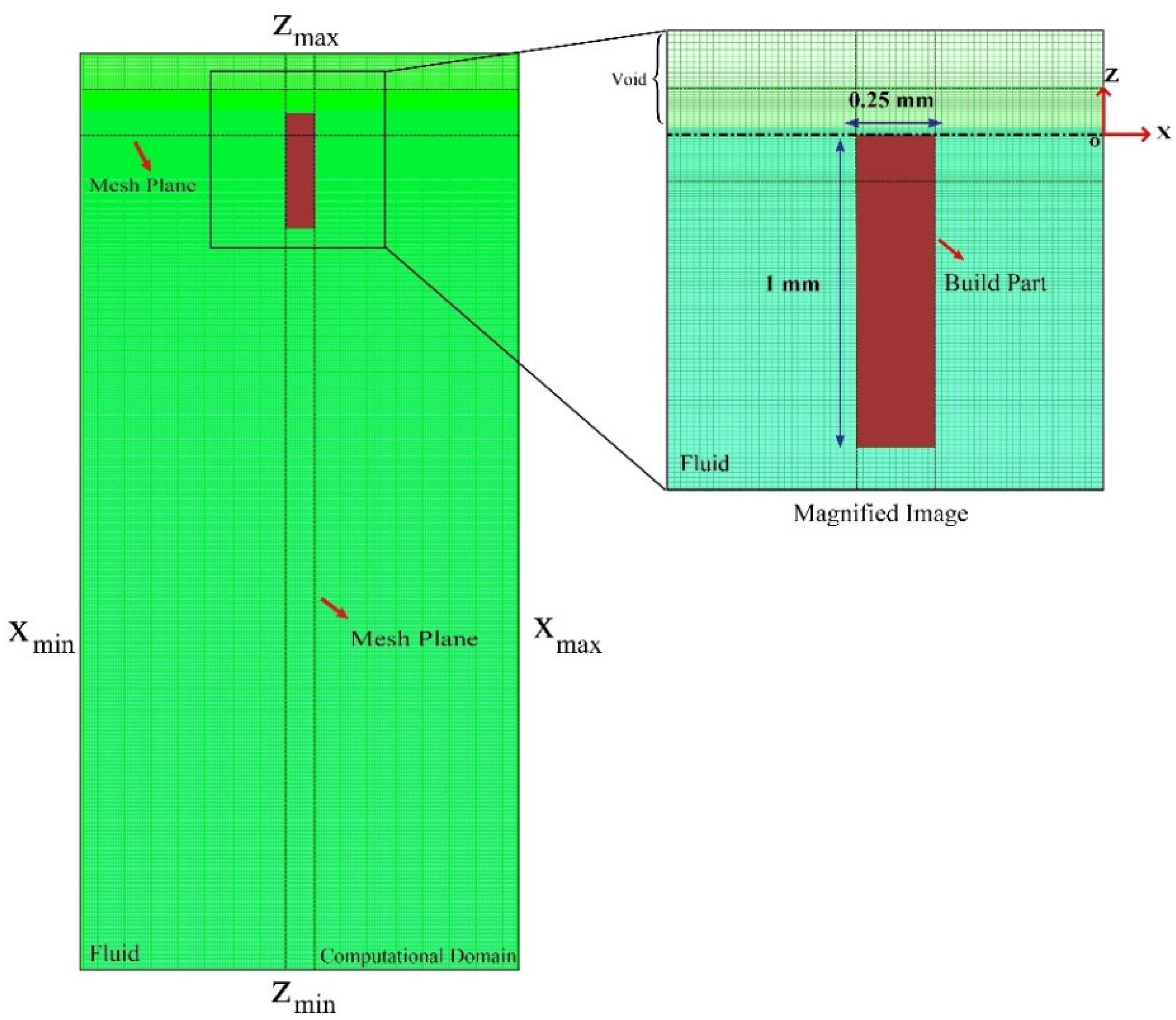

| Quantity | Unit | Mesh 1 | Mesh 2 | Mesh 3 |
|---|---|---|---|---|
| Number of cells | - | 33,108 | 68,580 | 104,091 |
| Maximum cell size (in X/Z direction) | 31.8/49 | 20.8/37.6 | 17.30/30.50 | |
| Minimum cell size (in X/Z direction) | 30.1/13.6 | 20.8/7.5 | 16.66/5.99 | |
| Maximum ratio of adjacent cell size ratio (in X/Z direction) | - | 1.02/1.22 | 1/1.23 | 1/1.20 |
| Maximum aspect ratio (X:Z ratio) | - | 2.33 | 2.77 | 2.88 |
| Case Numbers | Travelling Speed Ratio (-) | |||||
|---|---|---|---|---|---|---|
| Case 1 | 1100 | 0.05 | 1.5 | 1 | 50 | 6 |
| Case 2 | 0.1 | 1.5 | 1 | 50 | 6 | |
| Case 3 | 0.5 | 1.5 | 1 | 50 | 6 | |
| Case 4 | 1 | 1.5 | 1 | 50 | 6 | |
| Case 5 | 0.1 | 1 | 1 | 50 | 6 | |
| Case 6 | 0.1 | 2 | 1 | 50 | 6 | |
| Case 7 | 0.1 | 1.5 | 0.75 | 50 | 6 | |
| Case 8 | 0.1 | 1.5 | 1.25 | 50 | 6 | |
| Case 9 | 0.1 | 1.5 | 1 | 30 | 6 | |
| Case 10 | 0.1 | 1.5 | 1 | 70 | 6 | |
| Case 11 | 0.1 | 1.5 | 1 | 100 | 6 | |
| Case 12 | 0.1 | 1.5 | 1 | 50 | 3 | |
| Case 13 | 0.1 | 1.5 | 1 | 50 | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moghadasi, H.; Mollah, M.T.; Marla, D.; Saffari, H.; Spangenberg, J. Computational Fluid Dynamics Modeling of Top-Down Digital Light Processing Additive Manufacturing. Polymers 2023, 15, 2459. https://doi.org/10.3390/polym15112459
Moghadasi H, Mollah MT, Marla D, Saffari H, Spangenberg J. Computational Fluid Dynamics Modeling of Top-Down Digital Light Processing Additive Manufacturing. Polymers. 2023; 15(11):2459. https://doi.org/10.3390/polym15112459
Chicago/Turabian StyleMoghadasi, Hesam, Md Tusher Mollah, Deepak Marla, Hamid Saffari, and Jon Spangenberg. 2023. "Computational Fluid Dynamics Modeling of Top-Down Digital Light Processing Additive Manufacturing" Polymers 15, no. 11: 2459. https://doi.org/10.3390/polym15112459
APA StyleMoghadasi, H., Mollah, M. T., Marla, D., Saffari, H., & Spangenberg, J. (2023). Computational Fluid Dynamics Modeling of Top-Down Digital Light Processing Additive Manufacturing. Polymers, 15(11), 2459. https://doi.org/10.3390/polym15112459





