3.1. Raman Spectroscopy
The Raman spectra index of all bands found are disclosed in
Tables S1–S3 in the supplementary material. Based on
Figure 4a, the bands between 1400 and 1480 cm
−1 in the spectral region from 200 to 4000 cm
−1 correspond to methylene bending vibrations (𝛿(CH
2)). Additionally, in
Figure 4b, it can be observed that the band at 1440.00 cm
−1 refers to the D band present in the nanoplatelets, but with a displacement compared to the same band when analyzed separately, as discussed in
Figure 5. From the GNP/HDPE spectrum, one can notice a small band in 1580.80 cm
−1 attributed to the D band of the GNP. In addition, the crystalline phase is represented by the band at 1418.70 cm
−1, known as the crystallinity band [
45,
46,
47,
48]. This crystallinity band at 1418.70 cm
−1 is commonly used to determine the degree of orthorhombic crystallinity of the HDPE [
45]. The bands at 1060.00 and 1367.30 cm
−1 are attributed to the amorphous phase, while the Raman bands at 1060.80 and 1127.70 cm
−1 are attributed to the symmetric and asymmetric stretching vibrations of the C–C bonds. The Raman bands at 2849.70 cm
−1 and 2883.80 cm
−1 are attributed to the stretching of groups (CH
3), and the bands at 2907.70 cm
−1 and 3068.50 cm
−1 are assigned to the (C–H) group [
45,
46,
47,
48].
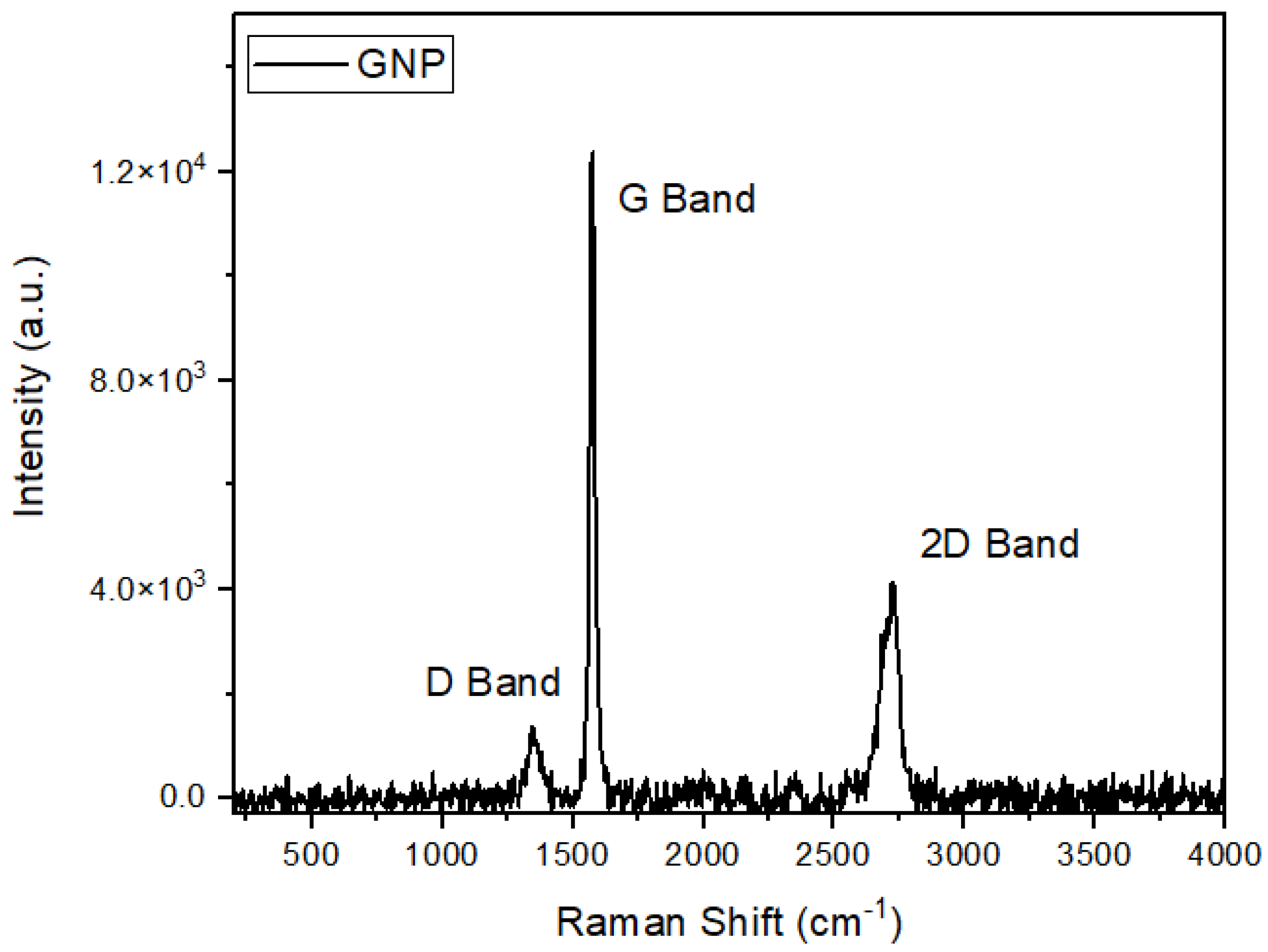
Based on
Figure 5, the Raman spectrum of the GNP revealed the presence of the G band at 1573.6 cm
−1 and the D band at 1347.7 cm
−1. The occurrence of the G band is attributed to the first-order scattering of the
E2g mode, while the D band is associated with defects in the graphite lattice, as explained by Krishnamoorthy et al. [
49]. Moreover, besides the changes observed in the G and D bands in the graphene sheets, significant alterations were also observed in the overtone band of graphene, which normally occurs at higher wavenumbers. In the case of the GNPs, 2D overtones were observed at 2715.9 cm
−1 [
49].
3.2. DSC Analysis
Differential scanning calorimetry (DSC) analyses were conducted on the HDPE and GNP/HDPE nanocomposites with 0.10 wt.% of GNP and different heating and cooling rates (5–20 °C/min). The results, presented in
Table 2, revealed the crystallization (T
c) and melting temperatures (T
m). Notably, with the incorporation of the GNP into the HDPE matrix, both T
c and T
m showed an average shift of 1 °C towards higher temperatures compared to pure HDPE. This observation supports the nucleation effect caused by the presence of graphene in the polymeric matrix, as emphasized by Evgin et al. [
40].
Furthermore, the crystallization behavior of the GNP/HDPE nanocomposites is influenced by the agglomeration of graphene nanoparticles, which may explain the observed increase in crystallization temperature with the increasing graphene content. The clustering of these nanoparticles can hinder the regular packing of HDPE polymeric chains, as pointed out by Evgin et al. [
40], resulting in reduced HDPE crystallinity despite acting as nucleating agents.
Moreover, it was observed that the crystallization and melting temperatures of the nanocomposites were slightly higher than those of pure HDPE, particularly at lower cooling rates. This can be attributed to the time-dependent nature of crystallization and melting processes, where lower cooling rates allow for increased fluidity and diffusivity of molecules due to lower viscosity and more time available for the completion of crystallization and melting. Consequently, both Tc and Tm temperatures increase with the decreasing cooling rate, as reported by Evgin et al. [
40] as well as Jiang and Drzal [
50]. These findings indicate that the amount of added GNPs plays a crucial role in the overall structure and properties of the composite.
In
Figure 6, the crystallization temperature of the HDPE and nanocomposites is plotted against the cooling rate. These results were obtained by analyzing the exothermic peaks in the DSC cooling curves, as depicted in
Figures S1 and S2 in the supplementary materials, with a heating rate of 10 °C/min. It can be observed that the crystallization peak temperature of the GNP/HDPE nanocomposites is slightly higher than that of pure HDPE for all cooling rates. This suggests that the presence of GNP particles in the HDPE matrix can induce heterogeneous nucleation by creating nucleation sites for the polymeric chains during melt crystallization, particularly at rates of 10 and 15 °C/min, where this effect is intensified.
Interestingly, at low cooling rates, the incorporation of GNP does not seem to significantly influence the crystallization temperature of the nanocomposites. However, for rates greater than 10 °C/min, crystallization temperatures show a slight increase with an increasing percentage of GNP in the HDPE matrix. These results suggest that the effect of GNP on crystallization temperature is more prominent at higher cooling rates, indicating a rate-dependent influence of GNP on the crystallization behavior of the nanocomposites.
As a result, from the DSC heating curves at a rate of 10 °C/min for the HDPE and GNP/HDPE films, shown in
Figures S3 and S4 in the supplementary materials, the degree of crystallinity for all nanocomposites was calculated using the melting enthalpy from the endothermic peak, applying Equation (1). The resulting values are as follows: HDPE (46.10%) and GNP/HDPE (62.19%).
Furthermore, in terms of crystallization kinetics, the heat of crystallization can be converted into the relative degree of crystallinity (
XT) by dividing the heat released at each crystallization temperature
T (Δ
HΤ) by the total heat (Δ
H0) corresponding to complete crystallization [
51]:
where
,
, and
represent the initial and final temperatures of crystallization at time
t and the final temperature of crystallization, respectively, while
represents the enthalpy of crystallization released during an infinitesimal temperature interval
: the crystallization time (
) can be obtained from the crystallization temperature using the following equation:
where
and
represent the temperature at the beginning and time of crystallization (
), respectively, and
φ is the cooling rate. The relative degree of crystallinity (
XT) is depicted in
Figure 7a,b as a function of temperature (
). Additionally,
Figure 7c,d illustrate the relative degree of crystallinity (
XT) as a function of time (
). These curves clearly exhibit a strong dependence of the crystallization process on the cooling rate. As crystallization progresses, the curves tend to approach a plateau due to the impact and crowding of the spherulites [
51]. Moreover, higher cooling rates result in shorter times required for crystallization to occur.
The time from the initiation of crystallization to the point where the relative degree of crystallinity reaches 50% was calculated from the curves in
Figure 7 and plotted for each cooling rate
φ, as illustrated in
Figure 8. It can be observed that the t
1/2 value of the GNP/HDPE nanocomposites is slightly higher compared to pure HDPE at a given cooling rate, particularly noticeable at lower cooling rates. This suggests that the addition of graphene filler complicates the time required for the polymer to achieve half the degree of crystallization, resulting in a lower rate of crystallization due to the effect of heterogeneous nucleation. Moreover, it appears that the charge load does not have a significant impact on the t
1/2 value in the GNP/HDPE nanocomposites.
In general, the kinetics of the crystallization transition has been traditionally interpreted using the Avrami and Ozawa equations [
40,
50,
51]. However, it has been noted in the literature that these methods may not fit well to non-isothermal crystallization data. Therefore, to better describe the non-isothermal crystallization process, Liu et al. [
52] proposed a combination of the Avrami and Ozawa equations:
The parameter F(T), defined as F(T) = [K(T)/Zt]1/m, where φ is the cooling rate and α is the ratio between the exponents Avrami and Ozawa n/m, carries a significant physical and practical meaning. It represents the critical cooling rate required to achieve a specific degree of crystallinity within a unit of crystallization time.
Figure 9a,b displays plots of
Log(
φ) versus
Log(
t) at various degrees of crystallinity for the HDPE and GNP/HDPE nanocomposites, respectively. Notably, these graphs exhibit excellent linearity, with most coefficient of determination (R-squared) values exceeding 0.95 in all cases, as one can notice in
Table 3.
The values of the α and Log[F(T)] parameters were determined from the intercepts and slopes of the fitted lines, respectively, as presented in
Table 3. It was observed that the
Log[
F(
T)] value increases with an increasing degree of crystallinity. This can be attributed to the fact that at low values of
XT, the polymeric matrix is in a molten state, resulting in a higher crystallization rate.
Furthermore, the
Log[
F(
T)] parameter for the GNP/HDPE nanocomposites exhibits slightly higher values compared to pure HDPE. This suggests that the presence of GNP particles did not facilitate the crystallization process in the HDPE composites, resulting in lower crystallization rates at higher crystalline fractions [
51,
53].
The
α values remain parallel and nearly constant for a given composition and different
XT values. Additionally, the ratio of the Avrami exponent to the Ozawa exponent ranges from 1.8 to 2.0, which is consistent with findings in the literature [
51,
53]. This suggests that significant growth of secondary crystallization accompanies primary crystallization during the non-isothermal crystallization period. The nucleation mechanism and crystal growth geometries are similar, indicating that the proposed method successfully describes the non-isothermal crystallization process of HDPE and its nanocomposites.
Furthermore, Friedman’s differential isoconversional method [
54] was employed to evaluate the effective activation energies, as shown:
where
is the instantaneous crystallization rate as a function of time for a given value of relative crystallinity (
), R is the universal gas constant, and
is the effective energy barrier of the process for a given value of
. This approach requires performing a series of experiments in different temperature programs to obtain this energy. Specifically, at various cooling rates, the values of
at a specific
are correlated with the corresponding crystallization temperature at this
, i.e.,
, a straight line, can be obtained by plotting
versus 1/
, and the slope is −
. The dependence of such an energy barrier on the relative crystallinity for HDPE and its GNP/HDPE nanocomposites based on the Friedman equation is shown in
Figure 10.
An analysis of
Figure 10 reveals that the GNP/HDPE nanocomposite exhibited lower activation energies for low crystallinity layers
, indicating a pronounced nucleating effect of GNP on the HDPE matrix, facilitating the initial crystallization process. However, for larger transformed layers
, graphene was found to cause an increase in activation energy. This could be attributed to the need to expel the GNP during crystal growth, resulting in a more complex and challenging process. This observation is consistent with the findings in
Figure 8, further supporting the conclusion.
3.3. Tensile Properties
Through the tensile tests, the tensile strength (σ
u), elastic modulus (E), ductility (ε
t) (deformation at break), and toughness (T) (area under the curve σ vs. ε) were obtained.
Figure 11 shows the results for the E of the 20J/HDPE and 20J/GNP/HDPE single nanocomposites.
The incorporation of nanoload is accompanied by an observed increase in the value of E, as depicted in
Figure 11. Thus, in terms of cost-effectiveness, smaller amounts of GNP are found to be more efficient in improving the mechanical behavior. This phenomenon may be associated with a points of stress concentration caused by the agglomeration of GNPs in the HDPE matrix, as noted in previous studies [
35,
55,
56].
However, the values of E obtained for the 20J/HDPE composite (1.32 ± 0.73 GPa) in this study are considerably higher than those reported in the literature (~1.0 GPa) [
14,
57,
58]. An increase of over 20% was demonstrated by the 20J/GNP/HDPE single nanocomposite (1.63 ± 0.15 GPa) compared to the 20J/HDPE studied in this work. Furthermore, when compared to the value reported in the literature, the increase exceeds 60% [
14,
57,
58].
As for tensile strength,
Figure 12 presents the average values and their standard deviations. Due to overlapping standard deviation bars, ANOVA and Tukey tests were conducted to ascertain whether the mean values exhibit any significant differences.
Based on the results of
Figure 12, it can be concluded that the mean values of tensile strength are equal. This suggests that the incorporation of GNPs did not significantly alter the tensile strength of the HDPE matrix. It can also be inferred that a lower nanoload content of GNPs performs better compared to higher amounts, likely due to the agglomeration and alignment of GNPs in the HDPE matrix, as reported in previous studies [
35,
59,
60,
61,
62].
Similarly, the results indicate that the inclusion of GNPs in the HDPE matrix did not have a significant influence on the ductility (ε
t) of the nanocomposite, 4.71%, as shown in
Figure 13. The lack of influence on ductility can be attributed to the low compatibility between GNPs and the HDPE matrix, resulting in voids around GNPs and their agglomeration in the HDPE matrix after plastic deformation, as reported in previous studies [
62]. These characteristics lead to a decrease in the surface area of GNPs, reducing the load transmission through the matrix, and maintaining the ductility of the polymer similar to that of pure HDPE.
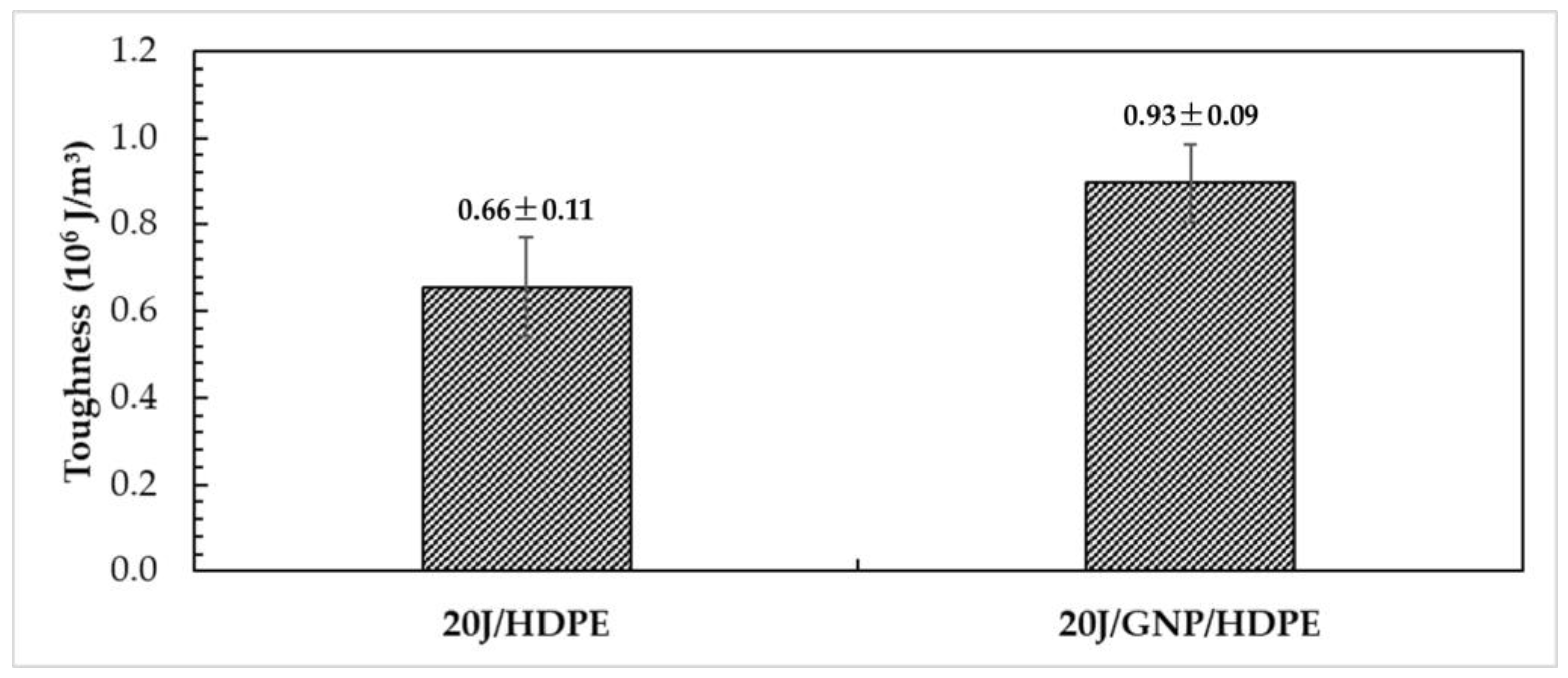
The data provided in
Figure 14 show that toughness, which is the energy required to cause fractures in a composite material, can be calculated from the stress–strain curve or from the tensile test data sheet. The data compare different nanocomposites made of HDPE, jute, and GNP.
The 20J/HDPE composite presented a toughness value of 0.66 MJ/m
3, as shown in
Figure 14. However, the incorporation of GNP into the HDPE matrix improves the toughness of the single nanocomposite 20J/GNP/HDPE to 0.93 MJ/m
3, which represents a more than 40% increase compared to 20J/HDPE. This indicates that the addition of GNP to the nanocomposite makes it more resistant to fracture. The increase in toughness can be attributed to the reinforcing effect of GNP, which improves the overall mechanical properties of the nanocomposite.
Figure 15a illustrates the typical shear band morphology and fracture characteristics of the 20J/HDPE composites. The fracture mechanism of the 20/J/HDPE composites differs from that of the 20J/GNP/HDPE nanocomposites, as evident in
Figure 15b. This fibrillation is observed as part of the tearing process due to significant localized plastic deformation. SEM micrographs of nanocomposite materials containing 0.10 wt.% of GNP show the presence of voids and the initiation of void cracking, with polymeric fibrils stabilizing the voids [
63].
The images in
Figure 15 reveal that the GNP/HDPE matrix deforms between the fibers of the jute fabric, indicating a strong adhesion of the HDPE and GNP/HDPE matrices to the jute fabric, filling the gaps between the fabric layers. SEM analysis confirms that shear is the mechanism governing the ductile fracture in the 20J/HDPE composites, while fibrillation and crazing fracture are the mechanisms for the 20J/GNP/HDPE nanocomposites with larger diameter sizes and GNP content [
63].
For the composites in group 2, a GNP concentration of 0.10 wt.% was chosen as it optimizes the tensile properties of all the composites in group 1, while minimizing the cost increase and reducing the likelihood of agglomerate formation and internal defects. Therefore, the tensile results for the composites in group 2 with 0.10 wt.% GNP are discussed below.
Figure 16 presents the tensile strength results corresponding to the ultimate stress reached by the single and hybrid nanocomposites. It is observed that as the number of aramid layers increases, the tensile strength tends to increase, indicating a better compatibility of the HDPE matrix with synthetic aramid fibers compared to natural fibers, such as jute.
Furthermore, there is a significant difference in the contribution to tensile strength between synthetic and natural fibers, with aramid fibers being approximately five times stronger than jute fibers [
33]. Based on these results, the ANOVA was conducted to verify the significant differences with 95% confidence, and the Tukey test was used to identify the differences between composites when compared pairwise.
The results of the ANOVA indicated that the calculated F-value of 254.09 was significantly higher than the critical F-value of 3.06, indicating that the values were not equal. The Tukey test was then conducted with a value of msd = 47.41, and the results are presented in
Table 4. It can be observed from the table that all the values showed significant differences in relation to each other. Furthermore, it can be noted that as the number of layers of aramid fabric increased, the differences between the averages also increased. Specifically, when compared to the 20J/GNP/HDPE single nanocomposite, the 15J/5A/GNP/HDPE, 10J/10A/GNP/HDPE, 5J/15A/GNP/HDPE, and 20A/GNP/HDPE hybrid nanocomposites exhibited differences in tensile strength of 195%, 591%, 1411%, and 1622%, respectively.
Figure 17 presents the average values for the E of single and hybrid nanocomposites with varying layers of jute and aramid fabrics. It can be observed that nanocomposites with higher layers of jute fabric tend to have relatively constant and lower values of E compared to composites with higher layers of aramid fabric. The results of the ANOVA indicated that the calculated F-value of 6.36 was greater than the critical F-value of 3.06, with a 95% reliability. This suggests that the incorporation of aramid fibers significantly influences the increase in the value of E of the hybrid nanocomposites.
Based on the Tukey test results, with an msd equal to 501.04 as shown in
Table 5, the 20A/GNP/HDPE single nanocomposite exhibited the most significant difference compared to the other composites. Specifically, in comparison to the 20J/GNP/HDPE single nanocomposite, the 20A/GNP/HDPE single nanocomposite demonstrated an increase of nearly 40% in the modulus of elasticity, suggesting better compatibility between the synthetic fibers and the HDPE matrix. However, for nanocomposites with layers below 50% of both synthetic and natural fibers, delamination was observed at the interface between the different fibers, resulting in an E similar to that of the 20J/GNP/HDPE single nanocomposite.
Figure 18 presents the mechanical toughness modulus results of the single and hybrid nanocomposites with varying layers of synthetic and natural fibers. This parameter is determined by calculating the area under the stress versus strain curve or by using the values provided by the equipment’s data. It represents the energy required to fracture the material under applied tensile stresses in a quasi-static manner. Notably, a significant increase in energy is observed with a higher incorporation of synthetic fibers, indicating the substantial improvement in mechanical properties achieved by using synthetic fibers in the hybrid nanocomposites.
Based on the ANOVA results, the calculated F value of 133.28 is greater than the critical F value of 3.06, indicating that the averages of the mechanical toughness values are not equal with 95% reliability. Further, the Tukey test with msd = 6.77, as shown in
Table 6, reveals that all hybrid nanocomposites with 10 layers of aramid fabric exhibit significant differences in mechanical toughness, with higher numbers of aramid layers promoting higher values of toughness. This underscores the potential of using different fibers in polymer matrix hybrid nanocomposites.
However, upon closer examination of
Table 6, it can be observed that the hybrid and single nanocomposites with 15 and 20 layers, respectively, of aramid fabric show similar mechanical toughness values. This suggests that both the hybrid nanocomposites 5J/15A/GNP/HDPE and 10J/10A/GNP/HDPE may be considered the most optimized in terms of mechanical toughness.
Furthermore, the 5J/15A/GNP/HDPE hybrid nanocomposite (37.92 ± 5.33 MJ/m3) exhibited a remarkable increase of 3977% compared to the 20J/GNP/HDPE single nanocomposite (0.93 ± 0.09 MJ/m3). Notably, the 10J/10A/GNP/HDPE hybrid nanocomposite (23.56 ± 1.60 MJ/m3) showed an impressive increase of 2433% in relation to the 20J/GNP/HDPE single nanocomposite in terms of mechanical toughness.
In terms of ductility, as shown in
Figure 19, defined by the maximum deformation achieved by the single and hybrid nanocomposites, a significant increase in maximum deformation is observed with increasing layers of aramid fabrics in the hybrid nanocomposite. For instance, the 10J/10A/GNP/HDPE hybrid nanocomposite exhibited a 462% increase in maximum deformation (26.47%) compared to the 20J/GNP/HDPE single nanocomposite (4.71%). This result underscores the potential of combining synthetic and natural fibers in the thermoplastic matrix, which could lead to the production of ballistic helmets with improved cost-effectiveness and superior mechanical properties, a critical aspect in helmet design.
The ANOVA results revealed that the calculated F value of 62.68 exceeded the critical F value of 3.06, indicating that the means are not equal with 95% reliability. Further analysis using the Tukey test with an msd value of 5.13 helped to identify the treatments that showed significant differences. Upon examining
Table 7, it is evident that all nanocomposites exhibited statistically significant differences from each other, except for those with a number of aramid layers greater than 10.
In
Figure 20, the fracture mechanisms of the hybrid nanocomposites are illustrated. The fracture surface indicates notable tearing and fibrillation of the HDPE, as well as delamination of the aramid and jute fabric. The insert in
Figure 20 also reveals that the GNP/HDPE matrix remained attached to the aramid fabric post the tensile test. This observation suggests that there is a harmonious relationship between the GNP/HDPE and the synthetic fabric.
Figure 20.
Fracture surface of the hybrid nanocomposites.
Figure 20.
Fracture surface of the hybrid nanocomposites.
Table 8.
Summary of the tensile properties discussed in the present work in comparison with other works in the literature.
Table 8.
Summary of the tensile properties discussed in the present work in comparison with other works in the literature.
| | Tensile Strength (MPa) | Elastic Modulus (GPa) | Ductility (%) | Toughness (MJ/m3) | Ref. |
|---|
| 20J/HDPE | 25.53 ± 3.69 | 1.32 ± 0.73 | 4.67 ± 0.51 | 0.66 ± 0.11 | PW |
| 20J/GNP/HDPE | 24.70 ± 0.72 | 1.63 ± 0.15 | 4.71 ± 0.75 | 0.93 ± 0.09 |
| 15J/5A/GNP/HDPE | 72.77 ± 9.74 | 1.66 ± 0.22 | 14.83 ± 1.61 | 6.42 ± 0.89 |
| 10J/10A/GNP/HDPE | 170.78 ± 30.60 | 1.60 ± 0.12 | 26.47 ± 3.22 | 23.56 ± 1.60 |
| 5J/15A/GNP/HDPE | 373.26 ± 8.94 | 1.85 ± 0.27 | 23.75 ± 3.43 | 37.92 ± 5.33 |
| 20A/GNP/HDPE | 425.42 ± 45.04 | 2.25 ± 0.39 | 24.80 ± 2.82 | 38.98 ± 5.80 |
| Curaua/Epoxy | 134.67 ± 23.01 | 3.08 ± 0.55 | 7.87 ± 1.17 | 5.83 ± 1.61 | [64] |
| Curaua/0.10%GO/Epoxy | 190.20 ± 31.75 | 4.95 ± 0.47 | 6.94 ± 0.90 | 7.50 ± 1.92 | [64] |
| Curaua non-woven/Epoxy | 44.48 ± 13.11 | 3.87 ± 0.43 | 2.71 ± 0.38 | 0.66 ± 0.25 | [65] |
| 19Aramid/Epoxy | 280.21 ± 53.79 | 11.40 ± 1.93 | 3.97 ± 0.30 | 5.41 ± 1.25 | [65] |
| 2Curaua/10Aramid/Epoxy | 156.13 ± 9.93 | 7.26 ± 1.42 | 4.01 ± 0.38 | 3.16 ± 0.50 | [65] |
| 2.0%PEG/SiO2/HDPE | 27.00 ± 1.50 | 0.80 ± 0.05 | 45.00 ± 5.00 | - | [66] |
| HDPE | 17.00 ± 2.00 | 0.45 ± 0.025 | 50.00 ± 4.00 | - | [67] |
Table 8 provides a summary of the properties discussed earlier for the aforementioned single and hybrid nanocomposites, as well as for some composites reported in the literature with thermoset matrices and pure HDPE. Notably, the 20J/HDPE composite exhibited an increase of 50% in strength and 193% in the value of E compared to the pure HDPE studied by Mendes et al. [
67]. Similarly, the 20J/GNP/HDPE single nanocomposite showed significant improvements, with a 45% increase in strength and a remarkable 262% increase in the E compared to pure HDPE. Regarding the 10J/10A/GNP/HDPE, it presented an increase superior to 900% in tensile strength, as well as 256% in the E. In addition, there was a reduction of 89% in ductility when compared with pure HDPE. These results highlight the potential of using a combination of synthetic and natural fibers to enhance the mechanical properties of thermoplastic matrix hybrid nanocomposites.
3.4. Izod Impact Test
Figure 21 depicts the average Izod impact absorption capacities of the 20J/HDPE composite and 20J/GNP/HDPE single nanocomposite. One can notice that the energy absorbed by the 20J/GNP/HDPE (349.70 ± 12.03 J/m) is significantly higher than that of the 20J/HDPE (308.00 ± 17.43 J/m), representing an increase of 14% in absorbed energy. These values are comparable to those of polymer composites reinforced with other natural fibers [
55,
67,
68].
Although the degree of crystallinity decreases the absorption energy capability of the matrix, the 20J/GNP/HDPE nanocomposite presented a higher impact resistance. This phenomenon could be attributed to the size of the GNP particles, which were larger than 25 μm, and were effective in absorbing the energy from the impact.
However, when evaluating the properties of the jute/aramid/GNP/HDPE hybrid nanocomposites, significantly larger values in the energy absorbed upon Izod impact is observed, as evidenced by
Figure 22. The ANOVA reveals that the calculated F value of 18.66 exceeds the critical F value of 3.06, indicating that the mean values are significantly different with a 95% confidence level. Hence, Tukey’s test was employed to identify the groups that exhibit significant differences in absorbed energy values.
As per the Tukey test, in
Table 9, with an msd of 91.88, all hybrid nanocomposites exhibited a significant difference compared to the 20J/HDPE composite. Notably, the 10J/10A/GNP/HDPE hybrid nanocomposite demonstrated the highest value of absorbed energy at 583.52 ± 48.59 J/m, as indicated in
Table 10 and
Figure 22. This represents a substantial increase of 89% compared to the 20J/HDPE composite, and a 20% increase compared to the 20A/HDPE composite.
The absorbed energy value of the 10J/10A/GNP/HDPE hybrid nanocomposite surpasses that of several other polymeric composites reported in the literature,
Table 10. Thus, with an increase in the number of aramid fabric layers, the absorbed energy upon Izod impact decreases after reaching 10 layers. This phenomenon is related to the fracture behavior of the composites, where at lower concentrations of aramid fibers, more fractures occur in the natural fibers and the HDPE matrix. On the other hand, with a higher aramid concentration, fewer fractures in the reinforcement are observed, resulting in lower energy absorption [
64]. This mechanism is supported by electron microscopy analysis of the specimens after the Izod impact test, shown in
Figure 23.
The fracture mechanism of the hybrid nanocomposites with both natural and synthetic fibers, as shown in
Figure 23, reveals more delamination and less fiber rupture, particularly in the aramid fibers. Additionally, defibrillation of the aramid fibers and a complete rupture of the jute fibers can be observed.