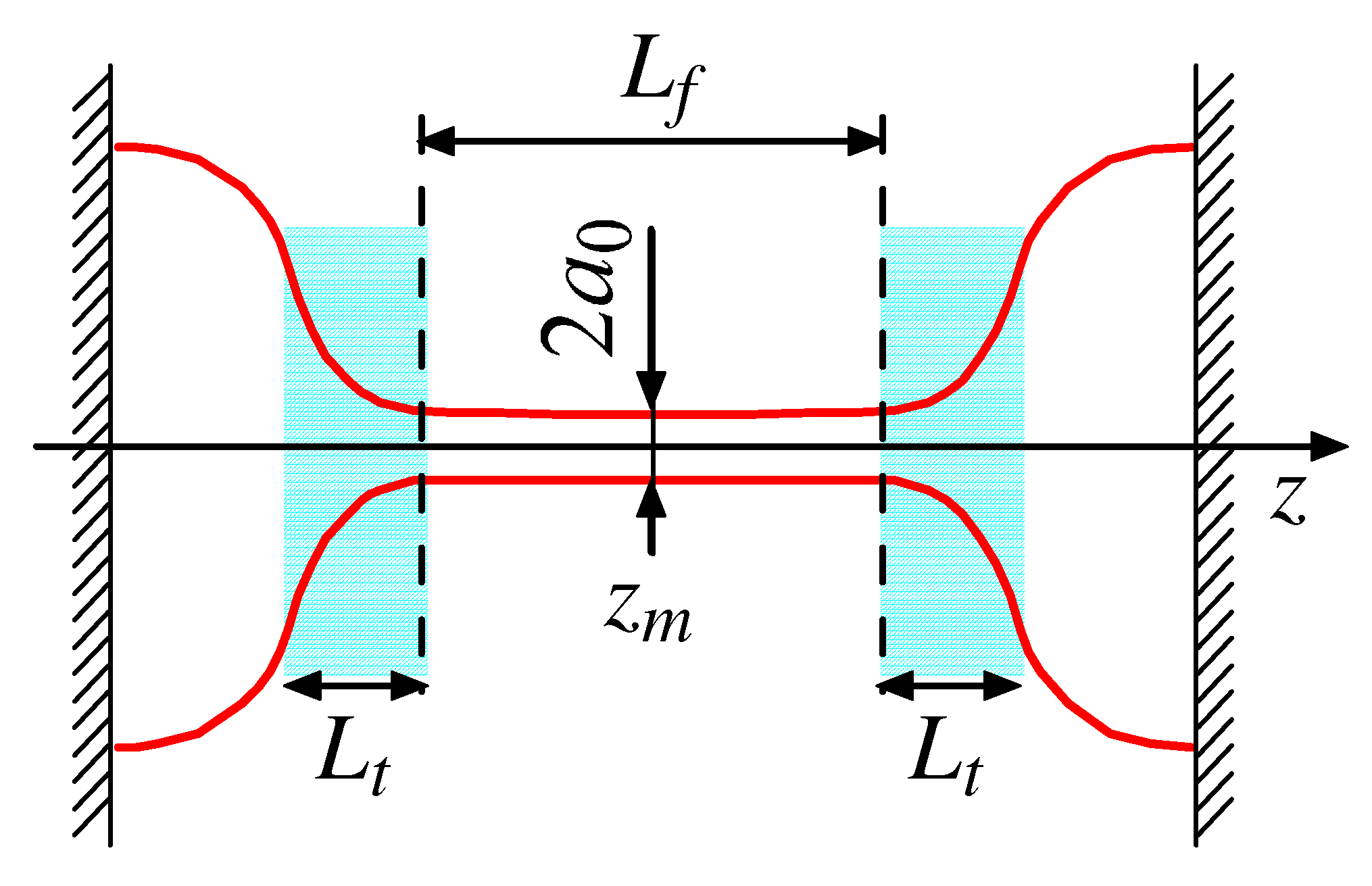
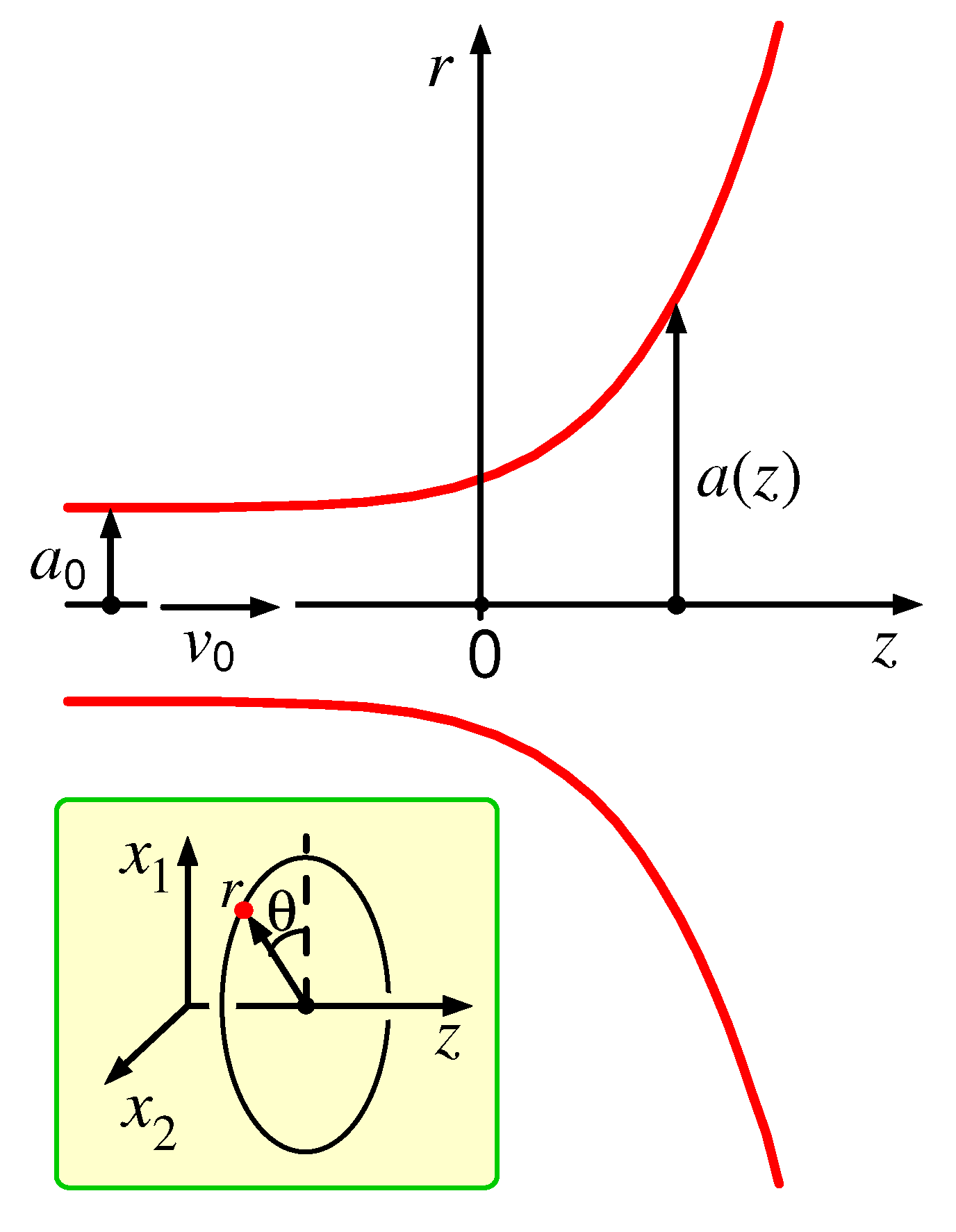
2. Capillary Thinning for the Oldroyd-B Model
Let us consider the typical setup: a thinning filament between two immobile semi-spherical droplets (
Figure 1). The liquid is an unentangled polymer solution. The filament length
is much larger than its radius
, which slowly decreases over time. This process is driven by capillary forces. It is slow due to the capillary-induced extension of polymer chains (upon the coil–stretch transition) leading to a dramatic increase in the solution viscosity [
14]. Five zones can be distinguished in
Figure 1: two end-droplets adjacent to solid plates, a nearly cylindrical filament of length
in the middle, and two transitions zones of length
(shown in cyan). The whole liquid bridge is assumed to be axially symmetric (around the
z-axis).
The filament is typically thin, long, and nearly uniform during the polymer extension process [
6]:
where
is the thickness in the middle of the thread
;
in the filament region. As the liquid is incompressible, the uniaxial extension rate in the thread is defined by the thinning rate (note that
in Equation (
3) is the (negative) extension rate in the radial direction, and that (by virtue of the incompressibility)
):
so the axial flow velocity is:
in the filament region of length
. Outside this region, the liquid cross-section increases rapidly, leading (by virtue of the incompressibility) to a decrease of
. Thus, the velocity maximum,
, is reached near the filament ends.
Let us turn to the force balance in the transition zones next to the filament ends where the surface shape deviates from a perfect cylinder and its radius shows a significant
z-dependence. The transition region between the thread and the second droplet is depicted in
Figure 2. (Note that the origin,
, is located near the righthand end of the thread. We define the point
by the condition
, where the factor
can be chosen as convenient; here it was set
.) As argued below, the axial size,
, of this region (where the droplet surface significantly deviates from both cylindrical and spherical) is relatively small,
.
To describe the flow and the free surface shape, we can benefit from two approximations. First, we neglect the inertial effects assuming that the ‘inertial pressure’ ∼
is much lower than the capillary pressure
(here,
is density and
is the surface tension of the liquid):
This is a natural condition since a uniform filament is not stable if inertial effects are significant [
3]. Second, we assume that polymer stress
) dominates over the viscous stress of the solvent:
. Again, this condition is obvious well inside the thread (as, otherwise, the polymer effect would be rheologically negligible, and the liquid would be equivalent to the Newtonian solvent there); however, it must be
assumed for the transition region. This assumption is justified if the capillary number
(defined in Equation (
71)) is small, as discussed in item 5 of
Section 4 (see text around Equation (
71)). It is also assumed that the liquid is incompressible:
where
is the velocity field.
The master dynamical equation is then reduced simply to the force balance:
where
are Cartesian components,
is the total stress tensor at the point
,
, and
is a derivative of a variable
Y along the coordinate
. It involves two contributions due to the pressure field (
)) and the extra polymer stress:
The polymer stress tensor is [
15]:
where
is the elastic free energy of a polymer chain with end-to-end vector
. Angular brackets here mean the statistical average,
c is the concentration of polymer segments (repeat units), and
N is their number in one chain (a monodisperse polymer is considered in the present paper). For polymer liquids in marginal or theta-solvent conditions [
16,
17] (and for concentrated polymer solutions) a Gaussian chain model is applicable during the coil–stretch transition when the chains are far from their full extension,
(here,
L is the chain contour length), so the elastic energy is [
15]:
where
T is temperature in energy units,
is the unperturbed coil size
is the polymer statistical segment,
is its Kuhn segment). Hence, recalling Equation (
8), we obtain:
where we took into account that all the chains in a fluid element are strongly stretched along the same axis (defined by some unit vector
), so that the end-to-end vector
of most chains is nearly parallel to
, and therefore,
, where
, and
is the root-mean-square (rms) of the end-to-end distance. For the sake of simplicity, in what follows, we omit the ‘bar’ over
and
R. (Thus, from now on,
R is simply the rms end-to-end distance of polymer chains, which is widely used in polymer physics.) Note that we consider the regime of significant chain extension,
, since, otherwise,
would be comparable with the ideal gas pressure of polymer molecules, which is low for long chains. Note also that
in Equation (
10) is the mean end-to-end vector which generally depends on the chain position
and time
t. (More precisely,
is the position of the chain center-of-mass. In all the cases, we assume that the fields such as
or
do not change much on the polymer length-scale
. This condition is satisfied if
.)
Obviously, well inside the thread, polymer chains must be stretched along its main axis
):
,
, where
is
(rms of polymer end-to-end distance) in the thread; thus, the only relevant component of the polymer elastic stress tensor is:
(other components being subdominant).
The model described above is virtually equivalent to the Oldroyd-B dumbbell model, as the polymer conformation is defined solely by the end-to-end vector
, and the polymer stress is quadratic in
. Using this model, it was established that the thinning of a polymer thread in the viscoelastic regime
) is quasi-exponential [
1,
8]:
where
is the stress relaxation time
, where
is the longest relaxation time of a polymer coil), and
t is the time passed since the beginning of coil stretching.
Equation (
12) (which is applicable in the transient regime during the polymer stretching stage) implies that the thinning rate
(cf. Equation (
3)) is constant,
. However, strictly speaking, the flow in the thread is not steady, as its radius
is decreasing. Nevertheless, the flow in the entrance region (the ‘corner flow’) can be considered at a different angle: The characteristic thinning time is
. Comparing it with the characteristic entering time
, we see that
, so:
This means that the entrance flow (at the interface between the thread and a large droplet) is
quasi-stationary to a good accuracy, since the ratio
is typically small in experiments,
[
3,
6,
7,
18]. Let us emphasize again that it is assumed here, following the previous theoretical studies [
1,
7,
8,
11,
12], that the thread is perfectly cylindrical, the flow velocity in the thread is parallel to the main axis
), and the chains are stretched along it. The force balance (cf. Equations (
6) and (
7)) in such a geometry demands that the pressure
p is constant (independent of both radial and axial coordinates),
, and that the polymeric stress
is
z-independent. In
Section 3, we show that well inside the thread, the stress
is also constant in the radial direction (cf. text below Equation (
56)). Note that, in contrast,
does depend on both
z and
r in the transition regions.
Since the entrance flow (see
Figure 2) can be considered as steady, its time dependence can be neglected at the relevant time scale
. The formal boundary conditions on the free liquid surface, defined by
, are: the surface must tend to a tube of radius
at
(here and below,
means that
and
), and to a sphere of large radius (which can be approximated by a flat plane) at
. (Note that we use cylindrical coordinates
,
, as shown in
Figure 2.) In the limit of no inertia, the equation of motion is reduced to the local force balance, which can be written as (see Equations (
6), (
7), and (
10)). (Most equations below are approximate, just like Equation (
10). However, the ‘=’ sign is used there for simplicity, except where it is important to emphasize their approximate nature.)
The pressure at the free surface is defined by its curvature
C:
where
and
p is the excess pressure on the top of atmospheric pressure. The flow is therefore defined by an interplay of capillary and viscoelastic effects.
The basic Equations (
5) and (
14) involve two unknown fields: polymer extension,
, and velocity
. However, in the entrance zone, these fields can be easily related to each other. The idea is that the polymer chains must be extended along the stationary streamlines, and their fragments (blobs) must simply follow the stream (i.e., a blob at point
moves with the velocity
). In fact, the relative motions of the blobs due to elastic forces can be neglected as being too slow since the relevant polymer relaxation time
) is much longer than
(see Equation (
13)). As a result, the chain extension vector
stays nearly proportional to the flow velocity
for kinematic reasons:
For a steady flow, the above equation follows from the kinematic equations
,
(cf. Equation (
80) with
), which ensure that if
at some point (which is the case for
,
), the latter equation must stay valid (with
) along the whole streamline in the transition region where the rate
can be neglected. Here,
means the full rate of change ‘following the fluid’ for a material element.
Of note, Equation (
17) remains valid in the
extended transition region, including the adjacent end part of the thread at
,
where
. The condition
ensures that the transition time (along the whole transition region including the
-part) is much shorter than the polymer relaxation time
, so that the polymer relaxation process can be neglected in the
-part. On the other hand, the condition
is sufficient to state that at
the thread is nearly perfectly cylindrical, so at
its radius is
, the rms chain extension is
and the flow velocity is
also being uniform in the cross-section. Then, applying Equation (
17) at
we obtain
and therefore
B is the same for all the streamlines. Equations (
10) and (
17) obviously agree with the convected Jeffreys (or Oldroyd-B) models with infinite relaxation time [
14] (cf. item 11 of the Discussion).
The force balance Equation (
14) then becomes:
where
and we took into account the flow incompressibility from Equation (
5). Equations (
18) and (
5), together with the boundary conditions in Equation (
15), an obvious condition
at the free surface (where
is the flow velocity component normal to the surface), and
completely define the flow, the pressure field, and the shape of the free surface in the entrance zone. (Recall that
physically means that
,
; in a similar fashion,
means
. Note also that we consider the limit of a very large droplet, so the excess pressure deeply inside it must tend to 0.) Obviously, Equations (
15) and (
16) also imply that:
There is only one essential non-dimensional parameter in the problem: the ratio
of polymer stress
to the capillary pressure well inside the filament,
. It was set to
in ref. [
8], while
was derived in ref. [
12]. (Note that the quantity
was denoted
X in ref. [
5];
was defined there as the ratio of the net tensile force in the thread to
. As follows from Table I of ref. [
5], the parameter
is as important as
itself for Newtonian liquids considered there. This parameter
) is even more important for polymer liquids as it highlights a relation between the main quantities of interest, the polymer stress
, and the capillary pressure
.) Below, we show that
X can be easily obtained based on the equations considered above. To this end, let us first analyze the pressure
p variation along a streamline. Equation (
18) gives (with
and the coordinate
u equal to the curvilinear distance along the streamline):
leading to
; hence,
This equation is applicable in the entrance zone, where the velocity is changing fast along streamlines. It connects the local pressure and velocity just like the Bernoulli’s principle does for an ideal fluid. We shall refer to Equation (
23) as the anti-Bernoulli law (due to the ‘minus’ sign leading to a higher pressure for a faster flow). The
in Equation (
23) can be easily found for the flow of
Figure 2: Recall that each streamline is coming from the uniform thread, where both
p and
are constant over a cross-section. Therefore,
in the whole entrance zone
). Note that Equations (
24) and (
23) are valid if the Newtonian solvent friction is negligible as assumed below Equation (
4) and as discussed in item 5 of the Discussion section (cf. Equation (
71)). The rhs in the above equation equals 0 since both
p and
must vanish deeply in the droplet region at
(cf. Equation (
20)). Thus, Equations (
20), (
21), and (
24) imply that
and we obtain
in the thread using Equations (
11) and (
19):
Hence, the parameter
X introduced below Equation (
21) is:
The total thread tension force
(defining the total momentum flux through its cross-section) is therefore:
The two terms in the middle of the above equation represent the surface and the internal axial stress contributions to the total tension
. Equations (
27) and (
28) agree with the results of ref. [
12].
It is worthwhile to note that Equations (
17)–(
24) are valid for a virtually arbitrary flow geometry (involving a long channel as a part of it). Using Equations (
18) and (
24), we obtain:
Let us now take into account that, typically, the experimental setup is such that both the free surface and the flow are axisymmetric. This symmetry is already implied in Equation (
15). For the flow velocity, it means that its axial and radial components
and
) do not depend on the polar angle
, while the polar velocity component
must vanish (here, we use cylindrical coordinates
, cf.
Figure 2):
The factor in brackets in Equation (
29) is related to the vorticity
where
is the Levi-Civita symbol. Therefore, Equation (
29) is equivalent to:
For an axisymmetric flow,
is always parallel to the azimuthal direction
); hence,
and
are orthogonal. Equation (
32) then gives
, so:
everywhere except at the stagnation points (where
), which are not expected in the entrance zone. Therefore, the flow is irrotational:
where
is a potential field which must satisfy the Laplace equation (in view of Equation (
5)):
Furthermore, on using Equations (
24) and (
25), the boundary condition, Equation (
15), transforms to:
while another condition at the free surface
simply says that the boundary curve
must be a streamline with
at
(obviously, the axisymmetric problem is essentially two-dimensional, so we can set
and
without loss of generality).
Further statements, which can facilitate numerical solution of the above equations for the velocity field
, can be proven in an elementary way. At large
, the flow is asymptotically similar to the electrostatic field of an electric charge:
where
is the position vector,
is the distance from the origin, and
Q is obtained based on the incoming volume flow rate, which is equal to
. Equation (
37) implies that at
, the pressure decreases as:
The pressure therefore becomes negligible in the droplet far from the entrance point, so the droplet shape there must be close to the static shape defined solely by the Laplace pressure. It leads to the condition of constant mean curvature,
, in the case of large droplet, so [
4]:
where
. The above equation is consistent with Equation (3).18 of ref. [
12].
Next, let us note that the structures of Equations (
35) and (
36) are such that a simple rescaling
,
, and
makes the problem free of any parameters (in other words, the solution is self-similar). It is therefore enough to solve the above equations for
,
and
. The unique rescaled flow field and the free surface curve
can be found numerically in two steps: (1) by setting a trial
and then solving the Laplace Equation (
35) in the region
,
, and
(see
Figure 2) with Neumann boundary conditions:
at the free surface
),
in the filament cross-section at
, and
at the hemisphere
inside the droplet (here
is unit vector normal to the surface); (2) by adjusting
iteratively so as to satisfy the anti-Bernoulli equation
at
.
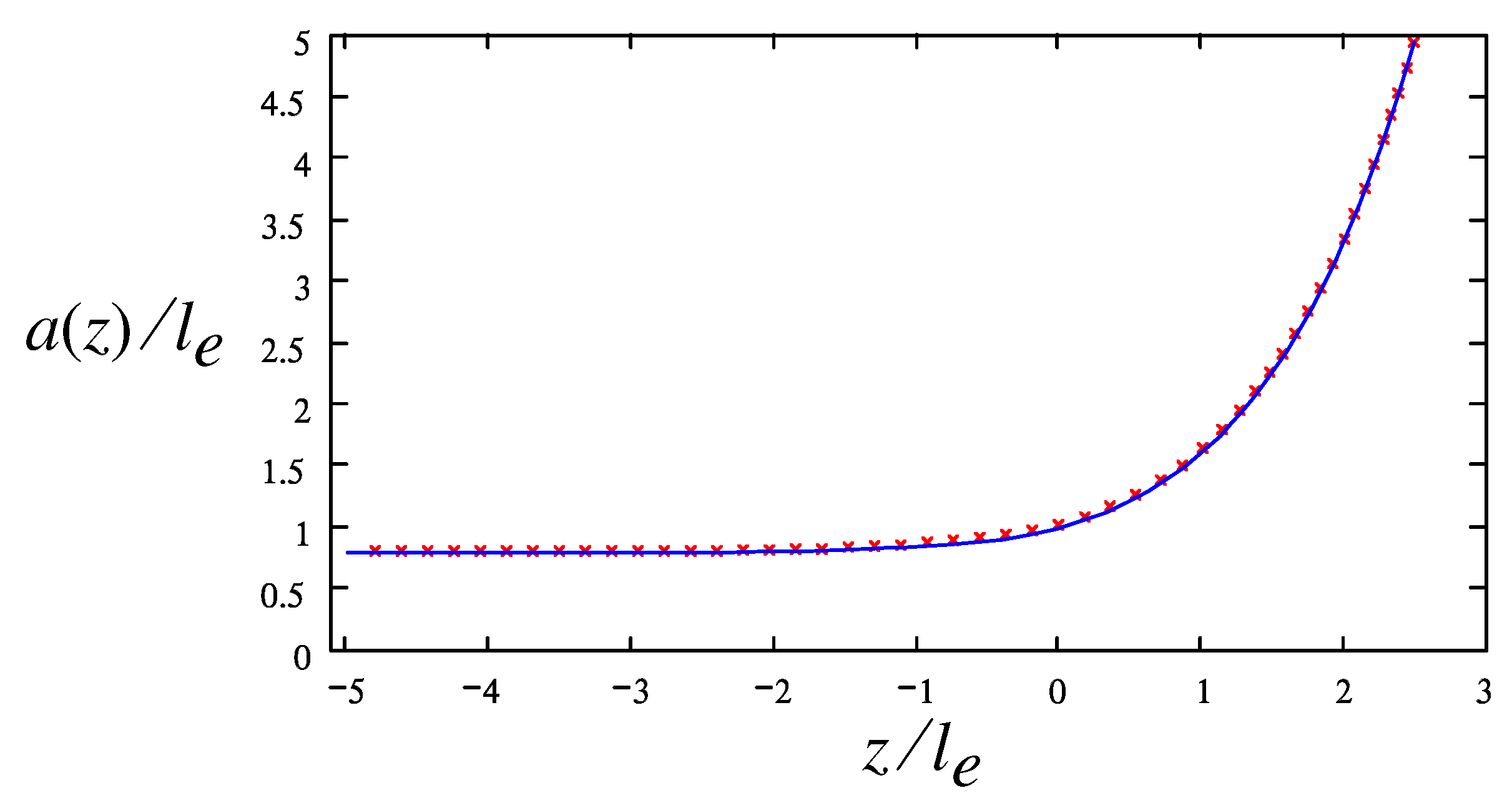
The resultant thread shape and streamlines in the entrance zone (obtained for
and
taken to obtain a well-converged solution to an accuracy of ∼
) are shown in
Figure 3. In the thread region,
, the free surface tends to a cylindrical shape in an exponential fashion:
where
. (The constant
is the lowest root of the characteristic equation
, which comes from the main correction to the potential field
at
:
, where
corresponds to a perfectly uniform flow. Here
are Bessel functions.)
The asymptotic behavior in the opposite regime,
, can be deduced from the force balance, which says that the total momentum flux in the cylindrical part (the thread tension
, cf. Equation (
28)) must be equal to the momentum flux,
, across a hemisphere
,
. The contribution of both polymer stress and pressure to
can be neglected since they rapidly tend to zero at large
:
(cf. Equation (
38)); hence,
at
. Therefore,
at
is defined solely by the surface tension
:
The equation
leads to
This asymptotic behavior was predicted [
12] using a similar argument. However, the point that the polymer stress can be neglected in the droplet region was not proven there. Of note, the numerical solution for
shown in
Figure 3 is in harmony with the asymptotic laws, Equations (
40) and (
42).
4. Discussion
1. In the present paper, we investigated the dynamics of a viscoelastic liquid bridge (a cylindrical ligament) connecting two large droplets (see
Figure 1). Its thinning is governed by capillary and viscoelastic forces and is coupled to the flow both in the ligament and in the transition zone between the thread and a droplet (see
Figure 2). As a fluid, we consider an unentangled polymer solution whose rheology can be described by either the Oldroyd-B or the FENE-P dumbbell models. The developed theory is focused on the regime of strongly stretched polymers whose conformational tensor
is dominated by a single eigenvalue (here,
is the end-to-end vector of a polymer chain). The models we used assume that the stress tensor contribution of a polymer chain is defined by the vector
and therefore is proportional to
. The prefactor in such a relation is either constant (cf. Equation (
10) for Oldroyd-B model) or depends on the degree of chain stretching
(for the FENE-P model). Both models ignore hydrodynamic interactions (HDI) in the system (see point 9 below).
As one of the main results, we have shown that for the Oldroyd-B model, the capillary-driven flow is nearly irrotational and satisfies the Laplace equation. In addition, we have established a general relation between the pressure and velocity fields (valid for a broad class of polymer flows) which is referred to as the anti-Bernoulli law (cf. Equation (
23); an equivalent static conservation law was derived for a neo-Hookean elastic solid [
12]). Using these results, we obtained a self-similar solution (involving a single length-scale, the radius
of the thread) for the shape of the free surface and for the pressure and velocity fields. In cylindrical coordinates
), the free surface is given by
. The numerically obtained free surface profile
for
and the corresponding flow structure are shown in
Figure 3. The calculated
is compared in
Figure 8 with the similarity solution for the bead-string structure of a neo-Hookean elastic body obtained in ref. [
12]. (Note that
was taken as a unit length in ref. [
12], so the data have been rescaled accordingly.) The obvious good agreement supports the conclusion of refs. [
12,
13] that (as conjectured earlier in refs. [
22,
23]) the neo-Hookean model asymptotically reproduces the geometry of a polymer liquid bridge formed in the course of its capillary thinning (according to the Oldroyd-B constitutive equation) in the regime of sufficiently long polymer relaxation time
. Of note, it was recently shown that the universal interfacial shapes obtained in ref. [
12] (and, therefore, the theoretical profile of
Figure 3 and
Figure 8) are in agreement with high-resolution experimental data on aqueous solutions of high-molecular-weight polymers (PEO) and biopolymers (hyaluronic acid) [
24,
25].
2. The conservation (anti-Bernoulli) law defining pressure in terms of the flow field (cf. Equation (
24)) was obtained here based on the steady-flow dynamical equations (Equations (
6) and (
17)). Of note, in the form of Equation (
56),
, this law is akin to the conservation law established for neo-Hookean solids [
12]. The main difference is that Equation (
56) is more general: it also accounts for non-linear elastic effects related to the finite extensibility of polymer chains.
3. To quantitatively establish the thinning kinetics,
, one needs a ‘closure’ relation between the pressure
and the axial polymer stress
in the thread. This relation cannot be obtained by considering a cylindrical thread as such. Long ago, Entov and Hinch [
8] assumed that the total axial stress in the thread
) must be equal to that in the droplet, i.e., to zero (if atmospheric pressure is subtracted from
):
. It is found here that the rigorous anti-Bernoulli law, Equation (
24), demands a different relation,
, in agreement with more recent predictions for the Oldroyd-B model [
7,
11,
12]. It is remarkable that a generalization of the anti-Bernoulli law for polymer chains with finite extensibility, Equation (
57), leads to a variable ratio
which depends on the degree of polymer extension
. While for
we obtain
, this ratio decreases with
s (see
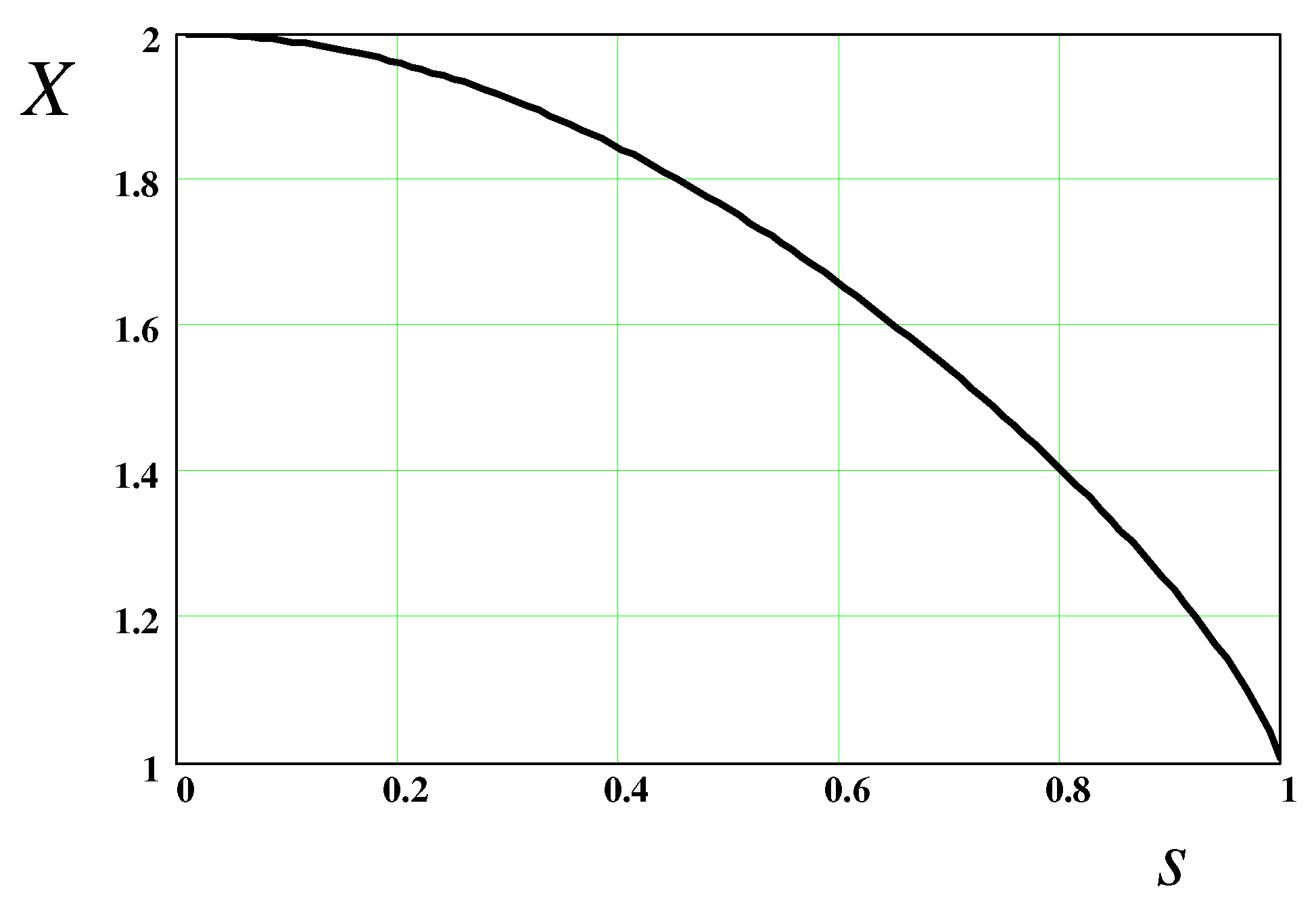
Figure 5), reaching its minimum,
, in the regime of completely stretched chains,
. Incidentally, it is the latter ratio that was assumed in ref. [
8].
It may seem that the model of a nearly uniform thread cannot be used for
s close to 1 since in this regime of highly extended chains the liquid behaves nearly as a Newtonian fluid with renormalized viscosity [
4,
26,
27,
28]
, where
) is a hydrodynamic factor [
29] and
is volume fraction of polymer. Thus, the classical Plateau–Rayleigh instability (undulations of the thread shape) must emerge in this regime (at
s close to 1,
), so that the uniform thread approximation seems to fail. The point, however, is that: (i) Before the instability (at
), the undulations are weak, and their amplitude (in radial direction) due to thermal fluctuations is
. (Here we make a plausible assumption that the amplitude of thermal fluctuations of the radius in the dynamically stable thread are comparable to that for a statically stable liquid cylinder of the same diameter.) Therefore,
, since, typically,
, while
. (ii) The growth rate of their amplitude (coming from the Rayleigh theory [
30]) is
, so it is comparable with the thread
thinning rate, [
4,
5]
. Therefore, as the thread thins by a factor of
k, the undulations grow by the same factor, so the thread radius
a becomes comparable with the undulation amplitude
for
. Considering
as a function of
s, we find, according to the theory of
Section 3.3 that
for
, that is,
. The above argument therefore shows that the thread undulations remain small (
) if
. Hence, the theory of
Section 3.3 is actually applicable in the regime where the chain extension degree
s is close to the maximum (=1): this is true in the region
since
. In this regime, the ratio
X indeed becomes very close to 1, as stated in the previous paragraph.
4. The developed theory was applied to obtain the thread thinning dynamics for the FENE-P model. While this problem was treated already in ref. [
8], it is treated here for the first time in a rigorous way. The numerically obtained thinning law,
(see
Figure 7) includes both the elasto-capillary (exponential thinning) and the terminal stage (quasi-linear thinning). It is based on the asymptotically exact dependence of the ratio
on the degree of chain stretching established in
Section 3 (see also point 3 above).
The predicted thinning law is universal (up to arbitrary horizontal and vertical shifts) when plotted in semilog scale vs.
. The theory is compared with experimental data on semidilute, unentangled polymer solutions (cf.
Figure 5 of ref. [
18]) in
Figure 9, where
for the theoretical curves is set to be the putative breakup point
. One can observe a good agreement down to the crossover regime; however, at later times (on the right to a red circle), the experimental curve deviates from the prediction. We attribute this discrepancy to a new regime most probably associated with the blistering (pearling) instability [
2,
31], which is normally accompanied by the polymer/solvent phase separation and formation of secondary solvent droplets (which can be both flow- and capillary-induced [
28,
29,
32,
33,
34]). Interestingly, according to
Figure 9, this transition occurs where the chains are not yet fully stretched, at
, corresponding to
.
5. Considering the thinning of a cylindrical polymer thread, we assumed that the pressure
p there is constant in the radial direction (i.e., it is homogeneous in a cross-section). This assumption was adopted in the previous theoretical studies on capillary thinning [
1,
7,
8,
11,
12]. In the case of negligible inertia, it simply follows from the force balance in the cylindrical geometry since the flow velocity
is parallel to the main axis, and so is the elastic force due to stretched polymer chains. In addition, however, the theory developed in
Section 2 and
Section 3 implies that the axial polymer stress
is also uniform (independent of
r) in the thread. For the Oldroyd-B model, this condition is justified in the limit of vanishing solvent viscosity as follows: First, it is straightforward to show that the argument (cf.
Section 2) leading to the anti-Bernoulli law, Equation (
24), is generally valid in the form:
(where
is the polymer stress component along the streamline). Obviously, in the thread,
and (as argued above)
. Therefore, Equation (
70) implies that
is also constant
-independent) there. The conjecture that for negligible solvent viscosity the stress profile in the thread is uniform [
12] is thus rigorously proved using a dynamical approach. (Of note, it was also established [
12] that the radial distribution of the axial stress is uniform for a soft neo-Hookean elastic solid. Hence, here, again, we confirm the correspondence between viscoelastic and elastic models [
13].) In
Section 3.2, we show that this statement is also valid for the models with finite chain extensibility.
Numerical studies of the Oldroyd-B model with a finite Newtonian solvent viscosity
[
12] reveal a weak radial dependence of
, which was attributed to an effect of
. We tend to agree with this interpretation. The effect of
(which was neglected in the present study) is unimportant as long as
, which is true everywhere (including the entrance region) if a capillary number is small:
The above condition was adopted in the previous sections. Note that for any
, this number
) can be made however small, provided that the polymer time
is sufficiently long. For a finite
, the polymer stress
in the thread may vary along the radius. We expect that (at least for a small
) a maximal relative variation of
in the radial direction should be defined by
. It may also be worth mentioning that an increase in the solvent’s viscosity does not necessarily lead to a higher
since the ratio
depends mainly on the polymer molecular weight rather than on
(note that
is nearly proportional to
if polymer volume fraction is low [
15,
35]).
6. It is well-known [
7,
11,
12,
36] that the elasto-capillary thread thinning (according to an exponential law, Equation (
12)) is preceded by a fast initial process of the thread formation, which is primarily governed by capillary and inertial forces. In a typical scenario, a cylinder of initial radius
and length
undergoes the Plateau instability. A thread of radius
is formed as a result of this process [
7,
11,
12,
36]. The characteristic time of this initial stage is inertial in nature,
. In the inertial regime,
also defines the period of oscillations of the emerging semi-droplets (connected by the thread). Their damping rate is proportional to the solvent viscosity
defining the dissipation rate, so the damping time is
. (Note that
as long as
, which literally means that initially the system falls in the inertial regime.) This time must not exceed
(since, otherwise, the thread thinning would be strongly perturbed by droplet oscillations). Hence, we have to demand that
This condition is compatible with Equation (
71) if
which simply means that
. Note that the condition (
73) also ensures that inertial effects are negligible in the thread:
, as was assumed in
Section 2 (cf. Equation (
4)). Thus, Equations (
71) and (
72) define the range of allowed
:
(Here, we assumed that the filament length is comparable with
,
, which was the case in the previous numerical studies [
7,
12,
23].) Obviously the conditions of Equation (
74) are always satisfied for a sufficiently long polymer relaxation time
.
7. The fluid dynamics considered here are dominated by the longitudinal polymer stress
(along a streamline). This property is quite natural in the regime of strongly stretched polymer chains, when the polymer chain end-to-end distance
R is much larger than the equilibrium coil size
,
. In fact, it was implicitly assumed that polymer chains are strongly stretched during an initial fast inertio-capillary stage of polymer thread development [
36], i.e., before the elasto-capillary regime of the thread thinning considered in this paper. Such initial process leads to a uniaxial polymer stress field, cf. Equation (
10), both in the thread (of radius
) and in the droplet/thread transition region of size
. However, the applicability of this approximation in the droplet at large distances from the transition region,
, may be questioned. Indeed,
(cf. Equations (
17) and (
37)) strongly decreases there with the distance
, so the chains become less stretched in the radial direction (along the streamline), and, more importantly, they become expanded in the lateral directions: the lateral size
grows as
. It leads to an emergence of the lateral stress
. The stress growth stops as soon as the travel time
for a fluid element to reach the distance
from the origin becomes comparable with the stress relaxation time
. Using Equation (
37) with
, we obtain
, so that
is reached at
. The maximum lateral stress is, therefore,
. This stress should lead to an additional curvature
of the free surface, which can be neglected if
, leading to the condition:
Here,
is nearly equivalent to the elasto-capillary number introduced in refs. [
7,
12] (with
). It is noteworthy that the same condition,
, also ensures that the chains are strongly stretched during the initial inertio-capillary process:
,
(cf. refs. [
7,
12]).
8. To sum up the previous two points, there are three main conditions of validity of the theory: Equations (
71), (
74), and (
75). It is noteworthy that Equations (
71) and (
75) are similar and are actually equivalent in the dilute/semidilute transition regime since the polymer contribution
to the total viscosity is
(for the Oldroyd-B model) and
at
, where
is the coil overlap concentration. Furthermore, in the semidilute regime
), Equation (
71) follows from Equation (
75).
9. In the present study, we totally neglected the hydrodynamic interactions (HDI), which are not incorporated either in the Oldroyd-B or FENE-P models. Such a simplification, which was also adopted in the previous theoretical works on the subject [
1,
7,
8,
11,
12,
37], may be appropriate in the semidilute or concentrated solution regime
). The effects related to topological constraints (entanglements between polymer chains) [
38] are disregarded here as well, so the region of applicability should be formally restricted to the unentangled polymer regime. It is worth noting, however, that both models employed here seem to also work well for dilute polymer solutions, at least as far as the capillary thinning kinetics are concerned [
8,
28,
32,
39]. Moreover, the main effect of the HDI is to modify the polymer relaxation time, which is completely irrelevant in the entrance zone with high deformation rate. Therefore, the approach to describe the flow in such zones (cf.
Section 2 and
Section 3.2) also remains valid for dilute polymer solutions.
10. In this paper, we ignored any effects of polymer/solvent separation assuming that polymer concentration
. It is well-known that an inhomogeneous polymer distribution in a solution may be generated by a flow, for example, due to the stress–concentration coupling (SCC) effect [
32,
40,
41,
42]. This effect is not relevant for the cylindrical thread where the stress is uniform, so the concentration is uniform as well. Moreover, while in principle, the SCC effect is present in the entrance zone, it is very weak there: in fact, we argued (cf.
Section 2) that polymer chains are extended along the streamlines which are curved in the entrance zone. This curvature generally leads to a net elastic force perpendicular to the streamline,
, acting on an internal part of the chain,
, where
R is the chain length,
is the typical streamline curvature, and
is the elastic tension of the chain (cf. Equation (
9)). The force,
, leads to the perpendicular velocity,
, of the chain relative to the solvent,
. The typical time the chain spends in the entrance zone is
, so its typical lateral displacement is
. The relative concentration change due to this displacement is
, where we recalled that
. Taking also into account that
, we find that
, so the SCC effect is indeed negligible and
in the system we considered.
11. The polymer stress tensor defined in Equation (
8), with the conditions specified before Equation (
10), can be written as:
Its rate-of-change prescribed by the Oldroyd-B model can be expressed in terms of the upper convective derivative:
as
(here,
is the full rate-of-change referred to a moving physical element of the fluid). The above equation is equivalent to the standard Oldroyd-B equation (see, e.g., Equation (2.2) in ref. [
12]). (Note that
here is the full polymer stress, while the polymer stress
in the standard Oldroyd-B model does not include the isotropic equilibrium polymer stress contribution
, so
.)
To further simplify the equations, we took into account that, in the thread (and, in particular, near its mid-point), all the chains are strongly stretched in a similar way along the filament axis
-axis). Therefore, the polymer stress tensor there must be dominated by a single eigenvalue corresponding to an eigenvector
parallel to this axis, as argued around Equation (
10):
The prefactor in the above equation is such that it makes sure that
is equal to the root-mean-square (rms) end-to-end distance of polymer chains in a fluid element. Equations (
77) and (
78) then ensure that if Equation (
79) is valid at some point (note that Equations (
76) and (
79) together are equivalent to Equation (
10)), it will be also valid at all the points downstream (as long as the polymer chains remain strongly stretched in a single direction), with vector
changing according to
where
. To derive Equation (
80), we neglected the second term in the rhs of Equation (
78): this term is small because
since the polymer (the dumbbell) is strongly stretched.
In the case of a steady flow, it is enough to know that Equation (
10) is applicable in a cross-section of the thread: then, it must also be valid in the whole volume downstream (as long as the eigenvalue of the tensor
associated with the eigenvector
remains strongly dominating). Note also that (again for a steady flow) the full rate of change of velocity is:
Interestingly, Equations (
80) and (
81) show that if
at some point at
, the two vectors remain parallel at all points downstream (along the streamline which includes the initial point):
with
. The validity of this statement can be demonstrated simply by substitution of the solution,
, in Equation (
80) to make sure that this equation is satisfied using Equation (
81).