Liquid Fraction Effect on Foam Flow through a Local Obstacle
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Procedure and Data Processing
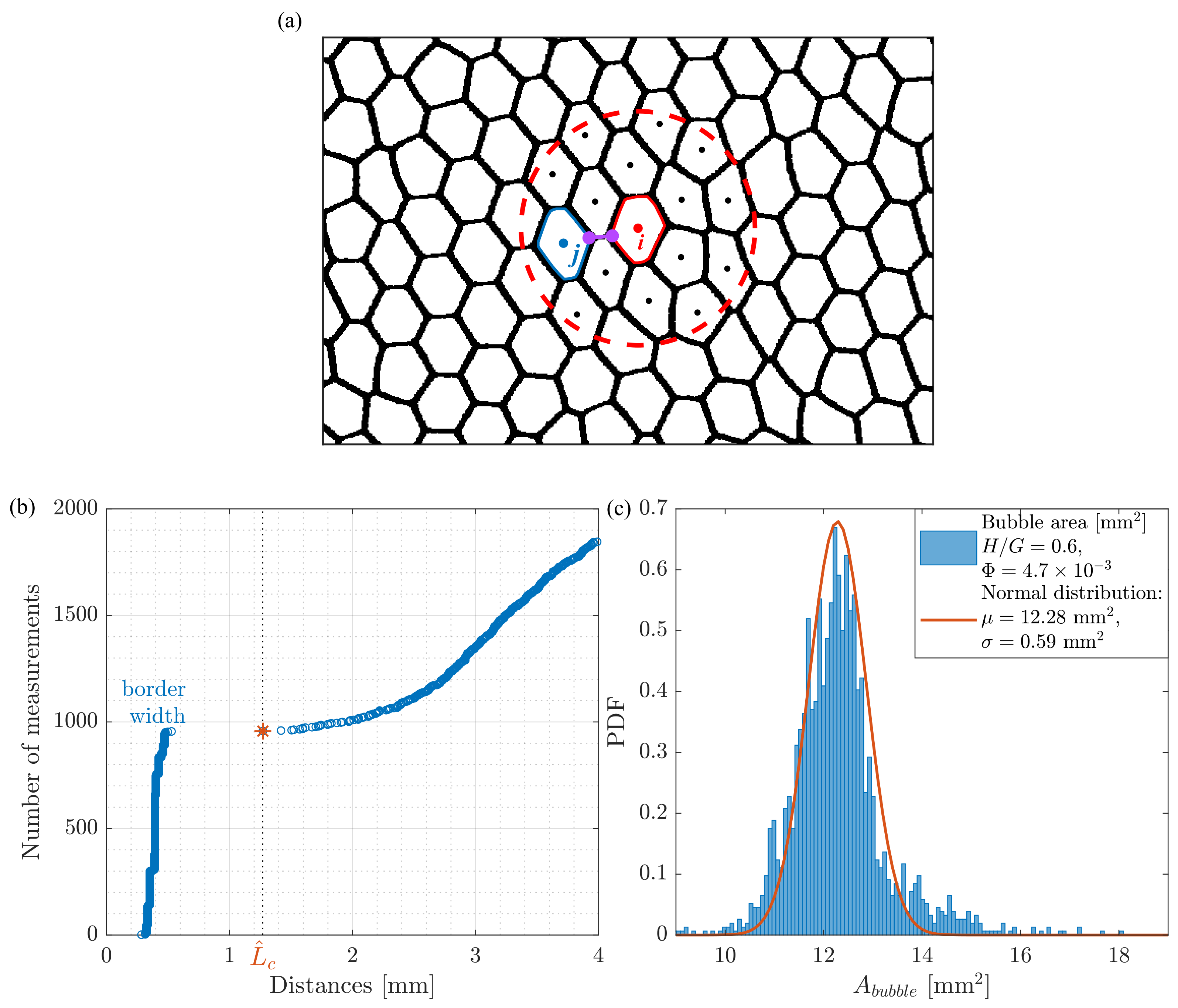
2.2. Computer Method for Liquid Fraction Calculation
3. Results
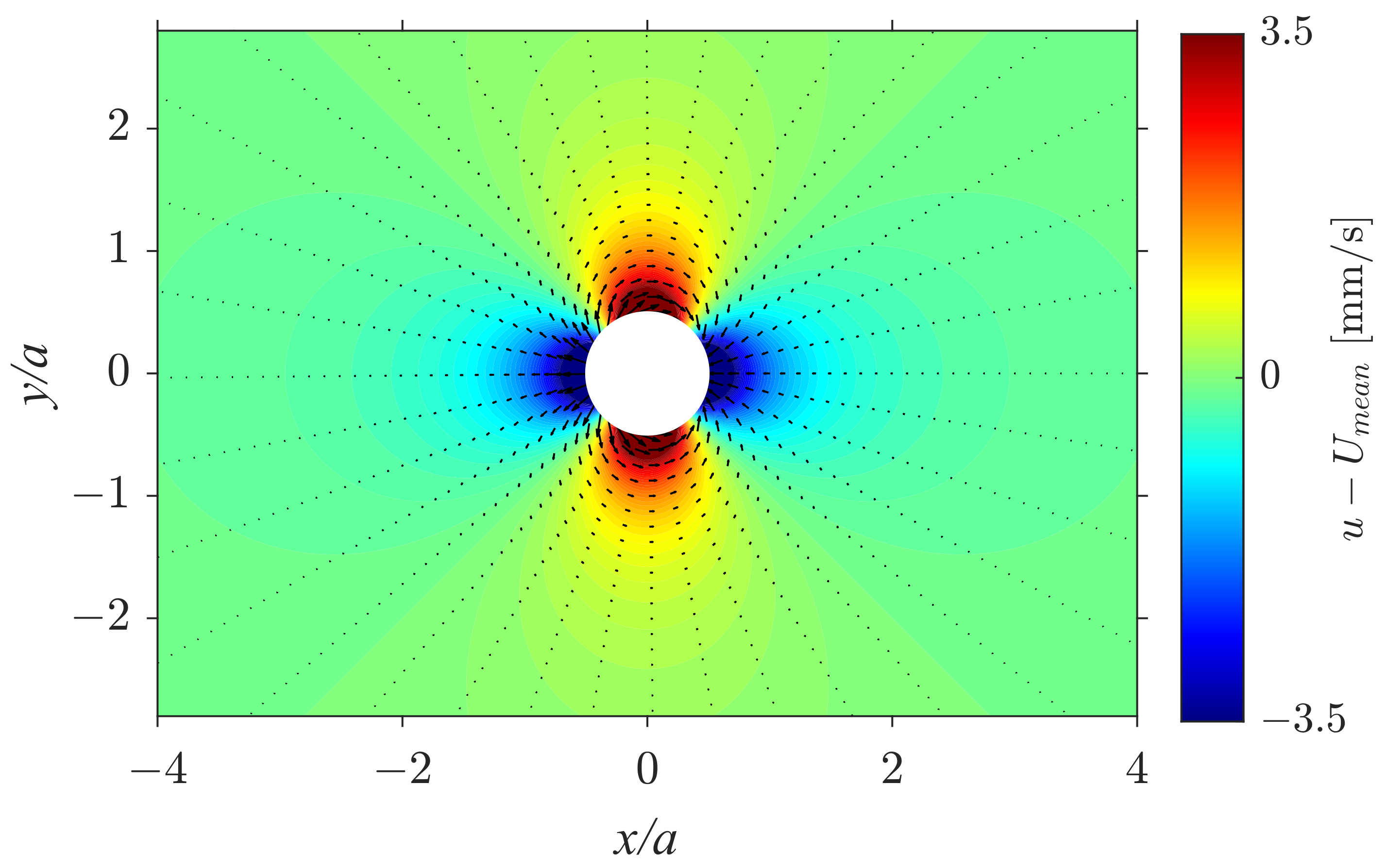
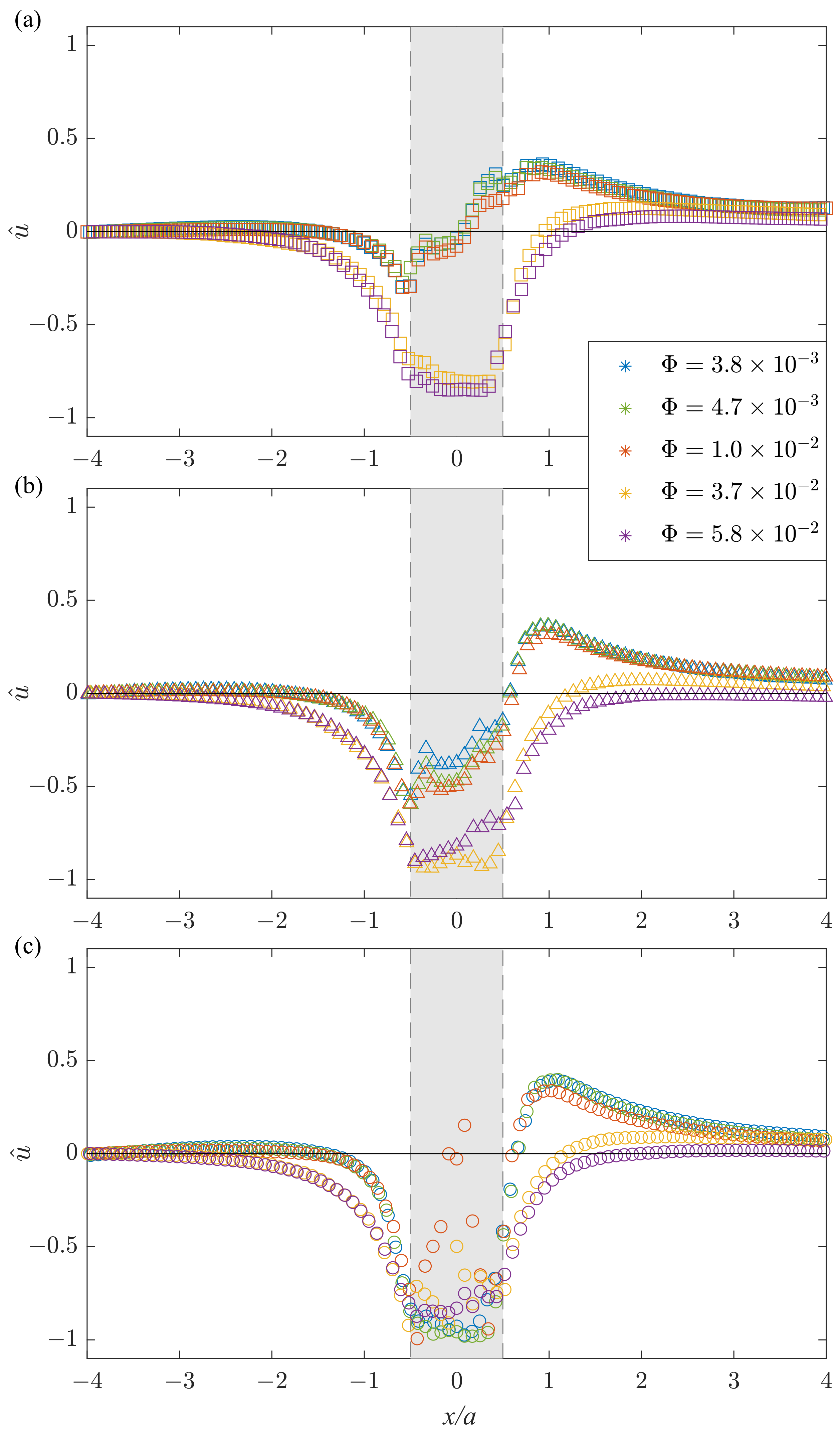
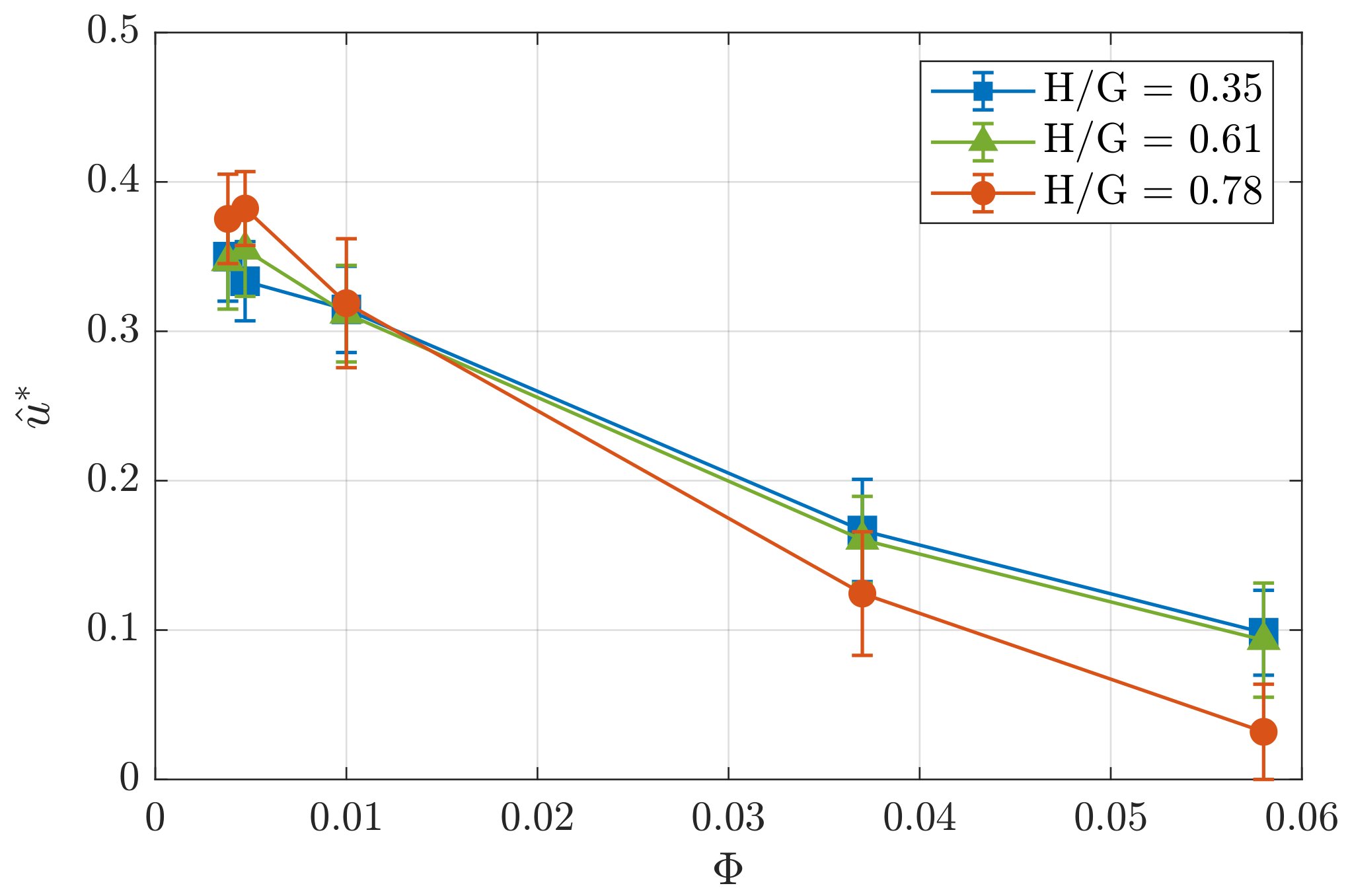
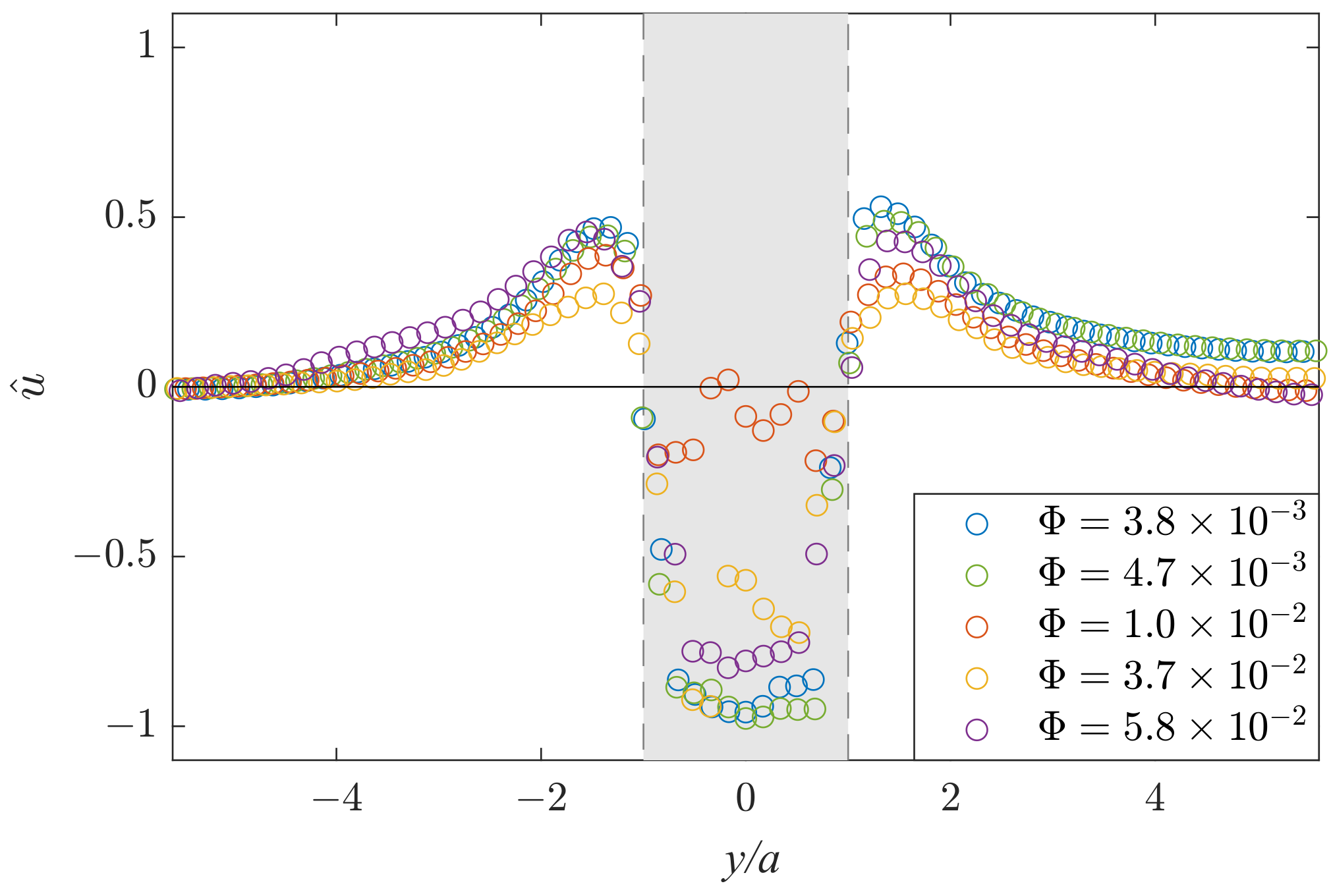
Velocity Field
4. Conclusions
- An increase in water content decreases the effect of a negative wake for the foam flowing around an obstacle, with full suppression of the effect in bubble flows;
- For drier foams, an increase in the obstacle height leads to an increase in the effect of a negative wake;
- The permeability of the local obstacle decreases significantly with an increase in the liquid fraction in the studied range of parameters and drops to a value of nearly zero for the liquid fraction above . The existence of a critical liquid fraction corresponding to the near-zero permeability factor at a permeable constriction is important for efficient flow control in applications related to the production of polymer materials based on aqueous foams.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weaire, D.L.; Hutzler, S. The Physics fo Foams; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Höhler, R.; Cohen-Addad, S. Rheology of liquid foam. J. Phys. Condens. Matter 2005, 17, R1041. [Google Scholar] [CrossRef]
- Reichler, M.; Rabensteiner, S.; Törnblom, L.; Coffeng, S.; Viitanen, L.; Jannuzzi, L.; Mäkinen, T.; Mac Intyre, J.R.; Koivisto, J.; Puisto, A.; et al. Scalable method for bio-based solid foams that mimic wood. Sci. Rep. 2021, 11, 24306. [Google Scholar] [CrossRef]
- Lai, C.Y.; Rallabandi, B.; Perazzo, A.; Zheng, Z.; Smiddy, S.E.; Stone, H.A. Foam-driven fracture. Proc. Natl. Acad. Sci. USA 2018, 115, 8082–8086. [Google Scholar] [CrossRef]
- Zhou, J.; Ranjith, P.G.; Wanniarachchi, W.A.M. Different strategies of foam stabilization in the use of foam as a fracturing fluid. Adv. Colloid Interface Sci. 2020, 276, 102104. [Google Scholar] [CrossRef] [PubMed]
- Tainio, O.; Sohrabi, F.; Janarek, N.; Koivisto, J.; Puisto, A.; Viitanen, L.; Timonen, J.V.; Alava, M. Correction: Chlamydomonas reinhardtii swimming in the Plateau borders of 2D foams. Soft Matter 2021, 17, 6675. [Google Scholar] [CrossRef] [PubMed]
- Ramesh, N.; Lee, S.; Park, C. Polymeric Foams: Science and Technology; Taylor and Francis Group, LLC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Wang, L.; Wu, Y.K.; Ai, F.F.; Fan, J.; Xia, Z.P.; Liu, Y. Hierarchical porous polyamide 6 by solution foaming: Synthesis, characterization and properties. Polymers 2018, 10, 1310. [Google Scholar] [CrossRef] [PubMed]
- Nam, P.H.; Maiti, P.; Okamoto, M.; Kotaka, T.; Nakayama, T.; Takada, M.; Ohshima, M.; Usuki, A.; Hasegawa, N.; Okamoto, H. Foam processing and cellular structure of polypropylene/clay nanocomposites. Polym. Eng. Sci. 2002, 42, 1907–1918. [Google Scholar] [CrossRef]
- Lee, J.W.; Wang, J.; Yoon, J.D.; Park, C.B. Strategies to achieve a uniform cell structure with a high void fraction in advanced structural foam molding. Ind. Eng. Chem. Res. 2008, 47, 9457–9464. [Google Scholar] [CrossRef]
- Amundson, K.; Van Blaaderen, A.; Wiltzius, P. Morphology and electro-optic properties of polymer-dispersed liquid-crystal films. Phys. Rev. E 1997, 55, 1646. [Google Scholar] [CrossRef]
- Tan, H.; Tu, S.; Zhao, Y.; Wang, H.; Du, Q. A simple and environment-friendly approach for synthesizing macroporous polymers from aqueous foams. J. Colloid Interface Sci. 2018, 509, 209–218. [Google Scholar] [CrossRef]
- Raufaste, C.; Dollet, B.; Cox, S.; Jiang, Y.; Graner, F. Yield drag in a two-dimensional foam flow around a circular obstacle: Effect of liquid fraction. Eur. Phys. J. E 2007, 23, 217–228. [Google Scholar] [CrossRef]
- Langevin, D. Aqueous foams and foam films stabilised by surfactants. Gravity-free studies. Comptes Rendus Mec. 2017, 345, 47–55. [Google Scholar] [CrossRef]
- Cantat, I.; Cohen-Addad, S.; Elias, F.; Graner, F.; Höhler, R.; Pitois, O.; Rouyer, F.; Saint-Jalmes, A. Foams; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Kraynik, A.M. Foam flows. Annu. Rev. Fluid Mech. 1988, 20, 325–357. [Google Scholar] [CrossRef]
- Buzza, D.; Lu, C.Y.; Cates, M. Linear shear rheology of incompressible foams. J. Phys. II 1995, 5, 37–52. [Google Scholar]
- Janiaud, E.; Weaire, D.; Hutzler, S. Two-dimensional foam rheology with viscous drag. Phys. Rev. Lett. 2006, 97, 038302. [Google Scholar] [CrossRef] [PubMed]
- Cox, S.J.; Vaz, M.; Weaire, D. Topological changes in a two-dimensional foam cluster. Eur. Phys. J. E 2003, 11, 29–35. [Google Scholar] [CrossRef]
- Vaz, M.F.; Cox, S.J. Two-bubble instabilities in quasi-two-dimensional foams. Philos. Mag. Lett. 2005, 85, 415–425. [Google Scholar] [CrossRef]
- Fritz, W. Berechnung des maximalvolumes von dampfblasen. Phys. Zeitschr 1935, 36, 379–384. [Google Scholar]
- Drenckhan, W.; Hutzler, S. Structure and energy of liquid foams. Adv. Colloid Interface Sci. 2015, 224, 1–16. [Google Scholar] [CrossRef]
- Thielicke, W.; Stamhuis, E. PIVlab—Towards User-friendly, Affordable and Accurate Digital Particle Image Velocimetry in MATLAB. J. Open Res. Softw. 2014, 2, e30. [Google Scholar] [CrossRef]
- Shmakova, N.; Chevalier, T.; Puisto, A.; Alava, M.; Raufaste, C.; Santucci, S. Quasi-two-dimensional foam flow through and around a permeable obstacle. Phys. Rev. Fluids 2020, 5, 093301. [Google Scholar] [CrossRef]
- Viitanen, L.; Mac Intyre, J.R.; Koivisto, J.; Puisto, A.; Alava, M. Machine learning and predicting the time-dependent dynamics of local yielding in dry foams. Phys. Rev. Res. 2020, 2, 023338. [Google Scholar] [CrossRef]
- Tainio, O.; Viitanen, L.; Mac Intyre, J.R.; Aydin, M.; Koivisto, J.; Puisto, A.; Alava, M. Predicting and following T1 events in dry foams from geometric features. Phys. Rev. Mater. 2021, 5, 075601. [Google Scholar] [CrossRef]
- Hassager, O. Negative wake behind bubbles in non-newtonian fluids. Nature 1979, 279, 402. [Google Scholar] [CrossRef]
- Dollet, B.; Graner, F. Two-dimensional flow of foam around a circular obstacle: Local measurements of elasticity, plasticity and flow. J. Fluid Mech. 2007, 585, 181–211. [Google Scholar] [CrossRef]
- Durian, D.J. Foam Mechanics at the Bubble Scale. Phys. Rev. Lett. 1995, 75, 4780. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stennikova, O.; Shmakova, N.; Carrat, J.-B.; Ermanyuk, E. Liquid Fraction Effect on Foam Flow through a Local Obstacle. Polymers 2022, 14, 5307. https://doi.org/10.3390/polym14235307
Stennikova O, Shmakova N, Carrat J-B, Ermanyuk E. Liquid Fraction Effect on Foam Flow through a Local Obstacle. Polymers. 2022; 14(23):5307. https://doi.org/10.3390/polym14235307
Chicago/Turabian StyleStennikova, Oksana, Natalia Shmakova, Jean-Bastien Carrat, and Evgeny Ermanyuk. 2022. "Liquid Fraction Effect on Foam Flow through a Local Obstacle" Polymers 14, no. 23: 5307. https://doi.org/10.3390/polym14235307
APA StyleStennikova, O., Shmakova, N., Carrat, J.-B., & Ermanyuk, E. (2022). Liquid Fraction Effect on Foam Flow through a Local Obstacle. Polymers, 14(23), 5307. https://doi.org/10.3390/polym14235307






