A Nonlinear Fractional Viscoelastic-Plastic Creep Model of Asphalt Mixture
Abstract
:1. Introduction
2. Theory
2.1. Viscoelastic-Plastic Creep Model Based on Nishihara Model
2.2. Viscoelastic-Plastic Creep Model Based on Fractional Differentiation
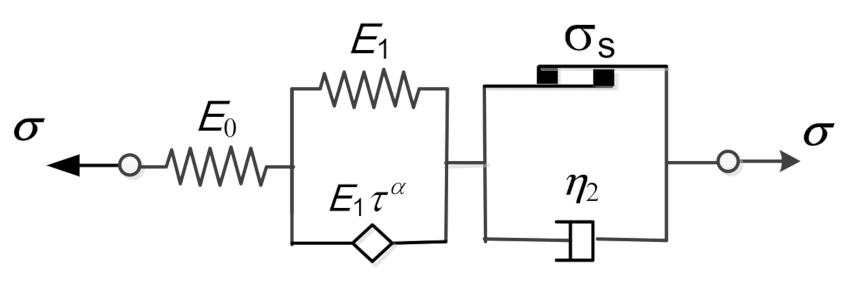
2.3. Nonlinear Fractional Viscoelastic-Plastic Creep Model Considering Damage Effect
3. Compressive Creep Tests
3.1. Material and Methodology
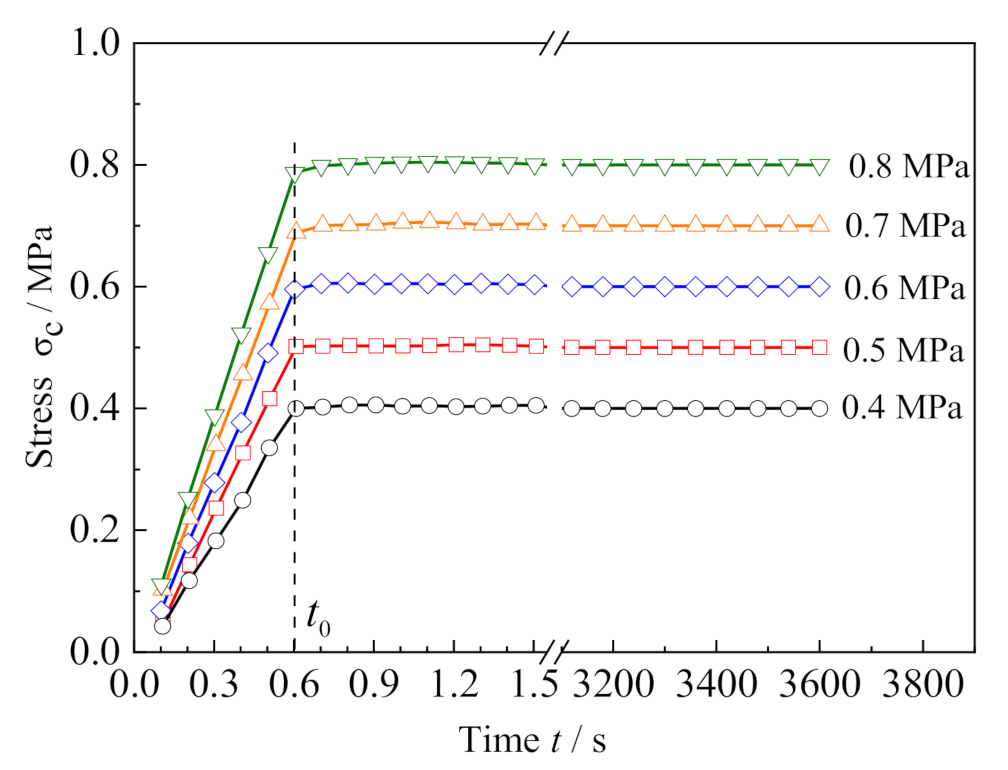
3.2. Test Results
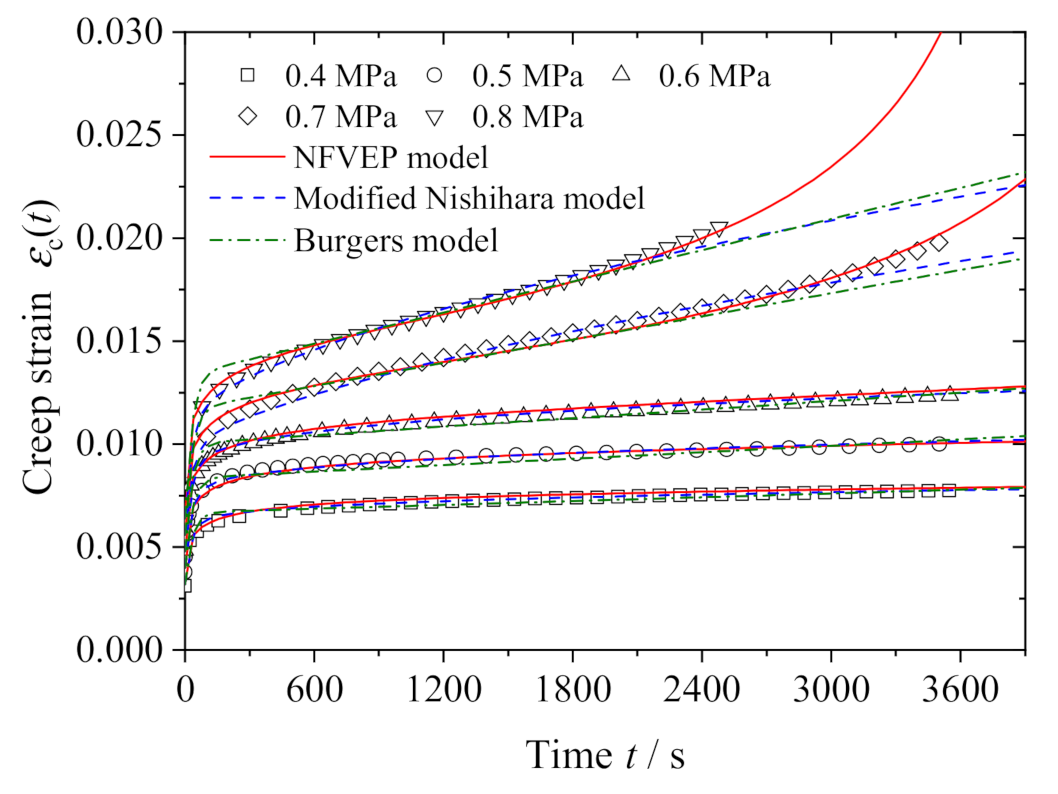
4. Analysis and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nguyen, Q.T.; Benedetto, H.D.; Sauzeat, C. Linear and nonlinear viscoelastic behaviour of bituminous mixtures. Mater. Struct. 2015, 48, 2339–2351. [Google Scholar] [CrossRef]
- Christensen, R.M. Theory of Viscoelasticity, an Introduction, 2nd ed.; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Luo, W.; Jazouli, S.; Vu-Khanh, T. Modeling of nonlinear viscoelastic creep of polycarbonate. E-Polymers 2007, 7, 191–201. [Google Scholar] [CrossRef] [Green Version]
- Monosmith, C.L.; Alexander, R.L.; Secor, K.E. Rheological behaviour of asphalt concrete. Assoc. Asph. Paving Technol. Proc. 1966, 35, 400–450. [Google Scholar]
- Airey, G.D.; Rahimzadeh, B.; Collop, A.C. Linear rheological behavior of bituminous paving materials. J. Mater. Civ. Eng. 2004, 16, 212–220. [Google Scholar] [CrossRef]
- Schapery, R.A. On the Characterization of nonlinear viscoelastic materials. Polym. Eng. Sci. 1969, 9, 295–310. [Google Scholar] [CrossRef]
- Findley, W.N.; Lai, J.S.; Onaron, K. Creep and Relaxation of Nonlinear Viscoelastic Materials; North-Holland Publishing Company: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Gao, D.; Wang, P.; Li, M.; Luo, W. Modelling of nonlinear viscoelastic creep behaviour of hot-mix asphalt. Constr. Build. Mater. 2015, 95, 329–336. [Google Scholar] [CrossRef]
- Arabani, M.; Jamshidi, R.; Sadeghnejad, M. Using of 2D finite element modeling to predict the glasphalt mixture rutting behavior. Constr. Build. Mater. 2014, 68, 183–191. [Google Scholar] [CrossRef]
- Imaninasab, R.; Bakhshi, B.; Shirini, B. Rutting performance of rubberized porous asphalt using Finite Element Method (FEM). Constr. Build. Mater. 2016, 106, 382–391. [Google Scholar] [CrossRef]
- Grishchenko, A.I.; Semenov, A.S.; Murgul, V. Effective methods of parameter identification for creep models with account of III stage. MATEC Web Conf. 2016, 53, 01041. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Q.; Qi, Y.; Wang, Z.; Zhou, C. An extended Nishihara model for the description of three stages of sandstone creep. Geophys. J. Int. 2013, 193, 841–854. [Google Scholar] [CrossRef]
- Li, X.; Liu, E.; Song, B.; Liu, X. An improved Nishihara model for frozen loess considering the influence of temperature. Adv. Mater. Sci. Eng. 2018, 2018, 9073435. [Google Scholar] [CrossRef] [Green Version]
- Qian, G.; Hu, K.; Gong, X.; Li, N.; Yu, H. Real-time flow behavior of hot mix asphalt (HMA) compaction based on rheological constitutive theory. Materials 2019, 12, 1711. [Google Scholar] [CrossRef] [Green Version]
- Fu, Q.; Xie, Y.-J.; Long, G.-C.; Meng, F.; Song, H. Temperature sensitivity and model of stress relaxation properties of cement and asphalt mortar. Constr. Build. Mater. 2015, 84, 1–11. [Google Scholar] [CrossRef]
- Zheng, J.L.; Lv, S.T.; Tian, X.G. Viscoelastic damage characteristics of asphalt based on creep test. Eng. Mech. 2008, 25, 193–196. (In Chinese) [Google Scholar]
- Alrub, R.K.A.; Darabi, M.K.; Masad, E. A straightforward numerical technique for finite element implementation of non-local gradient-dependent continuum damage mechanics theories. Int. J. Theor. Appl. Multiscale Mech. 2010, 1, 352. [Google Scholar]
- Zhang, J.; Zhu, C.; Li, X.; Pei, J.; Chen, J. Characterizing the three-stage rutting behavior of asphalt pavement with semi-rigid base by using UMAT in ABAQUS. Constr. Build. Mater. 2017, 140, 496–507. [Google Scholar] [CrossRef]
- Tao, B.; Wu, F.Q.; Guo, G.M.; Zhou, R. Flexibility of viscoelastoplastic model to rheological characteristics of rock and solution of rheological parameter. Chin. J. Rock Mech. Eng. 2005, 24, 3165–3171. (In Chinese) [Google Scholar]
- Xu, W.Y.; Yang, S.Q.; Chu, W.J. Nonlinear viscoelasto-plastic rheological model (Hohai model) of rock and its engineering application. Chin. J. Rock Mech. Eng. 2006, 25, 433–447. (In Chinese) [Google Scholar]
- Koeller, R.C. Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. 1984, 51, 299–307. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 1983, 27, 201–210. [Google Scholar] [CrossRef]
- Rabotnov, Y.N. Creep Problems in Structural Members; North-Holland Publishing Company: Amsterdam, The Netherlands, 1969. [Google Scholar]
- Leckie, F.A.; Hayhurst, D.R. Constitutive equations for creep rupture. Acta Metall. 1977, 25, 1059–1070. [Google Scholar] [CrossRef]
- Lemaitre, J. A Course on Damage Mechanics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Yin, Y.; Zhang, X. Dynamic viscoelastic behavior of asphalt mixtures based on fractional derivative. J. Cent South. Univ. 2013, 44, 3891–3897. (In Chinese) [Google Scholar]
- China Communications Bridge Techology Co. Ltd. Ed. JTG D50-2017, Specifications for Design of Highway Asphalt Pavemen; China Communicationa Press: Beijing, China, 2017. (In Chinese) [Google Scholar]
- Research Institute of Highway Ministry of Transport Ed. JTG F40-2004, Technical Specifications for Construction of Highway Asphalt Pavement; China Communicationa Press: Beijing, China, 2004. (In Chinese) [Google Scholar]
- Gonzalez, J.M.; Canet, J.M.; Oller, S.; Miro, R. A Viscoplastic constitutive model with strain rate variables for asphalt mixtures’ numerical simulation. Comput. Mater. Sci. 2007, 38, 543–560. [Google Scholar] [CrossRef] [Green Version]






| Penetration Degree (25 °C, 100 g, 5 s) (0.1 mm) | Softening Point (Ball-Circling Method) (°C) | Ductility (15 °C, 5 cm/min) (cm) | Density (25 °C) (kg/m3) |
|---|---|---|---|
| 68 | 47.5 | >150 | 1030 |
| Passing Rate/% | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (Sieve Size/mm) | ||||||||||
| 16 | 13.2 | 9.5 | 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 | |
| Upper limit | 100 | 100.0 | 85.0 | 68.0 | 50.0 | 38.0 | 28.0 | 20.0 | 15.0 | 8.0 |
| Lower limit | 100 | 90.0 | 68.0 | 38.0 | 24.0 | 15.0 | 10.0 | 7.0 | 5.0 | 4.0 |
| Screening result | 100 | 93 | 74 | 51 | 35 | 24 | 17 | 12 | 8 | 5 |
| E0/MPa | E1/MPa | τ/s | α | η2/(MPa·s) | n | q | c | m |
|---|---|---|---|---|---|---|---|---|
| 125 | 128 | 46 | 0.38 | 2000 | 0.26 | 1.27 | 0.00038 | 5.17 |
| σc/MPa | tr/s | R2 | ||||||
| 0.4 | 133,000 | 0.956 | ||||||
| 0.5 | 39,103 | 0.968 | ||||||
| 0.6 | 18,868 | 0.983 | ||||||
| 0.7 | 4833 | 0.989 | ||||||
| 0.8 | 3889 | 0.997 | ||||||
| σc/MPa | E0/MPa | E1/MPa | τ/s | η2/(MPa·s) | R2 |
|---|---|---|---|---|---|
| 0.4 MPa | 125 | 115 | 32 | 1168624.77 | 0.921 |
| 0.5 MPa | 125 | 115 | 32 | 879915.62 | 0.935 |
| 0.6 MPa | 125 | 115 | 32 | 811050.46 | 0.939 |
| 0.7 MPa | 125 | 115 | 32 | 351050.70 | 0.968 |
| 0.8 MPa | 125 | 115 | 32 | 301207.26 | 0.972 |
| σc/MPa | E0/MPa | E1/MPa | τ/s | η2/(MPa·s) | n | R2 |
|---|---|---|---|---|---|---|
| 0.4 MPa | 125 | 185 | 32 | 986.79 | 0.23 | 0.979 |
| 0.5 MPa | 125 | 185 | 32 | 1126.12 | 0.26 | 0.977 |
| 0.6 MPa | 125 | 185 | 32 | 1600.82 | 0.31 | 0.989 |
| 0.7 MPa | 125 | 185 | 32 | 13119.85 | 0.64 | 0.985 |
| 0.8 MPa | 125 | 185 | 32 | 9161.37 | 0.60 | 0.985 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Liu, X.; Yin, B.; Luo, W. A Nonlinear Fractional Viscoelastic-Plastic Creep Model of Asphalt Mixture. Polymers 2021, 13, 1278. https://doi.org/10.3390/polym13081278
Zhang Y, Liu X, Yin B, Luo W. A Nonlinear Fractional Viscoelastic-Plastic Creep Model of Asphalt Mixture. Polymers. 2021; 13(8):1278. https://doi.org/10.3390/polym13081278
Chicago/Turabian StyleZhang, Yongjun, Xiu Liu, Boyuan Yin, and Wenbo Luo. 2021. "A Nonlinear Fractional Viscoelastic-Plastic Creep Model of Asphalt Mixture" Polymers 13, no. 8: 1278. https://doi.org/10.3390/polym13081278
APA StyleZhang, Y., Liu, X., Yin, B., & Luo, W. (2021). A Nonlinear Fractional Viscoelastic-Plastic Creep Model of Asphalt Mixture. Polymers, 13(8), 1278. https://doi.org/10.3390/polym13081278







