Abstract
Polymer based textile composites have gained much attention in recent years and gradually transformed the growth of industries especially automobiles, construction, aerospace and composites. The inclusion of natural polymeric fibres as reinforcement in carbon fibre reinforced composites manufacturing delineates an economic way, enhances their surface, structural and mechanical properties by providing better bonding conditions. Almost all textile-based products are associated with quality, price and consumer’s satisfaction. Therefore, classification of textiles products and fibre reinforced polymer composites is a challenging task. This paper focuses on the classification of various problems in textile processes and fibre reinforced polymer composites by artificial neural networks, genetic algorithm and fuzzy logic. Moreover, their limitations associated with state-of-the-art processes and some relatively new and sequential classification methods are also proposed and discussed in detail in this paper.
1. Introduction
Classification of textiles and polymer based nanocomposites by computer added programs is relatively a new approach that develops the simulations of human brain in the form of algorithms to solve complex problems. Machine learning is a subcategory of artificial intelligence that provides the solution of various issues i.e., grading, classification, defects detection, quality control, prediction and process optimization, through advanced tools such as image processing, soft computing and computer vision algorithms. The adaptation of machine learning in textiles has aroused in recent years [1]. Durable, sustainable and quality products are produced with the help of machine learning algorithms with minimal effort. These algorithms are essential parts of modern artificial intelligence systems and researchers have been significantly used these systems for the betterment of textiles. Therefore, machine learning based automatic fabric defects detection system are integrated in modern textile machines to evaluate fiber grading, yarn quality and fabric performance.
Due to their economic benefits, textiles and polymers based composites have received tremendous attention and researchers used them in various fields due to their excellent mechanical, electrical and interfacial properties [2,3,4,5,6]. In terms of current research, the interfacial performance of fibre/resin for composites was observed to be sensitive to the actual service environment. The potential fibre/resin debonding may occur. In addition, the fatigue resistance is a key advantage of textile-based composites compared to the steel materials, that expands the application circle of composites in automobiles, aerospace, oil extraction industry, civil and building industry [7]. A group of researchers worked with the interfacial, mechanical and thermal properties of fibre reinforced composites and reported interesting results [8,9]. Li et al. worked with interfacial shear strength of pultruded rod made of carbon/glass. They investigated the effect of hydraulic pressure and water immersion on interfacial properties. The results revealed that the hydraulic pressure had positive impact on the interfacial performance of the carbon/glass composite and conversely, water immersion reduced the interfacial strength of carbon/glass rod [10]. In a recent study, Li et al. expanded their work on carbon/glass pultruded rod and investigated the interfacial, thermal and mechanical properties at elevated temperature. They reported that at elevated temperature, interfacial shear strength decreased with time for hybrid fibre reinforced composites. Longer exposure led to more degradation and plasticizing as well as hydrolysis observed due to the diffusion of water molecules [11]. In another study, Li et al. worked with the mechanical properties and life service evolution of unidirectional hybrid carbon/glass pultruded rod under harsh and elevated conditions. The results showed that fibre/resin debonding occurred under longer exposure and overall mechanical, thermal and interfacial properties decreased [12].
The use of machine learning in textiles, especially for classification, has shown its potential exponentially in the current era [13,14]. Zimmerling et al. reported the application of Gaussian regression algorithm to improve the geometrical shapes of fiber reinforced textile composites. This method significantly improved the assessment criterion for fibre reinforced plastics components. Based on the efficiency, they suggested machine learning as an economical tool than finite element method, for the evaluation of textile processes [15]. In another work, Seçkin et al. reported a production fault in gloves industry. They used time-series data for the simulation and forecasting of this problem and classified it with different machine learning algorithms [16]. Ribeiro et al. proposed an automatic method to predict different properties of woven fabrics based on design and finishing features [17]. Due to the complexities of their micro-structures and boundary conditions, the classification of overall characteristics of textiles and polymer composites is still a challenging task even for machine learning. Therefore, a highly efficient and accurate approach is required that can predict the microscopic structural performance under different geometries. Apart from the above discussion, hardware utilization and technical issues are two other major constrains during the application of machine learning in textiles. However, to address these problems, various machine learning and computer vision-based applications are reported in the literature as deterministic and non-deterministic models. Mathematical models, empirical models and computer aided models i.e., finite element method (FEM), are deterministic models. However, genetic algorithm (GA), artificial neural network (ANN), chaos theory (CT) and fuzzy logic (FL) are non-deterministic approaches. Figure 1 shows the difference between machine learning approaches and traditional deterministic engineering models.
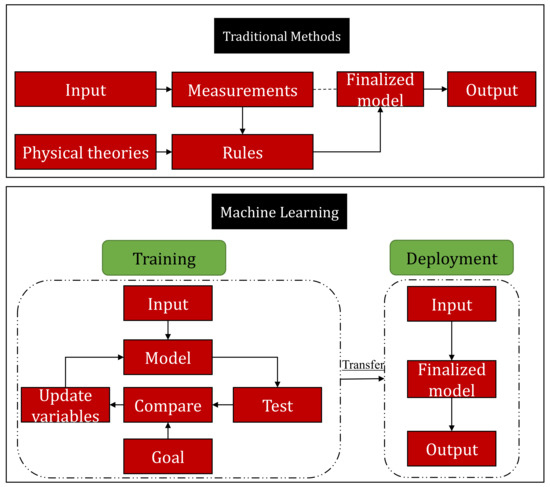
Figure 1.
Comparison of machine learning approaches with traditional deterministic models.
In recent years, considerable research efforts have been made to the development of machine learning tools for classification, prediction and defects detection. Although, the prediction and defects detection for textiles and polymer composites have been reviewed, the comprehensive review on the classification of fiber reinforced polymer composites is still missing. Therefore, our motivation is to provide a detail description about the used algorithms for fiber reinforced composites. This may help our readers to find out best possible algorithm for their future research endeavours. We categorized the applications of machine learning and computer vision algorithms into four classes based on standard textile manufacturing processes i.e., spinning, weaving, finishing and fiber reinforced polymer composites. In each of these four classes, we elucidated the recently reported work for defects detection, identification, classification and prediction by image segmentation-based approaches, color-based approaches, texture-based defect detection and by deep learning. In addition, we reviewed the limitations of existing state of the art methods and proposed a possible future research direction in textile composites using the sequential Monte Carlo methods.
After the introduction, this paper is organized in a following sequence: Section 2 focuses the utilization of machine learning in spinning, weaving, non-woven and textile finishing applications. The following Section 3 provides the limitations of widely used approaches. Section 4 explains the possibilities of future challenges for sequential Monte Carlo methods in textiles and polymer-based composites and the final Section 5 summarizes the paper with few suggestions to overcome the future challenges. Figure 2 explains the scheme that elucidates the methodology of the proposed paper. The authors believe that the approach delineates here opens up a new gateway for researchers to choose the best suitable machine learning tool in order to work with textile substrates and composites.

Figure 2.
A schematic illustration of this study.
2. Classification Based on Textile Processes
The necessity to process raw data and explore valuable information from it has become essential in every field of science, engineering, business and medicine. In textiles, even when a simple product e.g., a t-shirt is considered, bulk amount of data is generated from raw materials, quality parameters and machine settings. The data could be nonlinear and multivariable depend on the relationship between fiber properties and yarn properties or between fabric performance and machine settings. Moreover, improvements and innovations in textiles with the introduction of technical textiles have occurred with exceptional performance expectations at extreme conditions e.g., against sun, cold, impact, knife, bullet and microorganisms [18,19]. Therefore, the demand for data processing and discovery of valuable information from this data is continuous in textile industry. Many traditional models e.g., statistical and mathematical, have been reported in numerous studies to process textile data. However, these classical models remain incapable of discovering the complex relationship between the variables. To solve this challenge, machine learning models are implemented in almost all areas of textile engineering. In textile processes, the trend of reported literature elucidates that the researchers tried to establish a critical relationships among essential parameters of fibers, yarns and fabrics. Machine learning algorithms are robust and powerful tools for modeling and solving complex and nonlinear applications. In this context, Majumdar published a book on soft computing in textile engineering [20]. This book compiled various research studies based on ANN and FL approaches during yarn modelling, fabric manufacturing, garments modelling by FL, composites modelling for quasi-static mechanical properties, viscoelastic behaviour and fatigue behaviour using ANN, textile quality evaluation using image processing, ANN and FL approaches.
ANN has been widely studied for textile data since last decade and helped the researcher to get better efficiency for fiber classification, defect detection, prediction and modeling of yarn, fabric, color matching, color separation and their coordinates conversion [21]. Vassiliadis et al. introduced a comprehensive overview of ANN applications in fabric manufacturing [22]. ANN had been successfully utilised for fibrous properties (classification of fibers, color grading, selection of cotton bales, identification of control parameter), yarns parameters (detection of faults, prediction of tensile properties and shrinkage) and for fabrics properties (defects detection, prediction of thermophysiological, sensorial and comfort properties, bursting of woven and knitted fabrics).
The literature discussed above provides an overview of machine learning till 2011. Therefore, we will present a review of recent advanced works in this field. In this section, we categorized the textile applications using machine learning algorithms into four classes based on standard textile-based processes i.e., spinning, weaving, finishing and fiber reinforced polymer composites.
2.1. Classification Based on Yarn’s Production
Yarn is generally considered as a primary element for the manufacturing of high quality textiles and in recent years, numerous studies were conducted on the classification, modeling and prediction of essential yarn parameters as given below:
2.1.1. Fibre Maturity
Fibre maturity is an important and significantly crucial parameter especially when the researchers deal with yarns properties and desire excellent final product. In general, fibre maturity is considered as a functional and primary building block of any good textile product. Therefore, many researcher worked with the prediction of fibre maturity. Farook et al. proposed that ANN algorithms are excellent prediction tools in order to predict cotton fibre maturity [23]. They selected various fibre characteristics as an input variables and analysed fibre maturity as an output variable. The simulation results showed that ANN predicted cotton fibre maturity was higher when compared with the experimental values. However, there was no optimal result in this application.
2.1.2. Yarn Crimp
Malek et al. evaluated the performance of ANN for the prediction of yarn crimp in woven barrier fabrics [24]. They performed two experiments to predict yarn crimp. The purpose of both experiments was to predict the crimp in warp yarn and weft yarn respectively. The input variables were weave style, density of warp and weft yarns, fibre and filament fineness, shed time and loom speed. However, the only exception in the second experiment was the replacement of yarn fineness with filament fineness. ANN results showed good results for the prediction of yarn crimp with the exception of two small deviations between actual and predicted output. In a different work, Majumdar et al. introduced mathematical, statistical and ANNs models to predict breaking force at elongation of ring-spun cotton yarns [25]. The inputs for these three models were yarn count and cotton fiber properties. ANN model provided a better prediction performance compared to the statistical and mathematical models. Later, they reported the implementation of a hybrid neuro-fuzzy system for the prediction of yarn strength [26]. The results were compared with standard ANN and regression models for prediction accuracy. ANN showed better prediction results than others.
2.1.3. Yarn Types
Before the production of yarn, the prediction of quality parameters is important to overcome production faults. In an experimental study, Almetwally et al. used ANN and linear regression for the prediction of core spun yarn strength, elongation and rupture [27]. The results showed that ANN models provided significantly accurate prediction for yarn strength. Recently, Doran et al. reported the utilization of ANN and support vector machine (SVM) methods to avoid faulty fabric production [28]. In addition, they used statistical tools i.e., analysis of variance (ANOVA) and principal component analysis (PCA) to overcome input dimensions. The test results showed that both ANN and SVM methods provided effective predictions for yarn quality characteristics. However, SVM showed slightly better results than ANN for mean absolute percentage error (MAPE) and coefficient of correlation (R).
2.1.4. Yarn Tenacity
Dashti et al. worked with yarn tenacity through ANN and produced a decision support system by applying GA [29]. Experimental results showed that ANN offered an accurate prediction for yarn tenacity with less than error. In addition, GA was applied to obtain optimal input parameters for yarn production. The obtained tenacity was greater than the desired tenacity, therefore, a reduction in production cost was observed. The implementation of this strategy was useful to find good input conditions in order to achieve desired tenacity.
2.1.5. Yarn Strength Utilization
Mishra used ANN models during the production of cotton fabric for the prediction of yarn strength utilization [30]. The selected input parameters were yarn counts, initial crimps, total number of yarns and yarn strengths in longitudinal and transverse directions along with the weave float length. The experimental results showed that yarn strength utilization percentage increased with an increase in yarn number in both directions. However, a decrease in crimp percentage and float length was observed. Mozafary et al. proposed a combined approach, where they used K-means algorithm for data clustering and ANNs for defects detection i.e., yarn unevenness [31]. The feedforward ANN and Levenberg–Marquardt training function of back propagation were applied in this method and the effectiveness was demonstrated by a comparative analysis with standard ANN results. In an experimental study, Malik et al. applied a back propagation ANN to analyse the prediction efficiency of used model for tensile properties of even and uneven yarns extracted from polyester-cotton blend [32]. The selected parameters were twist multiplier, cot hardness and Break draft ratio. The reported results of linear regression and ANN for tensile properties were compared with standard methods. El-Geiheini et al. worked with different types of yarns and used ANN and image processing tools for modeling and simulation of yarn tenacity and elongation [33]. They reported that the proposed techniques were suitable for the estimation of various yarn properties with minimum error. In another study, Erbil et al. used ANN and regression tools for tensile strength prediction of ternary blended open-end rotor yarns [34]. They applied multiple linear regression (MLR) and trained ANN algorithm with Levenberg–Marquardt backpropagation function. Furthermore, they compared both models for prediction efficiency. The results demonstrated that ANN models gave better prediction output than MLR for both parameters i.e., breaking strength and elongation at break.
2.1.6. Yarn Twist
Yarn twist i.e., S twist, Z twist etc., is another important and noteworthy parameter in order to estimate end product’s performance. Therefore, different researcher worked with this variable and reported interesting results. Azimi et al. used ANN in order to predict twist type for textured yarns [35]. They investigated the effects of heater temperature, texturing speed and the effects of twist type on yarns crimp stability for hybrid yarns. The testing results demonstrated that ANN models were excellent for the prediction of yarn properties under selected variables.
2.2. Classification Based on Fabric Manufacturing
In this part, we classified the use of machine learning tools into three categories based on fabric manufacturing methods i.e., weaving, knitted and non-woven.
2.2.1. Weaving
The process of weaving is based on interlacing of yarns in warp and weft directions. However, with time, textile woven structures have become more and more complex by the addition of diagonal yarns in interlacing. Therefore, prediction of woven textiles is now a complex task that requires accumulated empirical knowledge about various parameters of woven textiles. Some of those variables are listed below where researchers performed machine learning algorithms to gain better performance and utilization of woven textiles.
Fabric Type
Woven structures are the mostly used structures not only in textile production but also in composites [36,37,38,39,40,41]. Ribeiro et al. proposed an automated machine learning method to predict the physical properties of woven fabrics based on finishing features and textile design. They investigated nine different properties including pilling, abrasion and elasticity and reported improved prediction results for all properties with low prediction error. They applied Cross-Industry Standard Process for Data Mining (CRISP-DM) iterations, where every iteration was based on the verification of standard input parameters. At CRISP-DM stage, an automated machine learning (AutoML) algorithm was performed to choose optimal regression model among six different machine learning algorithms. The results demonstrated that significantly better output was achieved by the selected codes for fixed sequence of yarns and fabric finishing treatment [17]. In an experimental study, Hussain et al. proposed a novel machine learning algorithm depends on transfer learning and data augmentation in order to recognize and classify the complex patterns of woven textiles. The texture and pattern of textiles are considered as essential factors to design and produce high-quality fabrics. The proposed algorithm worked with residual network through which textures of woven fabric were extracted and auto classified as an end-to-end manner. They suggested that the reported results would be effective even all of the fabric properties are altered [42].
Fabric Pilling, Drapability and Wrinkle Recovery
Fabric pilling, drapability and wrinkle recovery are the aesthetic properties of textiles and considered as performance indicator of textile fabrics for quality evaluation. Eldessouki et al. applied adaptive neuro-fuzzy models (ANFIS) for the evaluation of pilling resistance of woven fabrics. In this proposed approach, they classified the selected samples on the basis of texture patterns and compared their results with standard method of pilling resistance for correlation [43]. Xiao et al. predicted cotton-polyester fabric pilling with ANN (Back-propagation approach) and then used GA for optimization of their results. The optimized results revealed that GA algorithms were better in terms of root mean square error (RMSE), MAPE and mean absolute error (MAE) compared to ANN [44]. Drapability is one of the most important aesthetic properties that plays crucial role in providing graceful effects to textile fabrics. Drapability depends on experience and skills of humans and is judged subjectively. It renders the complexities during drape comparisons particularly when judged by different persons. Taieb et al. used ANN for the prediction of fabric drape ability under low stress. They reported that the application of ANN for the prediction of aesthetic properties including drapability is a promising one and is physical factors played crucial role during the prediction of fabric drape ability [45]. Hussain et al. compared ANN with adaptive neuro-fuzzy inference system (ANFIS) during the evaluation of fabrics wrinkle recovery [46]. They found that for both types of algorithms, the input conditions suitable for better wrinkle recovery were linear densities of both warp and weft sides. However, the suitable output variables were crease recovery angles of warp and weft yarns. The results demonstrated that simulation performed by ANN produced slightly better results than ANFIS with significant accuracy percentage. However, ANFIS process was more useful while drawing surface plots among variables. ANN algorithms do not have this feature.
Fabric Comfort Properties
Comfort evaluation is a noteworthy parameter in terms of fabric overall performance [47,48,49,50,51]. Majority of machine learning algorithms were applied on fabric’s thermophysiological and sensorial comfort. Malik et al. used ANN algorithm to predict woven fabrics thermophysiological property i.e., air permeability with respect to fabric construction, raw materials involved during production and process variables [52]. ANN algorithm was trained with feedforward neural function under a hybrid back propagation method composed of Bayesian regularization and Levenberg-Marquardt function. Simulation results showed that the proposed model provided promising results on test data with lower MAE. In addition, Malik et al. employed another ANN algorithm to show a relationship between loom parameters, used material and construction of fabric in terms of porosity, mean pore flow, mean pore size with air permeability [53]. The experimental result showed that ANN algorithms were excellent for the prediction of comfort properties with minimal error. Wong et al. applied a hybrid approach that combined ANN and fuzzy-logic for overall prediction of clothing comfort by considering physical properties as input variables [54]. Simulation results provided maximum correlation coefficient.
Optimization
Optimization of process variables in order to reduce cost and improve production efficiency is another important factor in textiles. Therefore, many studies were carried out to investigate the process of optimization. Xu et al. combined differential evolution and Kriging surrogate algorithms to study the optimization of enzyme washing and production cost incurred on indigo dyed cotton [55]. They selected Taguchi L16 orthogonal array algorithm for optimization and applied it in their study. temperature of bath and concentration of enzymes were chosen as input variables and enzymatic washing as output response. Kriging model was used to analyse the relationship between variables and results revealed that the applied method was significantly efficient for the optimization of overall cost and can be further utilized in the analysis of mean square error, absolute error and relative error.
2.2.2. Knitting
Knitting is another important production method in which prediction and modelling of knitting parameters are significantly complex tasks due to diversified variables i.e., knitted structures, knitting machine variables and selected yarn attributes etc. Several researchers have used different soft computing and machine learning algorithms to predict knitted fabric’s comfort properties, spirality, pilling, bursting strength as well as other aesthetic and physical properties.
Fabric Type and Pilling Behaviour
Pilling is a serious fault in textile production especially in knit wear. Therefore, machine learning is a useful tool to forecast pilling behaviour of knitted fabric. Unal et al. selected single jersey knitted fabrics for the evaluation of air permeability and combined ANN algorithm with regression methods for the prediction of bursting strength of knit structures [56]. Implementation of results showed that both methods were able to predict the properties of knitted fabrics. However, ANN had a slightly positive edge when used for prediction. Yang et al. identified knitted fabric pilling behaviour by modifying ANN into deep principle components analysis-based neural networks (DPCANNs) [57]. In DPCANNs, principle components automatically tracked down the fabric initial and after pilling test properties and then neural network was applied to evaluate pilling grades. The obtained results revealed that DPCANNs had above average classification efficiency for pilling behaviour of knitted fabric. Another important work using ANN was performed by Kayseri et al. where pilling tendency was predicted by selecting fabric cover factor as an input parameter [58]. They observed that by changing cover factor, fabric pilling was controlled to a greater extent. In this study, they concluded that pilling behaviour was the outcome of pilling grade, mean pilling height as well as covered pilling area. They reported that used algorithms had very good prediction power in determining fabric pilling behaviour.
Prediction of Comfort Properties
Fayla et al. applied ANN algorithm on knitted fabrics to predict thermal conductivity [59]. They selected yarn conductivity, porosity, fabric weight and air permeability as input conditions. The results revealed that ANN algorithm predicted the thermal conductivity with significantly high correlation coefficient. Majumdar used ANN to predict the thermal conductivity of cotton, bamboo and their blended yarns. The input variables were bamboo fiber proportion, linear density of yarn, thickness of fabric and areal density. The correlation coefficient of this study very high [60]. Knanat et al. used ANN for the prediction of thermal resistance of wet knitted fabrics [61]. Here, they used two different ANN networks for the prediction of thermal resistance. In the first network, the input variables were moisture content, yarn, fiber and fabric parameters. However, in the second network, input variables were yarn, fiber and fabric parameters, and the output response was thermal resistance under varying moisture level. The results from both networks showed efficient prediction of thermal resistance. Mitra et al. used ANN for the prediction of thermal resistance of handloomed cotton fabric [62]. The input fabric parameters were picks per inch (PPI), ends per inch (EPI), weft and warp count. The results revealed that used ANN algorithm achieved good prediction efficiency for thermal resistance under low MAE values. In addition, EPI, warp count and weft count were major contributors for the evaluation of thermal resistance.
2.2.3. Nonwoven
Machine learning algorithms have gained tremendous importance during the last few years to enhance productivity of nonwoven textiles by predicting various important parameters i.e., dimensional change, pilling behaviour and optimization of variables. Wang et al. measured the pilling of nonwoven fabrics using wavelet analysis [63]. The results demonstrated that wavelet analysis was quite similar to traditional method for pilling evaluation. Kalkanci et al. estimated fabric shrinkage by applying ANN algorithm inside relaxation methods [64]. Thermofixing, sanforizing, drying and washing were important processes applied on fabrics during finishing. Dimensional changes were predicted at the end of finishing processes by ANN. Two-layer feedforward perceptron function was used for ANN algorithm to evaluate the width of dimensional change. The experimental results showed that ANN gave better prediction results for dimensional change. Abhijit et al. applied a combination of GA and ANN as a hybrid algorithm to predict the comfort performance and the range of ultraviolet protection factor (UPF) [65]. ANN was applied as a prediction tool and GA was utilised as an optimization tool. For experimental purpose, a set of four samples were selected for the evaluation of functional properties. The proposed ANN–GA method was carried out until the required results were achieved. The results achieved by this method were in good agreement with the standard methods.
2.3. Classification Based on Finishing Processes
2.3.1. Handle Modifications (Softness and Stiffness)
Modification of textile end product by applying softeners and stiffeners is necessary to improve the aesthetic properties. The selection of these materials attracts the scientists and researchers to build and train special machine learning algorithms, special mathematical models and soft computing tools. Farooq et al. used ANN to predict the shade change of dyed knitted fabrics after finishing application [66]. The inputs were the shade percentage, dye color and finishing concentrations. The output was delta values with respect to standard samples. Simulations results showed that ANN provided high prediction accuracy for shade change that occurred during finishing with minimal value of error between actual and predicted values.
2.3.2. Functional Coatings
Malik et al. used ANN for the prediction of antimicrobial performance of chitosan/AgCl-TiO coated fabrics. The input variables were curing time and concentration of colloids [67]. Samples were developed with different blends of selected colloid under different curing time. Feedforward ANN was trained under a hybrid combination of Bayesian regularization and Levenberg Marqaurdt algorithms. The testing results had an acceptable MAE during network training. Furferi et al. introduced a novel ANN algorithm for the prediction of coating process on textile fabrics [68]. Testing results demonstrated the significance of ANN model for coating mechanism. Ni et al. proposed a novel online algorithm that detected and predicted the coating thickness of textiles by hyperspectral images [69]. The proposed algorithm was based on two different optimization modules i.e., the first module was called extreme learning machine (ELM) classifier whereas the second one was called a group of stacked autoencoders. The lateral module was designed to take data from hyperspectral images. However, ELM module optimized by a new optimizer known as grey wolf optimizer (GWO). GWO was used to determine the number of neurons and weights to get more accuracy during classification. The results explained that online detection performance significantly improved with a combination of VW-SAET with GWO-ELM that provided efficiency.
2.3.3. Fabric Defects and Detection
Fabrics are occasionally the end product of any textile manufacturing process and fabric defects inspection is very important in terms of post manufacturing processes i.e., marketing, merchandising and branding. In a simple term, Fabric defects detection is a crucial process applied to control the quality of textile production. Machine learning algorithms have also played their role in this detection/inspection process. The most famous machine learning tools used in defects detection are ANN and image processing algorithms that have been applied for defects detection and grading of woven, knitted and nonwoven textiles. Hanbay et al. presented a literature review about the methods used for the detection of fabric defects and explained that detection methods had several types including structural, hybrid, spectral, model-based and statistical [70]. Czimmermann et al. presented a detail review based on automatically detection of fabric faults and fabric defect [71]. Rasheed et al. reported a comprehensive study on faults detection methods of textiles [72]. The widely used detection methods are based on image segmentation, color coordinates, frequency domain, texture-based, image morphology operations and deep learning. Eldessouki et al. applied a defects detection method composed of a hybrid combination of sepctral (Fourier transform) and (spatial) statistical functions that detected the fabric defects from images [73]. They applied component analysis to overcome input characteristics of selected datasets. The use of PCA in this application increased the classification rate. Liu et al. proposed an algorithm composed of low-rank decomposition and multi-scale convolution neural networks for defects detection [74]. Convolution neural networks were applied to extract multiple characteristics of defects from images for the improvement of image characterization ability to deal with complex textures. However, low-rank decomposition tool was established to analyze matrix characteristics for background (low-rank part) and for (salient defects). Furthermore, the salient defects map produced by sparse matrix was further diversified under threshold to localize the defected area of fabric. The test results showed that extracted features by neural network were accurate enough to analyse fabric texture than traditional standard methods i.e., local binary pattern and histogram of the oriented gradient.
Many other researchers utilised machine learning algorithms for defects detection. Sezer et al. applied independent component analysis (ICA) for defects detection at block level using a sample image [75]. They reported that this method provided satisfactory results for plain weave fabrics. However, for twill and texture weave patterns, this method is not generalized yet. Yapi et al. proposed redundant contourlet transform (RCT) method for defects detection [76]. A finite mixture of generalized Gaussians (MoGG) was used for modeling RCT coefficients that constituted statistical signatures to differentiate the defected fabric from defect-free fabric. The proposed approach was based on three steps: (1) detection of basic pattern for image decomposition and signature calculation, (2) discrimination between defected and defect-free fabric through Bayes classifier (BC) based on labeled fabric samples, and (3) detection of defects during image inspection by testing local patches. Experimental results revealed that the used approach achieved good results compared to ICA, local binary patterns (LBPs) and slope difference distribution (SDD). Li et al. proposed Fisher criterion-based deep learning algorithm for defects detection of patterned fabrics [77]. A Fisher criterion-based stacked denoising method was used for fabric images to classify into defective and defect free categories. The experimental results showed that the accuracy of proposed method was excellent for patterned fabrics and more complex jacquard warp-knitted fabric. Han et al. proposed the stacked convolutional autoencoders for defect detection [78]. The autoencoders were trained through synthetic defected data and non-defected data by using expert-based knowledge of defect characteristics, where, input was used as a defected image produced artificially and output was the corresponding clean image. Jeffrey Kuo et al. detected the following four defects in embroidery textile patterns i.e., stitch missing, joint defect, yarn floating knit and unregistered defect recognition [79]. The results demonstrated that the applied procedure was more effective than back propagation for detects detection as it took less time to train the network. Huang et al. used machine learning tools and image analysis for pilling assessment of fleece [80]. The applied methods were discrete Fourier transform, Gaussian filtering and Daubechies wavelet, for the extraction of important features of image information i.e., pilling area, pilling density and number of pilling points. ANN and SVM were used to classify the textile grade. Experimental results showed that the use of Fourier-Gaussian method improved the efficiency of classification for ANN and SVM. Table 1 elucidates a comparison of related work for defects detection in textile processes.

Table 1.
A comparison of previously performed work for defects detection in textile processes.
2.4. Classification Based on Textile Polymer Composites
Composites are the most promising class of versatile and durable materials of modern age. Machine learning algorithms reduce time, cost and effort to search optimal conditions for selected variables of composite structures. Therefore, machine learning is an essential and effective tool for a comprehensive evaluation of composites. Machine learning is used to solve complex numerical and applied problems in composites. In general, the fabrication of fiber reinforced composites is considered more challenging than other anisotropic structures. Sapuan et al. presented a book on ANN applications for composite materials [88]. They reported the use of ANN for numerous tasks such as defects detection in composites and polymeric structures, localization of carbon fiber–reinforced plastics and perspex plates, prediction of mechanical behavior, aging cycles evaluation, fatigue life prediction and prediction of composites life under loading. Muzel et al. presented a comprehensive review on the applications of finite element method for composite materials, failure criteria, material properties and types of elements in aeronautics, aerospace, naval, automotive, energy, sports, civil, manufacturing and electronics [89]. Dixit et al. introduced a review on modelling approaches for the prediction of mechanical properties of textile based composites using finite element method [90]. However, there are many important parameters need to investigate for the development of new algorithms for composite materials. Therefore, In this study, we will discuss these variables in detail and propose new methods to develop machine learning algorithms for textiles and composite structures. Schimmack et al. used Extended Kalman Filter (EKF) algorithm as a virtual sensor for temperature detection, composed of metal-polymer fibre based heater structure [91]. The main purpose of this algorithm was to control temperature in case of overheating or in any other emergency condition. The results revealed the accuracy of proposed approach. In another study, Gonzalez et al. used CNN for the identification of flow disturbances of dissimilar materials in composites production [92]. Specifically, CNN was applied to detect the position, size and permeability of any embedded material on the surface of mould. In CNN, the region of dissimilar material was selected as an input variable in order to recognise disturbance flow. Altarazi et al. applied multiple algorithms at a time to predict and classify tensile strength of polymeric films of different compositions. The used algorithms were stochastic gradient descent (SGD), ANN, k-nearest neighbors (kNN), decision tree (DT), regression analysis, SVM, random forest (RF), logistic regression (LoR) and AdaBoost (AB) [93]. Experimental results demonstrated that SVM algorithm showed better prediction results. In addition, the results revealed that the classification ability of used algorithms was excellent for sorting films into conforming and non-conforming parts. Balcioglu et al. compared finite element analysis with machine learning algorithms (DT, KNN, RF, SVR) for fracture analysis of polymer composites [94]. Fracture behavior of laminated composites reinforced with pure carbon, glass and carbon/glass composition were tested and compared with standard samples. The RF algorithm showed the best result with lower MSE values compared to other algorithms.
2.4.1. Fiber Reinforced Polymer Composites
The use of natural fibers as a reinforcement in polymer composites has gained commercial success in terms of durable, economical and environmentally friendly materials. Khan et al. investigated the mechanical properties of cross-ply laminated fibre-reinforced polymer composites. They developed model for the prediction of mechanical properties using ANN [95]. The composite samples were developed by altering glass fibre layers with carbon fibre layers and polyphenylene sulphide with high-density polyethylene. The fibers were used as reinforcement and polyphenylene sulphide was used as a polymer matrix. Mechanical properties i.e., hardness, flexural modulus, impact and rupture strength were investigated for both directions. The input variables for ANN model were material type, matrix layers, composition and number of reinforcement. Simulation results showed that ANN predicted the mechanical properties with low MAE. In a study, Boon et al. provided a literature review on recent advances in optimization and design of fiber-reinforced polymer composites [96]. They stated that the best approach to provide accurate results was deep learning (DL). He et al. proposed a delamination detection approach for the detection of location, size and interfacial bonding of delamination in fiber-reinforced polymer composites. This method was based on frequency changes in multiple modes [97]. They employed a combination of different algorithms i.e., support vector machine, extreme learning machine and back propagation neural network for the detection of delamination parameters. Experimental results showed that SVM algorithms provided excellent prediction and classification performance as compared to other two algorithms.
Carbon fiber reinforced polymer composites (CFRP) are the most durable and promising modern age composite materials. By applying machine learning algorithms, researchers significantly reduced cost, efforts and time to determine optimal design points and process variables to develop CFRP structures. Mathematical modeling together with machine learning algorithms provide comprehensive analysis of CFRP structures. Matsuzaki et al. proposed an approach for state estimation and material properties of thermoset CFRP by using data assimilation [98]. Thermosetting simulation based on a non-linear state-space model that utilise ensemble Kalman filter (EnKF) for the estimation of state using data assimilation. This method estimated the degree of curing and the distribution of temperature model with thermal conductivity distribution. Simulation results showed that EnKF was successful in the estimation of the state of thermal conductivity distribution and model parameters. However, the estimation of thermal conductivity in complex distributions is still a challenging task. After the effectiveness of EnKF to estimate various CFRP thermoset molding attributes, they applied EnKF for the estimation of internal temperature during curing [99]. In this application, they selected three samples with altered thermal conductivity. The experimental results validated the efficiency of this approach using these types of specimens. Figure 3 shows a typical problem-solving method under machine learning algorithms validated for numerous types of fiber reinforced polymer composites including CFRP, glass fiber reinforced polymer composites (GFRP), basalt fiber reinforced polymer composites (BFRP) and aramid fiber reinforced polymer composites (AFRP).
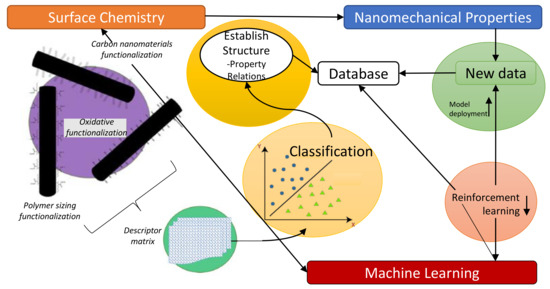
Figure 3.
Summary of machine learning procedure validated for fiber reinforced polymer composites including CFRP, GFRP, BFRP and AFRP etc. [100].
Gonzalez introduced different mathematical models to detect nonlinear flexural deformation of CFRP based on stiffness level in compression and polymer matrices under different strength [101]. The study further presented modeling of different properties of fiber reinforced composite beams [102]. The proposed mathematical model described nonlinear elastic three-point bending of isotropic and reinforced beams under stiffness and strength levels. The obtained results revealed that nonlinear properties of reinforced materials and polymer matrices carefully investigated when designing real structures. Zhang et al. predicted the delaminations through Gaussian process regression (GPR) algorithm for CFRP composites during drilling [103]. Taguchi and GPR approaches explained that more data set were required for the extraction of optimal variables from fewer experimental trials. Konstantopoulos et al. used nanoindentation mapping data with machine learning algorithms to identify interfacial reinforcement [100]. Normalization and k-means clustering were applied to process data by filtering out from epoxy matrix. The used processs was trained by ANN, support vector machines and classification trees. The intrinsic modifications at the interface of CFRP proved that machine learning algorithms effectively patterned data and best fit can be obtained through SVM. Qi et al. employed the decision tree (regression tree) model to establish a relationship between variables properties and macroscopic variables of composite materials [104]. Here, representative volume element (RVE) algorithms for single-layer and multi-layer CFRP were established by a cross-scale FEM and periodic boundary conditions were loaded in order to verified the obtained results. Table 2 illustrates a comparison of related work in fiber reinforced polymer composites.

Table 2.
Comparative study of related work in fiber reinforced polymer composites.
2.4.2. Prediction and Estimation of Reinforced Fibrous Material
Schimmack et al. applied a prediction approach based on wavelet for defects detection of any variable in a fiber reinforced polymer composite [111]. The applied algorithm was based on variance estimation for the local Lipschitz constant of any received signal over time. In addition, a modified recursive least squares (RLS) approach was applied to evaluated the various attributes of conductive multifilament fibers used as reinforcement during production process. The results proposed that RLS algorithms were useful for the estimation of time-varying sinusoidal disturbances as well as for inductance. Lui et al. developed a new strategy to predict the initial failure strength criterion of woven fabric reinforced composites based on micromechanical model by modifying deep learning neural network (DNN) and mechanics of structure genome (MSG) [112]. MGS is used to perform initial failure analysis of a square pack microscale model that trained the samples to detect yarn failure criterion. The effectiveness of this strategy was confirmed by testing yarns of mesoscale plain weave fabrics and fiber reinforced composite materials to compute the initial failure strength constants. Soman et al. used a novel algorithm based on Kalman Filter (KF) for load estimation in beam-like structures under complex loading [113]. Simulation results using experimental data showed that the used algorithm is efficient for classification and monitoring strains in continuous welded rails. In addition, Soman et al. used Kalman filter based neutral axis (NA) tracking algorithm for damage detection in composites structures under varying axial loading [114]. The proposed scheme was applied on a composite beam instrumented with fiber optic strain sensors. The change in neutral axis location is utilized to detect delamination in beams. Simulations results showed that the proposed formulation of KF for NA tracking provided more powerful use of NA location in various applications. Hallal et al. introduced a review on analytical modeling of elastic properties of textile composites [115]. Balokas et al. proposed FEM based multiscale prediction algorithm combined with ANN for the prediction of elastic properties of textile composites under different sources of aleatory uncertainty [116]. The results of sensitivity analysis showed that the proposed algorithm provided good prediction results for elastic yarn properties. Jiang et al. proposed an approach to predict elastic modulus of fiber braided composites with uncertainties using vibration test data [117]. Reference FEM was used for simulation of uncertain elastic parameters that reflected the dynamic characteristics of a braided composites. Statistical analysis of uncertain parameters revealed that uncertainties in elastic modulus can be identified by using modal data.
3. Limitations of the Proposed Techniques
The textile industry is benefited from machine learning tools by using them for different applications like prediction, classification, performance simulation, structural features modelling and image analysis etc. Table 3 summarizes mostly used machine learning techniques by various researcher in textile based applications.

Table 3.
Techniques used in textiles and fiber reinforced polymer composites.
In general, textile processes are mostly non-linear in nature. Therefore, it is difficult to obtain analytic models for the technical design of fabrics due to the difficulties and complex structure imposed by the raw materials. Therefore, most researchers applied ANN in textiles during the confrontation nonlinear and multiparameter problems, without an analytical solution. Furthermore, the use of ANN in textile data prediction, detection, identification and classification problems covers fabrics, fibers, yarns, color, wet processing and garments. In addition, ANN has shown its potential as a successful tool for the prediction of different textiles, fiber reinforced composites and in the evaluation of structural properties of polymer composites. The most common ANN type used in textile industry is multilayer perceptron that represents a class of feedforward ANN. A feedforward network consists of single hidden layer and sigmoid activation function is used extensively to solve textile processing problems. However, the limitations of ANN are: it is not applicable outside the data range for which it is trained. In simple, the durability of ANN is limited to the selected range of data. In addition, ANN cannot answer the relationship between input and output variables i.e., ANN cannot predict why the selected input variables result in a significant increase or decrease in output variables and vice versa. Textile processes parameters prediction in a hybrid situation is a complex task for ANN because of highly variable nature of natural fibers, spinning processes, functional materials and fabric end use requirements. The shortcoming of ANN is the implicit nature of ANN models. Rather than developing an explicit analytic expression i.e., linear or nonlinear, of input and output variables, ANN processes the variables in order to gain iterative knowledge and store it in the system. In such a case, ANN subsequently simulates the system and predicts the results.
Fuzzy logic has been applied in various fields of textiles including the prediction of melt-spun yarn count and tensile strength of fibers, classification of colored cotton into different classes, automatic recognition of fabric weave pattern and intelligent diagnosis system for fabric inspection. However, the use of fuzzy logic in a highly complex system may become an obstacle to the verification of system reliability. In addition, validation and verification of a fuzzy knowledge-based system need extensive testing with hardware. Genetic algorithms are widely used to solve various problems in textile processing right from fiber production to garment design and manufacturing. However, the major limitations of GA are: it cannot guarantee to find an optimal solution and it is time consuming. In addition, the solution quality deteriorates with the increase of the dimension of the problem. The neuro-fuzzy hybrid model was applied in several cases for the prediction of fiber, yarn and fabric properties. The prediction reliability of this hybrid model had outperformed the conventional multiple regression model and the ANN model. Supervised learning techniques such as SVM, SVR, DT, k-nearst, KNN and RT were used for classification, identification and prediction properties. However, the training for these algorithms requires a lot of computation time. Recently, deep learning has been used in some textile applications and has shown its performance in identification, defect detection and prediction. Like every method, DL has some limitations. It requires large training data to provide better performance than other methods. However, it has high computational cost to train complex data models.
Kalman filter, ensemble Kalman filter, extended Kalman filter were used to estimate and track the state of materials and their properties in fiber reinforced polymer composites. Kalman filter provides optimal solution only when the state is linear with Gaussian model. For nonlinear and non Gaussian state-space models, optimal estimation problems do not typically admit analytic solutions. Therefore, a numerical method is needed to approximate the state as EKF, EnKF and PFs. EKF relies on the linearization of nonlinear state and observations, and this may result in an erroneous estimation of the state, and in a highly nonlinear case, the filter may diverge. EnKF works better with the Gaussian model, and the accuracy of its estimation depends on number of samples. These algorithms are not effective when the model is highly non-Gaussian and/or nonlinear. The particle filters (PFs), also called Sequential Monte Carlo (SMC), are able to proceed better in these situations. PFs is a sequential Monte Carlo method to estimate the posterior density of the state in a sequential manner, and does not make any assumptions about the linearity of the system model [118].
4. Future Challenges
The main reason of machine learning algorithms shortcoming is to not fully utilization of valuable and persistent information about the dynamics and physiology of system. In majority of cases, the model structure of textile composites is related to physical information that may not incorporated explicitly into machine learning algorithms. Physiologically stable models, in contrast, for textiles and composites carry all available information related to system and underlying properties, can be developed using state-space framework. In general, state-space hidden Markov models allow extremely flexible frameworks for simulation and modeling of discrete time data. In a linear system with additive Gaussian noise, an optimal estimation is provided using the Kalman filter [119]. However, the textile application state-space models are highly nonlinear and may be non-Gaussian.
Sequential Monte Carlo (SMC) is a famous and reliable class of numerical methods to evaluate optimal designs related problems in nonlinear non-Gaussian systems [118]. SMC is a powerful sampling tool that works with a set of random weighted samples in order to predict the optimal solution. These samples are technically known as particles that are utilized during the approximation of state density and statistics of interest [118]. Given enough particles, the SMC will always perform better than the EKF or EnKF, albeit at the expense of computational requirements [119,120]. In addition, it provides the SMC converges almost to the optimal solution [121]. Figure 4 illustrates a general schematic layout of state estimation with data assimilation using SMC.
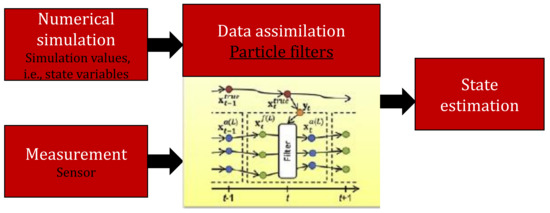
Figure 4.
A general schematic layout of the state estimation method with data assimilation.
4.1. Classical Sequential Monte Carlo
We consider the following constrained discrete state-space model, where model representation consists of a dynamical process that captures temporal evolution of system state. As a result, the measurement model explains the relationship between the system state and the system output.
where is the state transition vector and is the measurement vector. and are possibly nonlinear state transition and measurement functions, respectively. and are the process and measurement zero-mean white noise sequences with known probability density functions (pdfs) and , respectively.
In the Bayesian framework, the optimal inference of the state using the measurement history relies on the posterior density . Using Bayes’ rule, the posterior density can be computed recursively from the following prediction and update steps:
In fact, the Equations (3) and (4) represent only a conceptual solution in the nonlinear case, because the integrals defined are intractable.
Sequential Monte Carlo approximate the posterior density of the unknown state using a set of N particles and their associated weights :
where represents the dirac delta function. In the ideal case, the particles required to be generated from the true posterior , which is unknown. Thereby, another distribution named proposal distribution is used to generate the particles [118]. The importance weight of each particle is computed using:
where the normalized weights are given by .
The conditional mean estimate of the state is then given by:
The weights of the particles may perish and thus require resampling [118]. The particles are resampled according to their weights, i.e., removing particles with very small weights and duplicating particles with large weights. Thus, equal weights () are assigned to all selected N particles. The detailed steps of sequential Monte Carlo are presented in Algorithm 1.
| Algorithm 1 Classical sequential Monte Carlo |
Initialization for i = 1, 2, …, N do Generate . Compute the initial weights using Equation (6) and normalize. end for Estimation for k = 1, 2, …, T do for i = 1, 2, …, N do Generate sample from the system dynamics model (1). Compute weight using: . end for Normalize particle weights . Resample . Compute the weighted mean . end for |
4.2. Constrained Sequential Monte Carlo
Due to physical laws, kinematic constraints, mathematical properties such as target speed restrictions and road networks, technological limitations, geometric considerations, material balance, bounds on actuators and plants and maximum transmission capacity, various dynamical systems are limited within restricted regions [122,123,124]. Generally, these constraints may not indulged in state-space model without a major increase to avoid model complexities [119,124,125,126]. Nevertheless, it is not straightforward to take into account the physiological and modeling constraints on the state with SMC, due to the complex nature of computations in SMC. The current trend in constrained sequential Monte Carlo simply imposes the constraints on all particles of the SMC. These approaches are: (1) The acceptance/rejection approach, which enforces the constraints by simply rejecting the particles violating them [127,128]; (2) Constrained importance distribution, which imposes the constraints on all particles or equivalently sample from a constrained importance distribution [129,130,131,132,133]. The issue of how to impose the constraints -onto prior particles (particles before resampling), posterior particles (particles after resampling) or the estimated unconstrained conditional mean estimate- remains still open [129,134]. But these approach underlies the fundamental assumption that constraints on the conditional mean estimate (given in Equation (9)) can be effectively substituted by the same constraints on all particles. However, this is not true in general. It has been referred to these approaches as Point-wise Density Truncation (PoDeT) methods [135]. It was recently shown that such schemes result in incorrect estimate or irrelevant constraints altogether [135,136].
We consider a general constraint of the form [135,136]:
indicates the constraint function at time k. It is important to affirm that the constraint must only be satisfied by the state estimate provided by the conditional mean, defined as follows:
Recently, Amor et al. derived the optimal bounds of PoDeT [135]. They revealed that error estimation was bounded by the area of state posterior density that had not included constraining interval. Specifically, if most of the density lies within the interval, i.e., the density is well-localized in the constraining interval, then the PoDeT estimation error will be small. However, if a high probability region lies outside of the interval, i.e., the density is not well-localized in the constraining interval, then the PoDeT estimation error will be large [135]. Therefore, Amor et al. proposed a new algorithm referred as “Inductive Mean Density Truncation” (IMeDeT), which inductively samples particles that are guaranteed to satisfy the constraint on the mean of the unknown state [137]. The details the steps of IMeDeT algorithm are presented in Algorithm 2. They evaluated the robustness of the proposed algorithm on the dynamic brain source localization problem using EEG data. In addition, Amor et al. introduced a novel constrained particle filter algorithm called as “mean density truncation” (MiND) and established its convergence properties [136,138]. MiND is based on the principle of minimal perturbation strategy such that the constrained posterior density is “close”to the unconstrained posterior density. Specifically, they imposed the constraint on the mean of the unknown state by perturbing the unconstrained posterior density using only one particle. The details the steps of MiND algorithm are introduced in Algorithm 3. To assess the performance of the proposed algorithm, they applied MiND to solve the problem of movement identification for forearm prosthetic control using the non-negative synergy activation coefficients. The proposed algorithm provided an accurate result with error rates significantly lower than the state-of-the-art in the literature.
Many real-world applications in textile engineering and polymer composites [139,140,141], may take benefits from this research, i.e., constrained state estimation for nonlinear and non-Gaussian dynamical systems. The main objective of this paper is to emphasize the use of sequential Monte Carlo methods as well as their constrained formulation (IMeDeT and MiND) for the development and modelling of many applications in textile engineering based on, prediction, estimation, controlling, defect detection (See examples in Figure 5), identification and classification (See example in Figure 6) etc.
| Algorithm 2 Inductive Mean Density Truncation (IMeDeT) |
Initialization Denote by the constraint region::. for j = 1, 2, …, N do Generate . Compute the initial weights using Equation (6) and normalize. end for Unconstrained estimation fordo for do Generate sample from the system dynamics model (1). Calculate the weights of using Equation (6); then, normalize the weights.
Constrained estimation for i = 1, 2, …, j do if then Go to the next step. else Find a particle such that . end if end for end for Compute the constrained weighted mean . end for |

Figure 5.
Examples of: Defective fabric samples with different patterned textures (from a1–a5). Different types of defects in cotton fabric (from b1–b3). Defect with polymer composite (c1,c2).

Figure 6.
Example of identification and classification fabrics weave samples based on patterns.
| Algorithm 3 Mean Density Truncation (MiND) |
Initialization The same as initializing IMeDeT. for k = 1, 2, …, T do Unconstrained estimation for j = 1, 2, …, N do Generate sample from the system dynamics model (1). Compute weight using Equation (6). end for Normalize particle weights . Resample . Compute the weighted mean .
Constrained estimation if
then Remove the furthest particle . Add a new particle using and where and . Compute the constrained weighted mean . end if end for |
5. Future Direction and Summary
This study focuses on machine learning classification methods specifically designed for textiles and polymer composites. It elucidates how classification methods are applied in fiber reinforced composites to deal with problems. Based on discussed literature, this study clearly explains that machine learning classification receives significant consideration in textiles and composites industries. SVM and ANN are widely used classification methods as they provide better prediction accuracy. In addition, this study provides the classification of carbon fiber reinforced composites and the inclusion of polymeric fibers in composites formation. It elaborates recently used advanced machine learning algorithms for textile processes and carbon fiber reinforced composites. It provides critical and in-depth information regarding the algorithms applied during yarn production, fabric manufacturing and textile finishing processes. Drawbacks and limitations of each method are discussed in detail. This study proposes gateway and opens new avenues not only for researcher community but also for the readership of the journal. In addition, we suggest the use of sequential Monte Carlo methods, i.e., particle filters for control, monitoring, prediction, and identification, in textiles and composites.
For future work, some novel algorithms e.g., golden eagle optimiser are suggested to study the performance of fiber reinforced polymer composites, besides the classification method. Golden eagle optimiser is a recent method and only one or two studies have applied it so far. This can be beneficial to discover complex relationships and useful patterns between textiles and fiber reinforced polymer composites.
In textiles and composites industries, researchers mostly used single classifier. However, combining multiple algorithms may provide a more accurate and semantic vision for the classification of textile processes. Therefore, researchers should start to use hybrid models in order to achieve better results.
Author Contributions
N.A. and M.T.N. conceived, designed and performed experiments; analysed the results and wrote manuscript. M.P. analyzed the results, supervised and acquired funding. All of the authors participated in critical analysis and preparation of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Education, Youth and Sports of the Czech Republic and the European Union (European Structural and Investment Funds—Operational Programme Research, Development and Education) in the frames of the project “Modular platform for autonomous chassis of specialized electric vehicles for freight and equipment transportation”, Reg. No. CZ.02.1.01/0.0/0.0/16025/0007293.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Giri, C.; Jain, S.; Zeng, X.; Bruniaux, P. A Detailed Review of Artificial Intelligence Applied in the Fashion and Apparel Industry. IEEE Access 2019, 7, 95376–95396. [Google Scholar] [CrossRef]
- Noman, M.T.; Wiener, J.; Saskova, J.; Ashraf, M.A.; Vikova, M.; Jamshaid, H.; Kejzlar, P. In-situ development of highly photocatalytic multifunctional nanocomposites by ultrasonic acoustic method. Ultrason. Sonochem. 2018, 40, 41–56. [Google Scholar] [CrossRef]
- Noman, M.T.; Petrů, M. Functional Properties of Sonochemically Synthesized Zinc Oxide Nanoparticles and Cotton Composites. Nanomaterials 2020, 10, 1661. [Google Scholar] [CrossRef]
- Behera, P.; Noman, M.T.; Petrů, M. Enhanced Mechanical Properties of Eucalyptus-Basalt-Based Hybrid-Reinforced Cement Composites. Polymers 2020, 12, 2837. [Google Scholar] [CrossRef]
- Ashraf, M.; Wiener, J.; Farooq, A.; Šašková, J.; Noman, M. Development of Maghemite Glass Fibre Nanocomposite for Adsorptive Removal of Methylene Blue. Fibers Polym. 2018, 19, 1735–1746. [Google Scholar] [CrossRef]
- Jamshaid, H.; Mishra, R.; Militký, J.; Pechočiaková, M.; Noman, M. Mechanical, thermal and interfacial properties of green composites from basalt and hybrid woven fabrics. Fibers Polym. 2016, 17, 1675–1686. [Google Scholar] [CrossRef]
- Mahmood, A.; Noman, M.T.; Pechočiaková, M.; Amor, N.; Petrů, M.; Abdelkader, M.; Militký, J.; Sozcu, S.; Hassan, S.Z.U. Geopolymers and Fiber-Reinforced Concrete Composites in Civil Engineering. Polymers 2021, 13, 2099. [Google Scholar] [CrossRef]
- Sarr, M.M.; Inoue, H.; Kosaka, T. Study on the improvement of interfacial strength between glass fiber and matrix resin by grafting cellulose nanofibers. Compos. Sci. Technol. 2021, 211, 108853. [Google Scholar] [CrossRef]
- Liu, L.; Wang, X.; Wu, Z.; Keller, T. Tension-tension fatigue behavior of ductile adhesively-bonded FRP joints. Compos. Struct. 2021, 268, 113925. [Google Scholar] [CrossRef]
- Li, C.; Xian, G.; Li, H. Influence of immersion in water under hydraulic pressure on the interfacial shear strength of a unidirectional carbon/glass hybrid rod. Polym. Test. 2018, 72, 164–171. [Google Scholar] [CrossRef]
- Li, C.; Yin, X.; Liu, Y.; Guo, R.; Xian, G. Long-term service evaluation of a pultruded carbon/glass hybrid rod exposed to elevated temperature, hydraulic pressure and fatigue load coupling. Int. J. Fatigue 2020, 134, 105480. [Google Scholar] [CrossRef]
- Li, C.; Yin, X.; Wang, Y.; Zhang, L.; Zhang, Z.; Liu, Y.; Xian, G. Mechanical property evolution and service life prediction of pultruded carbon/glass hybrid rod exposed in harsh oil-well condition. Compos. Struct. 2020, 246, 112418. [Google Scholar] [CrossRef]
- Amor, N.; Noman, M.T.; Petrů, M. Prediction of functional properties of nano TiO2 coated cotton composites by artificial neural network. Sci. Rep. 2021, 11, 12235. [Google Scholar] [CrossRef]
- Amor, N.; Noman, M.T.; Petrů, M.; Mahmood, A.; Ismail, A. Neural network-crow search model for the prediction of functional properties of nano TiO2 coated cotton composites. Sci. Rep. 2021, 11, 13649. [Google Scholar] [CrossRef]
- Zimmerling, C.; Dörr, D.; Henning, F.; Kärger, L. A machine learning assisted approach for textile formability assessment and design improvement of composite components. Compos. Part A Appl. Sci. Manuf. 2019, 124, 105459. [Google Scholar] [CrossRef]
- Seçkin, M.; Çağdaş Seçkin, A.; Coşkun, A. Production fault simulation and forecasting from time series data with machine learning in glove textile industry. J. Eng. Fibers Fabr. 2019, 14, 1558925019883462. [Google Scholar] [CrossRef]
- Ribeiro, R.; Pilastri, A.; Moura, C.; Rodrigues, F.; Rocha, R.; Morgado, J.; Cortez, P. Predicting Physical Properties of Woven Fabrics via Automated Machine Learning and Textile Design and Finishing Features. In Artificial Intelligence Applications and Innovations; Maglogiannis, I., Iliadis, L., Pimenidis, E., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 244–255._21. [Google Scholar] [CrossRef]
- Noman, M.T.; Petru, M.; Louda, P.; Kejzlar, P. Woven Textiles Coated with Zinc Oxide Nanoparticles and Their Thermophysiological Comfort Properties. J. Nat. Fibers 2021, 1–13. [Google Scholar] [CrossRef]
- Noman, M.T.; Amor, N.; Petru, M.; Mahmood, A.; Kejzlar, P. Photocatalytic Behaviour of Zinc Oxide Nanostructures on Surface Activation of Polymeric Fibres. Polymers 2021, 13, 1227. [Google Scholar] [CrossRef] [PubMed]
- Majumdar, A. Soft Computing in Textile Engineering; Woodhead Publishing: Sawston, UK, 2011; pp. i–iii. [Google Scholar] [CrossRef]
- Mohammad, A.T.; Mahboubeh, M. Artificial Neural Network Prosperities in Textile Applications. In Artificial Neural Networks Industrial and Control Engineering Applications; Suzuki, K., Ed.; IntechOpen: Rijeka, Croatia, 2011; pp. 35–64. [Google Scholar] [CrossRef]
- Vassiliadis, S.; Rangoussi, M.; Cay, A.; Provatidis, C. Artificial Neural Networks and Their Applications in the Engineering of Fabrics. In Woven Fabric Engineering; Dubrovski, P.D., Ed.; Intechopen: London, UK, 2010; pp. 111–134. [Google Scholar] [CrossRef]
- Farooq, A.; Sarwar, M.I.; Ashraf, M.A.; Iqbal, D.; Hussain, A.; Malik, S. Predicting Cotton Fibre Maturity by Using Artificial Neural Network. Autex Res. J. 2018, 18, 429–433. [Google Scholar] [CrossRef]
- Malik, S.A.; Gereke, T.; Farooq, A.; Aibibu, D.; Cherif, C. Prediction of yarn crimp in PES multifilament woven barrier fabrics using artificial neural network. J. Text. Inst. 2018, 109, 942–951. [Google Scholar] [CrossRef]
- Majumdar, P.K.; Majumdar, A. Predicting the Breaking Elongation of Ring Spun Cotton Yarns Using Mathematical, Statistical, and Artificial Neural Network Models. Text. Res. J. 2004, 74, 652–655. [Google Scholar] [CrossRef]
- Majumdar, A.; Majumdar, P.K.; Sarkar, B. Application of an adaptive neuro-fuzzy system for the prediction of cotton yarn strength from HVI fibre properties. J. Text. Inst. 2005, 96, 55–60. [Google Scholar] [CrossRef]
- Almetwally, A.A.; Idrees, H.M.; Hebeish, A.A. Predicting the tensile properties of cotton/spandex core-spun yarns using artificial neural network and linear regression models. J. Text. Inst. 2014, 105, 1221–1229. [Google Scholar] [CrossRef]
- Doran, E.C.; Sahin, C. The prediction of quality characteristics of cotton/elastane core yarn using artificial neural networks and support vector machines. Text. Res. J. 2020, 90, 1558–1580. [Google Scholar] [CrossRef]
- Dashti, M.; Derhami, V.; Ekhtiyari, E. Yarn tenacity modeling using artificial neural networks and development of a decision support system based on genetic algorithms. J. AI Data Min. 2014, 2, 73–78. [Google Scholar] [CrossRef]
- Mishra, S. Prediction of Yarn Strength Utilization in Cotton Woven Fabrics using Artificial Neural Network. J. Inst. Eng. Ser. E 2015, 96, 151–157. [Google Scholar] [CrossRef]
- Mozafary, V.; Payvandy, P. Application of data mining technique in predicting worsted spun yarn quality. J. Text. Inst. 2014, 105, 100–108. [Google Scholar] [CrossRef]
- Malik, S.A.; Farooq, A.; Gereke, T.; Cherif, C. Prediction of Blended Yarn Evenness and Tensile Properties by Using Artificial Neural Network and Multiple Linear Regression. Autex Res. J. 2016, 16, 43–50. [Google Scholar] [CrossRef]
- El-Geiheini, A.; ElKateb, S.; Abd-Elhamied, M.R. Yarn Tensile Properties Modeling Using Artificial Intelligence. Alex. Eng. J. 2020, 59, 4435–4440. [Google Scholar] [CrossRef]
- Erbil, Y.; Babaarslan, O.; İlhami, I. A comparative prediction for tensile properties of ternary blended open-end rotor yarns using regression and neural network models. J. Text. Inst. 2018, 109, 560–568. [Google Scholar] [CrossRef]
- Azimi, B.; Tehran, M.A.; Mojtahedi, M.R.M. Prediction of False Twist Textured Yarn Properties by Artificial Neural Network Methodology. J. Eng. Fibers Fabr. 2013, 8, 97–101. [Google Scholar] [CrossRef]
- Noman, M.; Ashraf, M.A.; Jamshaid, H.; Ali, A. A Novel Green Stabilization of TiO2 Nanoparticles onto Cotton. Fibers Polym. 2018, 19, 2268–2277. [Google Scholar] [CrossRef]
- Azeem, M.; Noman, M.T.; Wiener, J.; Petru, M.; Louda, P. Structural design of efficient fog collectors: A review. Environ. Technol. Innov. 2020, 20, 1–17. [Google Scholar] [CrossRef]
- Yang, T.; Hu, L.; Xiong, X.; Petrů, M.; Noman, M.T.; Mishra, R.; Militký, J. Sound Absorption Properties of Natural Fibers: A Review. Sustainability 2020, 12, 8477. [Google Scholar] [CrossRef]
- Noman, M.; Ashraf, M.A.; Ali, A. Synthesis and applications of nano-TiO2: A review. Environ. Sci. Pollut. Res. 2018, 26, 3262–3291. [Google Scholar] [CrossRef]
- Noman, M.T.; Petru, M.; Militký, J.; Azeem, M.; Ashraf, M.A. One-Pot Sonochemical Synthesis of ZnO Nanoparticles for Photocatalytic Applications, Modelling and Optimization. Materials 2020, 13, 14. [Google Scholar] [CrossRef] [PubMed]
- Noman, M.; Amor, N.; Petru, M. Synthesis and applications of ZnO nanostructures (ZONSs): A review. Crit. Rev. Solid State Mater. Sci. 2021, 2, 1–44. [Google Scholar] [CrossRef]
- Hussain, M.; Khan, B.; Wang, Z.; Ding, S. Woven Fabric Pattern Recognition and Classification Based on Deep Convolutional Neural Networks. Electronics 2020, 9, 1048. [Google Scholar] [CrossRef]
- Eldessouki, M.; Hassan, M. Adaptive neuro-fuzzy system for quantitative evaluation of woven fabrics’ pilling resistance. Expert Syst. Appl. 2015, 42, 2098–2113. [Google Scholar] [CrossRef]
- Xiao, Q.; Wang, R.; Zhang, S.; Li, D.; Sun, H.; Wang, L. Prediction of pilling of polyester–cotton blended woven fabric using artificial neural network models. J. Eng. Fibers Fabr. 2020, 15, 1558925019900152. [Google Scholar] [CrossRef]
- Taieb, A.H.; Mshali, S.; Sakli, F. Predicting Fabric Drapability Property by Using an Artificial Neural Network. J. Eng. Fibers Fabr. 2018, 13, 87–93. [Google Scholar] [CrossRef]
- Hussain, T.; Malik, Z.A.; Arshad, Z.; Nazir, A. Comparison of artificial neural network and adaptive neuro-fuzzy inference system for predicting the wrinkle recovery of woven fabrics. J. Text. Inst. 2015, 106, 934–938. [Google Scholar] [CrossRef]
- Noman, M.T.; Petru, M. Effect of Sonication and Nano TiO2 on Thermophysiological Comfort Properties of Woven Fabrics. ACS Omega 2020, 5, 11481–11490. [Google Scholar] [CrossRef]
- Mansoor, T.; Hes, L.; Bajzik, V.; Noman, M.T. Novel method on thermal resistance prediction and thermo-physiological comfort of socks in a wet state. Text. Res. J. 2020, 90, 1987–2006. [Google Scholar] [CrossRef]
- Noman, M.; Petrů, M.; Amor, N.; Yang, T.; Mansoor, T. Thermophysiological comfort of sonochemically synthesized nano TiO2 coated woven fabrics. Sci. Rep. 2020, 10, 17204. [Google Scholar] [CrossRef]
- Ali, A.; Nguyen, N.H.A.; Baheti, V.; Ashraf, M.; Militky, J.; Mansoor, T.; Noman, M.T.; Ahmad, S. Electrical conductivity and physiological comfort of silver coated cotton fabrics. J. Text. Inst. 2018, 109, 620–628. [Google Scholar] [CrossRef]
- Noman, M.; Petrů, M.; Amor, N.; Louda, P. Thermophysiological comfort of zinc oxide nanoparticles coated woven fabrics. Sci. Rep. 2020, 10, 21080. [Google Scholar] [CrossRef]
- Malik, S.A.; Kocaman, R.T.; Kaynak, H.; Gereke, T.; Aibibu, D.; Babaarslan, O.; Cherif, C. Analysis and prediction of air permeability of woven barrier fabrics with respect to material, fabric construction and process parameters. Fibers Polym. 2017, 18, 2005–2017. [Google Scholar] [CrossRef]
- Malik, S.A.; Kocaman, R.T.; Gereke, T.; Aibibu, D.; Cherif, C. Prediction of the Porosity of Barrier Woven Fabrics with Respect to Material, Construction and Processing Parameters and Its Relation with Air Permeability. Fibres Text. East. Eur. 2018, 26, 71–79. [Google Scholar] [CrossRef]
- Wong, A.; Li, Y.; Yeung, P. Predicting Clothing Sensory Comfort with Artificial Intelligence Hybrid Models. Text. Res. J. 2004, 74, 13–19. [Google Scholar] [CrossRef]
- Xu, J.; He, Z.; Li, S.; Ke, W. Production cost optimization of enzyme washing for indigo dyed cotton denim by combining Kriging surrogate with differential evolution algorithm. Text. Res. J. 2020, 90, 1860–1871. [Google Scholar] [CrossRef]
- Unal, P.; Üreyen, M.; Mecit, D. Predicting properties of single jersey fabrics using regression and artificial neural network models. Fibers Polym. 2012, 13, 87–95. [Google Scholar] [CrossRef]
- Yang, C.S.; Lin, C.; Chen, W. Using deep principal components analysis-based neural networks for fabric pilling classification. Electronics 2019, 8, 474. [Google Scholar] [CrossRef]
- Özçelik Kayseri, G.; Kirtay, E. Part II. Predicting the Pilling Tendency of the Cotton Interlock Knitted Fabrics by Artificial Neural Network. J. Eng. Fibers Fabr. 2015, 10, 62–71. [Google Scholar] [CrossRef]
- Fayala, F.; Alibi, H.; Benltoufa, S.; Jemni, A. Neural Network for Predicting Thermal Conductivity of Knit Materials. J. Eng. Fibers Fabr. 2008, 3, 53–60. [Google Scholar] [CrossRef]
- Majumdar, A. Modelling of thermal conductivity of knitted fabrics made of cotton–bamboo yarns using artificial neural network. J. Text. Inst. 2011, 102, 752–762. [Google Scholar] [CrossRef]
- Kanat, Z.E.; Özdil, N. Application of artificial neural network (ANN) for the prediction of thermal resistance of knitted fabrics at different moisture content. J. Text. Inst. 2018, 109, 1247–1253. [Google Scholar] [CrossRef]
- Mitra, A.; Majumdar, A.; Majumdar, P.K.; Bannerjee, D. Predicting thermal resistance of cotton fabrics by artificial neural network model. Exp. Therm. Fluid Sci. 2013, 50, 172–177. [Google Scholar] [CrossRef]
- Wang, D.; Barber, J.; Lu, W.; Thouless, M. Use of wavelet analysis for an objective evaluation of the formation of pills in nonwoven fabrics. J. Ind. Text. 2019, 49, 663–675. [Google Scholar] [CrossRef]
- Kalkanci, M.; Sinecen, M.; Kurumer, G. Prediction of dimensional change in finished fabric through artificial neural networks. Tekst. Konfeksiyon 2018, 28, 43–51. [Google Scholar] [CrossRef]
- Majumdar, A.; Das, A.; Hatua, P.; Ghosh, A. Optimization of Woven Fabric Parameters for Ultraviolet Radiation Protection and Comfort Using Artificial Neural Network and Genetic Algorithm. Neural Comput. Appl. 2016, 27, 2567–2576. [Google Scholar] [CrossRef]
- Farooq, A.; Irshad, F.; Azeemi, R.; Iqbal, N. Prognosticating the Shade Change after Softener Application using Artificial Neural Networks. Autex Res. J. 2020, 79–84. [Google Scholar] [CrossRef]
- Malik, S.A.; Arain, R.A.; Khatri, Z.; Saleemi, S.; Cherif, C. Neural network modeling and principal component analysis of antibacterial activity of chitosan/AgCl-TiO2 colloid treated cotton fabric. Fibers Polym. 2015, 16, 1142–1149. [Google Scholar] [CrossRef]
- Furferi, R.; Governi, L.; Volpe, Y. Modelling and simulation of an innovative fabric coating process using artificial neural networks. Text. Res. J. 2012, 82, 1282–1294. [Google Scholar] [CrossRef]
- Ni, C.; Li, Z.; Zhang, X.; Sun, X.; Huang, Y.; Zhao, L.; Zhu, T.; Wang, D. Online Sorting of the Film on Cotton Based on Deep Learning and Hyperspectral Imaging. IEEE Access 2020, 8, 93028–93038. [Google Scholar] [CrossRef]
- Hanbay, K.; Talu, M.F.; Ozguvenc, O.F. Fabric defect detection systems and methods—A systematic literature review. Optik 2016, 127, 11960–11973. [Google Scholar] [CrossRef]
- Czimmermann, T.; Ciuti, G.; Milazzo, M.; Chiurazzi, M.; Roccella, S.; Oddo, C.M.; Dario, P. Visual-Based Defect Detection and Classification Approaches for Industrial Applications—A SURVEY. Sensors 2020, 20, 1459. [Google Scholar] [CrossRef] [PubMed]
- Rasheed, A.; Zafar, B.; Rasheed, A.; Ali, N.; Sajid, M.; Hanif Dar, S.; Habib, U.; Shehryar, T.; Mahmood, M.T. Fabric Defect Detection Using Computer Vision Techniques: A Comprehensive Review. Math. Probl. Eng. 2020, 2020, 8189403. [Google Scholar] [CrossRef]
- Eldessouki, M.; Hassan, M.; Qashqary, K.; Shady, E. Application of Principal Component Analysis to Boost the Performance of an Automated Fabric Fault Detector and Classifier. Fibres Text. East. Eur. 2014, 22, 51–57. [Google Scholar]
- Liu, Z.; Wang, B.; Li, C.; Yu, M.; Ding, S. Fabric defect detection based on deep-feature and low-rank decomposition. J. Eng. Fibers Fabr. 2020, 15, 1–12. [Google Scholar] [CrossRef]
- Sezer, O.; Ercil, A.; Ertuzun, A. Using perceptual relation of regularity and anisotropy in the texture with independent component model for defect detection. Pattern Recognit. 2007, 40, 121–133. [Google Scholar] [CrossRef]
- Yapi, D.; Allili, M.S.; Baaziz, N. Automatic Fabric Defect Detection Using Learning-Based Local Textural Distributions in the Contourlet Domain. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1014–1026. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, W.; Pan, J. Deformable Patterned Fabric Defect Detection With Fisher Criterion-Based Deep Learning. IEEE Trans. Autom. Sci. Eng. 2017, 14, 1256–1264. [Google Scholar] [CrossRef]
- Han, Y.J.; Yu, H.J. Fabric Defect Detection System Using Stacked Convolutional Denoising Auto-Encoders Trained with Synthetic Defect Data. Appl. Sci. 2020, 10, 2511. [Google Scholar] [CrossRef]
- Kuo, C.F.J.; Juang, Y. A study on the recognition and classification of embroidered textile defects in manufacturing. Text. Res. J. 2016, 86, 393–408. [Google Scholar] [CrossRef]
- Huang, M.L.; Fu, C.C. Applying Image Processing to the Textile Grading of Fleece Based on Pilling Assessment. Fibers 2018, 6, 73. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C. Automated vision system for fabric defect inspection using Gabor filters and PCNN. SpringerPlus 2016, 5, 765. [Google Scholar] [CrossRef]
- Sacco, C.; Radwan, A.; Harik, R.; Tooren, M.V. Automated Fiber Placement Defects: Automated Inspection and Characterization. In Proceedings of the SAMPE 2018 Conference and Exhibition, Long Beach, CA, USA, 25 May 2018; pp. 1–13. [Google Scholar]
- Liang, Z.; Xu, B.; Chi, Z.; Feng, D. Intelligent characterization and evaluation of yarn surface appearance using saliency map analysis, wavelet transform and fuzzy ARTMAP neural network. Expert Syst. Appl. 2012, 39, 4201–4212. [Google Scholar] [CrossRef]
- Jing, J.; Wang, Z.; Rätsch, M.; Zhang, H. Mobile-Unet: An efficient convolutional neural network for fabric defect detection. Text. Res. J. 2020, 0040517520928604. [Google Scholar] [CrossRef]
- Jeyaraj, P.R.; Nadar, E.R.S. Effective textile quality processing and an accurate inspection system using the advanced deep learning technique. Text. Res. J. 2020, 90, 971–980. [Google Scholar] [CrossRef]
- Wei, B.; Hao, K.; Tang, X.S.; Ding, Y. A new method using the convolutional neural network with compressive sensing for fabric defect classification based on small sample sizes. Text. Res. J. 2019, 89, 3539–3555. [Google Scholar] [CrossRef]
- Hu, G.; Huang, J.; Wang, Q.; Li, J.; Xu, Z.; Huang, X. Unsupervised fabric defect detection based on a deep convolutional generative adversarial network. Text. Res. J. 2020, 90, 247–270. [Google Scholar] [CrossRef]
- Sapuan, S.; Mujtaba, I. Composite Materials Technology: Neural Network Applications; CRC Press: Boca Raton, FL, USA, 2009; pp. 1–355. [Google Scholar]
- Müzel, S.D.; Bonhin, E.P.; Guimarães, N.; Guidi, E.S. Application of the Finite Element Method in the Analysis of Composite Materials: A Review. Polymers 2020, 12, 818. [Google Scholar] [CrossRef]
- Dixit, A.; Mali, H.S. Modeling techniques for predicting the mechanical properties of woven-fabric textile composites: A Review. Mech. Compos. Mater. 2013, 49, 1–20. [Google Scholar] [CrossRef]
- Schimmack, M.; Haus, B.; Leuffert, P.; Mercorelli, P. An Extended Kalman Filter for temperature monitoring of a metal-polymer hybrid fibre based heater structure. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 376–381. [Google Scholar] [CrossRef]
- González, C.; Fernández-León, J. A Machine Learning Model to Detect Flow Disturbances during Manufacturing of Composites by Liquid Moulding. J. Compos. Sci. 2020, 4, 71. [Google Scholar] [CrossRef]
- Altarazi, S.; Allaf, R.; Alhindawi, F. Machine Learning Models for Predicting and Classifying the Tensile Strength of Polymeric Films Fabricated via Different Production Processes. Materials 2019, 12, 1475. [Google Scholar] [CrossRef]
- Balcioglu, H.E.; Seckin, A.C. Comparison of machine learning methods and finite element analysis on the fracture behavior of polymer composites. Arch. Appl. Mech. 2020, 91, 223–239. [Google Scholar] [CrossRef]
- Khan, S.; Malik, S.A.; Gull, N.; Saleemi, S.; Islam, A.; Butt, M.T.Z. Fabrication and modelling of the macro-mechanical properties of cross-ply laminated fibre-reinforced polymer composites using artificial neural network. Adv. Compos. Mater. 2019, 28, 409–423. [Google Scholar] [CrossRef]
- Boon, Y.D.; Joshi, S.C.; Bhudolia, S.K.; Gohel, G. Recent Advances on the Design Automation for Performance-Optimized Fiber Reinforced Polymer Composite Components. J. Compos. Sci. 2020, 4, 61. [Google Scholar] [CrossRef]
- He, M.; Wang, Y.; Ramakrishnan, K.R.; Zhang, Z. A comparison of machine learning algorithms for assessment of delamination in fiber-reinforced polymer composite beams. Struct. Health-Monit. Int. J. 2020, 1997–2012. [Google Scholar] [CrossRef]
- Matsuzaki, R.; Tachikawa, T.; Ishizuka, J. Estimation of state and material properties during heat-curing molding of composite materials using data assimilation: A numerical study. Heliyon 2018, 4, e00554. [Google Scholar] [CrossRef]
- Ishizuka, J.; Matsuzaki, R.; Tachikawa, T. Data assimilation-based state estimation of composites during molding. Adv. Compos. Mater. 2019, 28, 225–243. [Google Scholar] [CrossRef]
- Konstantopoulos, G.; Koumoulos, E.P.; Charitidis, C.A. Classification of mechanism of reinforcement in the fiber-matrix interface: Application of Machine Learning on nanoindentation data. Mater. Des. 2020, 192, 108705. [Google Scholar] [CrossRef]
- Golushko, S. Mathematical Modeling and Numerical Optimization of Composite Structures; Intechopen: London, UK, 2019; pp. 13–34. [Google Scholar] [CrossRef]
- Golushko, S.; Buznik, V.; Nuzhny, G. Mathematical modeling and numerical analysis of reinforced composite beams. J. Phys. Conf. Ser. 2019, 1268, 012018. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, X. Predicting the delamination factor in carbon fibre reinforced plastic composites during drilling through the Gaussian process regression. J. Compos. Mater. 2020, 2061–2067. [Google Scholar] [CrossRef]
- Qi, Z.; Zhang, N.; Liu, Y.; Chen, W. Prediction of mechanical properties of carbon fiber based on cross-scale FEM and machine learning. Compos. Struct. 2019, 212, 199–206. [Google Scholar] [CrossRef]
- Liang, L.; Liu, M.; Martin, C.; Sun, W. A deep learning approach to estimate stress distribution: A fast and accurate surrogate of finite-element analysis. J. R. Soc. Interface 2018, 15, 20170844. [Google Scholar] [CrossRef]
- Shaban, Y.; Meshreki, M.; Yacout, S.; Balazinski, M.; Attia, H. Process control based on pattern recognition for routing carbon fiber reinforced polymer. J. Intell. Manuf. 2017, 28, 165–179. [Google Scholar] [CrossRef]
- Zhao, Z.; Yua, M.; Dong, S. Damage Location Detection of the CFRP Composite Plate Based on Neural Network Regression. In Proceedings of the 7th Asia-Pacific Workshop on Structural Health Monitoring, Hong Kong, China, 12–15 November 2018; pp. 1–10. [Google Scholar]
- Nasser, J.; Groo, L.; Sodano, H. Artificial neural networks and phenomenological degradation models for fatigue damage tracking and life prediction in laser induced graphene interlayered fiberglass composites. Smart Mater. Struct. 2021, 30, 085010. [Google Scholar] [CrossRef]
- Liu, K.; Ma, Z.; Liu, Y.; Yang, J.; Yao, Y. Enhanced Defect Detection in Carbon Fiber Reinforced Polymer Composites via Generative Kernel Principal Component Thermography. Polymers 2021, 13, 825. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Hu, S.J.; Freiheit, T. Feature-based quality classification for ultrasonic welding of carbon fiber reinforced polymer through Bayesian regularized neural network. J. Manuf. Syst. 2021, 58, 335–347. [Google Scholar] [CrossRef]
- Schimmack, M.; McGaw, D.; Mercorelli, P. Wavelet based Fault Detection and RLS Parameter Estimation of Conductive Fibers with a Simultaneous Estimation of Time-Varying Disturbance. IFAC-PapersOnLine 2015, 48, 1773–1778. [Google Scholar] [CrossRef]
- Liu, X.; Gasco, F.; Goodsell, J.; Yu, W. Initial failure strength prediction of woven composites using a new yarn failure criterion constructed by deep learning. Compos. Struct. 2019, 230, 111505. [Google Scholar] [CrossRef]
- Soman, R.; Ostachowicz, W. Kalman Filter Based Load Monitoring in Beam Like Structures Using Fibre-Optic Strain Sensors. Sensors 2019, 19, 103. [Google Scholar] [CrossRef]
- Soman, R.; Ostachowicz, W. Kalman Filter based Neutral Axis tracking for damage detection in composites structures under changing axial loading conditions. Compos. Struct. 2018, 206, 517–525. [Google Scholar] [CrossRef]
- Hallal, A.; Younes, R.; Fardoun, F. Review and comparative study of analytical modeling for the elastic properties of textile composites. Compos. Part B Eng. 2013, 50, 22–31. [Google Scholar] [CrossRef]
- Balokas, G.A.; Czichon, S.; Rolfes, R. Neural network assisted multiscale analysis for the elastic properties prediction of 3D braided composites under uncertainty. Compos. Struct. 2018, 183, 550–562. [Google Scholar] [CrossRef]
- Jiang, D.; Li, Y.; Fei, Q.; Wu, S. Prediction of uncertain elastic parameters of a braided composite. Compos. Struct. 2015, 126, 123–131. [Google Scholar] [CrossRef]
- Doucet, A.; Johansen, A.M. Handbook of Nonlinear Filtering; Oxford University Press: Oxford, UK, 2009; Volume 12, pp. 656–704. [Google Scholar]
- Simon, D. Optimal State Estimation: Kalman, H∞, and Nonlinear Approaches; Wiley: Hoboken, NJ, USA, 2006; p. 552. [Google Scholar] [CrossRef]
- Amor, N.; Meddeb, A.; Marrouchi, S.; Chebbi, S. A comparative study of nonlinear Bayesian filtering algorithms for estimation of gene expression time series data. Turk. J. Electr. Eng. Comput. Sci. 2019, 27, 2648–2665. [Google Scholar] [CrossRef]
- Crisan, D.; Doucet, A. A survery of convergence results on particle filtering methods for practitioners. IEEE Trans. Signal Process. 2002, 50, 736–746. [Google Scholar] [CrossRef]
- Huang, Y.; Werner, S.; Huang, J.; Kashyap, N.; Gupta, V. State Estimation in Electric Power Grids: Meeting New Challenges Presented by the Requirements of the Future Grid. IEEE Signal Process. Mag. 2012, 29, 33–43. [Google Scholar] [CrossRef]
- Battistello, G.; Ulmke, M. Exploitation of a-priori information for tracking maritime intermittent data sources. In Proceedings of the International Conference on Information Fusion, Chicago, IL, USA, 5–8 July 2011; pp. 1–8. [Google Scholar]
- Yang, C.; Bakich, M.; Blasch, E. Nonlinear constrained tracking of targets on roads. In Proceedings of the International Conference on Information Fusion, Sydney, NSW, Australia, 4–7 July 2005; pp. 235–242. [Google Scholar] [CrossRef]
- Agate, C.S.; Sullivan, K.J. Road-constrained target tracking and identification using a particle filter. In Proceedings of the Signal and Data Processing of Small Targets, San Diego, CA, USA, 5–7 August 2003; Volume 5204, pp. 532–543. [Google Scholar] [CrossRef]
- Ko, S.; Bitmead, R.R. State estimation for linear systems with state equality constraints. Automatica 2007, 43, 1363–1368. [Google Scholar] [CrossRef]
- Lang, L.; Chen, W.S.; Bakshi, B.R.; Goel, P.K.; Ungarala, S. Bayesian estimation via sequential Monte Carlo sampling Constrained dynamic systems. Automatica 2007, 43, 615–622. [Google Scholar] [CrossRef]
- Ungarala, S. A direct sampling particle filter from approximate conditional density function supported on constrained state space. Comput. Chem. Eng. 2011, 35, 1110–1118. [Google Scholar] [CrossRef]
- Shao, X.; Huang, B.; Lee, J.M. Constrained Bayesian state estimation: A comparative study and a new particle filter based approach. J. Process Control 2010, 20, 143–157. [Google Scholar] [CrossRef]
- Papi, F.; Podt, M.; Boers, Y.; Battistello, G. On constraints exploitation for particle filtering based target tracking. In Proceedings of the International Conference on Information Fusion, Singapore, 9–12 July 2012; pp. 455–462. [Google Scholar]
- Prakash, J.; Patwardhan, S.C.; Shah, S.L. On the choice of importance distributions for unconstrained and constrained state estimation using particle filter. J. Process Control 2011, 21, 3–16. [Google Scholar] [CrossRef]
- Straka, O.; Dunik, J.; Simandl, M. Truncation nonlinear filters for state estimation with nonlinear inequality constraints. Automatica 2012, 48, 273–286. [Google Scholar] [CrossRef]
- Zhao, Z.; Huang, B.; Liu, F. Constrained Particle Filtering Methods for State Estimation of Nonlinear Process; Wiley: Hoboken, NJ, USA, 2014; Volume 60, pp. 2072–2082. [Google Scholar] [CrossRef]
- Amor, N.; Rasool, G.; Bouaynaya, N.C. Constrained State Estimation—A Review. arXiv 2018, arXiv:eess.SP/1807.03463. [Google Scholar]
- Amor, N.; Bouaynaya, N.C.; Shterenberg, R.; Chebbi, S. On the convergence of the constrained particle filters. IEEE Signal Process. Lett. 2017, 24, 858–862. [Google Scholar] [CrossRef]
- Amor, N.; Rasool, G.; Bouaynaya, N.C.; Shterenberg, R. Constrained particle filtering for movement identification in forearm prosthesis. Signal Process. 2019, 161, 25–35. [Google Scholar] [CrossRef]
- Amor, N.; Bouaynaya, N.; Georgieva, P.; Shterenberg, R.; Chebbi, S. EEG Dynamic Source Localization using Constrained Particle Filtering. In Proceedings of the International Conference on Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Amor, N.; Rasool, G.; Bouaynaya, N.; Shterenberg, R. Hand Movement Discrimination Using Particle Filters. In Proceedings of the 2018 IEEE Signal Processing in Medicine and Biology Symposium (SPMB), Philadelphia, PA, USA, 1 December 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Ali, A.; Sattar, M.; Riaz, T.; Khan, B.A.; Awais, M.; Militky, J.; Noman, M.T. Highly stretchable durable electro-thermal conductive yarns made by deposition of carbon nanotubes. J. Text. Inst. 2021, 1–10. [Google Scholar] [CrossRef]
- Jamshaid, H.; Mishra, R.; Militký, J.; Noman, M.T. Interfacial performance and durability of textile reinforced concrete. J. Text. Inst. 2018, 109, 879–890. [Google Scholar] [CrossRef]
- Noman, M.T.; Militky, J.; Wiener, J.; Saskova, J.; Ashraf, M.A.; Jamshaid, H.; Azeem, M. Sonochemical synthesis of highly crystalline photocatalyst for industrial applications. Ultrasonics 2018, 83, 203–213. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).