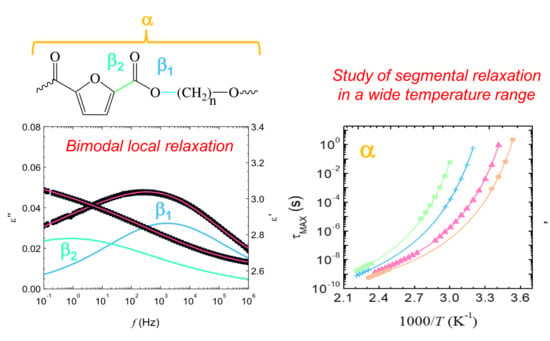
Broadband Dielectric Spectroscopy Study of Biobased Poly(alkylene 2,5-furanoate)s’ Molecular Dynamics
Abstract
1. Introduction
2. Materials and Methods
2.1. Samples
2.2. Broadband Dielectric Spectroscopy (BDS)
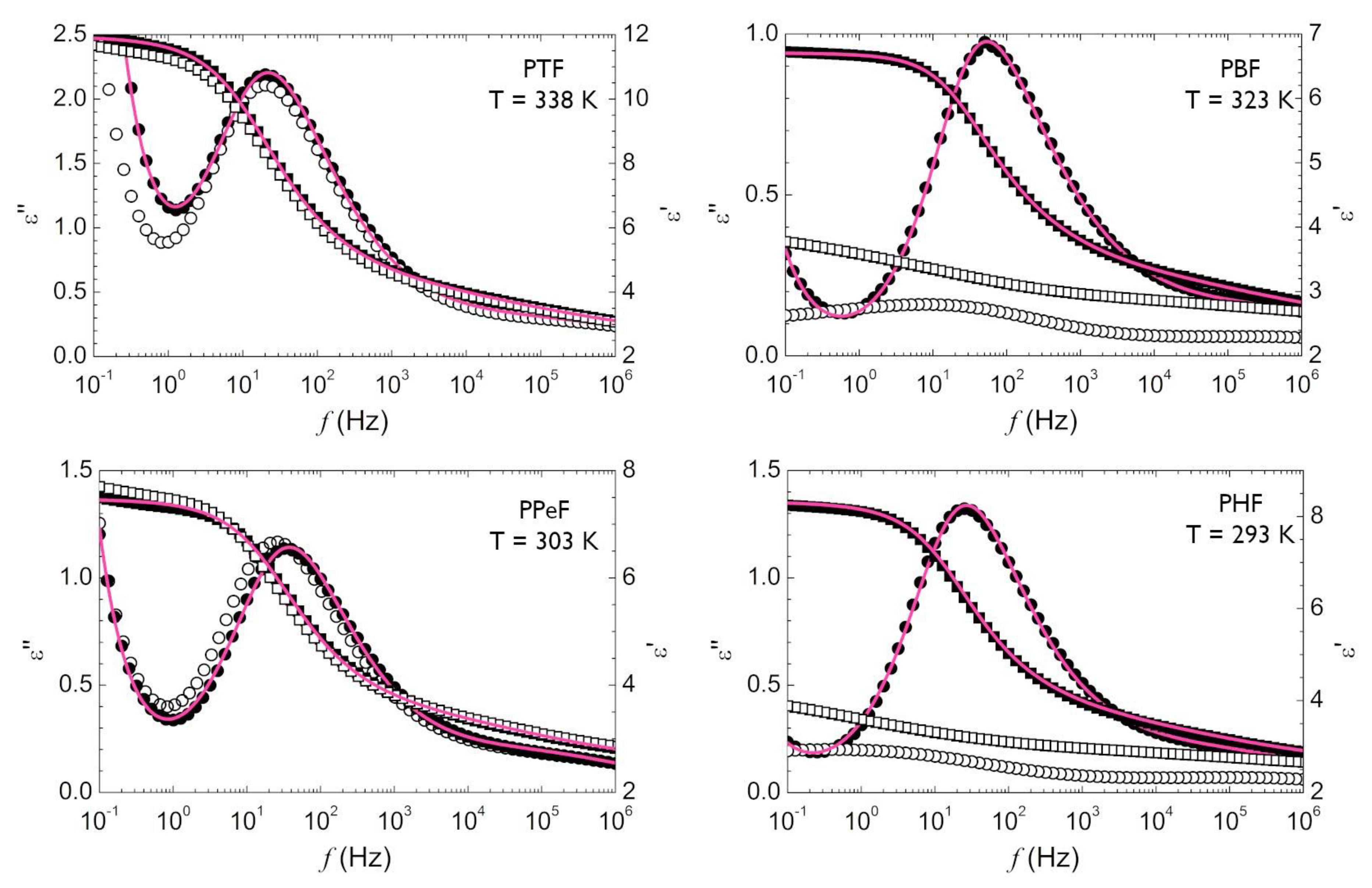
3. Results
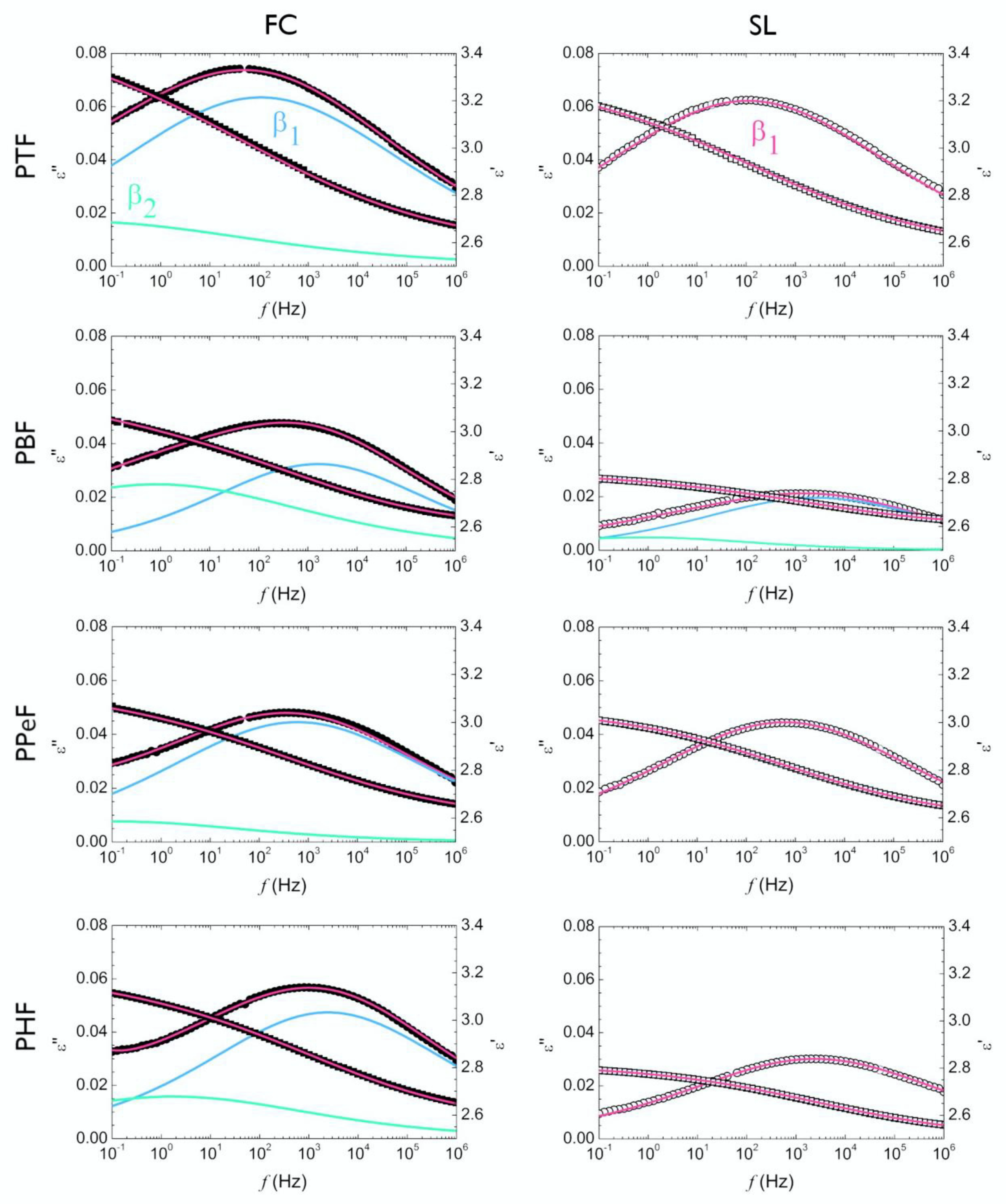
3.1. Local Dynamics of Poly(Alkylene 2,5-Furanoate)s (T « Tg)
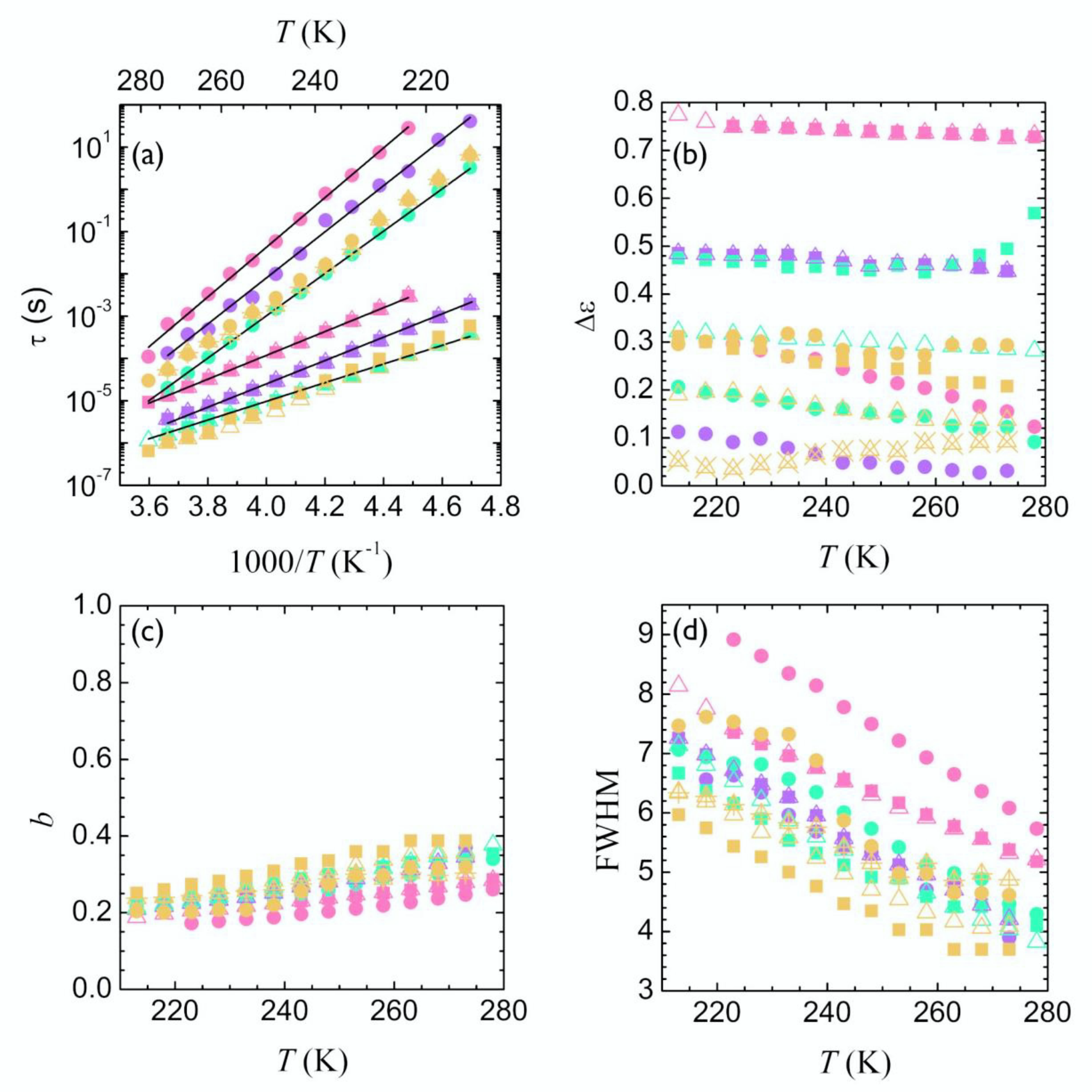
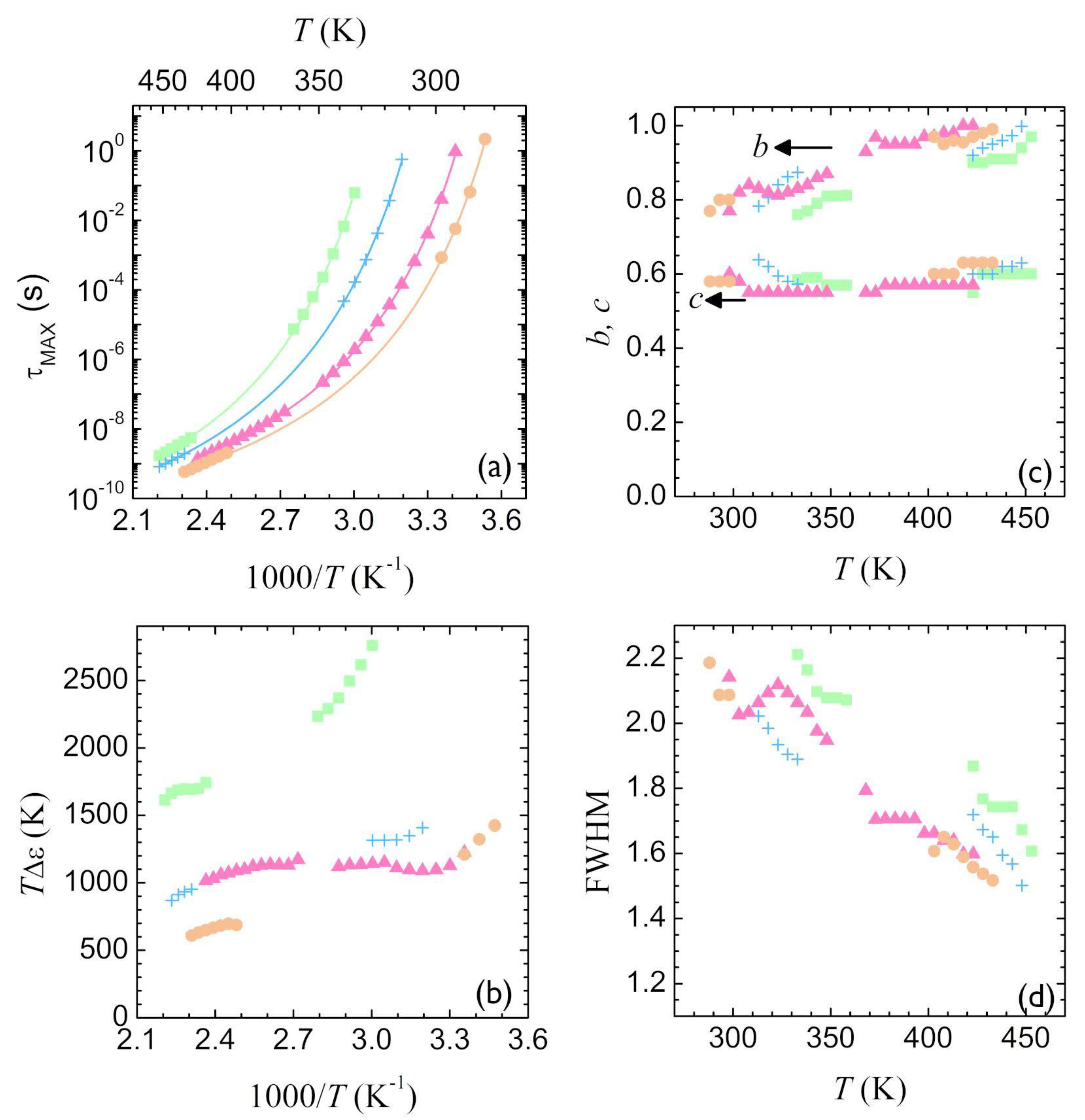
3.2. Segmental Dynamics of Poly(Alkylene Furanoate)s (T ≥ Tg)
4. Discussion
4.1. Local Relaxations
4.2. Segmental Relaxation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kremer, F.; Schönhals, A. Broadband Dielectric Spectroscopy; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Napolitano, S. Topical Issue on Dielectric Spectroscopy Applied to Soft Matter. Eur. Phys. J. E 2020, 43, 4. [Google Scholar] [CrossRef] [PubMed]
- Sanz, A.; Hansen, H.W.; Jakobsen, B.; Pedersen, I.H.; Capaccioli, S.; Adrjanowicz, K.; Paluch, M.; Gonthier, J.; Frick, B.; Lelièvre-Berna, E.; et al. High-pressure cell for simultaneous dielectric and neutron spectroscopy. Rev. Sci. Instrum. 2018, 89, 023904. [Google Scholar] [CrossRef] [PubMed]
- Markus, P.; Martínez-Tong, D.E.; Papastavrou, G.; Alegria, A. Effect of environmental humidity on the ionic transport of poly(ethylene oxide) thin films, investigated by local dielectric spectroscopy. Soft Matter 2020, 16, 3203–3208. [Google Scholar] [CrossRef]
- Bozell, J.J.; Petersen, G.R. Technology development for the production of biobased products from biorefinery carbohydrates—The US Department of Energy’s “Top 10” revisited. Green Chem. 2010, 12, 539–554. [Google Scholar] [CrossRef]
- Knoop, R.J.I.; Vogelzang, W.; van Haveren, J.; van Es, D.S. High molecular weight poly(ethylene-2,5-furanoate); critical aspects in synthesis and mechanical property determination. J. Polym. Sci. Part A Polym. Chem. 2013, 51, 4191–4199. [Google Scholar] [CrossRef]
- Codou, A.; Guigo, N.; van Berkel, J.; de Jong, E.; Sbirrazzuoli, N. Non-isothermal Crystallization Kinetics of Biobased Poly(ethylene 2,5-furandicarboxylate) Synthesized via the Direct Esterification Process. Macromol. Chem. Phys. 2014, 215, 2065–2074. [Google Scholar] [CrossRef]
- Papageorgiou, G.Z.; Tsanaktsis, V.; Bikiaris, D.N. Synthesis of poly(ethylene furandicarboxylate) polyester using monomers derived from renewable resources: Thermal behavior comparison with PET and PEN. Phys. Chem. Chem. Phys. 2014, 16, 7946–7958. [Google Scholar] [CrossRef]
- Burgess, S.K.; Leisen, J.E.; Kraftschik, B.E.; Mubarak, C.R.; Kriegel, R.M.; Koros, W.J. Chain Mobility, Thermal, and Mechanical Properties of Poly(ethylene furanoate) Compared to Poly(ethylene terephthalate). Macromolecules 2014, 47, 1383–1391. [Google Scholar] [CrossRef]
- Tsanaktsis, V.; Papageorgiou, D.G.; Exarhopoulos, S.; Bikiaris, D.N.; Papageorgiou, G.Z. Crystallization and Polymorphism of Poly(ethylene furanoate). Cryst. Growth Des. 2015, 15, 5505–5512. [Google Scholar] [CrossRef]
- Wu, J.; Xie, H.; Wu, L.; Li, B.-G.; Dubois, P. DBU-catalyzed biobased poly(ethylene 2,5-furandicarboxylate) polyester with rapid melt crystallization: Synthesis, crystallization kinetics and melting behavior. RSC Adv. 2016, 6, 101578–101586. [Google Scholar] [CrossRef]
- Pellis, A.; Haernvall, K.; Pichler, C.M.; Ghazaryan, G.; Breinbauer, R.; Guebitz, G.M. Enzymatic hydrolysis of poly(ethylene furanoate). J. Biotechnol. 2016, 235, 47–53. [Google Scholar] [CrossRef] [PubMed]
- Weinberger, S.; Canadell, J.; Quartinello, F.; Yeniad, B.; Arias, A.; Pellis, A.; Guebitz, G.M. Enzymatic Degradation of Poly(ethylene 2,5-furanoate) Powders and Amorphous Films. Catalysts 2017, 7, 318. [Google Scholar] [CrossRef]
- van Berkel, J.G.; Guigo, N.; Kolstad, J.J.; Sbirrazzuoli, N. Biaxial Orientation of Poly(ethylene 2,5-furandicarboxylate): An Explorative Study. Macromol. Mater. Eng. 2018, 303, 1700507. [Google Scholar] [CrossRef]
- Maini, L.; Gigli, M.; Gazzano, M.; Lotti, N.; Bikiaris, D.N.; Papageorgiou, G.Z. Structural Investigation of Poly(ethylene furanoate) Polymorphs. Polymers 2018, 10, 296. [Google Scholar] [CrossRef] [PubMed]
- Araujo, C.F.; Nolasco, M.M.; Ribeiro-Claro, P.J.A.; Rudić, S.; Silvestre, A.J.D.; Vaz, P.D.; Sousa, A.F. Inside PEF: Chain Conformation and Dynamics in Crystalline and Amorphous Domains. Macromolecules 2018, 51, 3515–3526. [Google Scholar] [CrossRef]
- Jiang, Y.; Woortman, A.J.J.; Alberda van Ekenstein, G.O.R.; Loos, K. A biocatalytic approach towards sustainable furanic–aliphatic polyesters. Polym. Chem. 2015, 6, 5198–5211. [Google Scholar] [CrossRef]
- Sousa, A.F.; Vilela, C.; Fonseca, A.C.; Matos, M.; Freire, C.S.R.; Gruter, G.-J.M.; Coelho, J.F.J.; Silvestre, A.J.D. Biobased polyesters and other polymers from 2,5-furandicarboxylic acid: A tribute to furan excellency. Polym. Chem. 2015, 6, 5961–5983. [Google Scholar] [CrossRef]
- Carlos Morales-Huerta, J.; Martínez de Ilarduya, A.; Muñoz-Guerra, S. Poly(alkylene 2,5-furandicarboxylate)s (PEF and PBF) by ring opening polymerization. Polymer 2016, 87, 148–158. [Google Scholar] [CrossRef]
- Papageorgiou, G.Z.; Papageorgiou, D.G.; Terzopoulou, Z.; Bikiaris, D.N. Production of bio-based 2,5-furan dicarboxylate polyesters: Recent progress and critical aspects in their synthesis and thermal properties. Eur. Polym. J. 2016, 83, 202–229. [Google Scholar] [CrossRef]
- Papageorgiou, D.G.; Guigo, N.; Tsanaktsis, V.; Exarhopoulos, S.; Bikiaris, D.N.; Sbirrazzuoli, N.; Papageorgiou, G.Z. Fast Crystallization and Melting Behavior of a Long-Spaced Aliphatic Furandicarboxylate Biobased Polyester, Poly(dodecylene 2,5-furanoate). Ind. Eng. Chem. Res. 2016, 55, 5315–5326. [Google Scholar] [CrossRef]
- Tsanaktsis, V.; Terzopoulou, Z.; Nerantzaki, M.; Papageorgiou, G.Z.; Bikiaris, D.N. New poly(pentylene furanoate) and poly(heptylene furanoate) sustainable polyesters from diols with odd methylene groups. Mater. Lett. 2016, 178, 64–67. [Google Scholar] [CrossRef]
- Genovese, L.; Lotti, N.; Siracusa, V.; Munari, A. Poly(Neopentyl Glycol Furanoate): A Member of the Furan-Based Polyester Family with Smart Barrier Performances for Sustainable Food Packaging Applications. Materials 2017, 10, 1028. [Google Scholar] [CrossRef] [PubMed]
- Guidotti, G.; Soccio, M.; Lotti, N.; Gazzano, M.; Siracusa, V.; Munari, A. Poly(propylene 2,5-thiophenedicarboxylate) vs. Poly(propylene 2,5-furandicarboxylate): Two Examples of High Gas Barrier Bio-Based Polyesters. Polymers 2018, 10, 785. [Google Scholar] [CrossRef] [PubMed]
- Maniar, D.; Jiang, Y.; Woortman, A.J.J.; van Dijken, J.; Loos, K. Furan-Based Copolyesters from Renewable Resources: Enzymatic Synthesis and Properties. ChemSusChem 2019, 12, 990–999. [Google Scholar] [CrossRef] [PubMed]
- Guidotti, G.; Soccio, M.; García-Gutiérrez, M.-C.; Gutiérrez-Fernández, E.; Ezquerra, T.A.; Siracusa, V.; Munari, A.; Lotti, N. Evidence of a 2D-Ordered Structure in Biobased Poly(pentamethylene furanoate) Responsible for Its Outstanding Barrier and Mechanical Properties. ACS Sustain. Chem. Eng. 2019, 7, 17863–17871. [Google Scholar] [CrossRef]
- Dimitriadis, T.; Bikiaris, D.N.; Papageorgiou, G.Z.; Floudas, G. Molecular Dynamics of Poly(ethylene-2,5-furanoate) (PEF) as a Function of the Degree of Crystallinity by Dielectric Spectroscopy and Calorimetry. Macromol. Chem. Phys. 2016, 217, 2056–2062. [Google Scholar] [CrossRef]
- Soccio, M.; Martínez-Tong, D.E.; Alegría, A.; Munari, A.; Lotti, N. Molecular dynamics of fully biobased poly(butylene 2,5-furanoate) as revealed by broadband dielectric spectroscopy. Polymer 2017, 128, 24–30. [Google Scholar] [CrossRef]
- Genovese, L.; Soccio, M.; Lotti, N.; Munari, A.; Szymczyk, A.; Paszkiewicz, S.; Linares, A.; Nogales, A.; Ezquerra, T.A. Effect of chemical structure on the subglass relaxation dynamics of biobased polyesters as revealed by dielectric spectroscopy: 2,5-furandicarboxylic acid vs. trans-1,4-cyclohexanedicarboxylic acid. Phys. Chem. Chem. Phys. 2018, 20, 15696–15706. [Google Scholar] [CrossRef]
- Bourdet, A.; Esposito, A.; Thiyagarajan, S.; Delbreilh, L.; Affouard, F.; Knoop, R.J.I.; Dargent, E. Molecular Mobility in Amorphous Biobased Poly(ethylene 2,5-furandicarboxylate) and Poly(ethylene 2,4-furandicarboxylate). Macromolecules 2018, 51, 1937–1945. [Google Scholar] [CrossRef]
- Papamokos, G.; Dimitriadis, T.; Bikiaris, D.N.; Papageorgiou, G.Z.; Floudas, G. Chain Conformation, Molecular Dynamics, and Thermal Properties of Poly(n-methylene 2,5-furanoates) as a Function of Methylene Unit Sequence Length. Macromolecules 2019, 52, 6533–6546. [Google Scholar] [CrossRef]
- Guidotti, G.; Soccio, M.; García-Gutiérrez, M.C.; Ezquerra, T.A.; Siracusa, V.; Munari, A.; Lotti, N. Fully biobased superpolymers of 2,5-furandicarboxylic acid with different functional properties: From rigid to flexible high performant packaging materials. ACS Sustain. Chem. Eng. 2020. [Google Scholar] [CrossRef]
- Soccio, M.; Costa, M.; Lotti, N.; Gazzano, M.; Siracusa, V.; Salatelli, E.; Manaresi, P.; Munari, A. Novel fully biobased poly(butylene 2,5-furanoate/diglycolate) copolymers containing ether linkages: Structure-property relationships. Eur. Polym. J. 2016, 81, 397–412. [Google Scholar] [CrossRef]
- Ma, J.; Yu, X.; Xu, J.; Pang, Y. Synthesis and crystallinity of poly(butylene 2,5-furandicarboxylate). Polymer 2012, 53, 4145–4151. [Google Scholar] [CrossRef]
- Sanz, A.; Nogales, A.; Lotti, N.; Munari, A.; Ezquerra, T.A. Complex nature of the β relaxation and fragility in aromatic polyesters. J. Non Cryst. Solids 2007, 353, 3989–3995. [Google Scholar] [CrossRef]
- Schwartz, G.A.; Colmenero, J.; Alegría, A. Single Component Dynamics in Miscible Poly(vinyl methyl ether)/Polystyrene Blends under Hydrostatic Pressure. Macromolecules 2007, 40, 3246–3255. [Google Scholar] [CrossRef]
- Bravard, S.P.; Boyd, R.H. Dielectric Relaxation in Amorphous Poly(ethylene terephthalate) and Poly(ethylene 2,6-naphthalene dicarboxylate) and Their Copolymers. Macromolecules 2003, 36, 741–748. [Google Scholar] [CrossRef]
- Alegría, A.; Mitxelena, O.; Colmenero, J. On the Molecular Motions Originating from the Dielectric γ-Relaxation of Bisphenol-A Polycarbonate. Macromolecules 2006, 39, 2691–2699. [Google Scholar] [CrossRef]
- Martínez-Tong, D.E.; Soccio, M.; Robles-Hernández, B.; Guidotti, G.; Iturrospe, A.; Arbe, A.; Arrese-Igor, S.; Munari, A.; Lotti, N.; Alegría, A. Impact of nanostructure development on the molecular dynamics of poly(pentamethylene 2,5-furanoate). 2020. Unpublished work. [Google Scholar]
- Robles-Hernández, B.; Soccio, M.; Castrillo, I.; Guidotti, G.; Lotti, N.; Alegria, A.; Martínez-Tong, D.E. Crystallization of poly(alkylene 2,5-furanoate)s thin films: Morphology and nanomechanical properties. ChemRxiv 2020. [Google Scholar] [CrossRef]
- Angell, C.A.; Ngai, K.L.; McKenna, G.B.; McMillan, P.F.; Martin, S.W. Relaxation in glass forming liquids and amorphous solids. J. Appl. Phys. 2000, 88, 3113–3157. [Google Scholar] [CrossRef]
- Ngai, K.L.; Roland, C.M. Chemical structure and intermolecular cooperativity: Dielectric relaxation results. Macromolecules 1993, 26, 6824–6830. [Google Scholar] [CrossRef]
- Musa, S.M. Nanoscale Spectroscopy with Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]

| Sample | Mn (kg/mol) | PDI | Tg (K) | Tm (K) |
|---|---|---|---|---|
| PTF [24] | 30 | 2.3 | 325 | 442 |
| PBF [28,33] | 36.1 * | - | 308 | 437 |
| PPeF [26] | 29.6 | 2.4 | 286 | - |
| PHF [32] | 28.9 | 2.3 | 286 | 414 |
| Sample | PTF kJ/mol | PBF (FC) [6] kJ/mol | PPeF kJ/mol | PHF kJ/mol |
|---|---|---|---|---|
| 52 ± 1 | 50 ± 2 | 52 ± 1 | 42 ± 1 | |
| 112 ± 2 | 89 ± 1 | 104 ± 2 | 96 ± 2 |
| Sample | PTF | PBF | PPeF | PHF |
|---|---|---|---|---|
| (s) | 10−12 (fixed) | |||
| D | 4.5 ± 0.1 | 4.8 ± 0.1 | 5.1 ± 0.06 | 5.0 ± 0.1 |
| (K) | 282 ± 1 | 266 ± 1 | 247 ± 1 | 240 ± 1 |
| (K) | 321 ± 1 | 306 ± 1 | 286 ± 1 | 277 ± 1 |
| m | 116 ± 3 | 106 ± 3 | 103 ± 3 | 105 ± 3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soccio, M.; Martínez-Tong, D.E.; Guidotti, G.; Robles-Hernández, B.; Munari, A.; Lotti, N.; Alegria, A. Broadband Dielectric Spectroscopy Study of Biobased Poly(alkylene 2,5-furanoate)s’ Molecular Dynamics. Polymers 2020, 12, 1355. https://doi.org/10.3390/polym12061355
Soccio M, Martínez-Tong DE, Guidotti G, Robles-Hernández B, Munari A, Lotti N, Alegria A. Broadband Dielectric Spectroscopy Study of Biobased Poly(alkylene 2,5-furanoate)s’ Molecular Dynamics. Polymers. 2020; 12(6):1355. https://doi.org/10.3390/polym12061355
Chicago/Turabian StyleSoccio, Michelina, Daniel E. Martínez-Tong, Giulia Guidotti, Beatriz Robles-Hernández, Andrea Munari, Nadia Lotti, and Angel Alegria. 2020. "Broadband Dielectric Spectroscopy Study of Biobased Poly(alkylene 2,5-furanoate)s’ Molecular Dynamics" Polymers 12, no. 6: 1355. https://doi.org/10.3390/polym12061355
APA StyleSoccio, M., Martínez-Tong, D. E., Guidotti, G., Robles-Hernández, B., Munari, A., Lotti, N., & Alegria, A. (2020). Broadband Dielectric Spectroscopy Study of Biobased Poly(alkylene 2,5-furanoate)s’ Molecular Dynamics. Polymers, 12(6), 1355. https://doi.org/10.3390/polym12061355