Using Finite Element Approach for Crashworthiness Assessment of a Polymeric Auxetic Structure Subjected to the Axial Loading
Abstract
1. Introduction
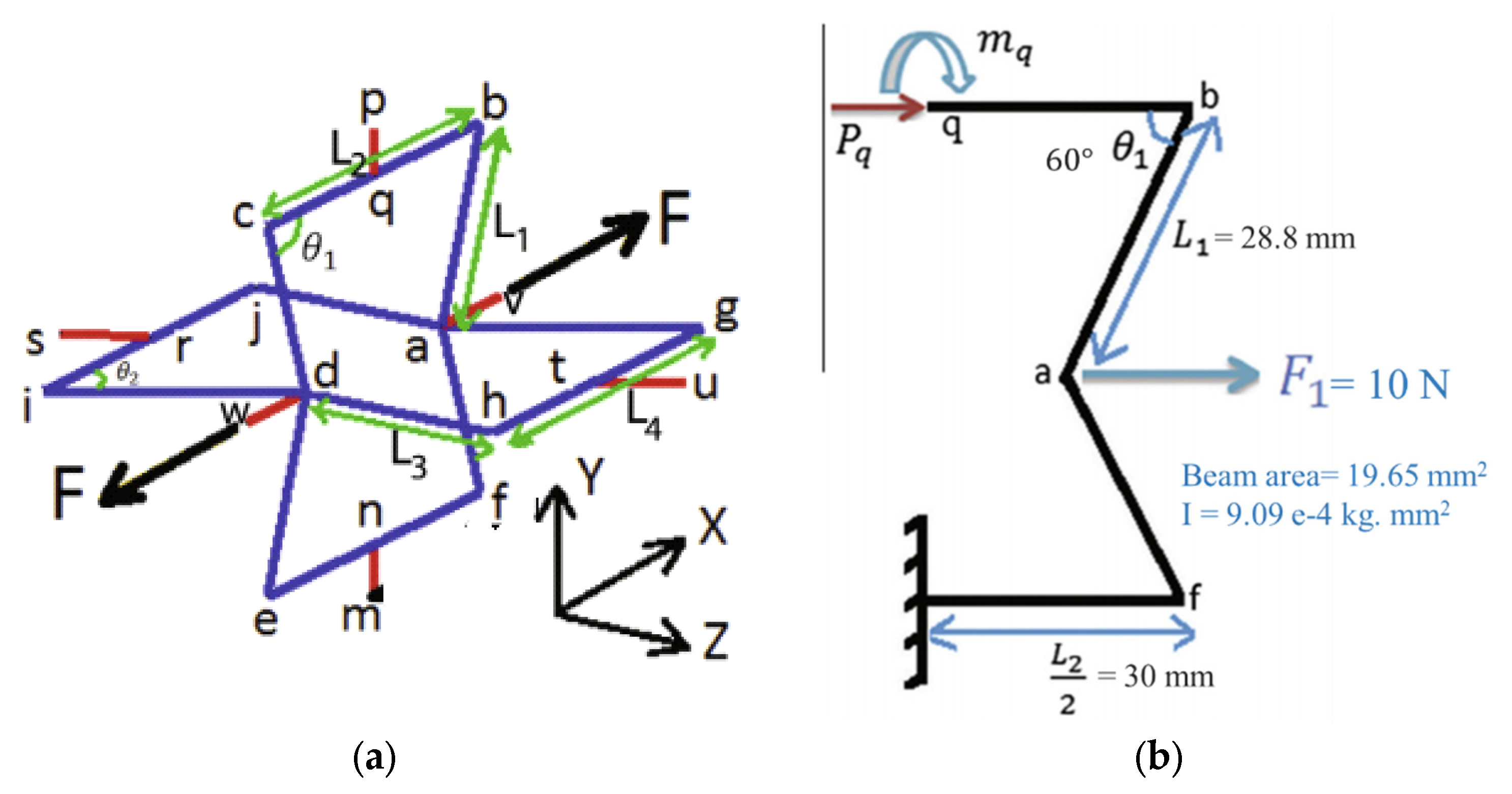
2. Analytical Solution for 3D Re-Entrant Cellular Structure
3. Finite Element Approaches and Simulation
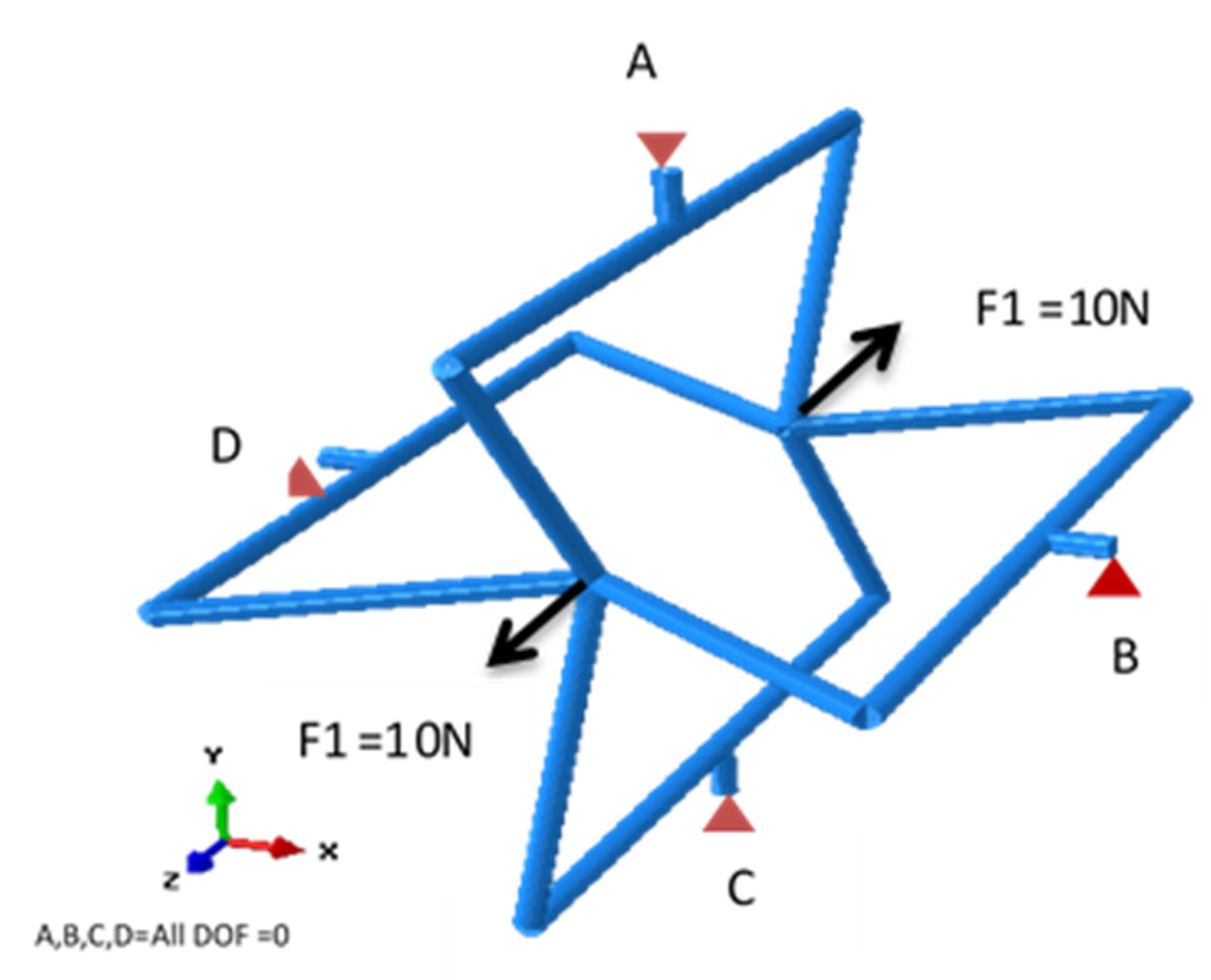
3.1. Unit Cell Modelling
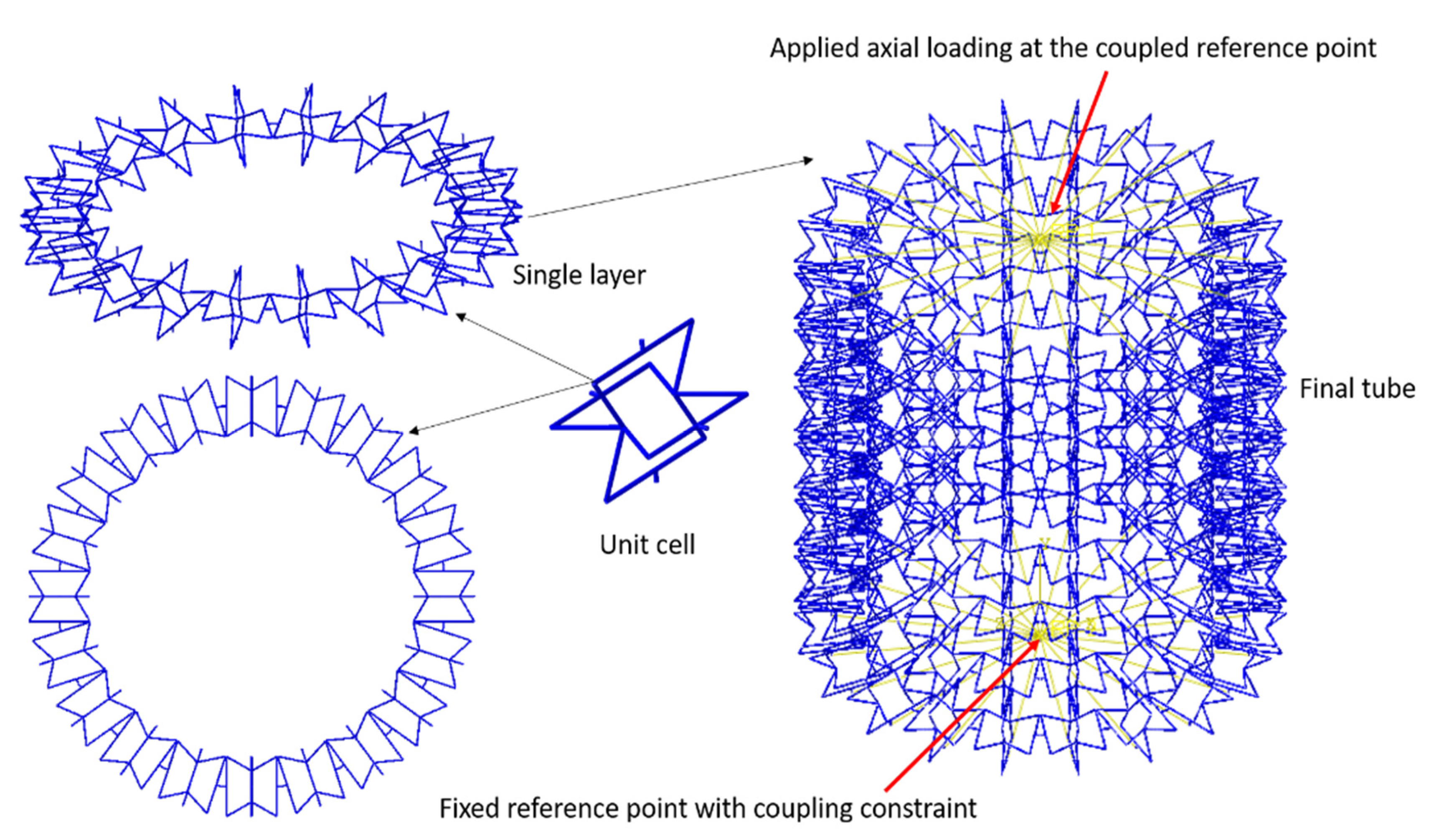
3.2. Cellular Tube Modelling
4. Results and Discussion
4.1. Unit Cell Modelling Results
4.1.1. H-Method Results for Convergence Study of a Unit Cell
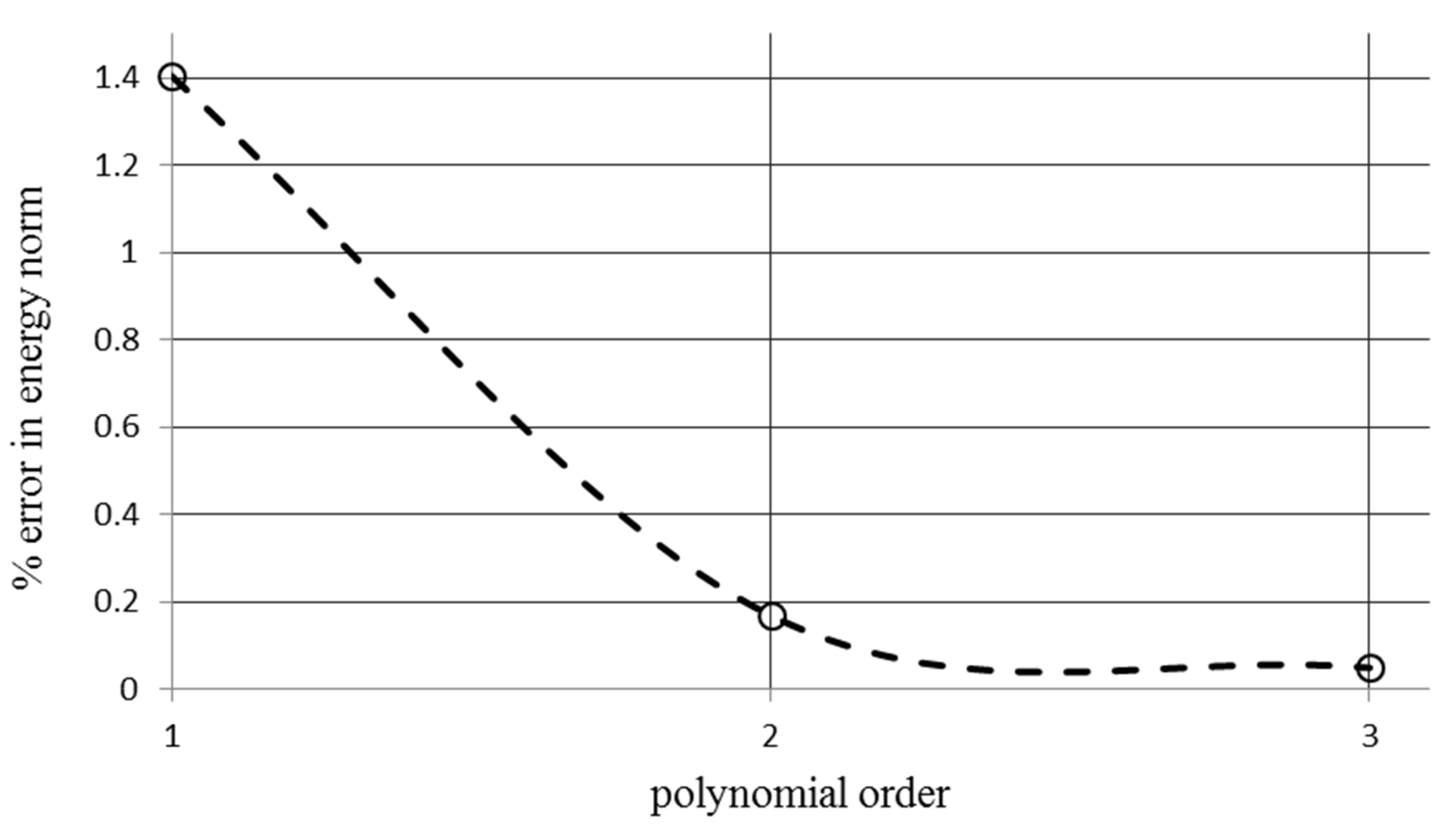
4.1.2. The P-Method Convergence Study for a Unit Cell
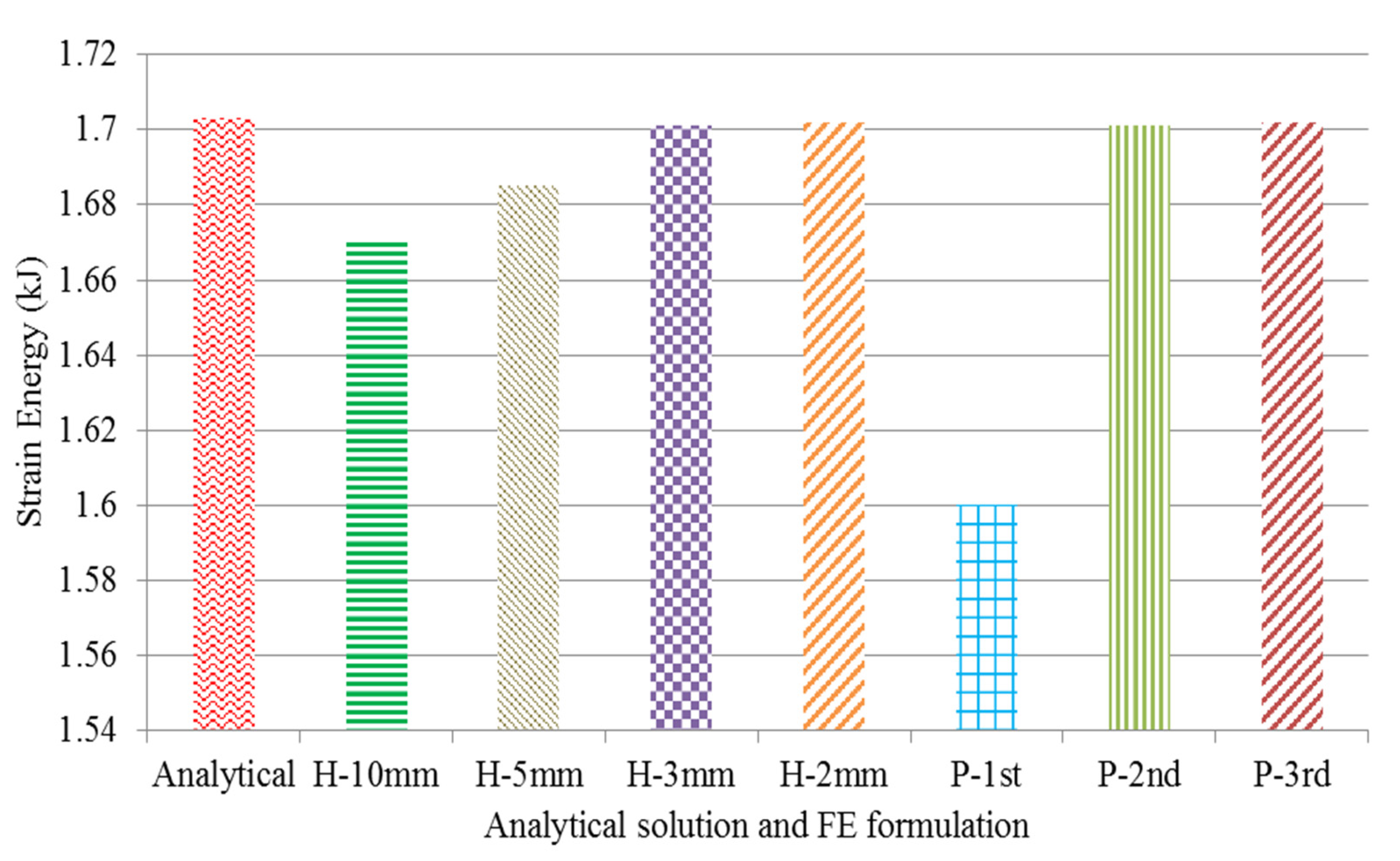
4.1.3. Unit Cell Strain Energy
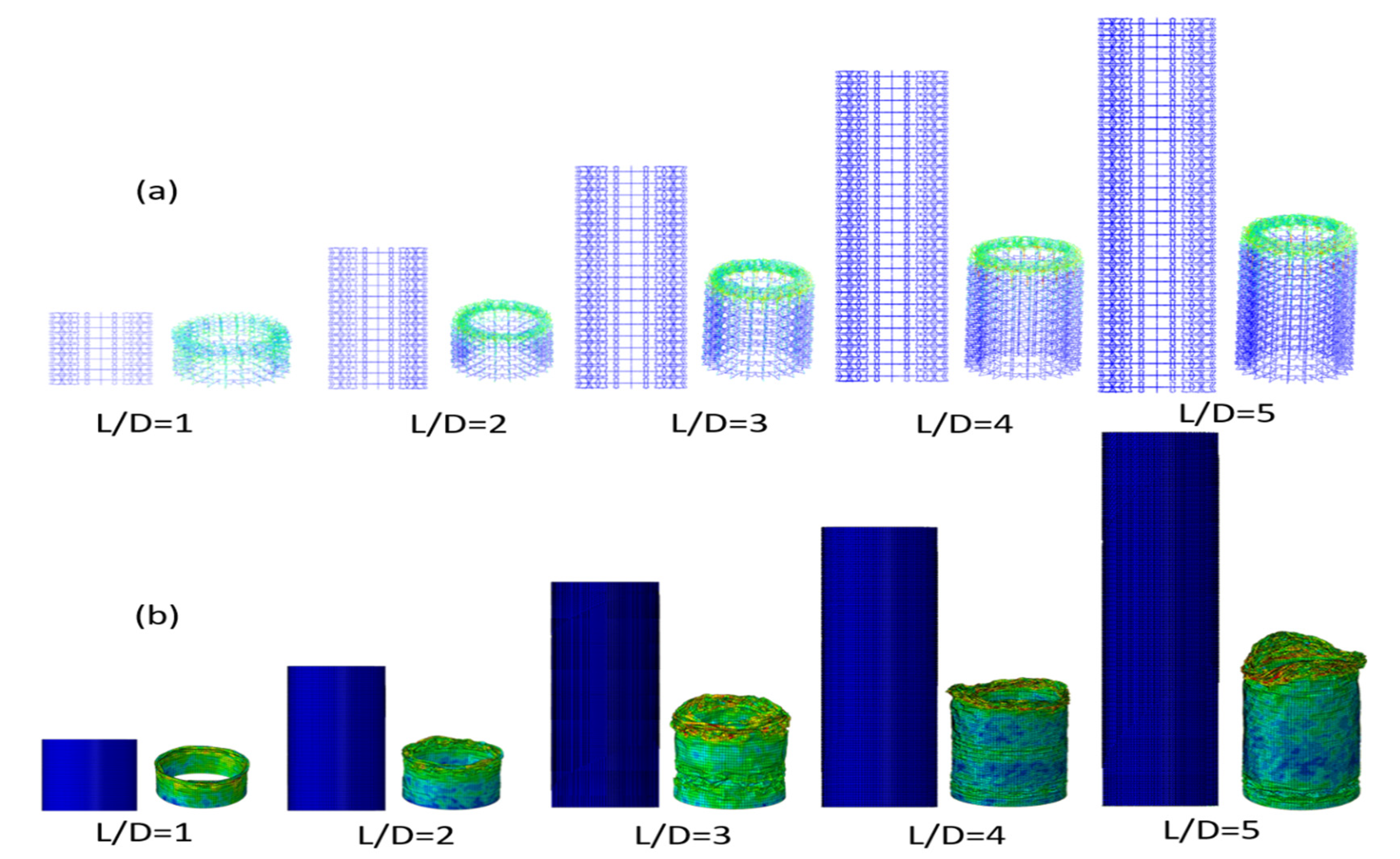
4.2. Cellular Tube’s Structure Results
4.2.1. Convergence Study for Cellular Tube Structure
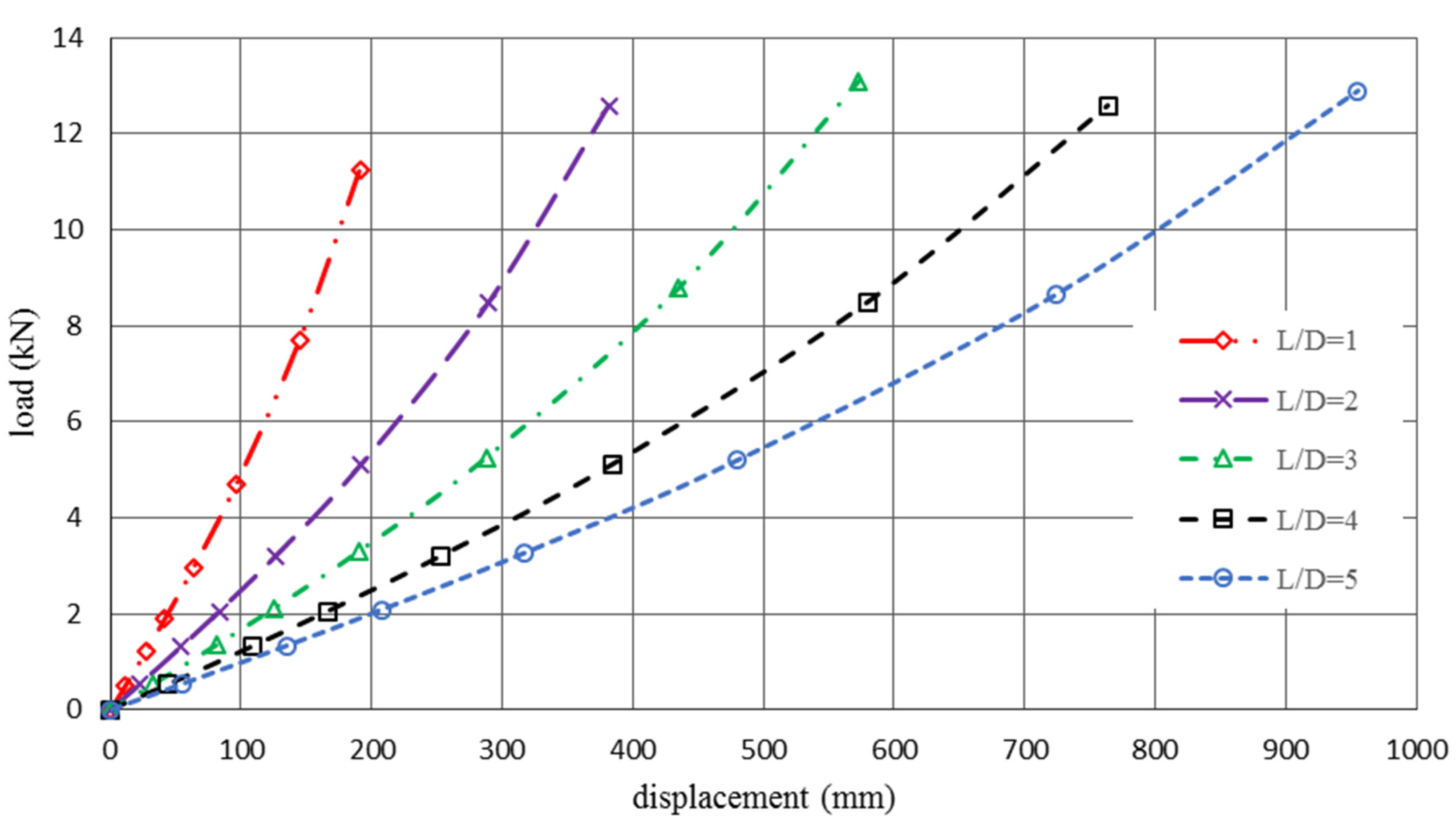
4.2.2. Structure Stiffness and Poisson’s Ratio
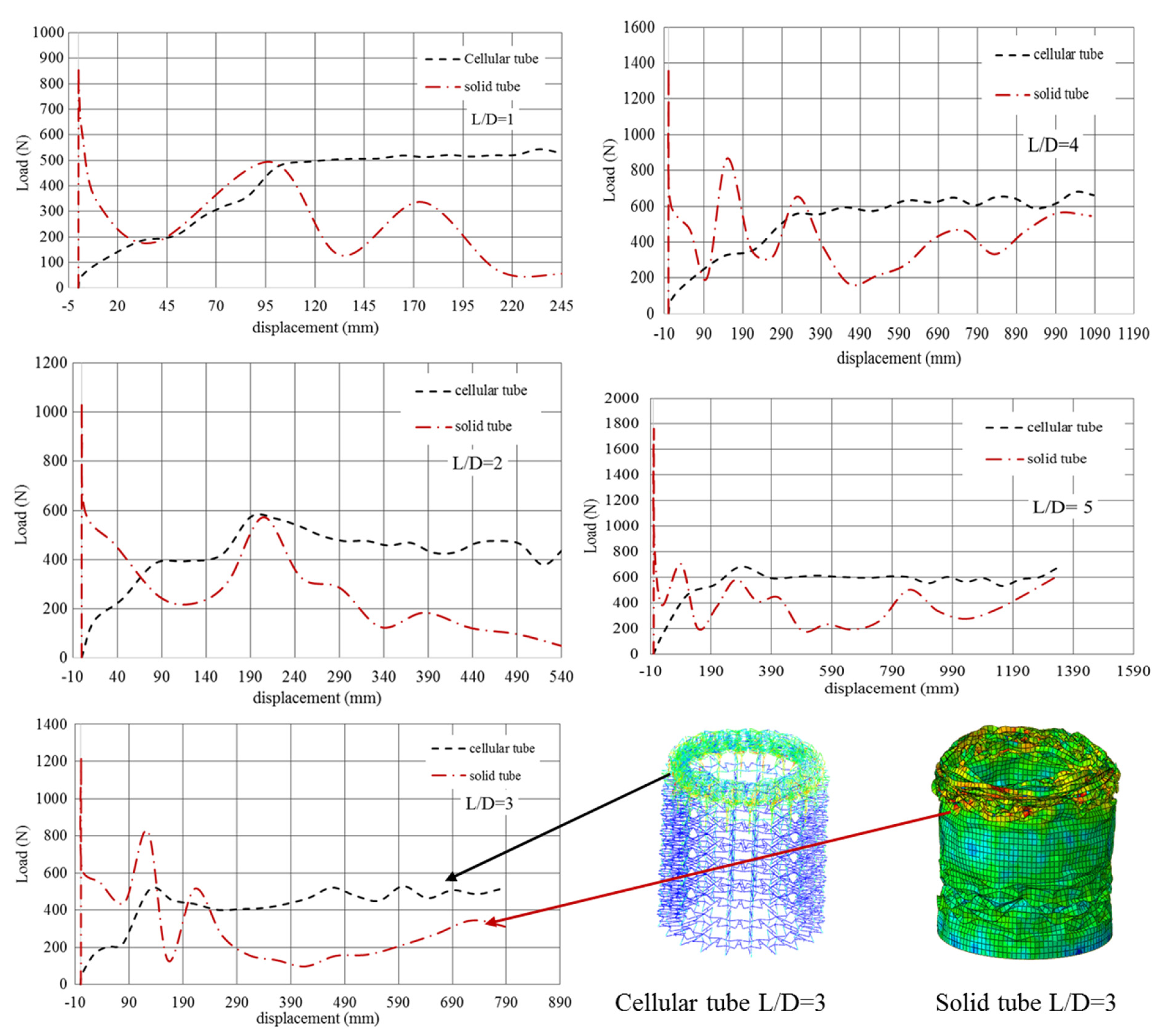
4.3. Energy Absorption Evaluation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Prawoto, Y. Seeing auxetic materials from the mechanics point of view: A structural review on the negative Poisson’s ratio. Comput. Mater. Sci. 2012, 58, 140–153. [Google Scholar] [CrossRef]
- Mohsenizadeh, S.; Alipour, R.; Shokri Rad, M.; Nejad, A.F.; Ahmad, Z. Crashworthiness assessment of auxetic foam-filled tube under quasi-static axial loading. Mater. Des. 2015, 88, 258–268. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, D. Mechanical properties of auxetic cellular material consisting of re-entrant hexagonal honeycombs. Materials 2016, 9, 900. [Google Scholar] [CrossRef]
- Yang, W.; Li, Z.-M.; Shi, W.; Xie, B.; Yang, M.-B. Review on auxetic materials. J. Mater. Sci. 2004, 39, 3269–3279. [Google Scholar] [CrossRef]
- Rad, M.S.; Hatami, H.; Alipouri, R.; Nejad, A.F.; Omidinasab, F. Determination of energy absorption in different cellular auxetic structures. Mech. Ind. 2019, 20, 302. [Google Scholar]
- Chan, N.; Evans, K.E. Fabrication methods for auxetic foams. J. Mater. Sci. 1997, 32, 5945–5953. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Non-chiral, molecular model of negative Poisson ratio in two dimensions. J. Phys. A 2003, 36, 11765. [Google Scholar] [CrossRef]
- Tretiakov, K.; Krzysztof, V.; Wojciechowski, W. Poisson’s ratio of simple planar ‘isotropic’ solids in two dimensions. Physica Status Solidi 2007, 244, 1038–1046. [Google Scholar] [CrossRef]
- Rad, M.S.; Prawoto, Y.; Ahmad, Z. Analytical solution and finite element approach to the 3D re-entrant structures of auxetic materials. Mech. Mater. 2014, 74, 76–87. [Google Scholar]
- Imbalzano, G.; Tran, P.; Ngo, T.; Lee, P.V.S. Three-dimensional modelling of auxetic sandwich panels for localised impact resistance. J. Sandw. Struct. Mater. 2017, 19, 291–316. [Google Scholar] [CrossRef]
- Rueger, Z.; Roderic, S. Lakes, Cosserat elasticity of negative Poisson’s ratio foam: Experiment. Smart Mater. Struct. 2016, 25, 054004. [Google Scholar] [CrossRef]
- Koumlis, S.; Lamberson, L. Strain Rate Dependent Compressive Response of Open Cell Polyurethane Foam. Exp. Mech. 2019, 59, 1087–1103. [Google Scholar] [CrossRef]
- Yao, Y.; Yun, L.; Xu, Y.; Wang, B.; Li, J.; Deng, L.; Lu, H. Fabrication and characterization of auxetic shape memory composite foams. Compos. Part B 2018, 152, 1–7. [Google Scholar] [CrossRef]
- Mohsenizadeh, S.; Alipour, R.; Nejad, A.F.; Rad, M.S.; Ahmad, Z. Experimental investigation on energy absorption of auxetic foam-filled thin-walled square tubes under quasi-static loading. Procedia Manuf. 2015, 2, 331–336. [Google Scholar] [CrossRef]
- Liu, Y.; Hong, H. A review on auxetic structures and polymeric materials. Sci. Res. Essays 2010, 5, 1052–1063. [Google Scholar]
- Rad, M.S.; Ahmad, Z.; Alias, A. Computational approach in formulating mechanical characteristics of 3D star honeycomb auxetic structure. Adv. Mater. Sci. Eng. 2015, 2015. [Google Scholar]
- Grima, J.N.; Elaine, M.; Daphne, A. Auxetic behaviour from connected different-sized squares and rectangles. Proc. R. Soc. A 2011, 467, 439–458. [Google Scholar] [CrossRef]
- Chetcuti, E.; Ellul, B.; Manicaro, E.; Brincat, J.-P.; Attard, D.; Gatt, R.; Grima, J.N. Modeling auxetic foams through semi-rigid rotating triangles. Physica Status Solidi 2014, 251, 297–306. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Alderson, A.; Evans, K.E. On the potential of connected stars as auxetic systems. Mol. Simul. 2005, 31, 925–935. [Google Scholar] [CrossRef]
- Gibson Lorna, J.; Michael, F.A. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Masters, I.G.; Evans, K.E. Models for the elastic deformation of honeycombs. Compos. Struct. 1996, 35, 403–422. [Google Scholar] [CrossRef]
- Rahmandoust, M.; Andreas, Ö. On finite element modeling of single-and multi-walled carbon nanotubes. J. Nanosci. Nanotechnol. 2012, 12, 8129–8136. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.C.; Ding, H.M.; An, L.Q.; Wang, X.L. Numerical investigation on dynamic crushing behavior of auxetic honeycombs with various cell-wall angles. Adv. Mech. Eng. 2015, 7, 679678. [Google Scholar] [CrossRef]
- Hu, L.; Fanfan, Y.; Tongxi, Y. Effect of cell-wall angle on the in-plane crushing behaviour of hexagonal honeycombs. Mater. Des. 2013, 46, 511–523. [Google Scholar] [CrossRef]
- Zou, Z.; Reid, S.R.; Tan, P.J.; Li, S.; Harrigan, J.J. Dynamic crushing of honeycombs and features of shock fronts. Int. J. Impact Eng. 2009, 36, 165–176. [Google Scholar] [CrossRef]
- Hu, L.L.; Yu, T.X. Dynamic crushing strength of hexagonal honeycombs. Int. J. Impact Eng. 2010, 37, 467–474. [Google Scholar] [CrossRef]
- Hu, L.L.; Yu, T.X. Mechanical behavior of hexagonal honeycombs under low-velocity impact–theory and simulations. Int. J. Solids Struct. 2013, 50, 3152–3165. [Google Scholar] [CrossRef]
- Lu, Z.-X.; Qiang, L.; Zhen-Yu, Y. Predictions of Young’s modulus and negative Poisson’s ratio of auxetic foams. Physica Status Solidi 2011, 248, 167–174. [Google Scholar] [CrossRef]
- Wang, H.; Lu, Z.; Yang, Z.; Li, X. A novel re-entrant auxetic honeycomb with enhanced in-plane impact resistance. Compos. Struct. 2019, 208, 758–770. [Google Scholar] [CrossRef]
- Zhao, X.; Gao, Q.; Wang, L.; Yu, Q.; Ma, Z.D. Dynamic crushing of double-arrowed auxetic structure under impact loading. Mater. Des. 2018, 160, 527–537. [Google Scholar] [CrossRef]
- Hu, L.L.; Zhou, M.Z.; Deng, H. Dynamic indentation of auxetic and non-auxetic honeycombs under large deformation. Compos. Struct. 2019, 207, 323–330. [Google Scholar] [CrossRef]
- Reid, S.R.; Peng, C. Dynamic uniaxial crushing of wood. Int. J. Impact Eng. 1997, 19, 531–570. [Google Scholar] [CrossRef]
- Ruan, D.; Lu, G.; Wang, B.; Yu, T.X. In-plane dynamic crushing of honeycombs—A finite element study. Int. J. Impact Eng. 2003, 28, 161–182. [Google Scholar] [CrossRef]
- Peirovi, S.; Pourasghar, M.; Nejad, A.F.; Hassan, M.A. A study on the different finite element approaches for laser cutting of aluminum alloy sheet. Int. J. Adv. Manuf. Technol. 2017, 93, 1399–1413. [Google Scholar] [CrossRef]
- Taghipour, A.; Parvizian, J.; Heinze, S.; Düster, A. p-version finite elements and finite cells for finite strain elastoplastic problems. PAMM 2016, 16, 243–244. [Google Scholar] [CrossRef]
- Zeng, J.; Hu, H. Finite Element Analysis of Three-Dimensional (3D) Auxetic Textile Composite under Compression. Polymers 2018, 10, 374. [Google Scholar] [CrossRef] [PubMed]
- Dobnik Dubrovski, P.; Novak, N.; Borovinšek, M.; Vesenjak, M.; Ren, Z. In-Plane Behavior of Auxetic Non-Woven Fabric Based on Rotating Square Unit Geometry under Tensile Load. Polymers 2019, 11, 1040. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Zhao, S.; Sun, R.; Scarpa, F.; Wang, J. In-Plane Mechanical Behavior of a New Star-Re-Entrant Hierarchical Metamaterial. Polymers 2019, 11, 1132. [Google Scholar] [CrossRef]
- Abaqus. Version. 6.14 Documentation; Dassault Systems Simulia Corporation: Providence, RI, USA, 2014. [Google Scholar]
- Marks, L.W.; Gardner, T.N. The use of strain energy as a convergence criterion in the finite element modelling of bone and the effect of model geometry on stress convergence. J. Biomed. Eng. 1993, 15, 474–476. [Google Scholar] [CrossRef]
- Lin, C.-L.; Chih-Han, C.; Chia-Shin, C.; Chau-Hsiang, W.; Huey-Er, L. Automatic finite element mesh generation for maxillary second premolar. Computer Methods Programs Biomed. 1999, 3, 187–195. [Google Scholar] [CrossRef]
- Lim, H.; Corbett, C.; Battaile, J.; Bishop, E.; James, W. Investigating mesh sensitivity and polycrystalline RVEs in crystal plasticity finite element simulations. Int. J. Plast. 2019, 121, 101–115. [Google Scholar] [CrossRef]
- Ng, T.P.; Koloor, S.S.R.; Djuansjah, J.R.P.; Kadir, M.A. Assessment of compressive failure process of cortical bone materials using damage-based model. J. Mech. Behave. Biomed. Mater. 2017, 66, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Koloor, S.S.R.; Rahimian-Koloor, S.M.; Karimzadeh, A.; Hamdi, M.; Petrů, M.; Tamin, M.N. Nano-level damage characterization of graphene/polymer cohesive interface under tensile separation. Polymers 2019, 11, 1435. [Google Scholar] [CrossRef] [PubMed]
- Koloor, S.S.R.; Karimzadeh, A.; Tamin, M.N.; Abd Shukor, M.H. Effects of Sample and Indenter Configurations of Nanoindentation Experiment on the Mechanical Behavior and Properties of Ductile Materials. Metals 2018, 8, 421. [Google Scholar]



| Symbol | Unit | Description |
|---|---|---|
| mm | Cellular wall length 1 | |
| mm | Cellular wall length 2 | |
| mm2 | Cross-section area for beam component | |
| N | Applied force to the cell | |
| The angle between and | ||
| J | Total elastic strain energy | |
| mm3 | Unit cell volume | |
| E | GPa | Young’s modulus of the beam |
| I | Kg·mm2 | Secondary moment of inertia |
| N | applied axial force | |
| N | Virtual applied axial force | |
| N·mm | Virtual bending moment |
| Property | Density | Poisson’s Ratio | Elastic Modulus | Yield Stress | Ultimate Stress | Strain Hardening Coefficient | Failure Strain |
|---|---|---|---|---|---|---|---|
| Unit | (kg/m3) | --- | (GPa) | (MPa) | (MPa) | --- | (%) |
| Symbol | υ | E | σy | σU | n | ||
| Value | 2700 | 0.3 | 56 | 60 | 215 | 0.26 | 36 |
| H-Method | P Method | ||||||
|---|---|---|---|---|---|---|---|
| Mesh 10 mm | Mesh 5 mm | Mesh 3 mm | Mesh 2 mm | 1st Order | 2nd Order | 3rd Order | |
| DOF | 300 | 588 | 996 | 1452 | 404 | 612 | 612 |
| Strain Energy [kJ] | 1.67 | 1.685 | 1.701 | 1.702 | 1.6 | 1.701 | 1.702 |
| CPU time [s] | 0.8 | 1.00 | 1.5 | 1.7 | 0.7 | 0.8 | 1 |
| Von Mises stress [MPa] | 23.2 | 24.54 | 25.01 | 25.02 | 24.3 | 25.02 | 25.02 |
| H-Method | P Method | ||||
|---|---|---|---|---|---|
| Mesh 5 mm | Mesh 3 mm | Mesh 2 mm | 2nd Order | 3rd Order | |
| DOF | 588 | 996 | 1452 | 22,562 | 22,562 |
| Strain Energy (kJ) | 376.89 | 386.75 | 387.15 | 387.12 | 387.12 |
| CPU time (s) | 426 | 570 | 696 | 418 | 447 |
| Von Mises stress (MPa) | 36.02 | 37.84 | 37.86 | 37.89 | 37.9 |
| Samples | P Max (N) | Pave (N) | CFE (%) | EA (J) | SEA (J/kg) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Solid Tube | Cellular Tube | Solid Tube | Cellular Tube | Solid Tube | Cellular Tube | Solid Tube | Cellular Tube | Solid Tube | Cellular Tube | |
| L/D = 1 | 842 | 496 | 271 | 435 | 32.07 | 87.8 | 627 | 975 | 1081 | 1681 |
| L/D = 2 | 1040 | 575 | 268 | 429 | 25 | 81.4 | 1422 | 2334 | 1225 | 2012 |
| L/D = 3 | 1215 | 513 | 302 | 430.1 | 24.8 | 83.8 | 2359 | 3361 | 1355 | 1931 |
| L/D = 4 | 1362 | 680 | 421 | 529 | 30.9 | 77.7 | 4552 | 5723 | 1962 | 2466 |
| L/D = 5 | 1752 | 682 | 375 | 563 | 21.4 | 82.5 | 4994 | 7506 | 1722 | 2588 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farokhi Nejad, A.; Alipour, R.; Shokri Rad, M.; Yazid Yahya, M.; Rahimian Koloor, S.S.; Petrů, M. Using Finite Element Approach for Crashworthiness Assessment of a Polymeric Auxetic Structure Subjected to the Axial Loading. Polymers 2020, 12, 1312. https://doi.org/10.3390/polym12061312
Farokhi Nejad A, Alipour R, Shokri Rad M, Yazid Yahya M, Rahimian Koloor SS, Petrů M. Using Finite Element Approach for Crashworthiness Assessment of a Polymeric Auxetic Structure Subjected to the Axial Loading. Polymers. 2020; 12(6):1312. https://doi.org/10.3390/polym12061312
Chicago/Turabian StyleFarokhi Nejad, Ali, Roozbeh Alipour, Mozafar Shokri Rad, Mohd Yazid Yahya, Seyed Saeid Rahimian Koloor, and Michal Petrů. 2020. "Using Finite Element Approach for Crashworthiness Assessment of a Polymeric Auxetic Structure Subjected to the Axial Loading" Polymers 12, no. 6: 1312. https://doi.org/10.3390/polym12061312
APA StyleFarokhi Nejad, A., Alipour, R., Shokri Rad, M., Yazid Yahya, M., Rahimian Koloor, S. S., & Petrů, M. (2020). Using Finite Element Approach for Crashworthiness Assessment of a Polymeric Auxetic Structure Subjected to the Axial Loading. Polymers, 12(6), 1312. https://doi.org/10.3390/polym12061312








