Fabrication of High-Quality Polymer Composite Frame by a New Method of Fiber Winding Process
Abstract
1. Introduction
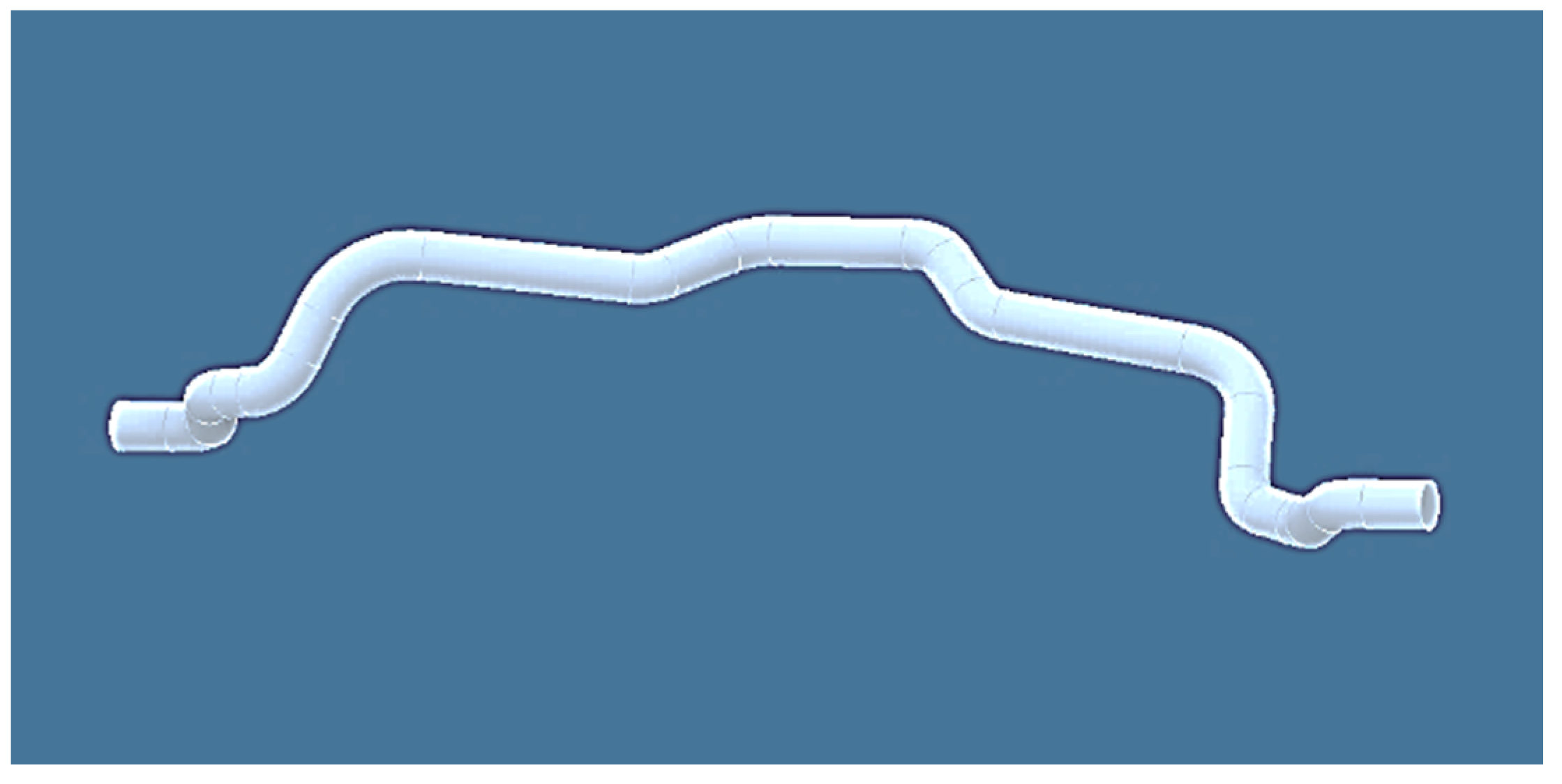
2. Manufacturing of Polymer Composite Frame
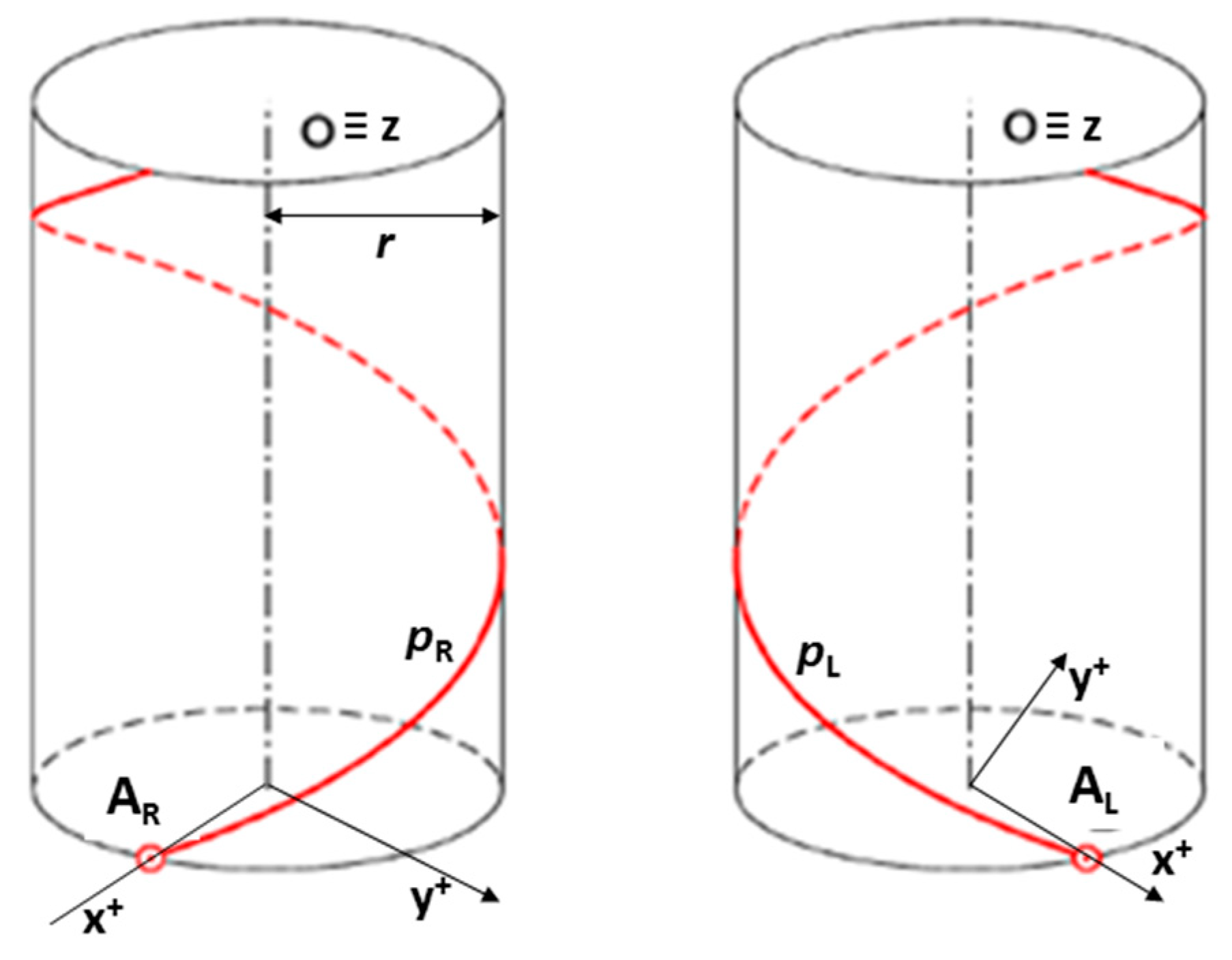
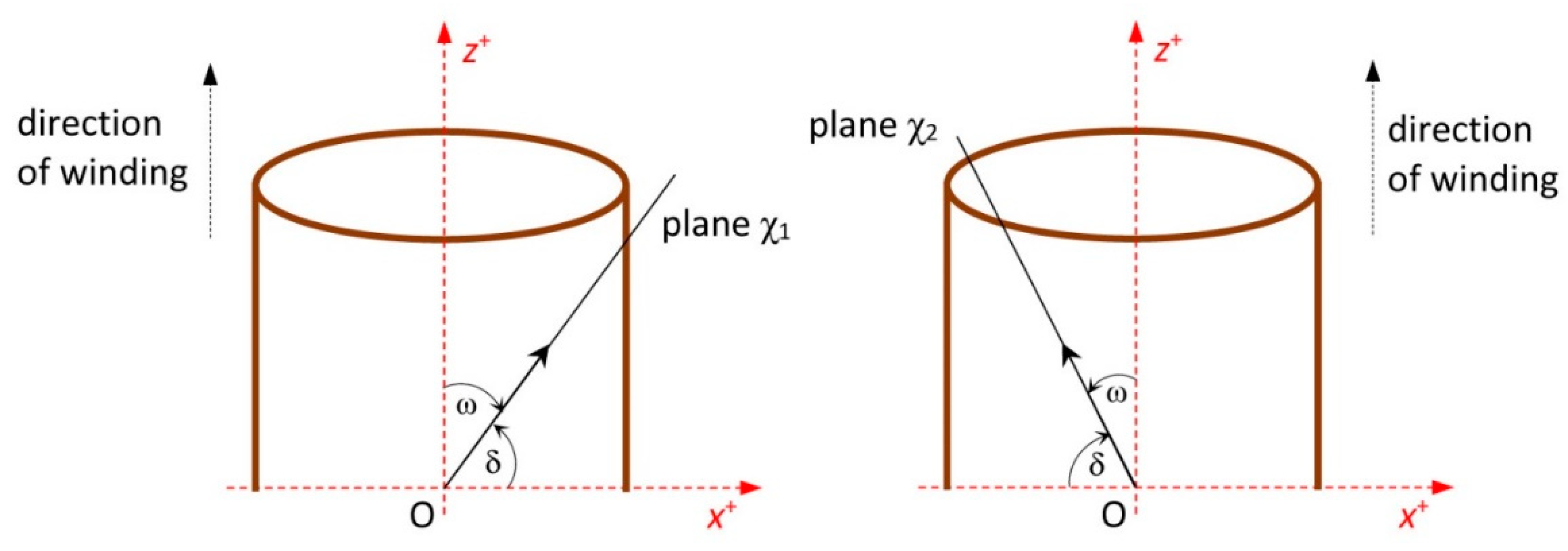
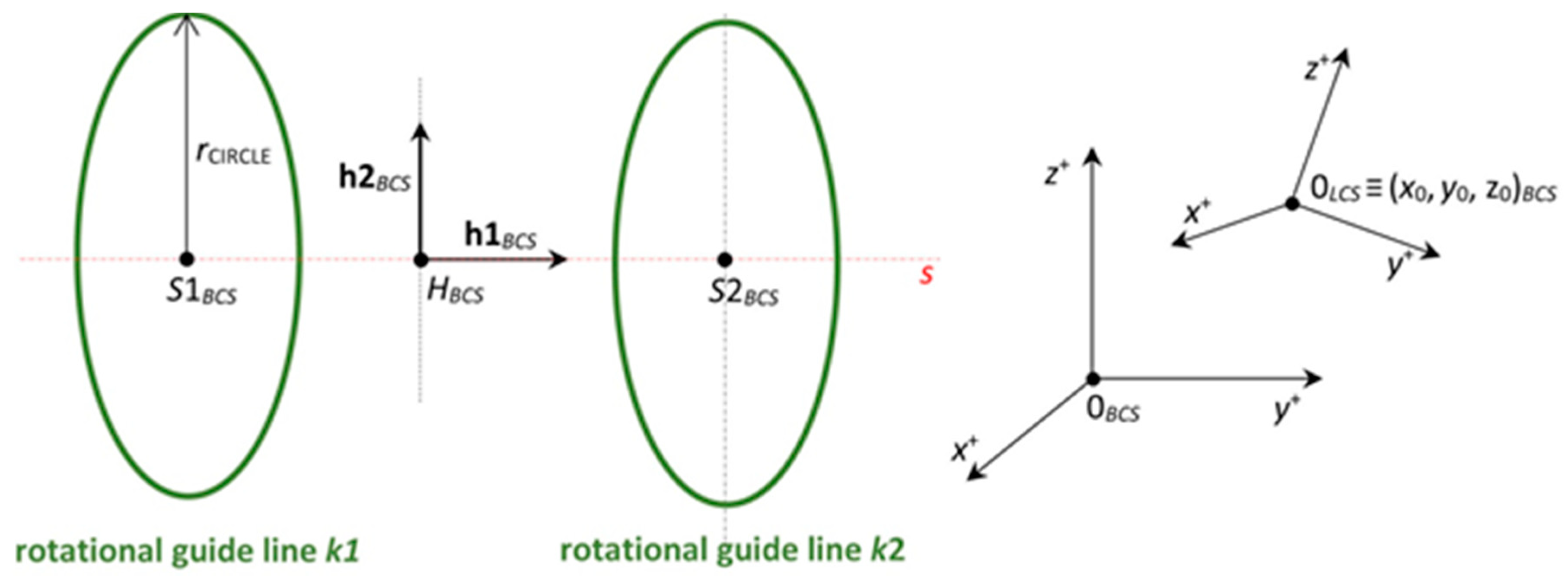
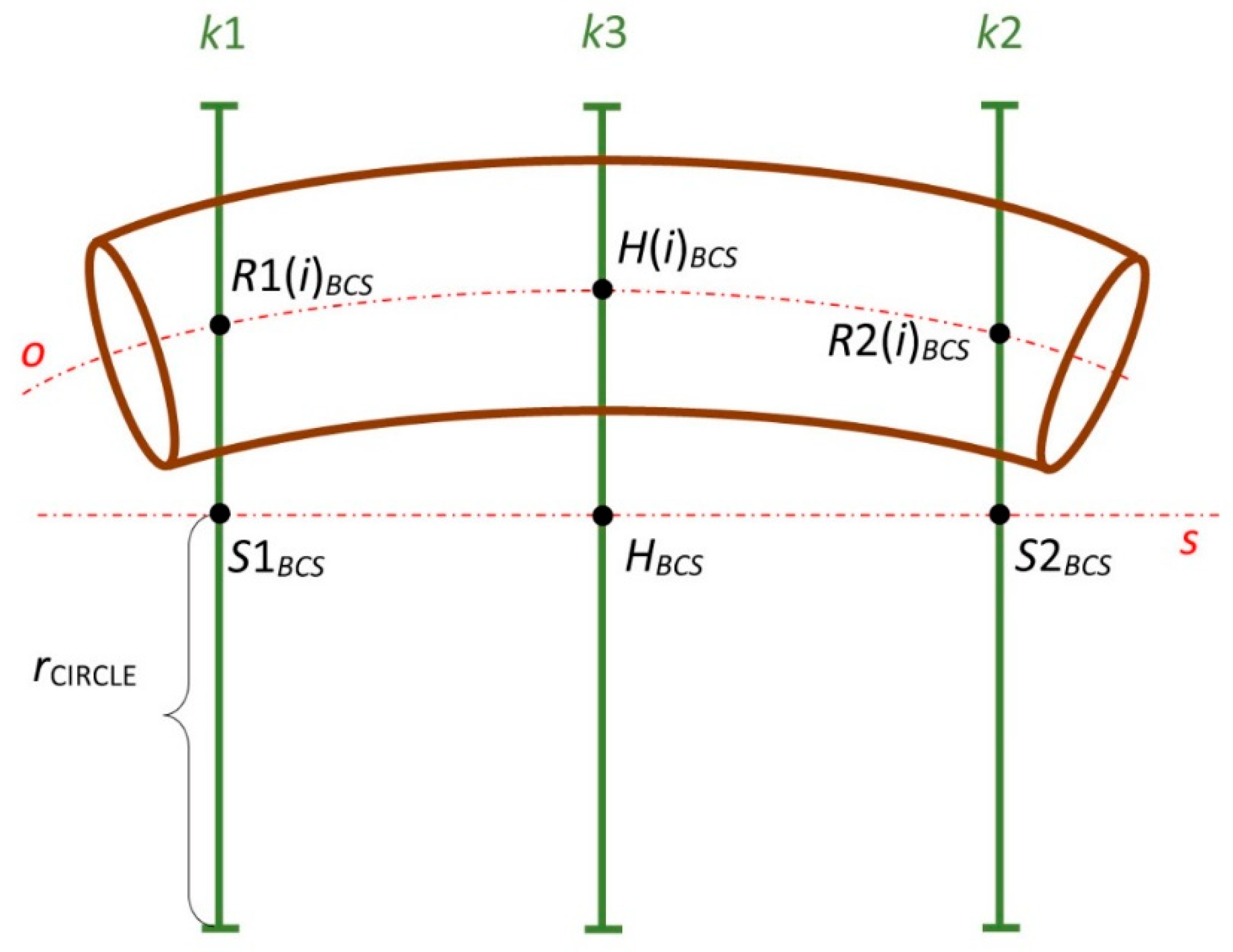
2.1. Fiber Winding Geometry
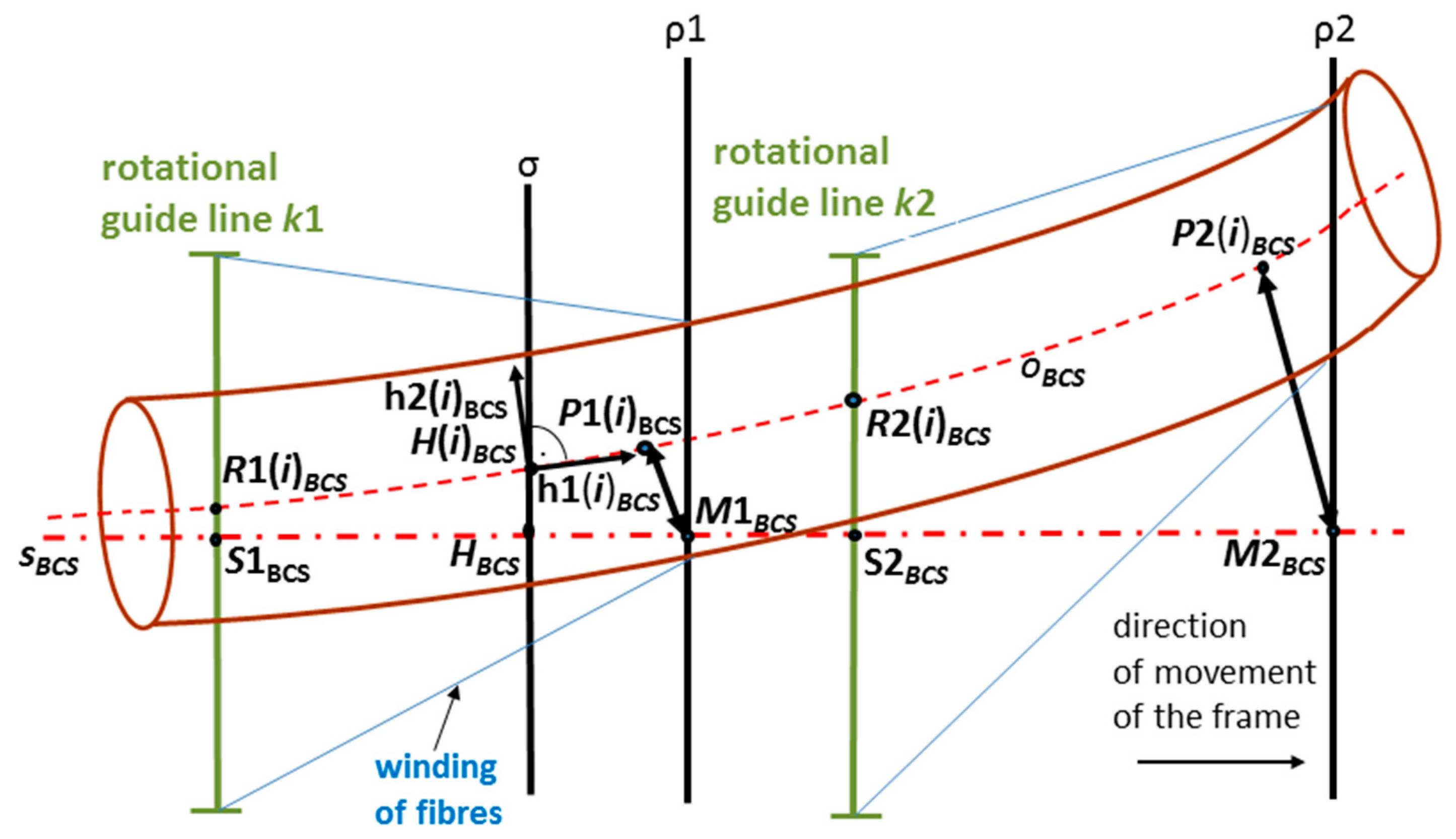
2.2. Mathematical Model of Winding Process
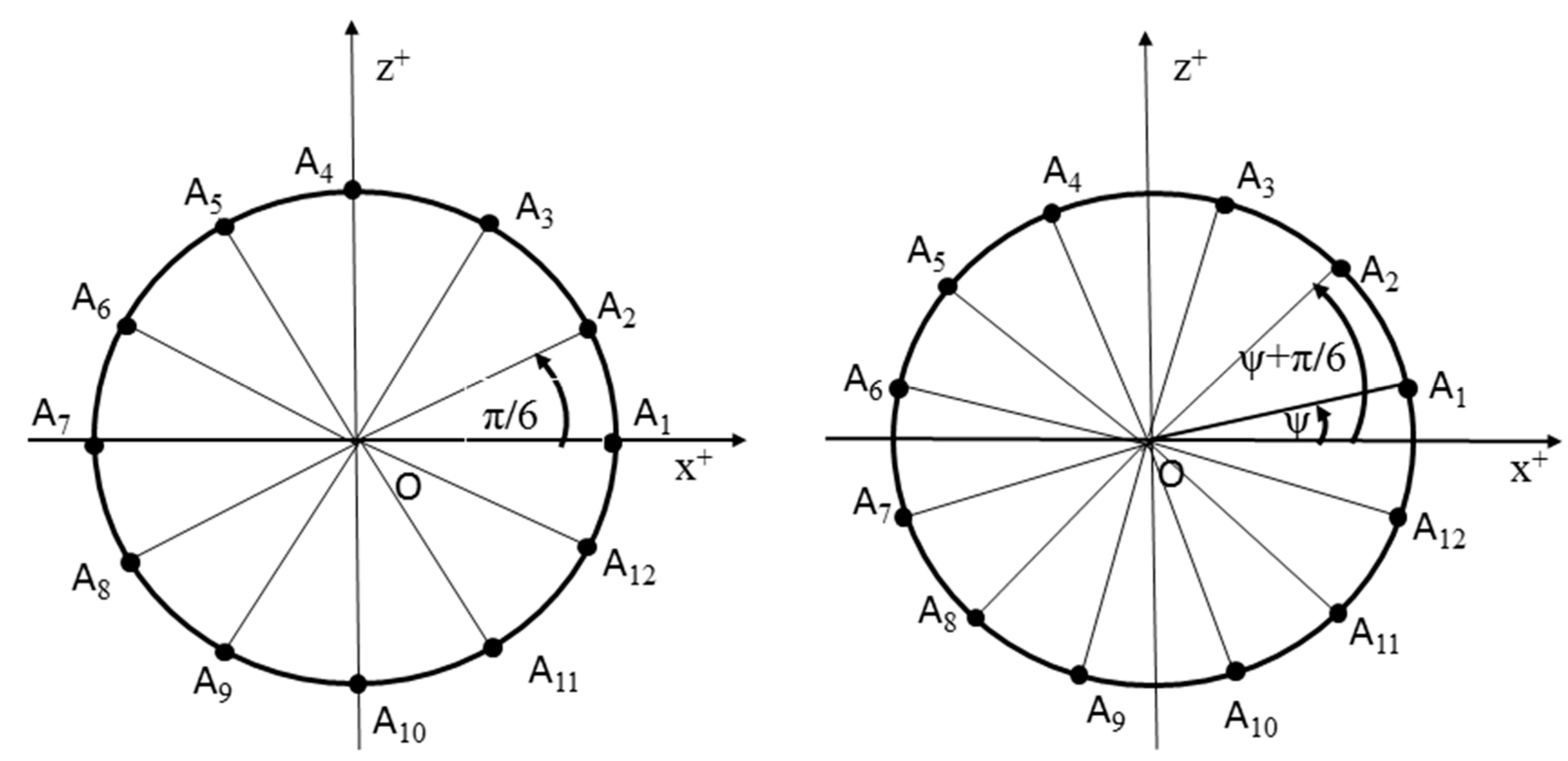
2.2.1. Fiber-Processing Head
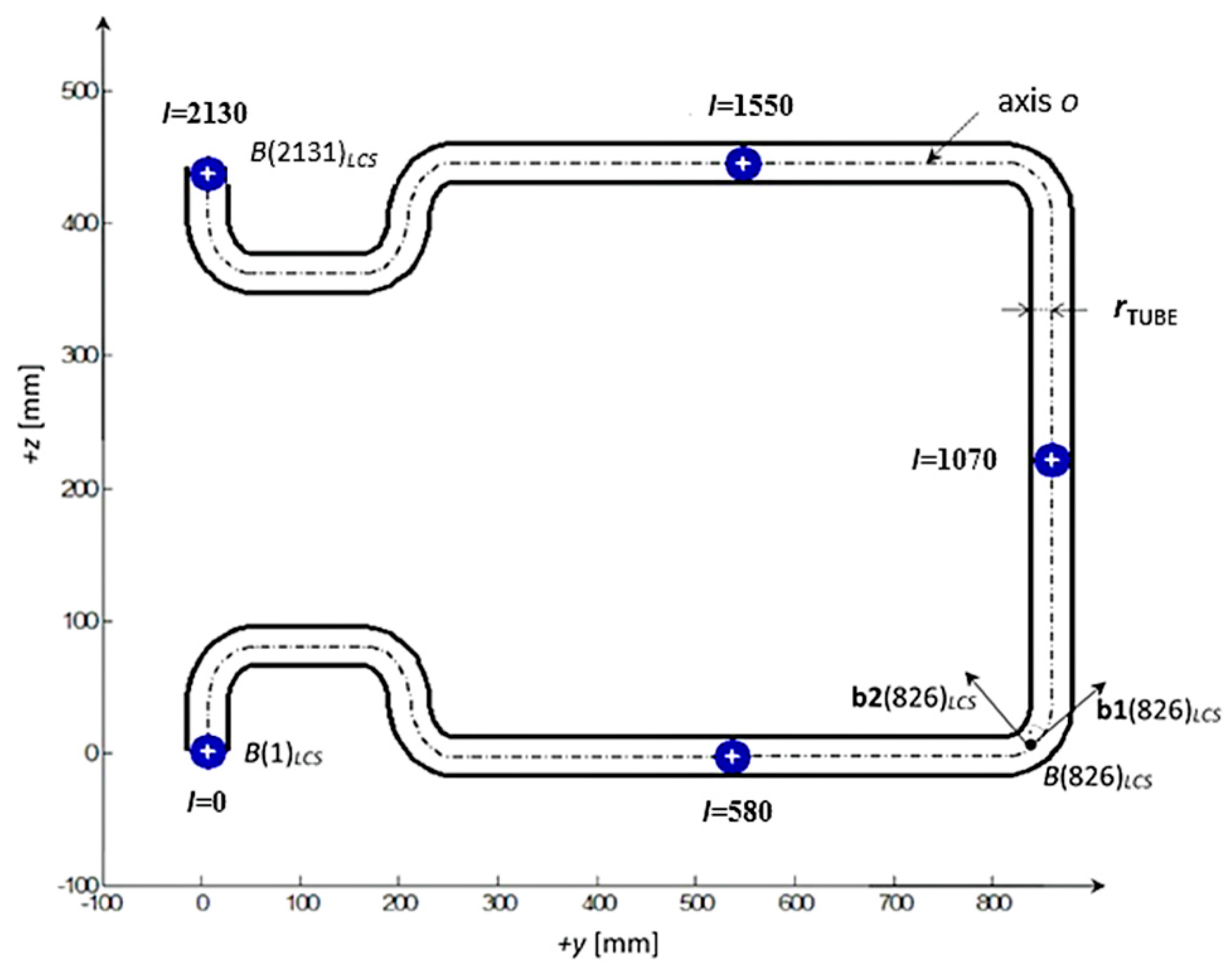
2.2.2. Non-Bearing Core Frame
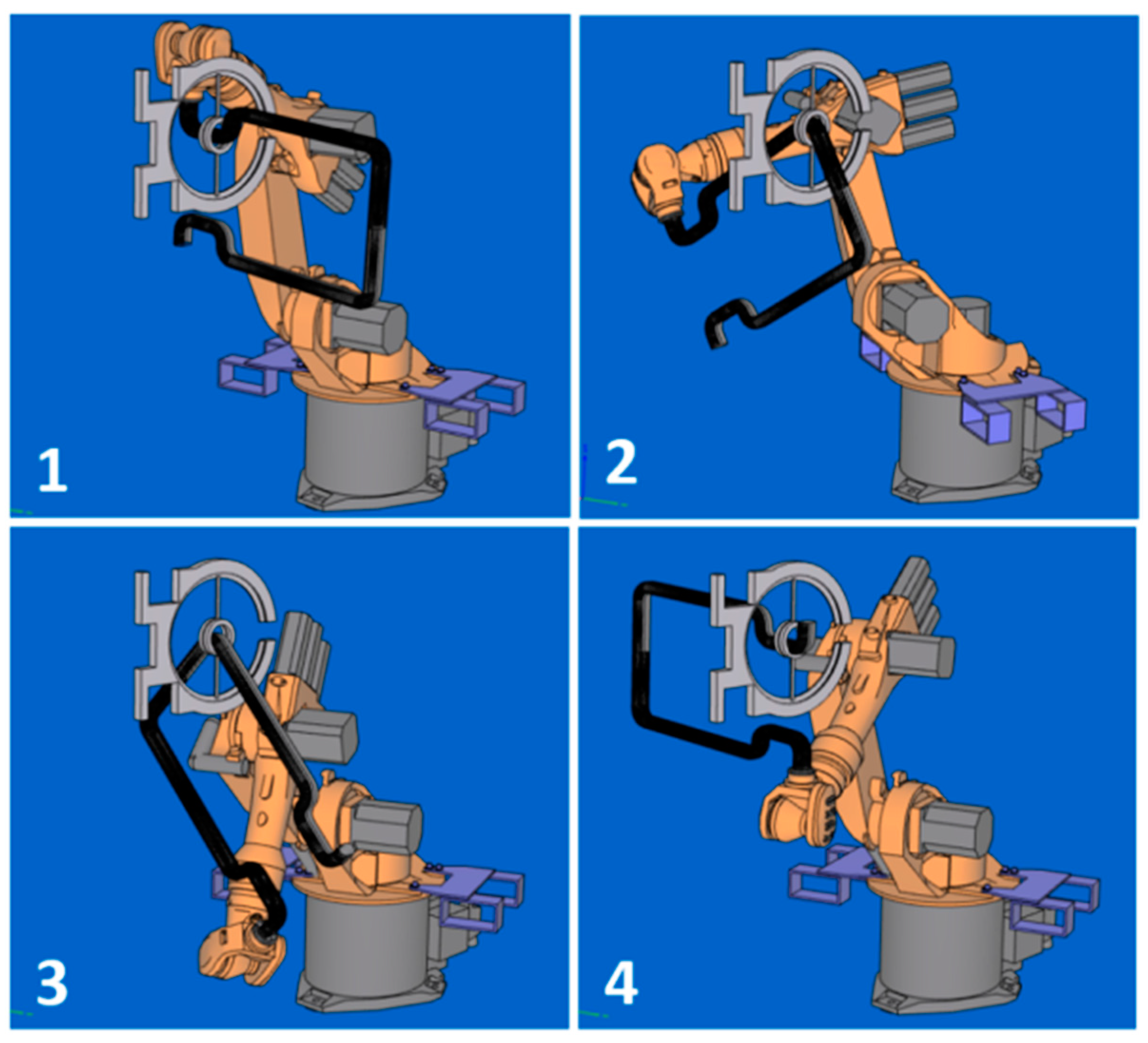
2.3. Robot Trajectory Optimization
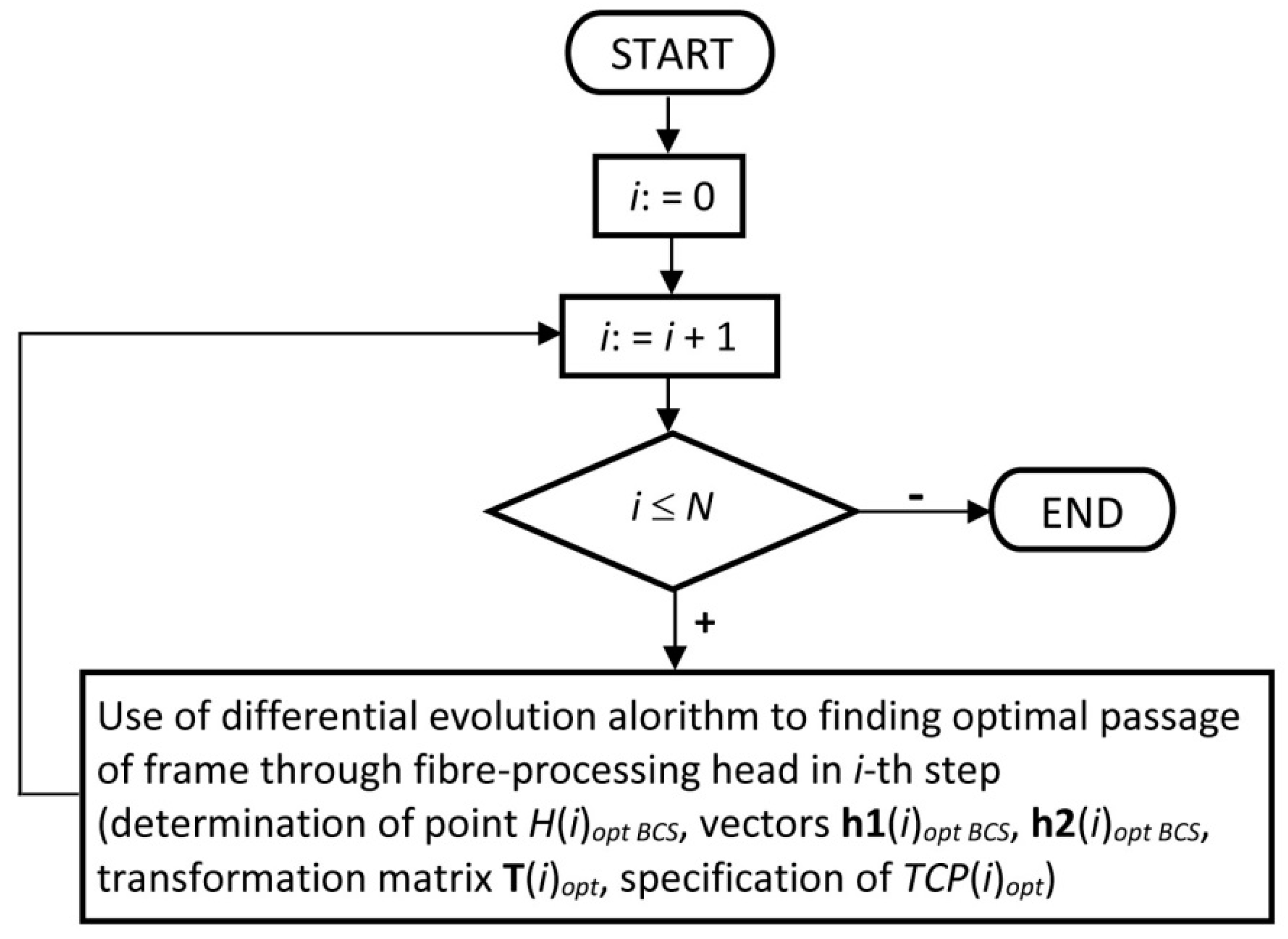
2.3.1. Schematic Representation of the Procedure for Calculating the Optimal REE Trajectory
- Specification of the fiber-processing head in (including coordinates of centers and of outer rotating guide lines and of the head, vectors and , common radius of circles and ).
- Loading of the location of composite frame in (including coordinates of points , vectors , and values for , radius of frame ).
- Determination of more points on frame axis and corresponding vectors and .
- Calculation of the optimal REE trajectory to ensure the high-quality of fiber winding on the composite frame. A differential evolution algorithm (see Section 4) is used for the optimization procedure. Determining the optimal sequence () is the result of calculation.
- Storing the calculated sequence of () in the central robot unit. Determining the optimal trajectory by linking individual corresponding parameters of consecutive following (using programming instruction of robot—linear interpolations or cubic splines).
2.3.2. Use of Differential Evolution Algorithm to REE Trajectory Optimization
2.3.3. Pseudo-Code of MDEA
| Algorithm 1. MDEA |
| Input: The number of calculated generations , crossover probability , mutation factor , generation size , the dimension of individuals , lower limits and upper limits , . Internal computation:
collision:=true repeat (i) randomly select index (ii) randomly select indices where for ; ; (iii) for step to do if or ) then else end for (j) (iv) Testing of possible collisions of the frame location in defined by and the fiber-processing head. if does not include collisions then collision = false until collision = false end repeat (v) if then else end if end for (m) b) Store individuals and their evolutions of the new generation -st generation in the matrix , . c) Find index which satisfies the condition for , , where satisfies (13) end while (k). Output: The best found individual is represented by the row of matrix that contains the corresponding value . Comments. The repeat until condition cycle is always executed at least once, since the controlling condition is checked at the end of the cycle. Function randomly picks a number from the interval . The notation means the j-th component of an individual in the k-th generation. The individual in pseudo-code of MDEA is the final solution and corresponds to designation that includes optimized parameters , . However, it should be noted that in general parameters , calculated by MDEA can only be optimized (and not optimal) parameters in relation to equation (9). This is due to the calculation of the final number of generations of individuals using MDEA. Therefore we mark calculated parameters as optimal parameters . |
3. Mechanical Performance of Polymer Composite Frame
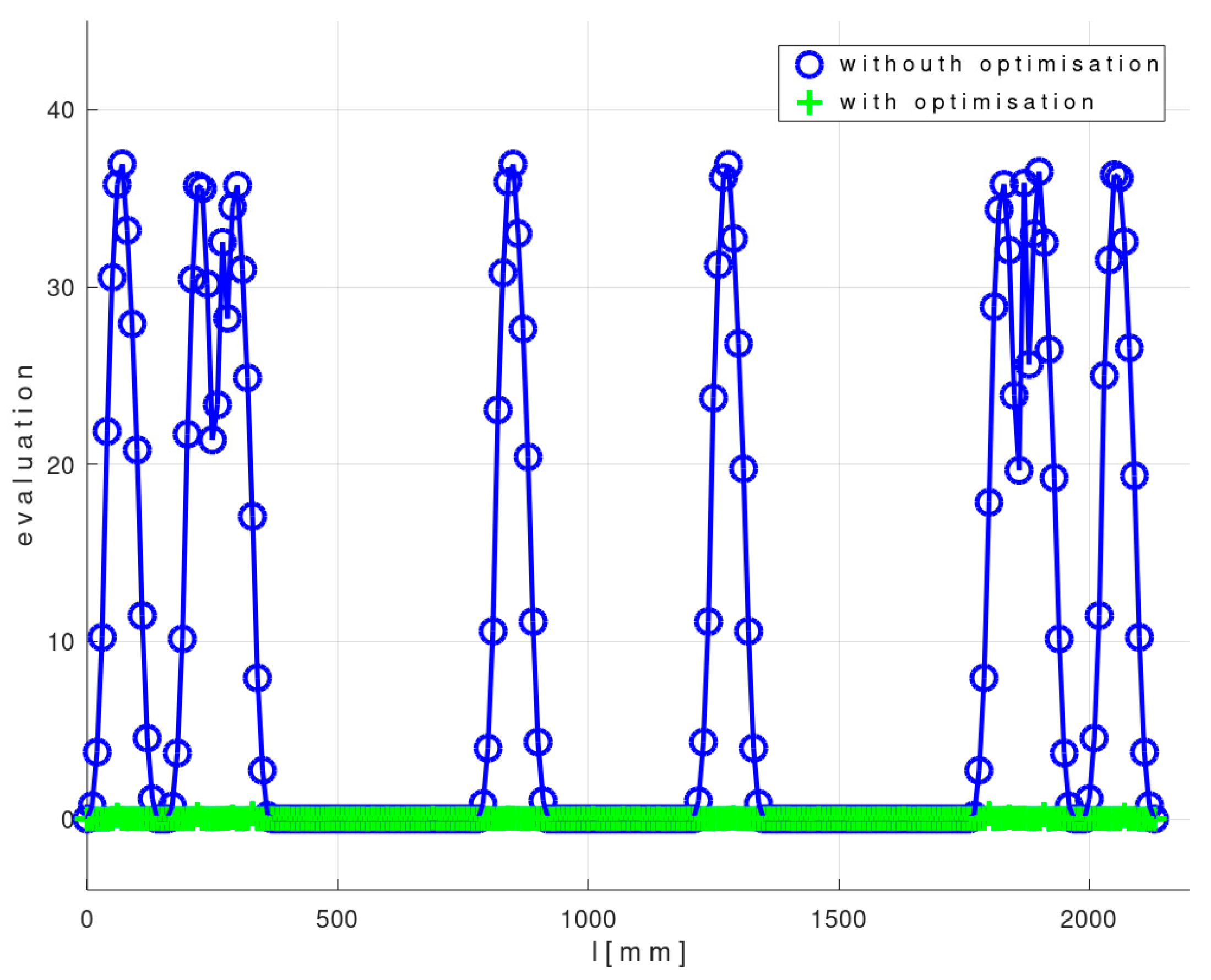
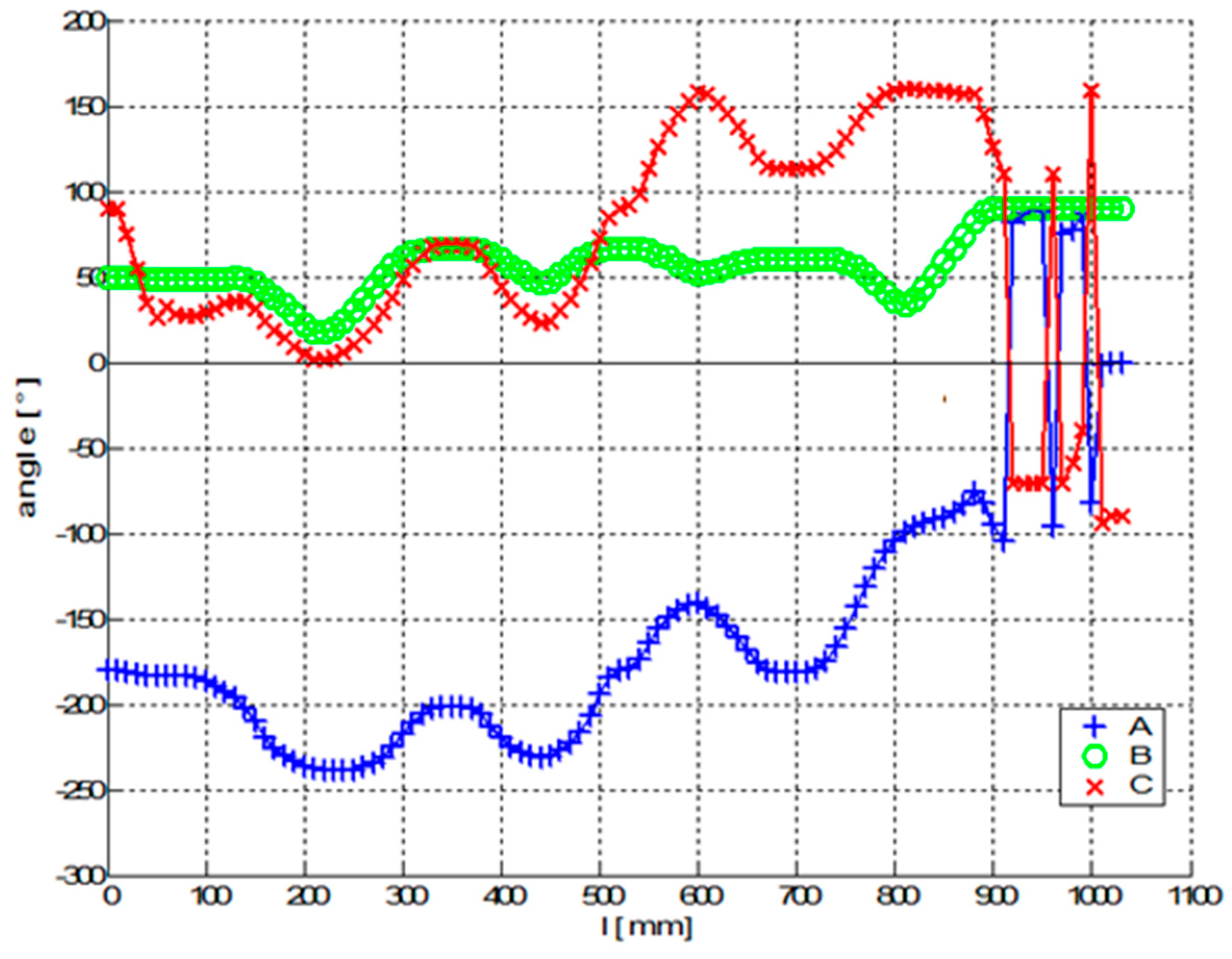
4. Practical Experimental Verification Tests of Optimization Procedure
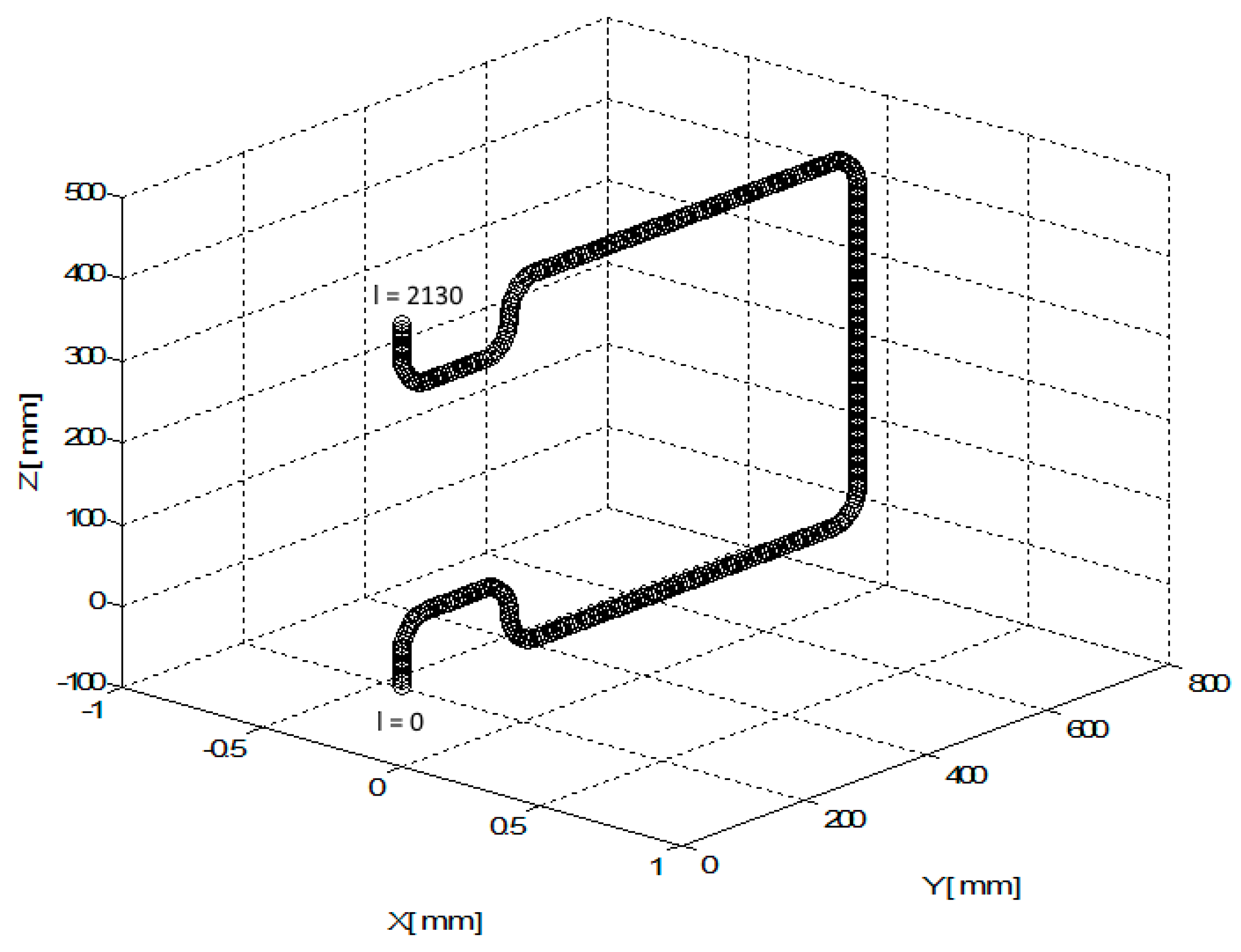
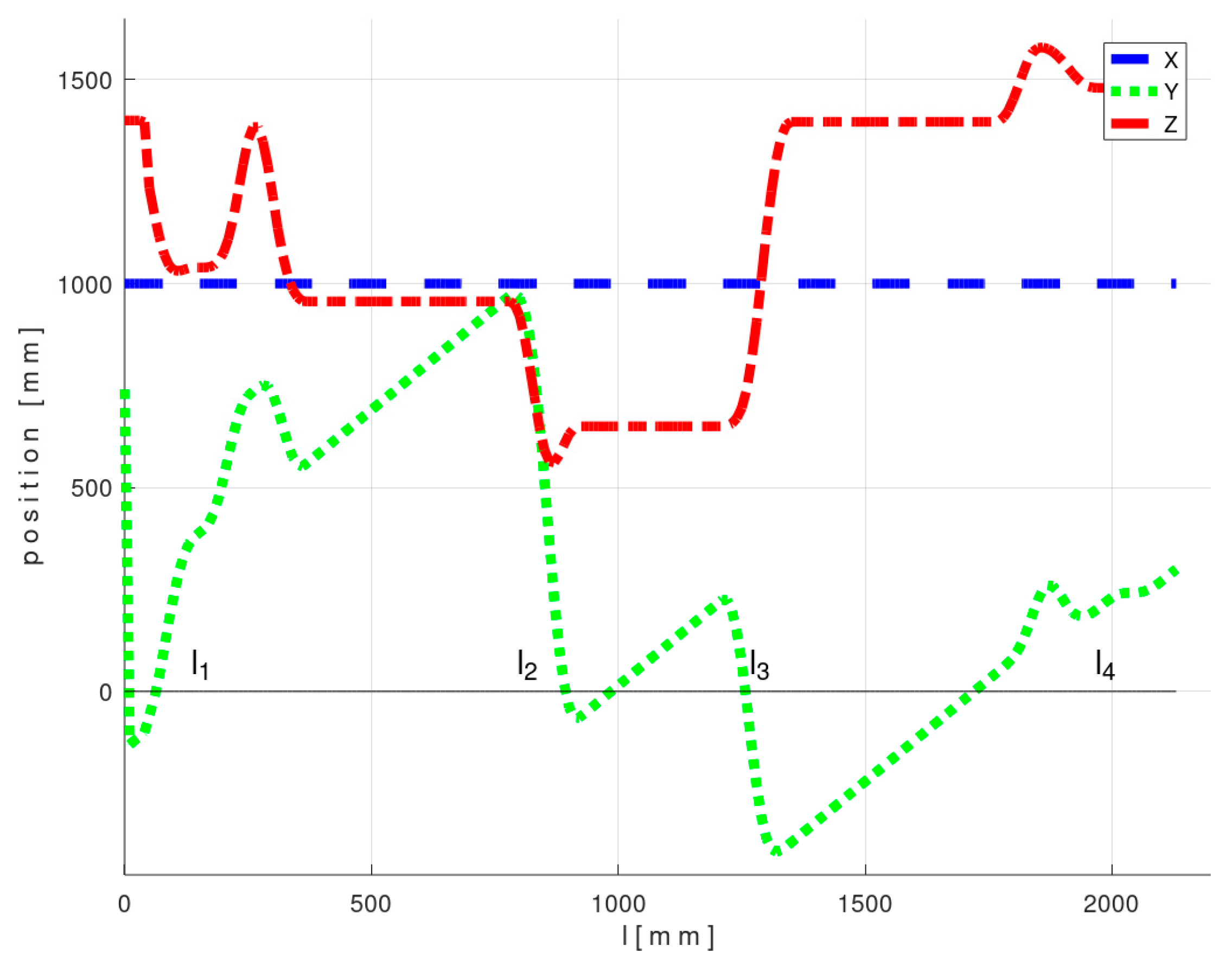
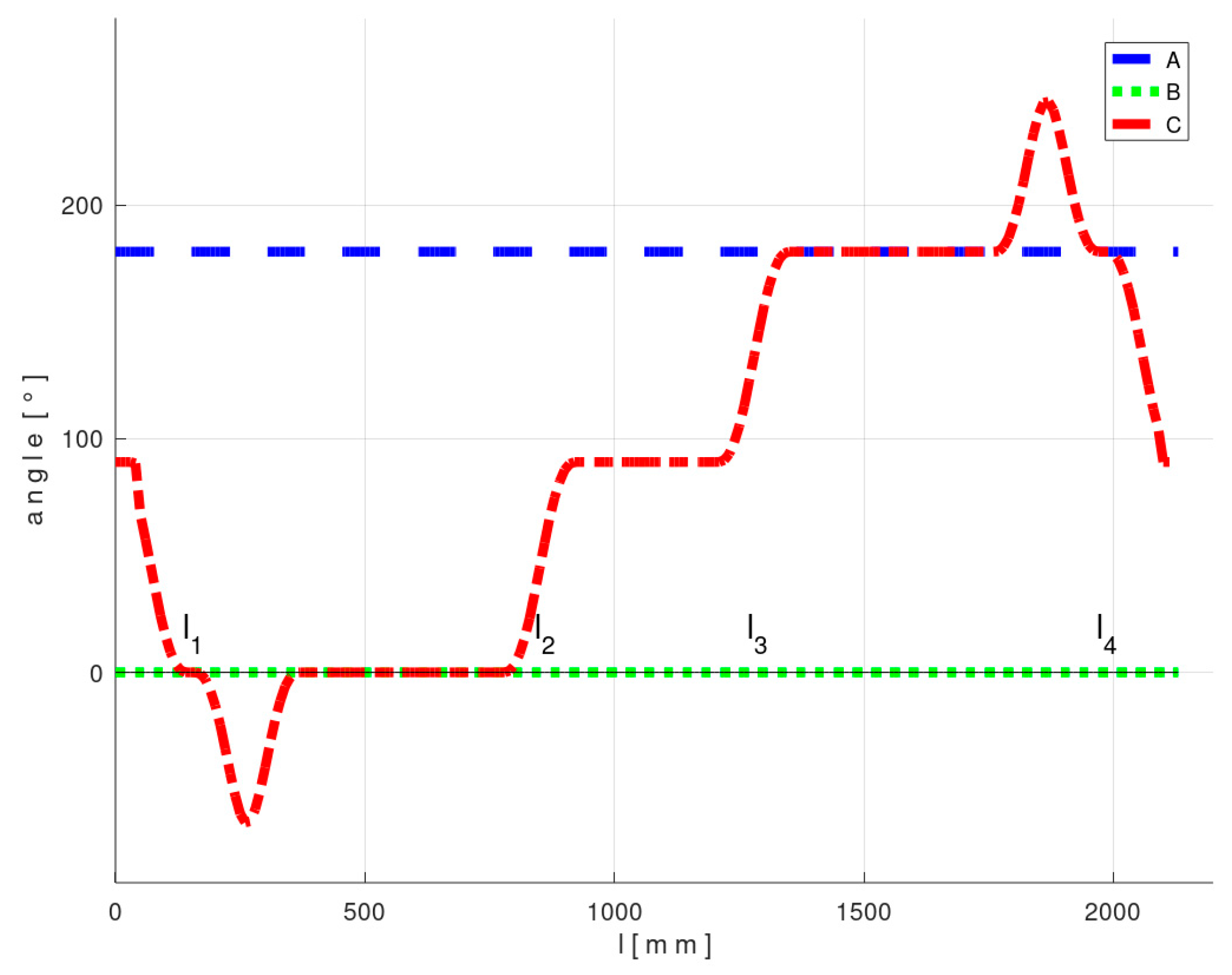
4.1. Experimental Test 1—Composite Non-Bearing Core Frame Shaped in 2D
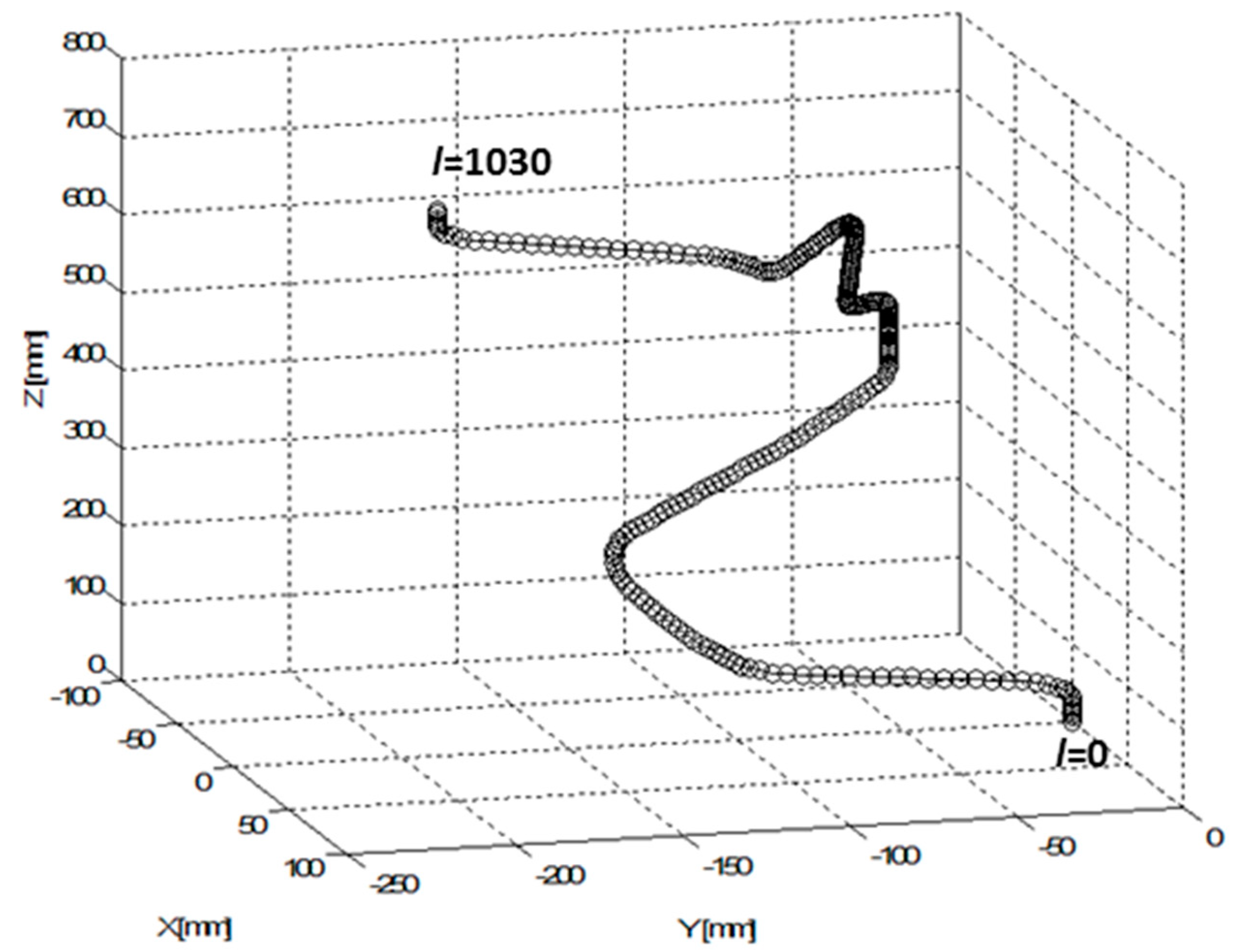
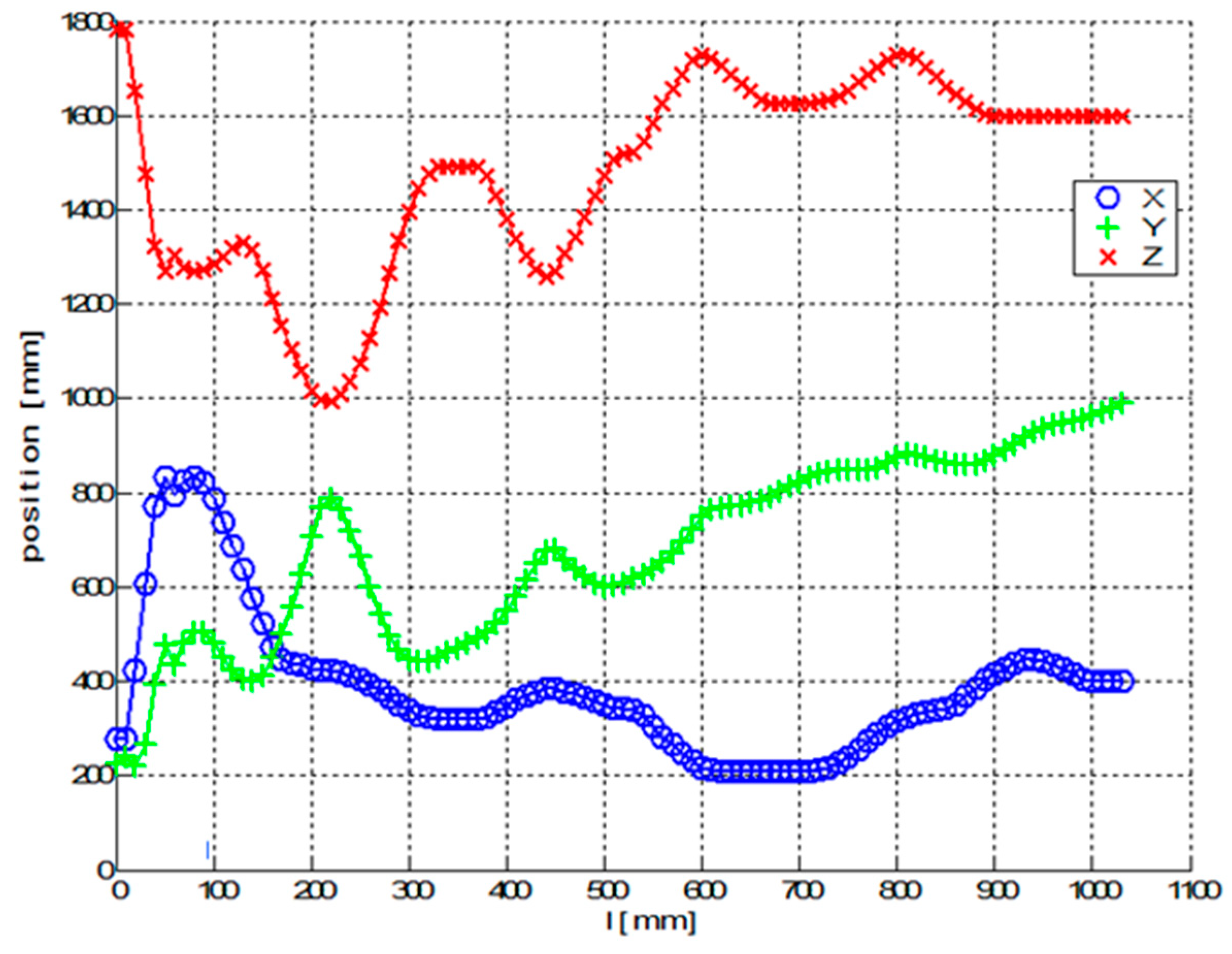
4.2. Experimental Test 2—3D Shape Non-Bearing Core Frame
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gay, D. Composite Materials: Design and Applications; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Koloor, S.S.R.; Tamin, M. Mode-II interlaminar fracture and crack-jump phenomenon in CFRP composite laminate materials. Compos. Struct. 2018, 204, 594–606. [Google Scholar] [CrossRef]
- Mlynek, J.; Petru, M.; Martinec, T. Optimization of Industrial Robot Trajectory in Composite Production. In Proceedings of the 2018 18th International Conference on Mechatronics-Mechatronika (ME), Brno, Czech Republic, 5–7 December 2018; pp. 1–6. [Google Scholar]
- Petrů, M.; Mlynek, J.; Martinec, T. Numerical modelling for optimization of fibres winding process of manufacturing technology for the non-circular aerospaces frames. Manuf. Technol. 2018, 18. [Google Scholar] [CrossRef]
- Kulhavy, P.; Syrovatkova, M.; Srb, P.; Petru, M.; Samkova, A. Irregular Winding of Pre-preg Fibres Aimed at the Local Improvement of Flexural Properties. Tekstilec 2017, 60. [Google Scholar] [CrossRef]
- Koloor, S.S.R.; Khosravani, M.R.; Hamzah, R.; Tamin, M. FE model-based construction and progressive damage processes of FRP composite laminates with different manufacturing processes. Int. J. Mech. Sci. 2018, 141, 223–235. [Google Scholar] [CrossRef]
- Wang, X.; Petrů, M.; Yu, H. The effect of surface treatment on the creep behavior of flax fiber reinforced composites under hygrothermal aging conditions. Constr. Build. Mater. 2019, 208, 220–227. [Google Scholar] [CrossRef]
- Sharma, S.; Sowntharya, L.; Kar, K.K. Polymer-Based Composite Structures: Processing and Applications. In Composite Materials; Springer: Berlin/Heidelberg, Germany, 2017; pp. 1–36. [Google Scholar]
- Agarwal, B.D.; Broutman, L.J.; Chandrashekhara, K. Analysis and Performance of Fiber Composites; John Wiley & Sons: New York, NY, USA, 2017. [Google Scholar]
- Sharifi Teshnizi, S.H.; Koloor, S.S.R.; Sharifishourabi, G.; Bin Ayob, A.; Yahya, M.Y. Effect of ply thickness on displacements and stresses in laminated GFRP cylinder subjected to radial load. Adv. Mater. Res. 2012, 488–489, 367–371. [Google Scholar] [CrossRef]
- Curliss, D.B.; Lincoln, J.E. Fiber Winding System for Composite Projectile Barrel Structure. U.S. Patent 10,168,117, 17 November 2016. [Google Scholar]
- Hernandez-Moreno, H.; Douchin, B.; Collombet, F.; Choqueuse, D.; Davies, P. Influence of winding pattern on the mechanical behavior of filament wound composite cylinders under external pressure. Compos. Sci. Technol. 2008, 68, 1015–1024. [Google Scholar] [CrossRef]
- Fowler, C.P.; Orifici, A.C.; Wang, C.H. A review of toroidal composite pressure vessel optimisation and damage tolerant design for high pressure gaseous fuel storage. Int. J. Hydrog. Energy 2016, 41, 22067–22089. [Google Scholar] [CrossRef]
- McIlhagger, A.; Archer, E.; McIlhagger, R. Manufacturing processes for composite materials and components for aerospace applications. In Polymer Composites in the Aerospace Industry; Elsevier: Cranfield, UK, 2020; pp. 59–81. [Google Scholar]
- Groppe, D. Robots improve the quality and cost-effectiveness of composite structures. Ind. Robot 2000, 27, 96–102. [Google Scholar] [CrossRef]
- Mlýnek, J.; Petrů, M.; Martinec, T. Design of composite frames used in agricultural machinery. In Proceedings of the 7th TAE, Prague, Czech Republic, 17–20 September 2019. [Google Scholar]
- Koloor, S.; Abdullah, M.; Tamin, M.; Ayatollahi, M. Fatigue damage of cohesive interfaces in fiber-reinforced polymer composite laminates. Compos. Sci. Technol. 2019, 183, 107779. [Google Scholar] [CrossRef]
- Quanjin, M.; Rejab, M.; Idris, M.; Kumar, N.M.; Merzuki, M. Robotic Filament Winding Technique (RFWT) in Industrial Application: A Review of State of the Art and Future Perspectives. Int. Res. J. Eng. Technol. 2018, 5, 1668–1676. [Google Scholar]
- Shirinzadeh, B.; Alici, G.; Foong, C.W.; Cassidy, G. Fabrication process of open surfaces by robotic fibre placement. Robot. Comput.-Integr. Manuf. 2004, 20, 17–28. [Google Scholar] [CrossRef]
- Meng, Z.; Yao, L.; Bu, J.; Sun, Y. Prediction method for offset compensation on three-dimensional mandrel with spatial irregular shape. J. Ind. Text. 2019. [Google Scholar] [CrossRef]
- Martinec, T.; Mlýnek, J.; Petrů, M. Calculation of the robot trajectory for the optimum directional orientation of fibre placement in the manufacture of composite profile frames. Robot. Comput.-Integr. Manuf. 2015, 35, 42–54. [Google Scholar] [CrossRef]
- Sofi, T.; Neunkirchen, S.; Schledjewski, R. Path calculation, technology and opportunities in dry fiber winding: A review. Adv. Manuf. Polym. Compos. Sci. 2018, 4, 57–72. [Google Scholar] [CrossRef]
- Polini, W.; Sorrentino, L. Influence of winding speed and winding trajectory on tension in robotized filament winding of full section parts. Compos. Sci. Technol. 2005, 65, 1574–1581. [Google Scholar] [CrossRef]
- Azevedo, C.B.; Almeida, J.H.S., Jr.; Flores, H.F.; Eggers, F.; Amico, S.C. Influence of mosaic pattern on hygrothermally-aged filament wound composite cylinders under axial compression. J. Compos. Mater. 2020. [Google Scholar] [CrossRef]
- Gao, J.; Pashkevich, A.; Caro, S. Manipulator motion planning in redundant robotic system for fiber placement process. In New Trends in Mechanism and Machine Science; Springer: Berlin, Germany, 2017; pp. 243–252. [Google Scholar]
- Chen, X.; Zhang, Y.; Xie, J.; Du, P.; Chen, L. Robot needle-punching path planning for complex surface preforms. Robot. Comput.-Integr. Manuf. 2018, 52, 24–34. [Google Scholar] [CrossRef]
- Andulkar, M.V.; Chiddarwar, S.S. Incremental approach for trajectory generation of spray painting robot. Ind. Robot 2015, 42, 228–241. [Google Scholar] [CrossRef]
- Gao, J.; Pashkevich, A.; Caro, S. Optimization of the robot and positioner motion in a redundant fiber placement workcell. Mech. Mach. Theory 2017, 114, 170–189. [Google Scholar] [CrossRef]
- Xiao, Y.; Du, Z.; Dong, W. Smooth and near time-optimal trajectory planning of industrial robots for online applications. Ind. Robot 2012, 39, 169–177. [Google Scholar] [CrossRef]
- Piao, S.; Zhong, Q.; Wang, X.; Gao, C. Optimal Trajectory Generation for Soccer Robot Based on Genetic Algorithms. In Proceedings of the International Workshop on Computer Science for Environmental Engineering and EcoInformatics, Kunming, China, 29–31 July 2011; pp. 447–451. [Google Scholar]
- Chen, Y.; Yan, L.; Wei, H.; Wang, T. Optimal trajectory planning for industrial robots using harmony search algorithm. Ind. Robot 2013, 40, 502–512. [Google Scholar] [CrossRef]
- Simba, K.R.; Uchiyama, N.; Sano, S. Real-time smooth trajectory generation for nonholonomic mobile robots using Bézier curves. Robot. Comput.-Integr. Manuf. 2016, 41, 31–42. [Google Scholar] [CrossRef]
- Hodgkinson, J.M. Mechanical Testing of Advanced Fibre Composites; Elsevier: Cambridge, UK, 2000. [Google Scholar]
- Gay, D.; Gambelin, J. Structural Modelling and Calculus: An Introduction; ISTE LTD: London, UK, 2008. [Google Scholar]
- Koloor, S.S.R.; Abdul-Latif, A.; Tamin, M.N. Mechanics of composite delamination under flexural loading. Key Eng. Mater. 2011, 462–463, 726–731. [Google Scholar] [CrossRef]
- Koloor, S.S.R.; Hussin, H.; Tamin, M.N. Mode i interlaminar fracture characterization of CFRP composite laminates. Adv. Mater. Res. 2012, 488–489, 552–556. [Google Scholar] [CrossRef]
- Sharifi Teshnizi, S.H.; Koloor, S.S.R.; Sharifishourabi, G.; Bin Ayob, A.; Yahya, M.Y. Mechanical behavior of GFRP laminated composite pipe subjected to uniform radial patch load. Adv. Mater. Res. 2012, 488–489, 542–546. [Google Scholar] [CrossRef]
- Sciavicco, L.; Siciliano, B. Modelling and Control of Robot Manipulators; Springer: London, UK, 2012. [Google Scholar]
- Rao, J.S.; Dukkipati, R.V. Mechanism and Machine Theory; Wiley: New York, NY, USA, 1989. [Google Scholar]
- Budinský, B. Analytic and Differential Geometry. In Mathematics for Technical Colleges; SNTL: Prague, Czech Republic, 1983. [Google Scholar]
- Jazar, R.N. Theory of Applied Robotics: Kinematics, Dynamics, and Control, 2nd ed.; Springer: Berlin, Germany, 2010. [Google Scholar]
- Mlýnek, J.; Martinec, T. Mathematical model of composite manufacture and calculation of robot trajectory. In Proceedings of the 16th International Conference on Mechatronics-Mechatronika 2014, Brno, Czech Republic, 3–5 December 2014; pp. 345–351. [Google Scholar]
- Antia, H.M. Numerical Methods for Scientists and Engineers; Birkhäuser: Basel, Switzerland, 2002. [Google Scholar]
- Tian, L.; Collins, C. An effective robot trajectory planning method using a genetic algorithm. Mechatronics 2004, 14, 455–470. [Google Scholar] [CrossRef]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Knobloch, R.; Mlýnek, J.; Srb, R. The classic differential evolution algorithm and its convergence properties. Appl. Math. 2017, 62, 197–208. [Google Scholar] [CrossRef]
- Hu, Z.; Xiong, S.; Su, Q.; Zhang, X. Sufficient conditions for global convergence of differential evolution algorithm. J. Appl. Math. 2013, 2013, 193196. [Google Scholar] [CrossRef]
- Mlýnek, J.; Knobloch, R. Model of shell metal mould heating in the automotive industry. Appl. Math. 2018, 63, 111–124. [Google Scholar] [CrossRef]
- Abdi, B.; Koloor, S.S.R.; Abdullah, M.R.; Ayob, A.; Yahya, M.Y.B. Effect of strain-rate on flexural behavior of composite sandwich panel. Appl. Mech. Mater. 2012, 229–231, 766–770. [Google Scholar] [CrossRef]
- Koloor, S.S.R.; Tamin, M.N. Effects of lamina damages on flexural stiffness of CFRP composites. In Proceedings of the 8th Asian-Australasian Conference on Composite Materials 2012, ACCM 2012—Composites: Enabling Tomorrow’s Industry Today, Kuala Lumpur, Malaysia, 6–8 November 2012; pp. 237–243. [Google Scholar]
- Schuecker, C.; Pettermann, H. Fiber reinforced laminates: Progressive damage modeling based on failure mechanisms. Arch. Comput. Methods Eng. 2008, 15, 163–184. [Google Scholar] [CrossRef]
- Xian, G.; Wang, Z. Carbon Fiber Reinforced Plastics—Properties. Comprehensive Composite Materials; Beaumont, Peter, W.R., Zweben, Carl, H., Eds.; Elsevier: New York, NY, USA, 2000; Volume 2. [Google Scholar]
- Hallett, S.R.; Jiang, W.-G.; Khan, B.; Wisnom, M.R. Modelling the interaction between matrix cracks and delamination damage in scaled quasi-isotropic specimens. Compos. Sci. Technol. 2008, 68, 80–89. [Google Scholar] [CrossRef]
- Maimi, P.; Camanho, P.; Mayugo, J.; Turon, A. Matrix cracking and delamination in laminated composites. Part II: Evolution of crack density and delamination. Mech. Mater. 2011, 43, 194–211. [Google Scholar] [CrossRef]
- Koloor, S.S.R.; Karimzadeh, A.; Yidris, N.; Petrů, M.; Ayatollahi, M.R.; Tamin, M.N. An energy-based concept for yielding of multidirectional FRP composite structures using a mesoscale lamina damage model. Polymers 2020, 12, 157. [Google Scholar] [CrossRef]
- Koloor, S.; Ayatollahi, M.; Tamin, M. Elastic-damage deformation response of fiber-reinforced polymer composite laminates with lamina interfaces. J. Reinf. Plast. Compos. 2017, 36, 832–849. [Google Scholar] [CrossRef]
- Slabaugh, G.G. Computing Euler angles from a rotation matrix. Retr. August 1999, 6, 39–63. [Google Scholar]
- Brunete, A.; Mateo, C.; Gambao, E.; Hernando, M.; Koskinen, J.; Ahola, J.M.; Seppälä, T.; Heikkila, T. User-friendly task level programming based on an online walk-through teaching approach. Ind. Robot 2016, 43, 153–163. [Google Scholar] [CrossRef]
- Luo, Z. (Ed.) Robotics, Automation, and Control in Industrial and Service Settings; IGI Global: Hershey, PA, USA, 2015; pp. 1–337. [Google Scholar] [CrossRef]
- Klimchik, A.; Ambiehl, A.; Garnier, S.; Furet, B.; Pashkevich, A. Efficiency evaluation of robots in machining applications using industrial performance measure. Robot. Comput.-Integr. Manuf. 2017, 48, 12–29. [Google Scholar] [CrossRef]









© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mlýnek, J.; Petrů, M.; Martinec, T.; Rahimian Koloor, S.S. Fabrication of High-Quality Polymer Composite Frame by a New Method of Fiber Winding Process. Polymers 2020, 12, 1037. https://doi.org/10.3390/polym12051037
Mlýnek J, Petrů M, Martinec T, Rahimian Koloor SS. Fabrication of High-Quality Polymer Composite Frame by a New Method of Fiber Winding Process. Polymers. 2020; 12(5):1037. https://doi.org/10.3390/polym12051037
Chicago/Turabian StyleMlýnek, Jaroslav, Michal Petrů, Tomáš Martinec, and Seyed Saeid Rahimian Koloor. 2020. "Fabrication of High-Quality Polymer Composite Frame by a New Method of Fiber Winding Process" Polymers 12, no. 5: 1037. https://doi.org/10.3390/polym12051037
APA StyleMlýnek, J., Petrů, M., Martinec, T., & Rahimian Koloor, S. S. (2020). Fabrication of High-Quality Polymer Composite Frame by a New Method of Fiber Winding Process. Polymers, 12(5), 1037. https://doi.org/10.3390/polym12051037






