Reliability Analysis of FRP-Confined Concrete at Ultimate using Conjugate Search Direction Method
Abstract
1. Introduction
2. Research Significance
3. Reliability Analysis-Based Conjugate Search Direction
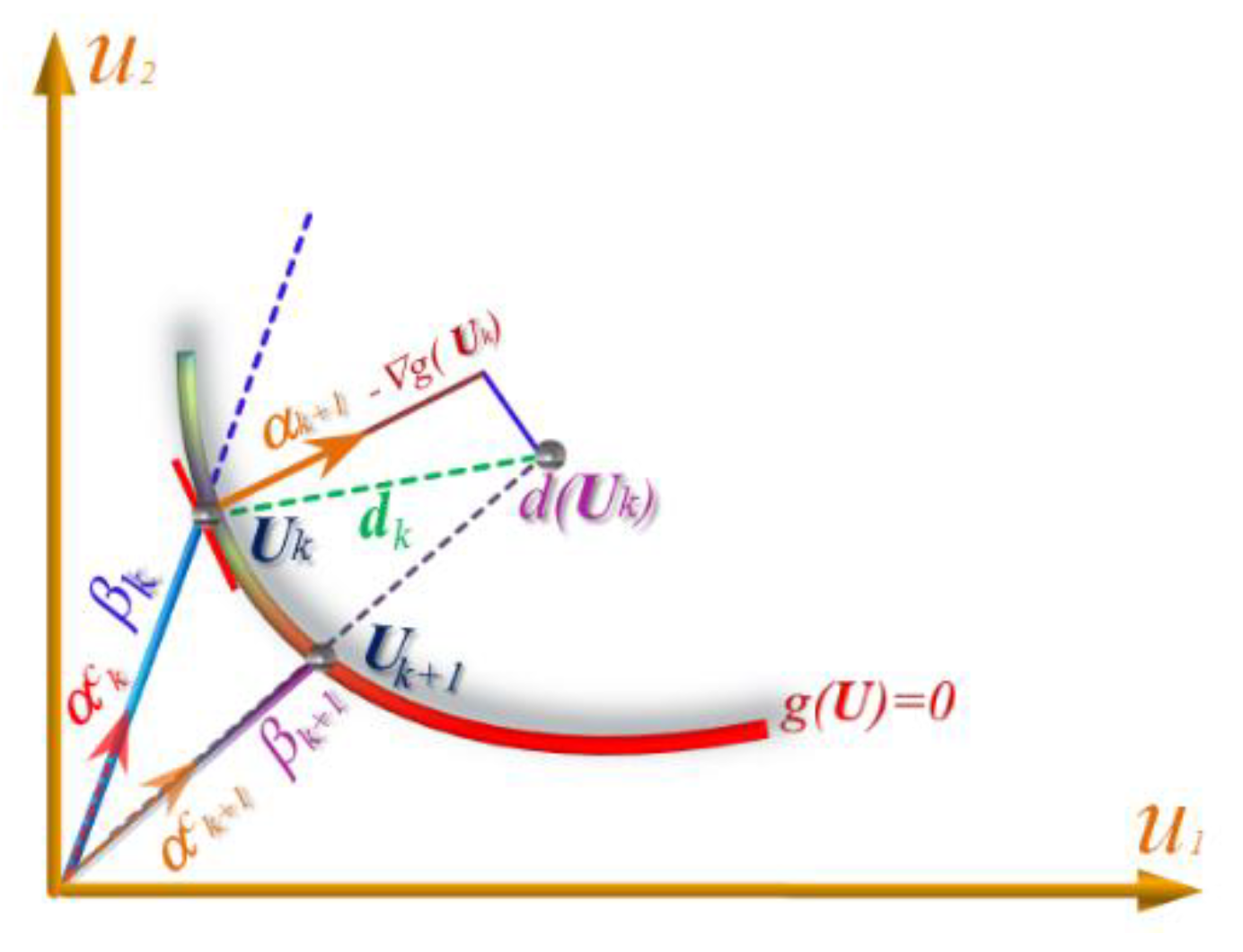
3.1. Conjugate Iterative Formula of FORM
3.2. CFORM Algorithm
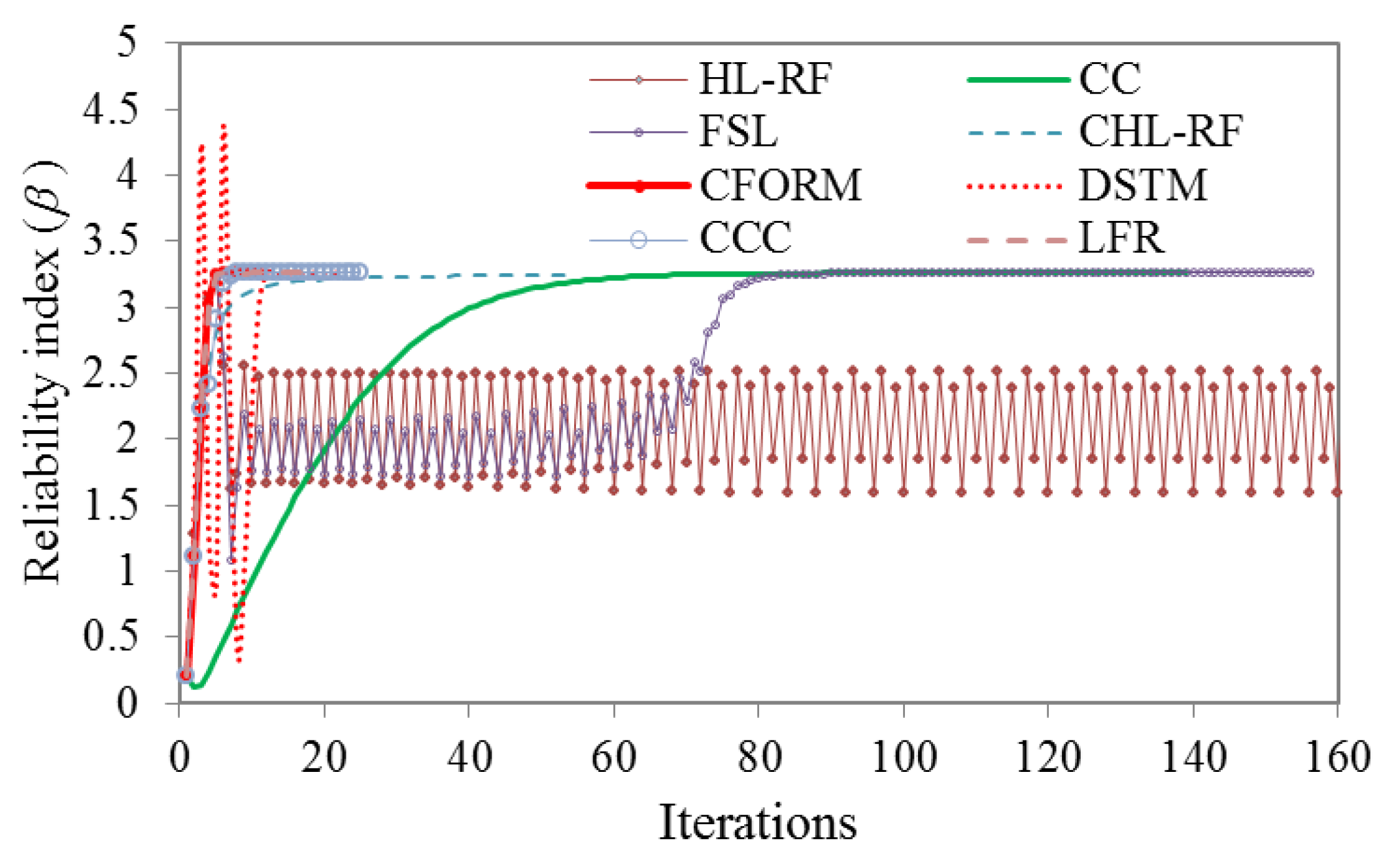
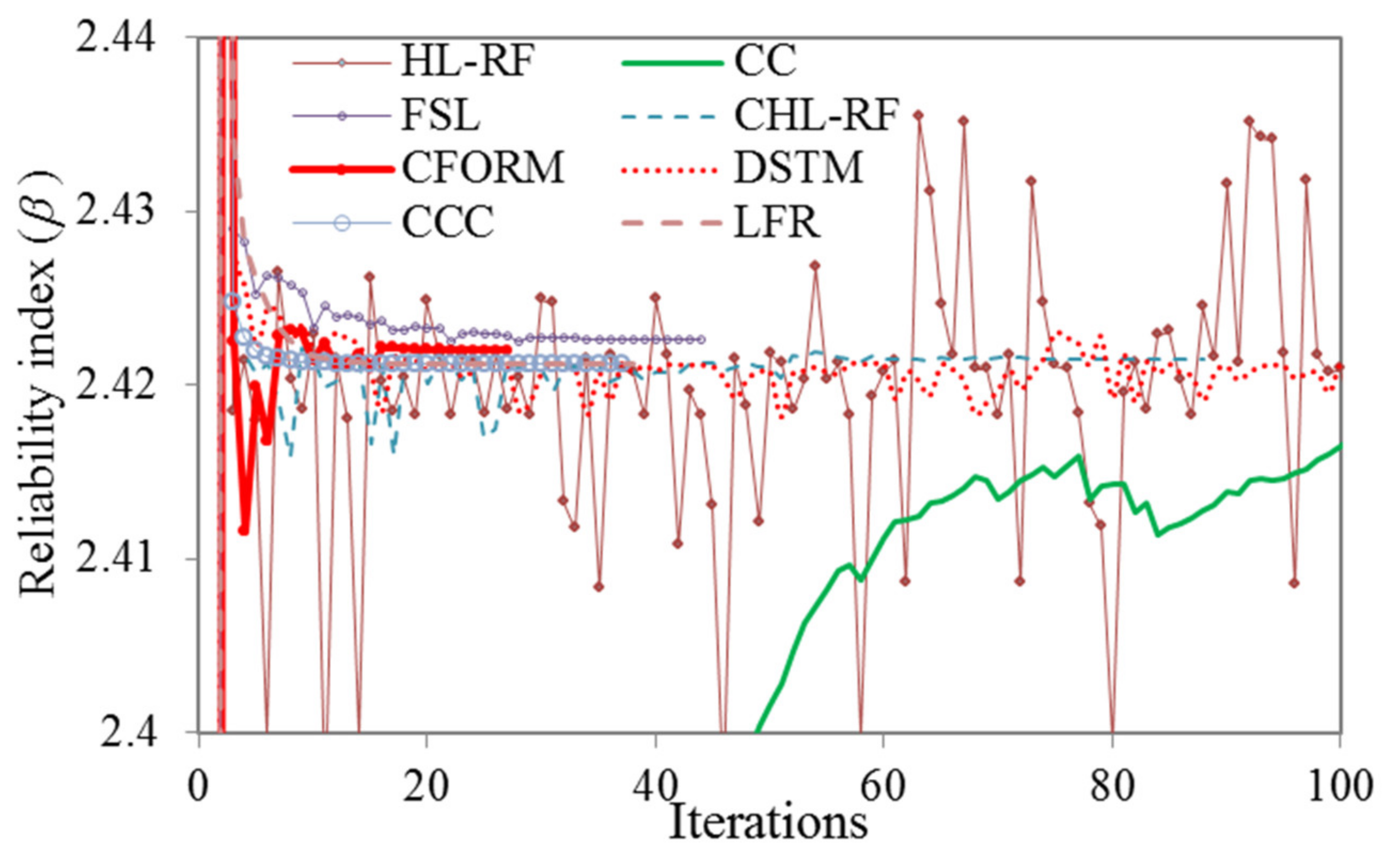
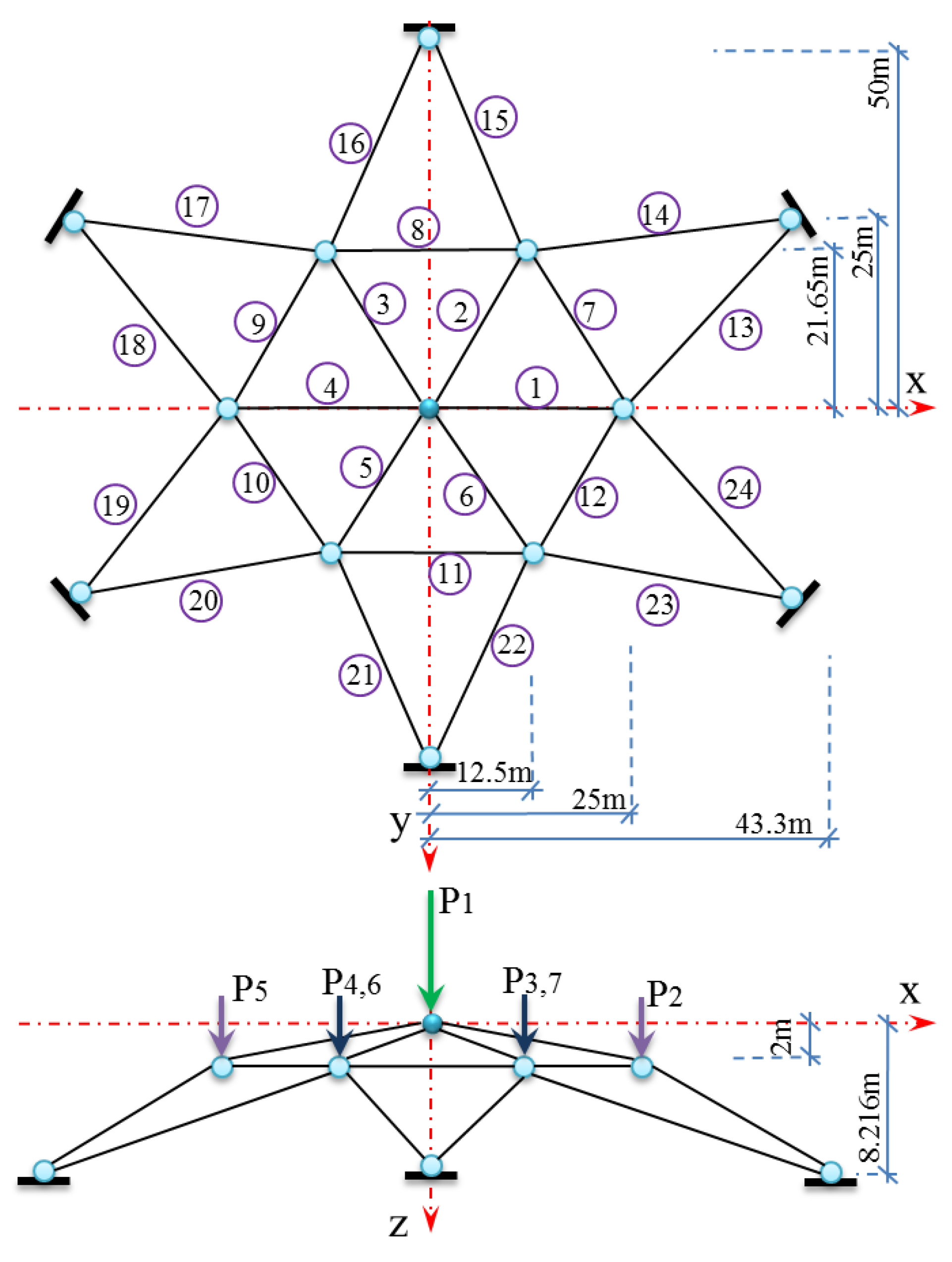
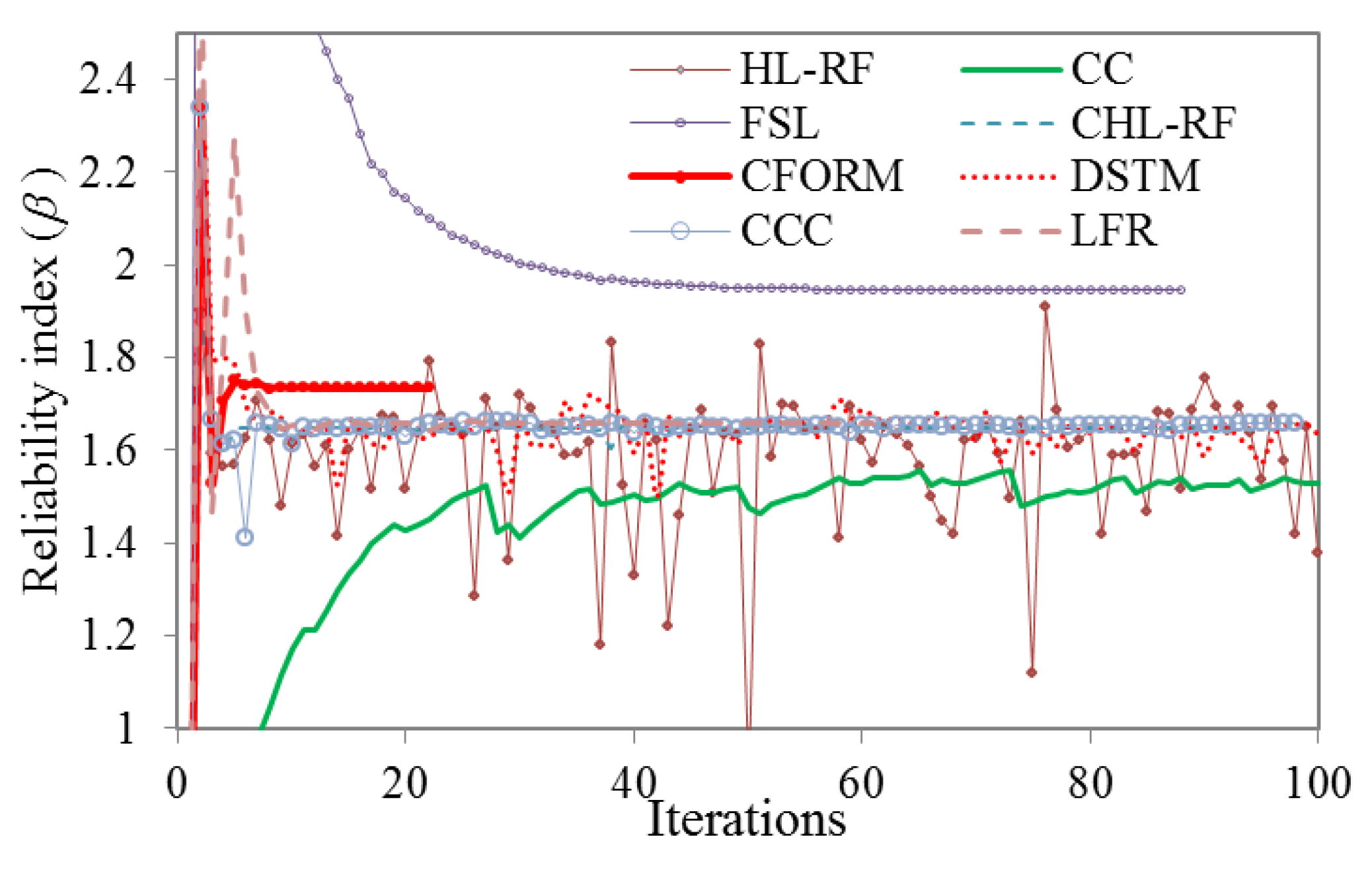
3.3. Validation of the Conjugate Reliability Analysis
4. Probabilistic Modeling of FRP-Confined Concrete
5. Reliability Analysis of FRP-Confined Concrete
5.1. Limit State Function for f′cc and εcu Results in the Database
5.2. Reliability Analysis of the Database
6. Conclusions
- (1)
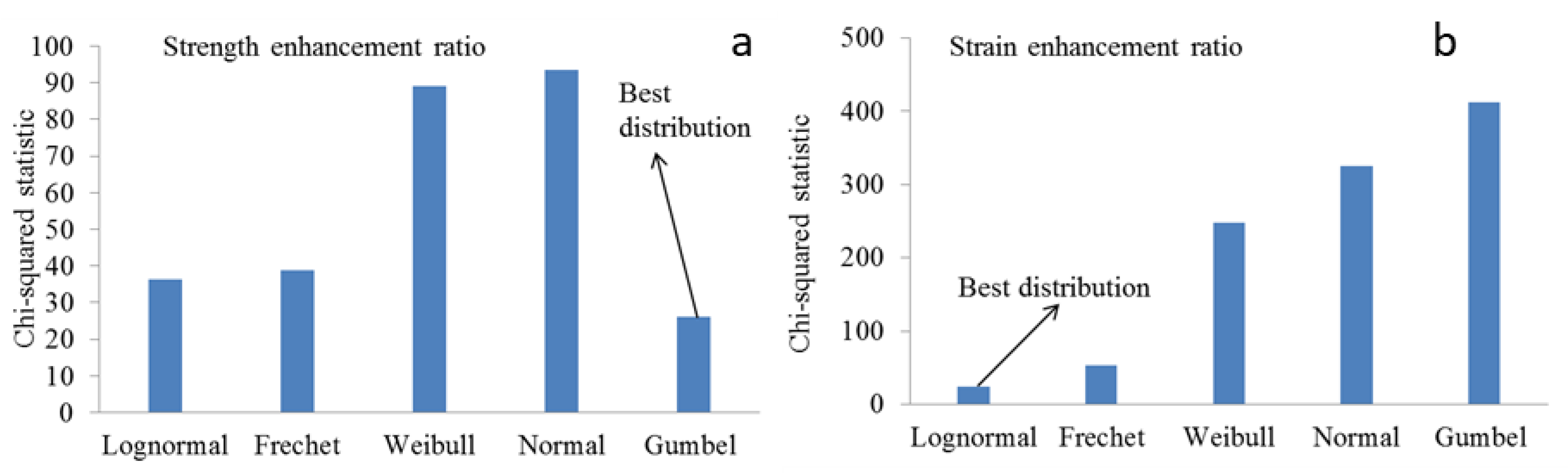
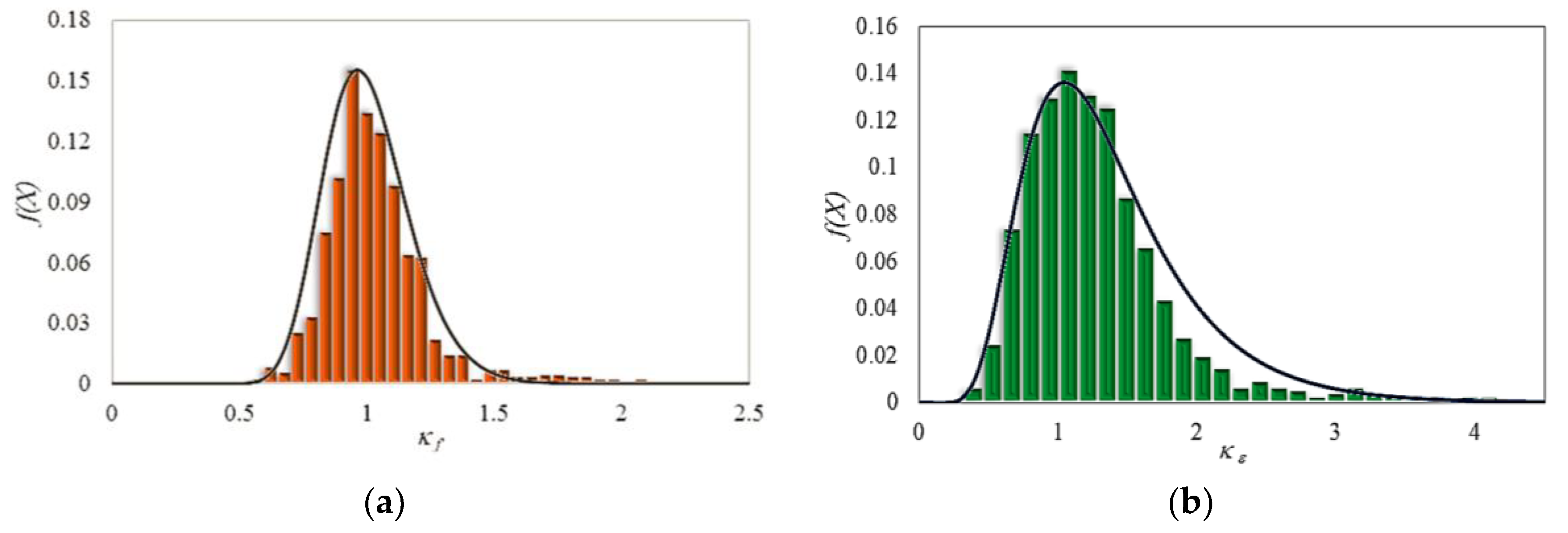
- Lognormal and Gumbel distributions provide the best fitness for κf and κε of FRP-confined concrete.
- (2)
- The segments of the database containing (i) NSC heavily confined (i.e., flu,a/f’co > 0.5) by low and normal modulus carbon fibers (i.e., Ef ≤ 260 GPa), and (ii) NSC moderately confined (i.e., 0.3 ≤ flu,a/f’co ≤ 0.5) by aramid fibers represent a very high safety level.
- (3)
- The segments of the database containing moderately and heavily confined (i.e., flu,a/f’co > 0.2) (i) NSC by high modulus carbon fibers (i.e,. Ef > 260 GPa), (ii) HSC by low and normal modulus carbon fibers (i.e., Ef ≤ 260 GPa), and iii) HSC by aramid fibers exhibit a high safety level.
- (4)
- The segments of the database containing (i) NSC moderately and heavily confined (i.e., flu,a/f’co > 0.3) by higher modulus glass fibers (i.e., Ef > 60 GPa), (ii) HSC lightly confined (i.e., flu,a/f’co ≤ 0.2) by highly modulus carbon fibers (i.e., Ef > 260 GPa), and (iii) HSC lightly confined (i.e., flu,a/f’co ≤ 0.2) by aramid fibers exhibit a moderate safety level.
- (5)
- The segments containing (i) HSC lightly and moderately confined (i.e., flu,a/f’co ≤ 0.5) by glass fibers, and (ii) HSC lightly confined (i.e., flu,a/f’co ≤ 0.15) by low and normal modulus carbon fibers (i.e., Ef ≤ 260 GPa) represent a low safety level.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| AFRP | Aramid fiber-reinforced polymer |
| CC | Chaos control |
| CCC | Chaotic conjugate control |
| CFORM | Conjugate first-order reliability method |
| CFRP | Carbon fiber-reinforced polymer |
| CHL-RF | Conjugate Hasofer-Lind and Rackwitz-Fiessler method |
| COV | Coefficients of variation |
| DSTM | Directional stability transformation method |
| FORM | First-order reliability method |
| FR | Fletcher and Reeves |
| FRP | Fiber-reinforced polymer |
| FSL | Finite-step length method |
| GFRP | Glass fiber-reinforced polymer |
| HL-RF | Hasofer-Lind and Rackwitz-Fiessler method |
| HSC | High strength concrete |
| IHL-RF | Improved Hasofer-Lind and Rackwitz-Fiessler method |
| LFR | Limited Fletcher and Reeves |
| MCS | Monte Carlo simulation |
| MPP | Most probable point |
| NSC | Normal strength concrete |
| Probability distribution function | |
| SORM | Second-order reliability method |
| STM | Stability transformation method |
| a | Chaos scalar factor |
| g | Distributed load |
| l | Length of truss |
| C | Involutory matrix |
| D | Diameter of concrete specimen |
| E | Young’s modulus |
| H | Height of concrete specimen |
| P | Concentric load |
| Normal standard random variables vector | |
| X | Original random variable vector |
| As | Cross sectional areas of steel bars |
| c1 | Adjusted factor |
| dk | Conjugate search direction vector |
| d(k) | Point-based conjugate search direction |
| Ec | Elastic modulus of reinforced concrete |
| Ef | Elastic modulus of fibers used in FRP jacket |
| Es | Elastic modulus of steel bars |
| Threshold confining pressure | |
| flu,a | Actual confining pressure |
| fX | Joint probability density function |
| g(X) | Limit state function |
| g(X) ≤ 0 | Failure region |
| Confinement stiffness of the FRP shell | |
| Pf | Failure probability |
| tf | Total thickness of fibers used in FRP jacket |
| f′cc | Concrete ultimate compressive strength |
| f′co | Unconfined concrete strength |
| U* | Most probable point (MPP) in U-space |
| k+1 | Unit normal vector |
| Conjugate unit normal vector at design point k | |
| β | Reliability index |
| λ | Finite-step length |
| δ | Limited conjugate factor |
| σ | Standard deviation |
| μ | Mean |
| εco | Axial strain corresponding to the f′co |
| εcu | Ultimate axial strain |
| εf | Ultimate tensile strength of fibers used in FRP jacket |
| εh,rup | Hoop rupture strain of the FRP |
| κf | Model error for ultimate strength |
| Model error for ultimate strain | |
| Φ | Standard normal cumulative distribution function |
| Maximum displacement at z-direction | |
| Gradient vector of the limit state function at point |
References
- Usman, M.; Farooq, S.H.; Umair, M.; Hanif, A. Axial compressive behavior of confined steel fiber reinforced high strength concrete. Constr. Build. Mater. 2020, 230, 117043. [Google Scholar] [CrossRef]
- Pour, A.F.; Gholampour, A.; Ozbakkaloglu, T. Influence of the measurement method on axial strains of FRP-confined concrete under compression. Compos. Struct. 2018, 188, 415–424. [Google Scholar] [CrossRef]
- Lim, J.C.; Ozbakkaloglu, T. Design model for FRP-confined normal- and high-strength concrete square and rectangular columns. Mag. Concr. Res. 2014, 66, 1020–1035. [Google Scholar] [CrossRef]
- Wu, Y.-F.; Wei, Y. General Stress-Strain Model for Steel- and FRP-Confined Concrete. J. Compos. Constr. 2015, 19, 04014069. [Google Scholar] [CrossRef]
- Pour, A.F.; Gholampour, A.; Zheng, J.; Ozbakkaloglu, T. Behavior of FRP-confined high-strength concrete under eccentric compression: Tests on concrete-filled FRP tube columns. Compos. Struct. 2019, 220, 261–272. [Google Scholar] [CrossRef]
- Ilki, A.; Peker, Ö.; Karamuk, E.; Demir, C.; Kumbasar, N. FRP Retrofit of Low and Medium Strength Circular and Rectangular Reinforced Concrete Columns. J. Mater. Civ. Eng. 2008, 20, 169–188. [Google Scholar] [CrossRef]
- Naderpour, H.; Kheyroddin, A.; Amiri, G.G. Prediction of FRP-confined compressive strength of concrete using artificial neural networks. Compos. Struct. 2010, 92, 2817–2829. [Google Scholar] [CrossRef]
- Wu, Y.-F.; Jiang, J.-F. Effective strain of FRP for confined circular concrete columns. Compos. Struct. 2013, 95, 479–491. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Lim, J.C.; Vincent, T. FRP-confined concrete in circular sections: Review and assessment of stress–strain models. Eng. Struct. 2013, 49, 1068–1088. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Gholampour, A.; Lim, J.C. Damage-Plasticity Model for FRP-Confined Normal-Strength and High-Strength Concrete. J. Compos. Constr. 2016, 20, 04016053. [Google Scholar] [CrossRef]
- Keshtegar, B.; Ozbakkaloglu, T.; Gholampour, A. Modeling the behavior of FRP-confined concrete using dynamic harmony search algorithm. Eng. Comput. 2016, 33, 415–430. [Google Scholar] [CrossRef]
- Gholampour, A.; Ozbakkaloglu, T. Behavior of steel fiber-reinforced concrete-filled FRP tube columns: Experimental results and a finite element model. Compos. Struct. 2018, 194, 252–262. [Google Scholar] [CrossRef]
- Hany, N.F.; Hantouche, E.G.; Harajli, M.H. Axial Stress-Strain Model of CFRP-Confined Concrete under Monotonic and Cyclic Loading. J. Compos. Constr. 2015, 19, 04015004. [Google Scholar] [CrossRef]
- Lim, J.C.; Ozbakkaloglu, T. Confinement Model for FRP-Confined High-Strength Concrete. J. Compos. Constr. 2014, 18, 04013058. [Google Scholar] [CrossRef]
- Pham, T.M.; Hadi, M.N. Confinement model for FRP confined normal- and high-strength concrete circular columns. Constr. Build. Mater. 2014, 69, 83–90. [Google Scholar] [CrossRef]
- Sadeghian, P.; Fam, A. Improved design-oriented confinement models for FRP-wrapped concrete cylinders based on statistical analyses. Eng. Struct. 2015, 87, 162–182. [Google Scholar] [CrossRef]
- Teng, J.; Jiang, T.; Lam, L.; Luo, Y.Z. Refinement of a Design-Oriented Stress–Strain Model for FRP-Confined Concrete. J. Compos. Constr. 2009, 13, 269–278. [Google Scholar] [CrossRef]
- Toutanji, H. Stress-strain characteristics of concrete columns externally confined with advanced fiber composite sheets. Mater. J. 1999, 96, 397–404. [Google Scholar]
- Skrzypczak, I.; Słowik, M.; Buda-Ożóg, L.; S?owik, M.; Buda-Ożóg, L. The Application of Reliability Analysis in Engineering Practice – Reinforced Concrete Foundation. Procedia Eng. 2017, 193, 144–151. [Google Scholar] [CrossRef]
- Der Kiureghian, A.; De Stefano, M. Efficient Algorithm for Second-Order Reliability Analysis. J. Eng. Mech. 1991, 117, 2904–2923. [Google Scholar] [CrossRef]
- Yang, D. Chaos control for numerical instability of first order reliability method. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 3131–3141. [Google Scholar] [CrossRef]
- Gong, J.-X.; Yi, P. A robust iterative algorithm for structural reliability analysis. Struct. Multidiscip. Optim. 2010, 43, 519–527. [Google Scholar] [CrossRef]
- Zou, Y.; Hong, H. Reliability assessment of FRP-confined concrete columns designed for buildings. Struct. Infrastruct. Eng. 2011, 7, 243–258. [Google Scholar] [CrossRef]
- Lim, J.; Lee, B.; Lee, I. Second-order reliability method-based inverse reliability analysis using Hessian update for accurate and efficient reliability-based design optimization. Int. J. Numer. Methods Eng. 2014, 100, 773–792. [Google Scholar] [CrossRef]
- Keshtegar, B.; Miri, M. Introducing conjugate gradient optimization for modified HL-RF method. Eng. Comput. 2014, 31, 775–790. [Google Scholar] [CrossRef]
- Keshtegar, B. Stability iterative method for structural reliability analysis using a chaotic conjugate map. Nonlinear Dyn. 2016, 84, 2161–2174. [Google Scholar] [CrossRef]
- Keshtegar, B.; Hao, P.; Meng, Z. A self-adaptive modified chaos control method for reliability-based design optimization. Struct. Multidiscip. Optim. 2016, 55, 63–75. [Google Scholar] [CrossRef]
- Seghier, M.E.A.B.; Keshtegar, B.; Correia, J.A.; Lesiuk, G.; De Jesus, A. Reliability analysis based on hybrid algorithm of M5 model tree and Monte Carlo simulation for corroded pipelines: Case of study X60 Steel grade pipes. Eng. Fail. Anal. 2019, 97, 793–803. [Google Scholar] [CrossRef]
- Rashki, M.; Miri, M.; Moghaddam, M.A. A simulation-based method for reliability based design optimization problems with highly nonlinear constraints. Autom. Constr. 2014, 47, 24–36. [Google Scholar] [CrossRef]
- Au, S.-K.; Beck, J.L. Estimation of small failure probabilities in high dimensions by subset simulation. Probabilistic Eng. Mech. 2001, 16, 263–277. [Google Scholar] [CrossRef]
- Huang, L.; Gao, C.; Yan, L.; Kasal, B.; Ma, G. Reliability assessment of confinement models of carbon fiber reinforced polymer-confined concrete. J. Reinf. Plast. Compos. 2016, 35, 996–1026. [Google Scholar] [CrossRef]
- Arab, H.G.; Rashki, M.; Rostamian, M.; Ghavidel, A.; Shahraki, H.; Keshtegar, B. Refined first-order reliability method using cross-entropy optimization method. Eng. Comput. 2018, 35, 1507–1519. [Google Scholar] [CrossRef]
- Val, D.V. Reliability of Fiber-Reinforced Polymer-Confined Reinforced Concrete Columns. J. Struct. Eng. 2003, 129, 1122–1130. [Google Scholar] [CrossRef]
- Sadeghian, P.; Okeil, A.; Fam, A. Reliability analysis of modeling concrete-filled frp tubes under flexural loading for bridge applications. In Proceedings of the 10th International Conference on Short and Medium Span Bridges, Quebec City, QC, Canada, 30 July– 3 August 2018. [Google Scholar]
- Rasheed, A.; Farooq, S.H.; Usman, M.; Hanif, A.; Khan, N.A.; Khushnood, R.A. Structural reliability analysis of superstructure of highway bridges on China-Pakistan Economic Corridor (CPEC): A case study. J. Struct. Integr. Maint. 2018, 3, 197–207. [Google Scholar] [CrossRef]
- Hasofer, A.M.; Lind, N.C. Exact and invariant second-moment code format. J. Eng. Mech. Div. 1974, 100, 111–121. [Google Scholar]
- Liu, P.-L.; Der Kiureghian, A. Optimization algorithms for structural reliability. Struct. Saf. 1991, 9, 161–177. [Google Scholar] [CrossRef]
- Keshtegar, B.; Miri, M. Reliability analysis of corroded pipes using conjugate HL–RF algorithm based on average shear stress yield criterion. Eng. Fail. Anal. 2014, 46, 104–117. [Google Scholar] [CrossRef]
- Baji, H.; Ronagh, H.; Li, C.-Q. Probabilistic assessment of FRP-confined reinforced concrete columns. Compos. Struct. 2016, 153, 851–865. [Google Scholar] [CrossRef]
- Zhang, D.; Gu, X.-L.; Yu, Q.-Q.; Huang, H.; Wan, B.; Jiang, C. Fully probabilistic analysis of FRP-to-concrete bonded joints considering model uncertainty. Compos. Struct. 2018, 185, 786–806. [Google Scholar] [CrossRef]
- Zhou, X.-Y.; Gosling, P.; Ullah, Z.; Kaczmarczyk, Ł.; Pearce, C.J. Exploiting the benefits of multi-scale analysis in reliability analysis for composite structures. Compos. Struct. 2016, 155, 197–212. [Google Scholar] [CrossRef]
- Keshtegar, B.; Chakraborty, S. A hybrid self-adaptive conjugate first order reliability method for robust structural reliability analysis. Appl. Math. Model. 2018, 53, 319–332. [Google Scholar] [CrossRef]
- Meng, Z.; Keshtegar, B. Adaptive conjugate single-loop method for efficient reliability-based design and topology optimization. Comput. Methods Appl. Mech. Eng. 2019, 344, 95–119. [Google Scholar] [CrossRef]
- Seghier, M.E.A.B.; Keshtegar, B.; Elahmoune, B. Reliability analysis of low, mid and high-grade strength corroded pipes based on plastic flow theory using adaptive nonlinear conjugate map. Eng. Fail. Anal. 2018, 90, 245–261. [Google Scholar] [CrossRef]
- Keshtegar, B. Limited conjugate gradient method for structural reliability analysis. Eng. Comput. 2016, 33, 621–629. [Google Scholar] [CrossRef]
- Keshtegar, B. Chaotic conjugate stability transformation method for structural reliability analysis. Comput. Methods Appl. Mech. Eng. 2016, 310, 866–885. [Google Scholar] [CrossRef]
- Keshtegar, B. Enriched FR conjugate search directions for robust and efficient structural reliability analysis. Eng. Comput. 2017, 34, 117–128. [Google Scholar] [CrossRef]
- Santos, S.R.d.; Matioli, L.C.; Beck, A.T. New optimization algorithms for structural reliability analysis. Comput. Model. Eng. Sci. (CMES) 2012, 83, 23–55. [Google Scholar]
- Keshtegar, B. A hybrid conjugate finite-step length method for robust and efficient reliability analysis. Appl. Math. Model. 2017, 45, 226–237. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Lim, J.C. Axial compressive behavior of FRP-confined concrete: Experimental test database and a new design-oriented model. Compos. Part B Eng. 2013, 55, 607–634. [Google Scholar] [CrossRef]
- Lim, J.C.; Ozbakkaloglu, T. Stress–strain model for normal- and light-weight concretes under uniaxial and triaxial compression. Constr. Build. Mater. 2014, 71, 492–509. [Google Scholar] [CrossRef]
- Lim, J.C.; Ozbakkaloglu, T. Influence of silica fume on stress–strain behavior of FRP-confined HSC. Constr. Build. Mater. 2014, 63, 11–24. [Google Scholar] [CrossRef]
- Lim, J.C.; Ozbakkaloglu, T. Influence of concrete age on stress–strain behavior of FRP-confined normal- and high-strength concrete. Constr. Build. Mater. 2015, 82, 61–70. [Google Scholar] [CrossRef]
- Xie, T.; Ozbakkaloglu, T. Behavior of steel fiber-reinforced high-strength concrete-filled FRP tube columns under axial compression. Eng. Struct. 2015, 90, 158–171. [Google Scholar] [CrossRef]
- Vincent, T.; Ozbakkaloglu, T. Influence of overlap configuration on compressive behavior of CFRP-confined normal- and high-strength concrete. Mater. Struct. 2015, 49, 1245–1268. [Google Scholar] [CrossRef]
- El Hassan, J.; Bressolette, P.; Chateauneuf, A.; El Tawil, K. Reliability-based assessment of the effect of climatic conditions on the corrosion of RC structures subject to chloride ingress. Eng. Struct. 2010, 32, 3279–3287. [Google Scholar] [CrossRef]
- Casella, G.; Berger, R.L. Statistical Inference; Duxbury Advanced Series; Cengage Learning Duxbury Press Thomson Learning: Pacific Grove, CA, USA, 2002. [Google Scholar]
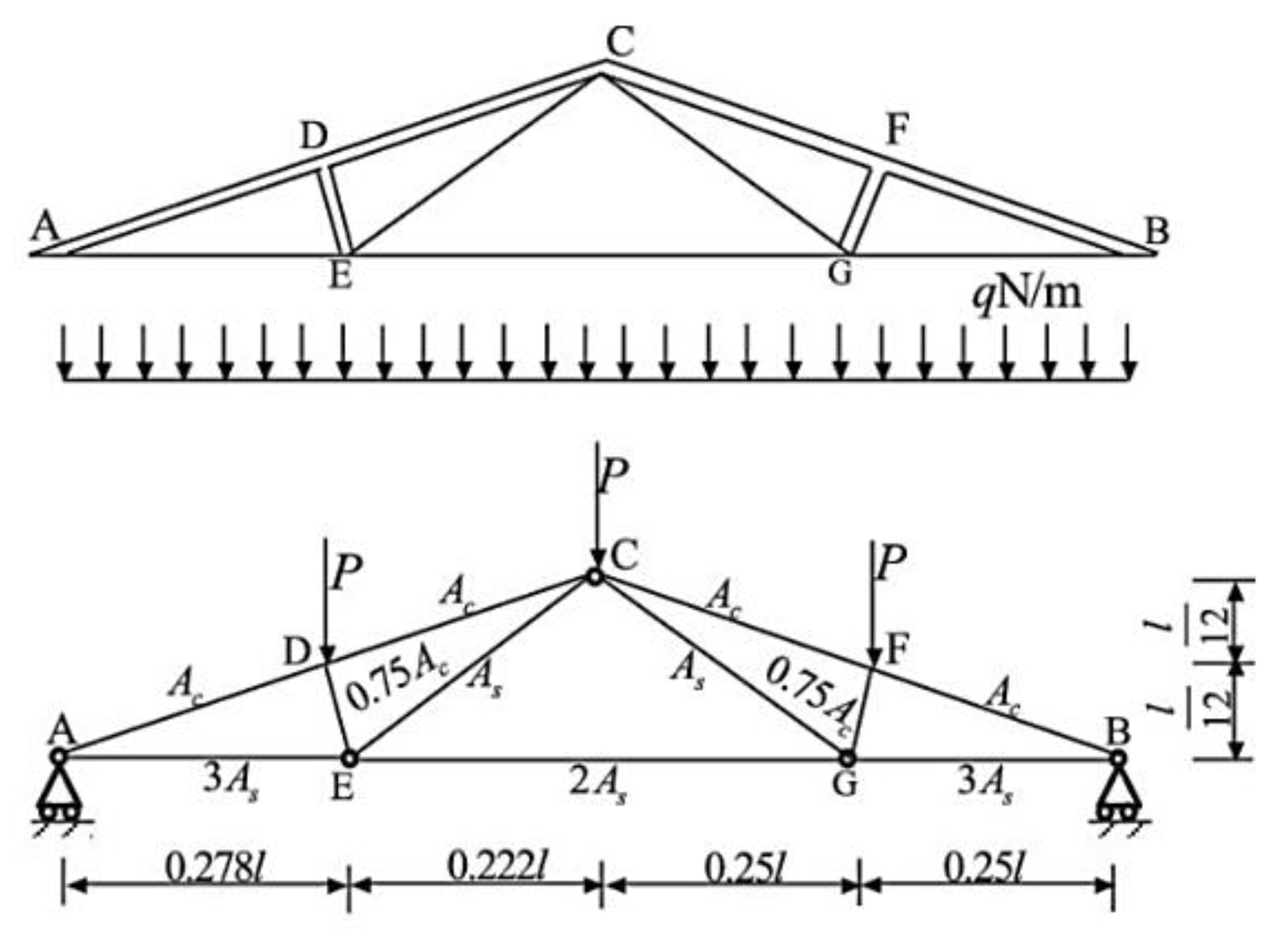
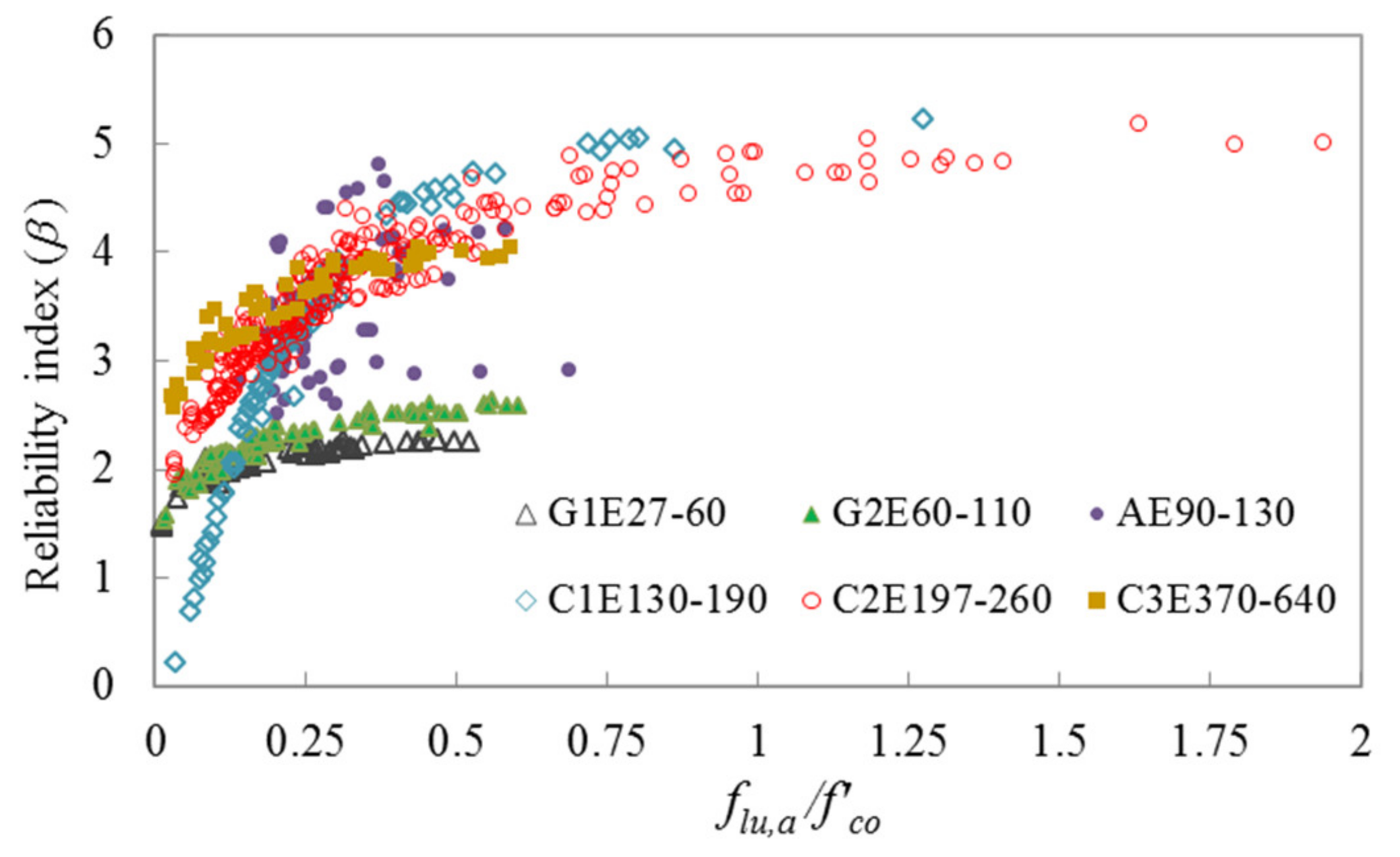
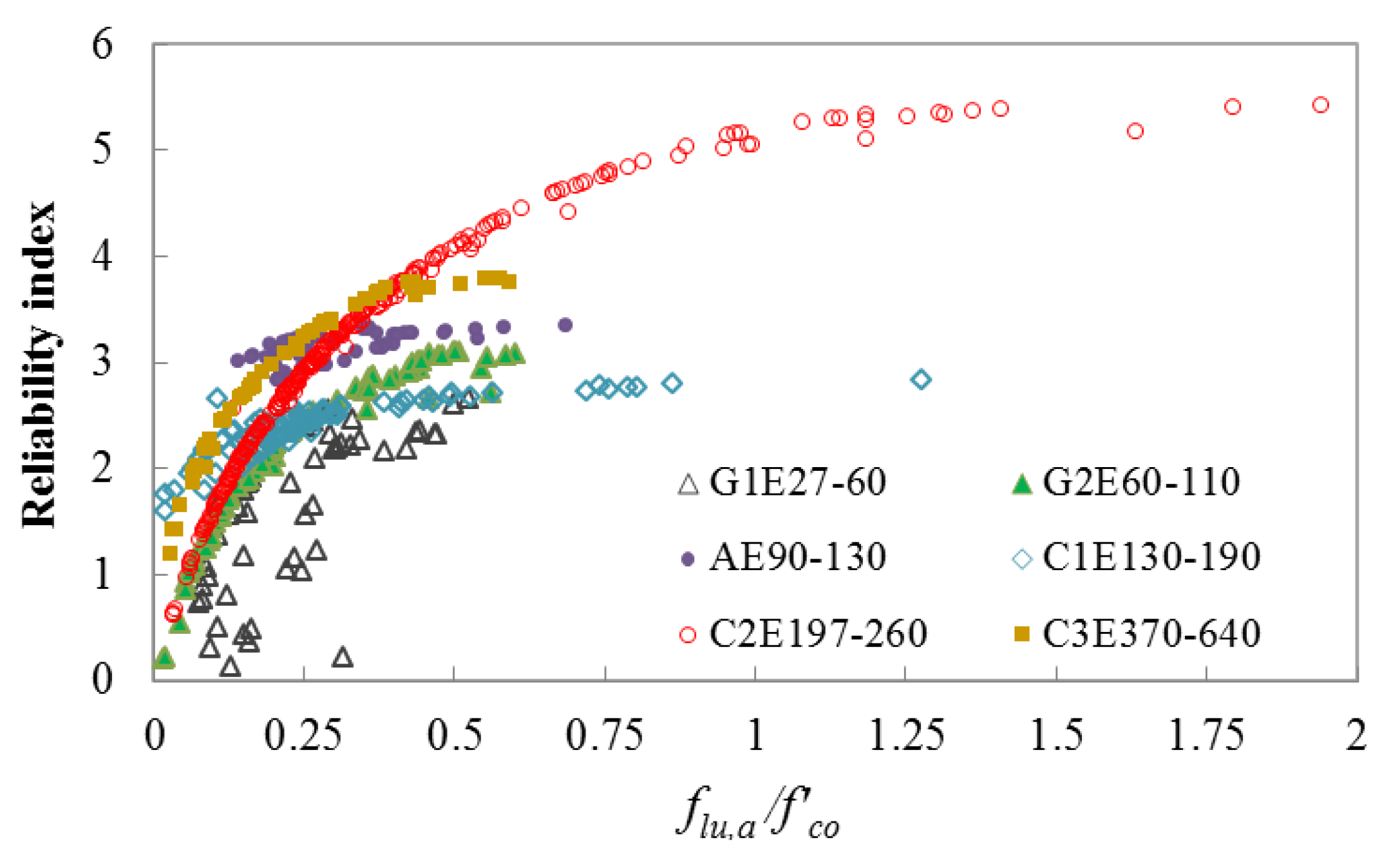
| Random Variable | l (m) | As (m2) | Ac (m2) | Es (Pa) | Ec (Pa) | |
|---|---|---|---|---|---|---|
| Mean | 20,000 | 12 | 9.82 × 10−4 | 0.04 | 1 × 1011 | 2 × 1010 |
| Standard deviation | 1400 | 0.12 | 5.98 × 10−5 | 0.0048 | 6 × 109 | 1.2 × 109 |
| Random Variable | A1–A6 (m2) | A7–A12 (m2) | A13–A24 (m2) | E (GPa) | P1 (kN) | P2–P7 (kN) |
|---|---|---|---|---|---|---|
| Mean | 0.013 | 0.01 | 0.016 | 205 | 20 | 10 |
| COV | 0.1 | 0.1 | 0.1 | 0.12 | 0.15 | 0.12 |
| Distribution | Normal | Normal | Normal | Normal | Gumbel | Gumbel |
| Parameter | C1E130-190 | C2E197-260 | C3E370-640 | G1E27-60 | G2E60-110 | AE90-130 |
|---|---|---|---|---|---|---|
| Ef (GPa) | 130–190 | 197–260 | 370–640 | 27–60 | 60–110 | 90–130 |
| εf (%) | 0.67–1.52 | 1.50–2.65 | 0.41–1.20 | 2.00–3.38 | 2.11–4.30 | 1.74–3.96 |
| tf (mm) | 0.10–3.51 | 0.20–2.26 | 0.15–0.85 | 0.60–3.90 | 0.15–2.55 | 0.15–1.20 |
| Categories | Data | Variable | Mean | COV | |
|---|---|---|---|---|---|
| C1E130-190 | 93 | tf (mm) | 1.198 | 0.085 | Lognormal |
| εf (%) | 1.01 | 0.352 | Gumbel | ||
| Ef (GPa) | 154.5 | 0.125 | Lognormal | ||
| κε | 1.207 | 0.337 | Gumbel | ||
| κf | 0.929 | 0.133 | Gumbel | ||
| C2E197-260 | 284 | tf (mm) | 1.124 | 0.081 | Weibull |
| εf (%) | 1.95 | 0.291 | Gumbel | ||
| Ef (GPa) | 237.5 | 0.086 | Lognormal | ||
| κε | 1.068 | 0.382 | Lognormal | ||
| κf | 0.997 | 0.175 | Lognormal | ||
| C3E370-640 | 61 | tf (mm) | 0.385 | 0.089 | Gumbel |
| εf (%) | 0.77 | 0.327 | Lognormal | ||
| Ef (GPa) | 418.6 | 0.095 | Frechet | ||
| κε | 1.095 | 0.220 | Lognormal | ||
| κf | 1.039 | 0.103 | Weibull | ||
| G1E27-60 | 58 | tf (mm) | 2.262 | 0.076 | Weibull |
| εf (%) | 2.57 | 0.377 | Lognormal | ||
| Ef (GPa) | 34.7 | 0.074 | Lognormal | ||
| κε | 1.098 | 0.418 | Lognormal | ||
| κf | 1.007 | 0.165 | Gumbel | ||
| G2E60-110 | 82 | tf (mm) | 0.921 | 0.113 | Gumbel |
| εf (%) | 3.12 | 0.391 | Gumbel | ||
| Ef (GPa) | 82.2 | 0.116 | Lognormal | ||
| κε | 1.142 | 0.362 | Lognormal | ||
| κf | 0.97 | 0.161 | Gumbel | ||
| AE90-130 | 63 | tf (mm) | 0.751 | 0.095 | Weibull |
| εf (%) | 2.62 | 0.218 | Gumbel | ||
| Ef (GPa) | 120.1 | 0.085 | Gumbel | ||
| κε | 1.284 | 0.167 | Lognormal | ||
| κf | 0.909 | 0.116 | Lognormal |
| Safety Level | C1E130-190 | C2E197-260 | C3E370-640 | G1E27-60 | G2E60-110 | AE90-130 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| flu,a/f’co | f’co (MPa) | flu,a/f’co | f’co (MPa) | flu,a/f’co | f’co (MPa) | flu,a/f’co | f’co (MPa) | flu,a/f’co | f’co (MPa) | flu,a/f’co | f’co (MPa) | ||
| Low | β < 2.5 | 0.03–0.15 | 35–170 | 0.07–0.15 | 50–130 | N.A. * | N.A. | 0.01–0.50 | 25–110 | 0.01–0.30 | 35–110 | N.A. | N.A. |
| Moderate | 2.5 ≤ β ≤ 3.25 | 0.16–0.20 | 30–130 | 0.16–0.31 | 35–170 | 0.14–0.25 | 30–85 | N.A. | N.A. | 0.31–0.71 | 30–50 | 0.14–0.3 | 40–120 |
| High | 3.25 < β ≤ 4.5 | 0.21–0.5 | 30–130 | 0.32–0.70 | 30–110 | 0.26–0.75 | 25–40 | N.A. | N.A. | N.A. | N.A. | 0.31–0.64 | 35–110 |
| Very high | β > 4.5 | 0.51–1.28 | 25–45 | 0.71–2.13 | 20–35 | N.A. | N.A. | N.A. | N.A. | N.A. | N.A. | 0.30–0.50 | 25–30 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Keshtegar, B.; Gholampour, A.; Ozbakkaloglu, T.; Zhu, S.-P.; Trung, N.-T. Reliability Analysis of FRP-Confined Concrete at Ultimate using Conjugate Search Direction Method. Polymers 2020, 12, 707. https://doi.org/10.3390/polym12030707
Keshtegar B, Gholampour A, Ozbakkaloglu T, Zhu S-P, Trung N-T. Reliability Analysis of FRP-Confined Concrete at Ultimate using Conjugate Search Direction Method. Polymers. 2020; 12(3):707. https://doi.org/10.3390/polym12030707
Chicago/Turabian StyleKeshtegar, Behrooz, Aliakbar Gholampour, Togay Ozbakkaloglu, Shun-Peng Zhu, and Nguyen-Thoi Trung. 2020. "Reliability Analysis of FRP-Confined Concrete at Ultimate using Conjugate Search Direction Method" Polymers 12, no. 3: 707. https://doi.org/10.3390/polym12030707
APA StyleKeshtegar, B., Gholampour, A., Ozbakkaloglu, T., Zhu, S.-P., & Trung, N.-T. (2020). Reliability Analysis of FRP-Confined Concrete at Ultimate using Conjugate Search Direction Method. Polymers, 12(3), 707. https://doi.org/10.3390/polym12030707









