1. Introduction
Block copolymers, i.e., polymers made of different chemically incompatible units, are known to spontaneously self-assemble into a rich variety of nanostructured patterns [
1,
2,
3]. The morphologies and dimensions of these morphologies can be varied by tuning the molecular weight and architecture of the constituent polymers. This makes them interesting for many applications such as drug delivery [
4], energy conversion [
5,
6], or soft lithography [
7,
8], as well as for fundamental research.
Theoretically, the self-consistent field (SCF) theory has proved to be a particularly valuable tool for studying self-assembled structures and morphological phase diagrams [
9,
10,
11,
12]. In parameter regimes where thermal fluctuations can be neglected, SCF models can often predict equilibrium self-assembled structures at a quantitative level. However, real materials often do not reach the true, fully ordered equilibrium state on experimental time scales. Defects form during the ordering process, which do not annihilate unless special techniques are applied [
13,
14,
15,
16,
17,
18,
19,
20]. Furthermore, intermediate states may appear, which may be interesting by themselves and can stabilized by crosslinking or freezing. The properties of these transition states not only depend on the characteristics of the constituent molecules, but also on the way the material is processed. For these reasons, considerable effort is also spent on studying the dynamics of block copolymer (BCP) ordering processes [
21].
SCF theories are often derived by field theoretical methods, i.e., first rewriting the partition function as a functional integral via insertion of Delta functionals, and then applying a saddle-point approximation. Similar approaches have recently been taken to derive a dynamic SCF theory [
22,
23], starting from the Martin–Siggia–Rose functional for Langevin dynamics [
24]. Solving the resulting dynamic SCF equations typically involves simulating an ensemble of independent chains moving in a co-evolving self-consistent field [
25], similar to the ‘self-consistent Brownian dynamics’ [
26,
27,
28], ‘single-chain in mean field’ [
29], or ‘MD-SCF’ simulation methods [
30] that have been used with great success to study polymer systems in and out of equilibrium.
Another popular class of dynamic extensions of the SCF theory is the class of dynamic self-sonsistent field or dynamic density functional theories (DDFTs), which combine the free energy functional of the SCF theory with a diffusive dynamical model for the polymer relaxation and do not require explicit chain simulations. The generic form of dynamical equation of an inhomogeneous (co)polymer system has the form [
31,
32,
33,
34]
where
denotes the local densities at position
and time
t of monomers of type
in vector notation,
a mobility matrix, and
is derived from the SCF free energy functional
via
. Hydrodynamics can be included by adding a convective term [
35] to Equation (
1) and combining it with a dynamical equation for fluid flow [
36,
37].
The mobility matrix relates the local thermodynamic force
on monomers at position
to the monomer density current at position
, taking into account the effect of chain connectivity. It thus incorporates the information on polymer dynamics, e.g., internal chain relaxation and possibly entanglements. It should be noted that an “exact” mobility matrix should also depend on frequency according to the Mori–Zwanzig theory [
38,
39,
40]. A generalized dynamic RPA (random phase approximation) theory that includes memory has recently been proposed by Wang et al. [
41]. The central assumption of Equation (
1) is that one can describe inhomogeneous polymer systems by an effective Markovian model which accounts for the multitude of relaxation time scales in polymer systems in terms of a suitable (effective) nonlocal mobility matrix.
The question is how to determine this mobility matrix. A number of expressions have been proposed in the literature [
31,
32,
34,
42,
43,
44], which rely on more or less heuristic assumptions. On the other hand, it was found that not only the time scales, but also the pathways of self-assembly may depend critically on the specific choice of the mobility matrix [
45,
46]. In a previous paper, we have therefore developed a more systematic approach, where the mobility matrix is constructed in a bottom-up manner from the single chain dynamic structure factor in particle-based reference simulations [
47]. We have tested it at the example of diblock copolymer melts with lamellar ordering and shown that DDFT calculations based on our approach can accurately reproduce the ordering and disordering kinetics in these systems. In fact, the DDFT results and the corresponding computer simulation data were found to be in similar quantitative agreement than SCF predictions and computer simulation data for equilibrium structures.
In Ref. [
47], the mobility matrix was determined from fine-grained simulation data. However, if reliable theoretical expressions for the single chain dynamic structure factor are available, our approach can also be used to derive analytic or semi-analytic expressions for the mobility matrix, without having to resort to fine-grained reference simulations. The purpose of the present paper is to provide such a description for melts of linear multiblock copolymers in the Rouse regime, i.e., the regime where chains are not entangled. We will first discuss the dynamic structure factor of Rouse copolymers and present a highly accurate analytical approximate expression, which can be used for efficiently calculating the mobility matrix of linear multiblock copolymers with arbitrary block sequence. To illustrate our approach, we will then apply the dynamic theory to a particularly interesting multiblock copolymer melt with two competing length scales [
48,
49], and show how the competition affects the pathways of self-assembly and the resulting final structures.
2. Theory
We consider melts of Gaussian chains of total length
N in the Rouse regime at total monomer density
. Single non-interacting chains are characterized by their radius of gyration
and the chain diffusion constant
, or, alternatively, the Rouse time
. Monomers have different types
, and the monomer sequence along the chains is described by a function
, with
if monomer
n is of type
, and
otherwise (
). Knowing
, one can calculate the overall fraction of monomers
in the chain
. The free energy of the melt is described by a free energy functional
, which depends on the rescaled local densities of type
monomers,
. In practice, we will consider block copolymers made of two types of monomers A and B, with Edwards-type interactions characterized by a Flory–Huggins parameter
and a Helfand compressibility parameter
[
50], and use the SCF free energy functional describing this class of systems. The relevant equations are summarized in
Appendix A.
As in Ref. [
47], we will use reduced quantities
,
and
to simplify the notation. Equation (
1) then takes the form
The thermodynamic driving field
is derived from the SCF functional of the copolymer system. The corresponding equations are given in
Appendix A.
Following Ref. [
47], we approximate the mobility matrix by that of a homogeneous reference system. This implies, in particular, that it is translationally invariant,
, hence we can conveniently rewrite Equation (
2) in Fourier space as
with the Fourier transform defined via
We determine
using the ”relaxation time approach” developed in Ref. [
47], i.e., we calculate it from the characteristic relaxation times of the single-chain dynamic structure factor
in the reference system:
This expression has been constructed such that the DDFT consistently reproduces
when used to study the relaxation dynamics of a single tagged chain. Further details can be found in Ref. [
47].
The central input quantity is thus the single chain dynamic structure, defined as
where
denotes the configurational average over all chain conformations, ⊗ the tensor product, and
gives the coordinates of monomer
n at time
t. In Ref. [
47], we propose to measure
from reference particle-based simulations. Here, we take an alternative approach and estimate it from the analytical solution for free Gaussian Rouse chains. For homopolymers, an exact expression is available [
51], which has been discussed extensively in the literature in various limiting regimes [
41,
51,
52]. The generalization to block copolymers is straightforward (see
Appendix B.2). However, using the resulting expression in the above formalism is not easy, because it involves an infinite sum over Rouse modes. To overcome this problem, we have derived an approximate expression, which avoids the sum, but still accurate reproduces
over the whole relevant range of
and
t. The derivation can be found in the
Appendix B.1. The result is
where Erf is the error function, and the scaled crossover time is set to
. As demonstrated in
Appendix B.2, the relative error of
with respect to the exact solution is less than
over the whole range of
and
t (see
Figure A1 in the
Appendix B).
Equation (
6) shows that the behavior of
features two time regimes: At small times
, the full spectrum of Rouse modes contributes to the dynamic structure factor in a collective manner that can be captured by a scaling function
. At large times
, only the leading Rouse mode contributes. In the limit
,
assumes the asymptotic behavior
This equation can also be derived independently, see
Appendix B.1, Equation (
A8). In the limit
and
, the double integral over
and
is dominated by the sharply peaked term
, i.e., by contributions of monomers that are close along the chain,
. In that limit, one obtains the scaling form
with the scaling function
, where
is defined as in Equation (
7). This corresponds to Equation (4.III.12) in Ref. [
51], generalized to linear multiblock copolymers.
Finally, at
, we have
for all
. For linear multiblocks containing a set
of blocks of type
with block length
, the integral Equation (
6) then gives
where
or
is the number of segments separating the blocks (
,
) or (
,
), respectively.
Using these results, we can now apply Equation (
4) to evaluate the mobility function. In the regime
, the time integral can be evaluated analytically
where
is the lower incomplete Gamma function. The other integrals have to be computed numerically.
It is possible to determine the limiting behavior of
in certain cases: In the limit
, the time integral in Equation (
4) is dominated by small times
. We can then use the scaling form Equation (
9) to evaluate
, giving
with
. The static single chain structure factor in this limit is given by
. Putting everything together, we obtain
In the limit
, we specifically examine the total mobility
, which corresponds to the mobility function for homopolymers. The relevant contribution to the time integral entering
stems from late times, thus we can replace
by the asymptotic expression Equation (
8), resulting in
. Furthermore, we have
at
. Together, we obtain
which essentially reflects the diffusion of the whole chain. Unfortunately, a similarly simple expression for the asymptotic behavior of the individual components
for block copolymers is not available, since they also include contributions from the internal modes, which relax on time scales of order
.
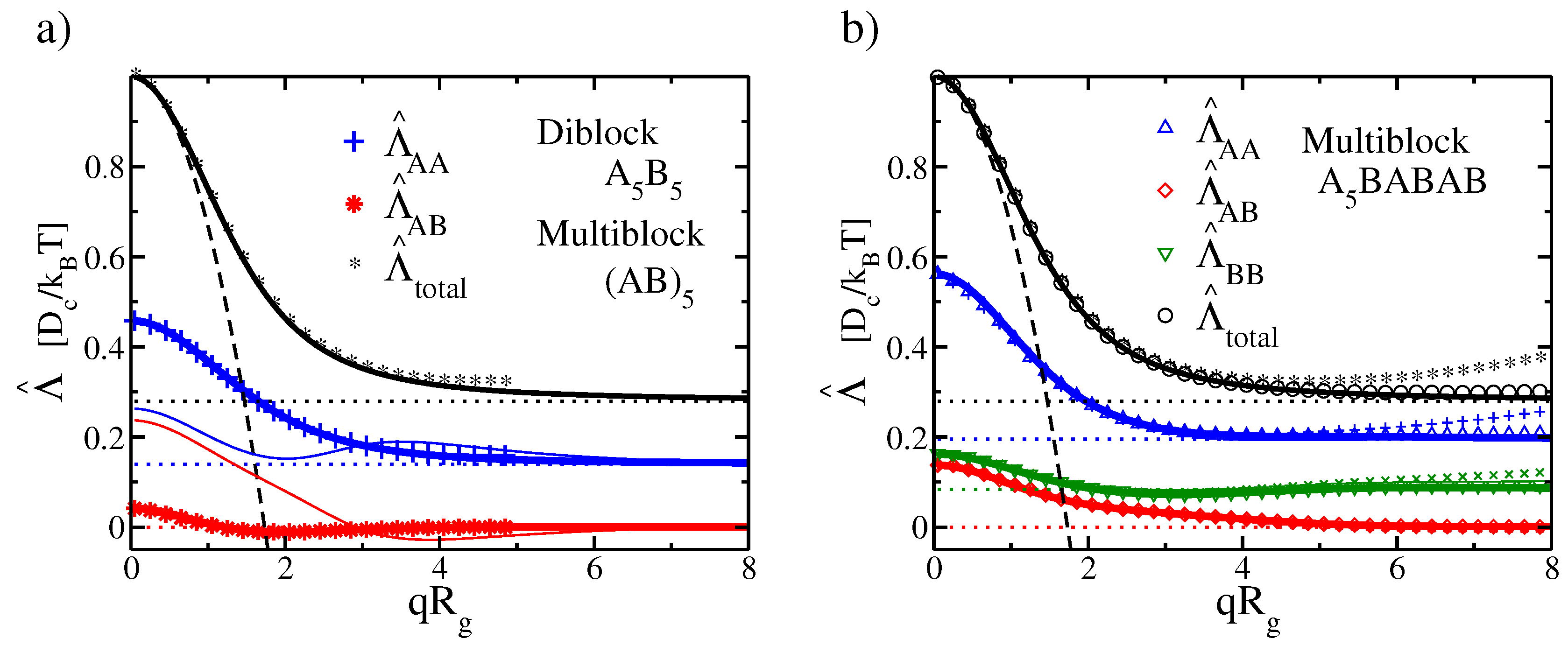
Figure 1 shows examples of mobility functions for three different types of linear multiblock copolymers containing two monomer species A and B. Additionally shown with dotted lines is the expected asymptotic behavior at
(Equation (
13)), and with black dashed lines, the expected asymptotic behavior of
, at
(Equation (
14)).
Figure 1a focusses on sequences that are symmetric with respect to exchanging A and B. The thick lines show the mobility function for symmetric diblock copolymers, the thin line the corresponding results for multiblock copolymers with sequence (A
B
)
. In the case of diblocks, we have also carried out particle-based simulations of discrete Gaussian chains of length
(symbols) for comparison. The data are in good agreement with the theory. The behavior of the dynamic mobilities of diblock and multiblock copolymers is qualitatively quite different: In diblock copolymers, the blocks move largely independent from each other: The mobility component
is close to zero in the whole range of
q. In contrast, in multiblock copolymers, the motion of blocks is highly cooperative at small
q and they start to decouple only at
. At
, they move independent from each other as expected, i.e.,
.
Figure 1b shows the mobility function for a more complicated asymmetric multiblock copolymer with sequence A
B
A
B
A
B
. It has a basic diblock structure, but one of the two blocks carries itself a periodic multiblock sequence. The mobility function combines features of the symmetric diblock and multiblock copolymer mobilities shown in
Figure 1a. The behavior of the A component resembles that in regular diblock copolymers. The B component tends to move cooperatively with the A component at small
q. The joint mobility
is nonzero over a range of
q which is even wider than in the case of pure periodic multiblock copolymers. The theoretical curves are again compared with simulation data for chains of length
(plus and stars) and
(circles, triangles, diamonds). The agreement is excellent at small
q. For large
q the simulation data for shorter chains start to deviate from the theory. This effect decreases with increasing chain length.
3. Application to Two-Length Scale Block Copolymers
To illustrate our DDFT approach, we will now use it to study the ordering kinetics of A
B
A
B
A
B
block copolymer melts. They belong to a class of polymers with a two-length-scale molecular architecture, which have attracted interest as promising candidates for responsive materials [
48]. In particular, linear copolymers consisting of one long uniform block and one periodic multiblock have been studied in some detail, mostly by ten Brinke and coworkers [
48,
49,
53,
54,
55]. At sufficiently high
, they form hierarchical patterns with small structures embedded in larger ones. These two length scales should be associated with two time scales, resulting in a complex ordering kinetics.
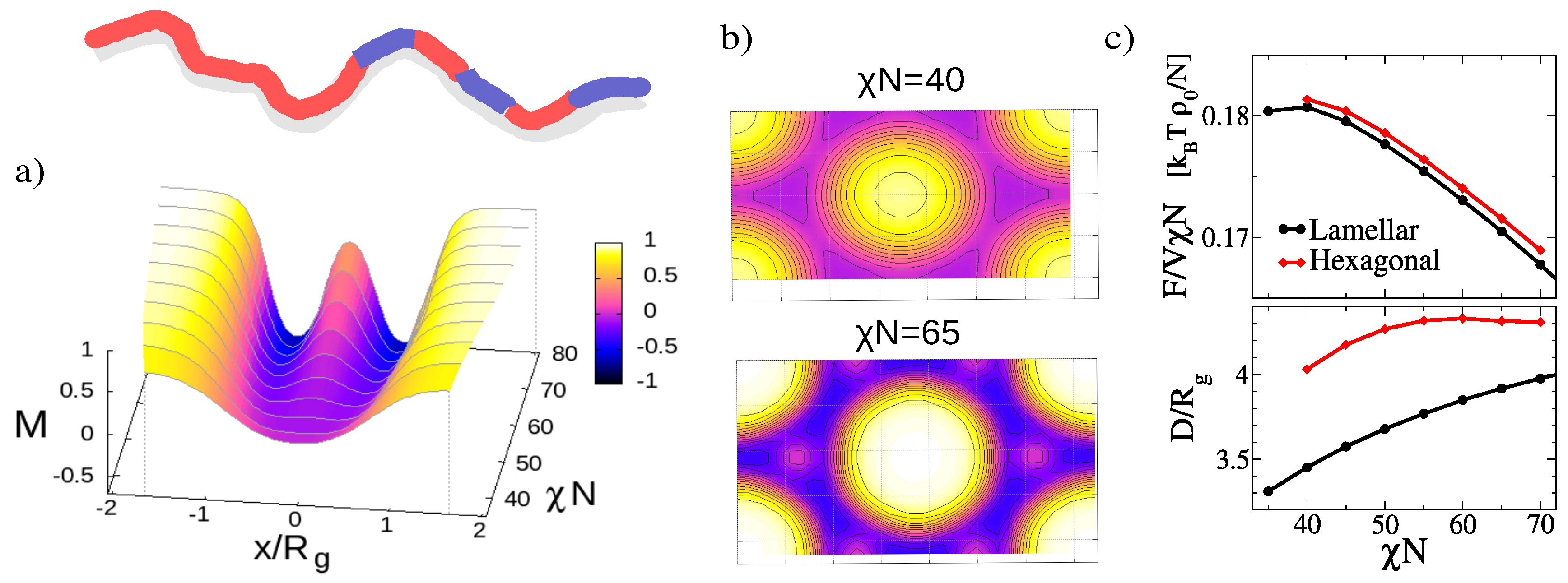
To set the stage, we have determined the equilibrium structures of A
B
A
B
A
B
copolymer melts using SCF theory for
. The results of the SCF analysis are summarized in
Figure 2. The equilibrium structure is basically lamellar, but with a lamellar-in-lamellar structure emerging at
, characterized by an internal substructure inside the B domains. The corresponding order parameter profiles are shown in
Figure 2a. Here, the order parameter is defined as
. The lamellar phase competes with a hexagonal phase, which also features substructures at higher
. Examples of order parameter maps of hexagonal structures corresponding to local free energy minima are shown in
Figure 2b. The SCF free energy of the lamellar phase is always slightly smaller than that of the hexagonal states, see
Figure 2c. Along with the minimum free energy per volume,
Figure 2c (lower panel) also shows the periodic distance/lattice parameter of the minimum structure.
Next we study the dynamic ordering process in this system using DDFT calculations with the mobility function calculated in the previous section (
Figure 1b). The calculations were carried out in two dimensions in periodic boxes of side length
, using
grid points. These dimensions were chosen such that, for every value of
studied here, at least one side length was roughly commensurate with the equilibrium lamellar distance and the lattice constant of the competing hexagonal pattern. The contour of the polymers was discretized with 100 ”segments”. The time step was chosen
depending on the system, where the time unit is
. We found that the results do not depend on the precise value of the time step, as long as the simulations were stable. If the time step was too large, the numerical procedure to determine the thermodynamic forces (see
Appendix A) failed, and we then reduced the time step. In most systems,
was sufficient, but we had to set
in the most strongly interacting systems with
. For numerical reasons, we impose a frequency cutoff
, i.e.,
may not exceed a cutoff value
. This is necessary because
in Equation (
3) diverges at large
q for
. The frequency cutoff slows down local ordering processes on very short time scales. Here, we use
. We also did shorter test runs on smaller systems with
(the value found to be sufficient in our earlier work on diblock copolymers [
47]) and found that the results do not change qualitatively. The initial configuration is a homogeneous melt, to which a small noise is added in order to initiate the ordering process.
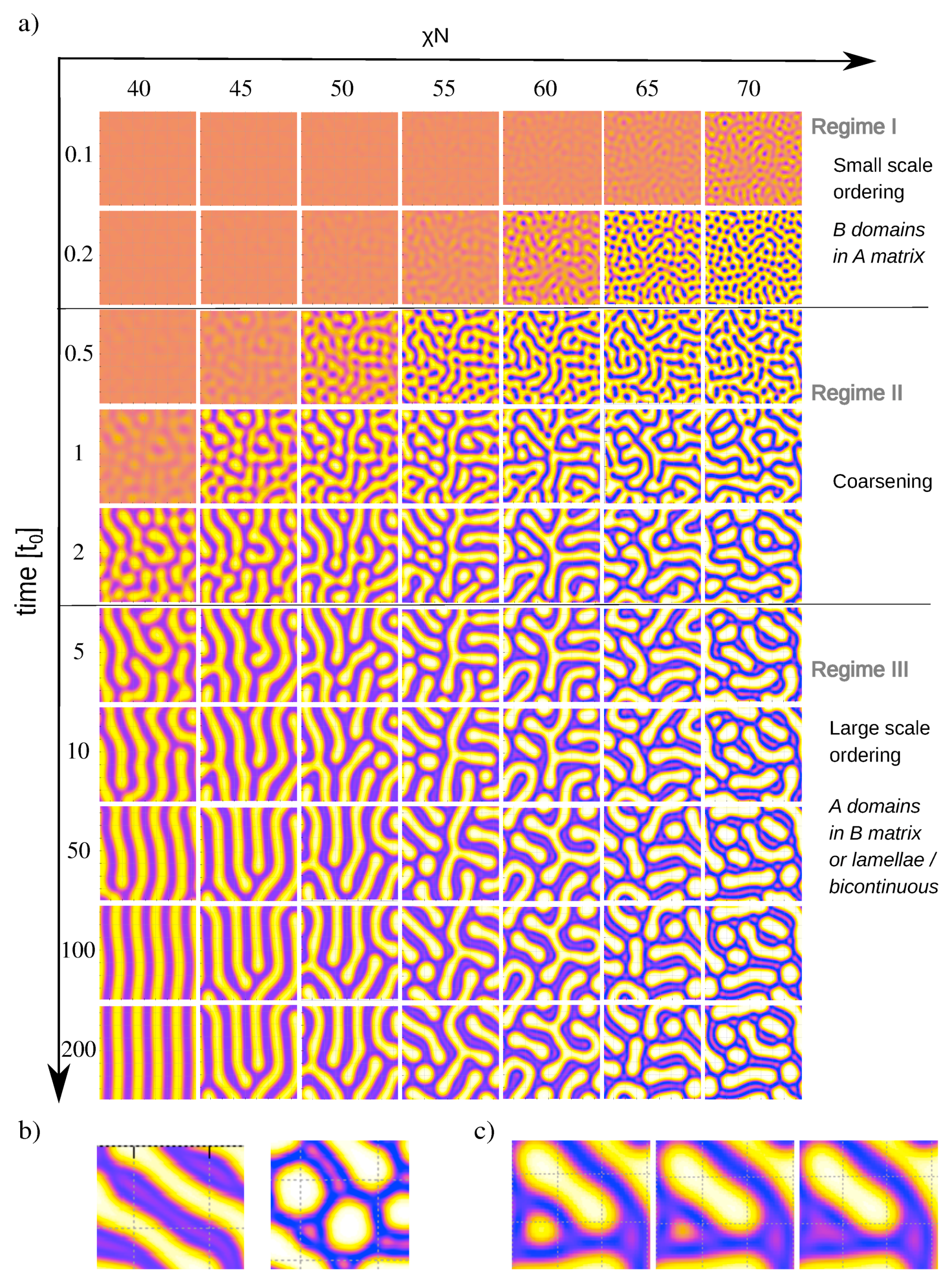
Figure 3a shows snapshots of melts during the ordering process for different
, starting from the same initial configuration. The ordering kinetics clearly reflects the two scale character of the block copolymer. At early times
(regime I), the local ordering is governed by the small characteristic length scale. Around
, the structures start to coarsen (regime II), until the second characteristic length scale is reached around
(regime III). The actual kinetic ordering pathway is governed by the interplay of these time-dependent ordering scales with yet another time scale, the time required for A-B segregation, which decreases with increasing incompatibility parameter
. As a result, the ordering process depends on
.
At low (e.g., ), the full segregation takes place in regime III. A defective lamellar phase forms, which subsequently orders by merging of A and/or B domains, resulting in an ordered lamellar phase. At intermediate , the segregation starts in regime II and continues in regime III. Thus the system initially orders on small scales, then coarsens by merging of B domains, but merging of A domains is also possible. The final structure is again lamellar.
Finally, at high
(
), the system segregates already in the time regime I. It initially orders into small circular
B domains, which then merge to form elongated connected structures. Then coarsening sets in, which is first mediated by rearrangement and further merging of B domains, and later by a thickening of B domains associated with substructure formation inside them. In most cases, A-rich substructures emerge spontaneously inside B domains. Sometimes, we also observe that a larger A island dissolves into a substructure (see
Figure 3c). Once regime III is reached, the topology of the structures inverts from B domains in an A matrix (in regime I) to A domains in a B matrix. At late times, the A domains straighten out, but the basic topology of the structure no longer changes. The final structure is characterized by A domains with defined thickness but variable length, ranging from circular to elongated. Thus these final structures combine elements of the equilibrium lamellar phase and the metastable hexagonal phase. They are kinetically arrested and the topologies do no longer change. To model their further relaxation, one would have to add stochastic thermal noise to the DDFT equations, following the lines outlined in Ref. [
47] (see next section). We should however note that thermal fluctuation amplitudes in copolymer melts are small [
33], therefore we expect similar long-lived structures to appear in real systems as well.
4. Conclusions and Outlook
To summarize, in this work, we have proposed a DDFT model for studying kinetic processes of linear (multi)block copolymer melts in the Rouse regime. The model builds on earlier work [
47], where we have showed how to construct such models systematically from fine-grained particle-based simulations. Here we use the same basic approach, but calculate the central input quantity— the mobility matrix—semi-analytically from the theory of Rouse dynamics. One key ingredient is an accurate approximate expression for the single chain dynamic structure factor of Rouse chains, which can be applied at all times and over a large wave vector range.
DDFT models make more approximations and are less versatile than self-consistent Brownian dynamics methods [
22,
23], which can also be used to study polymer systems far from equilibrium where the use of SCF free energy functional is no longer justified [
26]. On the other hand, they have the advantage that they establish a natural connection to other dynamic continuum theories such as Cahn–Hilliard theories. Furthermore, they require relatively modest computational effort. For example, the calculations presented here (
Figure 3) were run using own serial code on an Intel Core i7-6700 CPU processor. The CPU time per time step varied between 0.1 and 0.4 seconds, depending on the number of iterations required to determine the thermodynamic driving force self-consistently. In total, the cost for simulating one Rouse time
in our system of size 260
was roughly 12 CPU minutes for
, and 30 CPU minutes for
.
To illustrate our DDFT approach, we have studied the ordering kinetics in a melt of two-length-scale copolymers. The kinetic competition on different length and time scales leads to an intricate interplay of ordering processes and results in final structures that not necessarily correspond to a true free energy minimum. Specifically, we have studied situations where an initially disordered state was instantaneously quenched into an ordered region. In that case, the final structures strongly depend on initial small fluctuations and are hard to control. A better controlled ordering process might be achieved by using a slower, well-defined and tunable quenching protocol. Experimentally, it is found that well-ordered two-scale lamellar structures can be created by quenching the samples very slowly [
55]. This is consistent with our calculations where ordered structures are found to form when quenching into regions with lower
. We are not aware of published work on non-equilibrium morphologies that can be obtained if samples are quenched more rapidly. It would be interesting to compare them with our numerical calculations. We expect that it may be possible to stabilize novel structures when quenching with specially designed quenching protocols, possibly combined with periodic re-heating. This could also be studied DDFT simulations and will be an interesting direction for future work.
In the present work, we have employed a deterministic DDFT model that ignores thermal noise. Small thermal fluctuations can be included in a straightforward manner by adding a stochastic current to the DDFT equation, i.e., replacing Eqaution (
1) with
where the components of
are Gaussian random variables with zero mean (
) and correlations according to the fluctuation-dissipation theorem:
(here
are monomer types and
are cartesian coordinates). Equation (
15) implicitly assumes that the SCF free energy functional (from which
is derived) can be interpreted in the sense of a free energy landscape, which may be questionable if fluctuations are large. The relative amplitude of thermal noise is given by the inverse Ginzburg parameter [
11,
34]
. In dense systems of polymers with high molecular weight,
is small. Thus fluctuations are small and can be neglected in many cases, except when studying very soft modes (e.g., interfacial fluctuations) and/or dynamical pathways that involve the crossing of free energy barriers.
Our illustrative DDFT calculations were carried out in two-dimensions, i.e., we have imposed uniformity in the third dimension. This was motivated by the fact that the relevant competing SCF structures of our system are one- or two-dimensional. However, in reality, the initial structures will fluctuate in all three dimensions, e.g., one will find be three-dimensional, e.g., small-scale spheres instead of small-scale cylinders. This will have to be elucidated by full three dimensional calculations.
So far, the theory is restricted to linear multiblock copolymers, and we have assumed that monomers are structurally similar, i.e., they have the same flexibility and the same monomer friction. One goal of future work will be to develop similar semi-analytic approaches for other polymer architectures, for kinetically asymmetric copolymers, or (approximately) for polymers beyond the Rouse regime.