An Energy-Based Concept for Yielding of Multidirectional FRP Composite Structures Using a Mesoscale Lamina Damage Model
Abstract
1. Introduction
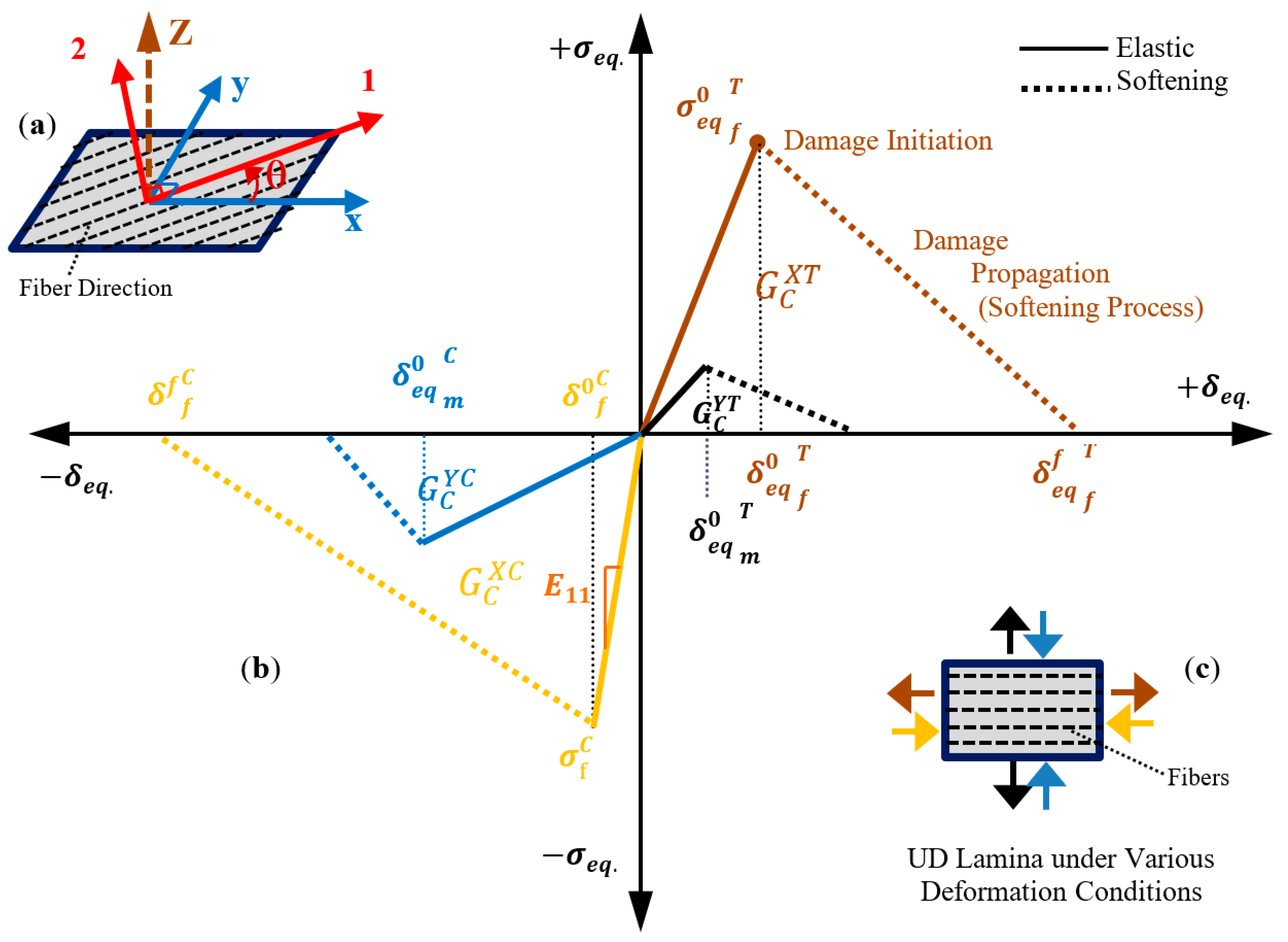
2. Damage Model of FRP Composite Lamina
2.1. Damage Initiation
2.2. Damage Propagation
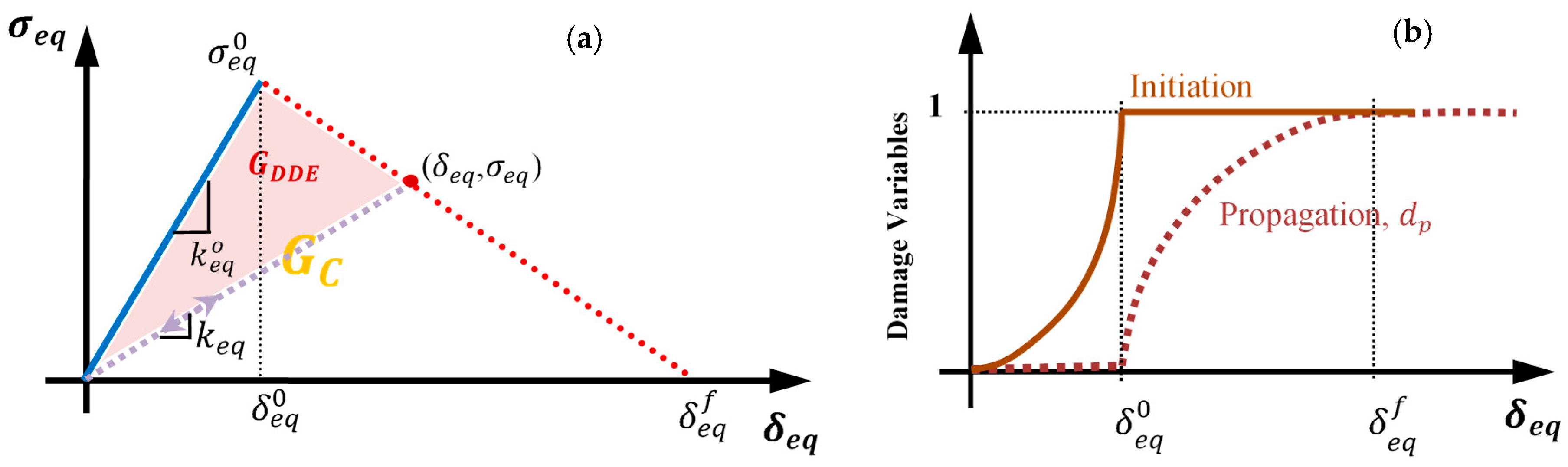
2.3. Damage Dissipation Energy
3. Materials and Experimental Procedures
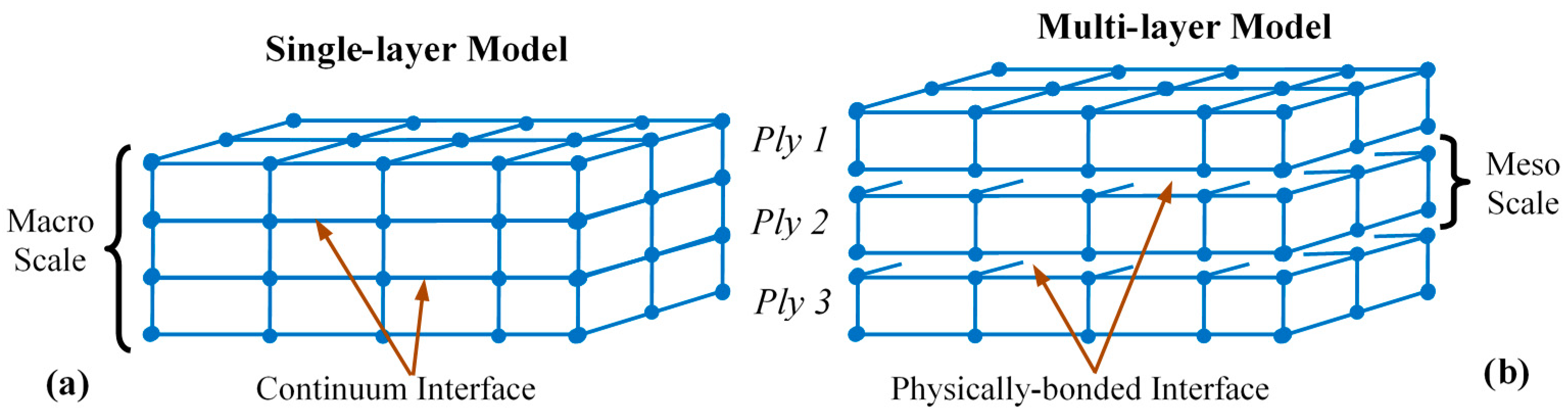
4. Finite Element Simulation
5. Results and Discussion
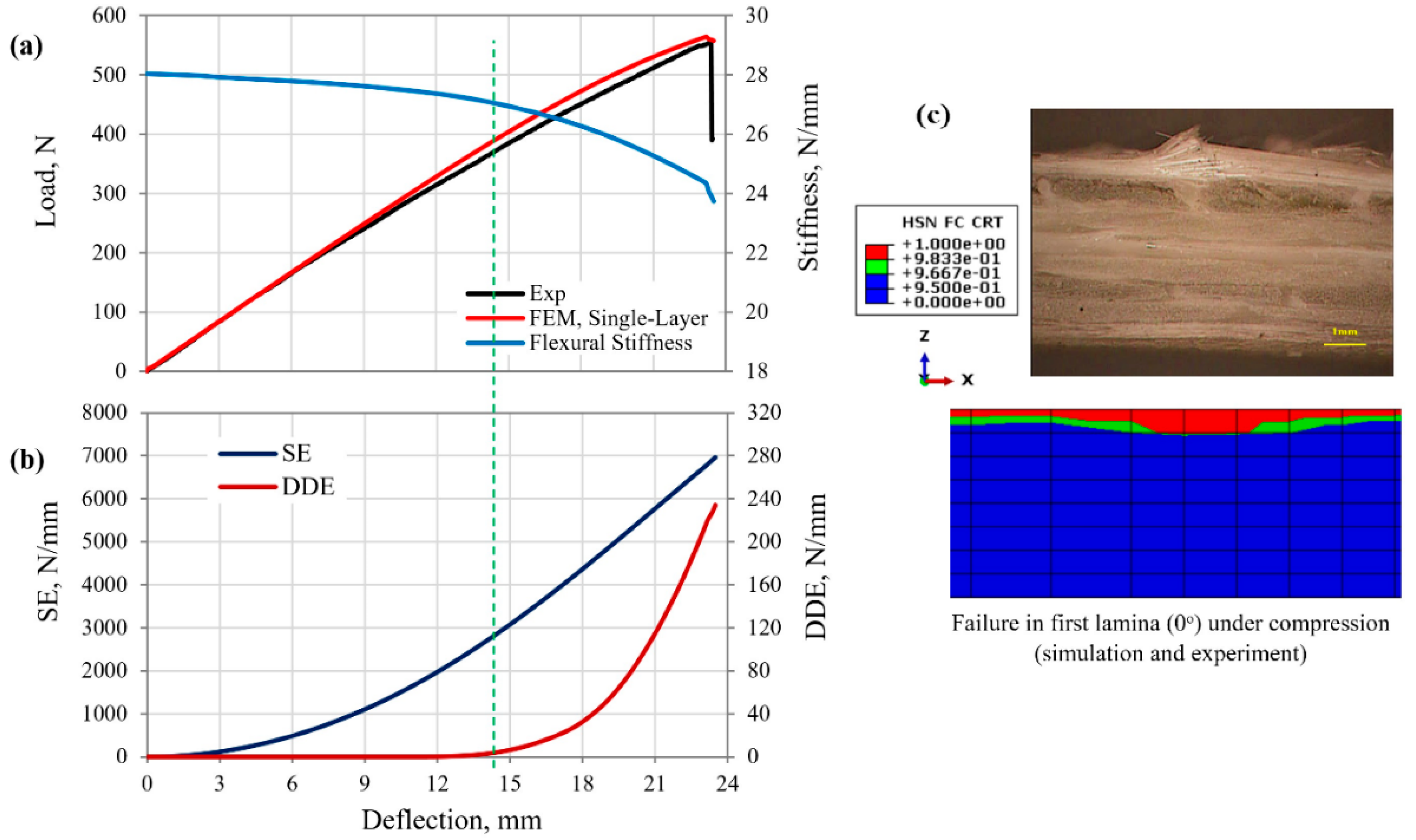
5.1. Structural Response and Damage Evolution of GFRP Composite Beam under Three-Point Bending
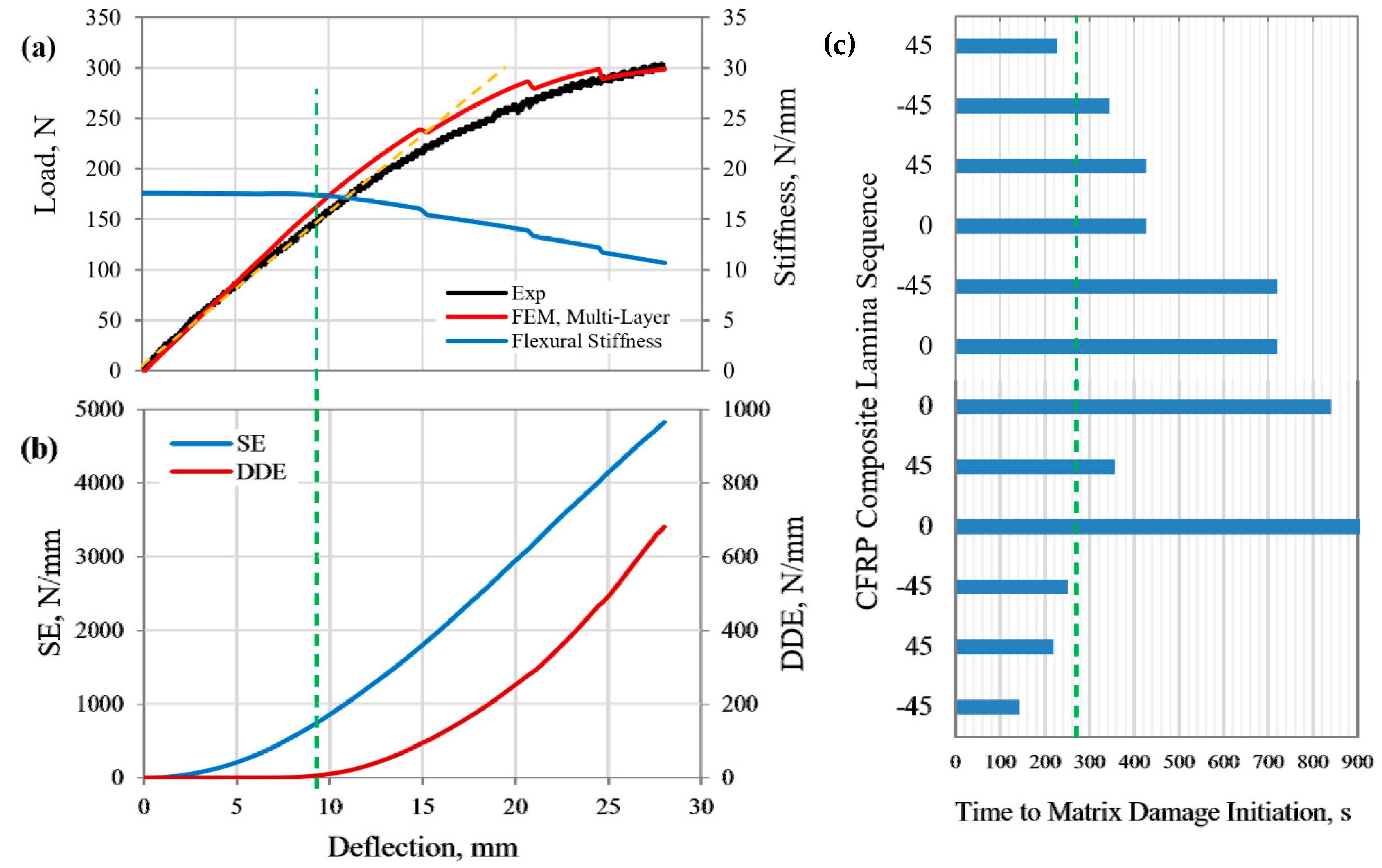
5.2. Structural Response and Damage Evolution of CFRP Composite Beam under Three-Point Bending Load
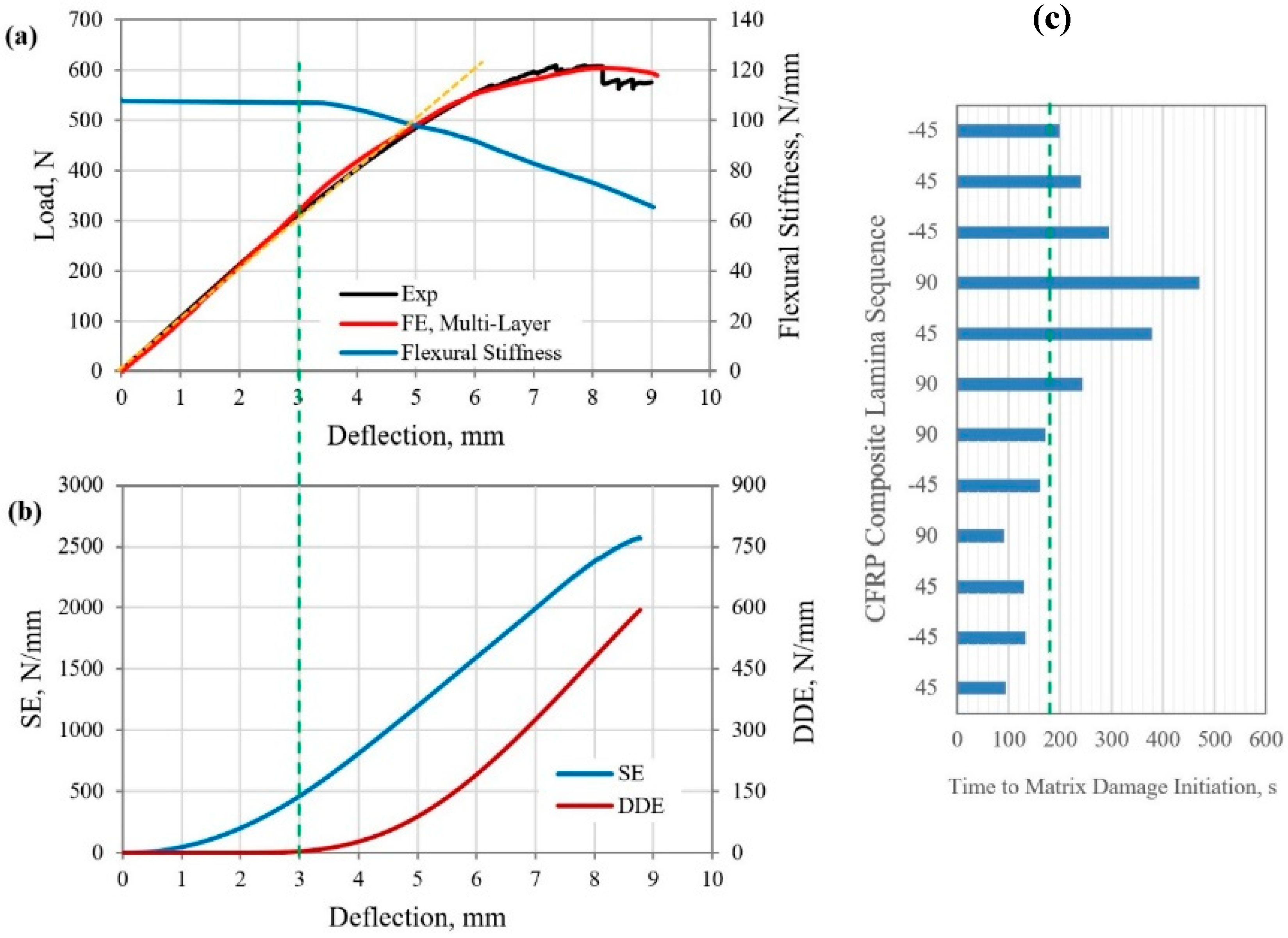
5.3. Structural Response and Damage Evolution of CFRP Composite Beam under Four-Point Bending
5.4. Comparison of the Estimated Yield Limits Based on UD Hashin Criteria and Energy-Based Criterion
6. Conclusions
- The yield point of the FRP composite laminate structures could be identified by a 5% increase in the initial slope of the DDE evolution curve with respect to the applied load parameters.
- At the yield point, the extent of damage by the various modes depended on material, lay-ups, load, and test configurations.
- The yield points of the MD GFRP and CFRP composite laminates (cases 1, 2, and 3) were identified to occur upon flexural loading when the rate of the DDE reached 0.914, 2.1, and 11.1 respectively. The corresponding deflections were 13.5, 9, and 3 mm, respectively.
- The initial flexural stiffness of the MD GFRP and CFRP composite structures (cases 1, 2, and 3) were measured at 28, 17.6, and 108.26 N/mm, reduced to 27.2, 17.44, and 107.1 N/mm at the yield point, indicating 3%, 0.91%, and 1.1% reductions in the stiffness of the beams, respectively. Therefore, an average 2% reduction in flexural stiffness could be suggested as a mean for the determination of the yield point in MD FRP composite structures under three- and four-point bending loads.
- In general, the UD criteria resulted in the assumption of structural yielding at 10%–20% maximum capacity of the structure (displacement or load), whereas, using the energy-based criterion, the yield limit could be safely increased to 30%–50% of the maximum capacity of the structure.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Effective stress of lamina (MPa) | |
| YT | Transverse tensile strength (MPa) |
| SL | Longitudinal shear strength (MPa) |
| ST | Transverse shear strength (MPa) |
| YC | Transverse compressive strength (MPa) |
| XT | Longitudinal tensile strength (MPa) |
| XC | Longitudinal compressive strength (MPa) |
| Matrix damage initiation variable in lamina under tensile load | |
| Matrix damage initiation variable in lamina under compressive load | |
| Fiber damage initiation variable in lamina under tensile load | |
| Fiber damage initiation variable in lamina under compressive load | |
| D | Damage operator in post-damage initiation process |
| , and | Internal damage variable corresponding to lamina fiber, matrix, and shear damage modes |
| GC | Fracture energy (N/mm) |
| GXT | Longitudinal tensile fracture energy (N/mm) |
| GXC | Longitudinal compressive fracture energy (N/mm) |
| GYT | Transverse tensile fracture energy (N/mm) |
| GYC | Transverse compressive fracture energy (N/mm) |
| GDDE | Damage dissipation energy (N/mm) |
| dp | Damage evolution variable |
| Equivalent elastic stiffness at the onset of damage (MPa) | |
| Equivalent displacement at the onset of damage (mm) | |
| Equivalent displacement at the separation of the material point (mm) | |
| and | Effective stresses (MPa) and strains at the onset of damage |
| Equivalent displacement at the state of damage initiation (mm) | |
| Equivalent displacement at failure (mm) | |
| Characteristic length of an element (mm) | |
| Internal energy (N/mm) | |
| Stress (MPa) | |
| Time rate of elastic, plastic, and creep strains | |
| Elastic strain energy (N/mm) | |
| Un-damaged stress (MPa) | |
| Undamaged elastic energy function | |
| Damage strain energy function | |
| EE and ED | Recoverable and irrecoverable energy (N/mm) |
| and | Interaction between the nodes-in-contact as separation and sliding motions (mm) |
| Interpolation function of the interface segments | |
| Interface segment curvature | |
| Stiffness matrix of interface with linear coupled elastic behavior (MPa) | |
| Force of interface node (N) | |
| Motion of interface node (mm) |
References
- Noël, M. Probabilistic fatigue life modelling of frp composites for construction. Constr. Build. Mater. 2019, 206, 279–286. [Google Scholar] [CrossRef]
- R. Koloor, S.S.; Tamin, M.N. Mode-ii interlaminar fracture and crack-jump phenomenon in cfrp composite laminate materials. Compos. Struct. 2018, 204, 594–606. [Google Scholar] [CrossRef]
- Karimzadeh, A.; R. Koloor, S.S.; Ayatollahi, M.R.; Bushroa, A.R.; Yahya, M.Y. Assessment of nano-indentation method in mechanical characterization of heterogeneous nanocomposite materials using experimental and computational approaches. Sci. Rep. 2019, 9, 15763. [Google Scholar] [CrossRef] [PubMed]
- Degenhardt, R.; Castro, S.G.P.; Arbelo, M.A.; Zimmerman, R.; Khakimova, R.; Kling, A. Future structural stability design for composite space and airframe structures. Thin Walled Struct. 2014, 81, 29–38. [Google Scholar] [CrossRef]
- Sharifi Teshnizi, S.H.; R. Koloor, S.S.; Sharifishourabi, G.; Bin Ayob, A.; Yahya, M.Y. Mechanical behavior of gfrp laminated composite pipe subjected to uniform radial patch load. Adv. Mater. Res. 2012, 488–489, 542–546. [Google Scholar] [CrossRef]
- Bertorello, C.; Argüelles, A.; Mollón, V.; Bonhomme, J.; Viña, I.; Viña, J. Use of a lhfb device for testing mode iii in a composite laminate. Polymers 2019, 11, 1243. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, J.; Guo, J.; Sun, X.; Xu, L. The study of thermal, mechanical and shape memory properties of chopped carbon fiber-reinforced tpi shape memory polymer composites. Polymers 2017, 9, 594. [Google Scholar] [CrossRef]
- Sriramula, S.; Chryssanthopoulos, M.K. Quantification of uncertainty modelling in stochastic analysis of frp composites. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1673–1684. [Google Scholar] [CrossRef]
- Zhou, A.; Qin, R.; Chow, C.L.; Lau, D. Structural performance of frp confined seawater concrete columns under chloride environment. Compos. Struct. 2019, 216, 12–19. [Google Scholar] [CrossRef]
- R. Koloor, S.S.; Khosravani, M.R.; Hamzah, R.I.R.; Tamin, M.N. Fe model-based construction and progressive damage processes of frp composite laminates with different manufacturing processes. Int. J. Mech. Sci. 2018, 141, 223–235. [Google Scholar] [CrossRef]
- R. Koloor, S.S.; Abdullah, M.A.; Tamin, M.N.; Ayatollahi, M.R. Fatigue damage of cohesive interfaces in fiber-reinforced polymer composite laminates. Compos. Sci. Technol. 2019, 183, 107779. [Google Scholar] [CrossRef]
- Sellitto, A.; Saputo, S.; Di Caprio, F.; Riccio, A.; Russo, A.; Acanfora, V. Numerical–experimental correlation of impact-induced damages in cfrp laminates. Appl. Sci. 2019, 9, 2372. [Google Scholar] [CrossRef]
- Filippatos, A.; Langkamp, A.; Gude, M. Influence of gradual damage on the structural dynamic behaviour of composite rotors: Simulation assessment. Materials 2018, 11, 2453. [Google Scholar] [CrossRef]
- Hong, B.; Xian, G.; Li, H. Comparative study of the durability behaviors of epoxy-and polyurethane-based cfrp plates subjected to the combined effects of sustained bending and water/seawater immersion. Polymers 2017, 9, 603. [Google Scholar] [CrossRef] [PubMed]
- Gere, J.M.; Goodno, B.J. Mechanics of Materials; Cengage Learning: Boston, MA, USA, 2008. [Google Scholar]
- Kassapoglou, C. Design and Analysis of Composite Structures: With Applications to Aerospace Structures; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Sharifi Teshnizi, S.H.; R. Koloor, S.S.; Sharifishourabi, G.; Bin Ayob, A.; Yahya, M.Y. Effect of ply thickness on displacements and stresses in laminated gfrp cylinder subjected to radial load. Adv. Mater. Res. 2012, 488–489, 367–371. [Google Scholar] [CrossRef]
- Abdi, B.; R. Koloor, S.S.; Abdullah, M.R.; Ayob, A.; Yahya, M.Y.B. Effect of strain-rate on flexural behavior of composite sandwich panel. Appl. Mech. Mater. 2012, 229–231, 766–770. [Google Scholar] [CrossRef]
- Zou, H.; Yin, W.; Cai, C.; Wang, B.; Liu, A.; Yang, Z.; Li, Y.; He, X. The out-of-plane compression behavior of cross-ply as4/peek thermoplastic composite laminates at high strain rates. Materials 2018, 11, 2312. [Google Scholar] [CrossRef]
- Rahimian-Koloor, S.M.; Moshrefzadeh-Sani, H.; Hashemianzadeh, S.M.; Shokrieh, M.M. The effective stiffness of an embedded graphene in a polymeric matrix. Curr. Appl. Phys. 2018, 18, 559–566. [Google Scholar] [CrossRef]
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. R. Soc. Lond. A Math. Phys. Eng. Sci. 1948, 193, 281–297. [Google Scholar]
- Tsai, S.W.; Wu, E.M. A general theory of strength for anisotropic materials. J. Compos. Mater. 1971, 5, 58–80. [Google Scholar] [CrossRef]
- Orifici, A.; Herszberg, I.; Thomson, R. Review of methodologies for composite material modelling incorporating failure. Compos. Struct. 2008, 86, 194–210. [Google Scholar] [CrossRef]
- Hashin, Z. Failure criteria for unidirectional fiber composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Chang, F.-K.; Lessard, L.B. Damage tolerance of laminated composites containing an open hole and subjected to compressive loadings: Part i—Analysis. J. Compos. Mater. 1991, 25, 2–43. [Google Scholar] [CrossRef]
- Puck, A.; Schürmann, H. Failure analysis of frp laminates by means of physically based phenomenological models. Compos. Sci. Technol. 2002, 62, 1633–1662. [Google Scholar] [CrossRef]
- Cuntze, R.; Freund, A. The predictive capability of failure mode concept-based strength criteria for multidirectional laminates. Compos. Sci. Technol. 2004, 64, 343–377. [Google Scholar] [CrossRef]
- Azizi, R.; Legarth, B.N.; Niordson, C.F. A new macroscopically anisotropic pressure dependent yield function for metal matrix composite based on strain gradient plasticity for the microstructure. J. Mech. Phys. Solids 2013, 61, 991–1009. [Google Scholar] [CrossRef]
- Daniel, I.M. Yield and failure criteria for composite materials under static and dynamic loading. Prog. Aerosp. Sci. 2016, 81, 18–25. [Google Scholar] [CrossRef]
- Christensen, R. Stress based yield/failure criteria for fiber composites. Int. J. Solids Struct. 1997, 34, 529–543. [Google Scholar] [CrossRef]
- Lissenden, C.J. Experimental investigation of initial and subsequent yield surfaces for laminated metal matrix composites. Int. J. Plast. 2010, 26, 1606–1628. [Google Scholar] [CrossRef]
- Daniel, I.M.; Daniel, S.M.; Fenner, J.S. A new yield and failure theory for composite materials under static and dynamic loading. Int. J. Solids Struct. 2018, 148–149, 79–93. [Google Scholar] [CrossRef]
- Hinton, M.; Kaddour, A. The background to the second world-wide failure exercise. J. Compos. Mater. 2012, 46, 2283–2294. [Google Scholar] [CrossRef]
- Kaddour, A.; Hinton, M.; Smith, P.; Li, S. A comparison between the predictive capability of matrix cracking, damage and failure criteria for fibre reinforced composite laminates—Part a of the third world-wide failure exercise. J. Compos. Mater. 2013, 47, 2749–2779. [Google Scholar] [CrossRef]
- Cherniaev, A.; Butcher, C.; Montesano, J. Predicting the axial crush response of cfrp tubes using three damage-based constitutive models. Thin Walled Struct. 2018, 129, 349–364. [Google Scholar] [CrossRef]
- Hinton, M.J.; Kaddour, A.S.; Soden, P.D. Failure Criteria in Fibre Reinforced Polymer Composites: The World-Wide Failure Exercise; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Zhuang, F.; Chen, P.; Arteiro, A.; Camanho, P.P. Mesoscale modelling of damage in half-hole pin bearing composite laminate specimens. Compos. Struct. 2019, 214, 191–213. [Google Scholar] [CrossRef]
- Eskandari, S.; Andrade Pires, F.M.; Camanho, P.P.; Marques, A.T. Intralaminar damage in polymer composites in the presence of finite fiber rotation: Part i—Constitutive model. Compos. Struct. 2016, 151, 114–126. [Google Scholar] [CrossRef]
- Maimí, P.; Camanho, P.P.; Mayugo, J.; Dávila, C. A continuum damage model for composite laminates: Part i–constitutive model. Mech. Mater. 2007, 39, 897–908. [Google Scholar] [CrossRef]
- Fakoor, M.; Mohammad Navid Ghoreishi, S. Experimental and numerical investigation of progressive damage in composite laminates based on continuum damage mechanics. Polym. Test. 2018, 70, 533–543. [Google Scholar] [CrossRef]
- Su, Z.C.; Tay, T.E.; Ridha, M.; Chen, B.Y. Progressive damage modeling of open-hole composite laminates under compression. Compos. Struct. 2015, 122, 507–517. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, X.; Wang, Y.-Q.; Gao, H.; Li, R.; Bao, Y. A progressive damage model for predicting damage evolution of laminated composites subjected to three-point bending. Compos. Sci. Technol. 2017, 151, 85–93. [Google Scholar] [CrossRef]
- R. Koloor, S.S. Simulation Methodology for Fracture Processes of Composite Laminates Using Damage-Based Models. Ph.D. Thesis, Universiti Teknologi Malaysia, Johor, Malaysia, 2016. [Google Scholar]
- R. Koloor, S.S.; Tamin, M. Effects of lamina damages on flexural stiffness of cfrp composites. In Proceedings of the 8th Asian-Australasian Conference on Composite Materials 2012, ACCM 2012, Kuala Lumpur, Malaysia, 6–8 November 2012; Volume 1, pp. 237–243. [Google Scholar]
- R. Koloor, S.S.; Ayatollahi, M.R.; Tamin, M.N. Elastic-damage deformation response of fiber-reinforced polymer composite laminates with lamina interfaces. J. Reinf. Plast. Compos. 2017, 36, 832–849. [Google Scholar] [CrossRef]
- Daniel, I.; Schaefer, J.; Werner, B. Yield criteria for matrix and composite materials under static and dynamic loading. In Proceedings of the 24th International Congress of Theoretical and Applied Mechanics (ICTAM 2016), Montreal, QC, Canada, 22 August 2016. [Google Scholar]
- Ahmed, A.; Wei, L. Introducing cfrp as an alternative material for engine hood to achieve better pedestrian safety using finite element modeling. Thin Walled Struct. 2016, 99, 97–108. [Google Scholar] [CrossRef]
- Durão, L.; Tavares, J.; de Albuquerque, V.; Marques, J.; Andrade, O. Drilling damage in composite material. Materials 2014, 7, 3802–3819. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Wang, J.; Hu, H.; Ni, A. A simplified computational strategy focused on resin damage to study matrix cracking of the cross-ply laminates under uniaxial tension load. Materials 2019, 12, 1984. [Google Scholar] [CrossRef]
- R. Koloor, S.S.; Rahimian-Koloor, S.M.; Karimzadeh, A.; Hamdi, M.; Petrů, M.; Tamin, M.N. Nano-level damage characterization of graphene/polymer cohesive interface under tensile separation. Polymers 2019, 11, 1435. [Google Scholar] [CrossRef] [PubMed]
- Capriotti, M.; Kim, H.E.; Scalea, F.L.D.; Kim, H. Non-destructive inspection of impact damage in composite aircraft panels by ultrasonic guided waves and statistical processing. Materials 2017, 10, 616. [Google Scholar] [CrossRef] [PubMed]
- R. Koloor, S.S.; Abdul-Latif, A.; Tamin, M.N. Mechanics of composite delamination under flexural loading. Key Eng. Mater. 2011, 462, 726–731. [Google Scholar] [CrossRef]
- Kaw, A.K. Mechanics of Composite Materials; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Murakami, S. Continuum Damage Mechanics: A Continuum Mechanics Approach to the Analysis of Damage and Fracture; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 185. [Google Scholar]
- Matzenmiller, A.; Lubliner, J.; Taylor, R. A constitutive model for anisotropic damage in fiber-composites. Mech. Mater. 1995, 20, 125–152. [Google Scholar] [CrossRef]
- Chaboche, J. The concept of effective stress applied elasticity and to viscoplasticity in presence of anisotropic damage. Mech. Behav. Anisotropic Solids 1979, 737–760. [Google Scholar]
- ABAQUS-6.9EF. Theory Manual. 2010. Available online: http://130.149.89.49:2080/v6.9ef/index.html (accessed on 3 January 2020).
- ASTM. D790-10. In Standard Test Methods for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials; ASTM International: Conshohocken, PA, USA, 2011; pp. 150–158. [Google Scholar]
- ASTM. D4762–18. Standard Guide for Testing Polymer Matrix Composite Materials. 2018. Available online: https://www.astm.org/Standards/D4762.htm (accessed on 3 January 2020).
- Ghelli, D. Some Issues Concerning the Dynamic Response and Damage of Composite Laminates Subjected to Low Velocity Impact; University of Bologna: Bologna, Italy, 2009. [Google Scholar]
- Nakatani, H.; Kosaka, T.; Osaka, K.; Sawada, Y. Damage characterization of titanium/gfrp hybrid laminates subjected to low-velocity impact. Compos. Part A Appl. Sci. Manuf. 2011, 42, 772–781. [Google Scholar] [CrossRef]
- Shi, Y.; Swait, T.; Soutis, C. Modelling damage evolution in composite laminates subjected to low velocity impact. Compos. Struct. 2012, 94, 2902–2913. [Google Scholar] [CrossRef]
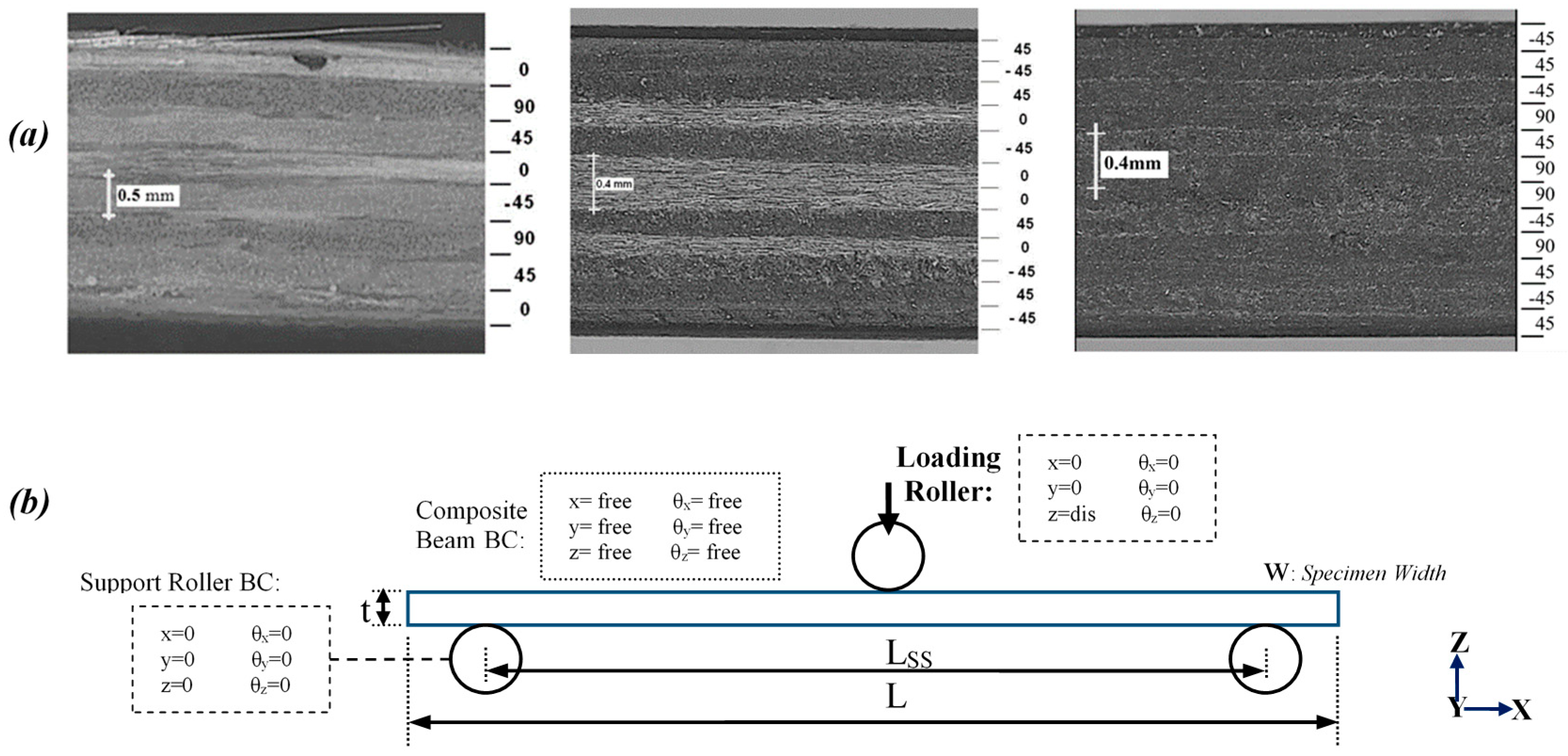
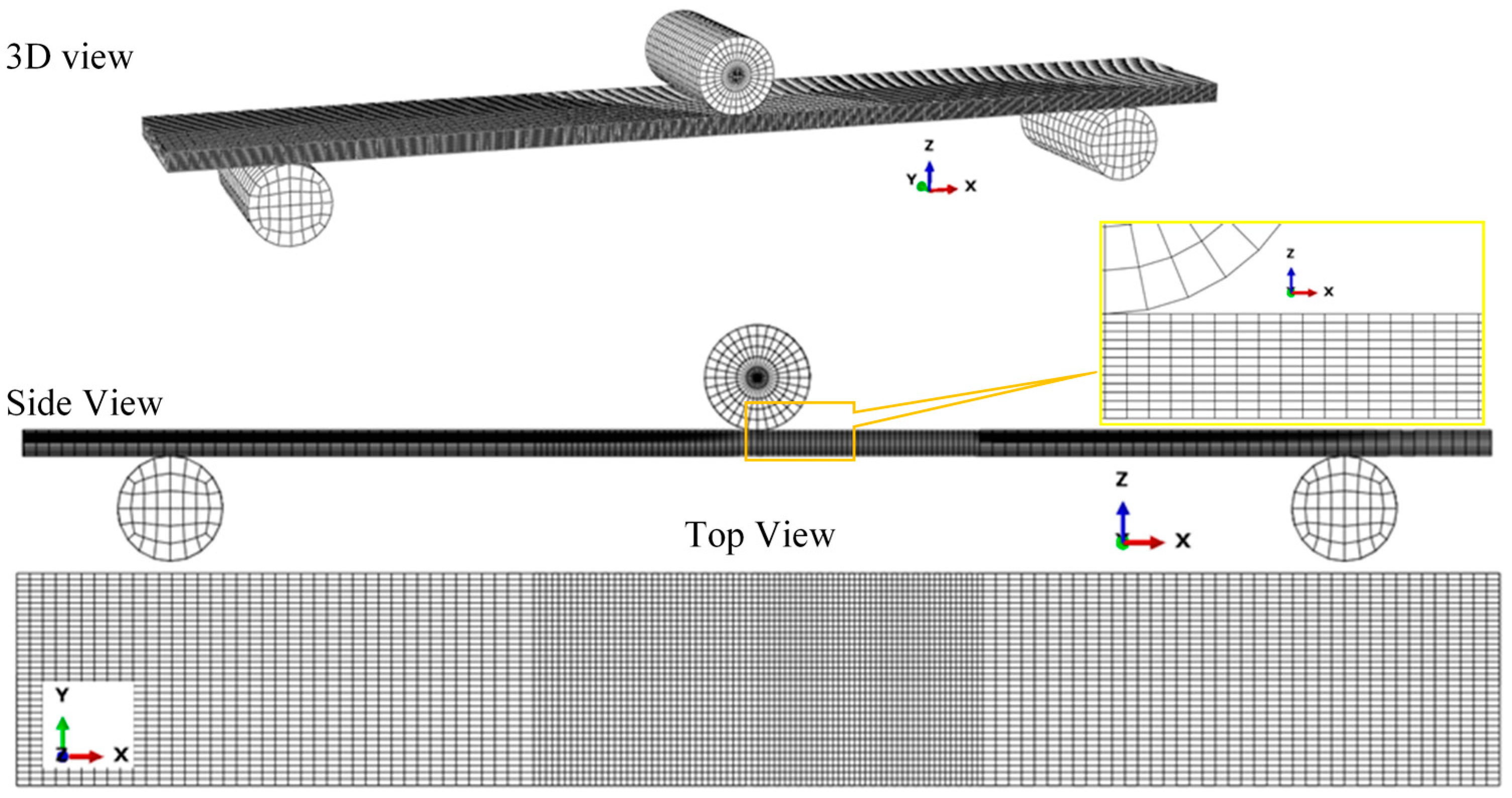
| Composite Panel (Case ID) | Laminate Sequences | Dimensions of the Beam Specimen (mm) | Loading Rate(mm/min) | Loading Type | ||||
|---|---|---|---|---|---|---|---|---|
| Length L | Width W | Laminate Thickness t | Lamina Thickness | Support Span Length LSS | ||||
| GFRP (Case 1) | [0/90/45/0/−45/90/45/0] | 210 | 25 | 4 | 0.5 | 170 | 2 | 3PB |
| CFRP (Case 2) | [45/−45/45/0/−45/0 /0/45/0/−45/45/−45] | 140 | 20 | 2.4 | 0.2 | 112 | 2 | 3PB |
| CFRP (Case 3) | [−45/45/−45/90/45/90/ 90/−45/90/45/−45/45] | 70 | 20 | 2.4 | 0.2 | 60 | 1 | 4PB |
| Lamina Constants | Constitutive Damage Model Parameters of Lamina | |||||
|---|---|---|---|---|---|---|
| GFRP | CFRP | GFRP | CFRP | |||
| E11, GPa | 36.9 | 105.5 | Longitudinal tensile strength, MPa | XT | 820 | 1340 |
| E22, GPa | 10 | 7.2 | Longitudinal compressive strength, MPa | XC | 500 | 1192 |
| E33, GPa | 10 | 7.2 | Transverse tensile strength, MPa | YT | 80.6 | 19.6 |
| G12, GPa | 3.3 | 3.4 | Transverse compressive strength, MPa | YC | 322 | 92.3 |
| G13, GPa | 3.3 | 3.4 | Longitudinal shear strength, MPa | SL | 54.5 | 51 |
| G23, GPa | 3.6 | 2.52 | Transverse shear strength, MPa | ST | 161.2 | 23 |
| ν12 | 0.32 | 0.34 | Longitudinal tensile fracture energy, N/mm | GXT | 32 | 48.4 |
| ν13 | 0.32 | 0.34 | Longitudinal compressive fracture energy, N/mm | GXC | 20 | 60.3 |
| ν23 | 0.44 | 0.378 | Transverse tensile fracture energy | GYT | 4.5 | 4.5 |
| Transverse compressive fracture energy, N/mm | GYC | 4.5 | 8.5 | |||
| Composite Panel (Case ID) | Yield Parameter | Maximum Capacity (MC) | Yield Point | Damage Type | |||
|---|---|---|---|---|---|---|---|
| UD Hashin Criteria | Energy-based Criteria | ||||||
| Value | Percentage to MC | Value | Percentage to MC | ||||
| GFRP (Case 1) | Deflection, mm | 23.4 | 13 | 55.5% | 13.5 | 57.7% | Single mode Fiber failure in first lamina (0°) |
| Load, N | 554.7 | 337 | 60.7% | 350 | 63.1% | ||
| CFRP (Case 2) | Deflection, mm | 28 | 4.7 | 16.8% | 9 | 32.1% | Mixed-matrix cracking and crushing events in different laminas |
| Load, N | 301 | 80.5 | 26.7% | 150 | 49.8% | ||
| CFRP (Case 3) | Deflection, mm | 8 | 1.5 | 18.7% | 3 | 37.5% | |
| Load, N | 600 | 161 | 26.8% | 313 | 52.2% | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahimian Koloor, S.S.; Karimzadeh, A.; Yidris, N.; Petrů, M.; Ayatollahi, M.R.; Tamin, M.N. An Energy-Based Concept for Yielding of Multidirectional FRP Composite Structures Using a Mesoscale Lamina Damage Model. Polymers 2020, 12, 157. https://doi.org/10.3390/polym12010157
Rahimian Koloor SS, Karimzadeh A, Yidris N, Petrů M, Ayatollahi MR, Tamin MN. An Energy-Based Concept for Yielding of Multidirectional FRP Composite Structures Using a Mesoscale Lamina Damage Model. Polymers. 2020; 12(1):157. https://doi.org/10.3390/polym12010157
Chicago/Turabian StyleRahimian Koloor, Seyed Saeid, Atefeh Karimzadeh, Noorfaizal Yidris, Michal Petrů, Majid Reza Ayatollahi, and Mohd Nasir Tamin. 2020. "An Energy-Based Concept for Yielding of Multidirectional FRP Composite Structures Using a Mesoscale Lamina Damage Model" Polymers 12, no. 1: 157. https://doi.org/10.3390/polym12010157
APA StyleRahimian Koloor, S. S., Karimzadeh, A., Yidris, N., Petrů, M., Ayatollahi, M. R., & Tamin, M. N. (2020). An Energy-Based Concept for Yielding of Multidirectional FRP Composite Structures Using a Mesoscale Lamina Damage Model. Polymers, 12(1), 157. https://doi.org/10.3390/polym12010157










