High Electromechanical Deformation Based on Structural Beta-Phase Content and Electrostrictive Properties of Electrospun Poly(vinylidene fluoride- hexafluoropropylene) Nanofibers
Abstract
:1. Introduction
2. Experimental
2.1. Materials
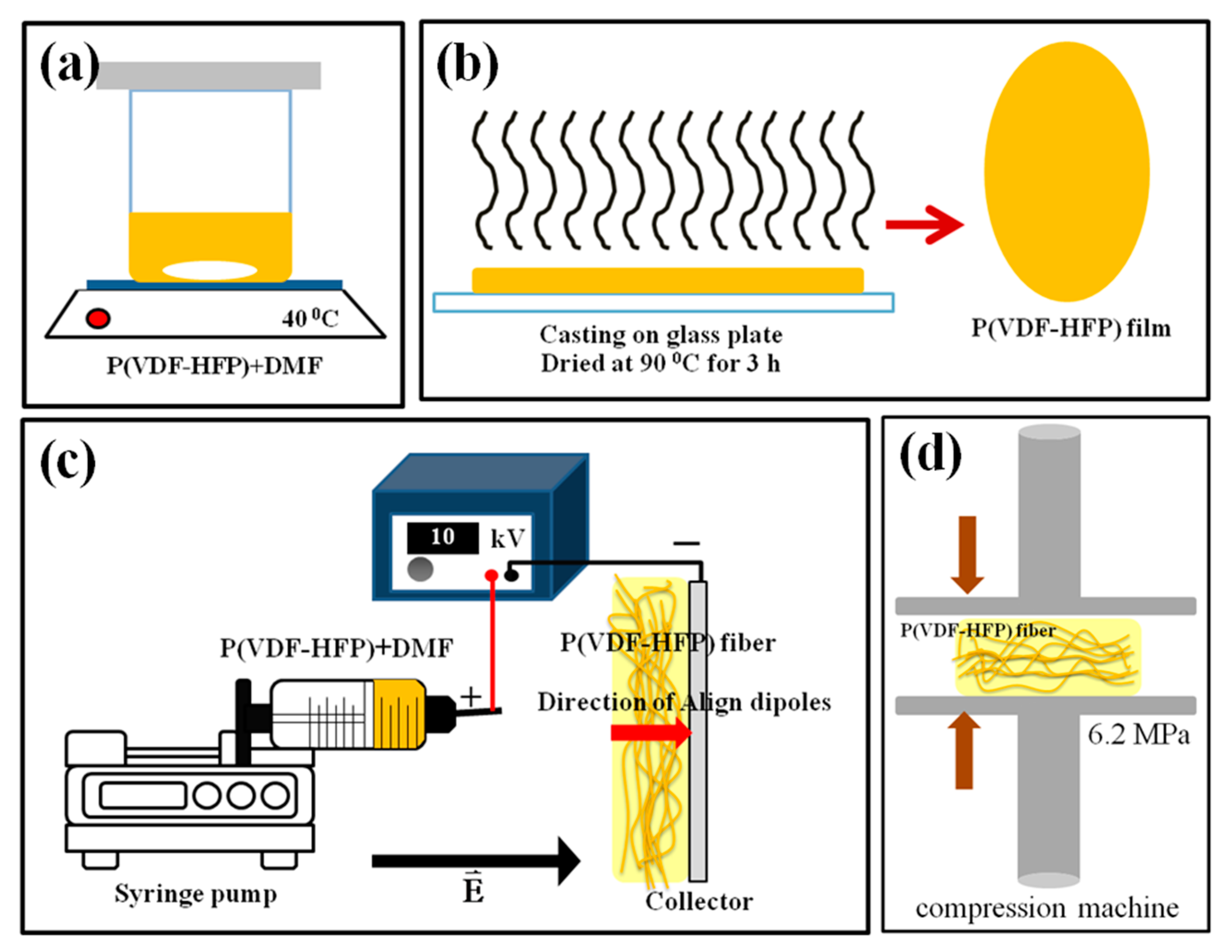
2.2. Synthesis of P(VDF-HFP) Films
2.3. Synthesis of P(VDF-HFP) Fiber
2.4. Material Characterization
2.4.1. Surface Topography
2.4.2. Crystalline Structure and Phase Investigation
2.4.3. Thermal Analysis
2.4.4. Mechanical Analysis
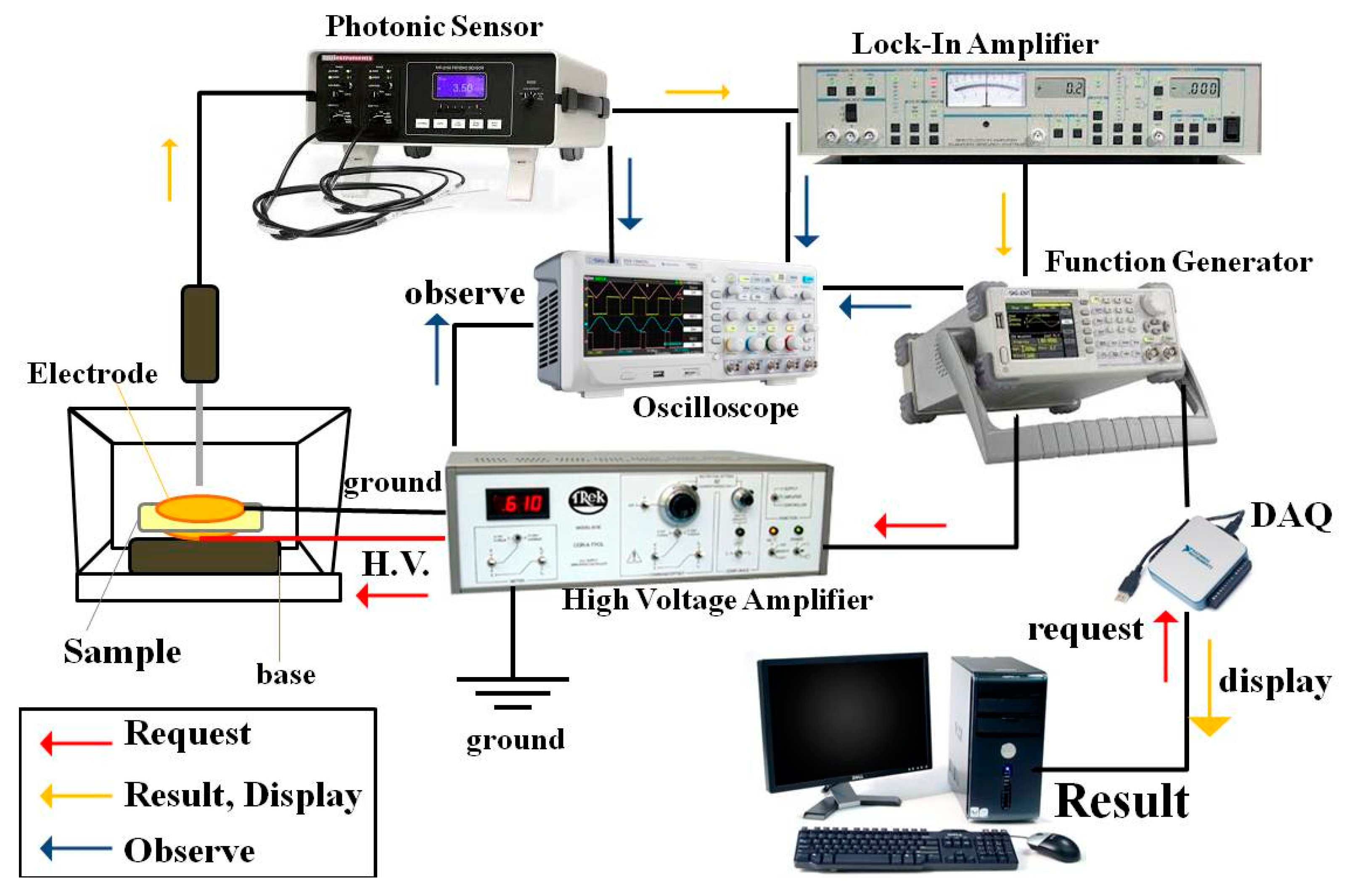
2.4.5. Electrical Properties
2.4.6. Electrostrictive Properties
3. Results and Discussion
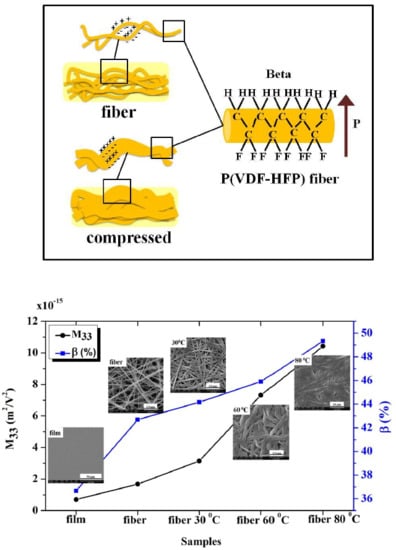
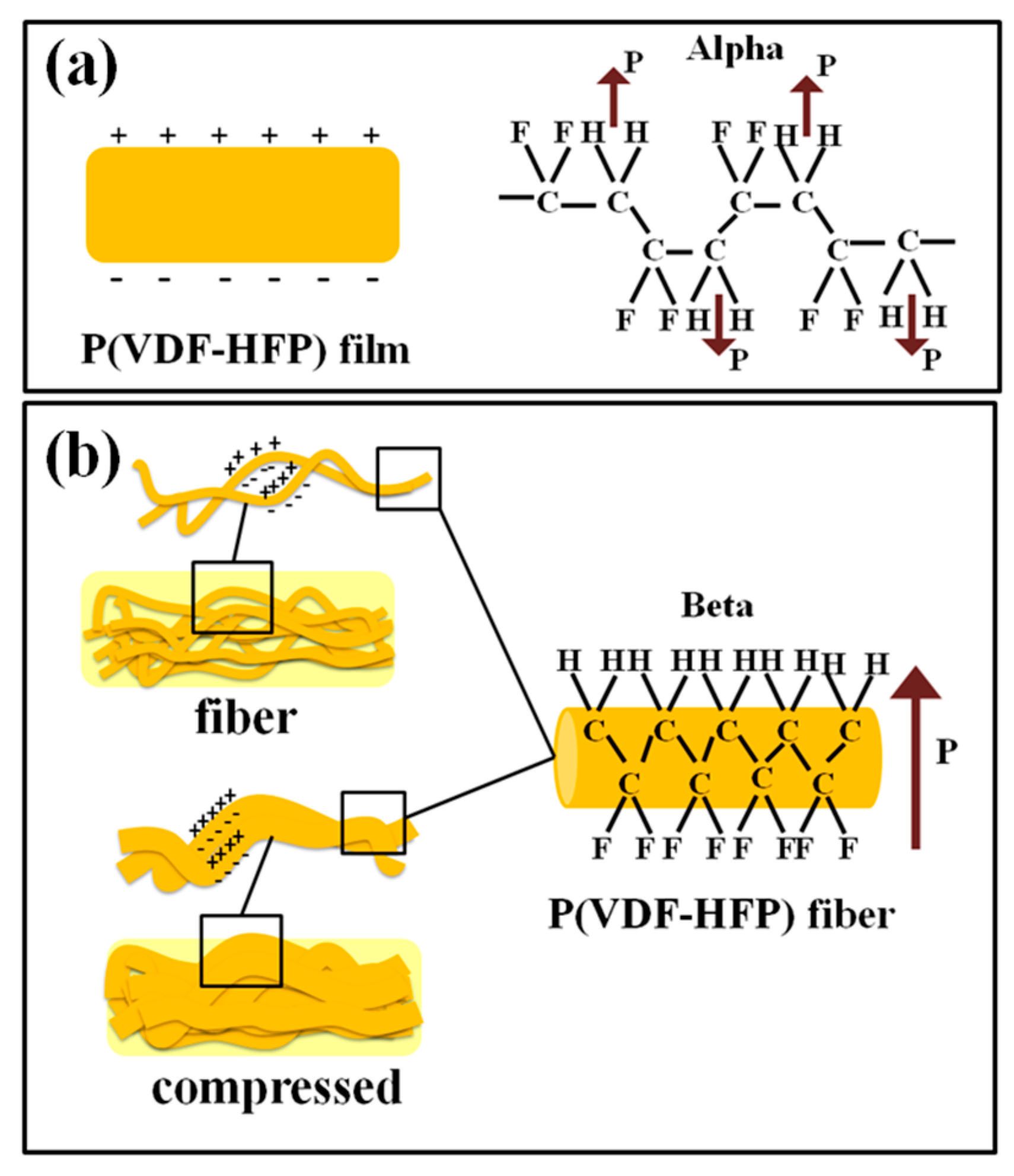
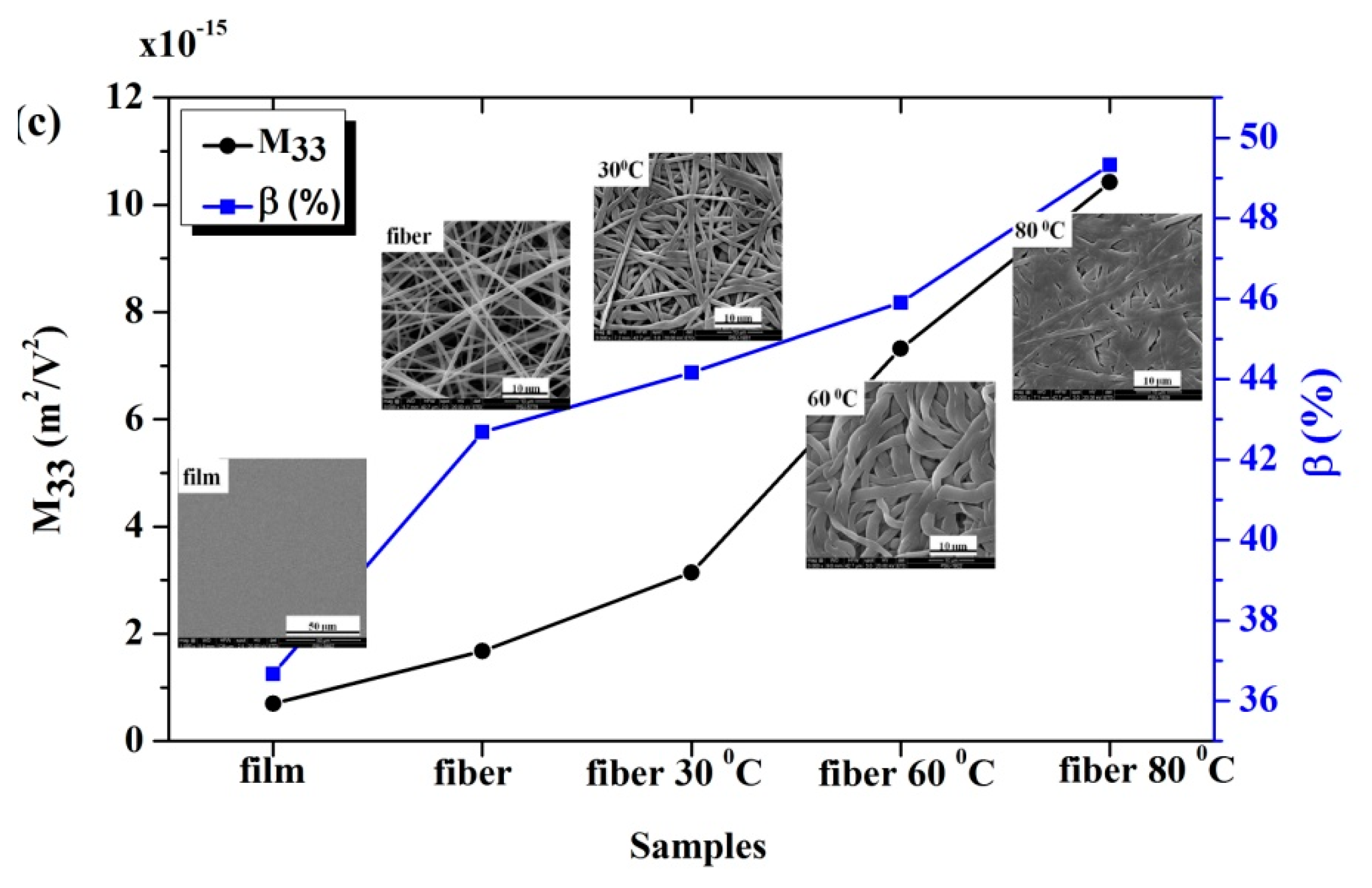
3.1. Structure and Morphology
3.2. X-ray Diffraction (XRD) Analysis
3.3. Fourier Transform Infrared Spectroscopy
3.4. Thermal Analysis
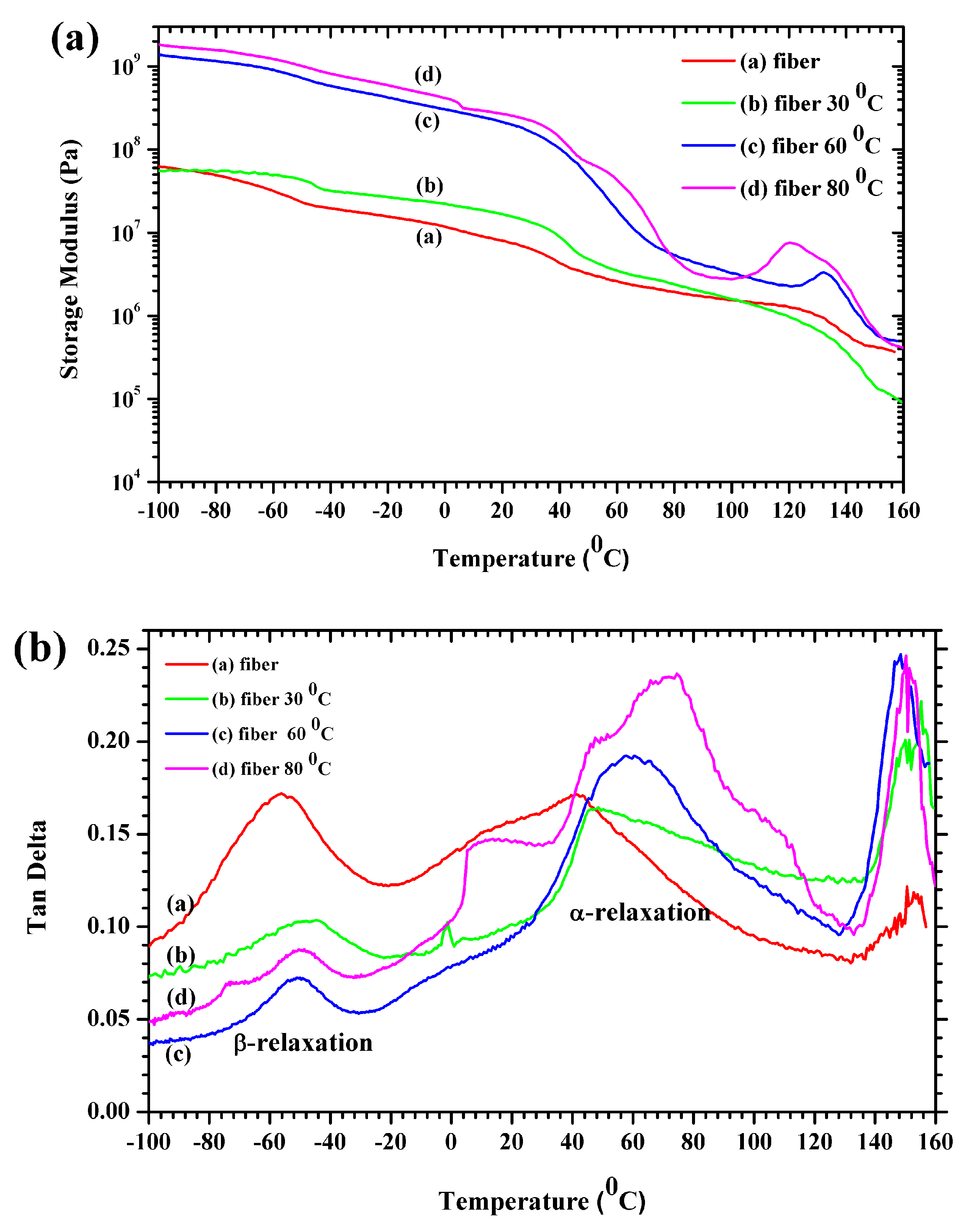
3.5. Mechanical Properties
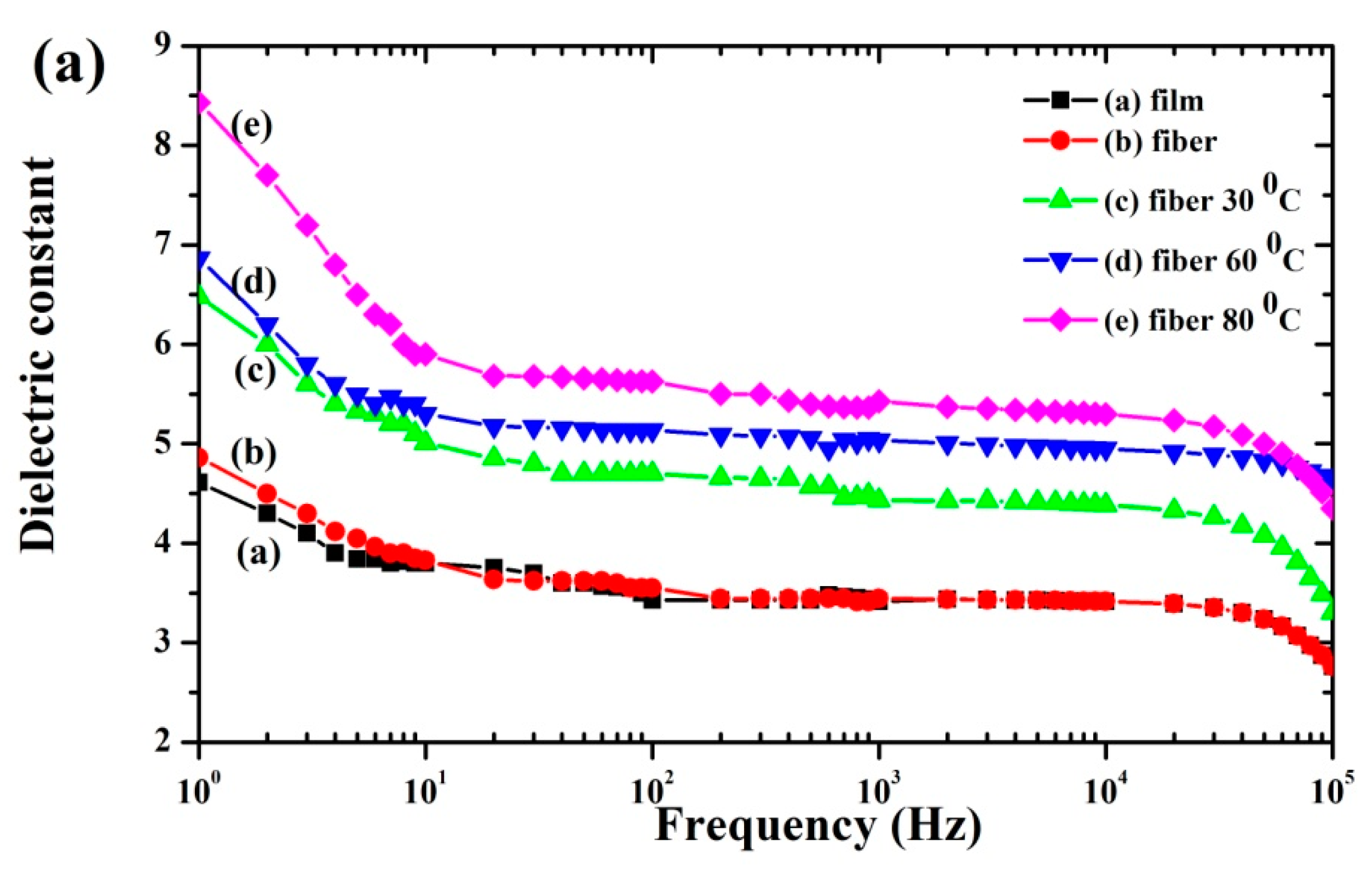
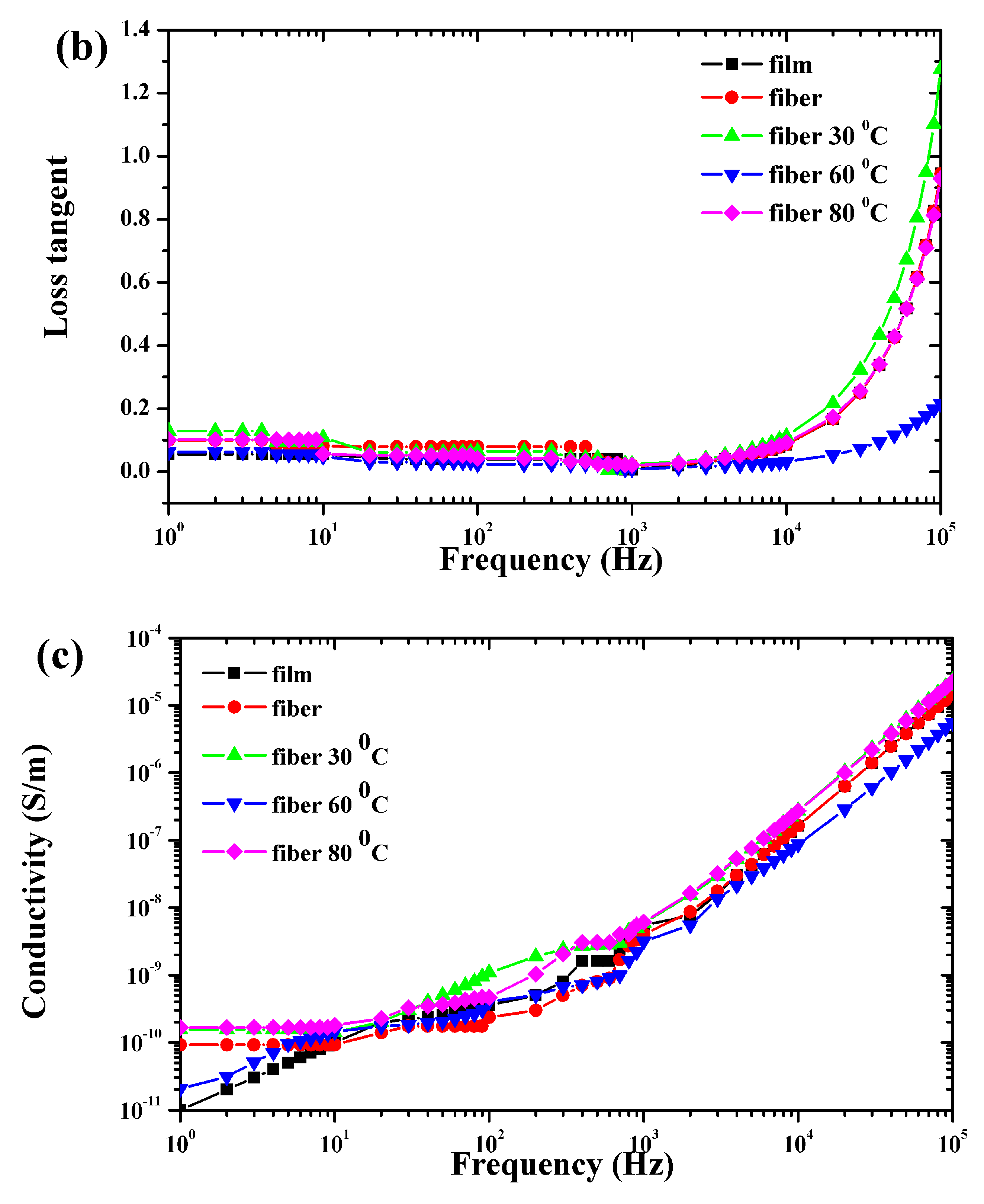
3.6. Electrical Properties
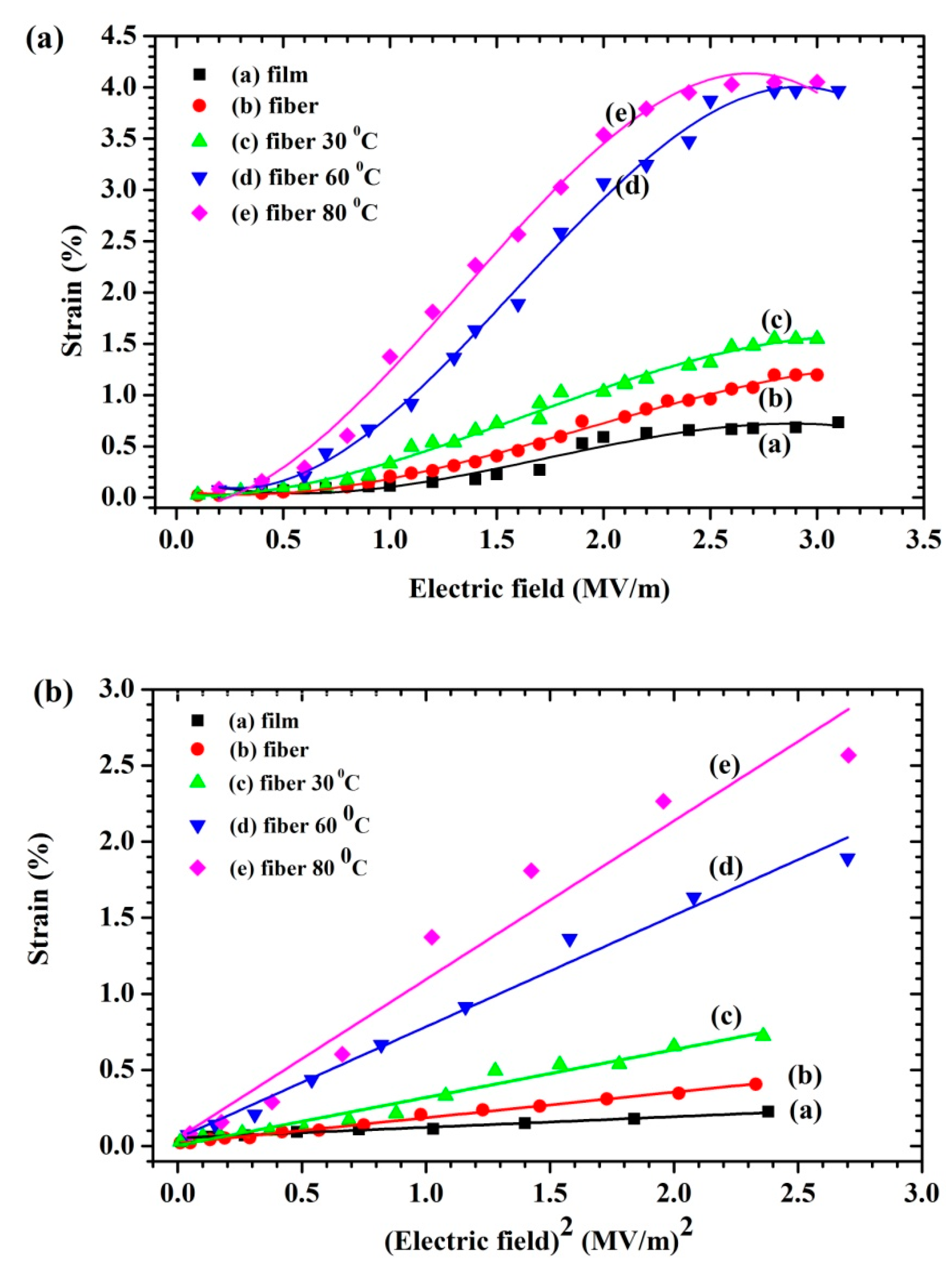
3.7. Electrostrictive Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brochu, P.; Pei, Q. Advances in dielectric elastomers for actuators and artificial muscles. Macromol. Rapid Commun. 2010, 31, 10–36. [Google Scholar] [CrossRef] [PubMed]
- Lang, S.B.; Muensit, S. Review of some lesser-known applications of piezoelectric and pyroelectric polymers. Appl. Phys. A 2006, 85, 125–134. [Google Scholar] [CrossRef]
- Putson, C.; Muensit, N. High electromechanical performance of modified electrostrictive polyurethane three-phase composites. Compos. Sci. Technol. 2018, 158, 164–174. [Google Scholar]
- Bharti, V.; Cheng, Z.Y.; Gross, S.; Xu, T.B.; Zhang, Q.M. High electrostrictive strain under high mechanical stress in electron-irradiated poly(vinylidene fluoride-trifluoroethylene) copolymer. Appl. Phys. Lett. 1999, 75, 2653–2655. [Google Scholar] [CrossRef]
- Cottinet, P.J.; Lallart, M.; Guyomar, D.; Guiffard, B.; Lebrun, L.; Sebald, G.; Putson, C. Analysis of ac-dc conversion for energy harvesting using an electrostrictive polymer P(VDF-TrFE-CFE). IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 30–42. [Google Scholar] [CrossRef] [PubMed]
- Xia, F.; Cheng, Z.Y.; Xu, H.S.; Li, H.F.; Zhang, Q.M.; Kavarnos, G.J.; Ting, R.Y.; Abdul-Sadek, G.; Belfield, K.D. High Electromechanical Responses in a Poly(vinylidene fluoride-trifluoroethylene-chlorofluoroethylene) Terpolymer. Adv. Mater. 2002, 14, 1574–1577. [Google Scholar] [CrossRef]
- Lu, X.; Schirokauer, A.; Scheinbeim, J. Giant electrostrictive response in poly(vinylidene fluoride-hexafluoropropylene) copolymers.). IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2000, 47, 1291–1295. [Google Scholar] [CrossRef]
- Wu, L.; Yuan, W.; Hu, N.; Wang, Z.; Chen, C.; Qiu, J.; Ying, J.; Li, Y. Improved piezoelectricity of PVDF-HFP/carbon black composite films. J. Phys. D Appl. Phys. 2014, 47, 135302. [Google Scholar] [CrossRef]
- Martins, P.; Lopes, A.C.; Lanceros-Mendez, S. Electroactive phases of poly(vinylidene fluoride): Determination, processing and applications. Prog. Polym. Sci. 2014, 39, 683–706. [Google Scholar] [CrossRef]
- Sencadas, V.; Gregorio, R.; Lanceros-Méndez, S. α to β Phase Transformation and Microestructural Changes of PVDF Films Induced by Uniaxial Stretch. J. Macromol. Sci. Part B 2009, 48, 514–525. [Google Scholar] [CrossRef]
- Thakur, P.; Kool, A.; Bagchi, B.; Hoque, N.A.; Das, S.; Nandy, P. Improvement of electroactive β phase nucleation and dielectric properties of WO3·H2O nanoparticle loaded poly(vinylidene fluoride) thin films. RSC Adv. 2015, 5, 62819–62827. [Google Scholar] [CrossRef]
- Sukwisute, P.; Muensit, N.; Soontaranon, S.; Rugmai, S. Micropower energy harvesting using poly(vinylidene fluoride hexafluoropropylene). Appl. Phys. Lett. 2013, 103, 063905. [Google Scholar] [CrossRef]
- Wang, F.; Frubing, P.; Wirges, W.; Gerhard, R.; Wegener, M. Enhanced Polarization in Melt-quenched and Stretched Poly(vinylidene Fluoride-Hexafluoropropylene) Films. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 1088–1095. [Google Scholar] [CrossRef]
- Scheinbeim, J.; Nakafuku, C.; Newman, B.A.; Pae, K.D. High-pressure crystallization of poly(vinylidene fluoride). J. Appl. Phys. 1979, 50, 4399–4405. [Google Scholar] [CrossRef]
- Ma, Y.; Tong, W.; Wang, W.; An, Q.; Zhang, Y. Montmorillonite/PVDF-HFP-based energy conversion and storage films with enhanced piezoelectric and dielectric properties. Compos. Sci. Technol. 2018, 168, 397–403. [Google Scholar] [CrossRef]
- Yuennan, J.; Sukwisute, P.; Boripet, B.; Muensit, N. Phase Transformation, Surface Morphology and Dielectric Property of P(VDF-HFP)/MgCl2·6H2O Nanocomposites. J. Phys. Conf. Ser. 2017, 901, 012085. [Google Scholar] [CrossRef]
- Roy, S.; Thakur, P.; Hoque, N.A.; Bagchi, B.; Das, S. Enhanced electroactive β-phase nucleation and dielectric properties of PVdF-HFP thin films influenced by montmorillonite and Ni(OH)2 nanoparticle modified montmorillonite. RSC Adv. 2016, 6, 21881–21894. [Google Scholar] [CrossRef]
- Zhou, T.; Zha, J.W.; Hou, Y.; Wang, D.; Zhao, J.; Dang, Z.M. Surface-functionalized MWNTs with emeraldine base: Preparation and improving dielectric properties of polymer nanocomposites. ACS Appl. Mater. Interfaces 2011, 3, 4557–4560. [Google Scholar] [CrossRef]
- Wongtimnoi, K.; Guiffard, B.; Bogner-Van de Moortele, A.; Seveyrat, L.; Cavaillé, J. Electrostrictive thermoplastic polyurethane-based nanocomposites filled with carboxyl-functionalized multi-walled carbon nanotubes (MWCNT-COOH): Properties and improvement of electromechanical activity. Compos. Sci. Technol. 2013, 85, 23–28. [Google Scholar] [CrossRef]
- Yan, J.; Jeong, Y.G. Roles of carbon nanotube and BaTiO 3 nanofiber in the electrical, dielectric and piezoelectric properties of flexible nanocomposite generators. Compos. Sci. Technol. 2017, 144, 1–10. [Google Scholar] [CrossRef]
- Tarhini, A.A.; Tehrani-Bagha, A.R. Graphene-based polymer composite films with enhanced mechanical properties and ultra-high in-plane thermal conductivity. Compos. Sci. Technol. 2019, 184, 107797. [Google Scholar] [CrossRef]
- Abolhasani, M.M.; Shirvanimoghaddam, K.; Naebe, M. PVDF/graphene composite nanofibers with enhanced piezoelectric performance for development of robust nanogenerators. Compos. Sci. Technol. 2017, 138, 49–56. [Google Scholar] [CrossRef] [Green Version]
- Dhakras, D.; Borkar, V.; Ogale, S.; Jog, J. Enhanced piezoresponse of electrospun PVDF mats with a touch of nickel chloride hexahydrate salt. Nanoscale 2012, 4, 752–756. [Google Scholar] [CrossRef] [PubMed]
- Sharma, M.; Srinivas, V.; Madras, G.; Bose, S. Outstanding dielectric constant and piezoelectric coefficient in electrospun nanofiber mats of PVDF containing silver decorated multiwall carbon nanotubes: Assessing through piezoresponse force microscopy. RSC Adv. 2016, 6, 6251–6258. [Google Scholar] [CrossRef]
- Wongtimnoi, K.; Guiffard, B.; Bogner-Van de Moortele, A.; Seveyrat, L.; Gauthier, C.; Cavaillé, J.Y. Improvement of electrostrictive properties of a polyether-based polyurethane elastomer filled with conductive carbon black. Compos. Sci. Technol. 2011, 71, 885–892. [Google Scholar] [CrossRef] [Green Version]
- Ribeiro, C.; Sencadas, V.; Ribelles, J.L.G.; Lanceros-Méndez, S. Influence of Processing Conditions on Polymorphism and Nanofiber Morphology of Electroactive Poly(vinylidene fluoride) Electrospun Membranes. Soft Mater. 2010, 8, 274–287. [Google Scholar] [CrossRef]
- Karan, S.K.; Mandal, D.; Khatua, B.B. Self-powered flexible Fe-doped RGO/PVDF nanocomposite: An excellent material for a piezoelectric energy harvester. Nanoscale 2015, 7, 10655–10666. [Google Scholar] [CrossRef]
- Low, Y.K.A.; Tan, L.Y.; Tan, L.P.; Boey, F.Y.C.; Ng, K.W. Increasing solvent polarity and addition of salts promote β-phase poly(vinylidene fluoride) formation. J. Appl. Polym. Sci. 2013, 128, 2902–2910. [Google Scholar] [CrossRef]
- Mano, J.F.; Sencadas, V.; Costa, A.M.; Lanceros-Méndez, S. Dynamic mechanical analysis and creep behaviour of β-PVDF films. Mater. Sci. Eng. A 2004, 370, 336–340. [Google Scholar] [CrossRef]
- Kang, J.; Sukigara, S. Development of bulk compression measurement for nonwoven sheets of electrospun nanofibers. Textile Res. J. 2013, 83, 1524–1531. [Google Scholar] [CrossRef]
- Patro, T.U.; Mhalgi, M.V.; Khakhar, D.V.; Misra, A. Studies on poly(vinylidene fluoride)–clay nanocomposites: Effect of different clay modifiers. Polymer 2008, 49, 3486–3499. [Google Scholar] [CrossRef]
- Prabakaran, K.; Mohanty, S.; Nayak, S.K. Influence of surface modified nanoclay on electrochemical properties of PVDF-HFP composite electrolytes. Int. J. Plast. Technol. 2014, 18, 349–361. [Google Scholar] [CrossRef]
- Du, C.-H.; Zhu, B.-K.; Xu, Y.-Y. The effects of quenching on the phase structure of vinylidene fluoride segments in PVDF-HFP copolymer and PVDF-HFP/PMMA blends. J. Mater. Sci. 2006, 41, 417–421. [Google Scholar] [CrossRef]
- Babu, K.S.; Reddy, A.R.; Sujatha, C.; Reddy, K.V.; Mallika, A.N. Synthesis and optical characterization of porous ZnO. J. Adv. Ceram. 2013, 2, 260–265. [Google Scholar] [CrossRef] [Green Version]
- Singh, M.; Lara, S.O.; Tlali, S. Effects of size and shape on the specific heat, melting entropy and enthalpy of nanomaterials. J. Taibah Univ. Sci. 2018, 11, 922–929. [Google Scholar] [CrossRef]
- Bikiaris, D.N.; Nianias, N.P.; Karagiannidou, E.G.; Docoslis, A. Effect of different nanoparticles on the properties and enzymatic hydrolysis mechanism of aliphatic polyesters. Polym. Degrad. Stab. 2012, 97, 2077–2089. [Google Scholar] [CrossRef]
- George, K.E.; Komalan, C.; Kumar, P.A.S.; Varughese, K.T.; Thomas, S. Dynamic mechanical analysis of binary and ternary polymer blends based on nylon copolymer/EPDM rubber and EPM grafted maleic anhydride compatibilizer. Express Polym. Lett. 2007, 1, 641–653. [Google Scholar]
- Prabakaran, K.; Mohanty, S.; Nayak, S.K. Improved electrochemical and photovoltaic performance of dye sensitized solar cells based on PEO/PVDF–HFP/silane modified TiO2 electrolytes and MWCNT/Nafion® counter electrode. RSC Adv. 2015, 5, 40491–40504. [Google Scholar] [CrossRef]
- Mahapatra, S.S.; Yadav, S.K.; Yoo, H.J.; Cho, J.W. Highly stretchable, transparent and scalable elastomers with tunable dielectric permittivity. J. Mater. Chem. 2011, 21, 7686. [Google Scholar] [CrossRef]
- Fan, B.H.; Zha, J.W.; Wang, D.R.; Zhao, J.; Dang, Z.M. Experimental study and theoretical prediction of dielectric permittivity in BaTiO3/polyimide nanocomposite films. Appl. Phys. Lett. 2012, 100, 092903. [Google Scholar] [CrossRef]
- Xing, C.; Guan, J.; Li, Y.; Li, J. Effect of a room-temperature ionic liquid on the structure and properties of electrospun poly(vinylidene fluoride) nanofibers. ACS Appl. Mater. Interfaces 2014, 6, 4447–4457. [Google Scholar] [CrossRef] [PubMed]
- Jana, S.; Garain, S.; Sen, S.; Mandal, D. The influence of hydrogen bonding on the dielectric constant and the piezoelectric energy harvesting performance of hydrated metal salt mediated PVDF films. Phys. Chem. Chem. Phys. 2015, 17, 17429–17436. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Wang, T.; Fang, M.; Wang, C.; Xiao, Y.; Pu, Y. Enhancement of dielectric and electrical properties in BFN/Ni/PVDF three-phase composites. Composites Sci. Technol. 2017, 146, 139–146. [Google Scholar] [CrossRef]


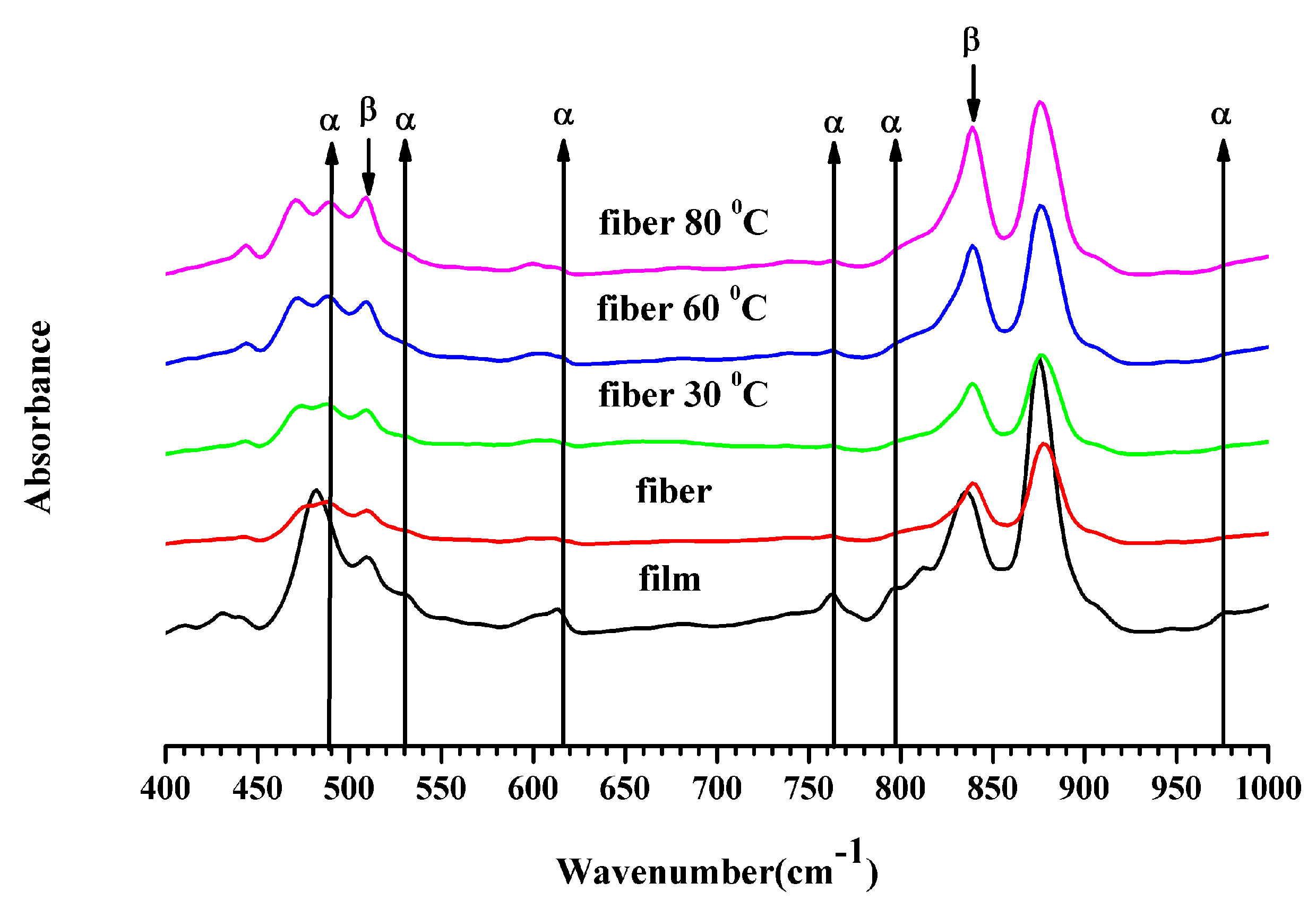
| Sample | Xc(%) | Aβ (cm−1) | Aα (cm−1) | F(β) (%) | %β |
|---|---|---|---|---|---|
| Film | 49.47 | 0.3161 | 0.0875 | 74.11 | 36.67 |
| Fiber | 49.69 | 0.1353 | 0.0176 | 85.90 | 42.68 |
| Fiber 30 °C | 50.88 | 0.1569 | 0.0189 | 86.80 | 44.16 |
| Fiber 60 °C | 52.44 | 0.2632 | 0.0297 | 87.53 | 45.90 |
| Fiber 80 °C | 55.03 | 0.327 | 0.0299 | 89.65 | 49.33 |
| Sample | ΔTm | ΔHm | ΔTc | ΔHc | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Film | 132.4 | 158.3 | 170.5 | 38.1 | 21.0 | 140.5 | 136.4 | 131.2 | 9.3 | −26.6 |
| Fiber | 136.0 | 160.1 | 170.1 | 34.1 | 22.7 | 140.9 | 137.1 | 131.7 | 9.2 | −25.2 |
| Fiber 30 °C | 143.0 | 159.0 | 170.8 | 27.8 | 25.2 | 142.2 | 136.4 | 130.8 | 11.4 | −27.0 |
| Fiber 60 °C | 137.2 | 158.3 | 171.8 | 34.6 | 29.3 | 139.1 | 134.3 | 129.1 | 10.0 | −27.0 |
| Fiber 80 °C | 135.5 | 158.2 | 170.9 | 35.4 | 36.3 | 138.6 | 134.2 | 129.6 | 9.0 | −26.2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tohluebaji, N.; Putson, C.; Muensit, N. High Electromechanical Deformation Based on Structural Beta-Phase Content and Electrostrictive Properties of Electrospun Poly(vinylidene fluoride- hexafluoropropylene) Nanofibers. Polymers 2019, 11, 1817. https://doi.org/10.3390/polym11111817
Tohluebaji N, Putson C, Muensit N. High Electromechanical Deformation Based on Structural Beta-Phase Content and Electrostrictive Properties of Electrospun Poly(vinylidene fluoride- hexafluoropropylene) Nanofibers. Polymers. 2019; 11(11):1817. https://doi.org/10.3390/polym11111817
Chicago/Turabian StyleTohluebaji, Nikruesong, Chatchai Putson, and Nantakan Muensit. 2019. "High Electromechanical Deformation Based on Structural Beta-Phase Content and Electrostrictive Properties of Electrospun Poly(vinylidene fluoride- hexafluoropropylene) Nanofibers" Polymers 11, no. 11: 1817. https://doi.org/10.3390/polym11111817
APA StyleTohluebaji, N., Putson, C., & Muensit, N. (2019). High Electromechanical Deformation Based on Structural Beta-Phase Content and Electrostrictive Properties of Electrospun Poly(vinylidene fluoride- hexafluoropropylene) Nanofibers. Polymers, 11(11), 1817. https://doi.org/10.3390/polym11111817