Experimental Study of Thermal Behavior of Insulation Material Rigid Polyurethane in Parallel, Symmetric, and Adjacent Building Façade Constructions
Abstract
:1. Introduction
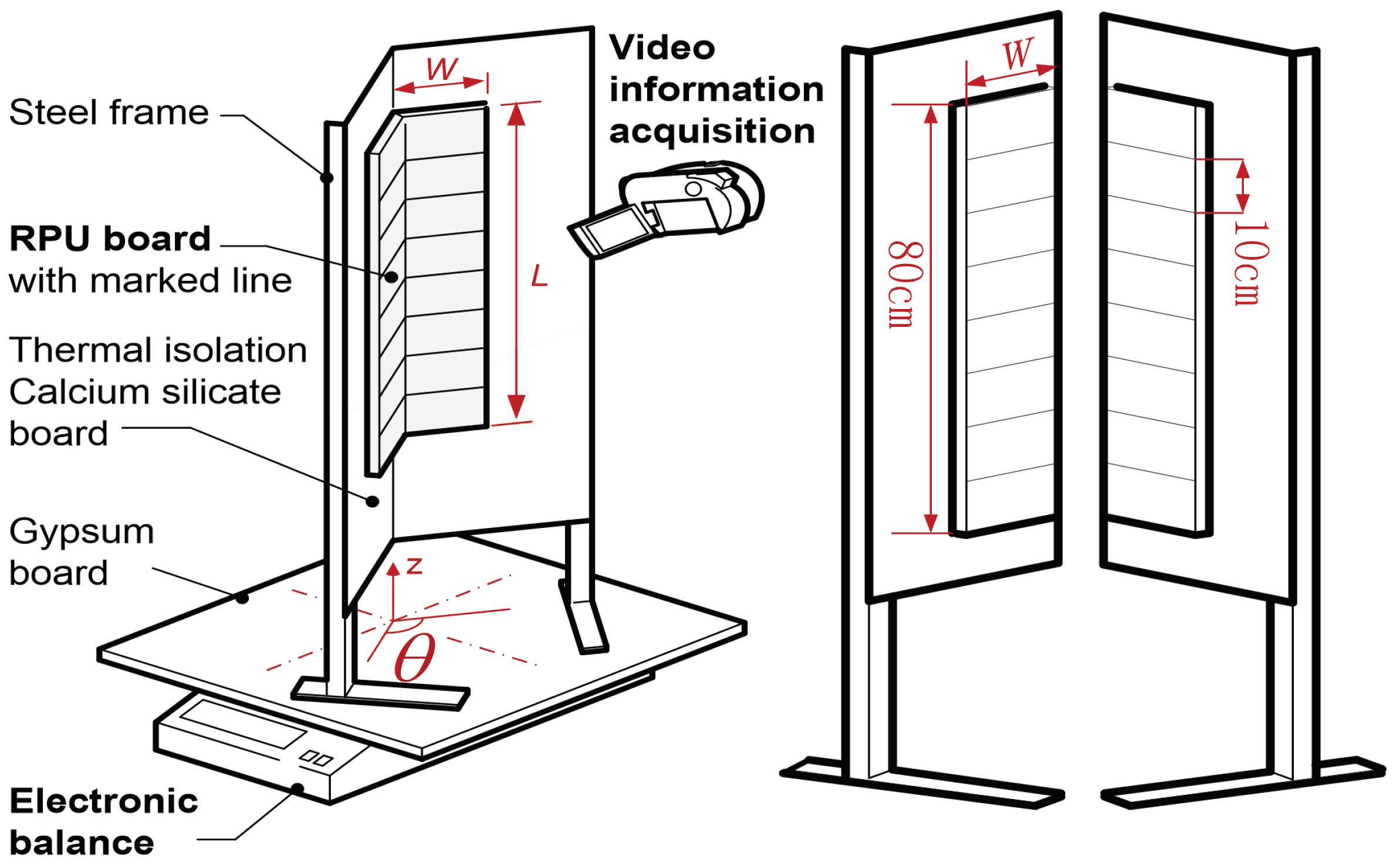
2. Materials and Methods
3. Results and Discussion
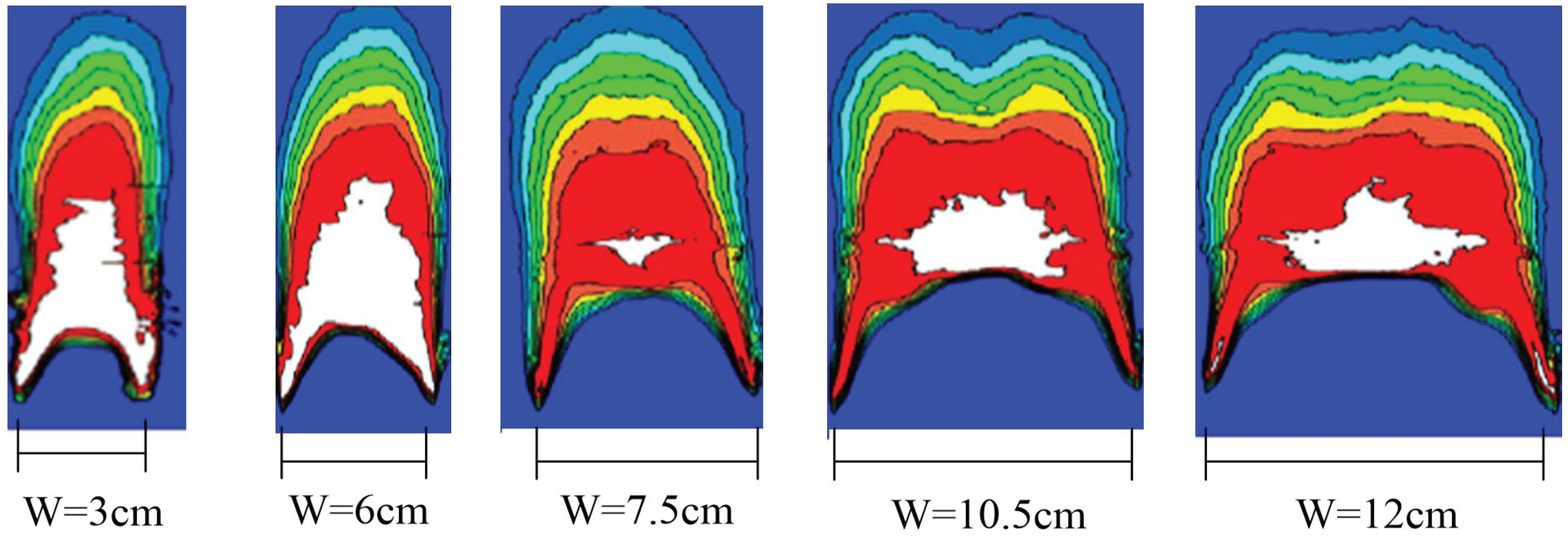
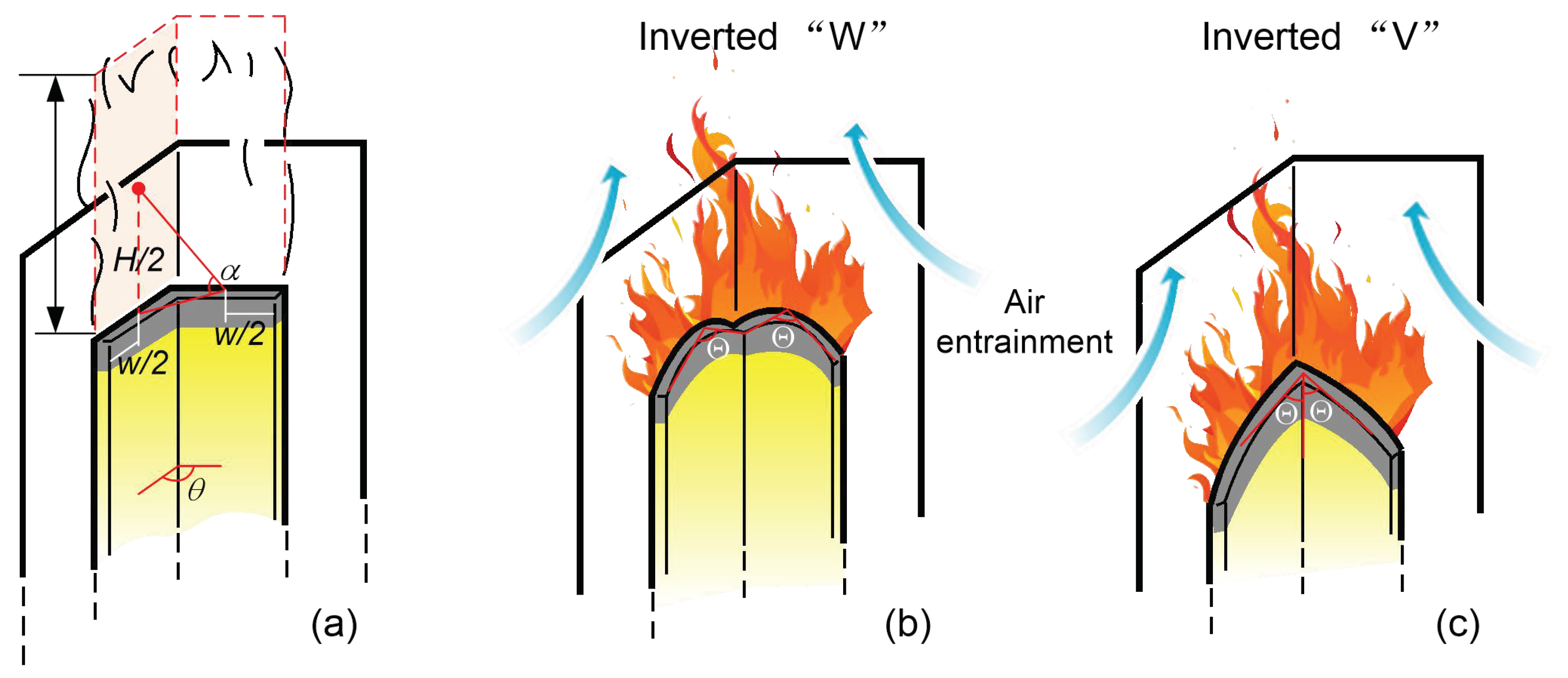
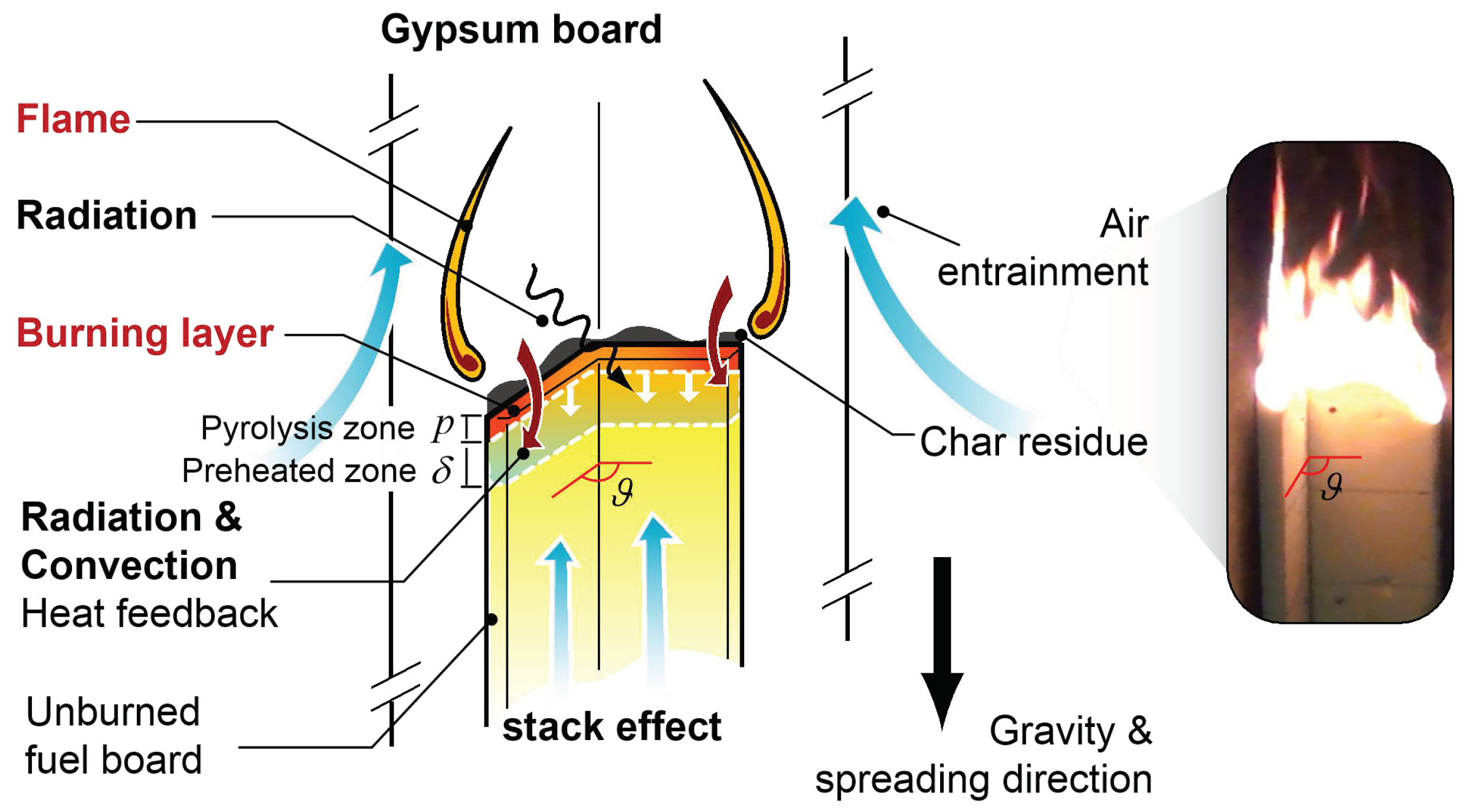
3.1. Flame morphology and Spreading Behavior
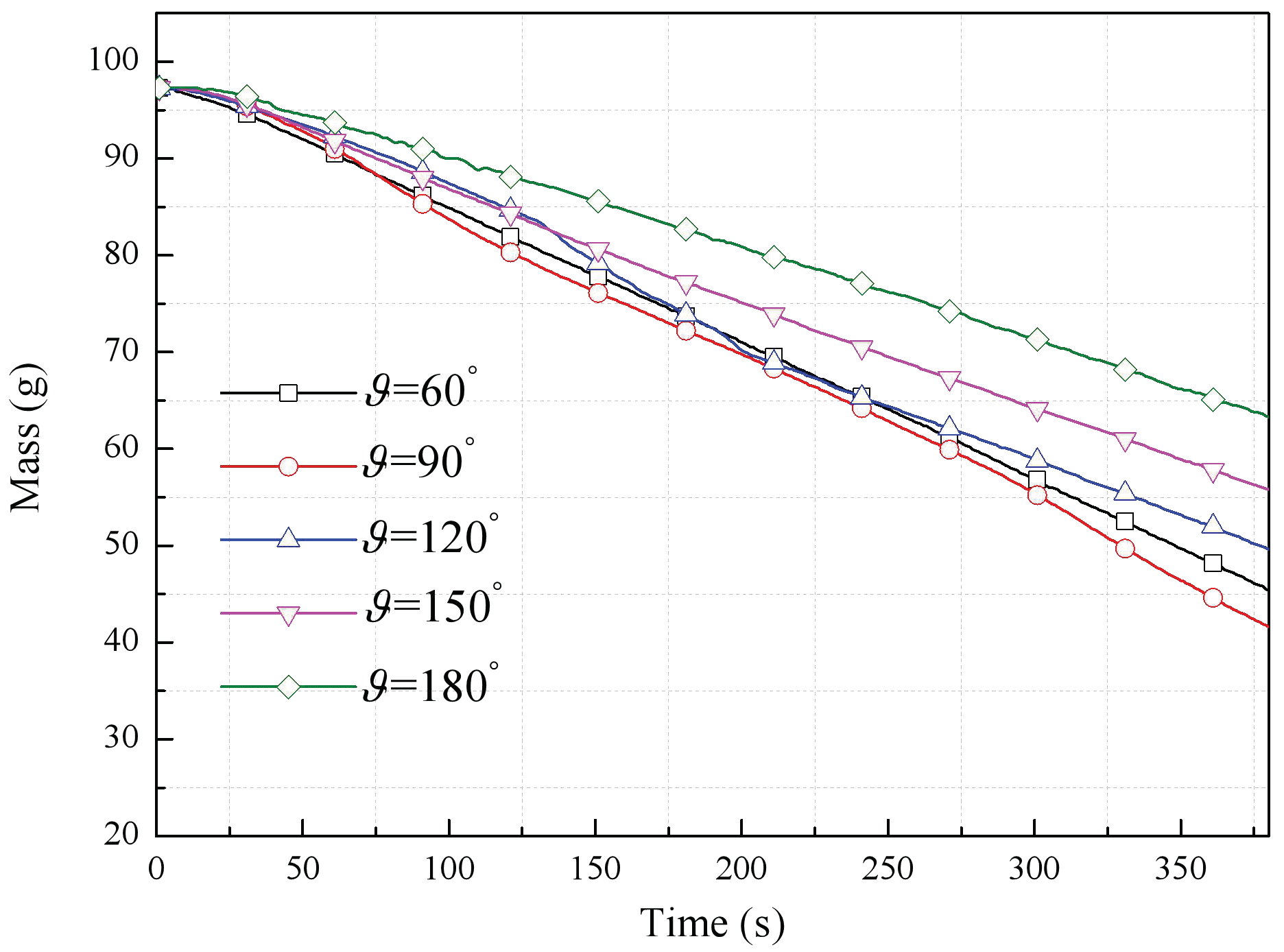
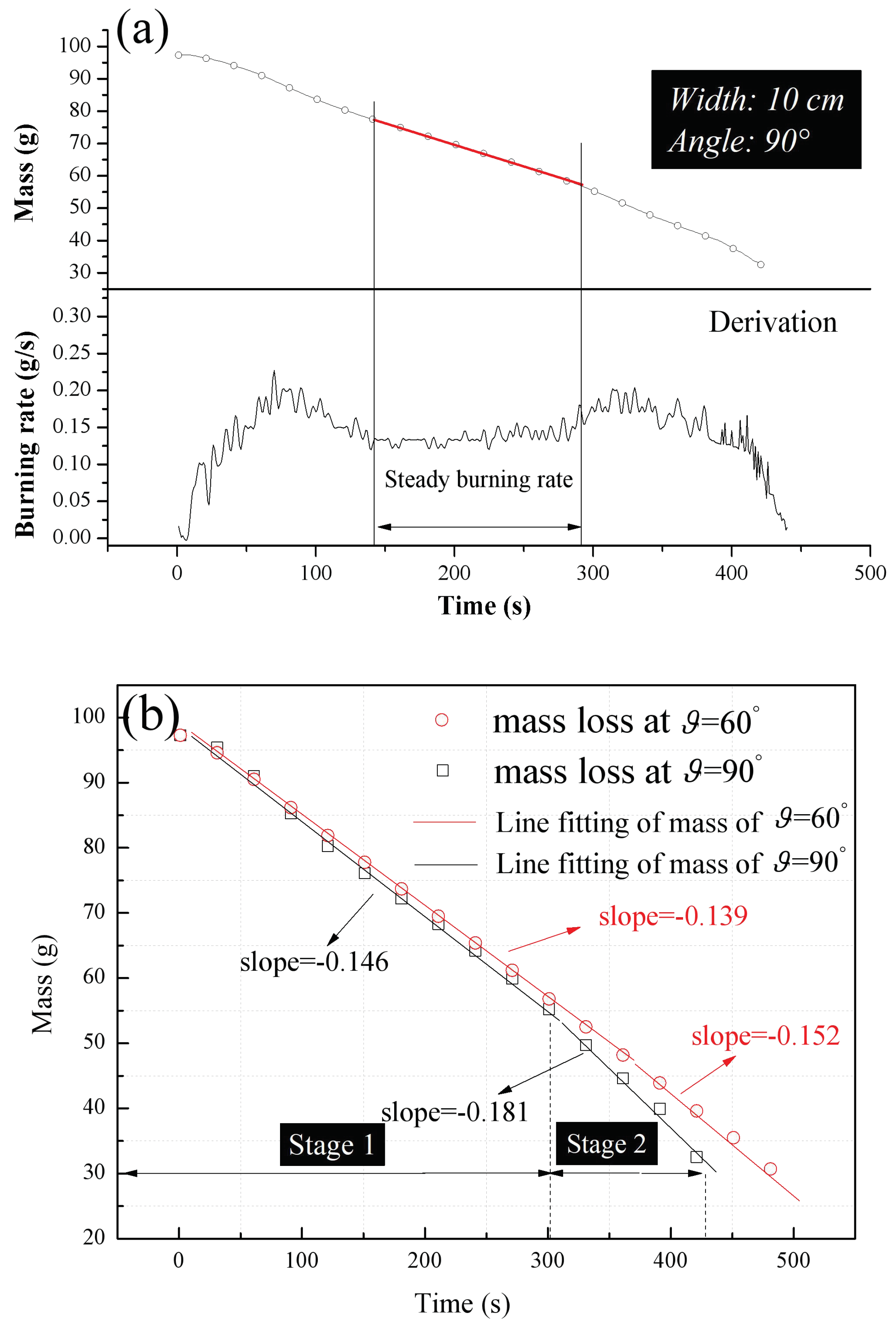
3.2. Overall Comparison of Burning Rates
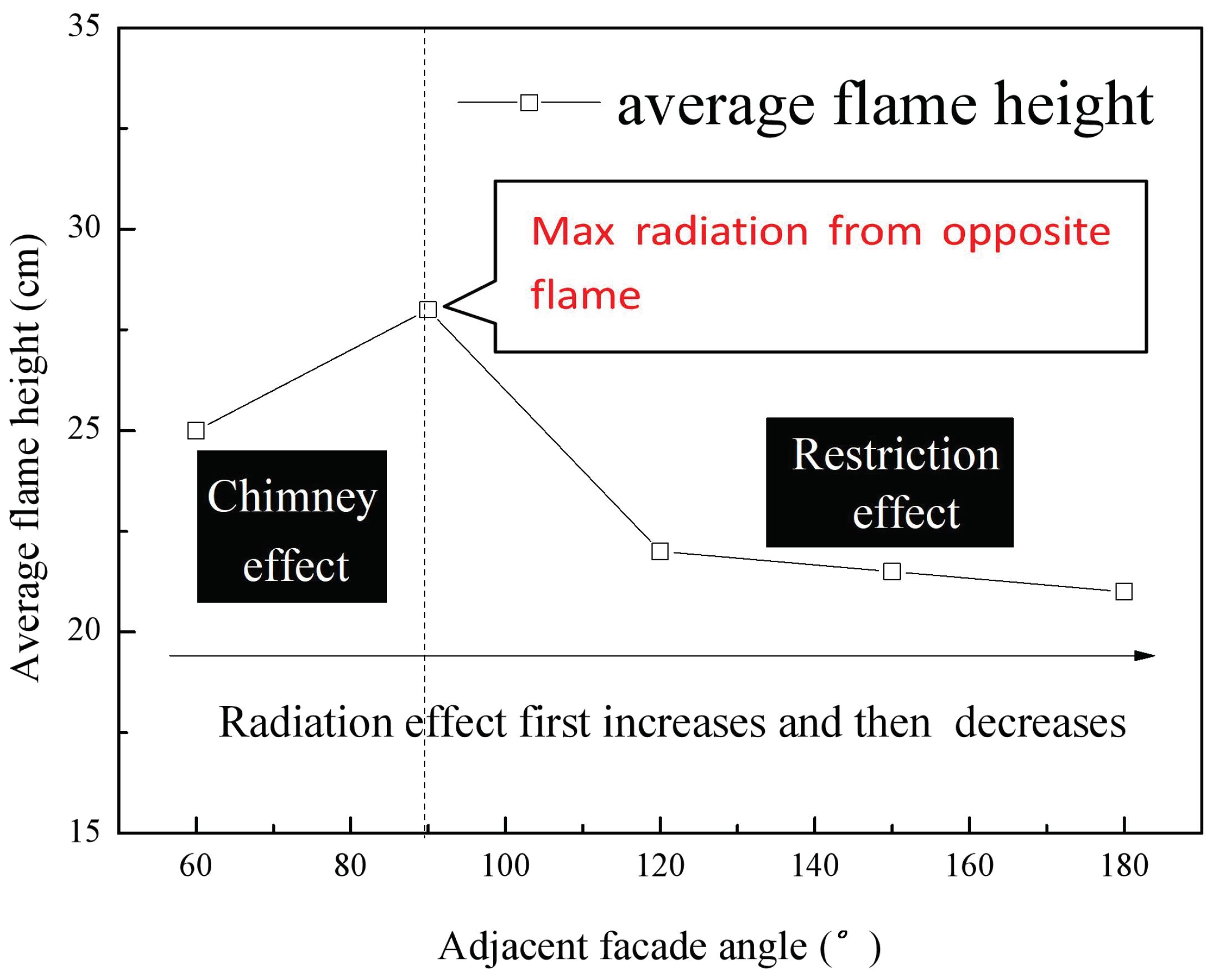
3.3. Flame Height and Flame Front Variations
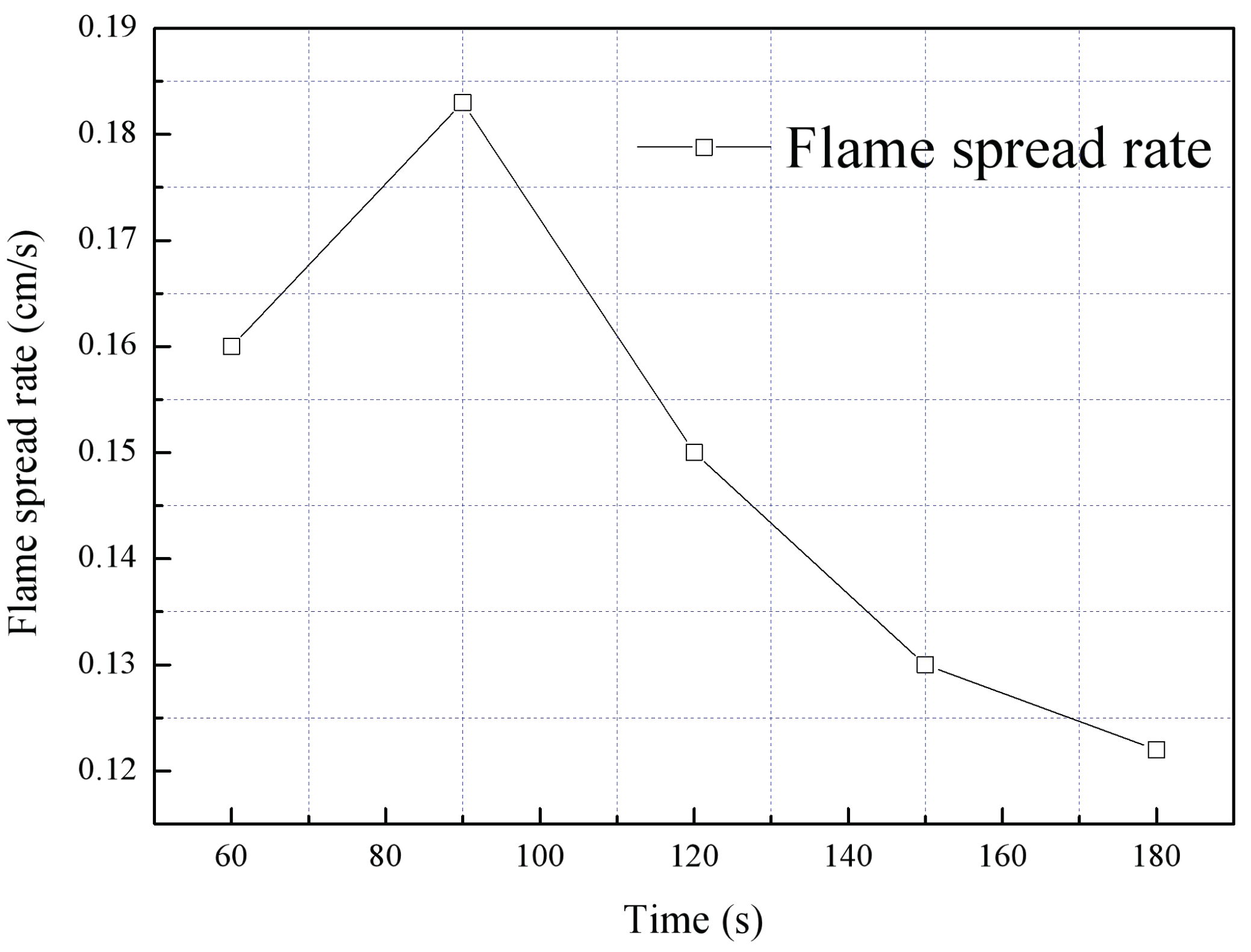
3.4. Flame Spreading Rates
4. Conclusions
- The parallel symmetric flame leading edge front was observed to change from one-dimensional to a unique morphology with an inverted ‘W’ shape, and finally exhibited an inverted ‘V’ shape. This occurred in conjunction with a narrow sample width due to the edge effect and the shear force that supplied additional heat feedback with enriched oxygen diffusion. The angle of the inverted ‘V’ shape was found to decrease as the flame spreading progressed.
- As the adjacent façade angle decreased, the burning rate varied in a nonlinear manner. This is attributed to the competition between the negative and positive effects of the parallel adjacent façade configuration. The downward flame spreading over the PUR was essentially stable during the early stage of flame spreading while accelerated flame spreading was observed during the later period. Phenomenological two-pass processing of the mass loss data showed complex combustion behavior that could complicate fire rescue.
- The average flame spreading rate and flame height both initially increased and then decreased with increases in the adjacent angle, similar to the trend displayed by the burning rate data. A critical angle of approximately was identified, due to the combined chimney and restriction effects induced by changes in the adjacent façade configuration. At smaller angles ( to ), the radiative heat transfer increased as a result of increases in the heat transfer from the opposite flame and the weakened chimney effect. At larger angles, the radiative heat transfer from the opposite flame and ember was gradually decreased, resulting in a lower flame spreading rate.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ma, X.; Tu, R.; Ding, C.; Zeng, Y.; Xu, L.; Fang, T.Y. Experimental study on thermal safety analysis of flexible polyurethane at various facade inclined structures under low ambient pressure condition. Eng Struct. 2018, 176, 11–19. [Google Scholar] [CrossRef]
- He, B.J.; Yang, L. Strategies for creating good wind environment around Chinese residences. Sustain Cities Soc. 2014, 10, 174–183. [Google Scholar] [CrossRef]
- Available online: https://en.wikipedia.org/wiki/Grenfell_Tower_fire (accessed on 3 October 2018).
- Ma, X.; Tu, R.; Xie, Q.Y. Study on downward flame spread behavior of flexible polyurethane board in external heat flux. J. Thermoplast compos. 2015, 28, 1693–1707. [Google Scholar] [CrossRef]
- De Ris, J.L.; Wu, P.K.; Heskestad, G. Radiation fire modeling. Proc. Combust. Inst. 2000, 28, 2751–2759. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; West, J. Determination of the spread rate in opposed flow flame spread over thick solid fuels in the thermal regime. Proc. Combust. Inst. 1996, 26, 1477–1485. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; King, M.D.; Takahashi, S.; Nagumo, T.; Wakai, K. Downward flame spread over poly(methyl)methacrylate. Proc. Combust. Inst. 2000, 28, 2891–2897. [Google Scholar] [CrossRef]
- Ma, X.; Tu, R.; Fang, T.Y. Thermal and fire risk analysis of low pressure on building energy conservation material flexible polyurethane with various inclined façade constructions. Constr. Build. Mater. 2018, 167, 449–456. [Google Scholar] [CrossRef]
- Ma, X.; Tu, R.; Xie, Q.Y. Experimental study on the burning behaviors of three typical thermoplastic materials liquid pool fire with different mass feeding rates. J. Therm. Anal. Calorim. 2015, 123, 329–337. [Google Scholar] [CrossRef]
- Umberto, B.; Nicholas, D. Thermal and fire characteristics of FRP composites for architectural applications. Polymers. 2015, 7, 2276–2289. [Google Scholar]
- Quintiere, J.; Harkleroad, M.; Hasemi, Y. Wall flames and implications of upward flame spread. Combust. Sci. Technol. 1986, 48, 191–222. [Google Scholar]
- Kashiwagi, H. Flame spread over an inclined thin fuel surface. Combust. Flame 1976, 26, 163–177. [Google Scholar] [CrossRef]
- Zhou, Y. Experimental investigation on downward flame spread over rigid polyurethane and extruded polystyrene foams. Exp. Therm. Fluid. Sci. 2018, 92, 346–352. [Google Scholar] [CrossRef]
- Sibulkin, M. The dependence of flame propagation on surface heat transfer I: Downward burning. Combust. Sci. Technol. 1976, 14, 43–56. [Google Scholar] [CrossRef]
- Shi, L.; Chew, M.Y.L.; Novozhilov, V.; Joseph, P. Modeling the pyrolysis and combustion behaviors of non-charring and intumescent-protected polymers using “Fires Cone”. Polymers. 2015, 7, 1979–1997. [Google Scholar] [CrossRef]
- An, W.G.; Pan, R.; Meng, Q.; Zhu, H. Experimental study on downward flame spread characteristics under the influence of parallel curtain wall. Appl. Therm. Eng. 2018, 128, 297–305. [Google Scholar] [CrossRef]
- Huan, Z.F.; Zhou, X.D.; Zhang, T.L.; Peng, F.; Wu, Z.B. F Flame spread rate over two parallel extruded polystyrene foam slab. Fire Safety Sci. 2014, 23, 190–194. [Google Scholar]
- Kurosaki, K. Downward flame spread along several vertical, parallel sheets of paper. Combust. Flame. 1985, 60, 269–277. [Google Scholar]
- Gong, J.H.; Zhou, X.; Deng, Z.; Yang, L. Influences of low atmospheric pressure on downward flame spread over thick PMMA slabs at different altitudes. J. Heat Mass Tran. 2013, 61, 191–200. [Google Scholar] [CrossRef]
- Gollner, M.J.; Williams, F.A.; Rangwala, A.S. Upward flame spread over corrugated cardboard. Combust. Flame. 2011, 7, 1404–1412. [Google Scholar] [CrossRef]
- Chilton, T.H.; Colburn, A.P. Mass Transfer (Absorption) Coefficients Prediction from Data on Heat Transfer and Fluid Friction. Ind. Eng. Chem. 1934, 26, 1183–1187. [Google Scholar] [CrossRef]
- Silver, R.S. Application of the Reynolds Analogy to Combustion of Solid Fuels. Nature. 1950, 165, 725–726. [Google Scholar] [CrossRef] [PubMed]




| Tested Material | Density (kg/m3) | Heat Capacity (J/kg·K) | Thermal Conductivity coefficient (W/m·K) | Pyrolysis Temperature (K) | Heat of Combustion (MJ/kg) |
|---|---|---|---|---|---|
| PUR | 60 | 1300 | 0.03 | 470 | 27 |
| Percentage (%) | 60° | 90° | 120° | 150° | 180° |
| 34.10% | 31.78% | 33.20% | 40.48% | 51.52% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Tu, R.; Cheng, X.; Zhu, S.; Ma, J.; Fang, T. Experimental Study of Thermal Behavior of Insulation Material Rigid Polyurethane in Parallel, Symmetric, and Adjacent Building Façade Constructions. Polymers 2018, 10, 1104. https://doi.org/10.3390/polym10101104
Ma X, Tu R, Cheng X, Zhu S, Ma J, Fang T. Experimental Study of Thermal Behavior of Insulation Material Rigid Polyurethane in Parallel, Symmetric, and Adjacent Building Façade Constructions. Polymers. 2018; 10(10):1104. https://doi.org/10.3390/polym10101104
Chicago/Turabian StyleMa, Xin, Ran Tu, Xudong Cheng, Shuguang Zhu, Jinwei Ma, and Tingyong Fang. 2018. "Experimental Study of Thermal Behavior of Insulation Material Rigid Polyurethane in Parallel, Symmetric, and Adjacent Building Façade Constructions" Polymers 10, no. 10: 1104. https://doi.org/10.3390/polym10101104
APA StyleMa, X., Tu, R., Cheng, X., Zhu, S., Ma, J., & Fang, T. (2018). Experimental Study of Thermal Behavior of Insulation Material Rigid Polyurethane in Parallel, Symmetric, and Adjacent Building Façade Constructions. Polymers, 10(10), 1104. https://doi.org/10.3390/polym10101104




