Effect of Dendrigraft Generation on the Interaction between Anionic Polyelectrolytes and Dendrigraft Poly(l-Lysine)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chemicals
2.2. Intergeneration Purification of DGL by Semi-Preparative Size-Exclusion Chromatography
2.3. Measurement of DGL Refractive Index Increments
2.4. Determination of the Molar Mass Distribution of DGL by Size-Exclusion Chromatography Coupled with Multi-Angle Laser Light Scattering (SEC–MALLS)
2.5. Preparation of Polyelectrolytes Mixtures
2.6. FACCE Procedure
3. Results and Discussions
3.1. Characterization of Purified DGL
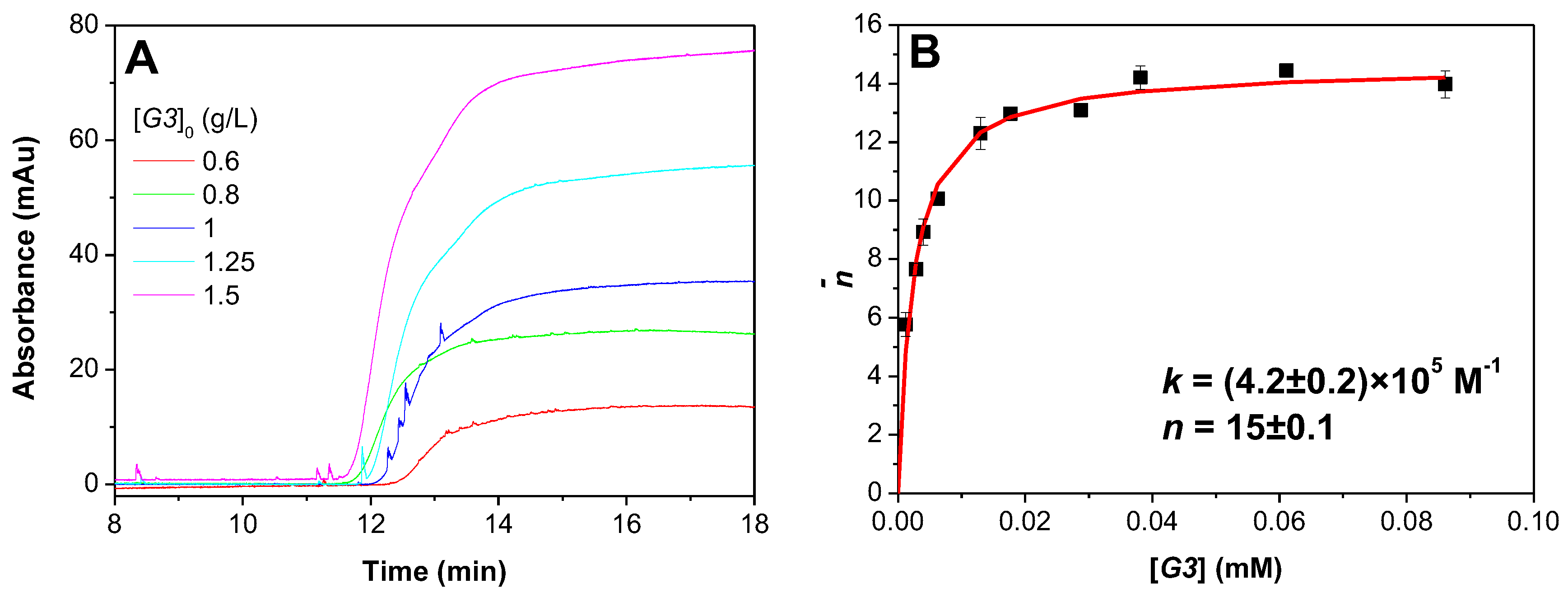
3.2. Determination of DGL-PAMAMPS Binding Parameters by FACCE
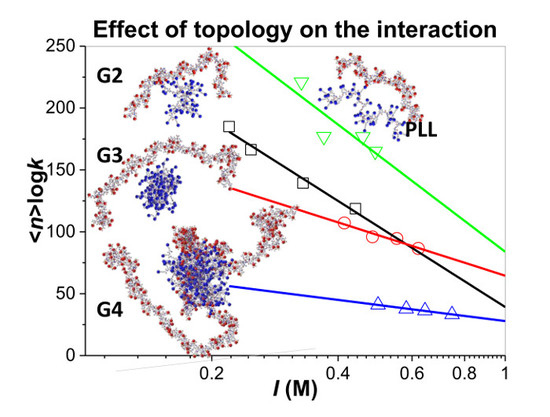
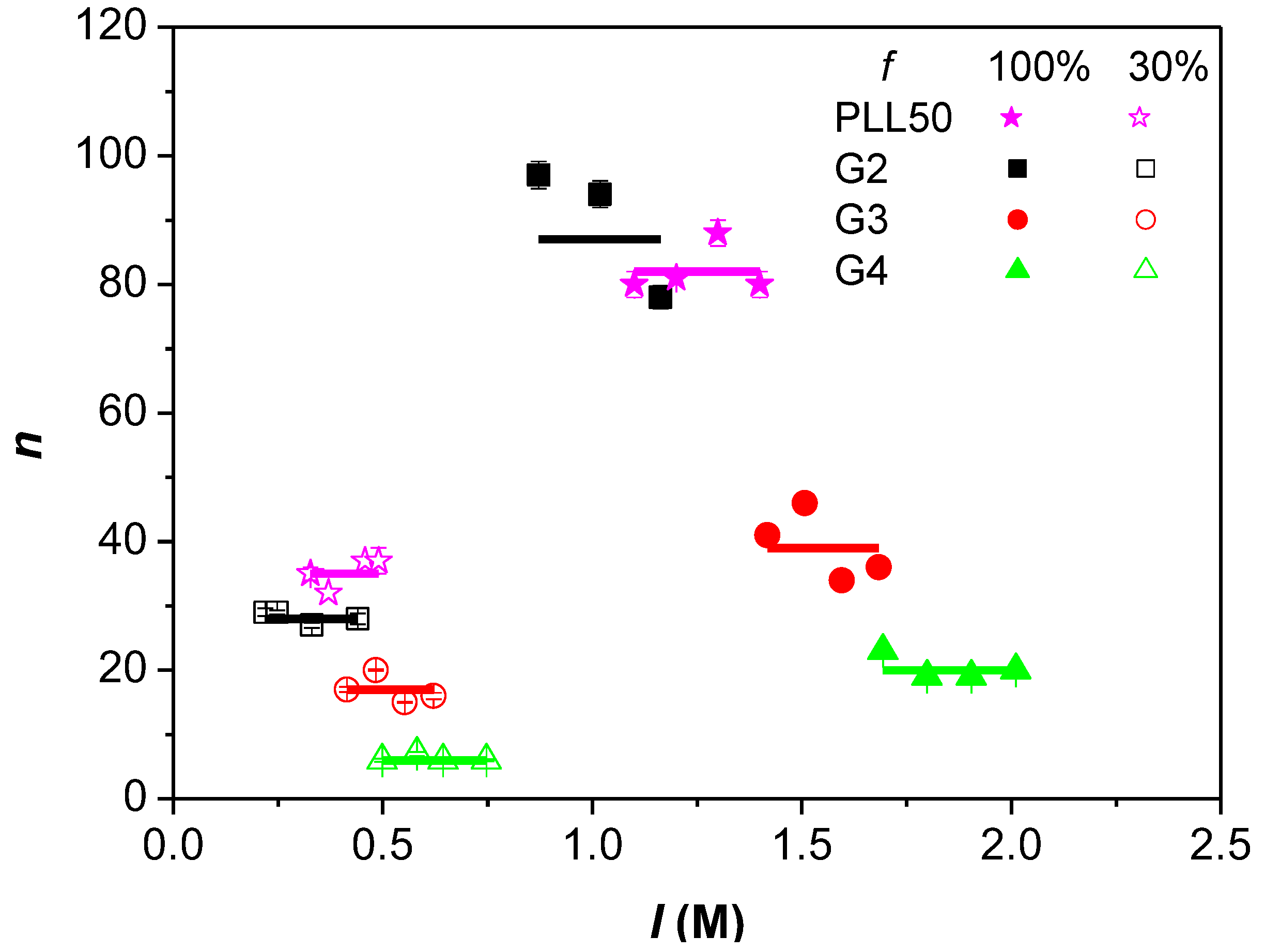
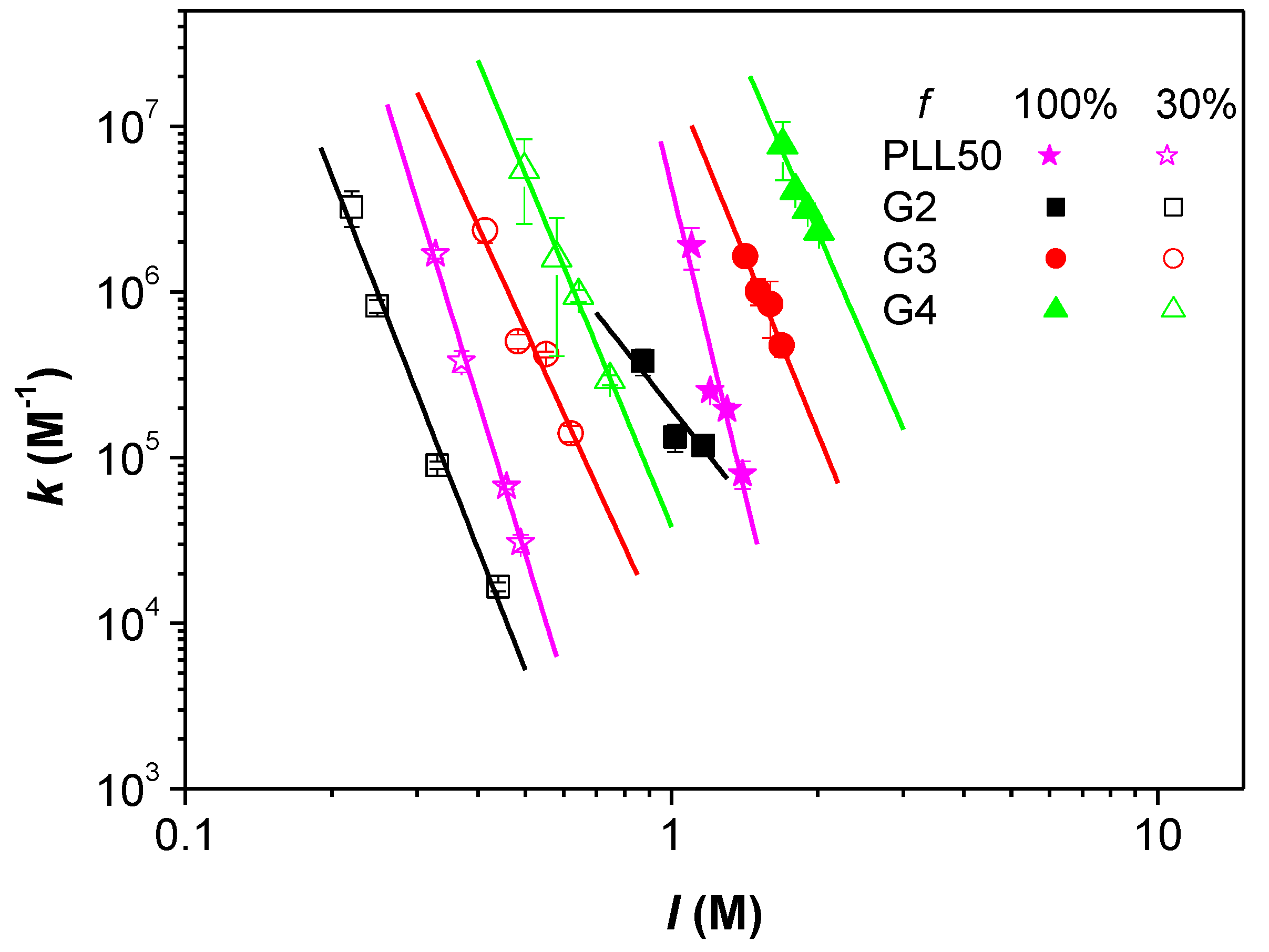
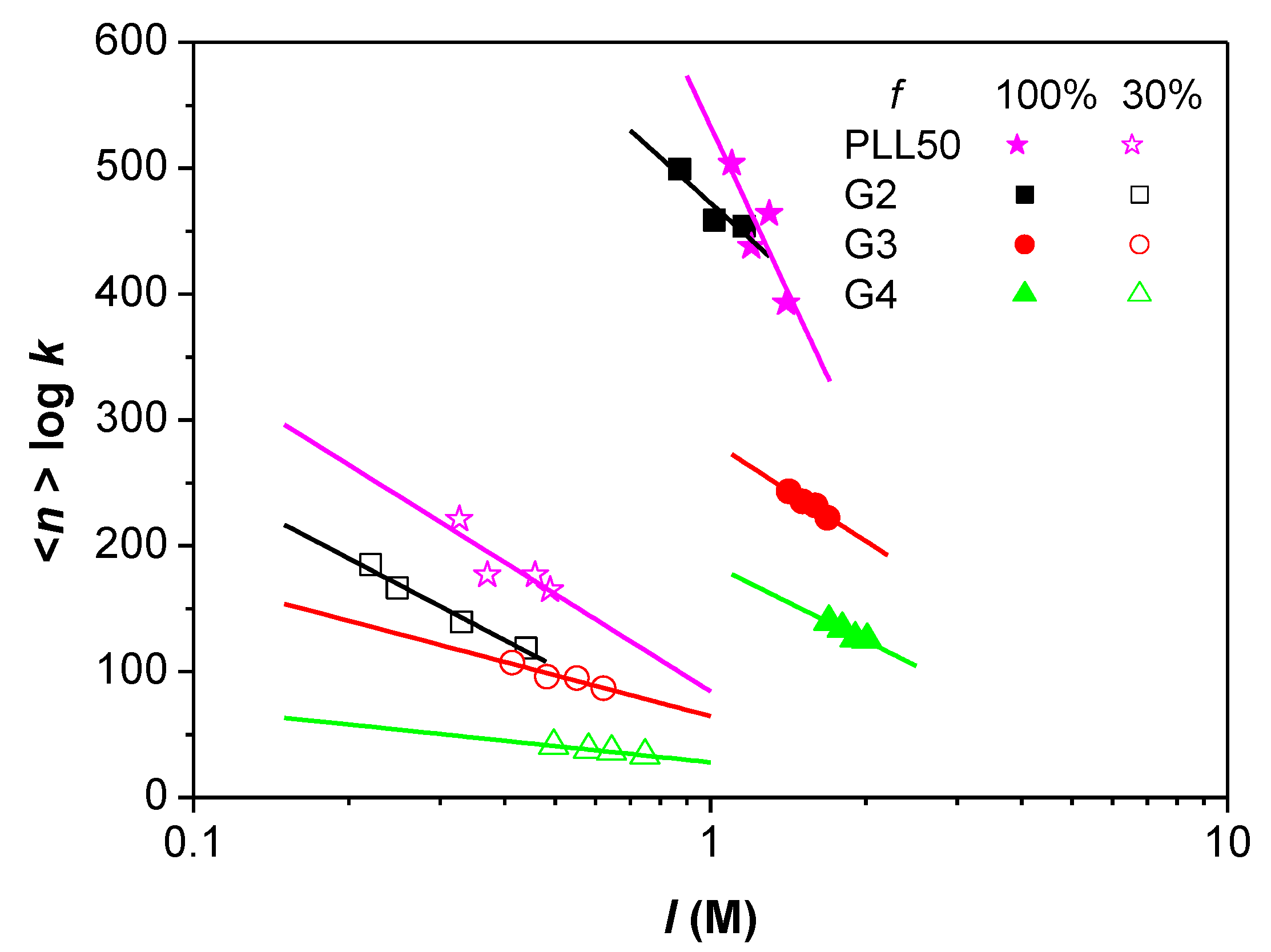
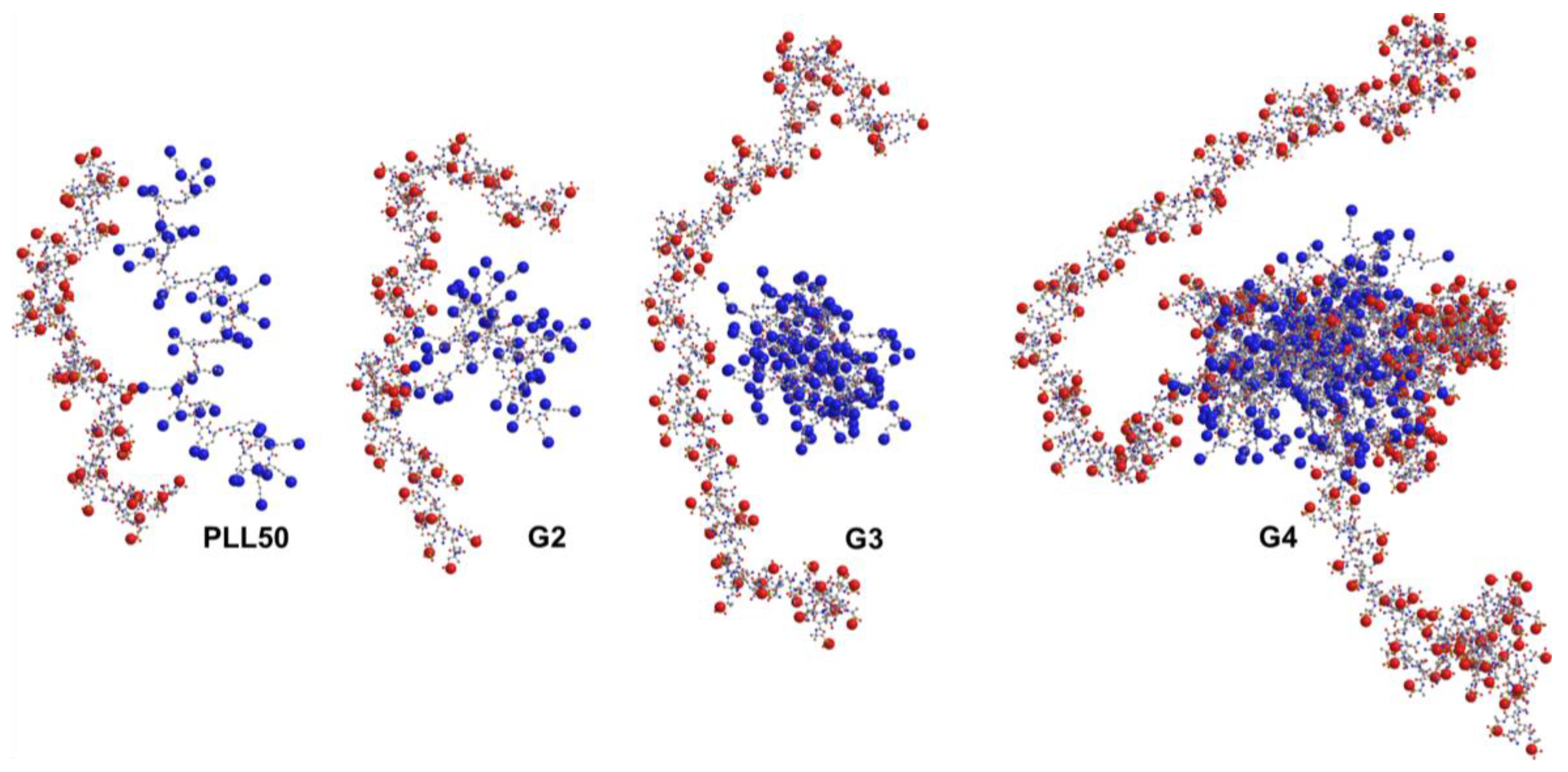
3.3. Influence of the Ionic Strength and DGL Generation on the Stoichiometry of Interaction
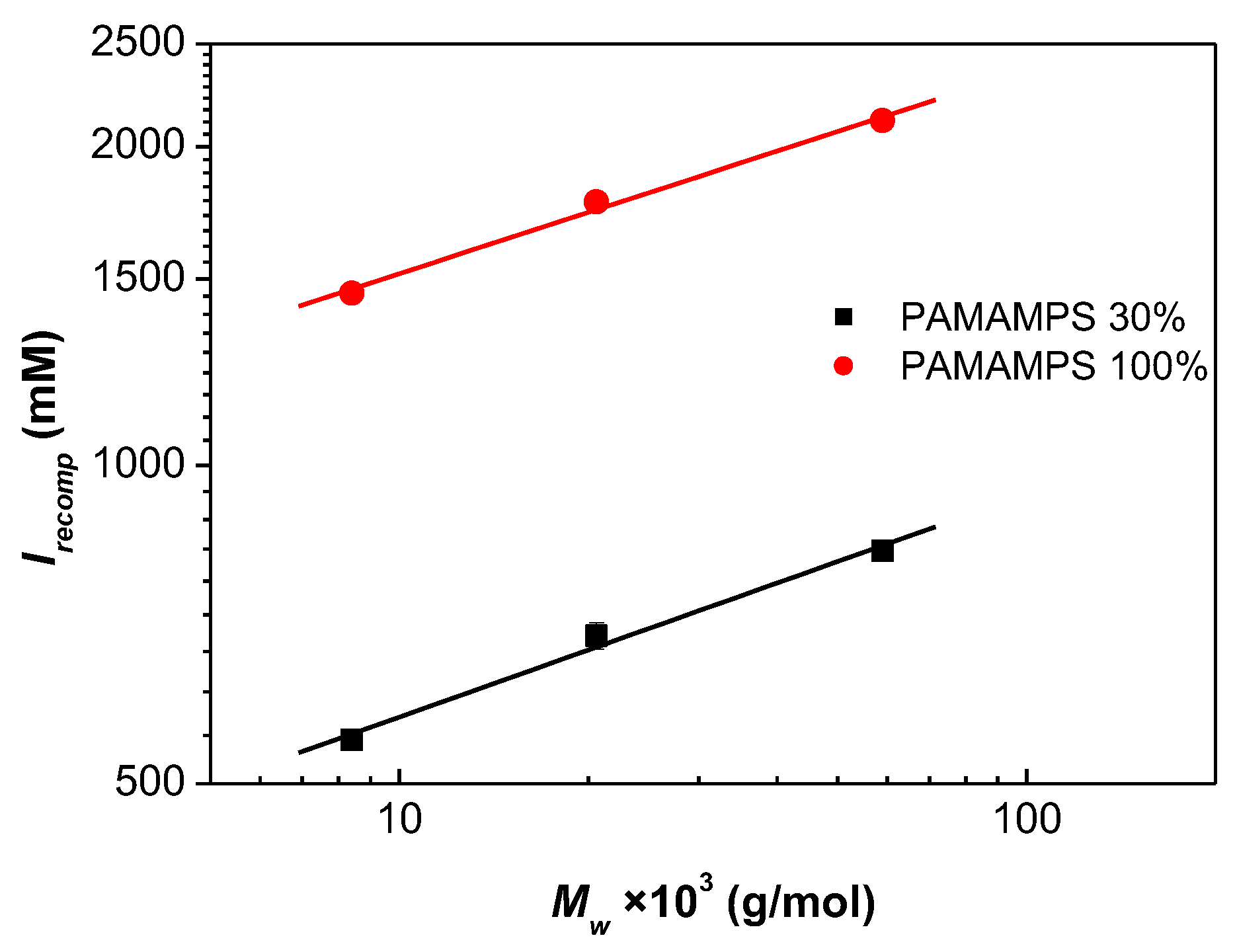
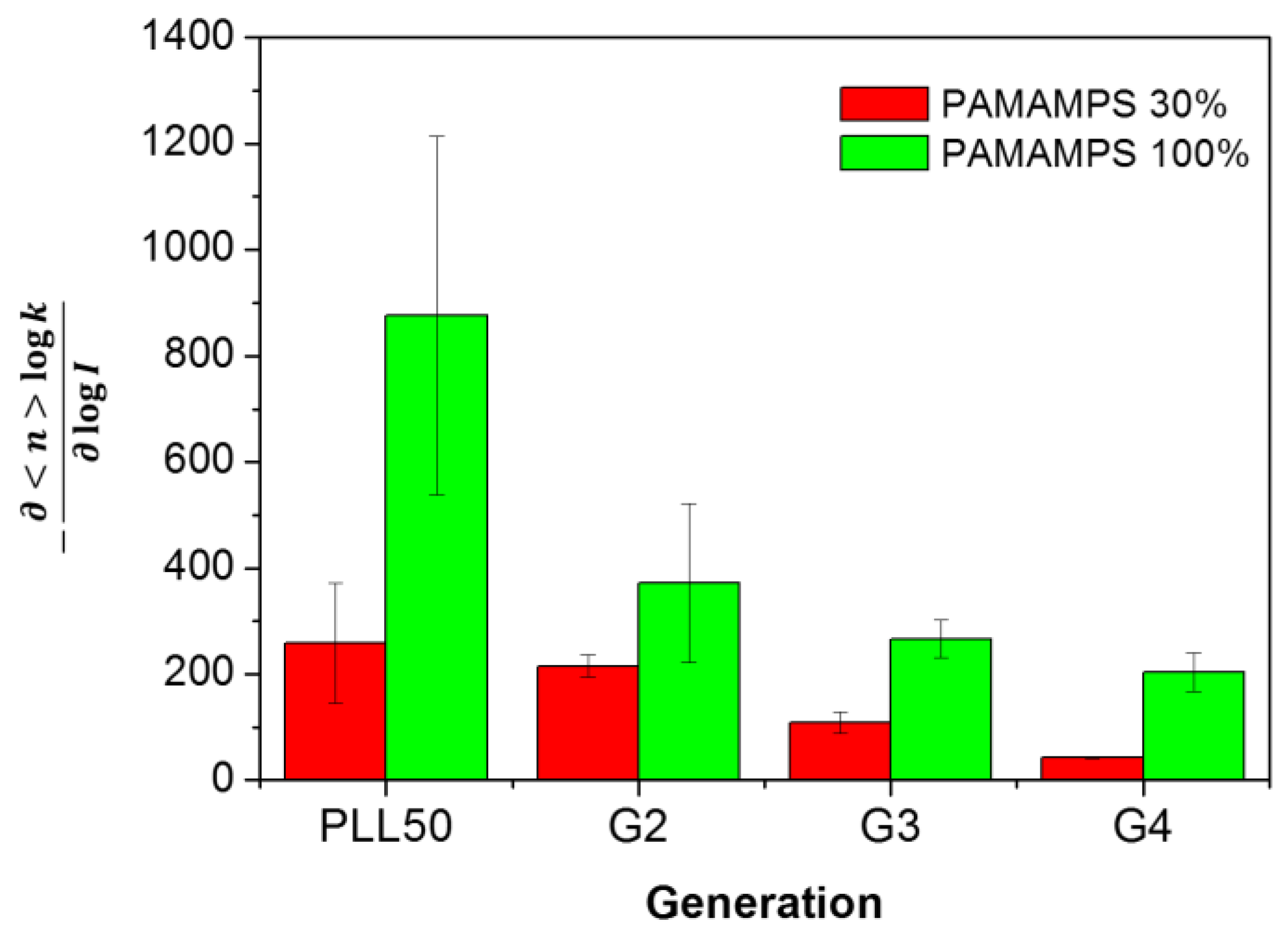
3.4. Influence of the Ionic Strength and DGL Generation on the Binding Constants
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Abbasi, E.; Aval, S.F.; Akbarzadeh, A.; Milani, M.; Nasrabadi, H.T.; Joo, S.W.; Hanifehpour, Y.; Nejati-Koshki, K.; Pashaei-Asl, R. Dendrimers: Synthesis, applications, and properties. Nanoscale Res. Lett. 2014, 9, 247. [Google Scholar] [CrossRef] [PubMed]
- Malkoch, M.; Malmström, E.; Nyström, A.M. Dendrimers: Properties and Applications. In Polymer Science: A Comprehensive Reference; Matyjaszewski, K., Möller, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Kesharwani, P.; Jain, K.; Jain, N.K. Dendrimer as nanocarrier for drug delivery. Prog. Polym. Sci. 2014, 39, 268–307. [Google Scholar] [CrossRef]
- Nanjwade, B.K.; Bechra, H.M.; Derkar, G.K.; Manvi, F.V.; Nanjwade, V.K. Dendrimers: Emerging polymers for drug-delivery systems. Eur. J. Pharm. Sci. 2009, 38, 185–196. [Google Scholar] [CrossRef] [PubMed]
- Svenson, S. Dendrimers as versatile platform in drug delivery applications. Eur. J. Pharm. Biopharm. 2009, 71, 445–462. [Google Scholar] [CrossRef] [PubMed]
- Wolinsky, J.; Grinstaff, M. Therapeutic and diagnostic applications of dendrimers for cancer treatment. Adv. Drug Deliv. Rev. 2008, 60, 1037–1055. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Hong, M.; Zhang, L.; Tang, G.; Jiang, Y.; Pei, Y. PEGylated PAMAM Dendrimer-Doxorubicin Conjugates: In Vitro Evaluation and In Vivo Tumor Accumulation. Pharm. Res. 2010, 27, 161–174. [Google Scholar] [CrossRef] [PubMed]
- Patil, M.L.; Zhang, M.; Taratula, O.; Garbuzenko, O.B.; He, H.; Minko, T. Internally Cationic Polyamidoamine PAMAM-OH Dendrimers for siRNA Delivery: Effect of the Degree of Quaternization and Cancer Targeting. Biomacromolecules 2009, 10, 258–266. [Google Scholar] [CrossRef] [PubMed]
- Longmire, M.; Choyke, P.L.; Kobayashi, H. Dendrimer-based contrast agents for molecular imaging. Curr. Top. Med. Chem. 2008, 8, 1180–1186. [Google Scholar] [CrossRef] [PubMed]
- Wijagkanalan, W.; Kawakami, S.; Hashida, M. Designing Dendrimers for Drug Delivery and Imaging: Pharmacokinetic Considerations. Pharm. Res. 2010, 28, 1500–1519. [Google Scholar] [CrossRef] [PubMed]
- Yiyun, C.; Tongwen, X.; Rongqiang, F. Polyamidoamine dendrimers used as solubility enhancers of ketoprofen. Eur. J. Med. Chem. 2005, 40, 1390–1393. [Google Scholar] [CrossRef] [PubMed]
- Yiyun, C.; Tongwen, X. Solubility of nicotinic acid in polyamidoamine dendrimer solutions. Eur. J. Med. Chem. 2005, 40, 1384–1389. [Google Scholar] [CrossRef] [PubMed]
- Milhem, O.M.; Myles, C.; McKeown, N.B.; Attwood, D.; D’Emanuele, A. Polyamidoamine Starburst dendrimers as solubility enhancers. Int. J. Pharm. 2000, 197, 239–241. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, M.-Y.; Jiang, T.-K.; Huang, W.-Z.; Wu, J.-Y. Low generational polyamidoamine dendrimers to enhance the solubility of folic acid: A “dendritic effect” investigation. Chin. Chem. Lett. 2014, 25, 815–818. [Google Scholar] [CrossRef]
- Sato, K.; Anzai, J.-I. Dendrimers in Layer-by-Layer Assemblies: Synthesis and Applications. Molecules 2013, 18, 8440–8460. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Astruc, D. Dendritic catalysis—Basic concepts and recent trends. Coord. Chem. Rev. 2013, 257, 2317–2334. [Google Scholar] [CrossRef]
- Astruc, D. Palladium catalysis using dendrimers: Molecular catalysts versus nanoparticles. Tetrahedron Asymmetry 2010, 21, 1041–1054. [Google Scholar] [CrossRef]
- Astruc, D.; Chardac, F. Dendritic Catalysts and Dendrimers in Catalysis. Chem. Rev. 2001, 101, 2991–3024. [Google Scholar] [CrossRef] [PubMed]
- Giri, J.; Diallo, M.S.; Simpson, A.J.; Liu, Y.; Goddard, W.A.; Kumar, R.; Woods, G.C. Interactions of Poly(amidoamine) Dendrimers with Human Serum Albumin: Binding Constants and Mechanisms. ACS Nano 2011, 5, 3456–3468. [Google Scholar] [CrossRef] [PubMed]
- Froehlich, E.; Mandeville, J.S.; Jennings, C.J.; Sedaghat-Herati, R.; Tajmir-Riahi, H.A. Dendrimers Bind Human Serum Albumin. J. Phys. Chem. B 2009, 113, 6986–6993. [Google Scholar] [CrossRef] [PubMed]
- Zou, T.; Oukacine, F.; Le Saux, T.; Cottet, H. Neutral Coatings for the Study of Polycation/Multicharged Anion Interactions by Capillary Electrophoresis: Application to Dendrigraft Poly-l-lysines with Negatively Multicharged Molecules. Anal. Chem. 2010, 82, 7362–7368. [Google Scholar] [CrossRef] [PubMed]
- Örberg, M.L.; Schillen, K.; Nylander, T. Dynamic light scattering and fluorescence study of the interaction between double-stranded DNA and poly(amido amine) dendrimers. Biomacromolecules 2007, 8, 1557–1563. [Google Scholar] [CrossRef] [PubMed]
- Ainalem, M.-L.; Campbell, R.A.; Khalid, S.; Gillams, R.J.; Rennie, A.R.; Nylander, T. On the Ability of PAMAM Dendrimers and Dendrimer/DNA Aggregates To Penetrate POPC Model Biomembranes. J. Phys. Chem. B 2010, 114, 7229–7244. [Google Scholar] [CrossRef] [PubMed]
- Kłos, J.S.; Sommer, J.U. Monte Carlo simulations of charged dendrimer-linear polyelectrolyte complexes and explicit counterions. J. Chem. Phys. 2011, 134, 204902. [Google Scholar] [CrossRef] [PubMed]
- Larin, S.V.; Darinskii, A.A.; Lyulin, A.V.; Lyulin, S.V. Linker Formation in an Overcharged Complex of Two Dendrimers and Linear Polyelectrolyte. J. Phys. Chem. B 2010, 114, 2910–2919. [Google Scholar] [CrossRef] [PubMed]
- Tian, W.-D.; Ma, Y.-Q. Complexation of a Linear Polyelectrolyte with a Charged Dendrimer: Polyelectrolyte Stiffness Effects. Macromolecules 2010, 43, 1575–1582. [Google Scholar] [CrossRef]
- Miura, N.; Dubin, P.L.; Moorefield, C.N.; Newkome, G.R. Complex Formation by Electrostatic Interaction between Carboxyl-Terminated Dendrimers and Oppositely Charged Polyelectrolytes. Langmuir 1999, 15, 4245–4250. [Google Scholar] [CrossRef]
- Kabanov, V.A.; Zezin, A.B.; Rogacheva, V.B.; Gulyaeva, Z.G.; Zansochova, M.F.; Joosten, J.G.H.; Brackman, J. Interaction of Astramol Poly(propyleneimine) Dendrimers with Linear Polyanions. Macromolecules 1999, 32, 1904–1909. [Google Scholar] [CrossRef]
- Leisner, D.; Imae, T. Polyelectrolyte Behavior of an Interpolyelectrolyte Complex Formed in Aqueous Solution of a Charged Dendrimer and Sodium Poly(l-glutamate). J. Phys. Chem. B 2003, 107, 13158–13167. [Google Scholar] [CrossRef]
- Vasumathi, V.; Maiti, P.K. Complexation of siRNA with Dendrimer: A Molecular Modeling Approach. Macromolecules 2010, 43, 8264–8274. [Google Scholar] [CrossRef]
- Froehlich, E.; Mandeville, J.S.; Weinert, C.M.; Kreplak, L.; Tajmir-Riahi, H.A. Bundling and Aggregation of DNA by Cationic Dendrimers. Biomacromolecules 2011, 12, 511–517. [Google Scholar] [CrossRef] [PubMed]
- Yevlampieva, N.; Dobrodumov, A.; Nazarova, O.; Okatova, O.; Cottet, H. Hydrodynamic Behavior of Dendrigraft Polylysines in Water and Dimethylformamide. Polymers 2012, 4, 20–31. [Google Scholar] [CrossRef]
- Sisavath, N.; Le Saux, T.; Leclercq, L.; Cottet, H. Effect of Dendrimer Generation on the Interactions between Human Serum Albumin and Dendrigraft Polylysines. Langmuir 2014, 30, 4450–4457. [Google Scholar] [CrossRef] [PubMed]
- Sisavath, N.; Leclercq, L.; Le Saux, T.; Oukacine, F.; Cottet, H. Study of interactions between oppositely charged dendrigraft poly-l-lysine and human serum albumin by continuous frontal analysis capillary electrophoresis and fluorescence spectroscopy. J. Chromatogr. A 2013, 1289, 127–132. [Google Scholar] [CrossRef] [PubMed]
- Salehi, A.; Larson, R.G. A Molecular Thermodynamic Model of Complexation in Mixtures of Oppositely Charged Polyelectrolytes with Explicit Account of Charge Association/Dissociation. Macromolecules 2016, 49, 9706–9719. [Google Scholar] [CrossRef]
- Sing, C.E.; Zwanikken, J.W.; Olvera de la Cruz, M. Ion Correlation-Induced Phase Separation in Polyelectrolyte Blends. ACS Macro Lett. 2013, 2, 1042–1046. [Google Scholar] [CrossRef]
- McCormick, C.L.; Chen, G.S. Water-soluble copolymers. IV. Random copolymers of acrylamide with sulfonated comonomers. J. Polym. Sci. A Polym. Chem. 1982, 20, 817–838. [Google Scholar] [CrossRef]
- Lounis, F.M.; Chamieh, J.; Gonzalez, P.; Cottet, H.; Leclercq, L. Prediction of Polyelectrolyte Complex Stoichiometry for Highly Hydrophilic Polyelectrolytes. Macromolecules 2016, 49, 3881–3888. [Google Scholar] [CrossRef]
- Gonzalez, P.; Leclercq, L.; Cottet, H. What is the Contribution of Counter-Ions to the Absolute Molar Mass of Polyelectrolytes Determined by SEC-MALLS? Macromol. Chem. Phys. 2016, 217, 2654–2659. [Google Scholar] [CrossRef]
- Ibrahim, A.; Koval, D.; Kašička, V.; Faye, C.; Cottet, H. Effective Charge Determination of Dendrigraft Poly-l-Lysine by Capillary Isotachophoresis. Macromolecules 2013, 46, 533–540. [Google Scholar] [CrossRef]
- Lounis, F.; Chamieh, J.; Leclercq, L.; Gonzalez, P.; Cottet, H. The Effect of Molar Mass and Charge Density on the Formation of Complexes between Oppositely Charged Polyelectrolytes. Polymers 2017, 9, 50. [Google Scholar] [CrossRef]
- Lounis, F.M.; Chamieh, J.; Leclercq, L.; Gonzalez, P.; Cottet, H. Modelling and predicting the interactions between oppositely and variously charged polyelectrolytes by frontal analysis continuous capillary electrophoresis. Soft Matter 2016, 12, 9728–9737. [Google Scholar] [CrossRef] [PubMed]
- Lounis, F.M.; Chamieh, J.; Leclercq, L.; Gonzalez, P.; Geneste, A.; Prelot, B.; Cottet, H. Interactions between Oppositely Charged Polyelectrolytes by Isothermal Titration Calorimetry: Effect of Ionic Strength and Charge Density. J. Phys. Chem. B 2017, 121, 2684–2694. [Google Scholar] [CrossRef] [PubMed]
- Anik, N.; Airiau, M.; Labeau, M.P.; Vuong, C.T.; Reboul, J.; Lacroix-Desmazes, P.; Gerardin, C.; Cottet, H. Determination of Polymer Effective Charge by Indirect UV Detection in Capillary Electrophoresis: Toward the Characterization of Macromolecular Architectures. Macromolecules 2009, 42, 2767–2774. [Google Scholar] [CrossRef]
- Lohman, T.M.; deHaseth, P.L.; Record, M.T., Jr. Pentalysine-deoxyribonucleic acid interactions: A model for the general effects of ion concentrations on the interactions of proteins with nucleic acids. Biochemistry 1980, 19, 3522–3530. [Google Scholar] [CrossRef] [PubMed]
- Lohman, T.M.; Mascotti, D.P. Thermodynamics of ligand-nucleic acid interactions. Methods Enzymol. 1992, 212, 400–424. [Google Scholar] [CrossRef] [PubMed]
- Mascotti, D.P.; Lohman, T.M. Thermodynamics of Oligoarginines Binding to RNA and DNA. Biochemistry 1997, 36, 7272–7279. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Bond, J.P.; Anderson, C.F.; Lohman, T.M.; Record, M.T. Large electrostatic differences in the binding thermodynamics of a cationic peptide to oligomeric and polymeric DNA. Proc. Natl. Acad. Sci. USA 1996, 93, 2511–2516. [Google Scholar] [CrossRef] [PubMed]
- Mascotti, D.P.; Lohman, T.M. Thermodynamic extent of counterion release upon binding oligolysines to single-stranded nucleic acids. Proc. Natl. Acad. Sci. USA 1990, 87, 3142–3146. [Google Scholar] [CrossRef] [PubMed]
- Hattori, T.; Hallberg, R.; Dubin, P.L. Roles of Electrostatic Interaction and Polymer Structure in the Binding of β-Lactoglobulin to Anionic Polyelectrolytes: Measurement of Binding Constants by Frontal Analysis Continuous Capillary Electrophoresis. Langmuir 2000, 16, 9738–9743. [Google Scholar] [CrossRef]
- Hattori, T.; Bat-Aldar, S.; Kato, R.; Bohidar, H.B.; Dubin, P.L. Characterization of polyanion-protein complexes by frontal analysis continuous capillary electrophoresis and small angle neutron scattering: Effect of polyanion flexibility. Anal. Biochem. 2005, 342, 229–236. [Google Scholar] [CrossRef] [PubMed]
- Seyrek, E.; Dubin, P.L.; Tribet, C.; Gamble, E.A. Ionic Strength Dependence of Protein-Polyelectrolyte Interactions. Biomacromolecules 2003, 4, 273–282. [Google Scholar] [CrossRef] [PubMed]
- Hileman, R.E.; Jennings, R.N.; Linhardt, R.J. Thermodynamic Analysis of the Heparin Interaction with a Basic Cyclic Peptide Using Isothermal Titration Calorimetry. Biochemistry 1998, 37, 15231–15237. [Google Scholar] [CrossRef] [PubMed]
- Pandav, G.; Ganesan, V. Computer Simulations of Dendrimer–Polyelectrolyte Complexes. J. Phys. Chem. B 2014, 118, 10297–10310. [Google Scholar] [CrossRef] [PubMed]
- Carrillo, J.-M.; Dobrynin, A. Salt Effect on Osmotic Pressure of Polyelectrolyte Solutions: Simulation Study. Polymers 2014, 6, 1897–1913. [Google Scholar] [CrossRef]
- Muthukumar, M. Theory of counter-ion condensation on flexible polyelectrolytes: Adsorption mechanism. J. Chem. Phys. 2004, 120, 9343–9350. [Google Scholar] [CrossRef] [PubMed]
| Generation | θ+ | M0 (g/mol) | DPn | DPw | Counter-Ion | dn/dC | Mw (g/mol) | PDI |
|---|---|---|---|---|---|---|---|---|
| G2 | 0.35 | 141 | 57 | 60 | Cl− | 0.1756 | 8400 | 1.05 |
| G3 | 0.65 | 152 | 136 | 137 | 0.1989 | 20723 | 1.01 | |
| G4 | 0.76 | 156 | 367 | 378 | 0.1749 | 58916 | 1.03 |
| f (%) a | θ− b | NNa+ c | Polycation | DPn d | θ+ e | I (M) | n(DGL/PAMAMPS) | <n> f | n(Lys/AMPS) | <n> g | Ncounter-ions h | Average% of Released Counter-Ions | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 30 | 0 | 0 | PLL50 | 50 | 0.5 | 0.327 | 35 | 35 | 1.60 | 1.56 | 887 | 258 ± 113 | 29 ± 3 |
| 0.37 | 32 | 1.42 | 792 | ||||||||||
| 0.458 | 37 | 1.56 | 916 | ||||||||||
| 0.49 | 37 | 1.66 | 919 | ||||||||||
| G2 | 57 | 0.35 | 0.22 | 29 | 28 | 1.35 | 1.31 | 584 | 215 ± 21 | 38 ± 4 | |||
| 0.25 | 29 | 1.36 | 587 | ||||||||||
| 0.33 | 27 | 1.24 | 537 | ||||||||||
| 0.44 | 28 | 1.3 | 560 | ||||||||||
| G3 | 136 | 0.65 | 0.41 | 17 | 17 | 1.93 | 1.96 | 102 | 108 ± 20 | 7 ± 2 | |||
| 0.48 | 20 | 2.45 | 1735 | ||||||||||
| 0.55 | 15 | 1.64 | 1290 | ||||||||||
| 0.62 | 16 | 1.82 | 1420 | ||||||||||
| G4 | 367 | 0.76 | 0.5 | 6 | 6 | 1.92 | 1.97 | 1653 | 43 ± 2 | 3 ± 0.2 | |||
| 0.58 | 7 | 2.12 | 1827 | ||||||||||
| 0.64 | 6 | 1.94 | 1673 | ||||||||||
| 0.75 | 6 | 1.89 | 1632 |
| f (%) a | θ− b | NNa+ c | Polycation | DPn d | θ+ e | I (M) | n(DGL/PAMAMPS) | <n> f | n(Lys/AMPS) | <n> g | N counter-ions h | Average% of Released Counter-Ions | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 100 | 0.67 | 2794 | PLL50 | 50 | 0.5 | 1.1 | 80 | 82 | 1.01 | 0.99 | 4801 | 876 ± 338 | 18 ± 2 |
| 1.2 | 81 | 0.97 | 4820 | ||||||||||
| 1.3 | 88 | 1.05 | 4988 | ||||||||||
| 1.4 | 80 | 0.96 | 4799 | ||||||||||
| G2 | 57 | 0.35 | 0.87 | 97 | 89 | 1.29 | 1.11 | 4722 | 372 ± 150 | 8 ± 3 | |||
| 1.02 | 94 | 1.12 | 4674 | ||||||||||
| 1.16 | 78 | 0.94 | 4342 | ||||||||||
| G3 | 136 | 0.65 | 1.42 | 41 | 39 | 1.23 | 1.18 | 6403 | 226 ± 36 | 4 ± 1 | |||
| 1.51 | 46 | 1.37 | 6827 | ||||||||||
| 1.6 | 34 | 1.07 | 5842 | ||||||||||
| 1.68 | 36 | 1.06 | 5940 | ||||||||||
| G4 | 367 | 0.76 | 1.69 | 23 | 20 | 1.96 | 1.75 | 9153 | 204 ± 37 | 2 ± 0.5 | |||
| 1.80 | 19 | 1.63 | 8071 | ||||||||||
| 1.91 | 19 | 1.65 | 8132 | ||||||||||
| 2.01 | 20 | 1.74 | 8440 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lounis, F.M.; Chamieh, J.; Leclercq, L.; Gonzalez, P.; Rossi, J.-C.; Cottet, H. Effect of Dendrigraft Generation on the Interaction between Anionic Polyelectrolytes and Dendrigraft Poly(l-Lysine). Polymers 2018, 10, 45. https://doi.org/10.3390/polym10010045
Lounis FM, Chamieh J, Leclercq L, Gonzalez P, Rossi J-C, Cottet H. Effect of Dendrigraft Generation on the Interaction between Anionic Polyelectrolytes and Dendrigraft Poly(l-Lysine). Polymers. 2018; 10(1):45. https://doi.org/10.3390/polym10010045
Chicago/Turabian StyleLounis, Feriel Meriem, Joseph Chamieh, Laurent Leclercq, Philippe Gonzalez, Jean-Christophe Rossi, and Hervé Cottet. 2018. "Effect of Dendrigraft Generation on the Interaction between Anionic Polyelectrolytes and Dendrigraft Poly(l-Lysine)" Polymers 10, no. 1: 45. https://doi.org/10.3390/polym10010045
APA StyleLounis, F. M., Chamieh, J., Leclercq, L., Gonzalez, P., Rossi, J.-C., & Cottet, H. (2018). Effect of Dendrigraft Generation on the Interaction between Anionic Polyelectrolytes and Dendrigraft Poly(l-Lysine). Polymers, 10(1), 45. https://doi.org/10.3390/polym10010045