2. Elliptic Curves and Discrete Logarithm Structures
An elliptic curve
over a number field
is a non-singular curve (i.e., with a unique tangent at every point) with points in
that are the solutions of a cubic equation. Therefore, elliptic curves can be thought of as the set of solutions in the field
of equations in the form [
47]:
where the coefficients
A and
B belong to
and satisfy the non-singular condition
for the discriminant
that excludes cusps or self-intersections (i.e., knots) [
47,
48]. Elliptic curves specified as in the equation above are said to be given in the Weierstrass normal form. When
coincides with the set of real numbers
, we can graph
and view its solutions
as actual points of a plane curve. An example is shown in
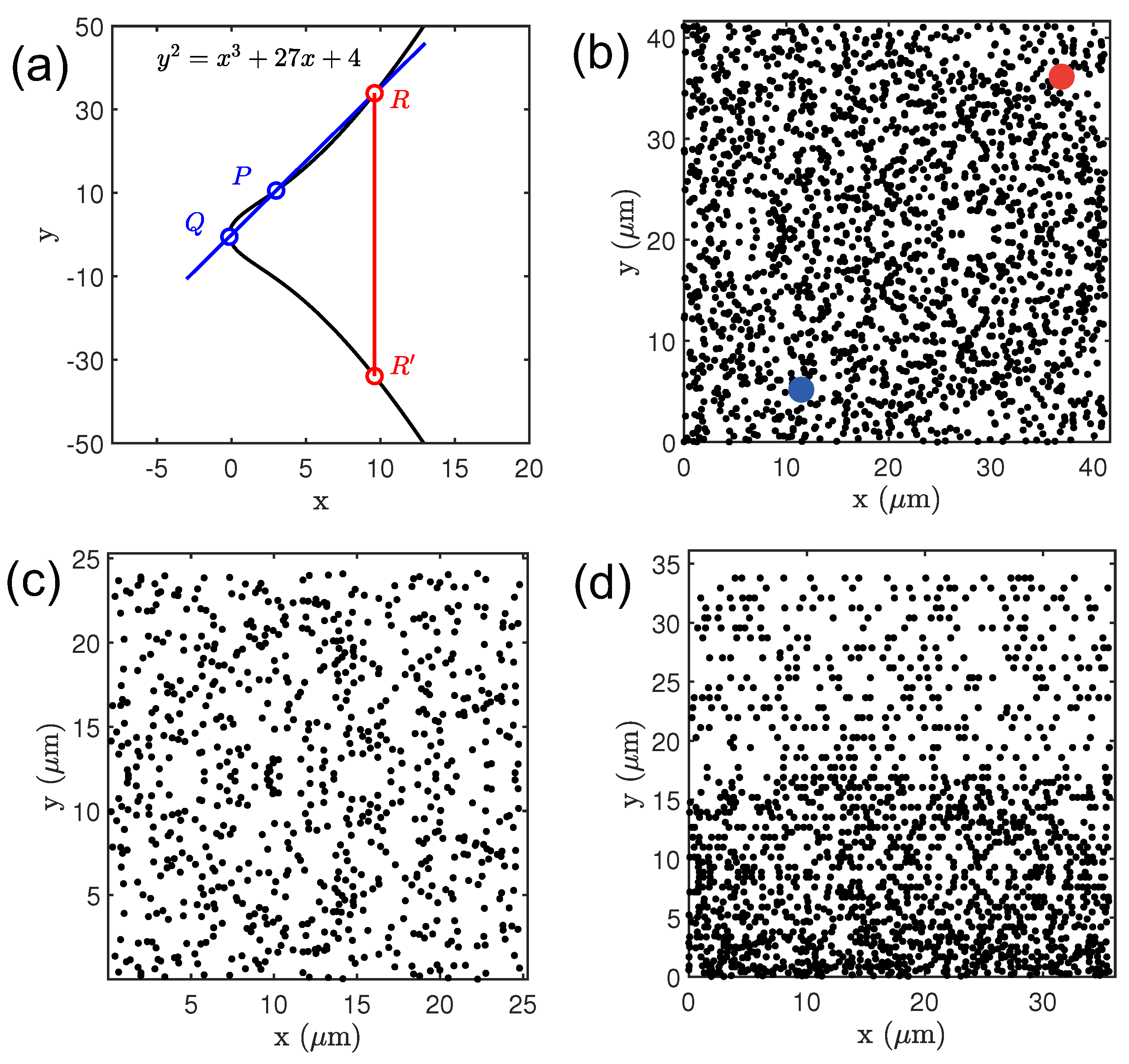
Figure 1a for a representative elliptic curve (
) over the real numbers defined by the parameters
and
. Clearly, different choices for the field
will result in different sets of solutions for the same cubic equation, since elliptic curves can also be regarded as particular examples of algebraic varieties. Algebraic varieties over the field of rational numbers
have been investigated already by post-classical Greek mathematicians, most notably by Diophantus, who lived around 270
in Alexandria, Egypt. In his honor, we refer to a polynomial equation in one or more variables whose solutions are sought among the integers or rational numbers as a ‘Diophantine equation’. The history of Diophantine equations and elliptic curves runs central to the development of the most advanced ideas of number theory that led to the proof of the celebrated Fermat’s last theorem by the British mathematician Andrew Wiles in 1995 [
49].
The study of elliptic curves constitutes a major area of current research in number theory with important applications to cryptography and integer factorization. Interestingly, when endowed with an extra point
at infinity, the points of elliptic curves acquire the structure of an Abelian group with the point
serving as the neutral group element. In particular, the group of rational points (solutions in
) of the elliptic curve
is finitely generated (Mordell’s theorem) and can be decomposed into the direct sum of
with finite cyclic groups [
47,
48]. More specifically, one can also show the group of rational points has the form:
where
T is a finite group consisting of torsion points (i.e., a point
satisfying
is called a point of order
m in the group
E. All points of finite order form an Abelian subgroup called the torsion group of
E) and
r is a non-negative number, called the algebraic rank of the elliptic curve
E, which somehow characterizes its size [
48,
50].
An example of the composition group law for the previously introduced elliptic curve over the real numbers is illustrated in
Figure 1a where two points with real-valued coordinates
P and
Q are summed to obtain the point
. The simplest way to introduce the group composition law is to implement the following geometrical construction [
47,
48]: we first draw the line that intersects
P and
Q. This line will generally intersect the cubic at a third point, called
R. We then define the addition
as the point
, i.e., the point opposite
R. It is possible to prove that this definition for addition works except in a few special cases related to the point at infinity and intersection multiplicity [
47,
48].
The type of elliptic curves that we will investigate in this paper are defined over the finite field
where
p is an odd prime number. This is the set of integers modulo
p, which is an algebraic field when
p is prime. An elliptic curve over
is still defined by Equation (
1) where the equal sign is replaced by the congruence operation:
where the coefficients
and the discriminant
in this case must be incongruent to 0 when reduced modulo the prime
p. Since
is a finite group with
p elements, the elliptic curve defined above has only a finite number of points which we expect to be approximately
in number (remember the necessity to add the extra point at infinity). It turns out that the actual number of points
of the curve
fluctuates from
within a bound
, which is a result proved in 1933 by Helmut Hesse. More precisely, if we define the quantity
Hesse’s theorem states that
[
47,
48]. One of the most challenging yet unsolved problems in mathematics, which is also a millennium prize problem of the Clay Mathematics Institute [
51], is the Birch and Swinnerton-Dyer conjecture (BSD) that identifies the algebraic and the analytic rank of an elliptic curve [
48,
52]. The analytic rank of a curve
E is equal to the order of vanishing of the associated Dirichlet
L-function
at
. The
L-function
mentioned above is a complex-valued function that is constructed based on the numbers
[
53]. This function, which is analogous to the Riemann zeta function
and the Dirichlet
L-series, can be analytically continued over the whole complex plane and it encodes information on the number of solutions of
E modulo a prime onto the properties of the associated complex function
. Moreover,
satisfies a Riemann-type functional equation connecting its values
and
for any
s. According to the Sato–Tate conjecture, the random looking fluctuations observed in the ‘error term’
when the prime
p is varied are captured by a ‘sine-squared’ probability distribution. This conjecture has been proved in 2008 by Richard Taylor limited to particular types of elliptic curves [
54].
In
Figure 1b we show the elliptic curve over
with
that has the same parameters as the curve
previously shown in
Figure 1a. We note that the curve has been rescaled by a constant parameter so that the average separation between points equals 450 nm, which enables resonant scattering responses across the visible spectrum. Apart from this irrelevant scaling, the points on this curve appear to be randomly distributed in stark contrast with its counterpart defined over the field of real numbers. Moreover, working with
over finite fields allows one to define the associated discrete logarithm problem that plays an essential role in elliptic curves cryptography due to its non-polynomial complexity [
47,
50]. Let
be an elliptic curve over
(see
Figure 1b) and
M (blue circle marker) and
W (red circle marker) two points on the curve. The discrete logarithm problem is the problem of finding an integer
k such that
. By fixing a starting point
W and applying this group operation repeatedly to all the points
M on the curve
E in
Figure 1b, we can obtain the point patterns shown in
Figure 1c,d, which are the physical representations of the abstract discrete logarithm problem on the original curve
E. Specifically,
Figure 1c,d display curves characterized by the coordinates
and
rescaled in order to have an average interparticle separtion equal to 450 nm, respectively. These types of aperiodic deterministic structures are referred to as the elliptic curve discrete logarithm (
). Clearly, the distribution of points in
strongly depends on the choice of the initial point
W on the starting
. In our work we have uniformly sampled 9 starting points on
E. We have found that the resulting
curves can be divided into two main categories:
point patterns that are symmetric with respect to the
x-axis (
Figure 1c) and others that do not show this structural symmetry and are generally less homogeneous (
Figure 1d). Moreover, the number of elements
cannot be controlled exactly because it depends on the value of the integer
k. The complexity of the discrete logarithm problem for elliptic curves over finite fields is at the heart elliptic-curve cryptography (ECC), which is the most advanced approach to public-key cryptography that protects highly secure communications (up to to-secret classification) using key that are significantly smaller compared to alternative methods such as RSA-based cryptosystems [
47,
50]. In what follow we will apply the statistical methods of point pattern analysis and the theory of multiple light scattering in order to investigate the structural, spectral, and scattering properties of these number-theoretic structures regarded as aperiodic photonic systems of scattering point-particles.
3. Structural and Spectral Properties of Elliptic Curves and Discrete Logarithm Arrays
In order to obtain quantitative information on the degree of local structural order of
and
point patterns, we have computed their radial distribution functions
, which give the probability of finding two particles separated by a distance
r [
55]. In
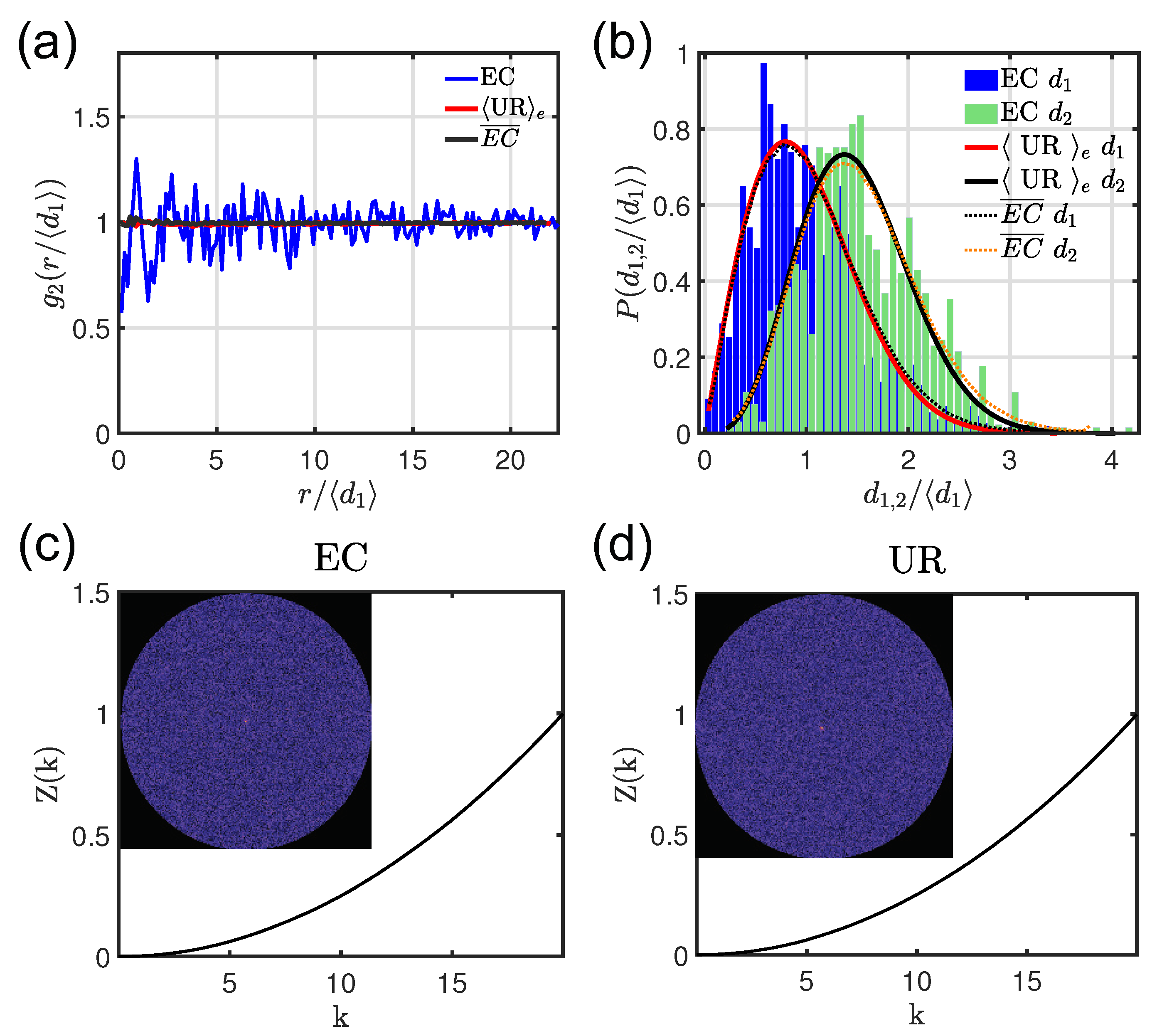
Figure 2a we display the
of the representative
point pattern shown in
Figure 1b (blue line) and we compare it with the disorder-averaged
of a uniform random (
) structure considering 200 realizations of disorder (red line). In order to systematically analyze the correlation properties of
structures, we have considered 900 different elliptic curves generated by a uniform sample of the integer parameters
A and
B in the range (1, 30). The arithmetic average value of the
for all the investigated
structures is shown by the black line in
Figure 2a. This quantity clearly demonstrates the uncorrelated nature of
structures akin to the average behavior of Poisson random point patterns. To gain more information on the peculiar geometrical arrangements of the points compared to
systems we studied the probability density functions of the first (
) and second (
) neighbor distances [
25,
55]. The results of this analysis are presented in panel
Figure 2b. The
and
functions can be analytically approximated using the following expression:
where
is probability density function for the
k-neighbor particle spacing of homogeneous Poisson point patterns with intensity
evaluated as
. Here
N is the number of points in the array, which varies between 1926 and 2106, and
R is the maximum radial coordinate of the system [
31,
55]. We notice that while the
and
distributions for a single
array fluctuate significantly, their average over the 900 investigated
structures with different
A and
B parameters can be precisely fitted using the analytical expression in Equation (
3).
Aperiodic deterministic structures are complex structures with varying degrees of order and spatial correlations ranging from quasicrystals to more disordered amorphous structures with diffuse spectra [
25,
56,
57]. In order to characterize the structural order of
point patterns, we have analyzed their spatial Fourier spectra by evaluating the static structure factor as
Interestingly, the inset of
Figure 2c shows that
aperiodic structures are characterized by diffuse diffraction spectra that are typically associated to homogenuous and isotropically disordered media (see the inset of
Figure 2d). In order to get more information on the nature of these spectra, we have analyzed the behavior of the integrated intensity function defined as [
22]:
For two-dimensional (2D) arrays, this function characterizes the distribution of the diffracted intensity peaks contained within a square region, centered at the origin, with a maximum size of
in the reciprocal space [
43]. Interestingly, Equation (
5) has also been recently used as a tool to quantitatively characterize the type of hyperuniformity of quasicrystalline point sets generated by projection method by studying its scaling behavior as
k tends to zero [
58,
59]. We recall that any diffraction intensity pattern can be regarded as a spectral measure
that, thanks to the well-known Lebesgue’s decomposition theorem [
56,
57,
60], can be uniquely decomposed in term of three kinds of primitive spectral components, or a mixture of them. Specifically, any diffraction spectra measure can be expressed as
, where
,
and
refer to the pure-point, singular continuous, and absolutely continuous spectral components, respectively [
22,
23,
56]. In particular, in both periodic and quasiperiodic structures there are regions where
is constant due to the pure point nature of the spectrum. Therefore, over spectral gap regions
remains constant and presents jump discontinuities every time an isolated Bragg peak is integrated over. On the contrary, for structures with absolutely continuous Fourier spectra the integrated intensity function is continuous and differentiable. Finally, in the case of structures with singular-continuous spectra like the ones generated by the distribution of the prime number on complex quadratic fields and quaternion rings [
43], the Bragg peaks are no longer well-separated but clustered into a hierarchy of self-similar contributions giving rise to a weak continuous component in the spectrum that smoothly increases the value of
in between consecutive plateaus. In
Figure 2c,d we report the calculated
for
and
configurations, respectively. The results did not show any appreciable difference compared to
systems, indicating that elliptic curves are structures characterized by an absolutely continuous diffraction spectral measure.
We now investigate the scattering spectra and wave localization properties of the elliptic curves defined over the finite field
by using the Green’s matrix method. This formalism allows for a full description of open three-dimensional (3D) scattering resonances of large-scale structures at a relatively low computational cost if compared to traditional numerical methods such as finite difference time domain (FDTD) or finite element method (FEM) techniques [
25,
31,
61]. Moreover, this approach provides access to all the scattering resonances of a system composed of vector electric dipoles in vacuum and accounts for all the multiple scattering orders. The point-scatterer assumption implies that the scatterer size must be much smaller than the wavelength. Specifically, in this limit each scatterer is described by a Breit–Wigner resonance at frequency
and width
(
). The scattering resonances or quasi-modes of an array can be identified with the eigenvectors of the Green’s matrix
which, for
N vector dipoles, is a
matrix with components [
20]:
has the form:
when
and 0 for
, and where
is the wavevector of light, the integer indexes
refer to different particles,
is the 3 × 3 identity matrix,
is the unit vector position from the
i-th and
j-th scatter while
identifies its magnitude. This method is an excellent tool to study light scattered by atomic clouds but also provides fundamental insights into the physics of periodic, aperiodic, and uniform random systems of small and sufficiently well-separated scattering particles [
4,
20,
21,
25,
31,
43,
61,
62,
63,
64,
65,
66,
67,
68]. The Green’s matrix (
6) is a non-Hermitian matrix. As a consequence, it has complex eigenvalues
(
) with
and
[
20,
65,
66,
67,
68]. Moreover, it is important to realize that the Green’s matrix method is an eigenvalue method that captures the fundamental physics of multiple scattering of vector waves for any assembly of electric scattering point dipoles. In addition, this powerful method enables a clear separation between the geometry of the scattering arrays (the arrangement of the dipoles) and the material properties and sizes of the individual particles that are captured by a retarded polarizability or by the refractive index. As a result, the predictions of the Green’s approach should be considered “universal” in the limit of electric dipole scatterers, meaning that the size and the refractive index of the particles can be taken into account after the diagonalization of the Green’s matrix by extracting the frequency
and
from the central position and the lineshape of the scattering cross section (computed using for example the Mie–Lorentz theory in the dipole limit) of a single particle.
We have applied this formalism to both
and
arrays and studied the light scattering properties in the plane of these arrays by analyzing the behavior of their scattering resonances embedded in 3D. In order to do that, we have diagonalized numerically the
Green’s matrix (
7). The distribution of the resonant complex poles
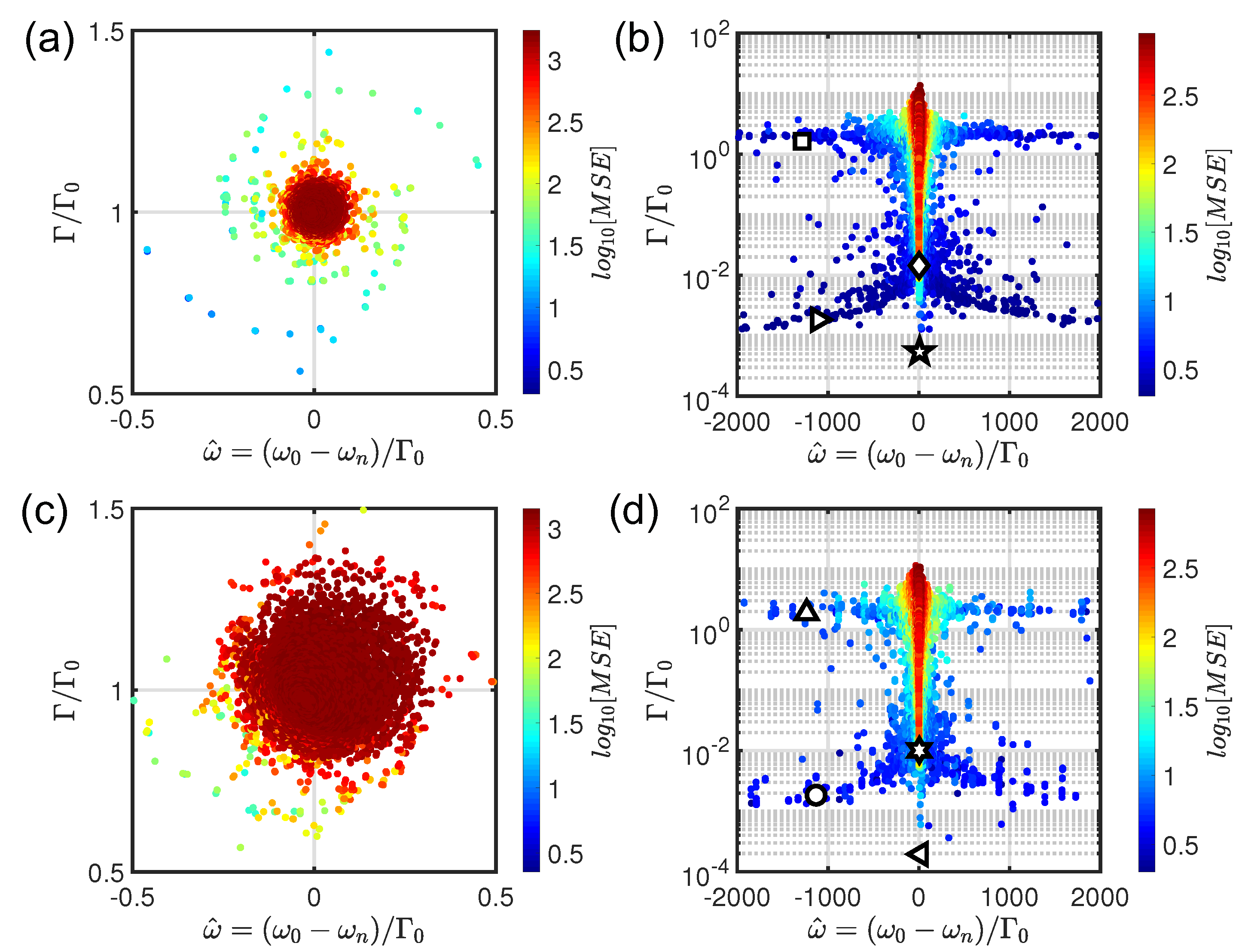
, color coded according to the
values of the modal spatial extent (MSE), is reported in
Figure 3a,b for the
and in
Figure 3c,d for the representative
configuration shown in
Figure 1b, respectively. Specifically, panels (a,c) and panels (b,d) refer to low and high optical density
, respectively. Here
is the number of particles per unit area while
is the optical wavelength and
is a measure of the scattering strength of the systems. Instead, the MSE parameter characterizes the spatial extent of a photonic mode [
69]. It is important to emphasize that the dimensionality of the studied electromagnetic problem is 3D, but the electromagnetic field of a scattering resonance is not only spatially confined in the plane of the array but it also leaks out from such a plane with a characteristic time proportional to its quality factor [
31].
At low optical density (
), the distribution of the complex poles of
electric point dipoles randomly located inside a circular region is highly uniform and is characterized by a circular shape with distinctive spiral arms that are weakened when the electric dipoles are arranged in
geometries (see
Figure 3c). These spectral regions are typically populated by scattering resonances localized over small clusters of scatterers, down to only two particles [
21,
67]. The subradiant dark states, also called proximity resonances, are characterized by MSE = 2 [
67,
70] (see also
Figure 4a,b). Interestingly, the absence of these scattering resonances in a class of aperiodic spirals, called Vogel spirals, was recently connected to the ability of these structures to localize vector waves thanks to their peculiar correlation properties [
31].
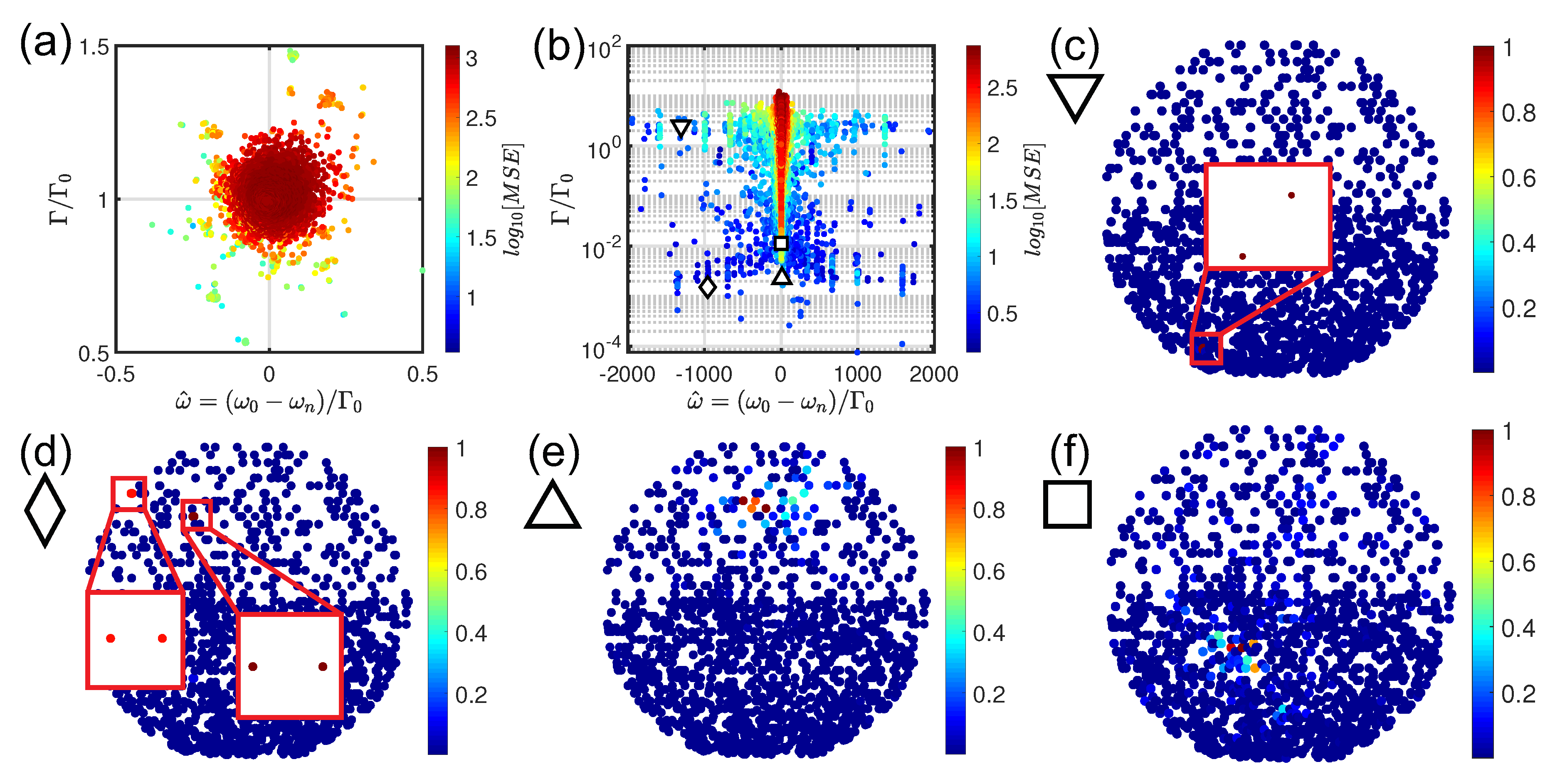
In order to understand the nature of the scattering resonances that characterize EC-based structures in the strong scattering regime (
), we have analyzed the spatial distributions of a few representative optical modes identified by the symbols shown in
Figure 3b,d.
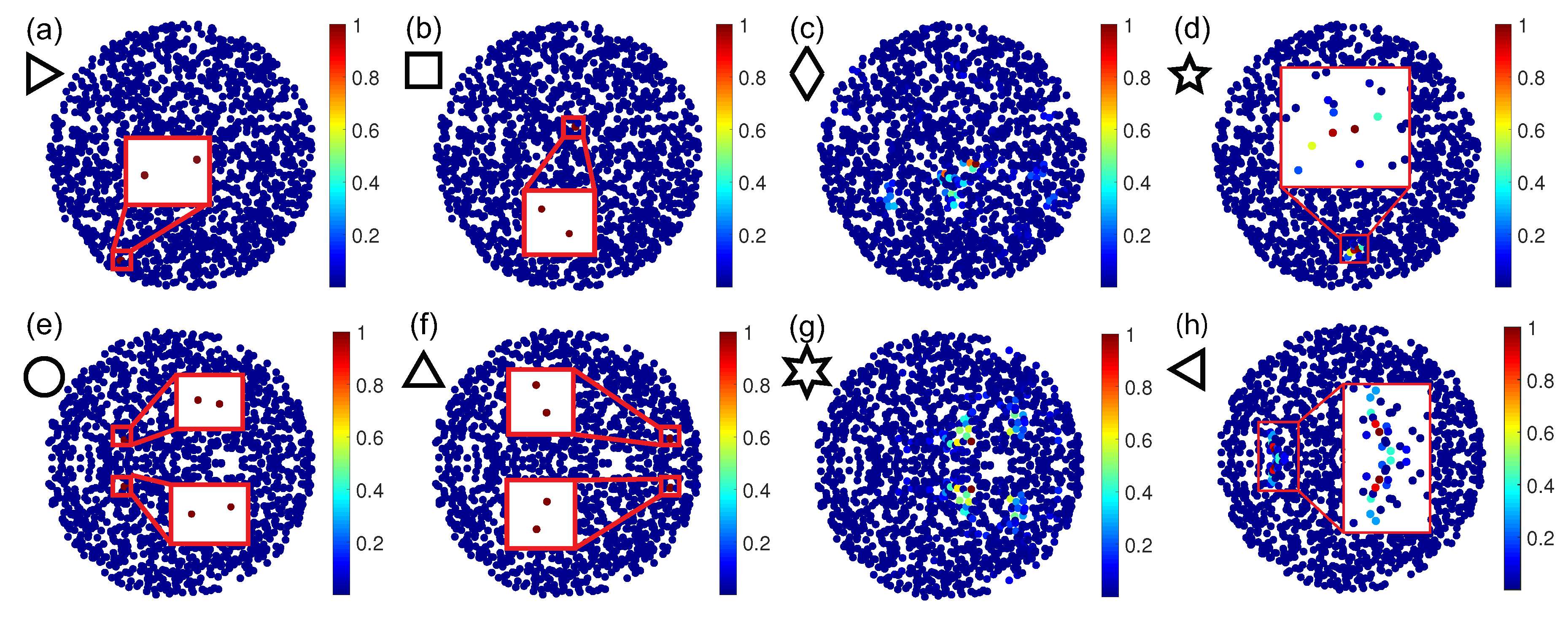
Figure 4 shows a survey of representative spatial distribution of the Green’s eigenvectors for
(panels (a–d)) and
geometries (panels (e–h)), respectively. From the complex eigenvalues distribution and from the selected spatial field profiles, we can clearly distinguish among three different types of scattering resonances. Let us start by analyzing the
configuration. The first type of scattering resonances correspond to short-lived quasi-modes (
) that are delocalized across the all arrays (
). Moreover, this spectral region is also populated by proximity resonances, as shown in
Figure 4b. This is a clear signature of the fact that proximity resonances are not related to interference-driven light localization because they do not require multiple scattering in order to occur [
25,
31,
67,
70]. Finally, there are resonances that populate the dispersion branch around
with
. These quasi-modes are long-lived resonances with
in the range
extended over almost all the particles (see
Figure 4c) or clustered over few particles near the array boundaries (see also the discussion of Figure 6a for more details). However, even if the main characteristics of the complex eigenvalues distribution of
structures is very similar to the
ones, a deeper analysis unveils important differences. First of all, strictly speaking
structures do not show traditional proximity resonances but clustered quasi-modes (
) associated to the structural mirror symmetry along the
x-axis, as shown in
Figure 4e,f. Another important difference arises when looking at the dispersion branch around
. Indeed, the
-based arrays feature longer-lived and clustered resonances (
with
12) compared to standard
structures, see
Figure 4h. These more extended, long-lived resonances are similar to the critical scattering resonances that are typical of fractal and multifractal systems. These optical modes characterized by a power-law envelope localization and multifractal field intensity oscillations [
25,
26,
33,
39,
43,
71].
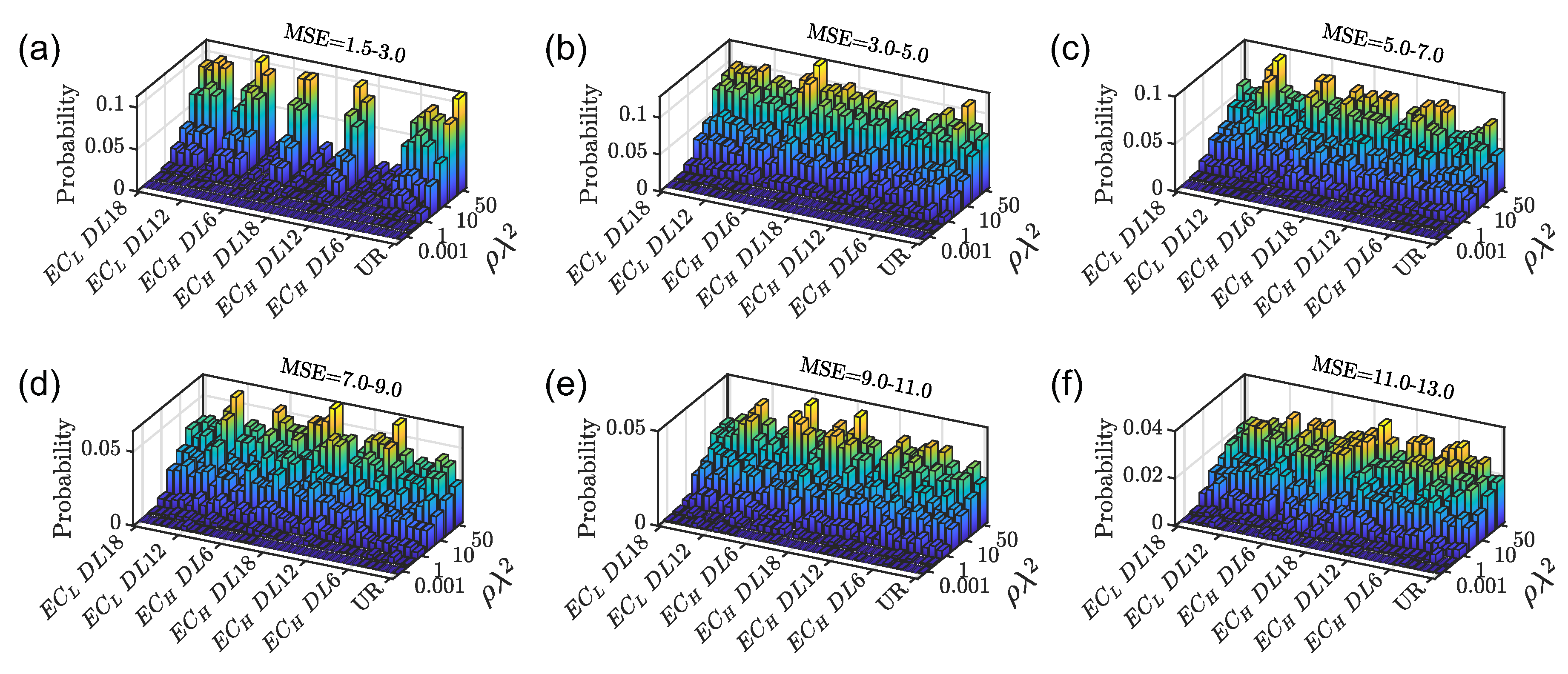
To gain additional insights on the nature of the scattering resonances of
-based arrays compared to
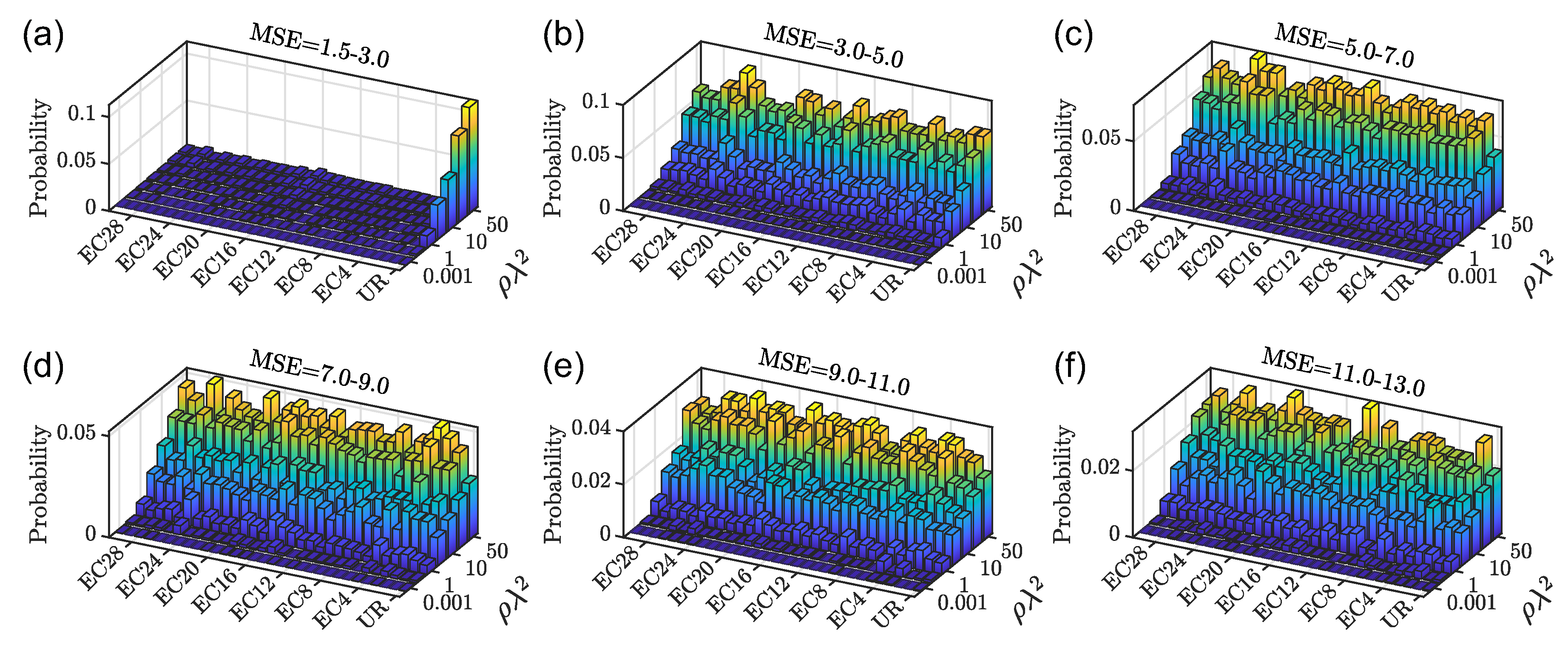
systems, we have evaluated the proportion of modes that extend over a number of particles specified by the range of the MSE values considered. In particular, we computed the probability of the number of scattering resonances in different MSE ranges and at different optical densities.
Figure 5 shows the results of this study. First of all,
Figure 5a indicates that for
point patterns the probability of obtaining resonances localized over at most three scatterers is negligible compared to UR structures, shown in the first column of
Figure 5. This is regardless of the value of the optical density. In contrast, proximity resonances do appear in UR systems even at low optical density (
). By increasing the
threshold, the probability of finding scattering resonances localized over large clusters of particles is always larger for the analyzed
configurations compared to the UR reference structures. Therefore, our analysis provides evidence that, differently from the case of uniform random systems, the mechanism of localization in EC-based structures proceeds through wave tunneling and trapping over few-particle clusters via the formation of Efimov-like resonances [
72].
In order to analyze the light localization behavior, we have evaluated the modal average lifetime [
31,
62,
63], the Thouless conductance
g, also called Thouless number [
73,
74,
75], and the level spacing distribution [
76,
77]. The average modal lifetime, defined as
, provides the mean-time that light spends inside a medium [
31,
62,
63].
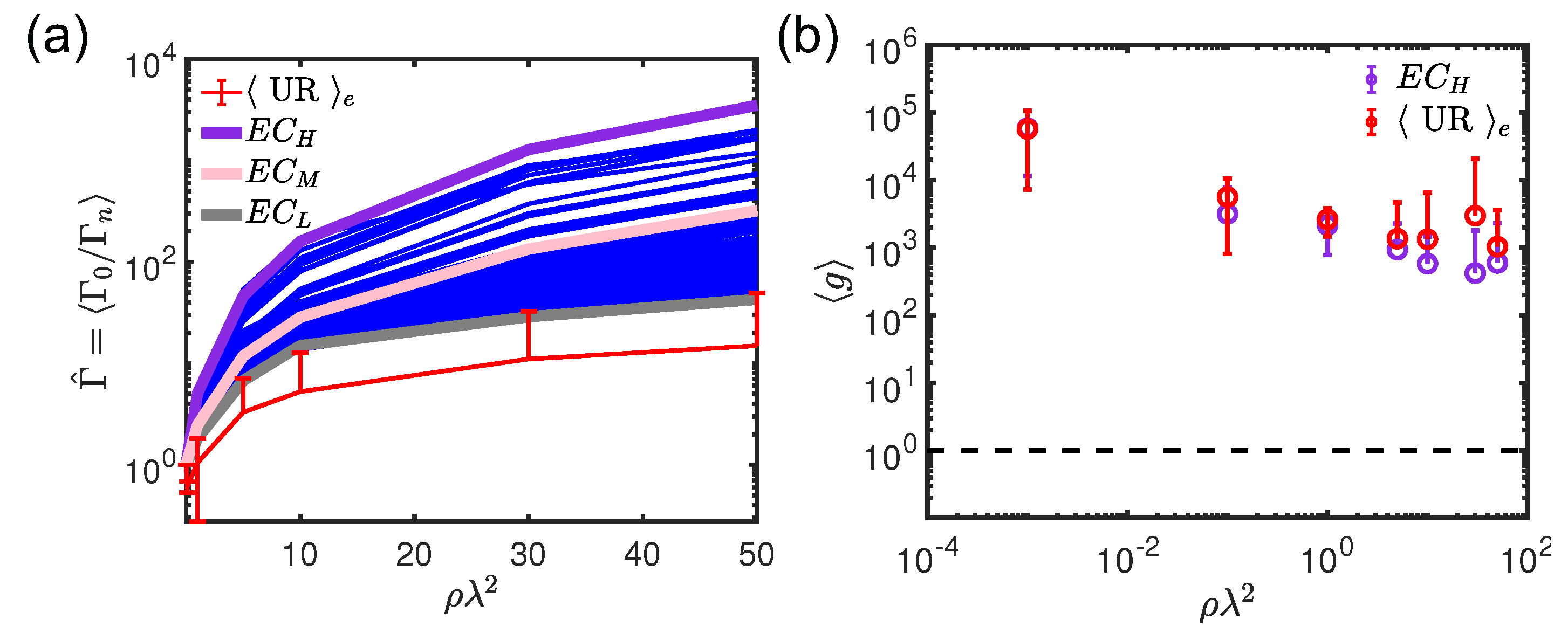
Figure 6a compares the averaged modal lifetime of the 900 different elliptic curves over
with respect to the value of
produced by 10 different realizations of
structures. Interestingly, all the
structures show a larger average modal lifetime for all the analyzed
values demonstrating enhanced light-matter interaction compared to random uniform random systems. The ability to confine and eventually localized light is also described by the Thouless conductance, which is a parameter that characterizes the degree of spectral overlap between different optical scattering resonances. In order to demonstrate light localization, the Thouless conductance, which is proportional to the scattering mean free path, must decrease below the value 1 when increasing the scattering strength, i.e., increasing the optical density
. Within the Green’s matrix formalism, it is defined as the ratio of the dimensionless lifetime
to the spacing of nearest dimensionless resonance frequencies
[
20]:
where
indicates the average of
g over a frequency interval of width 2
centered in
. This frequency stripe selection is necessary due to the strong frequency dependence of the light localization behavior [
31]. On the other hand, averaging over all scattering frequencies will produce biased results due to the mixing of different types of light regimes [
75]. Differently from the uniform random media, we do not need to consider any ensemble averages because the
structures are deterministic.
Figure 6b compares the semilog plot of the Thouless conductance, as a function of
, obtained by using Equation (
8) after diagonalizing the
Green’s matrix of the
structure with the highest
(violet line in
Figure 6a) with respect to the uniform random scenario. Even though
structures are characterized by longer-lived critical resonances than
systems, the
parameter clearly indicates that the light localization transition is never achieved, since
is always larger than 1. This is due to two factors: the presence of degenerate proximity resonances (like the ones shown in
Figure 4e,f) and the absence of any structural correlations. The absence of structural correlations was recently identified as the factor preventing light localization to occur in uniform random arrays when the vector nature of light is taken into account [
20,
31,
66].
In order to further investigate the spectral properties of
arrays we considered the distribution of level spacing
that provides important information about the electromagnetic propagation for both closed- and open-scattering systems [
25]. Indeed, the shape of
depends on the spatial extent of the system eigenmodes. In particular, for open weakly disordered random media the probability density function of spacings between nearest eigenvalues
and
is described by:
where
is the normalized eigenvalue spacing [
66,
76,
77]. The important feature of this equation is the so-called level-repulsion phenomenon:
when
. The level repulsion is a characteristic of extended/delocalized scattering resonances that repel each other in the complex plane [
25,
66]. On the contrary, the appearance of localized states leads to a suppression of the eigenvalue repulsion because two spatially localized states hardly influence each other when strongly localized in different parts of the medium. Consequently, distinct modes with infinitely close energies are allowed and the distribution of level spacings is described in this more localized regime by the Poisson distribution:
Notably, the level spacing statistics is very well described by Equation (
10) in the strong scattering regime for closed as well as for open (dissipative) systems [
25,
76].
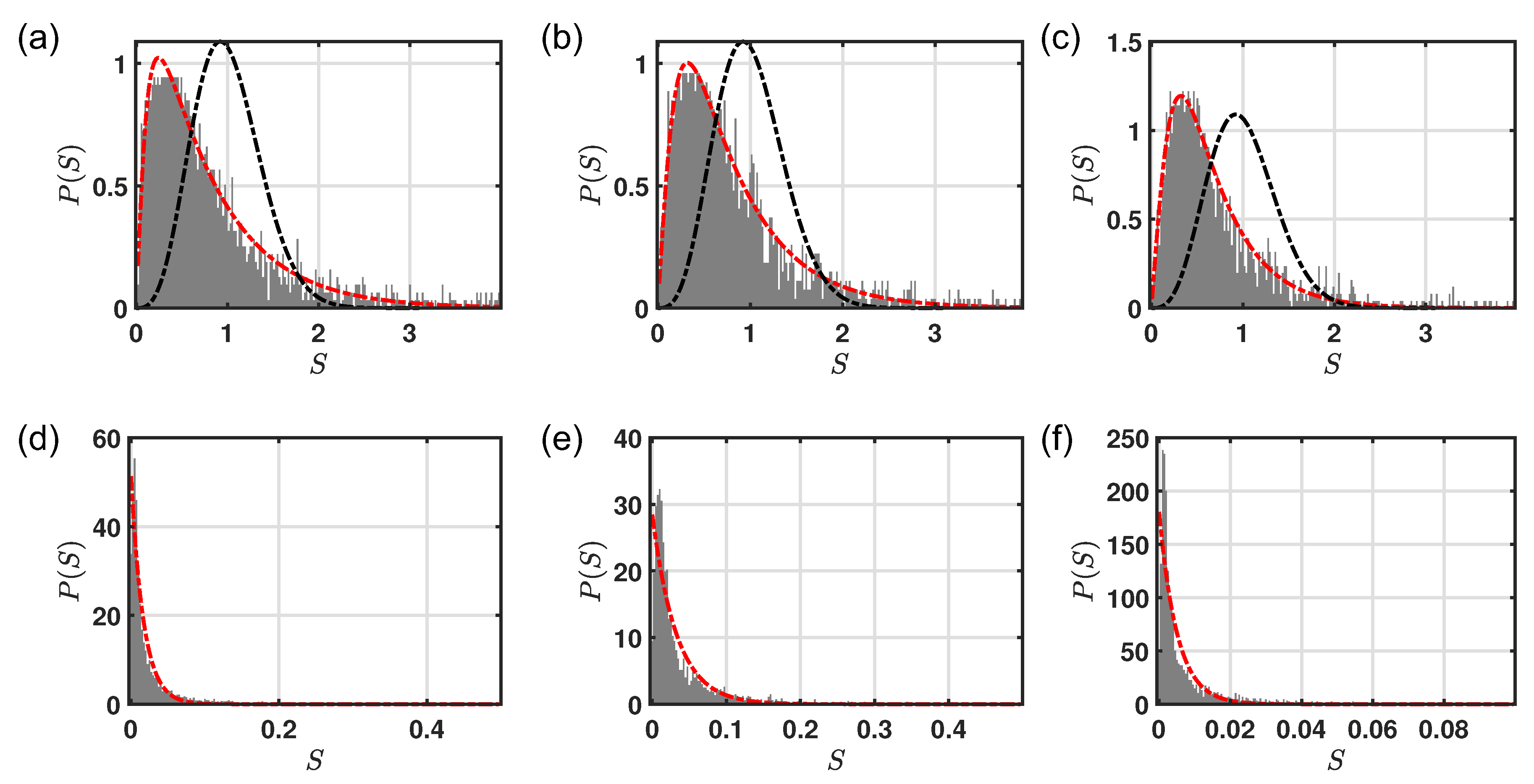
However, the level statistics of deterministic aperiodic systems displays different features with respect to the uniform random scenario. In our previous works, we have investigated the transition from the presence to the absence of level repulsion by increasing
in different open, deterministic, and aperiodic planar systems [
25,
31,
43]. We have found that the distribution obeys at
< 1 the critical cumulative probability density:
where
and
are fitting parameters. This is attributed to the formation of a large number of critical scattering resonances. Indeed, Equation (
11) was successfully applied to describe the energy level spacing distribution of an Anderson Hamiltonian containing
lattice sites at the critical disorder value, i.e., at the metal–insulator threshold where it is known that all the wave functions exhibit multifractal scaling properties [
46]. We remark that the presence of a critical statistics in the spectral behavior of
structures occurs over a broad range of optical densities compared to the case of random media in which criticality is achieved only at the threshold density
[
25,
31,
43].
The results shown in
Figure 7 demonstrate that the critical behavior is a generic attribute of all the investigated
structures. Indeed, panels (a,d), (b,e), (c,f) show a transition from the presence to the absence of level repulsion by increasing
for the
,
, and
point patterns, defined in
Figure 6a, respectively. At low optical density (panels (a–c)), the
of the
point patterns and
configurations are well described by, respectively, Equation (
11) (dotted dashed red lines) and Equation (
9) (dotted dashed black lines). On the other hand,
follows the Poisson distribution (
10) for both
and
configurations for high optical density (
). Since the presence of a critical statistics is associated to the multifractal nature of the spectrum, the criticality discovered in
structures opens intriguing opportunities to engineer wave transport in these novel aperiodic systems [
11,
29].
We now address the structural and spectral properties of aperiodic point patterns obtained by the solution of the discrete logarithm problem, as discussed in
Section 2.
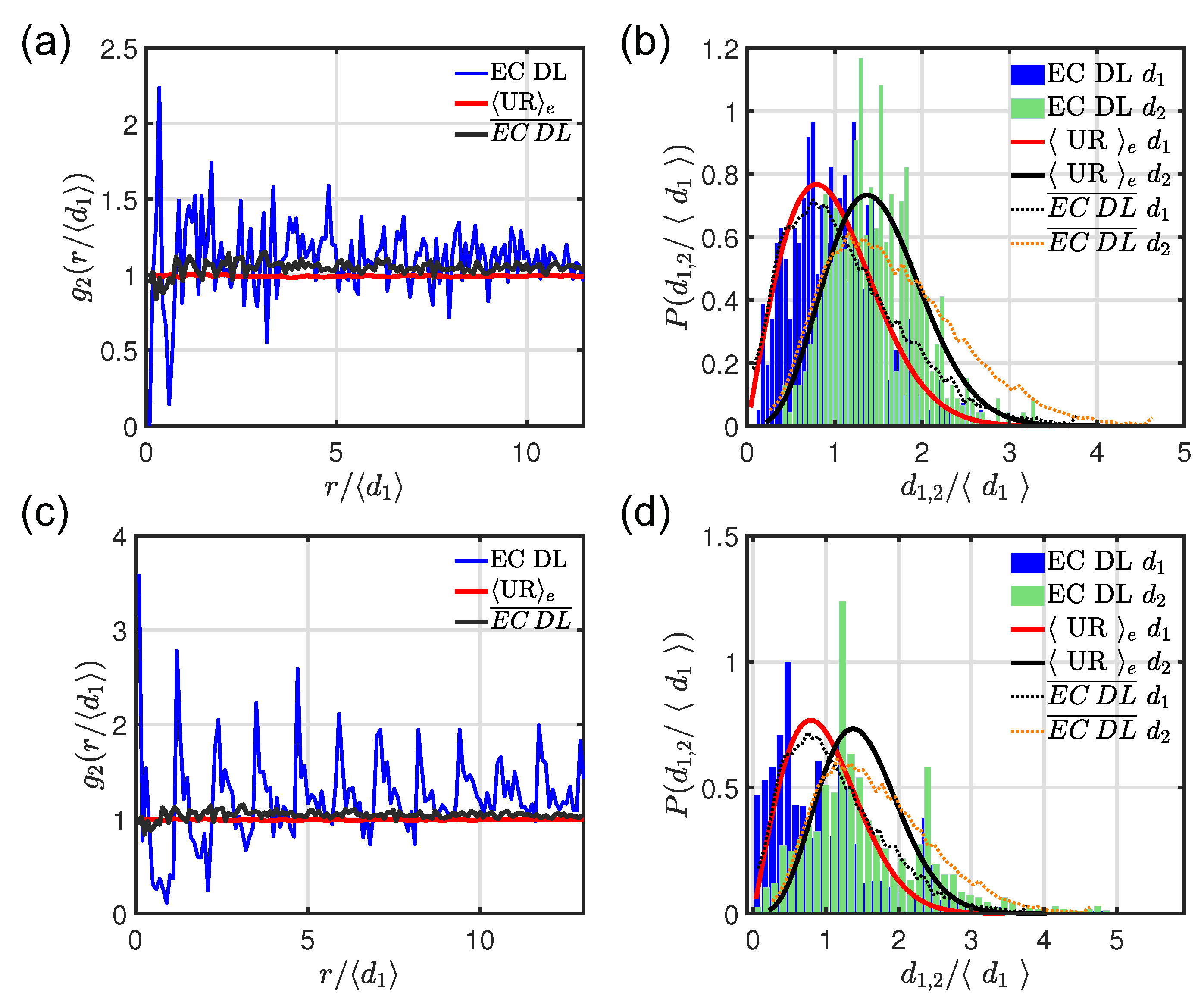
Figure 8 displays the main results of the structural analysis, based on the radial distribution function and on the first and second neighbor distributions.
structures, generated by the coordinate
, show higher degree of structural correlations than the
that are symmetric with respect to the
x-axis, i.e., produced by the pairs
. However, after averaging over 72 different
arrays generated by randomly selecting the starting point
W from the
and
point patterns (the elliptic curve configurations that show the highest and lowest modal lifetime, as reported in
Figure 6a), the
becomes constant and very close to 1 in value, indicating absence of any structural correlations (see the black lines in
Figure 8a,c). Moreover, also the averaged first (black dash dotted lines in
Figure 8b,d) and second (orange dash dotted lines in
Figure 8b,d) neighbor distributions are very similar to the analytical expression of Equation (
3) valid for homogeneous Poisson point processes [
55]. Therefore, we have found that on average also the
structures are spatially uncorrelated point patterns (incidentally, this property explains why the discrete logarithm problem on elliptic curve is a very hard problem). This behavior is also confirmed by analyzing their spectral properties via the diagonalization of the matrix (
7). Indeed, the results of
Figure 9 are very similar to the ones reported in
Figure 3 for the EC structures. Specifically, the complex eigenvalues distribution of
point patterns at low optical density (
) shows the same characteristics of elliptic curves: a circular disk region as for the
structures but without the distinctive spiral arms populated by the proximity resonances (see
Figure 9a). Instead, the distribution of the complex scattering poles at large optical density shows similar features in both
and
arrays. In particular, both proximity and clustered quasi-modes, with
, are present. Proximity resonances populate mostly the spectral region with
, while these clustered optical modes characterize the sub-radiant spiral arms (see
Figure 9c,d). Moreover, the dispersion branch around
is characterized by both scattering resonances clustered on few particles near the array boundaries, similar to the
scenario, and by critical quasi-modes, as shown in
Figure 9e,f, respectively. Indeed, a clear spectral region characterized by longer-lived modes with large value of
is clearly visible is
Figure 9b when
and
.
In order to understand how critical quasi-modes influence the light-matter interaction properties of
geometry, we have also evaluated their probability density function by selecting different
ranges. We discovered that the probability of finding scattering resonances localized over a clusters of scatterers is always larger than in the
scenario (see
Figure 10). Of particular interest is the situation depicted in
Figure 10a where the
range is fixed between 1.5 and 3, i.e., the resonances are localized over at most 3 particles. Whereas
point patterns are always characterized by the absence of proximity resonances,
structures instead show the presence of long-lived, strongly localized sub-radiant states even for the lowest
range considered. Specifically, we observed that proximity resonances are always present in the type of
point patterns that lack reflection symmetry, discussed in
Section 2. Moreover, the modal average lifetime (
Figure 11a), the Thouless conductance (
Figure 11b), and the level spacing statistics (
Figure 12) clearly demonstrate the role played by the critical scattering resonances also for the case of
structures. However, we found that the average modal lifetime of 36
aperiodic structures is always larger than the
scenario. Moreover, the Thouless conductance of the
and
structures with the largest
(orange and violet line in
Figure 6a and
Figure 11a, respectively) are comparable and both larger than what can be achieved in
systems, demonstrating the potential to obtain stronger light-matter interaction in these novel aperiodic arrays.
4. Light Scattering Properties and the Extended Green’s Matrix Method
As discussed in the previous section, the Green’s matrix spectral method is an excellent approximation to study light scattering by atomic clouds and can give fundamental insights into the physics of multiple scattered light by small particles within the dipole approximation. However, this method is an oversimplification in the case of realistic scatterers that are, instead, characterized by higher-order multipolar resonances. The number of these peaks depends by the scatterer material and by the size parameter
x defined as
, where
k is the wavelength number, while
R is the scatterer radius. Specifically, light scattering by a homogeneous, isotropic and spherical particle with radius
R illuminated by a linearly polarized plane wave traveling in the z-direction
can be calculated by using the Mie–Lorentz theory [
78]. If the size of scatterers in an array is smaller than the incident wavelength and they are far enough from each others, the light scattering problem can be described by using only the dipolar term in the general multipolar expansion [
79]. However, the interplay between the electric and magnetic dipolar responses of small particles is a key ingredient in determining their directional scattering features. Therefore, in order to obtain a more realistic description of light scattering from these complex arrays we must go beyond the simple electric dipole framework. For this reason, we provide an extension of the Green’s matrix method that takes into account both the first-order Mie–Lorentz coefficients, referred to as the electric and magnetic coupled dipole approximation (EMCDA) [
78,
80]. In this approximation, each particle is characterized by two dipoles (electric dipole (ED) and magnetic dipole (MD)) corresponding to the induced electric and a magnetic polarizability [
81].
In order to derive rigorously the EMCDA approximation, we must start from the electric
and magnetic fields
at a distance
r and direction
produced by an electric dipole
. In the
cgs unit system, we have [
82]:
Equivalently, the field
and
produced by a magnetic dipole
are give by [
82]
By introducing the coefficients
a,
b, and
d defined as [
78,
80]
We can rewrite Equations (
12) and (
13) in a shorter notation:
As a first step, our goal is to evaluate the total electric and magnetic fields at the
ith particle (
and
) resulting from the electric and magnetic dipole moments of the
jth particle. Explicitly, we can write, by using Equation (
17),
and
as:
where the electric and magnetic dipole moments at the
jth particle position are defined as
and
, respectively [
83]. The electric and magnetic polarizabilities
and
(that have units of a volume) are related to the first order Mie–Lorentz coefficients
and
as [
81,
84]:
Here,
is the wavenumber of the background medium, while
and
are derived from the equation
where
R is the radius of the spherical scatterer, and
n is the relative refractive index of the nanosphere with respect to the background medium.
and
are the Riccati–Bessel functions constructed from spherical Bessel functions via
and
. In addition,
is the spherical Bessel function of the first type, and
is the spherical Hankel function of the first type. By substituting the dipole moments expressions into Equation (
18), we finally obtain the total electric and magnetic fields at the
i-th particle in the form:
To solve these coupled equations, it is convenient to express the various vector products in Equations (
21) and (
22) as matrix products [
78,
83]. In detail, by introducing the
matrices
and
, defined as:
where
(
and
z) are the components of the direction vector from the
jth to the
ith particle, we can re-write Equations (
21) and (
22) in the compact form:
where
and
are 3×3 diagonal matrices containing the polarizability
and
defined by Equation (
19) in the case of isotropic materials.
Equation (
25) defines the dyadic Green’s matrix
that connects the electromagnetic field of the
i-th-particle with the electromagnetic field of the
j-th-particle. Specifically,
is obtained as:
The dyadic symbol
is used to stress the fact that we are taking into account all the field components. Therefore,
is a
matrix. Moreover, one of the advantages of using cgs system unit is that the symmetry relations between electric and magnetic quantities are preserved, i.e.,
=
and
=
[
83].
The generalization of the formalism for N scatterers is straightforward. Equations (
21) and (
22) can be assembled using the a Foldy–Lax scheme such that the local fields at the position of the
ith scatterer
and
are the sum of the scattered term of all the other particles plus the incident field (
;
) on the
ith particle
These last two equations can be rewritten as:
where
is the vector containing the electric
and magnetic field
, while
is a linear integral operator describing the interactions between the scatterers. To solve Equation (
29), successive approximations must be used. The first step is characterized by the Rayleigh–Gans–Debye (RGD) approximation [
78,
81]. Within this approximation,
is equal to
. In this way, we can compute the first-order estimation for every particles. After that, the iterative scheme is obtained by inserting the
j-th interaction of the fields
into the right side of Equation (
29) and evaluating the next interaction in the left side. The solution of Equation (
29) is, therefore,
which is a direct implementation of the well-know Neumann series
where
is the unitary operator. A necessary and sufficient condition for the convergence of the Neumann-series is
. From a physical point of view, this iterative self consistent method lies in successive calculations of interactions between different scatterers. Therefore, the zero order level accounts for no interactions, the first approximation takes into account the influence of the scattering of each dipole on the others once, and so on.
It is very instructive to write down the compact matrix form of Equations (
27) and (
28) because it defines the full Green’s matrix
. Explicitly, the full Green’s matrix has the form
where
represents the
zeros matrix, while the
sub-block are expressed by the matrix (
26). The
is a
elements where
N expresses the total number of scattereres.
Within this formalism, the extinction efficiency of a generic array of scattering particles can be directly obtained from the forward-scattering amplitude using the optical theorem for vector waves for both electric and magnetic polarizations, which results in [
85]:
where
,
,
R is the particle radius, N is the particle number, and the asterisk denotes the complex conjugate. Similarly, the absorption efficiency can be obtained by considering the energy dissipation of both dipoles in the system producing:
The scattering efficiency can be always obtained by the difference of the extinction and the absorption efficiency, i.e.,
. However, this operation requires high numerical accuracy in the computation of both
and
[
83]. To avoid this problem it is possible to directly calculate the scattering efficiency
by evaluating the power radiated in the far field by the oscillating electric and magnetic dipoles, which is [
86]:
where
is an unit vector in the direction of scattering. Moreover, Equation (
34) defines the differential scattering efficiency in the backward and forward direction when
is equal to the tern
and
, respectively, if the excitation is assumed along the z-axis. Explicitly, the forward and backward scattering efficiencies are defined as:
where
is the azimuthal angle.
5. Scattering Properties of Elliptic Curves and Discrete Logarithm Structures
Using the EMCDA framework introduced above we now discuss the scattering properties of aperiodic TiO
nanoparticles arrays generated according to elliptic curves over
and the corresponding discrete logarithm problem. The magnetic permittivity of the sphere and the surrounding medium is assumed to be 1. All the calculations are performed in air (
) under plane wave illumination with
= 0
assuming transverse electric polarized light described by
where
, while the symbol
identifies the unit axes vector.
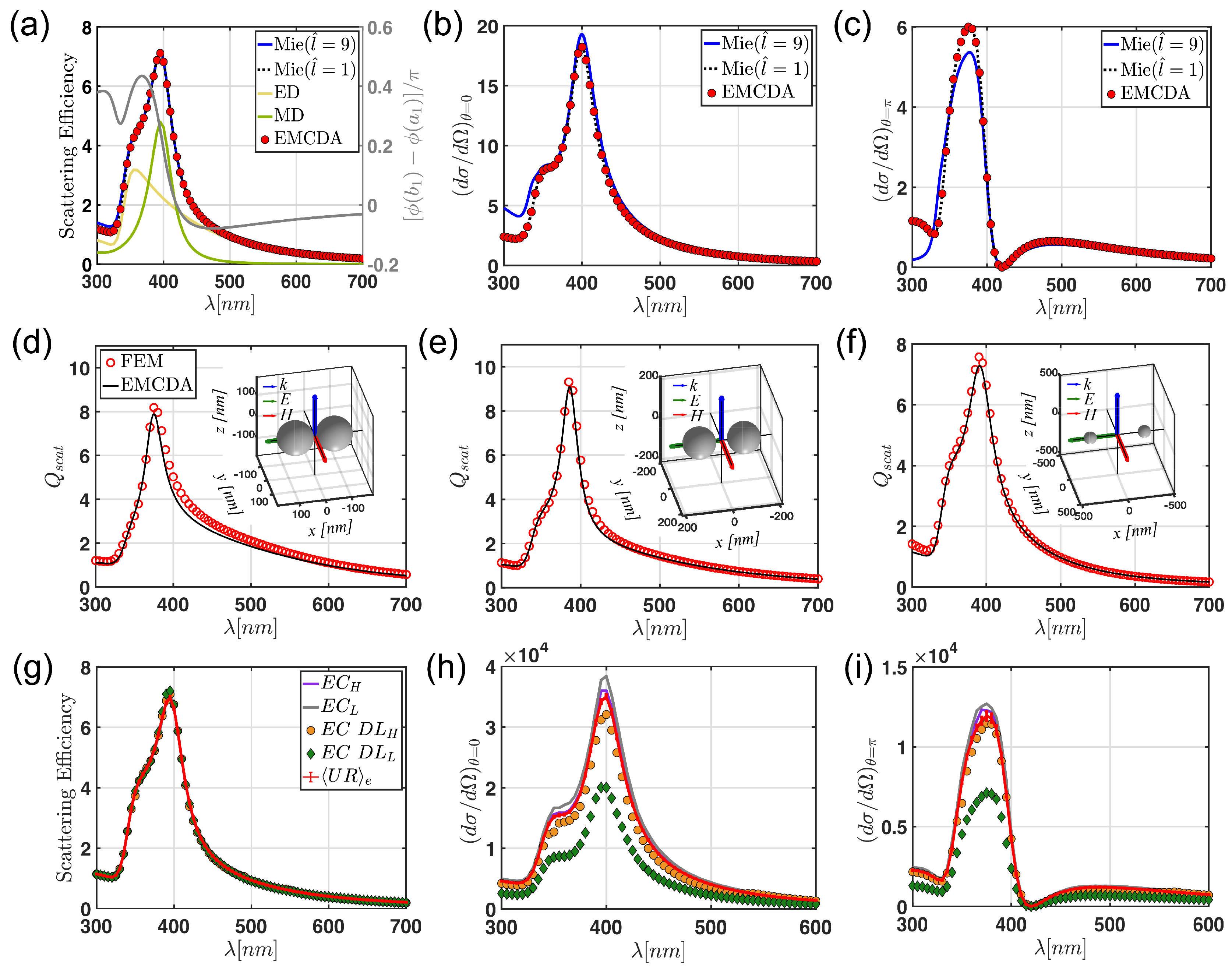
Before analyzing the scattering properties of the arrays, we performed different benchmarks of the EMCDA method with respect to the analytical full-wave Mie theory [
88,
89] applied to a single TiO
nanoparticle with a radius of 70 nm.
Figure 13a–c show the results of this comparison. In particular,
Figure 13a displays the scattering efficiency computed using the analytical Mie–Lorentz theory by truncating the multipolar expansion up to the convergence order provided by
[
87] (
x is the size parameter) as compared to both the analytical result with only the dipolar contribution (
) and the numerical EMCDA calculation (red circle markers). The agreements between the EMCDA and the Mie theory with only the dipolar contribution is almost perfect. Moreover, the relative error due to the dipolar approximation, evaluated from the ratio of the area beyond the blue and the black dotted curves, is 1.5%. Therefore, the scattering properties of these small nanoparticles are sufficiently well-described by considering only the electric (
) and magnetic (
) dipole terms of the Mie expansion [
79].
Figure 13b,c display, respectively, the differential scattering efficiency in the forward and backward direction evaluated by using Equations (
35) and (
36), respectively, (red circle markers) and compare to the results from the equations:
that are derived from the Mie theory [
88,
89] when
(blue curve) and
(dotted black line). Again, the matching between the EMCDA and the Mie theory with
is excellent. On the other hand, the relative error due to the dipolar approximation is approximately 10% for both comparisons. This is due to the fact that the higher-order multipoles interfere with the dipole moments for fixed scattering directions. We remark that Equation (
38) describes a coherent sum between all the multipole moments. On the other hand, no interference effects contribute to the total scattering efficiency [
88]. Interestingly,
Figure 13c shows that the backscattered light is completely suppressed around
nm, where the relative phase between the electric (
) and magnetic (
) dipoles crosses zero, as shown in the grey
y-axis of
Figure 13a (see also [
90] for more details).
In order to analyze the scattering properties of the
and
arrays, we have selected the structures that showed significantly different modal lifetime behavior. Namely,
,
,
, and
. To avoid the occurrence of overlapping nanoparticles (remember that we are considering now a real scattering object characterized by a size and a material through the polarizabilities expressed by Equation (
19)), we have rescaled these aperiodic arrays by fixing the minimum particle separation to be of the order of
nm. We carefully verified the accuracy of the EMCDA simulations by comparing them with simulations performed using the finite element method (FEM) in a dimer nanoparticle configuration with 10 nm gap separation. The FEM model was meshed with 5.6 nm maximum element size and 0.56 nm minimum element size. The total degrees of freedom of the FEM simulation were 1,420,416. We performed the simulations using a 40 core cluster (Intel Xeon(R) CPU E5-2698 v4) with 256Gb total RAM. Typical time to complete full-spectrum simulations was approximately 4 h and only approximately 3 min using the EMCDA method on the same geometry. Moreover, the Green’s matrix spectral method provides fundamental physical information about the light transport properties of open scattering systems that cannot be easily accessed via other numerical methods, such as finite difference time domain (FDTD) or finite elements (FEM). Indeed, in contrast to numerical mesh-based methods, the Green’s matrix spectral method and its EMCDA extension allow one not only to obtain the frequency positions and lifetimes of all the scattering resonances, but also to fully characterize their spectral statistics and measurable scattering parameters. Finally, these methods enable the understanding of the full spectral characteristics of the deterministic aperiodic arrays containing several thousand interacting nanoparticles, which are well beyond the reach of mesh-based numerical methods.
The validation results (shown in
Figure 13d–f for the longitudinal polarization) yield a small (
) discrepancy compared to the ones obtained using our EMCDA method. On the other hand, the results of the EMCDA analysis on the arrays are reported in
Figure 13g–i. Since only a small fraction (<
) of the particles in the arrays are separated by the 10 nm minimum gap distance, the application of the EMCDA method to these geometries is fully justified and the contribution of higher-order electromagnetic multipoles can be safely neglected. Our findings show that the scattering spectra of the investigated
and
structures overlap very well with the spectrum of the ensemble-averaged
system across the entire visible spectrum. This is in agreement with the uncorrelated nature of the
arrays and of the
arrays with the largest and the smallest modal lifetimes. However, structural differences between these systems can be identified by considering the spectral behavior of their directional scattering parameters. This has been achieved by computing the forward and the backward scattering spectra, which are shown in
Figure 13h,i, respectively. In particular, we observe that the data obtained on
feature significantly reduced forward and backscattering intensities, reflecting a more correlated spatial structure compared to all the other systems. Smaller differences are also visible among the other
-based structures when compared to the ensemble-averaged
case.
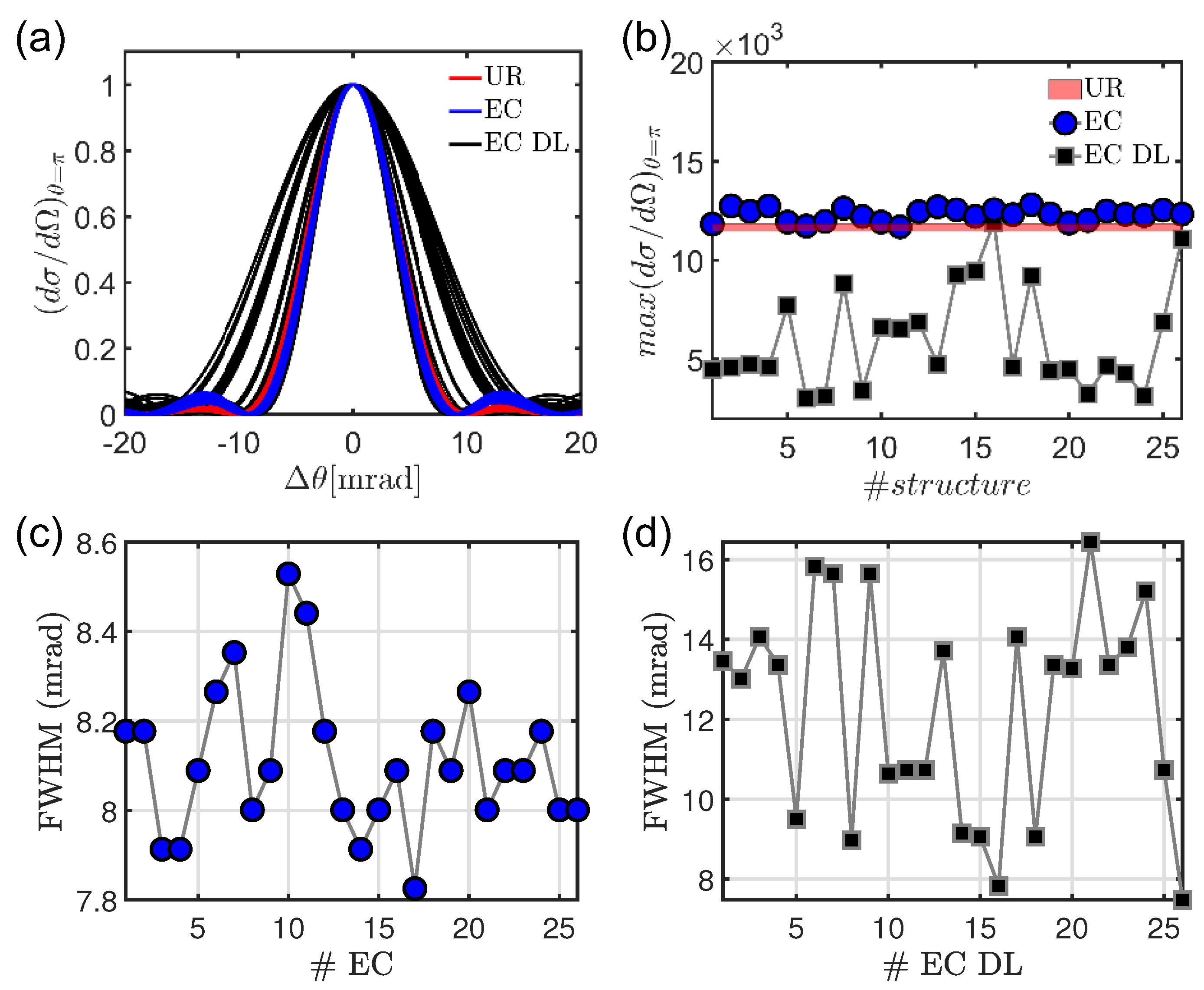
In order to more precisely address the subtle modifications in the directional scattering parameters we analyzed in
Figure 14 the linewidth and the maximal differential scattering efficiency in the backward direction for the different arrays. The analysis is performed considering 26 representative
and
structures. In order to uniformly sample the vast space of structural parameters that we have examined in the
Section 3, we have selected 52 aperiodic arrays by using as discriminator the average modal lifetime
, as reported in
Figure 6 and
Figure 11. Specifically, 26
arrays were chosen between the 900 different elliptic curves point patterns generated by the integer coefficients
A and
B in the range (1, 30) ordered by following the trend of
. Specifically, 26 different
structures were selected with parameter values that are equidistant between the
and the
structure. In the same way, the 26
arrays were selected equidistantly between the 36 different structures discussed in
Figure 11. All these 52 arrays were scaled to avoid the occurrence of overlapping nanoparticles.
Table 1 summarizes the averaged structural parameters of all the investigated structures. All share approximately the same minimum and averaged first-neighbor particle separation, as well as the same particle density.
The normalized lineshapes of the backscattering are displayed in
Figure 14a and show a significant variability. The backscattering of a
representative realization is also shown for comparison in red. The significant differences in the width of the backscattering angular spectrum (computed at the wavelength of maximum scattering) evidence subtle differences in the structural properties of the arrays that cannot otherwise be resolved by total scattering analysis. The more sensitive interference effects that contribute to the width and intensity of the backscattering cone allow us to differentiate between different
and
structures for the first time. Note that simply considering the maximum backscattering efficiency, shown in
Figure 14b, would not lead to a clear discrimination between a
and the different
structures. The full-width-at-half-maximum (FWHM) results obtained for all the investigated structures are plotted in
Figure 14c,d, which demonstrate a great variability across the analyzed sample. We should appreciate that the FWHM of the backscatering cone varies by almost a factor of two across the different
structures, which is evidence of significant modifications in the underlying geometrical structure of the arrays. Therefore, our findings not only establish that
and
are remarkably different from uniform random systems, but they may also provide an optical approach to rapidly identify the potential vulnerabilities of modern
-based cryptosystems by investigating coherent light scattering effects in the associated photonic structures.