Application of GISAXS in the Investigation of Three-Dimensional Lattices of Nanostructures
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. General Properties of GISAXS Intensity Maps
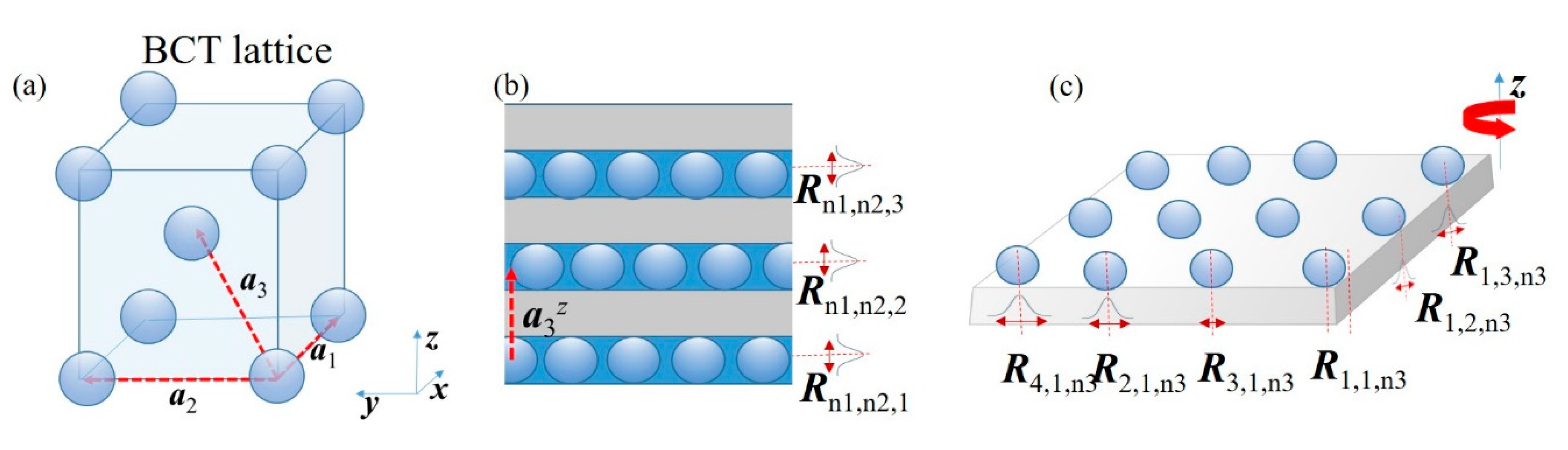
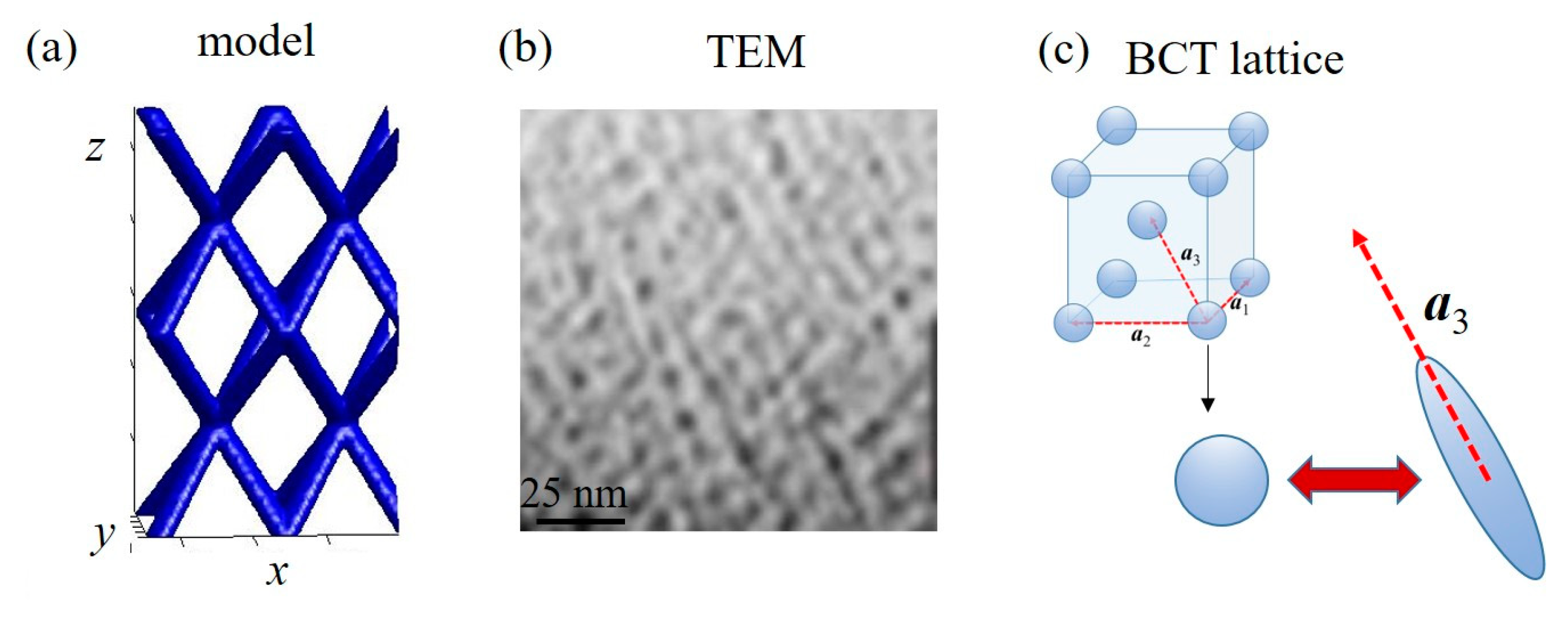
3.2. Ordering Types in Nanostructured Materials
4. Examples
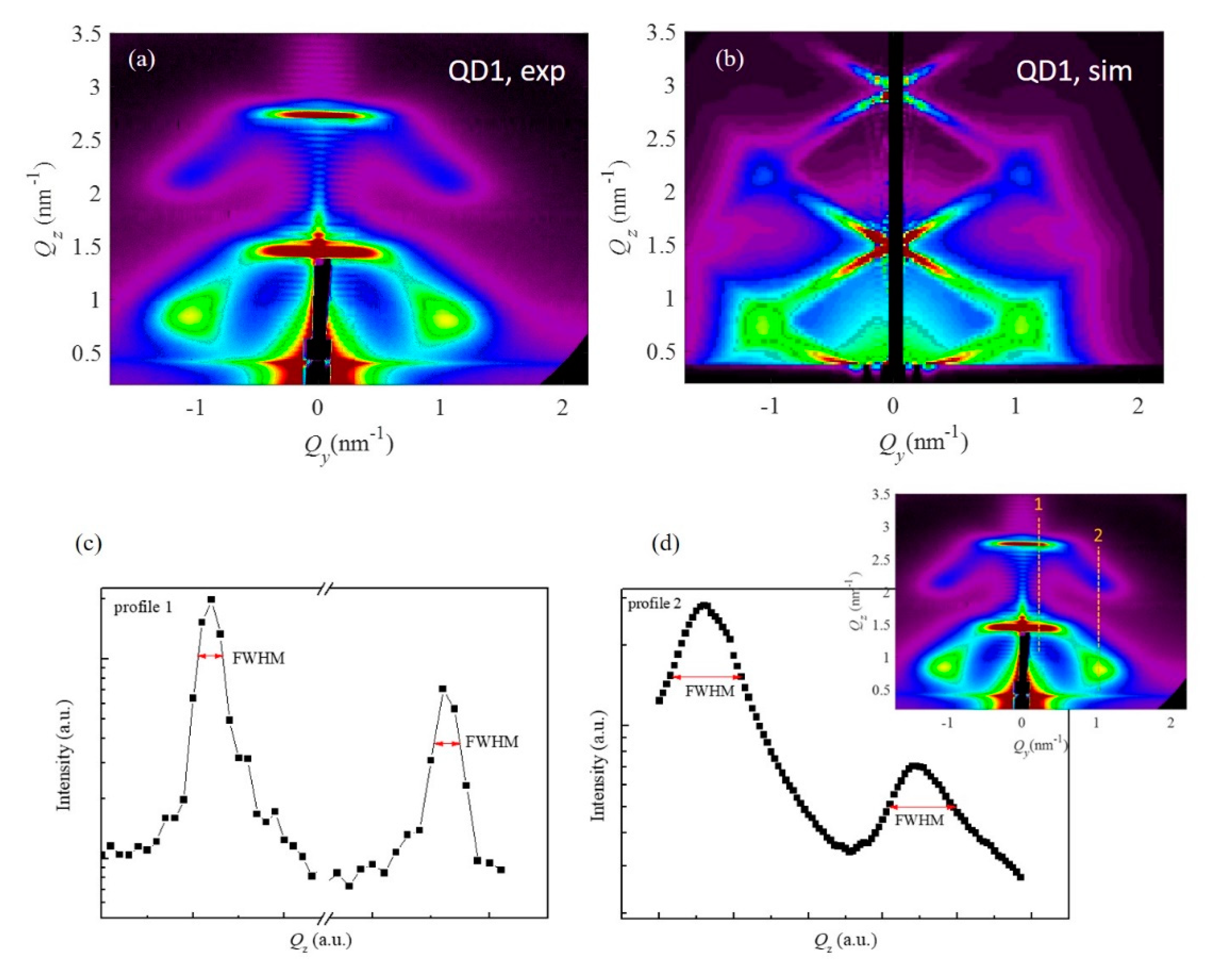
4.1. 3D Ge Quantum Dot Lattices
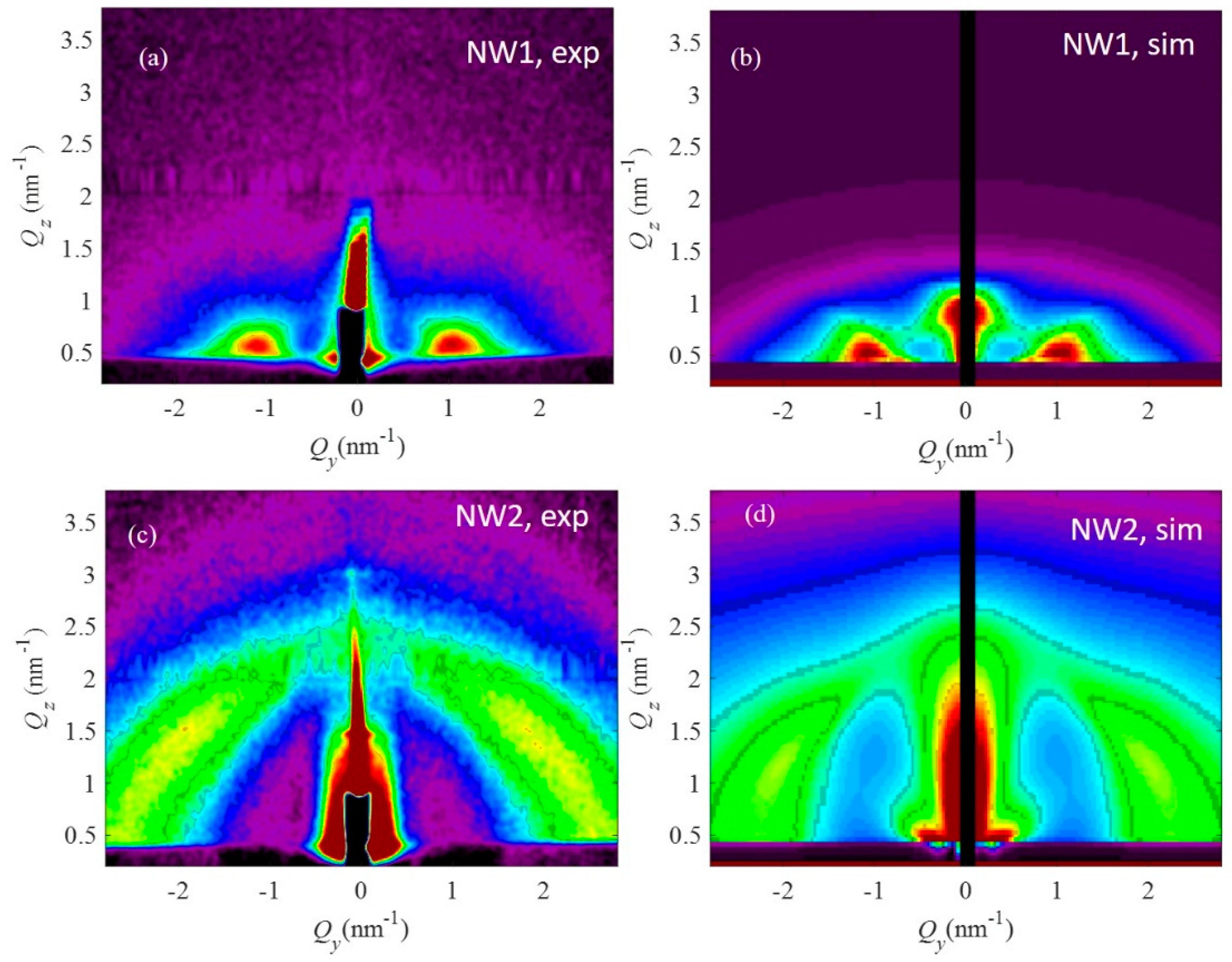
4.2. 3D Networks of Ge Nanowires
4.3. Lattices of Core/Shell Quantum Dots
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Renaud, J.; Lazzari, R.; Leroy, F. Probing surface and interface morphology with Grazing Incidence Small Angle X-Ray Scattering. Surf. Sci. Rep. 2009, 64, 255–380. [Google Scholar] [CrossRef]
- Buljan, M.; Karlušić, M.; Nekić, N.; Jerčinović, M.; Bogdanović-Radović, I.; Bernstorff, S.; Radić, N.; Mekterović, I. GISAXS analysis of ion beam modified films and surfaces. Comp. Phys. Commun. 2017, 212, 69–81. [Google Scholar] [CrossRef]
- Buljan, M.; Radić, N.; Bernstorff, S.; Dražić, G.; Bogdanović-Radović, I.; Holý, V. Grazing incidence small angle x-ray scattering: Application to the study of quantum dot lattices. Acta Cryst. A 2012, 68, 124–138. [Google Scholar] [CrossRef] [PubMed]
- Buljan, M.; Desnica, U.V.; Ivanda, M.; Radić, N.; Dubček, P.; Dražić, G.; Salamon, K.; Bernstorff, S.; Holý, V. Formation of three-dimensional quantum-dot superlattices in amorphous systems: Experiments and Monte Carlo simulations. Phys. Rev. B 2009, 79, 035310. [Google Scholar] [CrossRef]
- Buljan, M.; Pinto, S.R.C.; Rolo, A.G.; Martín-Sánchez, J.; Gomes, M.J.M.; Grenzer, J.; Mücklich, A.; Bernstorff, S.; Holý, V. Self-Assembling of Ge quantum dots in an alumina matrix. Phys. Rev. B 2010, 82, 235407. [Google Scholar] [CrossRef]
- Buljan, M.; Jerčinović, M.; Siketić, Z.; Bogdanović-Radović, I.; Delač Marion, I.; Kralj, M.; Ivanda, M.; Turković, A.; Dražić, G.; Bernstorff, S.; et al. Tuning the growth properties of Ge quantum dot lattices in amorphous oxides by matrix type. J. Appl. Cryst. 2013, 46, 1490–1500. [Google Scholar] [CrossRef]
- Buljan, M.; Roshchupkina, O.; Šantić, A.; Holý, V.; Baehtz, C.; Mücklich, A.; Horák, L.; Valeš, V.; Radić, N.; Bernstorff, S.; et al. Growth of a three-dimensional anisotropic lattice of Ge quantum dots in an amorphous alumina matrix. J. Appl. Cryst. 2013, 46, 709–715. [Google Scholar] [CrossRef]
- Buljan, M.; Radić, N.; Ivanda, M.; Bogdanović-Radović, I.; Karlušić, M.; Grenzer, J.; Prucnal, S.; Dražić, G.; Pletikapić, G.; Svetličić, V.; et al. Ge quantum dot lattices in Al2O3 multilayers. J. Nanopart Res. 2013, 15, 1485. [Google Scholar] [CrossRef]
- Jerčinović, M.; Radić, N.; Buljan, M.; Grenzer, J.; Delač-Marion, I.; Kralj, M.; Bogdanović-Radović, I.; Hübner, R.; Dubček, P.; Salamon, K.; et al. Self-Assembled growth of Ni nanoparticles in amorphous alumina matrix. J. Nanopart Res. 2014, 16, 2296. [Google Scholar] [CrossRef]
- Buljan, M.; Radić, N.; Sancho-Paramon, J.; Janicki, V.; Grenzer, J.; Bogdanović-Radović, I.; Siketić, Z.; Ivanda, M.; Utrobičić, A.; Hübner, R.; et al. Production of three-dimensional quantum dot lattice of Ge/Si core–shell quantum dots and Si/Ge layers in an alumina glass matrix. Nanotechnology 2015, 26, 065602. [Google Scholar] [CrossRef] [PubMed]
- Nekić, N.; Sancho Parramon, J.; Bogdanović-Radović, I.; Grenzer, J.; Huebner, R.; Ivanda, M.; Buljan, M. Ge/Si core/shell quantum dots in alumina: Tuning the optical absorption by the core and shell size. Nanophotonics 2017, 6, 1055–1062. [Google Scholar] [CrossRef][Green Version]
- Nekić, N.; Šarić, I.; Salamon, K.; Basioli, L.; Sancho-Parramon, J.; Grenzer, J.; Hübner, R.; Bernstorff, S.; Petravić, M.; Mičetić, M. Preparation of non-oxidized Ge quantum dot lattices in amorphous Al2O3, Si3N4 and SiC matrices. Nanotechnology 2019, 30, 335601. [Google Scholar] [CrossRef] [PubMed]
- Sinha, S.K.; Sirota, E.B.; Garoff, S.; Stanley, H.B. X-ray and neutron scattering from rough surfaces. Phys. Rev. B 1988, 38, 2297–2311. [Google Scholar] [CrossRef] [PubMed]
- Lazzari, R. IsGISAXS: A program for grazing-incidence small-angle X-ray scattering analysis of supported islands. J. Appl. Cryst. 2002, 35, 406–421. [Google Scholar] [CrossRef]
- Tate, M.P.; Urade, V.N.; Kowalski, J.D.; Wei, T.C.; Hamilton, B.D.; Eggiman, B.W.; Hillhouse, H.W. Simulation and interpretation of 2D diffraction patterns from self-assembled nanostructured films at arbitrary angles of incidence: From grazing incidence (above the critical angle) to transmission perpendicular to the substrate. J. Phys. Chem. B 2006, 110, 9882–9892. [Google Scholar] [CrossRef] [PubMed]
- Babonneau, D. FitGISAXS: Software package for modelling and analysis of GISAXS data using IGOR Pro. J. Appl. Cryst. 2010, 43, 929–936. [Google Scholar] [CrossRef]
- Chourou, S.; Sarje, A.; Li, X.S.; Chan, E.; Hexemer, A. HipGISAXS: A High Performance Computing Code for Simulating Grazing Incidence X-Ray Scattering Data. J. Appl. Crystallogr. 2013, 46, 1781–1795. [Google Scholar] [CrossRef]
- Durniak, C.; Ganeva, M.; Pospelov, G.; Van Herck, W.; Wuttke, J. BornAgain—Software for Simulating and Fitting X-ray and Neutron Small-Angle Scattering at Grazing Incidence 2015. Available online: http://juser.fz-juelich.de/record/255761 (accessed on 11 September 2019).
- Mekterović, I.; Basioli, L.; Mičetić, M. GISAXStudio 2019. Available online: http://homer.zpr.fer.hr/gisaxstudio/doku.php?id=install (accessed on 11 September 2019).
- Ragulskaya, A.V.; Andreeva, M.A.; Rogachev, A.V.; Yakunin, S.N. The investigation of [Fe/Cr] multilayer by GISAXS. Superlattices Microstruct. 2019, 125, 16–25. [Google Scholar] [CrossRef]
- Eads, J.L.; Millane, R.P. Diffraction by the ideal paracrystal. Acta Cryst. A 2001, 57, 507–517. [Google Scholar] [CrossRef] [PubMed]
- Ray, N.; Gupta, N.; Adhikary, M.; Nekić, N.; Basioli, L.; Dražić, G.; Bernstorff, S.; Mičetić, M. Influence of Structure on Electronic Charge Transport in 3D Ge Nanowire Networks in an Alumina Matrix. Sci. Rep. 2019, 9, 5432. [Google Scholar] [CrossRef] [PubMed]
- Mekterović, I.; Basioli, L.; Bernstorff, S.; Mičetić, M. GisaxStudio—Software platform for GISAXS analysis of nanostructured materials. Unpublished work. 2019. [Google Scholar]

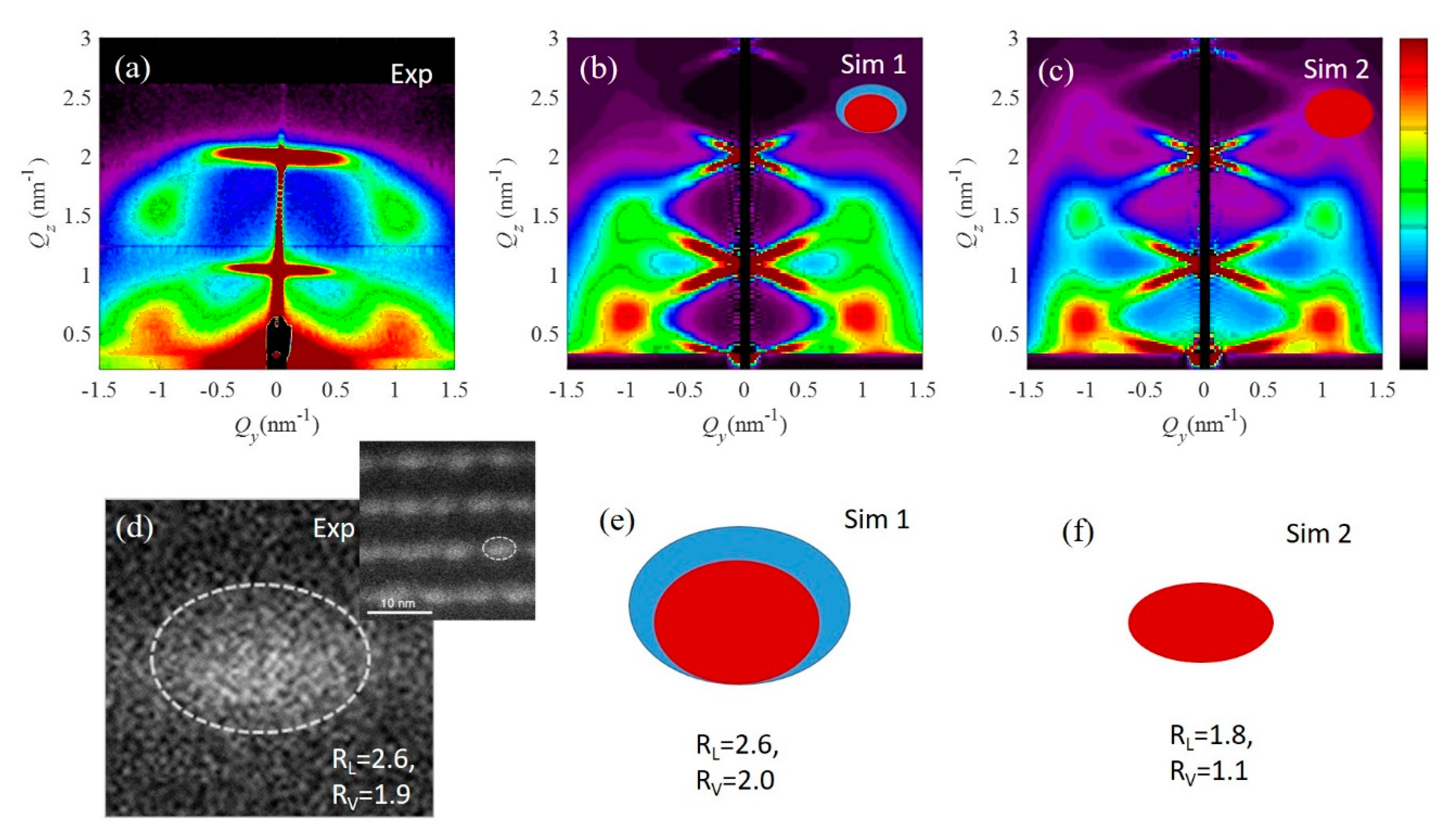
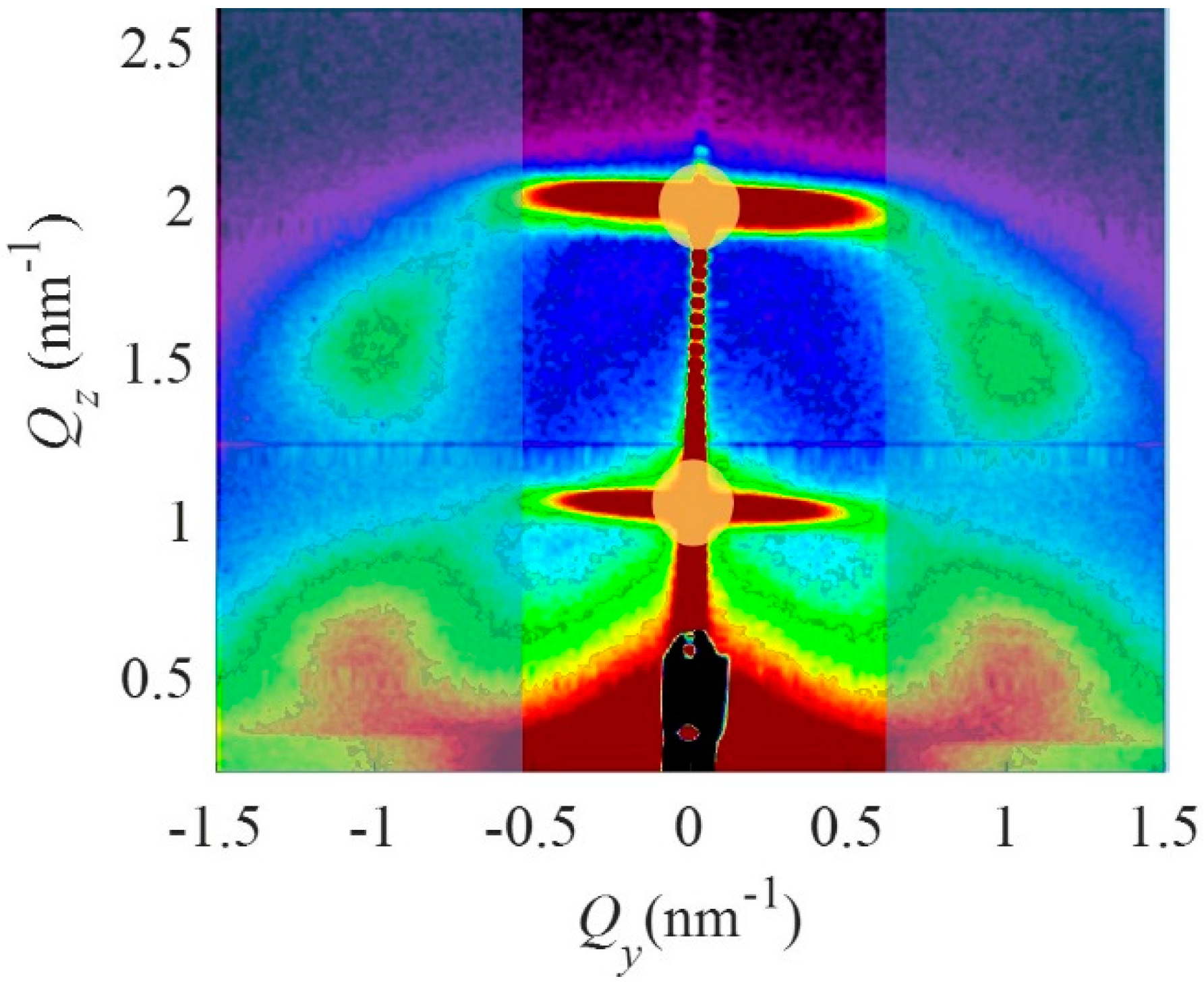
| Parameter (nm) | a | c | σ1,2x,y | σ1,2z | σ3x,y | σ3z | Rx,y | Rz | σR |
|---|---|---|---|---|---|---|---|---|---|
| QD1 | 5.1 | 4.2 | 1.6 | 0.2 | 0.7 | 0.2 | 1.6 | 1.0 | 0.4 |
| Parameter (nm) | a | c | σ1,2x,y | σ1,2z | σ3x,y | σz | Rx,y | Rz | σR |
|---|---|---|---|---|---|---|---|---|---|
| NW1 | 5.5 | 6.3 | 1.2 | 1.8 | 0.8 | 1.6 | 1.0 | 2.3 | 0.4 |
| NW2 | 2.9 | 1.9 | 0.9 | 0.9 | 1.2 | 3.7 | 0.4 | 0.8 | 0.1 |
| Parameter (nm) | a | c | σ1,2x,y | σ1,2z | σ3x,y | σz | Rx,y | Rz | σR | t | d |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sim1 | 5.2 | 6.3 | 1.5 | 0.2 | 1.4 | 0.6 | 2.6 | 2.0 | 0.3 | 0.9 | 0.3 |
| Sim2 | 5.2 | 6.5 | 1.9 | 0.3 | 1.1 | 0.5 | 1.8 | 1.1 | 0.3 | --- | --- |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basioli, L.; Salamon, K.; Tkalčević, M.; Mekterović, I.; Bernstorff, S.; Mičetić, M. Application of GISAXS in the Investigation of Three-Dimensional Lattices of Nanostructures. Crystals 2019, 9, 479. https://doi.org/10.3390/cryst9090479
Basioli L, Salamon K, Tkalčević M, Mekterović I, Bernstorff S, Mičetić M. Application of GISAXS in the Investigation of Three-Dimensional Lattices of Nanostructures. Crystals. 2019; 9(9):479. https://doi.org/10.3390/cryst9090479
Chicago/Turabian StyleBasioli, Lovro, Krešimir Salamon, Marija Tkalčević, Igor Mekterović, Sigrid Bernstorff, and Maja Mičetić. 2019. "Application of GISAXS in the Investigation of Three-Dimensional Lattices of Nanostructures" Crystals 9, no. 9: 479. https://doi.org/10.3390/cryst9090479
APA StyleBasioli, L., Salamon, K., Tkalčević, M., Mekterović, I., Bernstorff, S., & Mičetić, M. (2019). Application of GISAXS in the Investigation of Three-Dimensional Lattices of Nanostructures. Crystals, 9(9), 479. https://doi.org/10.3390/cryst9090479







