A First-Principles Exploration of NaxSy Binary Phases at 1 atm and Under Pressure
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
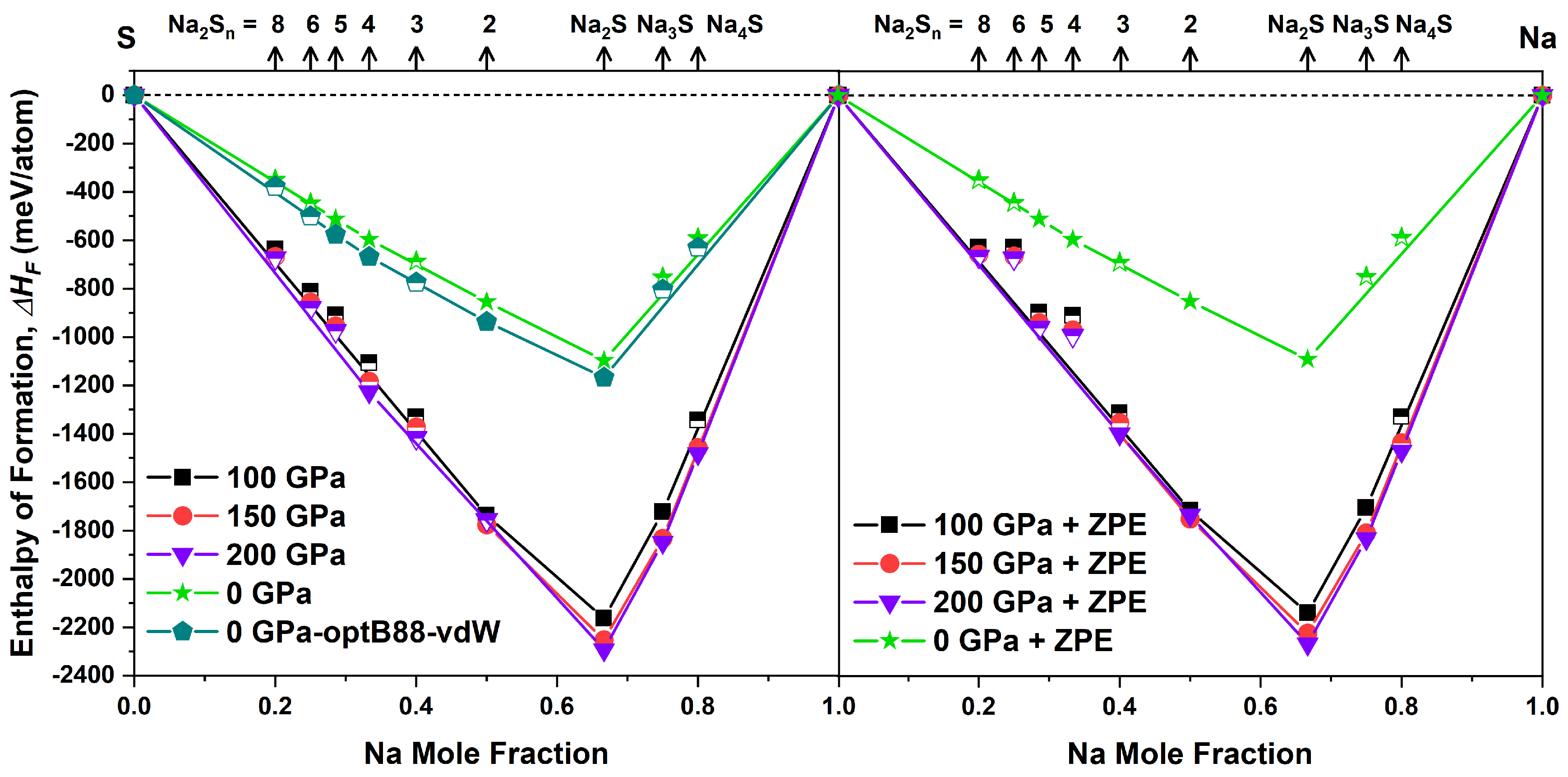
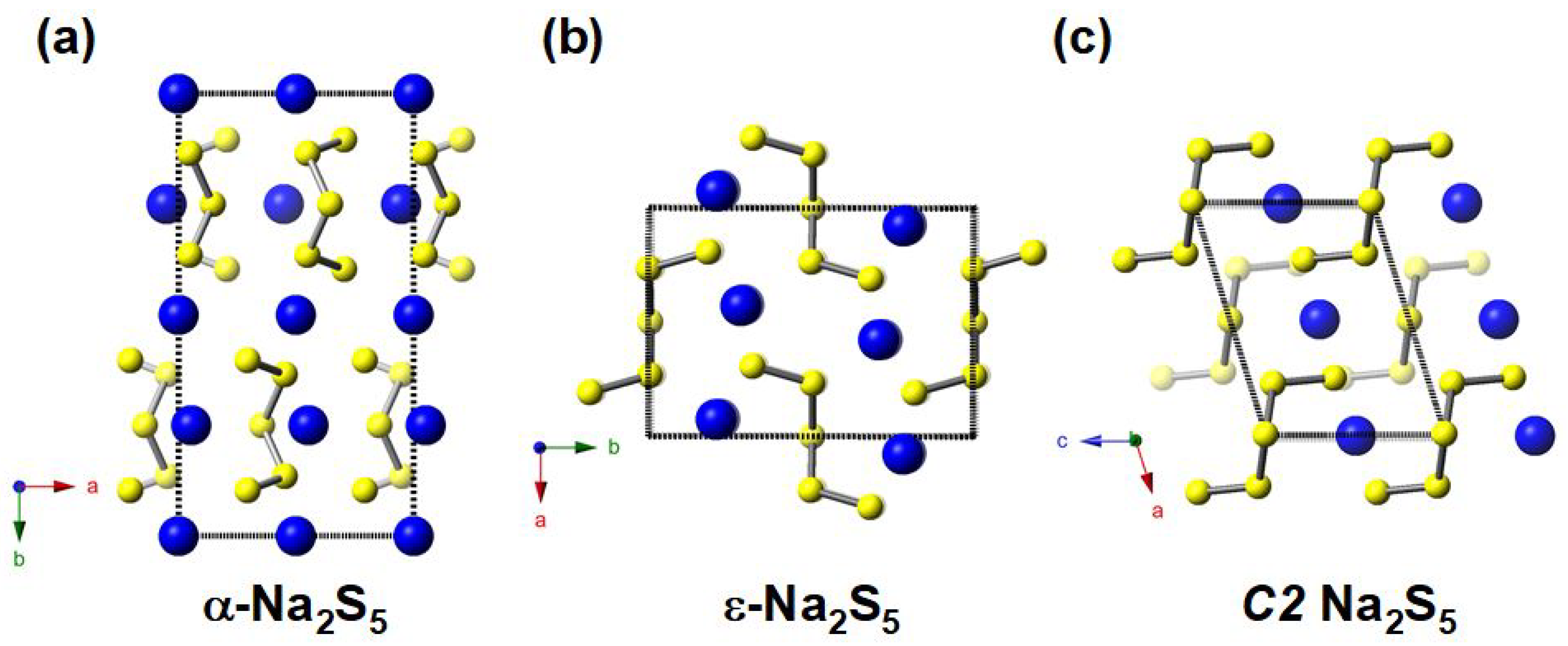
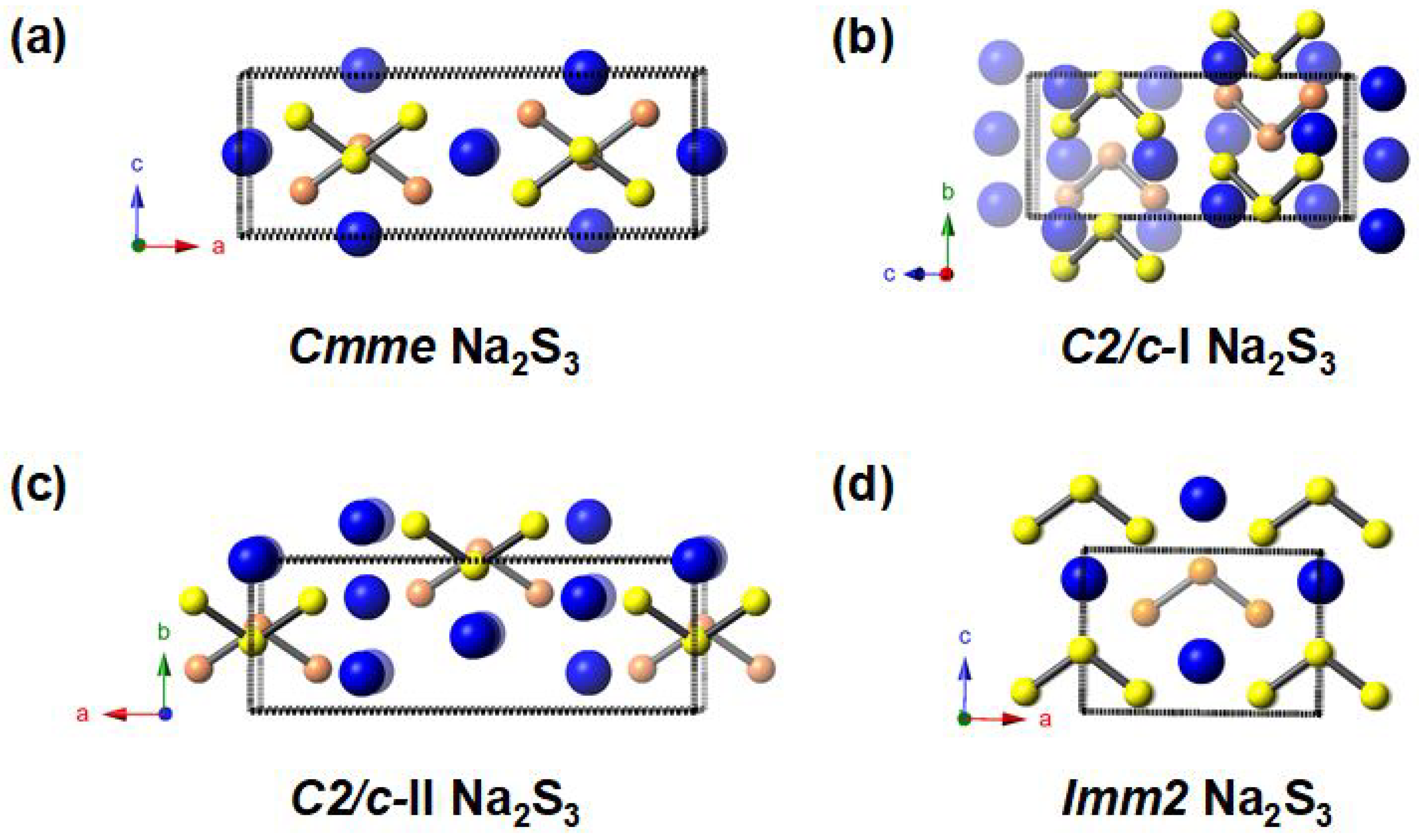
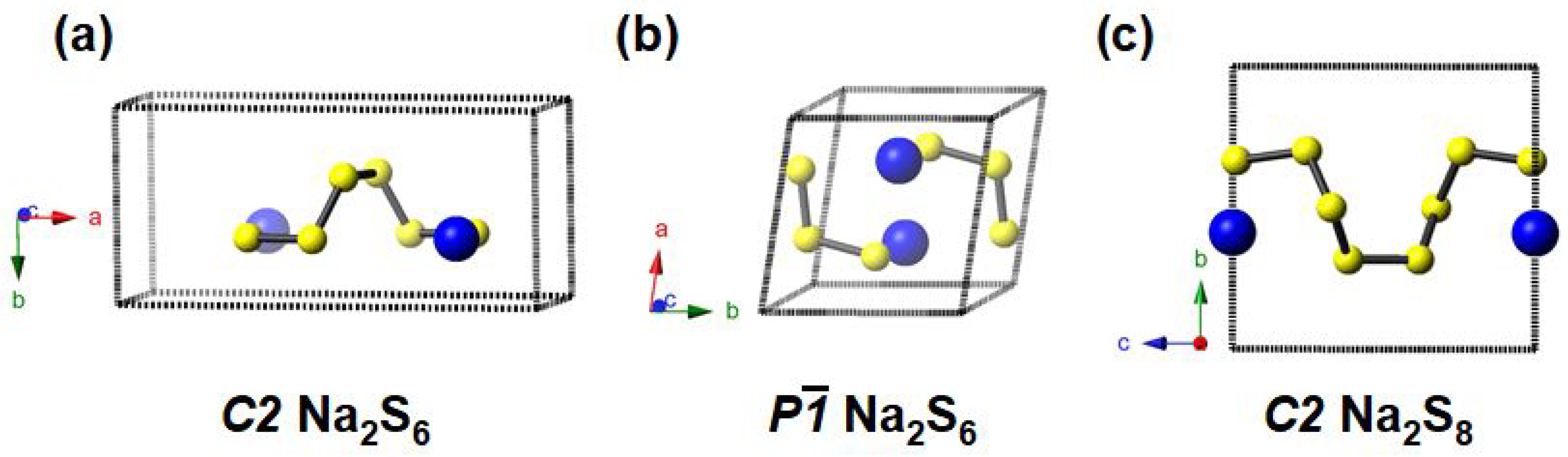
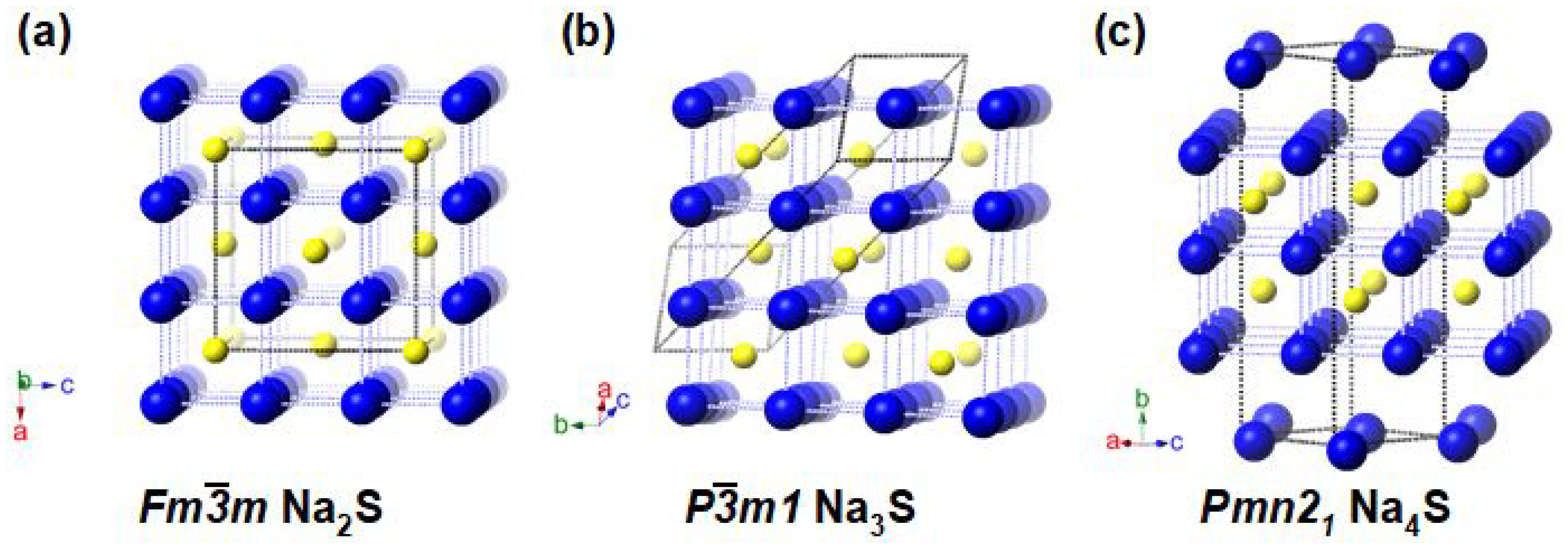
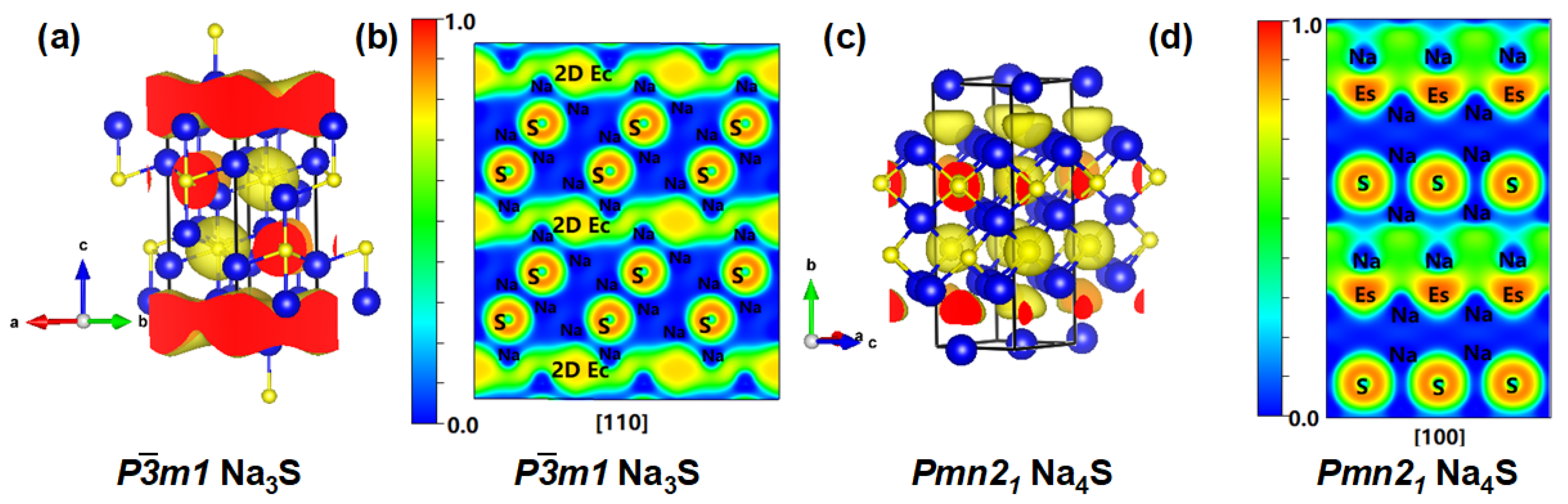
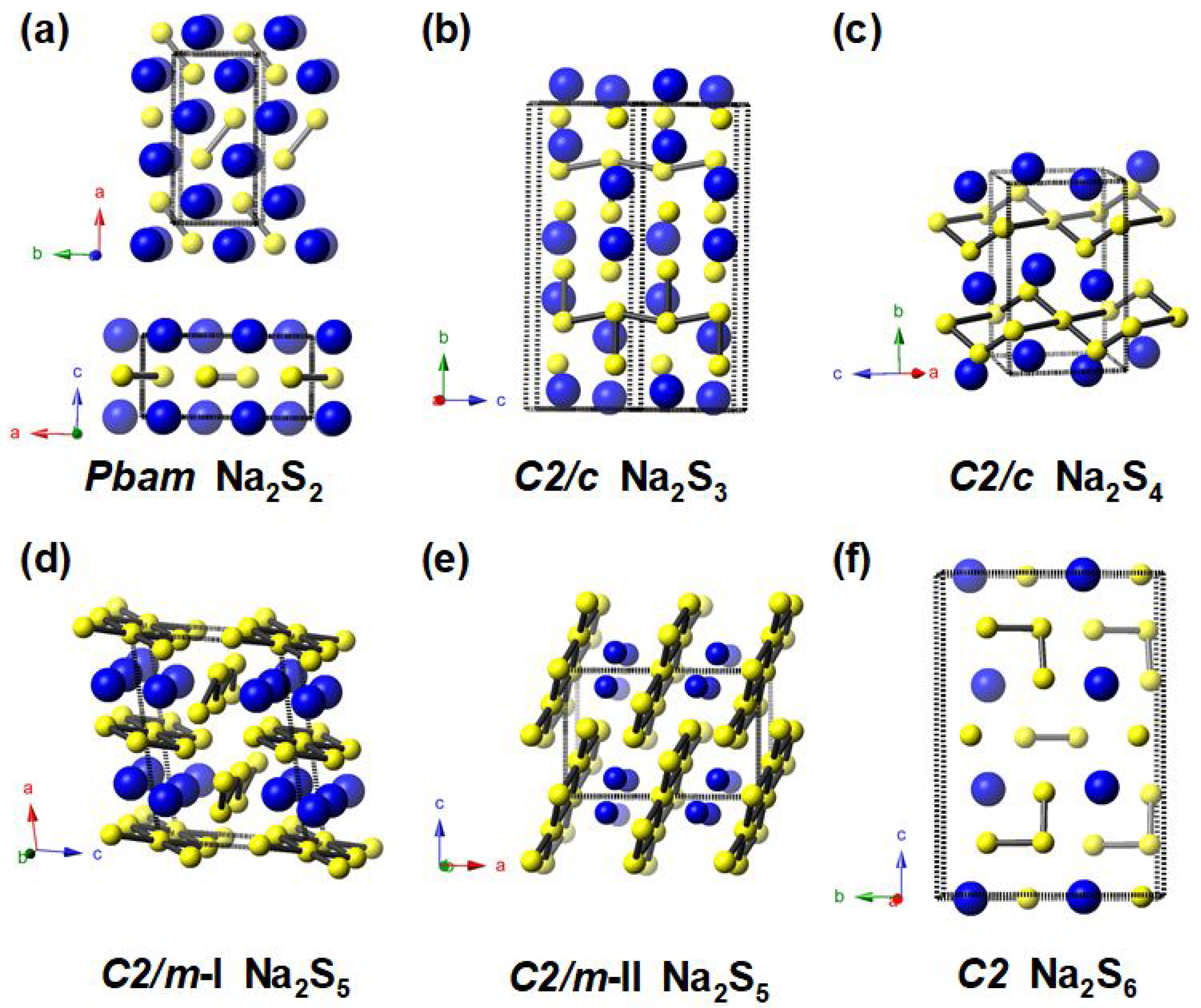
3.1. Stable and Metastable Na-S Phases at Atmospheric Conditions
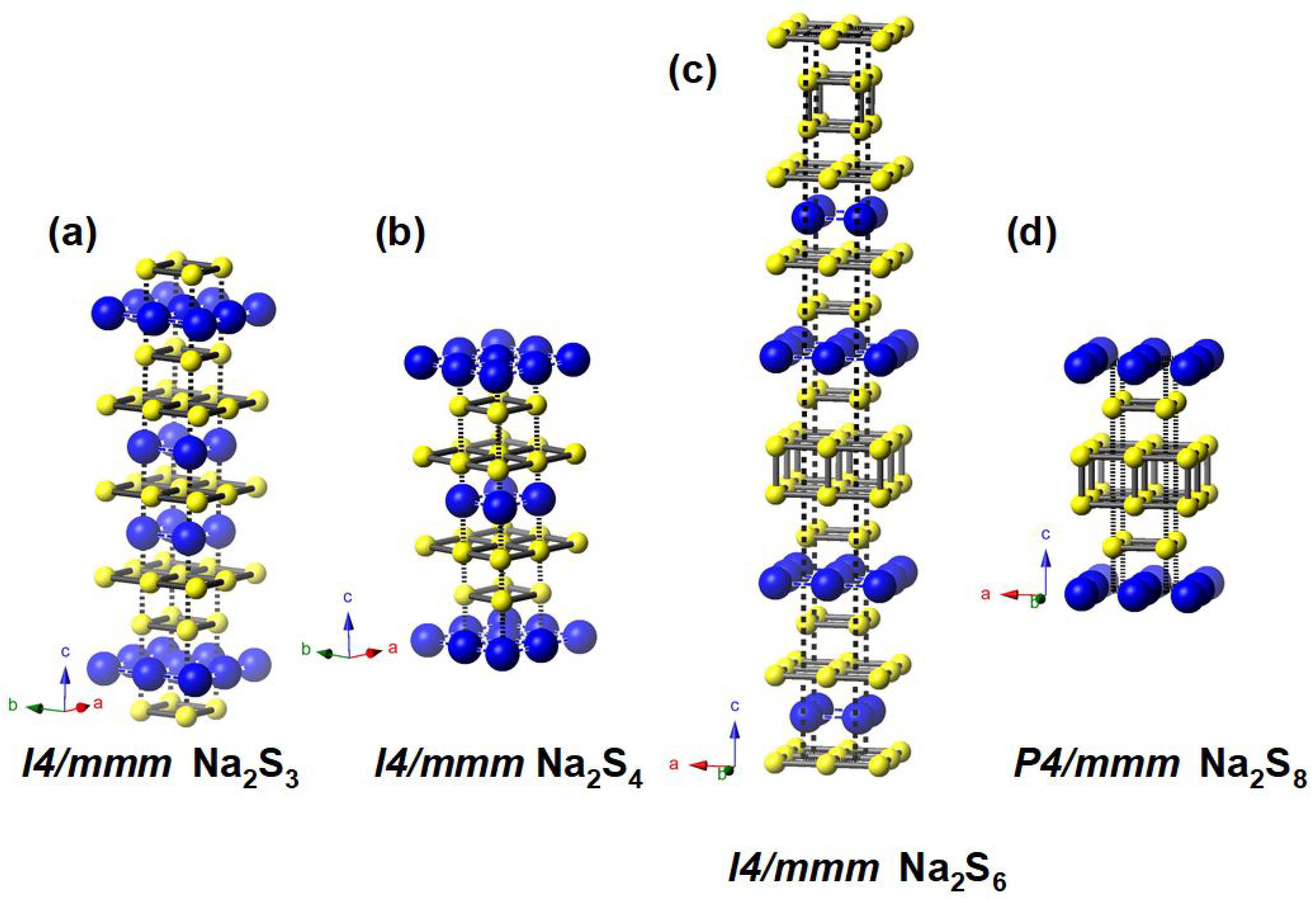
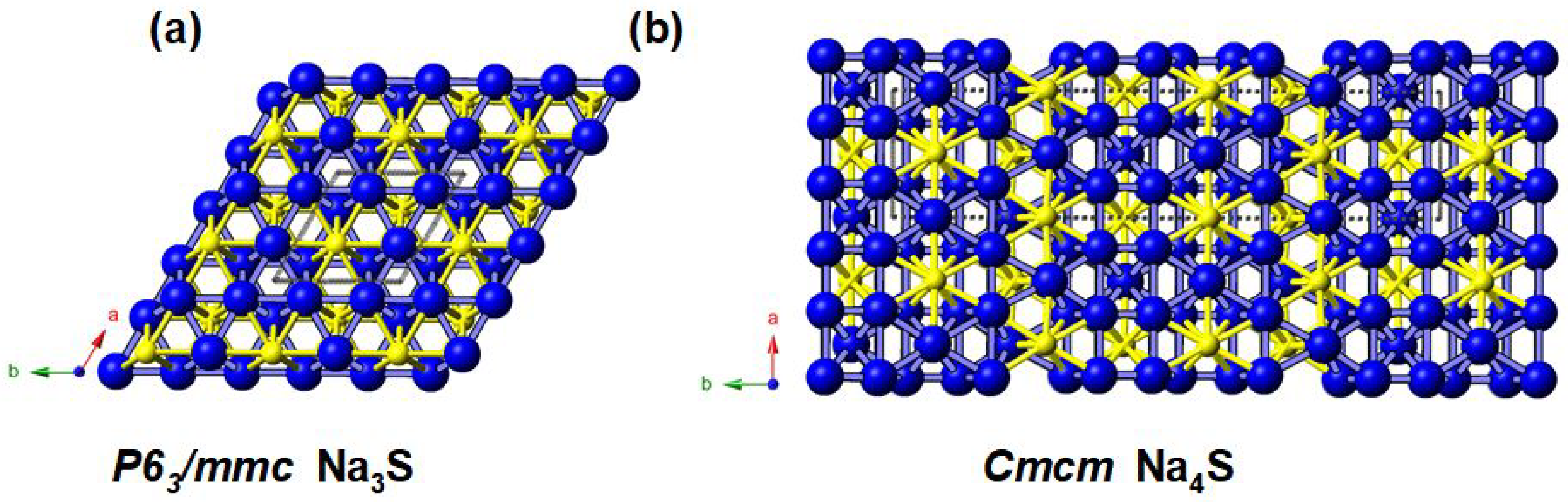
3.2. Na-S System at High Pressure
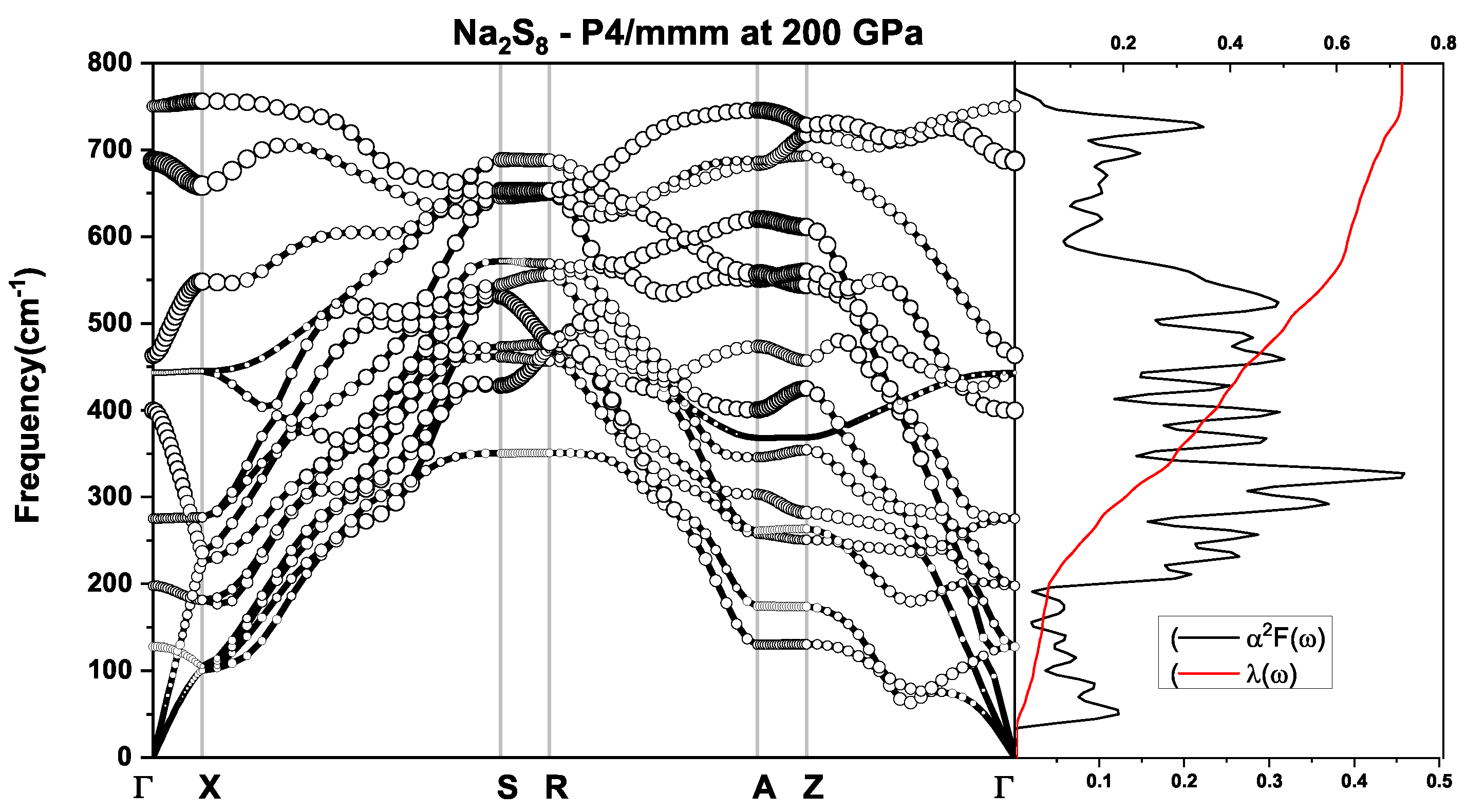
3.3. Electronic Structure and Superconductivity under Pressure
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Okamoto, H. The Li-S (lithium-sulfur) system. J. Phase Equilib. 1995, 16, 94–97. [Google Scholar] [CrossRef]
- Janz, G.J.; Coutts, J.W.; Downey, J.R.; Roduner, E. Raman studies of sulfur-containing anions in inorganic polysulfides. Potassium polysulfides. Inorg. Chem. 1976, 15, 1755–1759. [Google Scholar] [CrossRef]
- Sangster, J.; Pelton, A.D. The K-S (potassium-sulfur) system. J. Phase Equilib. 1997, 18, 82–88. [Google Scholar] [CrossRef]
- Sangster, J.; Pelton, A.D. The Rb-S (rubidium-sulfur) system. J. Phase Equilib. 1997, 18, 97–100. [Google Scholar] [CrossRef]
- Sangster, J.; Pelton, A.D. The Cs-S (cesium-sulfur) system. J. Phase Equilib. 1997, 18, 78–81. [Google Scholar] [CrossRef]
- Oei, D.G. Sodium-sulfur system. I. Differential thermal analysis. Inorg. Chem. 1973, 12, 435–437. [Google Scholar] [CrossRef]
- Sangster, J.; Pelton, A.D. The Na-S (sodium-sulfur) system. J. Phase Equilib. 1977, 18, 89–96. [Google Scholar] [CrossRef]
- Rosen, E.; Tegman, R. A preparative and X-ray powder diffraction study of the polysulfides Na2S2, Na2S4 and Na2S5. Acta Chem. Scand. 1971, 25, 3329–3336. [Google Scholar] [CrossRef][Green Version]
- Föppl, H.; Busmann, E.; Frorath, F.K. Die kristallstrukturen von α-Na2S2 und K2S2, β-Na2S2 und Na2Se2. Z. Anorg. Allg. Chem. 1962, 314, 12–20. [Google Scholar] [CrossRef]
- Oei, D.G. Sodium-sulfur system. II. Polysulfides of sodium. Inorg. Chem. 1973, 12, 438–441. [Google Scholar] [CrossRef]
- Böttcher, P.; Keller, R. Die kristallstruktur des α-Na2S5/The crystal structure of α-Na2S5. Z. Naturforsch. B 1984, 39, 577–581. [Google Scholar] [CrossRef]
- Weber, N. Ford gives Na-S battery details. Chem. Eng. News 1966, 44, 32–33. [Google Scholar]
- Kummer, J.T.; Weber, N. Battery Having a Molten Alkali Metal Anode and Molten Sulfur Cathode. U.S. Patent 3,413,150, 26 November 1968. [Google Scholar]
- Yao, Y.F.Y.; Kummer, J.T. Ion exchange properties of and rates of ionic diffusion in beta-alumina. J. Inorg. Nucl. Chem. 1967, 29, 2453–2475. [Google Scholar]
- Ellis, B.L.; Nazar, L.F. Sodium and sodium-ion energy storage batteries. Curr. Opin. Solid State Mater. Sci. 2012, 16, 168–177. [Google Scholar] [CrossRef]
- Hueso, K.B.; Armand, M.; Rojo, T. High temperature sodium batteries: Status, challenges and future trends. Energy Environ. Sci. 2013, 6, 734–749. [Google Scholar] [CrossRef]
- Dunn, B.; Kamath, H.; Tarascon, J.M. Electrical energy storage for the grid: A battery of choices. Science 2011, 334, 928–935. [Google Scholar] [CrossRef] [PubMed]
- Nikiforidis, G.; van de Sanden, M.C.M.; Tsampas, M.N. High and intermediate temperature sodium-sulfur batteries for energy storage: Development, challenges and perspectives. RSC Adv. 2019, 9, 5649–5673. [Google Scholar] [CrossRef]
- Momida, H.; Yamashita, T.; Oguchi, T. First-principles study on structural and electronic properties of α-S and Na–S crystals. J. Phys. Soc. Jpn. 2014, 83, 124713. [Google Scholar] [CrossRef]
- Mali, G.; Patel, M.U.M.; Mazaj, M.; Dominko, R. Stable crystalline forms of Na polysulfides: Experiment versus ab initio computational prediction. Chem. Eur. J. 2016, 22, 3355–3360. [Google Scholar] [CrossRef]
- Wang, Y.; Hao, Y.; Xu, L.C.; Yang, Z.; Di, M.Y.; Liu, R.; Li, X. Insight into the discharge products and mechanism of room-temperature sodium-sulfur batteries: A first-principles study. J. Phys. Chem. C 2019, 123, 3988–3995. [Google Scholar] [CrossRef]
- Zintl, E.; Harder, A.; Dauth, B. Gitterstruktur der oxyde, sulfide, selenide und telluride des lithiums, natriums und kaliums. Z. Elektrochem. Angew. Phys. Chem. 1934, 40, 588–593. [Google Scholar]
- May, K. Die kristallstruktur des rubidium-sulfids Rb2S. Z. Kristallogr. 1936, 94, 412–413. [Google Scholar] [CrossRef]
- Sommer, H.; Hoppe, R. Die Kristallstruktur von Cs2S. mit einer Bemerkung über Cs2Se, Cs2Te, Rb2Se und Rb2Te. Z. Anorg. Allg. Chem. 1977, 429, 118–130. [Google Scholar] [CrossRef]
- Grzechnik, A.; Vegas, A.; Syassen, K.; Loa, I.; Hanfland, M.; Jansen, M. Reversible antifluorite to anticotunnite phase transition in Li2S at high pressures. J. Solid State Chem. 2000, 154, 603–611. [Google Scholar] [CrossRef]
- Vegas, A.; Grzechnik, A.; Syassen, K.; Loa, I.; Hanfland, M.; Jansen, M. Reversible phase transitions in Na2S under pressure: A comparison with the cation array in Na2SO4. Acta Crystallogr. 2001, B57, 151–156. [Google Scholar] [CrossRef]
- Barkalov, O.I.; Naumov, P.G.; Felser, C.; Medvedev, S.A. Pressure-induced transition to Ni2In-type phase in lithium sulfide(Li2S). Solid State Sci. 2016, 61, 220–224. [Google Scholar] [CrossRef]
- Santamaría-Pérez, D.; Vegas, A.; Muehle, C.; Jansen, M. High-pressure experimental study on Rb2S: Antifluorite to Ni2In-type phase transitions. Acta Crystallogr. 2011, B67, 109–115. [Google Scholar] [CrossRef]
- Santamaría-Pérez, D.; Vegas, A.; Muehle, C.; Jansen, M. Structural behaviour of alkaline sulfides under compression: High-pressure experimental study on Cs2S. J. Chem. Phys. 2011, 135, 054511. [Google Scholar] [CrossRef]
- Schön, J.C.; Čančarević, Ž.; Jansen, M. Structure prediction of high-pressure phases for alkali metal sulfides. J. Chem. Phys. 2004, 121, 2289–2304. [Google Scholar] [CrossRef]
- Verma, A.K.; Modak, P.; Sharma, S.M. Structural phase transitions in Li2S, Na2S and K2S under compression. J. Alloy. Compd. 2017, 710, 460–467. [Google Scholar] [CrossRef]
- Li, Y.; Jin, X.; Cui, T.; Zhuang, Q.; Lv, Q.; Wu, G.; Meng, X.; Bao, K.; Liu, B.; Zhou, Q. Structural stability and electronic property in K2S under pressure. RSC Adv. 2017, 7, 7424–7430. [Google Scholar] [CrossRef]
- Yao, Y.; Tse, J.S. Superconducting hydrogen sulfide. Chem. Eur. J. 2018, 24, 1769–1778. [Google Scholar] [CrossRef]
- Drozdov, A.P.; Eremets, M.I.; Troyan, I.A.; Ksenofontov, V.; Shylin, S.I. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 2015, 525, 73–76. [Google Scholar] [CrossRef]
- Kokail, C.; Heil, C.; Boeri, L. Search for high-Tc conventional superconductivity at megabar pressures in the lithium-sulfur system. Phys. Rev. B 2016, 94, 060502. [Google Scholar] [CrossRef]
- Li, Y.; Jin, X.; Cui, T.; Zhuang, Q.; Zhang, D.; Meng, X.; Bao, K.; Liu, B.; Zhou, Q. Unexpected stable stoichiometries and superconductivity of potassium-rich sulfides. RSC Adv. 2017, 7, 44884–44889. [Google Scholar] [CrossRef]
- Duan, D.; Liu, Y.; Tian, F.; Li, D.; Huang, X.; Zhao, Z.; Yu, H.; Liu, B.; Tian, W.; Cui, T. Pressure-induced metallization of dense (H2S)2H2 with high-Tc superconductivity. Sci. Rep. 2014, 4, 6968. [Google Scholar] [CrossRef]
- Lonie, D.C.; Zurek, E. XtalOpt: An open-source evolutionary algorithm for crystal structure prediction. Comput. Phys. Commun. 2011, 182, 372–387. [Google Scholar] [CrossRef]
- XtalOpt. Available online: http://xtalopt.github.io (accessed on 19 August 2019).
- Avery, P.; Falls, Z.; Zurek, E. XtalOpt Version r10: An open-source evolutionary algorithm for crystal structure prediction. Comput. Phys. Commun. 2017, 217, 210–211. [Google Scholar] [CrossRef]
- Lonie, D.C.; Zurek, E. Identifying duplicate crystal structures: XtalComp, an open-source solution. Comput. Phys. Commun. 2012, 183, 690–697. [Google Scholar] [CrossRef]
- Avery, P.; Zurek, E. RandSpg: An open-source program for generating atomistic crystal structures with specific spacegroups. Comput. Phys. Commun. 2017, 213, 208–216. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Maintz, S.; Deringer, V.L.; Tchougréeff, A.L.; Dronskowski, R. LOBSTER: A tool to extract chemical bonding from plane-wave based DFT. J. Comput. Chem. 2016, 37, 1030–1035. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Klimeš, J.; Bowler, D.R.; Michaelides, A. Chemical accuracy for the van der Waals density functional. J. Phys. Condens. Matter 2010, 22, 022201. [Google Scholar] [CrossRef]
- Klimeš, J.; Bowler, D.R.; Michaelides, A. Van der Waals density functionals applied to solids. Phys. Rev. B 2011, 83, 195131. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Parlinski, K.; Li, Z.Q.; Kawazoe, Y. First-principles determination of the soft mode in cubic ZrO2. Phys. Rev. Lett. 1997, 78, 4063–4066. [Google Scholar] [CrossRef]
- Chaput, L.; Togo, A.; Tanaka, I.; Hug, G. Phonon-phonon interactions in transition metals. Phys. Rev. B 2011, 84, 094302. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Dal Corso, A. Pseudopotentials periodic table: From H to Pu. Comput. Mater. Sci. 2014, 95, 337–350. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef]
- Allen, P.B.; Dynes, R.C. Transition temperature of strong-coupled superconductors reanalyzed. Phys. Rev. B 1975, 12, 905–922. [Google Scholar] [CrossRef]
- Hanfland, M.; Loa, I.; Syassen, K. Sodium under pressure: Bcc to fcc structural transition and pressure-volume relation to 100 GPa. Phys. Rev. B 2002, 65, 184109. [Google Scholar] [CrossRef]
- Gregoryanz, E.; Lundegaard, L.F.; McMahon, M.I.; Guillaume, C.; Nelmes, R.J.; Mezouar, M. Structural diversity of sodium. Science 2008, 320, 1054–1057. [Google Scholar] [CrossRef]
- McMahon, M.I.; Gregoryanz, E.; Lundegaard, L.F.; Loa, I.; Guillaume, C.; Nelmes, R.J.; Kleppe, A.K.; Amboage, M.; Wilhelm, H.; Jephcoat, A.P. Structure of sodium above 100 GPa by single-crystal x-ray diffraction. Proc. Natl. Acad. Sci. USA 2007, 104, 17297–17299. [Google Scholar] [CrossRef]
- Ma, Y.; Eremets, M.; Oganov, A.R.; Xie, Y.; Trojan, I.; Medvedev, S.; Lyakhov, A.O.; Valle, M.; Prakapenka, V. Transparent dense sodium. Nature 2009, 458, 182–185. [Google Scholar] [CrossRef]
- Meyer, B. Elemental sulfur. Chem. Rev. 1976, 76, 367–388. [Google Scholar] [CrossRef]
- Zakharov, O.; Cohen, M.L. Theory of structural, electronic, vibrational, and superconducting properties of high-pressure phases of sulfur. Phys. Rev. B 1995, 52, 12572–12578. [Google Scholar] [CrossRef]
- Gavryushkin, P.N.; Litasov, K.D.; Dobrosmislov, S.S.; Popov, Z.I. High-pressure phases of sulfur: Topological analysis and crystal structure prediction. Phys. Status Solidi B 2017, 254, 1600857. [Google Scholar] [CrossRef]
- Luo, H.; Greene, R.G.; Ruoff, A.L. β-Po phase of sulfur at 162 GPa: X-ray diffraction study to 212 GPa. Phys. Rev. Lett. 1993, 71, 2943–2946. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Lozano, A.; Escribano, B.; Akhmatskaya, E.; Carrasco, J. Assessment of van der Waals inclusive density functional theory methods for layered electroactive materials. Phys. Chem. Chem. Phys. 2017, 19, 10133–10139. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Constantin, L.A.; Terentjevs, A.; Della Sala, F.; Fabiano, E. Gradient-dependent upper bound for the exchange-correlation energy and application to density functional theory. Phys. Rev. B 2015, 91, 041120. [Google Scholar] [CrossRef]
- Peng, H.; Perdew, J.P. Rehabilitation of the Perdew-Burke-Ernzerhof generalized gradient approximation for layered materials. Phys. Rev. B 2017, 95, 081105. [Google Scholar] [CrossRef]
- Terentjev, A.V.; Constantin, L.A.; Pitarke, J. Dispersion-corrected PBEsol exchange-correlation functional. Phys. Rev. B 2018, 98, 214108. [Google Scholar] [CrossRef]
- Peng, H.; Yang, Z.H.; Perdew, J.P.; Sun, J. Versatile van der Waals density functional based on a meta-generalized gradient approximation. Phys. Rev. X 2016, 6, 041005. [Google Scholar] [CrossRef]
- Rettig, S.J.; Trotter, J. Refinement of the structure of orthorhombic sulfur, α-S8. Acta Cryst. 1987, C43, 2260–2262. [Google Scholar] [CrossRef]
- Wagman, D.D.; Evans, W.H.; Parker, V.B.; Schumm, R.H.; Halow, I.; Bailey, S.M.; Churney, K.L.; Nuttall, R.L. The NBS tables of chemical thermodynamic properties. J. Phys. Chem. Ref. Data 1982, 11 (Suppl. 2), 1–392. [Google Scholar]
- Tegman, R. The crystal structure of sodium tetrasulphide, Na2S4. Acta Cryst. 1973, B29, 1463–1469. [Google Scholar] [CrossRef]
- Kelly, B.; Woodward, P. Crystal structure of dipotassium pentasulphide. J. Chem. Soc. Dalton Trans. 1976, 1314–1316. [Google Scholar] [CrossRef]
- Böttcher, P. Synthesis and crystal structure of the dirubidiumpentachalcogenides Rb2S5 and Rb2Se5. Z. Kristallogr. Cryst. Mater. 1979, 150, 65–73. [Google Scholar] [CrossRef]
- Böttcher, P.; Kruse, K. Darstellung und kristallstruktur von dicaesiumpentasulfid (Cs2S5). J. Less Common Met. 1982, 83, 115–125. [Google Scholar] [CrossRef]
- Janz, G.J.; Downey, J.R.; Roduner, E.; Wasilczyk, G.J.; Coutts, J.W.; Eluard, A. Raman studies of sulfur-containing anions in inorganic polysulfides. Sodium polysulfides. Inorg. Chem. 1976, 15, 1759–1763. [Google Scholar] [CrossRef]
- Te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- ADF2018. SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands. Available online: http://www.scm.com (accessed on 19 August 2019).
- Feng, J.; Hennig, R.G.; Ashcroft, N.; Hoffmann, R. Emergent reduction of electronic state dimensionality in dense ordered Li-Be alloys. Nature 2008, 451, 445–458. [Google Scholar] [CrossRef]
- Miao, M. Helium chemistry: React with nobility. Nat. Chem. 2017, 9, 409–410. [Google Scholar] [CrossRef]
- Liu, Z.; Botana, J.; Hermann, A.; Zurek, E.; Yan, D.; Lin, H.; Miao, M. Reactivity of He with ionic compounds under high pressure. Nat. Commun. 2018, 9, 951. [Google Scholar] [CrossRef]
- Zarifi, N.; Liu, H.; Tse, J.S.; Zurek, E. Crystal structures and electronic properties of Xe-Cl compounds at high pressure. J. Phys. Chem. C 2018, 122, 2941–2950. [Google Scholar] [CrossRef]
- Mishra, A.K.; Muramatsu, T.; Liu, H.; Geballe, Z.M.; Somayazulu, M.; Ahart, M.; Baldini, M.; Meng, Y.; Zurek, E.; Hemley, R.J. New calcium hydrides with mixed atomic and molecular hydrogen. J. Phys. Chem. C 2018, 122, 19370–19378. [Google Scholar] [CrossRef]
- Gregoryanz, E.; Degtyareva, O.; Somayazulu, M.; Hemley, R.J.; Mao, H.K. Melting of dense sodium. Phys. Rev. Lett. 2005, 94, 185502. [Google Scholar] [CrossRef]
- Neaton, J.B.; Ashcroft, N.W. On the constitution of sodium at higher densities. Phys. Rev. Lett. 2001, 86, 2830–2833. [Google Scholar] [CrossRef]
- Tutchton, R.; Chen, X.; Wu, Z. Is sodium a superconductor under high pressure? J. Chem. Phys. 2017, 146, 014705. [Google Scholar] [CrossRef]
- Struzhkin, V.V.; Hemley, R.J.; Mao, H.K.; Timofeev, Y.A. Superconductivity at 10–17 K in compressed sulphur. Nature 1997, 390, 382–384. [Google Scholar] [CrossRef]
- Rudin, S.P.; Liu, A.Y. Predicted simple-cubic phase and superconducting properties for compressed sulfur. Phys. Rev. Lett. 1999, 83, 3049–3052. [Google Scholar] [CrossRef]
- Monni, M.; Bernardini, F.; Sanna, A.; Profeta, G.; Massidda, S. Origin of the critical temperature discontinuity in superconducting sulfur under high pressure. Phys. Rev. B 2017, 95, 064516. [Google Scholar] [CrossRef]
- Center for Computational Research, University at Buffalo. Available online: http://hdl.handle.net/10477/79221 (accessed on 19 August 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, N.; Bi, T.; Zarifi, N.; Yan, Y.; Zurek, E. A First-Principles Exploration of NaxSy Binary Phases at 1 atm and Under Pressure. Crystals 2019, 9, 441. https://doi.org/10.3390/cryst9090441
Geng N, Bi T, Zarifi N, Yan Y, Zurek E. A First-Principles Exploration of NaxSy Binary Phases at 1 atm and Under Pressure. Crystals. 2019; 9(9):441. https://doi.org/10.3390/cryst9090441
Chicago/Turabian StyleGeng, Nisha, Tiange Bi, Niloofar Zarifi, Yan Yan, and Eva Zurek. 2019. "A First-Principles Exploration of NaxSy Binary Phases at 1 atm and Under Pressure" Crystals 9, no. 9: 441. https://doi.org/10.3390/cryst9090441
APA StyleGeng, N., Bi, T., Zarifi, N., Yan, Y., & Zurek, E. (2019). A First-Principles Exploration of NaxSy Binary Phases at 1 atm and Under Pressure. Crystals, 9(9), 441. https://doi.org/10.3390/cryst9090441






