Comparing Cyclic Tension-Compression Effects on CoCrFeMnNi High-Entropy Alloy and Ni-Based Superalloy
Abstract
1. Introduction
2. Materials and Methods
3. Results
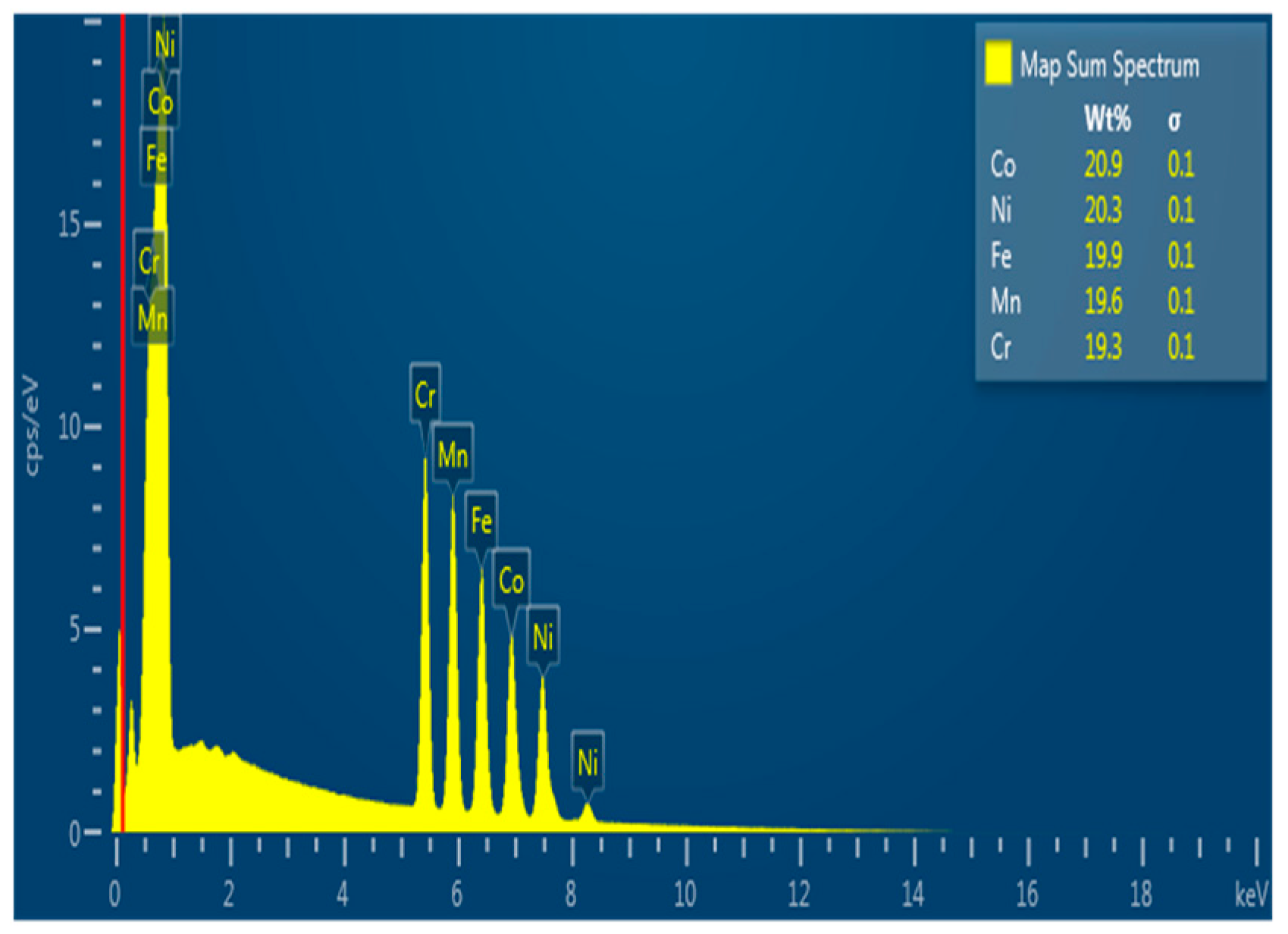
3.1. Chemical Composition of Alloying Elements in CoCrFeMnNi
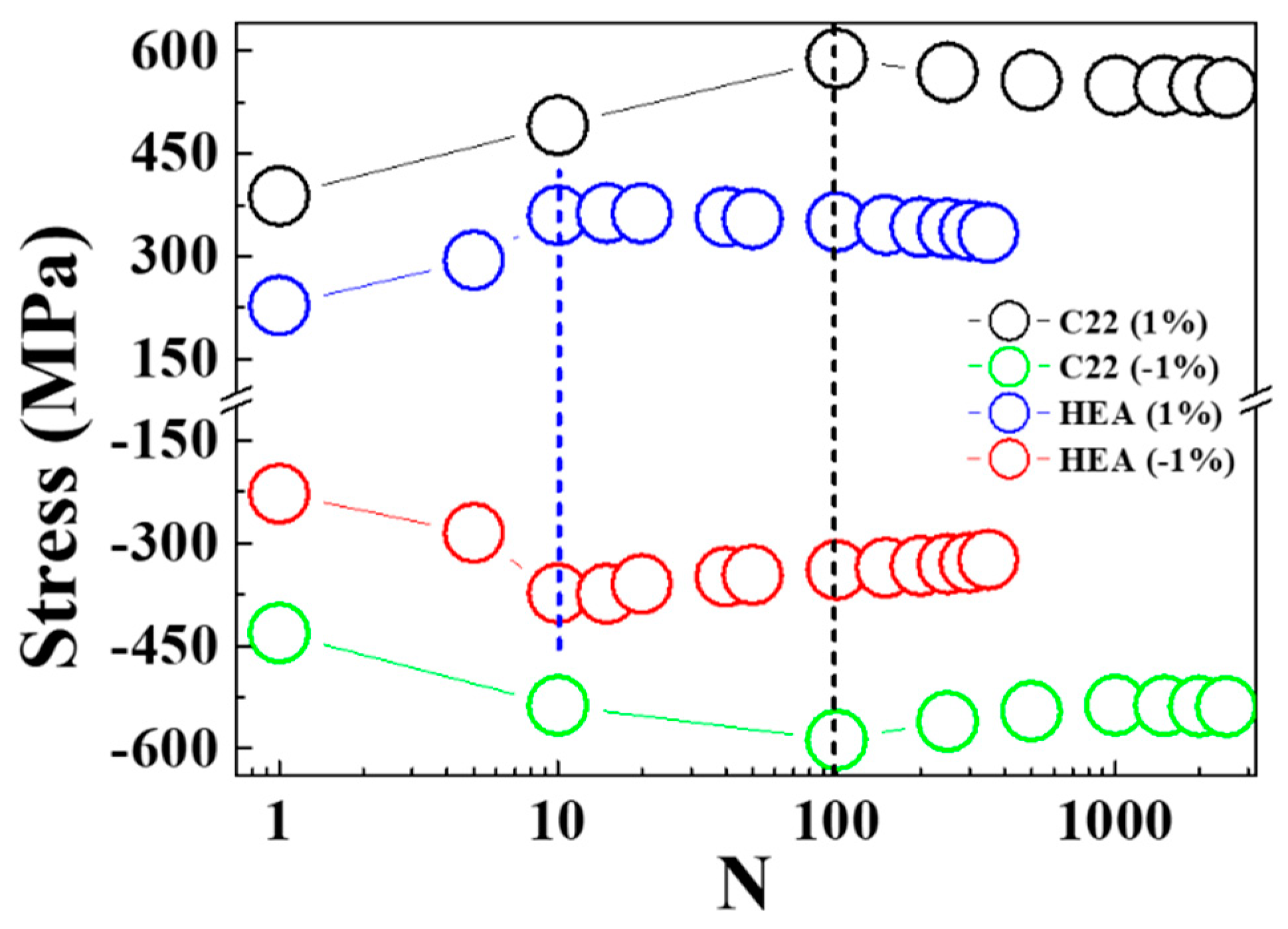
3.2. Low-Cycle Fatigue Experiments
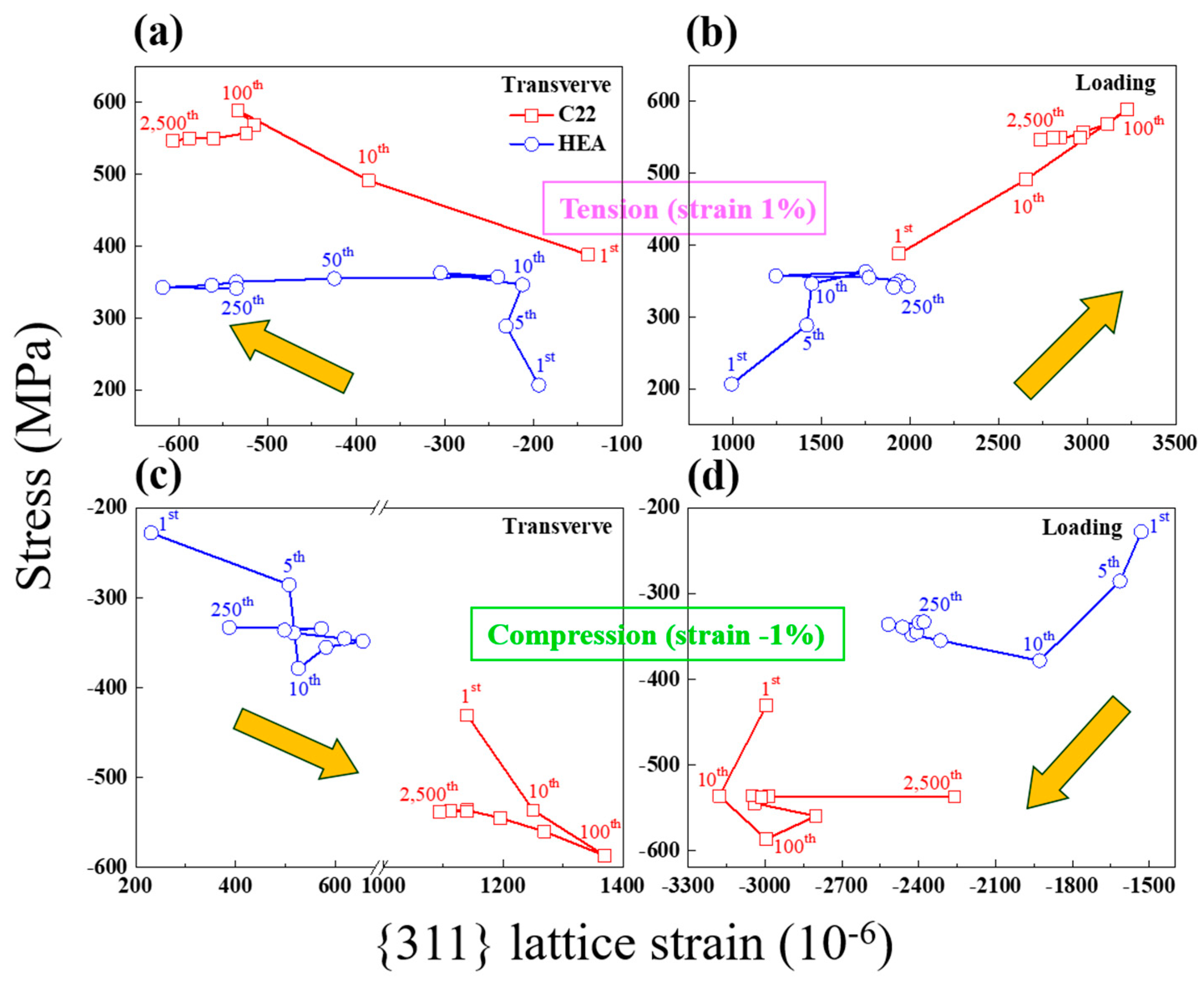
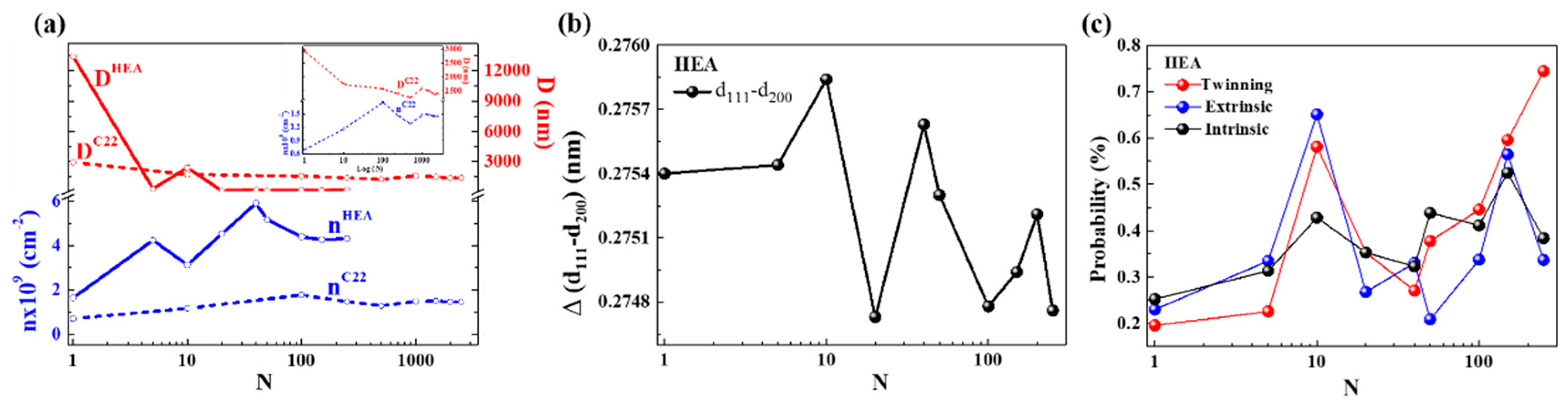
3.3. Lattice Strain Evolution during Tension-Compression Cyclic Loadings
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Seifi, M.; Li, D.; Yong, Z.; Liaw, P.K.; Lewandowski, J.J. Fracture Toughness and Fatigue Crack Growth Behavior of As-Cast High-Entropy Alloys. Jom 2015, 67, 2288–2295. [Google Scholar] [CrossRef]
- Hemphill, M.A.; Yuan, T.; Wang, G.Y.; Yeh, J.W.; Tsai, C.W.; Chuang, A.; Liaw, P.K. Fatigue behavior of Al0.5CoCrCuFeNi high entropy alloys. Acta Materialia 2012, 60, 5723–5734. [Google Scholar] [CrossRef]
- Tang, Z.; Yuan, T.; Tsai, C.W.; Yeh, J.W.; Lundin, C.D.; Liaw, P.K. Fatigue behavior of a wrought Al0.5CoCrCuFeNi two-phase high-entropy alloy. Acta Materialia 2015, 99, 247–258. [Google Scholar] [CrossRef]
- Chen, P.; Lee, C.; Wang, S.Y.; Seifi, M.; Lewandowski, J.J.; Dahmen, K.A.; Jia, H.; Xie, X.; Chen, B.; Yeh, J.W.; et al. Fatigue behavior of high-entropy alloys: A review. Sci. China Technol. Sci. 2017, 61, 168–178. [Google Scholar] [CrossRef]
- Thurston, K.V.S.; Gludovatz, B.; Hohenwarter, A.; Laplanche, G.; George, E.P.; Ritchie, R.O. Effect of temperature on the fatigue-crack growth behavior of the high-entropy alloy CrMnFeCoNi. Intermetallics 2017, 88, 65–72. [Google Scholar] [CrossRef]
- Niendorf, T.; Wegener, T.; Li, Z.; Raabe, D. Unexpected cyclic stress-strain response of dual-phase high-entropy alloys induced by partial reversibility of deformation. Scr. Mater. 2018, 143, 63–67. [Google Scholar] [CrossRef]
- Niu, C.; LaRosa, C.R.; Miao, J.; Mills, M.J.; Ghazisaeidi, M. Magnetically-driven phase transformation strengthening in high entropy alloys. Nat. Commun. 2018, 9, 1363. [Google Scholar] [CrossRef]
- Tracy, C.L.; Park, S.; Rittman, D.R.; Zinkle, S.J.; Bei, H.; Lang, M.; Ewing, R.C.; Mao, W.L. High pressure synthesis of a hexagonal close-packed phase of the high-entropy alloy CrMnFeCoNi. Nat. Commun. 2017, 8, 15634. [Google Scholar] [CrossRef]
- Zhang, F.; Wu, Y.; Lou, H.; Zeng, Z.; Prakapenka, V.B.; Greenberg, E.; Ren, Y.; Yan, J.; Okasinski, J.S.; Liu, X.; et al. Polymorphism in a high-entropy alloy. Nat. Commun. 2017, 8, 15687. [Google Scholar] [CrossRef]
- Huang, E.W.; Lin, C.M.; Jain, J.; Shieh, S.R.; Wang, C.P.; Chuang, Y.C.; Liao, Y.F.; Zhang, D.Z.; Huang, T.; Lam, T.-N.; et al. Irreversible phase transformation in a CoCrFeMnNi high entropy alloy under hydrostatic compression. Mater. Today Commun. 2018, 14, 10–14. [Google Scholar] [CrossRef]
- Huang, E.W.; Barabash, R.I.; Clausen, B.; Liaw, P.K. Cyclic-Loading Induced Lattice-Strain Asymmetry in Loading and Transverse Directions. Metall. Mater. Trans. A 2012, 43, 1454–1461. [Google Scholar] [CrossRef]
- Huang, E.W.; Barabash, R.I.; Wang, Y.; Clausen, B.; Li, L.; Liaw, P.K.; Ice, G.E.; Ren, Y.; Choo, H.; Pike, L.M.; et al. Plastic behavior of a nickel-based alloy under monotonic-tension and low-cycle-fatigue loading. Int. J. Plast. 2008, 24, 1440–1456. [Google Scholar] [CrossRef]
- Huang, E.W.; Barabash, R.I.; Clausen, B.; Liu, Y.L.; Kai, J.J.; Ice, G.E.; Woods, K.P.; Liaw, P.K. Fatigue-induced reversible/irreversible structural-transformations in a Ni-based superalloy. Int. J. Plast. 2010, 26, 1124–1137. [Google Scholar] [CrossRef]
- Huang, E.; Clausen, B.; Wang, Y.; Choo, H.; Liaw, P.; Benson, M.; Pike, L.; Klarstrom, D. A neutron-diffraction study of the low-cycle fatigue behavior of HASTELLOY® C-22HSTM alloy. Int. J. Fatigue 2007, 29, 1812–1819. [Google Scholar] [CrossRef]
- Huang, E.W.; Chang, C.K.; Liaw, P.K.; Suei, T.R. Fatigue induced deformation and thermodynamics evolution in a nano particle strengthened nickel base superalloy. Fatigue Fract Eng Mater Struct. 2016, 39, 675–685. [Google Scholar] [CrossRef]
- Huang, E.W.; Barabash, R.I.; Ice, G.E.; Liu, W.; Liu, Y.L.; Kai, J.J.; Liaw, P.K. Cyclic-loading-induced accumulation of geometrically necessary dislocations near grain boundaries in an Ni-based superalloy. JOM: J. Miner., Met. Mater. Sci. 2009, 61, 53–58. [Google Scholar] [CrossRef]
- Huang, E.W.; Barabash, R.; Jia, N.; Wang, Y.D.; Ice, G.E.; Clausen, B.; Horton, J.; Liaw, P.K. Slip-System-Related Dislocation Study from In-Situ Neutron Measurements. Metall. Mater. Trans. A 2008, 39, 3079. [Google Scholar] [CrossRef]
- Huang, E.W.; Lin, C.M.; Juang, J.Y.; Chang, Y.J.; Chang, Y.W.; Wu, C.S.; Tsai, C.W.; Yeh, A.C.; Shieh, S.R.; Wang, C.P.; et al. Deviatoric deformation kinetics in high entropy alloy under hydrostatic compression. J. Alloys. Compd. 2019, 792, 116–121. [Google Scholar] [CrossRef]
- Huang, E.W.; Yu, D.; Yeh, J.W.; Lee, C.; An, K.; Tu, S.Y. A study of lattice elasticity from low entropy metals to medium and high entropy alloys. Scr. Mater. 2015, 101, 32–35. [Google Scholar] [CrossRef]
- Woo, W.; Huang, E.W.; Yeh, J.W.; Choo, H.; Lee, C.; Tu, S.Y. In-situ neutron diffraction studies on high-temperature deformation behavior in a CoCrFeMnNi high entropy alloy. Intermetallics 2015, 62, 1–6. [Google Scholar] [CrossRef]
- Von Dreele, R.B.; Larson, A.C. General Structure Analysis System (GSAS). Los Alamos Natl. Lab. Rep. LAUR 2004, 86–748. [Google Scholar]
- Ribárik, G.; Ungár, T.; Ungár, J. MWP-fit a program for multiple whole-profile fitting of diffraction peak profiles by ab initio theoretical functions. J. Appl. Crystallogr. 2001, 34, 669–676. [Google Scholar] [CrossRef]
- Velterop, L.; Delhez, R.; de Keijser, Th.H.; Mittemeijera, E.J.; Reefman, D. X-ray diffraction analysis of stacking and twin faults in f.c.c. metals. J. Appl. Cryst. 2000, 33, 296–306. [Google Scholar] [CrossRef]
- Suzuki, Y.; Egami, T. Shear deformation of glassy metals: Breakdown of cauchy relationship and anelasticity. J. Non. Cryst. Solids 1985, 75, 361–366. [Google Scholar] [CrossRef]
- Mughrabi, H. Dislocation clustering and long-range internal stresses in monotonically and cyclically deformed metal crystals. Rev. Phys. Appl. (Paris) 1988, 23, 367–379. [Google Scholar] [CrossRef]
- Laplanche, G.; Kostka, A.; Horst, O.M.; Eggeler, G.; George, E.P. Microstructure evolution and critical stress for twinning in the CrMnFeCoNi high-entropy alloy. Acta Materialia 2016, 118, 152–163. [Google Scholar] [CrossRef]
- Yu, P.F.; Cheng, H.; Zhang, L.J.; Zhang, H.; Ma, M.Z.; Li, G.; Liaw, P.K.; Liu, R.P. Nanotwin’s formation and growth in an AlCoCuFeNi high-entropy alloy. Scr. Mater. 2016, 114, 31–34. [Google Scholar] [CrossRef]
- Ungár, T. Microstructural parameters from X-ray diffraction peak broadening. Scr. Mater. 2004, 51, 777–781. [Google Scholar] [CrossRef]
- Warren, B.E. X-ray diffraction. Phys. Today 1970, 23, 53. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lam, T.-N.; Chou, Y.-S.; Chang, Y.-J.; Sui, T.-R.; Yeh, A.-C.; Harjo, S.; Lee, S.Y.; Jain, J.; Lai, B.-H.; Huang, E.-W. Comparing Cyclic Tension-Compression Effects on CoCrFeMnNi High-Entropy Alloy and Ni-Based Superalloy. Crystals 2019, 9, 420. https://doi.org/10.3390/cryst9080420
Lam T-N, Chou Y-S, Chang Y-J, Sui T-R, Yeh A-C, Harjo S, Lee SY, Jain J, Lai B-H, Huang E-W. Comparing Cyclic Tension-Compression Effects on CoCrFeMnNi High-Entropy Alloy and Ni-Based Superalloy. Crystals. 2019; 9(8):420. https://doi.org/10.3390/cryst9080420
Chicago/Turabian StyleLam, Tu-Ngoc, You-Shiun Chou, Yao-Jen Chang, Tsung-Ruei Sui, An-Chou Yeh, Stefanus Harjo, Soo Yeol Lee, Jayant Jain, Bo-Hong Lai, and E-Wen Huang. 2019. "Comparing Cyclic Tension-Compression Effects on CoCrFeMnNi High-Entropy Alloy and Ni-Based Superalloy" Crystals 9, no. 8: 420. https://doi.org/10.3390/cryst9080420
APA StyleLam, T.-N., Chou, Y.-S., Chang, Y.-J., Sui, T.-R., Yeh, A.-C., Harjo, S., Lee, S. Y., Jain, J., Lai, B.-H., & Huang, E.-W. (2019). Comparing Cyclic Tension-Compression Effects on CoCrFeMnNi High-Entropy Alloy and Ni-Based Superalloy. Crystals, 9(8), 420. https://doi.org/10.3390/cryst9080420





