An Accurate Method for Crystallographic Reconstruction of Parent Austenite from Inherited Martensite in a Low-Alloy Steel

Abstract

The microstructure of austenite at high temperatures, which cannot be reserved at room temperatures, determines the properties of its transformed phase in low-alloy steels. Consequently, an accurate method is herein developed to reconstruct local orientations of the parent austenite ($\mathsf{\gamma }$) phase from electron backscatter diffraction maps of the martensite (${\alpha }^{\prime }$) microstructure. The orientation map of ${\alpha }^{\prime }$ is cropped into a grid of data squares as the reconstruction unit. The cropped square is then divided into the square inherited from only one $\mathsf{\gamma }$ grain and the square inherited from more than one $\mathsf{\gamma }$ grain. The local orientations around parent $\mathsf{\gamma }$ grain boundaries are more accurately determined using a newly proposed reconstruction criterion. Furthermore, the solution spaces for the orientation relationship and the parent $\mathsf{\gamma }$ orientation are refined, which simultaneously improves the calculation accuracy and efficiency of reconstruction procedure. The validated reconstruction method is applied to obtain local orientations of the deformed $\mathsf{\gamma }$ microstructure accurately.

1. Introduction

In low-alloy steels, the grain size, morphology, and crystallographic orientations of the austenite $\left(\mathsf{\gamma }\right)$ phase at high temperature are known to determine the microstructures and properties of the product phase. Therefore, knowledge of the evolution of $\mathsf{\gamma }$ microstructure during hot deformation contributes to clarifying the mechanism of microstructural evolution and optimizing the processing parameters. However, due to unavoidable transformation during cooling, the $\mathsf{\gamma }$ phase at high temperatures cannot be reserved and characterized at room temperature [1]. Various methods have been attempted to overcome the issue but have evident drawbacks. For example, although metallographic etching can be used to reveal prior $\mathsf{\gamma }$ grain boundaries from quenched martensitic microstructures, it often fails owing to low concentration of impurities along prior $\mathsf{\gamma }$ grain boundaries. Moreover, it is impossible to recover the crystallography of the parent phase through this method [2]. Another method is the use of model steels that retain their austenitic structure down to room temperature. As the model steels must be high in alloying elements, the metallurgical phenomenon observed in these steels is not applicable to the studied low-alloy steels [3]. Consequently, there is a need for a more direct and explicit method to observe the $\mathsf{\gamma }$ microstructure.

Recently, reconstruction of the parent $\mathsf{\gamma }$ microstructure from inherited martensite (${\alpha }^{\prime }$) orientation maps measured by electron backscatter diffraction (EBSD) has been proposed for a direct characterization of $\mathsf{\gamma }$ microstructure. There are two main approaches to reconstruct the orientation of parent $\mathsf{\gamma }$ from its inherited variants [4]. First, a reconstruction procedure based on the two-step “nuclei identification” and “nuclei spreading” strategy was proposed by German et al. [5,6]. The method has been used and validated by some reacher in the literature [2,7]. In this method, the domains with preset misorientation tolerance are sorted into different parent grains with robust algorithms and only an average orientation of grain is recovered. Thus, the orientation gradient within grains cannot be obtained in detail using this method. Second, Miyamoto et al. proposed another method to reconstruct the parent $\mathsf{\gamma }$ orientation: minimizing the angular deviation between the experimental ${\alpha }^{\prime }$ orientations and the predicted ones [8,9]. This method includes subdivision of the EBSD map using a grid of squares and calculating the local $\mathsf{\gamma }$ orientation for each square. Therefore, it is more appropriate to deformed microstructures with orientation gradients in parent $\mathsf{\gamma }$ grains. A fundamental aspect of this method is to seek the $\mathsf{\gamma }$ orientation, which transforms into ${\alpha }^{\prime }$ orientations in accordance with the orientation relationship (OR). However, when the cropped region around the grain boundaries of the parent phase contains ${\alpha }^{\prime }$ variants transformed from distinctly different $\mathsf{\gamma }$ grains, a mis-indexing $\mathsf{\gamma }$ orientation will be figured out. In addition, this method is time-consuming, because it intends to use all the scanned data for the calculation of $\mathsf{\gamma }$ orientation. This restricts the calculation efficiency and accuracy [10].

To obtain local orientations of parent $\mathsf{\gamma }$ microstructure, the reconstruction method of the present work focuses on overcoming the limitations above. The local orientations around the grain boundaries of the parent phase are correctly determined using the new reconstruction criterion proposed in this study. Moreover, considering the calculation accuracy and efficiency of the method, a reduced solution space of Euler angles for OR is also proposed. Then, the potential $\mathsf{\gamma }$ orientations for each cropped square can be refined by the thought of reverse phase transformation. Based on the validated reconstruction method, an automatic reconstruction program is developed and applied to the reconstruction of deformed $\mathsf{\gamma }$ microstructure from the orientation maps of inherited ${\alpha }^{\prime }$.

2. Experiment

Fe-0.15C-1.11Cr-1.05Mn-0.27Si-0.06Ti (mass %) alloy is used for the study. Cylindrical specimens of the steel with 8 mm in diameter and 12 mm in length are prepared via machining and then applied in isothermal compression tests on a Gleeble-3500 thermal simulator (Dynamic Systems Inc., Austin, TX, USA). The specimens are heated to 1100 °C with 5 °C/s and austenitized for 300 s. Then, in order to obtain different orientation gradients inside $\mathsf{\gamma }$ grains, the specimens are compressed with a height reduction of 50% at a strain rate of 0.01 and 1 s⁻¹, and quenched to reserve the microstructure. For EBSD observation, specimens are sectioned along the axial direction and then polished in an electrolyte comprising 8% perchloric acid and 92% ethanol at a voltage of 20 V for 15s. Orientation data are acquired with a step size of 0.2–0.4 μm, using a TSL system attached to an FEI Siron200 scanning electron microscopes (SEM, FEI Co., Hillsboro, OR, USA). TSL OIM Analysis software is used to perform data processing of ${\alpha }^{\prime }$ orientations, as well as reconstructed $\mathsf{\gamma }$ orientations.

3. Reconstruction Method

A schematic diagram for reconstruction procedure is given in Figure 1. The intersections of thin dashed lines are the points with ${\alpha }^{\prime }$ orientations, which can be obtained using EBSD. Different colors represent different parent $\mathsf{\gamma }$ grains. Thick lines between them are parent $\mathsf{\gamma }$ grain boundaries (PAGB). In order to analyze the local orientation of parent $\mathsf{\gamma }$, the ${\alpha }^{\prime }$ orientation map is cropped into small data squares (indicated by red boxes in Figure 1). The squares can be divided into two types: one is the square inside the parent $\mathsf{\gamma }$ grain (indicated by S1), where the ${\alpha }^{\prime }$ orientations in this type of square possess a same parent $\mathsf{\gamma }$ orientation. The other is the square covering PAGB (indicated by S2). The procedure of cropping is automatically carried out according to the parameters of L and D. L is the length of one side of the cropped square and D is the distance between neighboring squares. The setting of L needs to ensure that there are at least two different ${\mathsf{\alpha }}^{\prime }$ variants in each square [11]. The ratio of L to D is usually between two and four and it should be adjusted by trial and error for every EBSD mapping.

Figure 1. Schematic representation of a scanned orientation map and cropped data squares.

For the square type of S1, the parent $\mathsf{\gamma }$ orientation can be obtained according to the method proposed in [9] (the calculated orientation satisfies the OR with all the ${\alpha }^{\prime }$ orientations in the square). Then, the determined $\mathsf{\gamma }$ orientation is assigned to the geometric center. However, this method is not appropriate for the square type of S2. This is because S2 contains ${\alpha }^{\prime }$ orientations transformed from both Grain 1 and Grain 2. It is unable to calculate a single $\mathsf{\gamma }$ orientation that satisfies the OR with all of these ${\alpha }^{\prime }$ orientations. However, it is noted that the parent $\mathsf{\gamma }$ orientation of the geometric center is consistent with the parent $\mathsf{\gamma }$ orientation of the partial ${\alpha }^{\prime }$ orientations in this square type. Consequently, the ${\alpha }^{\prime }$ orientations inherited from the grain covering the geometric center, are selected to reconstruct the $\mathsf{\gamma }$ orientation of this square. As shown in the enlarged chart on the right side of Figure 1, the parent $\mathsf{\gamma }$ orientation should be determined only using the ${\alpha }^{\prime }$ orientations from Grain 1. Through this reconstruction method, it is guaranteed that the determined $\mathsf{\gamma }$ orientation for every cropped square is consistent with the grain where the geometric center is located, which improves the reconstruction accuracy.

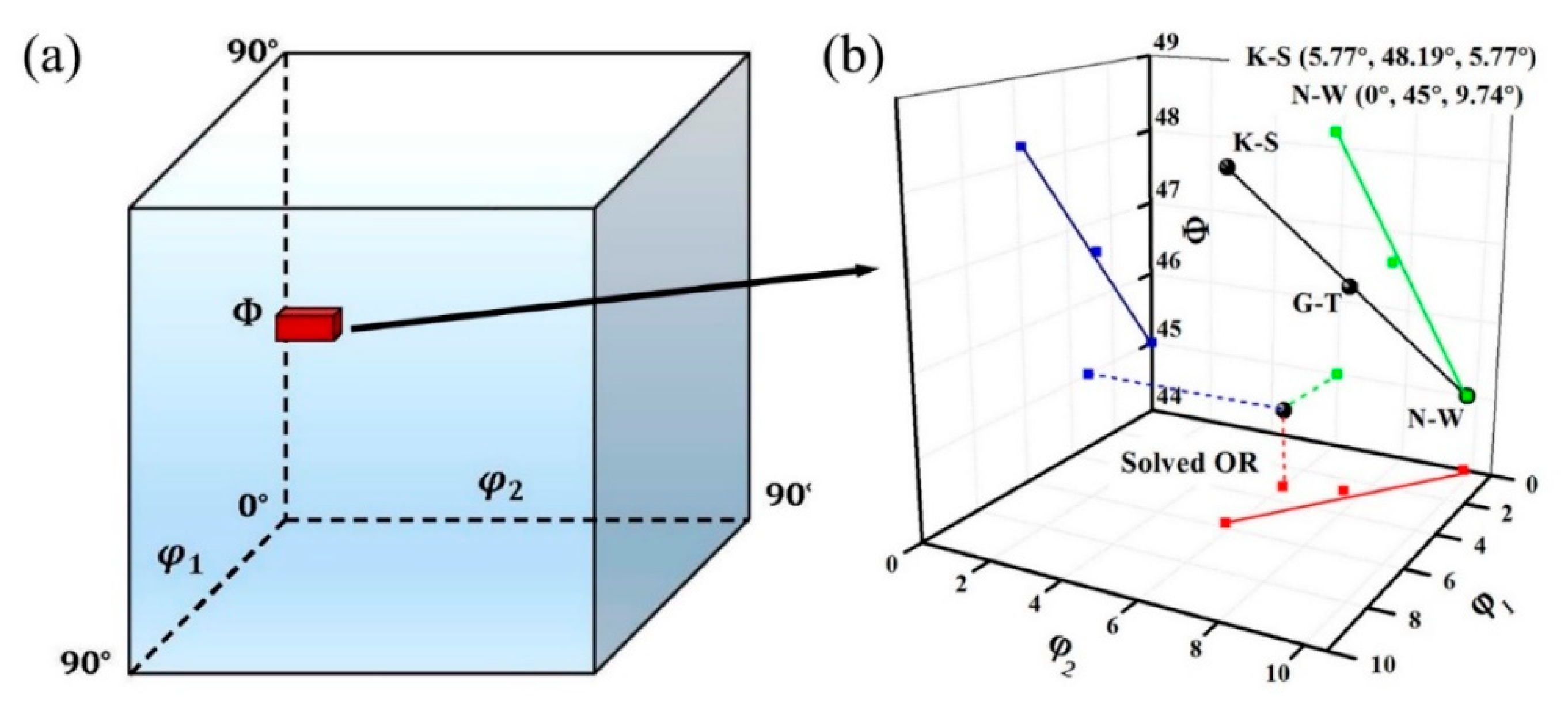
3.1. Precise Solution of the OR

OR defines the possible ${\alpha }^{\prime }$ orientations $\mathrm{inherited}$ from a parent $\mathsf{\gamma }$ orientation. The results of the reconstruction are highly sensitive to the selection of an appropriate OR [7]. It has been proven that the average OR of steels is influenced by their chemical composition and cooling condition during phase transformation [12]. Consequently, the OR should be first determined for the material.

If a region contains at least two ${\alpha }^{\prime }$ variants transformed from a single $\mathsf{\gamma }$ grain, the parent $\mathsf{\gamma }$ orientation ($M^{\gamma }$) and the OR (${\mathrm{V}}^{\gamma \to {\alpha }^{\prime }}$) can be simultaneously obtained through numerical fitting [9]. Firstly, the possible orientations of ${\alpha }^{\prime }$ variants can be calculated as [13]:

$$M_n^{{\alpha }^{\prime }}={\mathrm{V}}^{\gamma \to {\alpha }^{\prime }}{C}_n{M}^{\gamma }$$

(1)

where $C_n$ is the nth conversion matrix of 24 symmetry operations for the cubic system. ${\mathrm{V}}^{\gamma \to {\alpha }^{\prime }}{C}_n$ corresponds to 24 variants of OR. The region contains N data points of $\alpha$ orientations; the ith data point in the region is referred to as $M_i^{\alpha }$. Then, the deviation matrix between calculated and experimental ${\alpha }^{\prime }$ orientations for each $M_i^{\alpha }$ is estimated by [9]:

$$D_i=\left({\mathrm{V}}^{\gamma \to {\alpha }^{\prime }}{C}_n{M}^{\gamma }\right){\left(C_m{M}_i^{{\alpha }^{\prime }}\right)}^{-1}$$

(2)

$C_n$ and $C_m$ are chosen as deviation angle of $D_i$ ($\Delta {\theta }_i$) being minimal for each $M_i^{\alpha }$. At last, for N data points of ${\alpha }^{\prime }$ orientations, the average deviation angle is given by:

$$\Delta {\theta }_{ave}={\displaystyle \sum }_N\Delta {\theta }_i/N$$

(3)

As individual variables, $M^{\gamma }$ and ${\mathrm{V}}^{\gamma \to \alpha }$ can be determined by minimizing $\Delta {\theta }_{ave}$, which is considered as the reconstruction criterion of the selected region.

In a cubic crystal system, all the orientations can be found in a space of Euler angles (${\phi }_1:0-90°$, $\mathsf{\Phi }:0-90°$, ${\phi }_2:0-90°$), which is seen as the entire solution space for ${\mathrm{V}}^{\gamma \to {\alpha }^{\prime }}$ (Figure 2a). The entire space is too large to solve the ${\mathrm{V}}^{\gamma \to \alpha }$ accurately and efficiently. Consequently, the solution space should be reduced. It is noted that ${\mathrm{V}}^{\gamma \to \alpha }$ needs to represent any of the 24 variants and the rest of the variants can be calculated by ${\mathrm{V}}^{\gamma \to {\alpha }^{\prime }}{C}_n$. Thus, the solution space can be reduced according to the classical ORs (Kurdjumov-Sachs (KS), Nishiyama-Wasserman (NW), and Greninger-Troiano (GT)) in low-alloy steels [14]. For the three ORs, a selected variant is described by a combination of two close-packed planes (CPs) and two close-directions (CDs), as well as Euler angles [15]. As shown in Table 1, only KS OR satisfies parallel CPs and parallel CDs, but NW and GT ORs are closed to the parallel relation. Accordingly, the Euler angles of the three ORs are similar. ${\phi }_1$ and ${\phi }_2$ are within the range of $0°$ to $10°$ and $\mathsf{\Phi }$ is within the range of $44°$ to $49°$. It has been proved that the real OR for martensitic transformation always has several degrees of deviations from KS or NW OR [16]. Moreover, ORs measured in steels from EBSD and TEM experimental studies are usually intermediate between KS OR and NW OR [17,18]. As shown in Figure 2b, GT OR is such an OR. Consequently, the solution space for ${\mathrm{V}}^{\gamma \to {\alpha }^{\prime }}$ can be restricted as ${\phi }_1:0-10°;\mathsf{\Phi }:44-49°;{\phi }_2:0-10°$ for numerical fitting (Figure 2b).

Figure 2. (a) Position of reduced solution space in the entire space of Euler angles. (b) Range of the reduced solution space.

Table 1. Miller notations and the corresponding Euler angles for different classical orientation relationships (ORs) [15].

OR	Miller Notation		Euler Angles $\left({\mathit{\phi }}_1 \mathbf{\Phi } {\mathit{\phi }}_2\right)$
	Plane	Direction
KS	${\left(111\right)}_{\gamma }\parallel {\left(110\right)}_{\alpha }$	${\left[1\overline{1}0\right]}_{\gamma }\parallel {\left[1\overline{1}1\right]}_{\alpha }$	$\left(5.77°48.2°5.77°\right)$
NW	${\left(111\right)}_{\gamma }\parallel {\left(110\right)}_{\alpha }$	${\left[1\overline{1}0\right]}_{\gamma }5.2°\mathrm{from}{\left[1\overline{1}1\right]}_{\alpha }$	$\left(0°45°9.74°\right)$
GT	${\left(111\right)}_{\gamma }1°\mathrm{from}{\left(110\right)}_{\alpha }$	${\left[1\overline{1}0\right]}_{\gamma }2.5°\mathrm{from}{\left[1\overline{1}1\right]}_{\alpha }$	$\left(2.7°46.6°7.5°\right)$

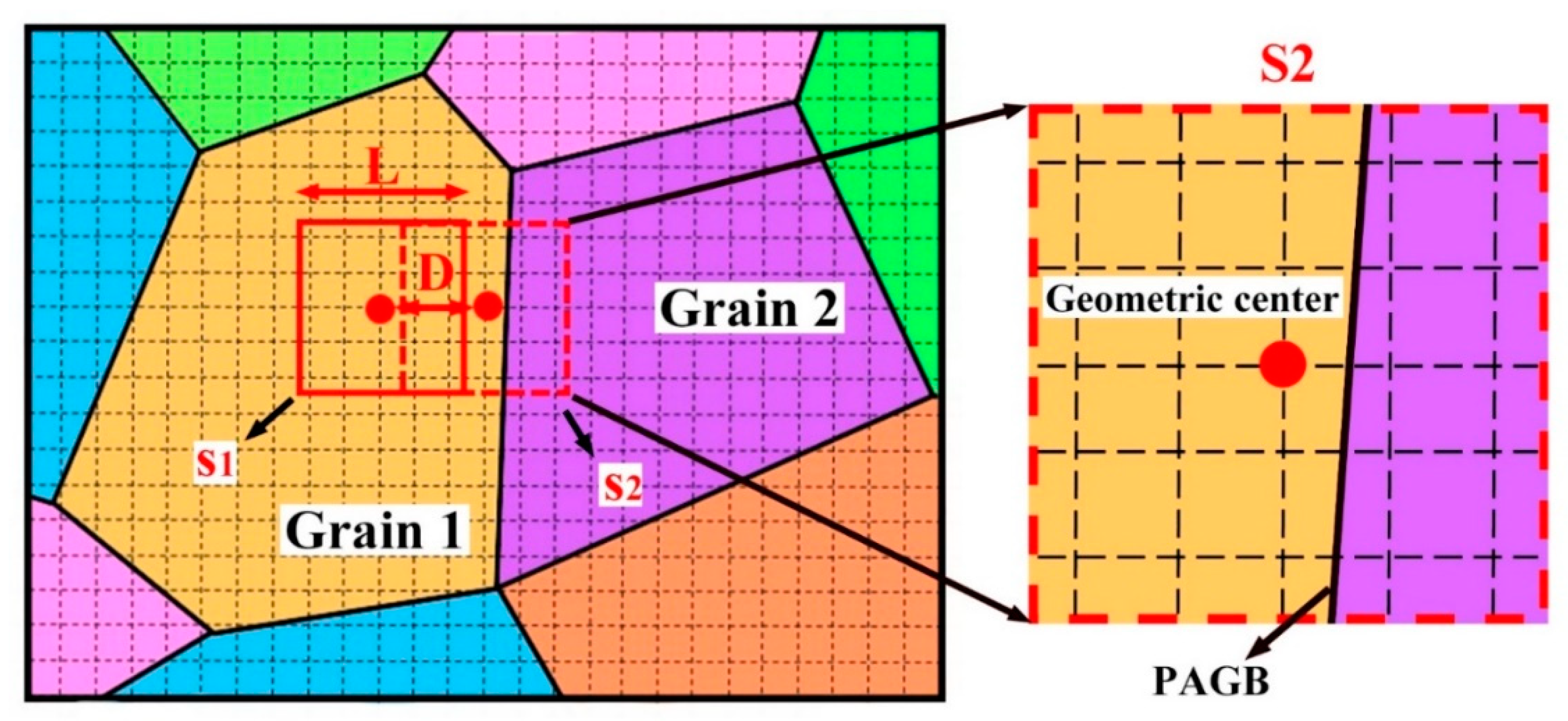
3.2. Determination of the Local $\gamma$ Orientation

In previous studies, the parent $\mathsf{\gamma }$ orientation was determined from the entire solution space, which can be refined in this step. First, the 24 potential parent orientations of every data point in the cropped square are calculated using the OR solved in Section 3.1. Subsequently, these orientations can be assembled as potential $\mathsf{\gamma }$ orientations for the cropped square. The calculation is derived as follows:

$$M_{i,j}^{\gamma }={\left({\mathrm{V}}^{\gamma \to {\alpha }^{\prime }}{C}_n\right)}^{-1}\left(C_m{M}_i^{{\alpha }^{\prime }}\right)$$

(4)

The minimum $\Delta {\theta }_{ave}$ is calculated for every cropped square from $M_{i,j}^{\gamma }$. If the minimum $\Delta {\theta }_{ave}$ is lower than a predefined distinguishing angle (${\theta }_d)$, the ${\alpha }^{\prime }$ variants in the cropped square are transformed from only one$\mathsf{\gamma }$ grain. Then, the $M^{\gamma }$ is correctly determined through $\Delta {\theta }_{ave}$ minimization. If not, the cropped square contains ${\alpha }^{\prime }$ variants inherited from more than one $\mathsf{\gamma }$ grain. The determination of $M^{\gamma }$ is operated in a different way. Notably, the geometric center of the cropped square is always located at the parent $\mathsf{\gamma }$ grain, which provides the majority of ${\alpha }^{\prime }$ orientations. Based on this idea, a new reconstruction criterion is proposed as follows.

After substituting the candidate value of $M^{\gamma }$ from $M_{i,j}^{\gamma }$ into Equation (2), the $\Delta {\mathsf{\theta }}_i$ value for the ith measured point can be obtained. The data point for which $\Delta {\mathsf{\theta }}_i<{\theta }_d$ is considered as the qualified point satisfying the OR. The number of qualified points is expressed as ${\mathrm{N}}_{\Delta {\mathsf{\theta }}_i<{\theta }_d}$. The percentage of qualified points among N measured points for every candidate $M_{i,j}^{\gamma }$ is given as:

$$\mathrm{P}={\mathrm{N}}_{\Delta {\mathsf{\theta }}_i<{\theta }_d}/N$$

(5)

Finally, $M^{\gamma }$ is determined from $M_{i,j}^{\gamma }$ by maximizing P for the cropped square with ${\alpha }^{\prime }$ variants from different parent $\mathsf{\gamma }$ grains.

The reconstruction criterion for both types of squares can be summarized and expressed as follows:

$$\mathrm{C}=\left[\left(\mathrm{F}-1\right)·\Delta {\theta }_{ave}+\left(F+1\right)·P\right]/2$$

(6)

where F is defined as the discriminant factor for cropped squares, and is expressed as:

$$\mathrm{F}=\left|\Delta {\theta }_{ave}-{\mathsf{\theta }}_d\right|/\left(\Delta {\theta }_{ave}-{\mathsf{\theta }}_d\right)$$

(7)

When $\Delta {\theta }_{ave}$ is less than ${\mathsf{\theta }}_d$ (F = −1), the cropped square is from a parent $\mathsf{\gamma }$ grain. When $\Delta {\theta }_{ave}$ is greater than ${\mathsf{\theta }}_d$ (F = 1), the cropped square contains ${\alpha }^{\prime }$ orientations from more than one parent $\mathsf{\gamma }$ grain. The local $\mathsf{\gamma }$ orientation can be determined for all cropped squares only when C is at a maximum.

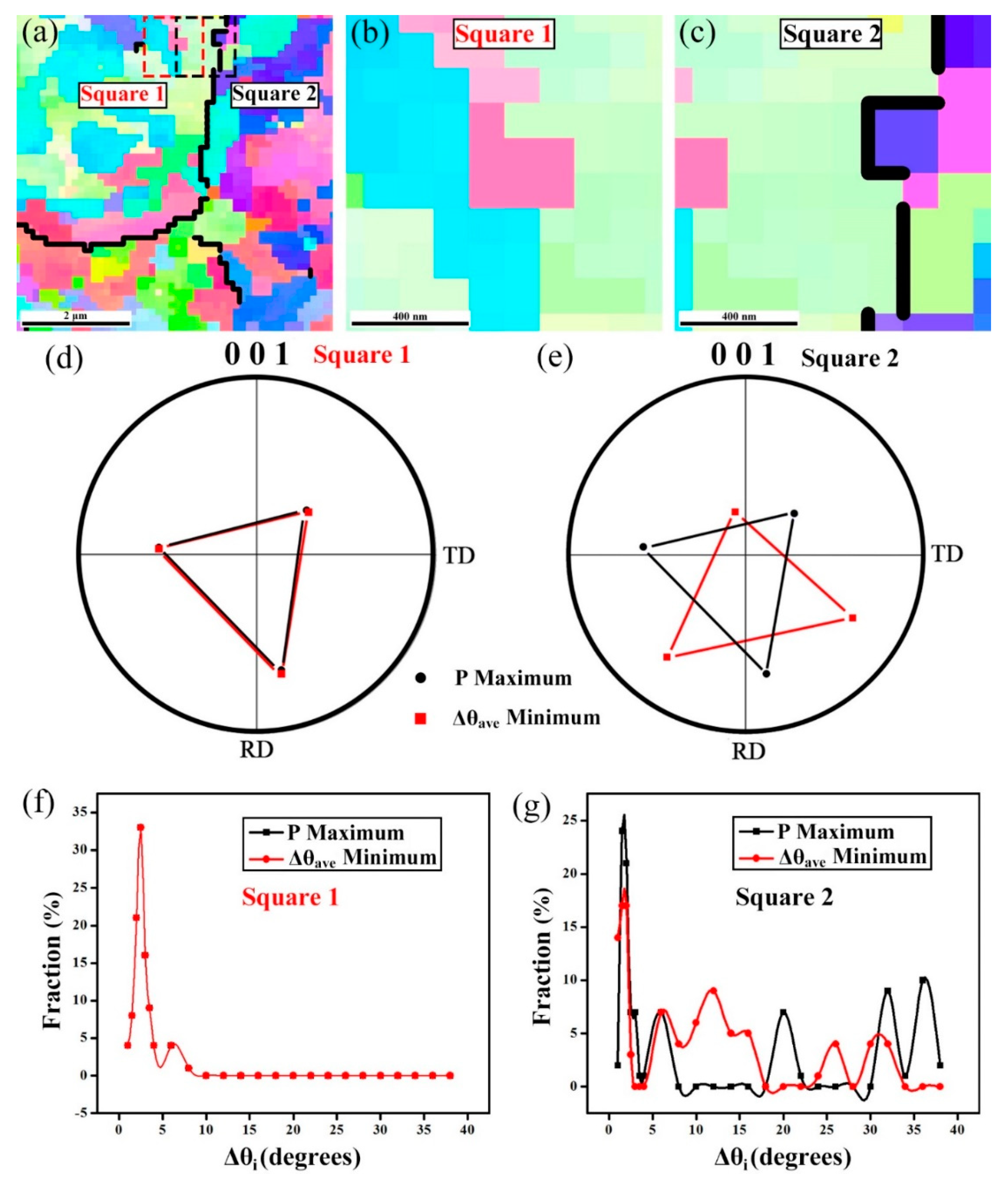
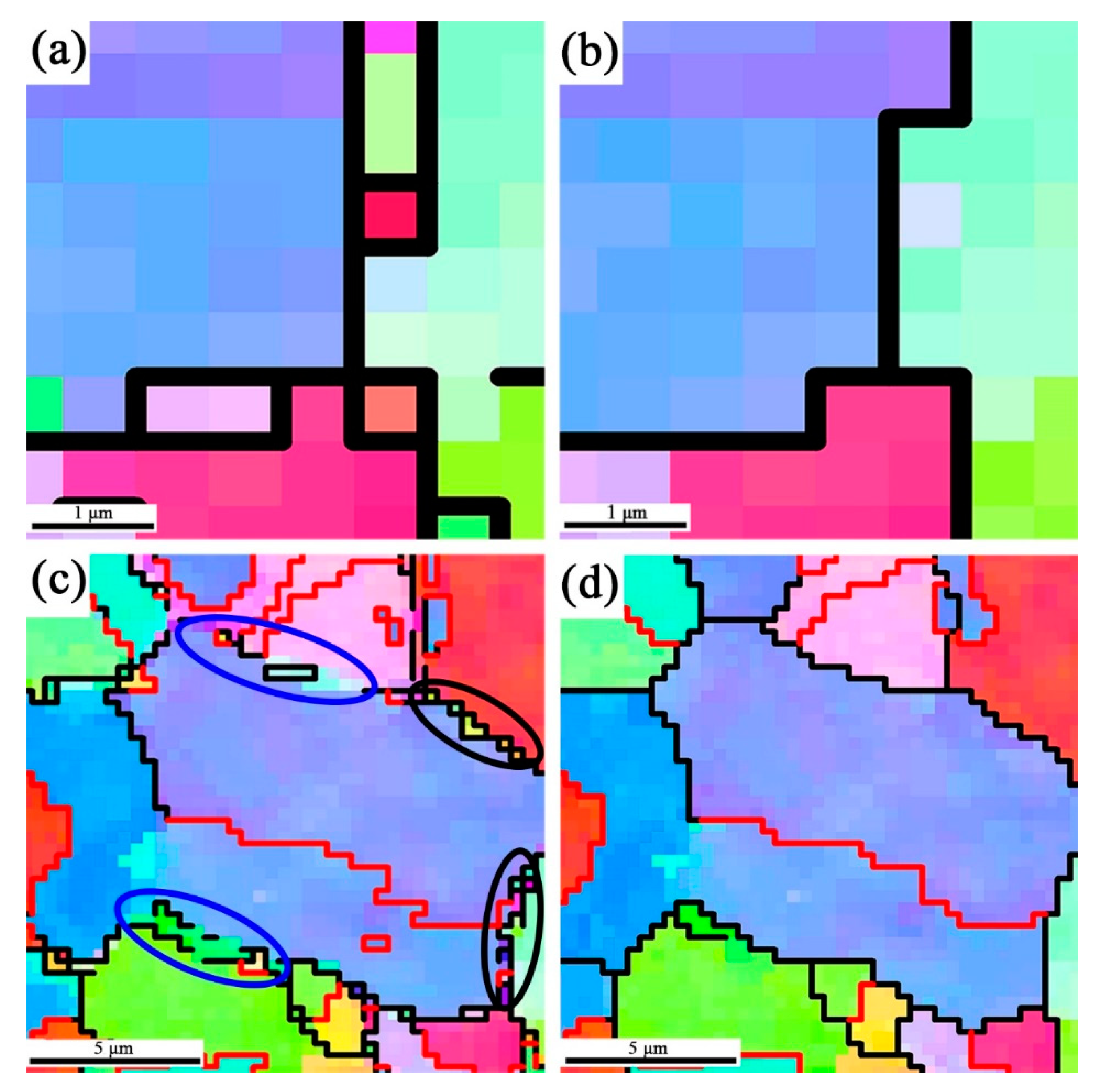
4. Experimental Verification and Application

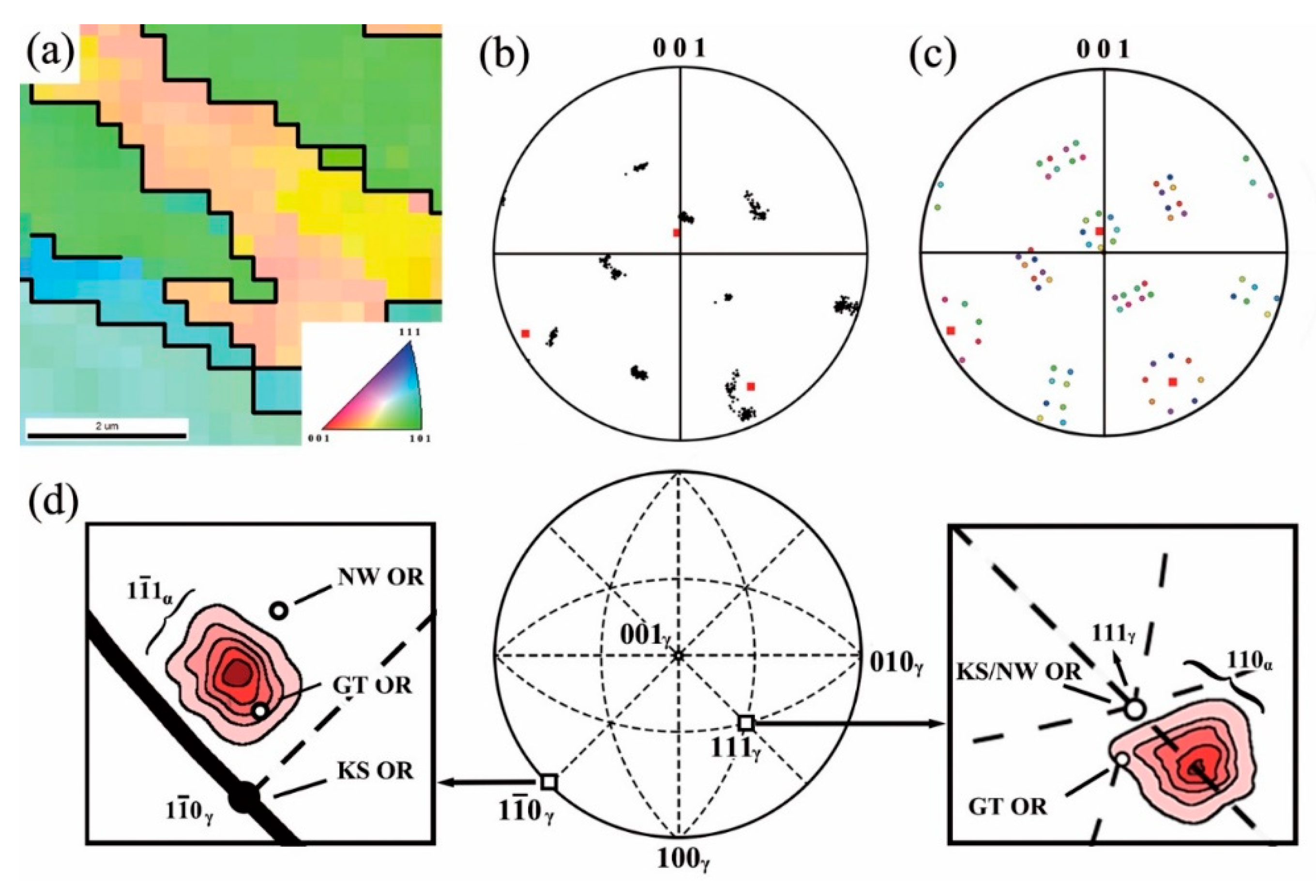
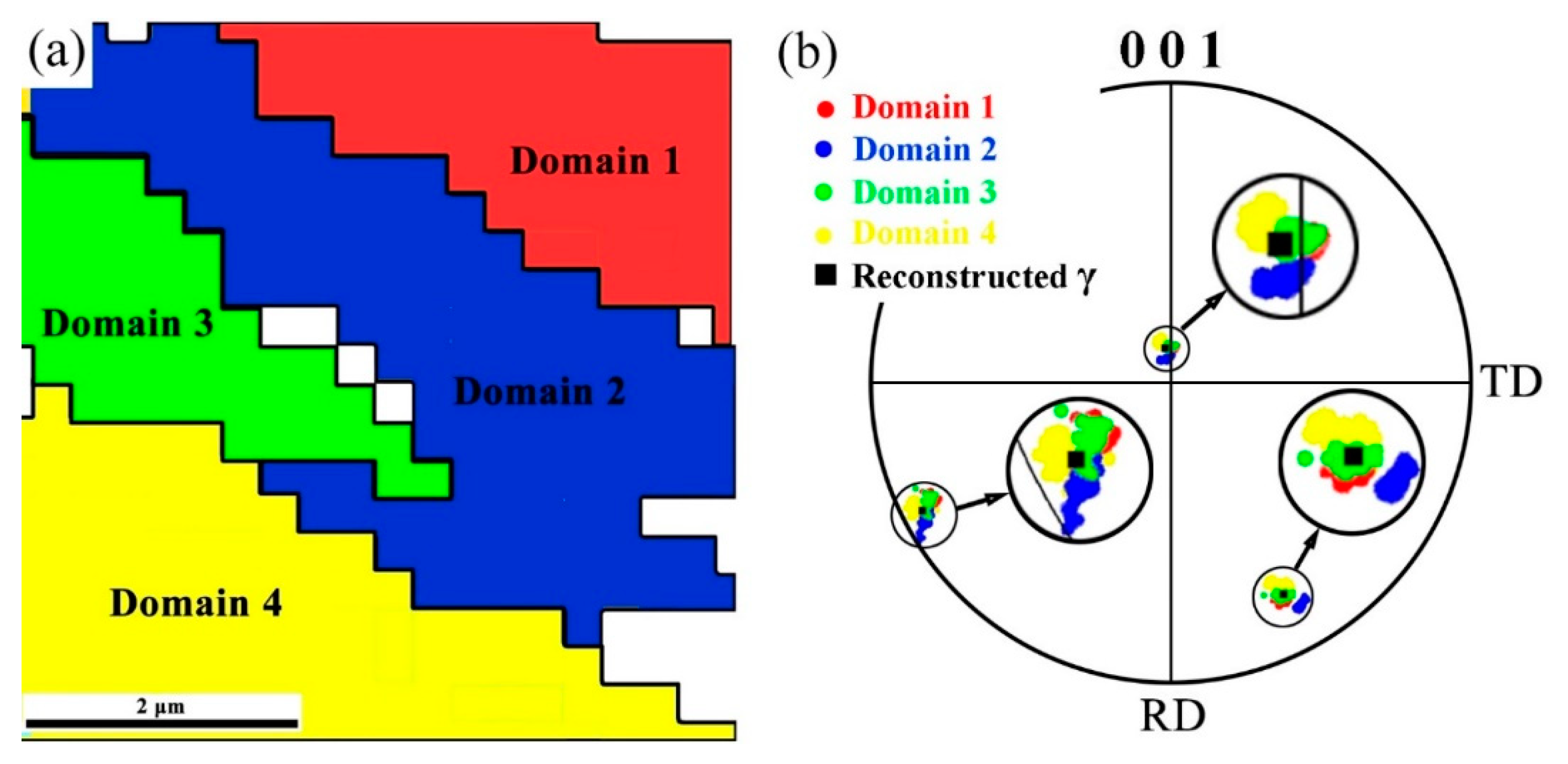
4.1. Verification

Figure 3a shows the inverse pole figure (IPF) map of a manually cropped region with several variants transformed from one $\mathsf{\gamma }$ grain. Using the reduced solution space of Euler angles proposed in Section 3.1, the OR and the parent $\mathsf{\gamma }$ orientation were determined by numerical fitting for this region. The 001 pole figure of the measured ${\alpha }^{\prime }$ orientations in Figure 3a, as well as the reconstructed $\mathsf{\gamma }$ orientation, are presented in Figure 3b. In addition, the 001 pole figure of all ${\alpha }^{\prime }$ orientations predicted by the solved OR and the reconstructed $\mathsf{\gamma }$ orientation are shown in Figure 3c. The measured ${\alpha }^{\prime }$ orientations (black dots in Figure 3c) and predicted ${\alpha }^{\prime }$ orientations (colored dots in Figure 3d) indicate good agreement between the experimental and calculated data. It was proven that the reduced solution space of Euler angles could be effectively used to solve the OR. The quantity of data in Figure 3a is not sufficient to determine the average OR appropriate for all the $\mathsf{\gamma }$ grains [11]. Therefore, data regions inside different $\mathsf{\gamma }$ grains were selected. Figure 1d shows a 001_γ standard stereographic projections, indicating a deviation from the parallel relations of CP (${\left(111\right)}_{\gamma }$ and ${\left(110\right)}_{\alpha }$) and CD (${\left[1\overline{1}0\right]}_{\gamma }$ and ${\left[1\overline{1}1\right]}_{\alpha }$), which was satisfied in KS OR. The density contours were calculated using ORs solved from different regions. Furthermore, the peak position was considered as the average OR. Thus, the average OR of this low-alloy steel was solved as ${\phi }_1:3.3°;\mathsf{\Phi }:45.1°;{\phi }_2:6.2°$. For this average OR, the angle between the CPs was $2°$, while the angle between the CDs was $3.5°$.

Figure 3. (a) The inverse pole figure (IPF) map of $\alpha$ orientations transformed from one $\mathsf{\gamma }$ grain. (b) 001 pole figure of $\alpha$ orientations (black dots) and the reconstructed $\mathsf{\gamma }$ orientation (red square dots) in (a). (c) 001 pole figure of the $\alpha$ orientations (colored dots) predicted by the solved orientation relationship (OR) and the reconstructed $\mathsf{\gamma }$ orientation (red square dots). (d) 001_γ standard stereographic projections on which the $\alpha$ directions of $1\overline{1}{1}_{\alpha }$ and ${110}_{\alpha }$ are represented by iso-density contours.

After identifying the average OR of the steel, the solution space for the parent $\mathsf{\gamma }$ orientation of every cropped square was refined using Equation (4). It should be further discussed whether the potential orientations in the refined space can cover the real parent $\mathsf{\gamma }$ orientation. The parent $\mathsf{\gamma }$ orientation of the ${\alpha }^{\prime }$ orientation map in Figure 3a was determined from the entire solution space. Then, every ${\alpha }^{\prime }$ orientation in the map was sorted into one of 24 variants. As shown in Figure 4a, the orientation map was mainly divided into four different domains. In each domain, ${\alpha }^{\prime }$ orientations were considered bearing the same variant of the OR. Then, the potential $\mathsf{\gamma }$ orientations around the target $\mathsf{\gamma }$ orientation (black dots) were calculated by Equation (4) and shown in the 001 pole figure (Figure 4b). The ${\alpha }^{\prime }$ orientations inside each domain were not consistent owing to orientation scatterings during martensitic transformation [19]. Therefore, the reversely calculated $\mathsf{\gamma }$ orientations for each domain were also scattered. As shown in Figure 4b, these orientations not only cover the$\mathsf{\gamma }$ orientation to be determined but were densely dispersed around the real parent $\mathsf{\gamma }$ orientation. Consequently, the refined solution space also guaranteed the reconstruction accuracy.

Figure 4. (a) Domains bearing the same variant of the OR in Figure 3a. (b) 001 pole figure of the potential $\mathsf{\gamma }$ orientations around the reconstructed $\mathsf{\gamma }$ orientation for Domains 1–4.

The ${\alpha }^{\prime }$ orientation map in Figure 5a was cropped into 225 squares for reconstruction of the $\mathsf{\gamma }$ microstructure. The black lines in the map represent boundaries with misorientation angles between $21°$ and $47°$, which partially reveal PAGB [20]. Therefore, the cropped squares could not avoid covering the $\mathsf{\gamma }$ grain boundaries. The minimum $\Delta {\theta }_{ave}$ was calculated for every cropped square. The frequency of minimum $\Delta {\theta }_{ave}$ is shown in Figure 5a. The values of minimum $\Delta {\theta }_{ave}$ for cropped squares inside the parent $\mathsf{\gamma }$ grains concentrate in the low-value zone follow a normal distribution. In this case, the deviation angle was mainly due to the true variation of OR between the product and parent phases, as previously indicated by Kelly et al. [16], as well as by errors in the EBSD measurements. However, for the cropped square containing $\alpha$ orientations from different parent $\mathsf{\gamma }$ grains, the minimum $\Delta {\theta }_{ave}$ presented a large value. As shown in the partial enlargement of Figure 4a, the descent stage of normal distribution tended to increase owing to the latter cropped squares. The value of the first inflection point was considered as the distinguishing value (${\theta }_d$) for two types of cropped squares. The value of ${\theta }_d$ is $3.3°$ for the map in Figure 5a. Through the analysis of various EBSD data of this steel, the values of ${\theta }_d$ were in the range of $3.2-3.7°$.

Figure 5. (a) IPF map of $\alpha$ with parent $\mathsf{\gamma }$ grain boundaries (PAGB). (b) Frequency of the minimum $\Delta {\theta }_{ave}$ of 225 cropped squares from Figure 5a.

To validate the proposed criterion of P maximization, an IPF map of ${\alpha }^{\prime }$ with evident PAGB was selected from the dashed box in Figure 5a. There were two adjacent cropped squares called Squares 1 and 2 (Figure 6a). Both squares consisted of 100 data points. Square 1 was in the interior of parent $\mathsf{\gamma }$ grain, whereas Square 2 covered two $\mathsf{\gamma }$ grains (Figure 6c). With the criteria of $\Delta {\theta }_{ave}$ minimization and P maximization for Square 1, the reconstructed $\mathsf{\gamma }$ orientations were obtained and shown in the 001 pole figure (Figure 6d). The parent $\mathsf{\gamma }$ orientations determined by the two criteria and the distributions of $\Delta {\mathsf{\theta }}_i$ were almost the same (Figure 6f). More than 90% of $\Delta {\mathsf{\theta }}_i$ was less than $3.3°$. However, using the criteria of $\Delta {\theta }_{ave}$ minimization and P maximization in Square 2, two different $\mathsf{\gamma }$ orientations were determined and shown in the 001 pole figure (Figure 6e). Most ${\alpha }^{\prime }$ orientations in Square 2 were inherited from the grain on the left side, where all orientations in Square 1 belong. Thus, the solved parent $\mathsf{\gamma }$ orientation of Square 2 should be the same as that of Square 1. As shown in Figure 6e, the criterion of P maximization satisfied the requirement, whereas the criterion of $\Delta {\theta }_{ave}$ minimization yielded a mis-indexing orientation. The distributions of $\Delta {\mathsf{\theta }}_i$ for the reconstructed $\mathsf{\gamma }$ orientations obtained by the two criteria were shown in Figure 6g. The $\mathsf{\gamma }$ orientation obtained by the criterion of P maximization had more measured points whose $\Delta {\mathsf{\theta }}_i$ was less than $3.3°$.

Figure 6. (a) Enlarged IPF map of the dashed box in 5(a). IPF maps of cropped Squares 1 (b) and 2 (c). (d) 001 pole figure of the $\mathsf{\gamma }$ orientations determined by two different criteria for Square 1 (d) and Square 2 (e). Distribution of $\Delta {\mathsf{\theta }}_i$ of the determined $\mathsf{\gamma }$ orientations by two different criteria for Square 1 (f) and Square 2 (g).

The map in Figure 6a was reconstructed using only the conventional criterion of $\Delta {\theta }_{ave}$ minimization. There were mis-indexing orientations along the PAGB, as shown in Figure 7a. When the newly proposed criterion of C maximization was applied, the reconstruction quality along PAGB was evidently improved (Figure 7b). The entire map in Figure 5a was also reconstructed using the conventional and newly proposed criteria (Figure 7c,d). As shown in Figure 7c, the reconstructed map exhibited failures around the PAGB. Two-layer grain boundaries were generated in the black oval. In addition, prior boundaries were not presented clearly in the blue oval. Both of these features were unfavorable for grain size statistics. The reconstructed map in Figure 7d showed a more unambiguous morphology of the grains than that in Figure 7c. During hot deformation of austenitic materials, dynamic recrystallization (DRX) always generated small grains around the initial grain boundaries. Therefore, the newly proposed reconstruction criterion enhanced the capacity of characterization of the microstructure around the PAGB. Furthermore, many twins were generated in austenitic materials, which also required high quality of reconstructed boundaries [21].

Figure 7. Reconstructed IPF map for measured data in Figure 6a by the criterion of $\Delta {\theta }_{ave}$ minimization (a) and the newly proposed criterion (b). Reconstructed IPF map for measured data in Figure 5a by the criterion of $\Delta {\theta }_{ave}$ minimization (c) and the newly proposed criterion (d). (Black lines: misorientation angles >$15°$; Red lines: $\mathsf{\Sigma }3$ boundaries).

4.2. Application

According to the improved reconstruction method, an automatic program was written in C language. The IPF maps with the misorientation angle distribution (MAD) charts of the $\alpha$ microstructure at strain rates of 0.01 and 1 s⁻¹ are shown in Figure 8a,c. The boundaries of black lines with misorientation angles between $21-47°$ were also shown in the $\alpha$ maps. The IPF map showed a morphology of fully lath martensite. The MAD of $\alpha$ transformed from $\mathsf{\gamma }$ deformed at different strain rates were similar. Furthermore, 95% misorientation angels were concentrated in the range of $0-15°$ and $50-60°$. This is related to the crystallographic relationship of the adjacent variants obtained from the KS-based OR [22]. Moreover, the MAD of the ${\alpha }^{\prime }$ map was not evidently influenced by different strain rates. The IPF maps of the reconstructed $\mathsf{\gamma }$ microstructure were obtained using the improved reconstruction procedure, shown in Figure 8b,d. Overall, the reconstructed $\mathsf{\gamma }$ grain boundaries (>$15°$) appear to be consistent with the black lines in Figure 8a,c. The MAD of the reconstructed $\mathsf{\gamma }$ at low and high strain rates showed different tendencies. There were fewer low angle boundaries ($<15°$) existing at 1 s⁻¹ than that at 0.01 s⁻¹. This indicates the fraction of DRX is more obvious at 1 s^-1. Furthermore, more $\mathsf{\Sigma }3$ twin boundaries were generated at a high strain rate. This is because the formation of $\mathsf{\Sigma }3$ twin boundaries was promoted by DRX [23,24].

Figure 8. IPF maps with misorientation angle distribution (MAD) charts of $\alpha$ and reconstructed $\mathsf{\gamma }$ deformed at strain rate of 0.01 ${\mathrm{s}}^{-1}$ (a,b) and 1 ${\mathrm{s}}^{-1}$ (c,d). (Black lines: misorientation angles >$15°$; Red lines: $\mathsf{\Sigma }3$ boundaries in (b,d)).

When analyzing the behavior of DRX using EBSD, it is necessary to obtain the distribution of low angle boundaries and high angle boundaries. The reconstruction procedure proposed in this study precisely reconstructed orientation gradients and low angle boundaries. It was difficult for the reconstruction approach of the nuclei identification and spreading strategy to satisfy this requirement. The proposed reconstruction criterion enhanced the manipulation of reconstruction around PAGB as well as some special boundaries. It was proven that the characterization of twin boundaries by the procedure was consistent with the existing studies. Thus, the proposed reconstruction method had a strong capacity for indexing local orientations of parent $\mathsf{\gamma }$ microstructure.

5. Conclusions

An accurate method to reconstruct the local $\mathsf{\gamma }$ orientation has been presented and applied to the martensitic structure of a low-alloy steel. The following results were obtained:

• A reduced solution space of Euler angles for the OR to be determined was proposed, based on the classical ORs. Thus, an average OR for this steel can be accurately determined with high calculation efficiency. The angular deviations between CPs and CDs were found to be $2°$ and $3.5°$, respectively.
• Further, the solution range of the parent $\mathsf{\gamma }$ orientation for every square was refined. The 24 potential parent $\mathsf{\gamma }$ orientations of every measured point in the cropped square were reversely calculated using the solved OR and assembled as the candidate $\mathsf{\gamma }$ orientations for numerical fitting.
• Cropped squares containing variants inherited from different parent $\mathsf{\gamma }$ grains were separated from those inherited from one parent $\mathsf{\gamma }$ grain, i.e., a discriminant factor (F). A unified criterion of C maximization was proposed, appropriate to both types of squares.
• The present method was applied to the EBSD maps of martensitic phase in the studied steel. It verified that the method accurately reconstructs morphology and crystallography of deformed parent $\mathsf{\gamma }$ grains.