Fe Melting Transition: Electrical Resistivity, Thermal Conductivity, and Heat Flow at the Inner Core Boundaries of Mercury and Ganymede
Abstract
1. Introduction
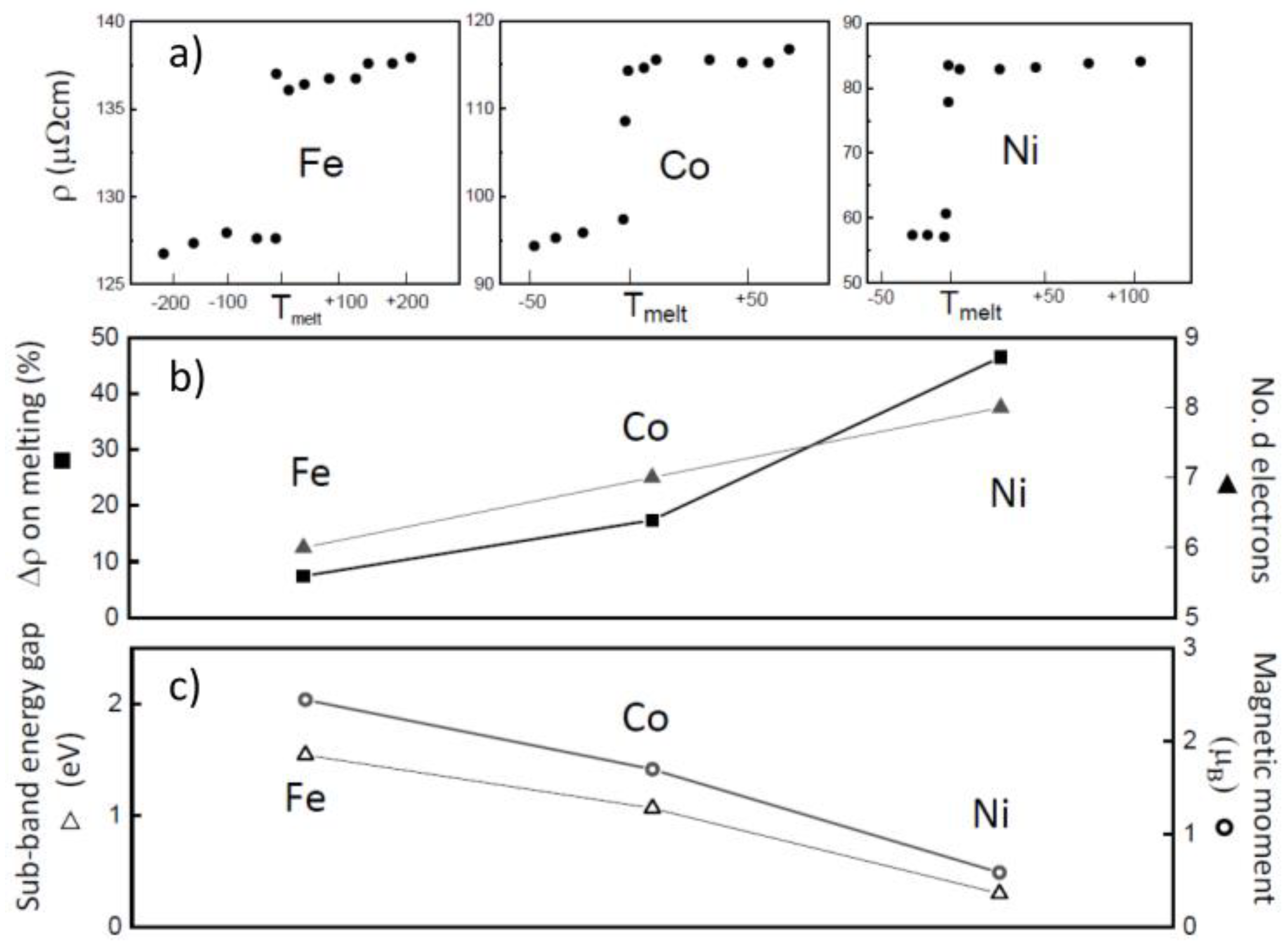
2. Electronic Scattering in Ferromagnetic Metals
3. Results and Discussion
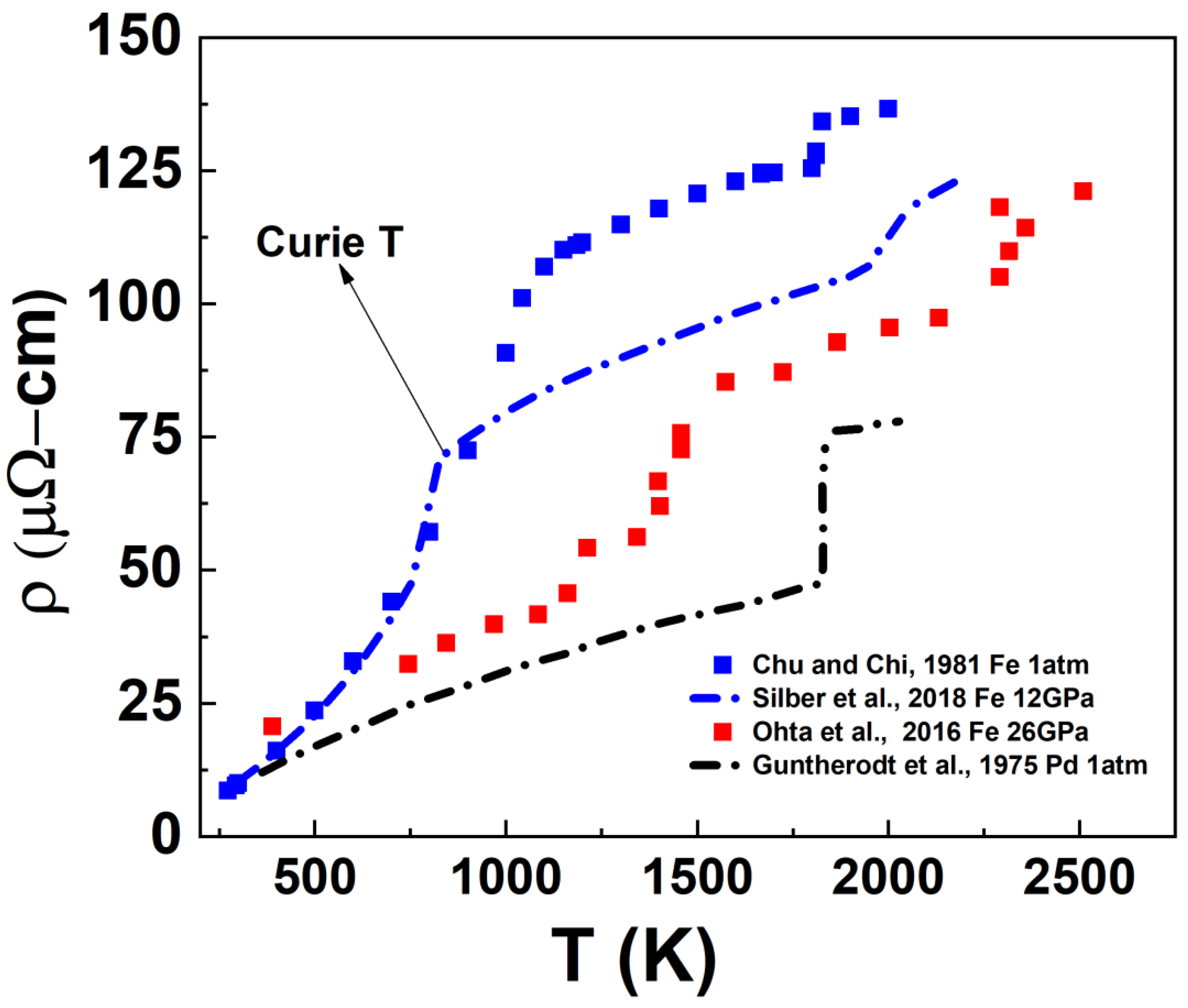
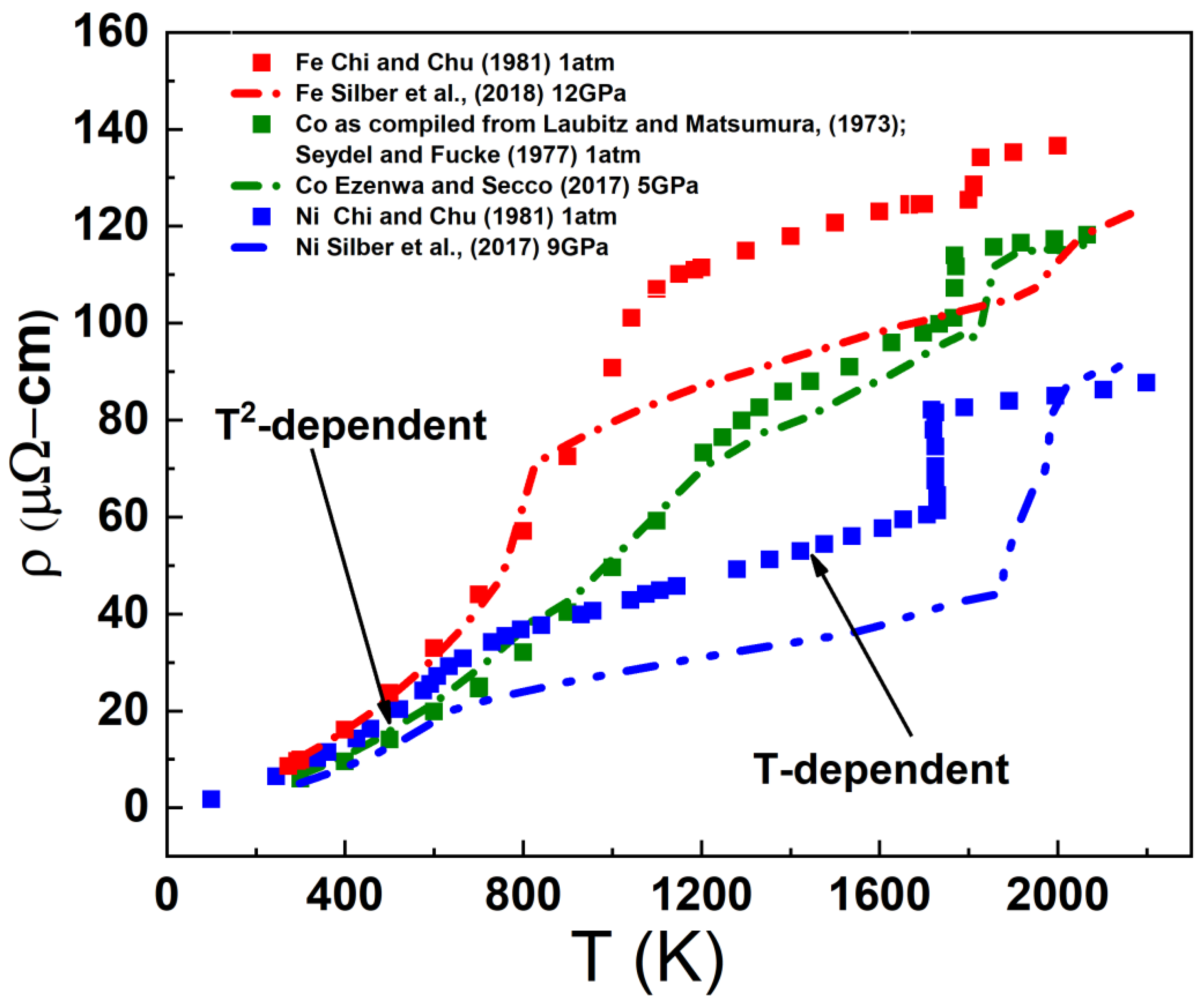
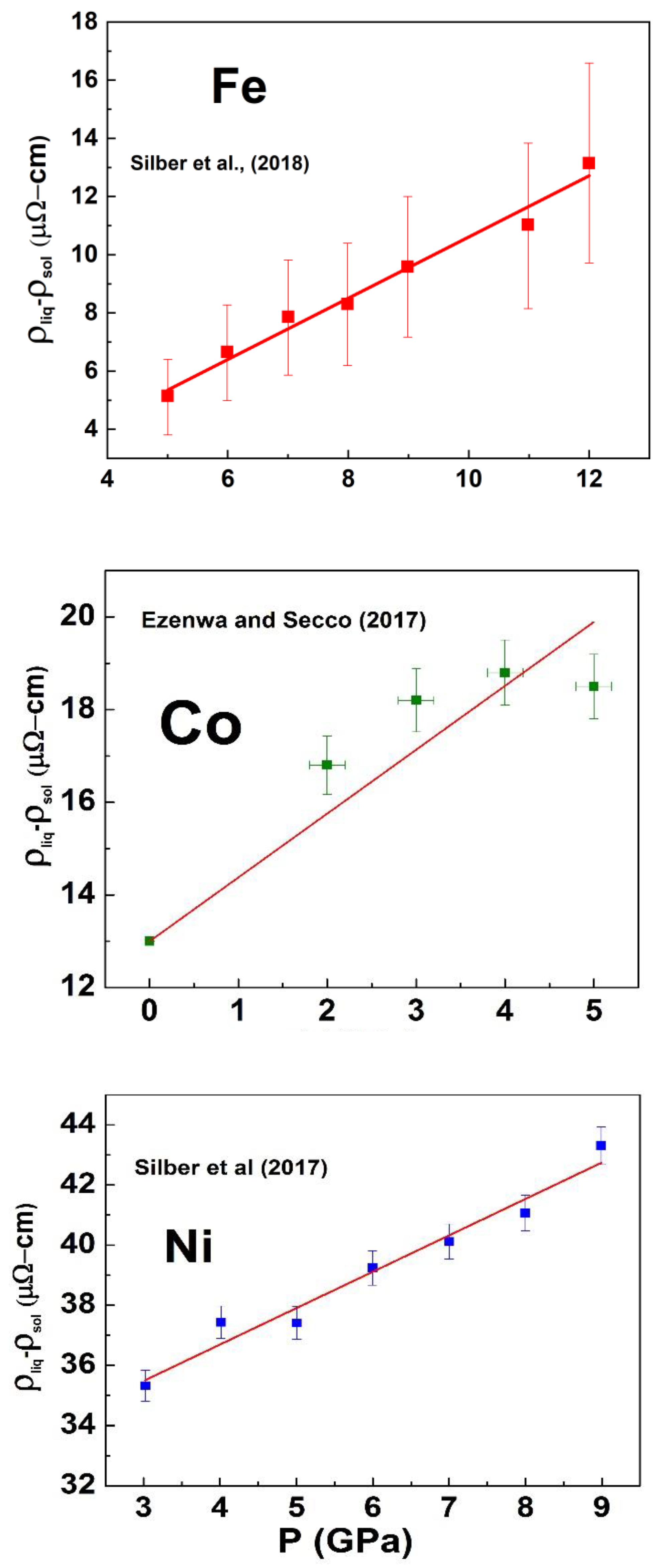
3.1. Electrical Resistivity and Thermal Conductivity at the Melting Transition
3.2. Heat Flow at the Inner Core Boundaries of Mercury and Ganymede
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aharonson, O.; Zuber, M.T.; Solomon, S.C. Crustal remanence in an internally magnetized non-uniform shell: A possible source for Mercury’s magnetic field? Earth Planet. Sci. Lett. 2004, 218, 261–268. [Google Scholar] [CrossRef]
- Christensen, U.R. A deep dynamo generating Mercury’s magnetic field. Nature 2006, 444, 1056–1058. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, F.; Shimizu, H.; Tsunakawa, H. Mercury’s anomalous magnetic field caused by a symmetry-breaking self-regulating dynamo. Nat. Commun. 2019, 10, 208. [Google Scholar] [CrossRef] [PubMed]
- Margot, J.L.; Peale, S.J.; Jurgens, R.F.; Slade, M.A.; Holin, I.V. Large longitude libration of Mercury reveals a molten core. Science 2007, 316, 710–714. [Google Scholar] [CrossRef]
- Margot, J.L.; Peale, S.J.; Solomon, S.C.; Hauck, S.A.; Ghigo, F.D.; Jurgens, R.F.; Yseboodt, M.; Giorgini, J.D.; Padovan, S.; Campbell, D.B. Mercury’s moment of inertia from spin and gravity data. J. Geophys. Res. Planets 2012, 117. [Google Scholar] [CrossRef]
- Hauck, S.A.; Margot, J.L.; Solomon, S.C.; Phillips, R.J.; Johnson, C.L.; Lemoine, F.G.; Perry, M.E. The curious case of Mercury’s internal structure. J. Geophys. Res. Planets 2013, 118, 1204–1220. [Google Scholar] [CrossRef]
- Stark, A.; Oberst, J.; Preusker, F.; Peale, S.J.; Margot, J.L.; Phillips, R.J.; Neumann, G.A.; Smith, D.E.; Zuber, M.T.; Solomon, S.C. First MESSENGER orbital observations of Mercury’s librations. Geophys. Res. Lett. 2015, 42, 7881–7889. [Google Scholar] [CrossRef]
- Ness, N.F.; Behannon, K.W.; Lepping, R.P.; Whang, Y.C.; Schatten, K.H. Magnetic field observations near Mercury: Preliminary results from Mariner 10. Science 1974, 185, 151–160. [Google Scholar] [CrossRef]
- Stevenson, D.J.; Spohn, T.; Schubert, G. Magnetism and thermal evolution of the terrestrial planets. Icarus 1983, 54, 466–489. [Google Scholar] [CrossRef]
- Genova, A.; Goossens, S.; Mazarico, E.; Lemoine, F.G.; Neumann, G.A.; Kuang, W.; Sabaka, T.J.; Hauck, I.I.; Smith, D.E.; Solomon, S.C.; et al. Geodetic evidence that Mercury has a solid inner core. Geophys. Res. Lett. 2019, 46, 3625–3633. [Google Scholar] [CrossRef]
- Stanley, S.; Bloxham, J.; Hutchison, W.E.; Zuber, M.T. Thin shell dynamo models consistent with Mercury’s weak observed magnetic field. Earth Planet. Sci. Lett. 2005, 234, 27–38. [Google Scholar] [CrossRef]
- Kimura, J.; Nakagawa, T.; Kurita, K. Size and compositional constraints of Ganymede’s metallic core for driving an active dynamo. Icarus 2009, 202, 216–224. [Google Scholar] [CrossRef]
- Schubert, G.; Zhang, K.; Kivelson, M.G.; Anderson, J.D. The magnetic field and internal structure of Ganymede. Nature 1996, 384, 544–545. [Google Scholar] [CrossRef]
- Verhoogen, J. Energetics of the Earth; National Academy Press: Washington, DC, USA, 1980. [Google Scholar]
- Hirose, K.; Morard, G.; Sinmyo, R.; Umemoto, K.; Hernlund, J.; Helffrich, G.; Labrosse, S. Crystallization of silicon dioxide and compositional evolution of the Earth’s core. Nature 2017, 543, 99. [Google Scholar] [CrossRef] [PubMed]
- O’Rourke, J.G.; Stevenson, D.J. Powering Earth’s dynamo with magnesium precipitation from the core. Nature 2016, 529, 387. [Google Scholar] [CrossRef] [PubMed]
- Du, Z.; Jackson, C.; Bennett, N.; Driscoll, P.; Deng, J.; Lee, K.M.; Greenberg, E.; Prakapenka, V.B.; Fei, Y. Insufficient energy from MgO exsolution to power early geodynamo. Geophys. Res. Lett. 2017, 44, 11376–11381. [Google Scholar] [CrossRef]
- Badro, J.; Aubert, J.; Hirose, K.; Nomura, R.; Blanchard, I.; Borensztajn, S.; Siebert, J. Magnesium partitioning between Earth’s mantle and core and its potential to drive an early exsolution geodynamo. Geophys. Res. Lett. 2018, 45, 13240–13248. [Google Scholar] [CrossRef]
- Gomi, H.; Ohta, K.; Hirose, K.; Labrosse, S.; Caracas, R.; Verstraete, M.J.; Hernlund, J.W. The high conductivity of iron and thermal evolution of the Earth’s core. Phys. Earth Planet. Inter. 2013, 224, 88–103. [Google Scholar] [CrossRef]
- Ohta, K.; Kuwayama, Y.; Hirose, K.; Shimizu, K.; Ohishi, Y. Experimental determination of the electrical resistivity of iron at Earth’s core conditions. Nature 2016, 534, 95–98. [Google Scholar] [CrossRef] [PubMed]
- Silber, R.E.; Secco, R.A.; Yong, W.; Littleton, J.A. Electrical resistivity of liquid Fe to 12 GPa: Implications for heat flow in cores of terrestrial bodies. Sci. Rep. 2018, 8, 10758. [Google Scholar] [CrossRef] [PubMed]
- Williams, Q. The thermal conductivity of Earth’s core: A key geophysical parameter’s constraints and uncertainties. Annu. Rev. Earth Planet. Sci. 2018, 46, 47–66. [Google Scholar] [CrossRef]
- Stacey, F.D.; Anderson, O.L. Electrical and thermal conductivities of Fe–Ni–Si alloy under core conditions. Phys. Earth Planet. Inter. 2001, 124, 153–162. [Google Scholar] [CrossRef]
- Stacey, F.D.; Loper, D.E. A revised estimate of the conductivity of iron alloy at high pressure and implications for the core energy balance. Phys. Earth Planet. Inter. 2007, 161, 13–18. [Google Scholar] [CrossRef]
- Konôpková, Z.; McWilliams, R.S.; Gómez-Pérez, N.; Goncharov, A.F. Direct measurement of thermal conductivity in solid iron at planetary core conditions. Nature 2016, 534, 99. [Google Scholar]
- Pozzo, M.; Davies, C.; Gubbins, D.; Alfe, D. Thermal and electrical conductivity of iron at Earth’s core conditions. Nature 2012, 485, 355–358. [Google Scholar] [CrossRef]
- De Koker, N.; Steinle-Neumann, G.; Vlček, V. Electrical resistivity and thermal conductivity of liquid Fe alloys at high P and T, and heat flux in Earth’s core. Proc. Natl. Acad. Sci. USA 2012, 109, 4070–4073. [Google Scholar] [CrossRef] [PubMed]
- Wagle, F.; Steinle-Neumann, G. Electrical resistivity discontinuity of iron along the melting curve. Geophys. J. Int. 2017, 213, 237–243. [Google Scholar] [CrossRef]
- Ezenwa, I.C.; Secco, R.A. Invariant electrical resistivity of Co along melting boundary. Earth Planet. Sci. Lett. 2017, 474, 120–127. [Google Scholar] [CrossRef]
- Silber, R.E.; Secco, R.A.; Yong, W. Constant electrical resistivity of Ni along the melting boundary up to 9 GPa. J. Geophys. Res. Solid Earth 2017, 122, 5064–5081. [Google Scholar] [CrossRef]
- Secco, R.A.; Schloessin, H.H. The electrical resistivity of solid and liquid Fe at pressures up to 7 GPa. J. Geophys. Res. Solid Earth 1989, 94, 5887–5894. [Google Scholar] [CrossRef]
- Deng, L.; Seagle, C.; Fei, Y.; Shahar, A. High pressure and temperature electrical resistivity of iron and implications for planetary cores. Geophys. Res. Lett. 2013, 40, 33–37. [Google Scholar] [CrossRef]
- Pommier, A. Influence of sulfur on the electrical resistivity of a crystallizing core in small terrestrial bodies. Earth Planet. Sci. Lett. 2018, 496, 37–46. [Google Scholar] [CrossRef]
- Landrum, G.A.; Dronskowski, R. The orbital origins of magnetism: From atoms to molecules to ferromagnetic alloys. Angew. Chem. Int. Ed. 2000, 39, 1560–1585. [Google Scholar] [CrossRef]
- Mott, N.F. The electrical conductivity of transition metals. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1936, 153, 699–717. [Google Scholar]
- Matula, R.A. Electrical resistivity of copper, gold, palladium, and silver. J. Phys. Chem. Ref. Data 1979, 8, 1147–1298. [Google Scholar] [CrossRef]
- Powell, R.W.; Tye, R.P. The promise of platinum as a high temperature thermal conductivity reference material. Br. J. Appl. Phys. 1963, 14, 662. [Google Scholar] [CrossRef]
- Güntherodt, H.J.; Hauser, E.; Künzi, H.U.; Müller, R. The electrical resistivity of liquid Fe, Co, Ni and Pd. Phys. Lett. A 1975, 54, 291–292. [Google Scholar] [CrossRef]
- Laubitz, M.J.; Matsumura, T. Transport properties of the ferromagnetic metals. i Cobalt. Can. J. Phys. 1973, 51, 1247–1256. [Google Scholar] [CrossRef]
- Laubitz, M.J.; Matsumura, T.; Kelly, P.J. Transport properties of the ferromagnetic metals. II. Nickel. Can. J. Phys. 1976, 54, 92–102. [Google Scholar] [CrossRef]
- Seydel, U.; Fucke, W. Sub-microsecond pulse heating measurements of high temperature electrical resistivity of the 3d-transition metals iron, cobalt, and nickel. Chem. Inf. 1977, 32, 994–1002. [Google Scholar] [CrossRef]
- Chu, T.K.; Chi, T.C. McGram-Hill/CICADAS data series on materials properties. In Properties of Selected Ferrous Aloying Elements, Vol. III-1; Touloukian, Y.S., Ho, C.Y., Eds.; McGraw-Hill: New York, NY, USA, 1981. [Google Scholar]
- Campbell, I.A.; Fert, A. Chapter 9 Transport properties of ferromagnets. In Handbook of Ferromagnetic Materials; Wohlfarth, E.P., Ed.; Elsevier: Amsterdam, The Netherlands, 1982; pp. 747–804. [Google Scholar]
- Gold, A.V. Review paper: Fermi surfaces of the ferromagnetic transition metals. J. Low Temp. Phys. 1974, 16, 3–42. [Google Scholar] [CrossRef]
- Coleman, R.V.; Morris, R.C.; Sellmyer, D.J. Magnetoresistance in Iron and Cobalt to 150 kOe. Phys. Rev. B 1973, 8, 317–331. [Google Scholar] [CrossRef]
- Angadi, M.A.; Fawcett, E.; Rasolt, M. High field magnetoresistance and quantum oscillations in iron whiskers. Can. J. Phys. 1975, 53, 284–298. [Google Scholar] [CrossRef]
- Himpsel, F.J.; Heimann, P.; Eastman, D.E. Band structure measurements and multi-electron effects (satellites) for nearly-filled d-band metals: Fe, Co, Ni, Cu, Ru, and Pd. J. Appl. Phys. 1981, 52, 1658–1663. [Google Scholar] [CrossRef]
- Eastman, D.E.; Himpsel, F.J.; Knapp, J.A. Experimental exchange-split energy-band dispersions for Fe, Co, and Ni. Phys. Rev. Lett. 1980, 44, 95–98. [Google Scholar] [CrossRef]
- Korenman, V.; Prange, R.E. Local-band-theory analysis of spin-polarized, angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 1984, 53, 186–189. [Google Scholar] [CrossRef]
- Chikazumi, S.; Graham, C.D. Physics of Ferromagnetism 2e (No. 94); Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Iota, V.; Klepeis, J.H.P.; Yoo, C.S.; Lang, J.; Haskel, D.; Srajer, G. Electronic structure and magnetism in compressed 3d transition metals. Appl. Phys. Lett. 2007, 90, 042505. [Google Scholar] [CrossRef]
- Ross, M.; Boehler, R.; Errandonea, D. Melting of transition metals at high pressure and the influence of liquid frustration: The late metals Cu, Ni, and Fe. Phys. Rev. B 2007, 76, 184117. [Google Scholar] [CrossRef]
- McMahan, A.K.; Albers, R.C. Insulating nickel at a pressure of 34 TPa. Phys. Rev. Lett. 1982, 49, 1198. [Google Scholar] [CrossRef]
- McMahan, A.K. Pressure effects on the electronic structure of 4f and 5f materials. J. Less Common Met. 1989, 149, 1–11. [Google Scholar] [CrossRef]
- Gaspari, G.D.; Gyorffy, B.L. Electron-phonon interactions, d resonances, and superconductivity in transition metals. Phys. Rev. Lett. 1972, 28, 801–805. [Google Scholar] [CrossRef]
- Brown, J.S. D resonance calculation of the resistivity and thermopower of liquid Ni and Pd. J. Phys. F Met. Phys. 1973, 3, 1003–1007. [Google Scholar] [CrossRef]
- Shvets, V.T. Influence of sd hybridization of the electrical conductivity of liquid transition metals. Theor. Math. Phys. 1982, 53, 1040–1046. [Google Scholar] [CrossRef]
- Shvets, V.T.; Savenko, S.; Datsko, S. Perturbation theory for electrical resistivity of liquid transition metals. Condens. Matter Phys 2002, 5, 511–522. [Google Scholar] [CrossRef]
- McWilliams, R.S.; Konôpková, Z.; Goncharov, A.F. A flash heating method for measuring thermal conductivity at high pressure and temperature: Application to Pt. Phys. Earth Planet. Inter. 2015, 247, 17–26. [Google Scholar] [CrossRef]
- Silber, R.E.; Secco, R.A.; Yong, W.; Littleton, J.A. Heat flow in Earth’s core from invariant electrical resistivity of Fe-Si on the melting boundary to 9 GPa: Do light elements matter? J. Geophys. Res. Solid Earth 2019, 124. [Google Scholar] [CrossRef]
- Ezenwa, I.C.; Secco, R.A.; Yong, W.; Pozzo, M.; Alfè, D. Electrical resistivity of solid and liquid Cu up to 5GPa: Decrease along the melting boundary. J. Phys. Chem. Solids 2017, 110, 386–393. [Google Scholar] [CrossRef]
- Littleton, J.A.; Secco, R.A.; Yong, W. Decreasing electrical resistivity of silver along the melting boundary up to 5 GPa. High Press. Res. 2018, 38, 99–106. [Google Scholar] [CrossRef]
- Berrada, M.; Secco, R.A.; Yong, W. Decreasing electrical resistivity of gold along the melting boundary up to 5 GPa. High Press. Res. 2018, 38, 367–376. [Google Scholar] [CrossRef]
- Ezenwa, I.C.; Secco, R.A. Constant electrical resistivity of Zn along the melting boundary up to 5 GPa. High Press. Res. 2017, 37, 319–333. [Google Scholar] [CrossRef]
- Klemens, P.G.; Williams, R.K. Thermal conductivity of metals and alloys. Int. Met. Rev. 1986, 31, 197–215. [Google Scholar] [CrossRef]
- Breuer, D.; Rueckriemen, T.; Spohn, T. Iron snow, crystal floats, and inner-core growth: Modes of core solidification and implications for dynamos in terrestrial planets and moons. Prog. Earth Planet. Sci. 2015, 2, 39. [Google Scholar] [CrossRef]
- Secco, R.A. Thermal conductivity and Seebeck coefficient of Fe and Fe-Si alloys: Implications for variable Lorenz number. Phys. Earth Planet. Inter. 2017, 265, 23–34. [Google Scholar] [CrossRef]
- Sohl, F.; Spohn, T.; Breuer, D.; Nagel, K. Implications from Galileo observations on the interior structure and chemistry of the Galilean satellites. Icarus 2002, 157, 104–119. [Google Scholar] [CrossRef]
- Rivoldini, A.; Van Hoolst, T. The interior structure of Mercury constrained by the low-degree gravity field and the rotation of Mercury. Earth Planet. Sci. Lett. 2013, 377, 62–72. [Google Scholar] [CrossRef]
- Desai, P.D. Thermodynamic properties of iron and silicon. J. Phys. Chem. Ref. Data 1986, 15, 967–983. [Google Scholar] [CrossRef]
- Hussmann, H.; Sotin, C.; Lunine, J.I. Interiors and evolution of icy satellites. In Treatise on Geophysics; Schubert, G., Ed.; Elsevier: Amsterdam, The Netherlands, 2007; Volume 10. [Google Scholar]
- Jeanloz, R. Properties of iron at high pressures and the state of the core. J. Geophys. Res. Solid Earth 1979, 84, 6059–6069. [Google Scholar] [CrossRef]
- Schubert, G.; Anderson, J.D.; Spohn, T.; McKinnon, W.B. Interior composition, structure and dynamics of the Galilean satellites. Jupit. Planet Satell. Magnetos. 2004, 1, 281–306. [Google Scholar]
| Parameter | Mercury | Ref. | Ganymede | Ref. |
|---|---|---|---|---|
| PICB—pressure at ICB | 5 GPa | [6] | 9 GPa | [68] |
| TICB—temperature at ICB | 1880 K | [66] | 2200 K | [71] |
| Lo—Lorenz number | 2.445 × 10−8 WΩ/K2 | [67] | 2.445 × 10−8 WΩ/K2 | [67] |
| kesolid—electronic thermal conductivity of solid | 39 W/m K | 46 W/m K | ||
| keliquid—electronic thermal conductivity of solid | 37 W/m K | 39 W/m K | ||
| α—thermal expansion | 8.9 × 10−5 K−1 | [67] | 4.8 × 10−5 K−1 | [72] |
| g—gravitational acceleration | 4.0 m/s2 | [69] | 4.36 m/s2 | |
| CP—specific heat | 835 J/kg K | [70] | 835 J/kg K | [70] |
| Qcond solid—conducted heat on solid side of ICB | 31 mW/m2 | 23 mW/m2 | ||
| Qcond liquid—conducted heat on liquid side of ICB | 30 mW/m2 | 19 mW/m2 | ||
| rICB—radius of ICB | 800–1400 km | [10,69] | 650 km | [73] |
| total adiabatic heat flow on solid side of ICB | 0.25–0.77 TW | 0.12 TW | ||
| total adiabatic heat flow on liquid side of ICB | 0.24–0.75 TW | 0.10 TW |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ezenwa, I.C.; Secco, R.A. Fe Melting Transition: Electrical Resistivity, Thermal Conductivity, and Heat Flow at the Inner Core Boundaries of Mercury and Ganymede. Crystals 2019, 9, 359. https://doi.org/10.3390/cryst9070359
Ezenwa IC, Secco RA. Fe Melting Transition: Electrical Resistivity, Thermal Conductivity, and Heat Flow at the Inner Core Boundaries of Mercury and Ganymede. Crystals. 2019; 9(7):359. https://doi.org/10.3390/cryst9070359
Chicago/Turabian StyleEzenwa, Innocent C., and Richard A. Secco. 2019. "Fe Melting Transition: Electrical Resistivity, Thermal Conductivity, and Heat Flow at the Inner Core Boundaries of Mercury and Ganymede" Crystals 9, no. 7: 359. https://doi.org/10.3390/cryst9070359
APA StyleEzenwa, I. C., & Secco, R. A. (2019). Fe Melting Transition: Electrical Resistivity, Thermal Conductivity, and Heat Flow at the Inner Core Boundaries of Mercury and Ganymede. Crystals, 9(7), 359. https://doi.org/10.3390/cryst9070359





