High pO2 Floating Zone Crystal Growth of the Perovskite Nickelate PrNiO3
Abstract
:1. Introduction
2. Experimental Section
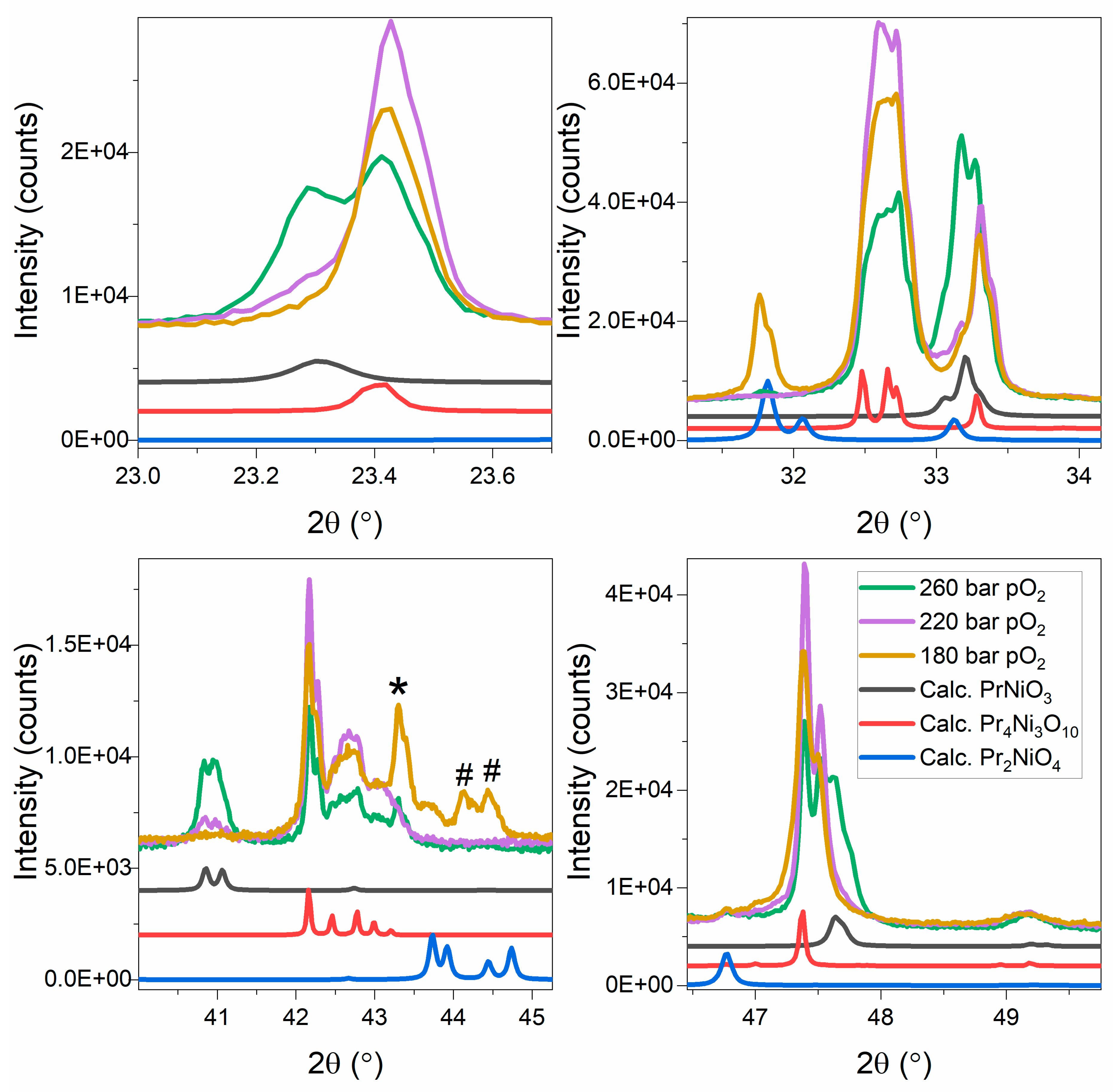
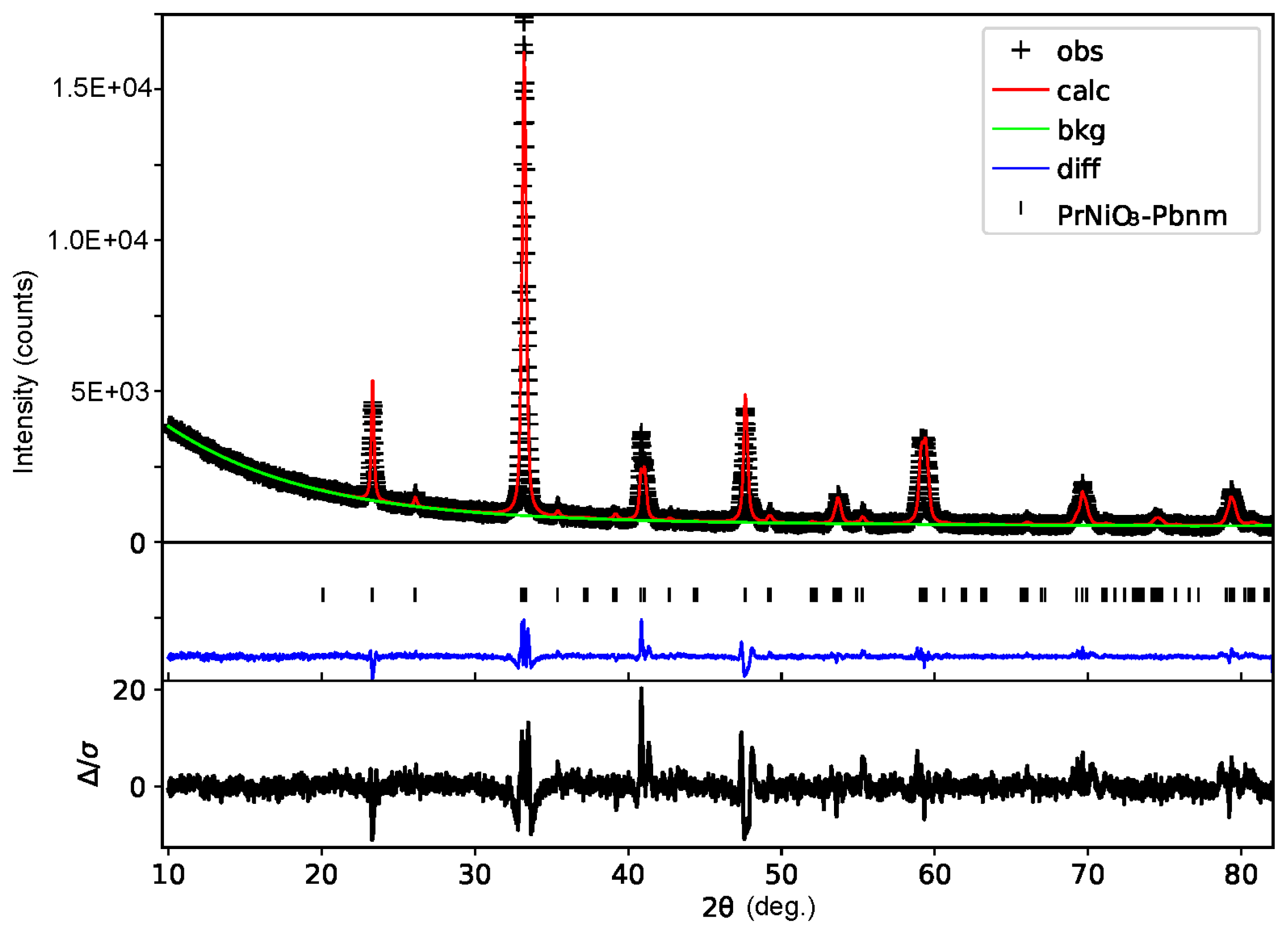
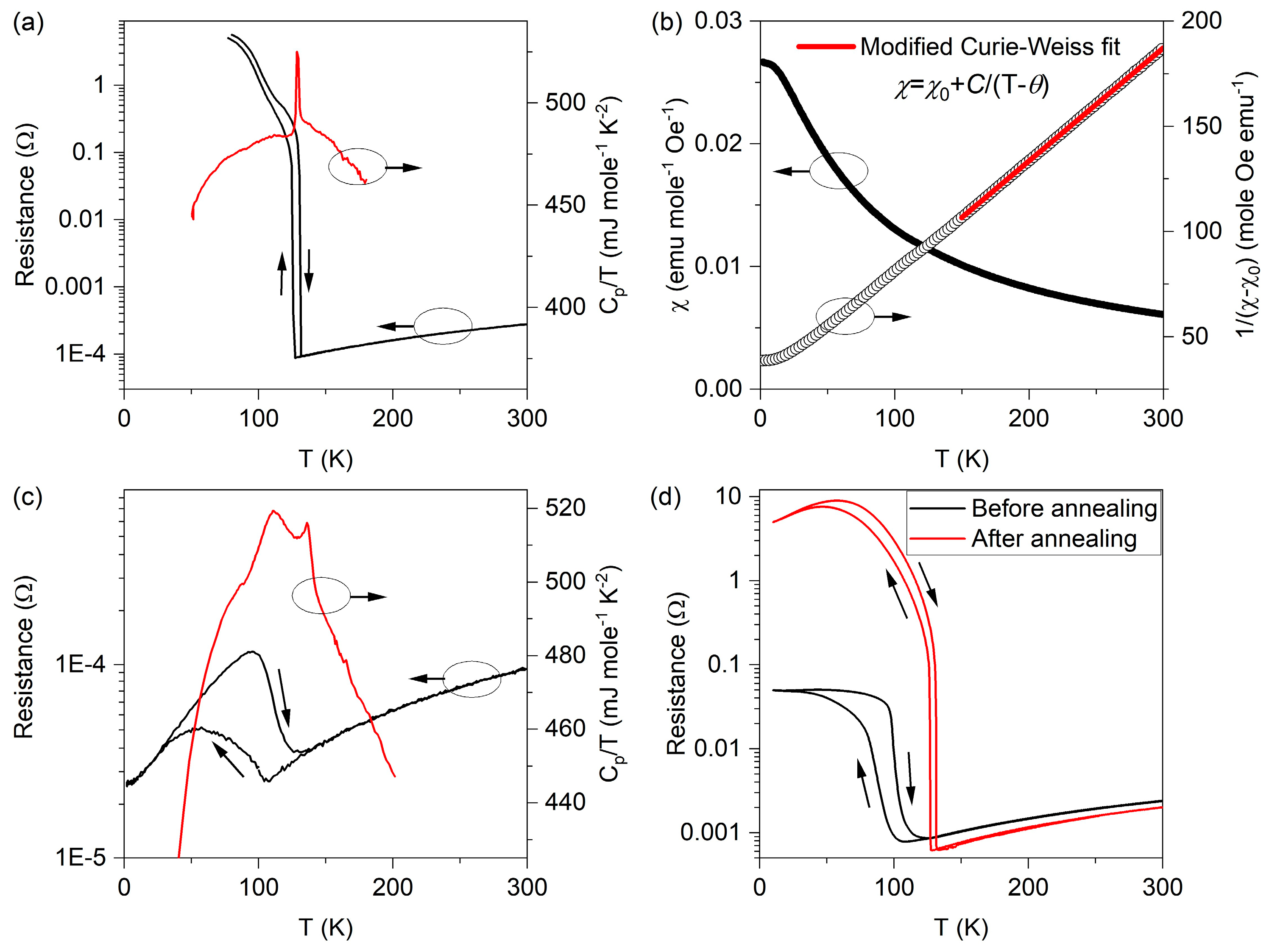
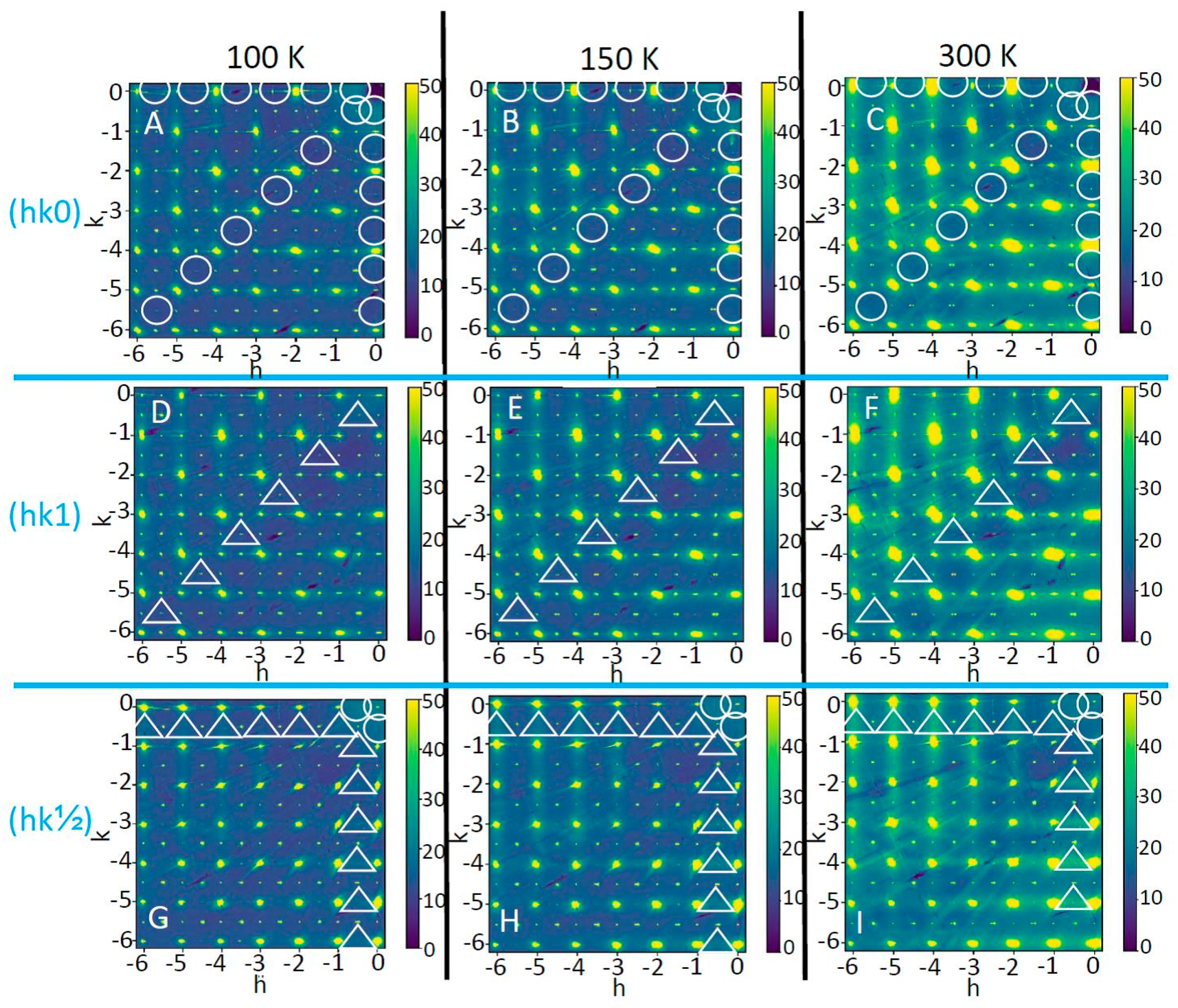
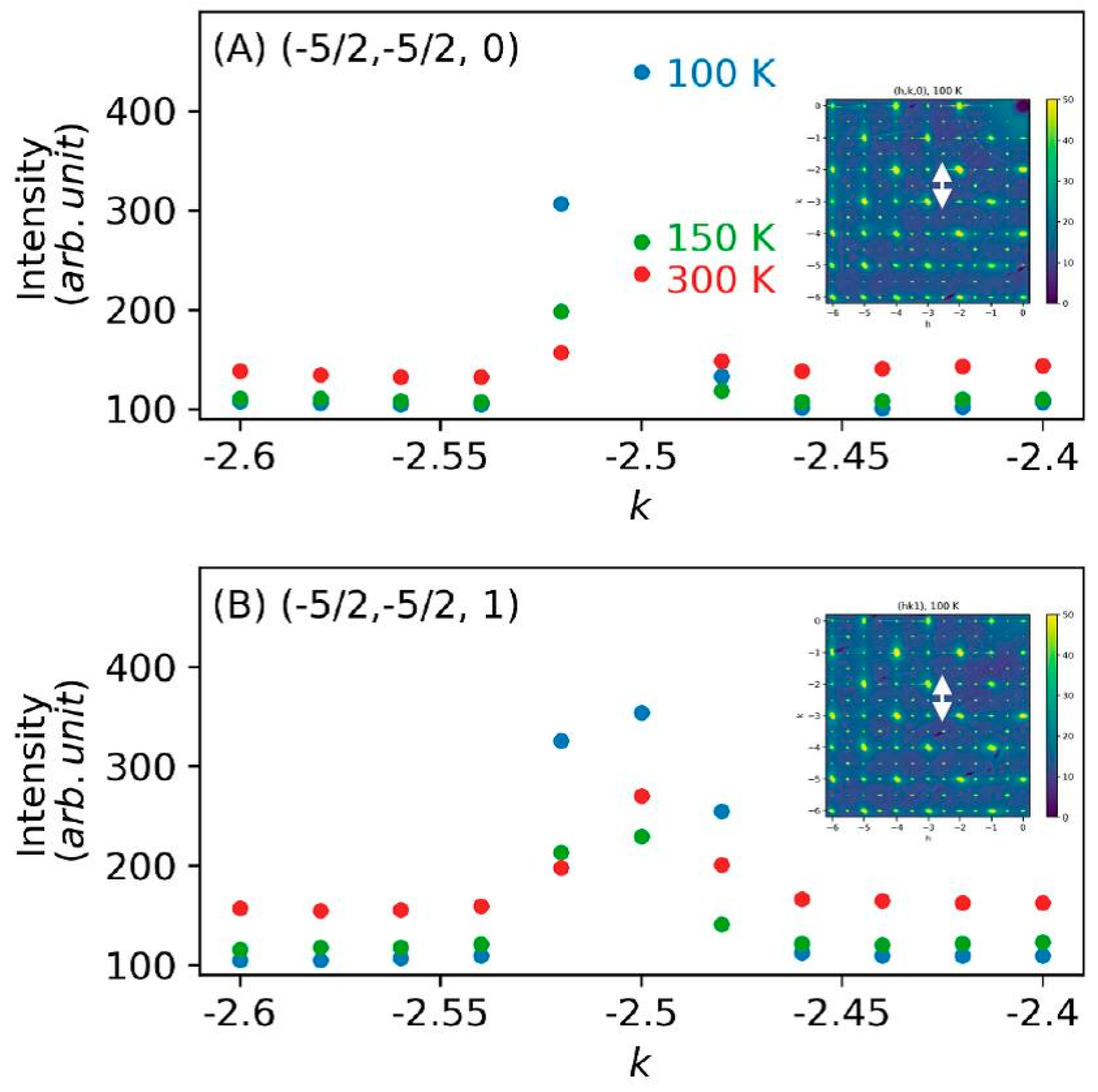
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Catalano, S.; Gibert, M.; Fowlie, J.; Íñiguez, J.; Triscone, J.M.; Kreisel, J. Rare-earth nickelates RNiO3: Thin films and heterostructures. Rep. Prog. Phys. 2018, 81, 046501. [Google Scholar] [CrossRef] [PubMed]
- Catalan, G. Progress in perovskite nickelate research. Phase Transit. 2008, 81, 729–749. [Google Scholar] [CrossRef]
- María Luisa, M. Structural, magnetic and electronic properties of RNiO3 perovskites (R = rare earth). J. Phys. Condens. Matter 1997, 9, 1679. [Google Scholar]
- Shamblin, J.; Heres, M.; Zhou, H.; Sangoro, J.; Lang, M.; Neuefeind, J.; Alonso, J.A.; Johnston, S. Experimental evidence for bipolaron condensation as a mechanism for the metal-insulator transition in rare-earth nickelates. Nat. Commun. 2018, 9, 86. [Google Scholar] [CrossRef] [PubMed]
- Bisogni, V.; Catalano, S.; Green, R.J.; Gibert, M.; Scherwitzl, R.; Huang, Y.; Strocov, V.N.; Zubko, P.; Balandeh, S.; Triscone, J.M.; et al. Ground-state oxygen holes and the metal–insulator transition in the negative charge-transfer rare-earth nickelates. Nat. Commun. 2016, 7, 13017. [Google Scholar] [CrossRef] [PubMed]
- Allen, S.J.; Hauser, A.J.; Mikheev, E.; Zhang, J.Y.; Moreno, N.E.; Son, J.; Ouellette, D.G.; Kally, J.; Kozhanov, A.; Balents, L.; et al. Gaps and pseudogaps in perovskite rare earth nickelates. APL Mater. 2015, 3, 062503. [Google Scholar] [CrossRef]
- Misra, D. Possible ground states of rare-earth nickelates (RNiO3, R = La, Nd, Pr): A mean-field study. Phase Transit. 2014, 87, 398–407. [Google Scholar] [CrossRef]
- Jaramillo, R.; Ha, S.D.; Silevitch, D.M.; Ramanathan, S. Origins of bad-metal conductivity and the insulator-metal transition in the rare-earth nickelates. Nat. Phys. 2014, 10, 304–307. [Google Scholar] [CrossRef]
- Lau, B.; Millis, A.J. Theory of the magnetic and metal-insulator transitions in RNiO3 bulk and layered structures. Phys. Rev. Lett. 2013, 110, 126404. [Google Scholar] [CrossRef]
- Kumar, D.; Rajeev, K.P.; Alonso, J.A.; Martínez-Lope, M.J. Spin-canted magnetism and decoupling of charge and spin ordering in NdNiO3. Phys. Rev. B 2013, 88, 014410. [Google Scholar] [CrossRef]
- Caviglia, A.D.; Först, M.; Scherwitzl, R.; Khanna, V.; Bromberger, H.; Mankowsky, R.; Singla, R.; Chuang, Y.D.; Lee, W.S.; Krupin, O.; et al. Photoinduced melting of magnetic order in the correlated electron insulator NdNiO3. Phys. Rev. B 2013, 88, 220401. [Google Scholar] [CrossRef]
- Lee, S.; Chen, R.; Balents, L. Landau theory of charge and spin ordering in the nickelates. Phys. Rev. Lett. 2011, 106, 016405. [Google Scholar] [CrossRef] [PubMed]
- Bodenthin, Y.; Staub, U.; Piamonteze, C.; Garcia-Fernandez, M.; Martinez-Lope, M.J.; Alonso, J.A. Magnetic and electronic properties of RNiO3 (R = Pr, Nd, Eu, Ho and Y) perovskites studied by resonant soft x-ray magnetic powder diffraction. J. Phys. Condens. Matter 2011, 23, 036002. [Google Scholar] [CrossRef] [PubMed]
- Medarde, M.; Dallera, C.; Grioni, M.; Delley, B.; Vernay, F.; Mesot, J.; Sikora, M.; Alonso, J.A.; Martinez-Lope, M.J. Charge disproportionation in RNiO3 perovskites (R = rare earth) from high-resolution x-ray absorption spectroscopy. Phys. Rev. B 2009, 80, 245105. [Google Scholar] [CrossRef]
- Giovannetti, G.; Kumar, S.; Khomskii, D.; Picozzi, S.; van den Brink, J. Multiferroicity in rare-earth nickelates RNiO3. Phys. Rev. Lett. 2009, 103, 156401. [Google Scholar] [CrossRef] [PubMed]
- Medarde, M.; Fernández-Díaz, M.T.; Lacorre, P. Long-range charge order in the low-temperature insulating phase of PrNiO3. Phys. Rev. B 2008, 78, 212101. [Google Scholar] [CrossRef]
- Scagnoli, V.; Staub, U.; Mulders, A.M.; Meijer, G.I.; Hammerl, G.; Tonnerre, J.M. Magnetic and orbital ordering in NdNiO3. Phys. B 2006, 378–380, 541–542. [Google Scholar] [CrossRef]
- Zhou, J.S.; Goodenough, J.B.; Dabrowski, B. Pressure-induced non-Fermi-liquid behavior of PrNiO3. Phys. Rev. Lett. 2005, 94, 226602. [Google Scholar] [CrossRef]
- Piamonteze, C.; Tolentino, H.C.N.; Ramos, A.Y.; Massa, N.E.; Alonso, J.A.; Martinez-Lope, M.J.; Casais, M.T. Short-range charge order in RNiO3 perovskites (R = Pr, Nd, Eu, Y) probed by X-ray-absorption spectroscopy. Phys. Rev. B 2005, 71, 012104. [Google Scholar] [CrossRef]
- Zhou, J.S.; Goodenough, J.B.; Dabrowski, B.; Klamut, P.W.; Bukowski, Z. Enhanced susceptibility in LNiO3 Perovskites (L= La, Pr, Nd, Nd0.5Sm0.5). Phys. Rev. Lett. 2000, 84, 526–529. [Google Scholar] [CrossRef]
- Rosenkranz, S.; Medarde, M.; Fauth, F.; Mesot, J.; Zolliker, M.; Furrer, A.; Staub, U.; Lacorre, P.; Osborn, R.; Eccleston, R.S.; et al. Crystalline electric field of the rare-earth nickelates RNiO3 (R = Pr, Nd, Sm, Eu, and Pr1-xLax, 0 ≤ x ≤ 0.7) determined by inelastic neutron scattering. Phys. Rev. B 1999, 60, 14857–14867. [Google Scholar] [CrossRef]
- Medarde, M.; Lacorre, P.; Conder, K.; Fauth, F.; Furrer, A. Giant oxygen isotope effect on the metal-insulator transition of RNiO3 perovskites. J. Supercond. 1999, 12, 189–191. [Google Scholar] [CrossRef]
- Alonso, J.A.; Martinez-Lope, M.J.; Casais, M.T.; Aranda, M.A.G.; Fernandez-Diaz, M.T. Metal-insulator transitions, structural and microstructural evolution of RNiO3 (R = Sm, Eu, Gd, Dy, Ho, Y) perovskites: Evidence for room-temperature charge disproportionation in monoclinic HoNiO3 and YNiO3. J. Am. Chem. Soc. 1999, 121, 4754–4762. [Google Scholar] [CrossRef]
- Liu, C.; Wrobel, F.; Hoffman, J.D.; Hong, D.; Pearson, J.E.; Benckiser, E.; Bhattacharya, A. Counter-thermal flow of holes in high-mobility LaNiO3 thin films. Phys. Rev. B 2019, 99, 041114. [Google Scholar] [CrossRef]
- Wang, B.X.; Rosenkranz, S.; Rui, X.; Zhang, J.; Ye, F.; Zheng, H.; Klie, R.F.; Mitchell, J.F.; Phelan, D. Antiferromagnetic defect structure in LaNiO3-δ single crystals. Phys. Rev. Mater. 2018, 2, 064404. [Google Scholar] [CrossRef]
- Guo, H.; Li, Z.W.; Zhao, L.; Hu, Z.; Chang, C.F.; Kuo, C.Y.; Schmidt, W.; Piovano, A.; Pi, T.W.; Sobolev, O.; et al. Antiferromagnetic correlations in the metallic strongly correlated transition metal oxide LaNiO3. Nat. Commun. 2018, 9, 43. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zheng, H.; Ren, Y.; Mitchell, J.F. High-pressure floating-zone growth of perovskite nickelate LaNiO3 single crystals. Cryst. Growth Des. 2017, 17, 2730–2735. [Google Scholar] [CrossRef]
- Li, B.; Louca, D.; Yano, S.; Marshall, L.G.; Zhou, J.; Goodenough, J.B. Insulating Pockets in Metallic LaNiO3. Adv. Electron. Mater. 2016, 2, 1500261. [Google Scholar] [CrossRef]
- Zhou, J.S.; Marshall, L.G.; Goodenough, J.B. Mass enhancement versus Stoner enhancement in strongly correlated metallic perovskites: LaNiO3 and LaCuO3. Phys. Rev. B 2014, 89, 245138. [Google Scholar] [CrossRef]
- King, P.D.C.; Wei, H.I.; Nie, Y.F.; Uchida, M.; Adamo, C.; Zhu, S.; He, X.; Bozovic, I.; Schlom, D.G.; Shen, K.M. Atomic-scale control of competing electronic phases in ultrathin LaNiO3. Nat. Nanotech. 2014, 9, 443–447. [Google Scholar] [CrossRef]
- Fernandez-Diaz, M.T.; Alonso, J.A.; Martinez-Lope, M.J.; Casais, M.T.; Garcia-Munoz, J.L.; Aranda, M.A.G. Charge disproportionation in RNiO3 perovskites. Phys. B 2000, 276, 218–221. [Google Scholar] [CrossRef]
- Scagnoli, V.; Staub, U.; Janousch, M.; Mulders, A.; Shi, M.; Meijer, G.; Rosenkranz, S.; Wilkins, S.; Paolasini, L.; Karpinski, J.; et al. Charge disproportionation and search for orbital ordering in NdNiO3 by use of resonant x-ray diffraction. Phys. Rev. B 2005, 72, 155111. [Google Scholar] [CrossRef]
- Alonso, J.A.; Martinez-Lope, M.J.; Presniakov, I.A.; Sobolev, A.V.; Rusakov, V.S.; Gapochka, A.M.; Demazeau, G.; Fernandez-Diaz, M.T. Charge disproportionation in RNiO3 (R = Tm, Yb) perovskites observed in situ by neutron diffraction and Fe-57 probe Mossbauer spectroscopy. Phys. Rev. B 2013, 87, 184111. [Google Scholar] [CrossRef]
- García-Muñoz, J.L.; Aranda, M.A.G.; Alonso, J.A.; Martínez-Lope, M.J. Structure and charge order in the antiferromagnetic band-insulating phase of NdNiO3. Phys. Rev. B 2009, 79, 134432. [Google Scholar] [CrossRef]
- Lacorre, P.; Torrance, J.B.; Pannetier, J.; Nazzal, A.I.; Wang, P.W.; Huang, T.C. Synthesis, crystal structure, and properties of metallic PrNiO3: Comparison with metallic NdNiO3 and semiconducting SmNiO3. J. Solid State Chem. 1991, 91, 225–237. [Google Scholar] [CrossRef]
- Demazeau, G.; Marbeuf, A.; Pouchard, M.; Hagenmuller, P. Sur une série de composés oxygènes du nickel trivalent derivés de la perovskite. J. Solid State Chem. 1971, 3, 582–589. [Google Scholar] [CrossRef]
- Alonso, J.A.; Martínez-Lope, M.J.; Casais, M.T.; Martínez, J.L.; Demazeau, G.; Largeteau, A.; García-Muñoz, J.L.; Muñoz, A.; Fernández-Díaz, M.T. High-pressure preparation, crystal structure, magnetic properties, and phase transitions in GdNiO3 and DyNiO3 perovskites. Chem. Mater. 1999, 11, 2463–2469. [Google Scholar] [CrossRef]
- Saito, T.; Azuma, M.; Nishibori, E.; Takata, M.; Sakata, M.; Nakayama, N.; Arima, T.; Kimura, T.; Urano, C.; Takano, M. Monoclinic distortion in the insulating phase of PrNiO3. Phys. B 2003, 329–333 Pt 2, 866–867. [Google Scholar] [CrossRef]
- Azuma, M.; Saito, T.; Ishiwata, S.; Yamada, I.; Kohsaka, Y.; Takagi, H.; Takano, M. Single crystal growth of transition metal oxides at high pressures of several GPa. Phys. C 2003, 392–396 Pt 1, 22–28. [Google Scholar] [CrossRef]
- Alonso, J.A.; Muñoz, A.; Largeteau, A.; Demazeau, G. Crystal growth of NdNiO3 perovskite under high oxygen pressure. J. Phys. Condens. Matter 2004, 16, S1277. [Google Scholar] [CrossRef]
- Phelan, W.A.; Zahn, J.; Kennedy, Z.; McQueen, T.M. Pushing boundaries: High pressure, supercritical optical floating zone materials discovery. J. Solid State Chem. 2018, 270, 705–709. [Google Scholar] [CrossRef]
- Toby, B.H.; Von Dreele, R.B. GSAS-II: The genesis of a modern open-source all purpose crystallography software package. J. Appl. Crystallogr. 2013, 46, 544–549. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, H.; Chen, Y.S.; Ren, Y.; Yonemura, M.; Huq, A.; Mitchell, J.F. High oxygen pressure floating zone growth and crystal structure of the layered nickelates R4Ni3O10 (R = La, Pr). arXiv 2019, arXiv:1904.10048. Available online: https://arxiv.org/ftp/arxiv/papers/1904/1904.10048.pdf (accessed on 21 June 2019).
- Zhang, J.; Botana, A.S.; Freeland, J.W.; Phelan, D.; Zheng, H.; Pardo, V.; Norman, M.R.; Mitchell, J.F. Large orbital polarization in a metallic square-planar nickelate. Nat. Phys. 2017, 13, 864–869. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Takeda, Y.; Hashimoto, H.; Sato, A.; Imanishi, N.; Yamamoto, O. Oxygen deficiency and electrical conductivity in LnNiO3−z (Ln=La, Pr) and LaCuO3−z. J. Jpn. Soc. Powder Powder Metall. 1992, 39, 345–348. [Google Scholar] [CrossRef]
- Gawryluk, D.J.; Rodríguez-Carvajal, J.; Lacorre, P.; Fernández-Díaz, M.T.; Medarde, M. Distortion mode anomalies in bulk PrNiO3. arXiv 2018, arXiv:1809.10914. Available online: https://arxiv.org/pdf/1809.10914.pdf (accessed on 21 June 2019).

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, H.; Zhang, J.; Wang, B.; Phelan, D.; Krogstad, M.J.; Ren, Y.; Phelan, W.A.; Chmaissem, O.; Poudel, B.; Mitchell, J.F. High pO2 Floating Zone Crystal Growth of the Perovskite Nickelate PrNiO3. Crystals 2019, 9, 324. https://doi.org/10.3390/cryst9070324
Zheng H, Zhang J, Wang B, Phelan D, Krogstad MJ, Ren Y, Phelan WA, Chmaissem O, Poudel B, Mitchell JF. High pO2 Floating Zone Crystal Growth of the Perovskite Nickelate PrNiO3. Crystals. 2019; 9(7):324. https://doi.org/10.3390/cryst9070324
Chicago/Turabian StyleZheng, Hong, Junjie Zhang, Bixia Wang, Daniel Phelan, Matthew J. Krogstad, Yang Ren, W. Adam Phelan, Omar Chmaissem, Bisham Poudel, and J. F. Mitchell. 2019. "High pO2 Floating Zone Crystal Growth of the Perovskite Nickelate PrNiO3" Crystals 9, no. 7: 324. https://doi.org/10.3390/cryst9070324
APA StyleZheng, H., Zhang, J., Wang, B., Phelan, D., Krogstad, M. J., Ren, Y., Phelan, W. A., Chmaissem, O., Poudel, B., & Mitchell, J. F. (2019). High pO2 Floating Zone Crystal Growth of the Perovskite Nickelate PrNiO3. Crystals, 9(7), 324. https://doi.org/10.3390/cryst9070324






