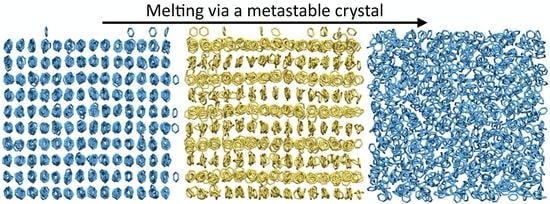
Stepwise Homogeneous Melting of Benzene Phase I at High Pressure
Abstract
1. Introduction
2. Methods
2.1. Force Field
2.2. MD Simulations
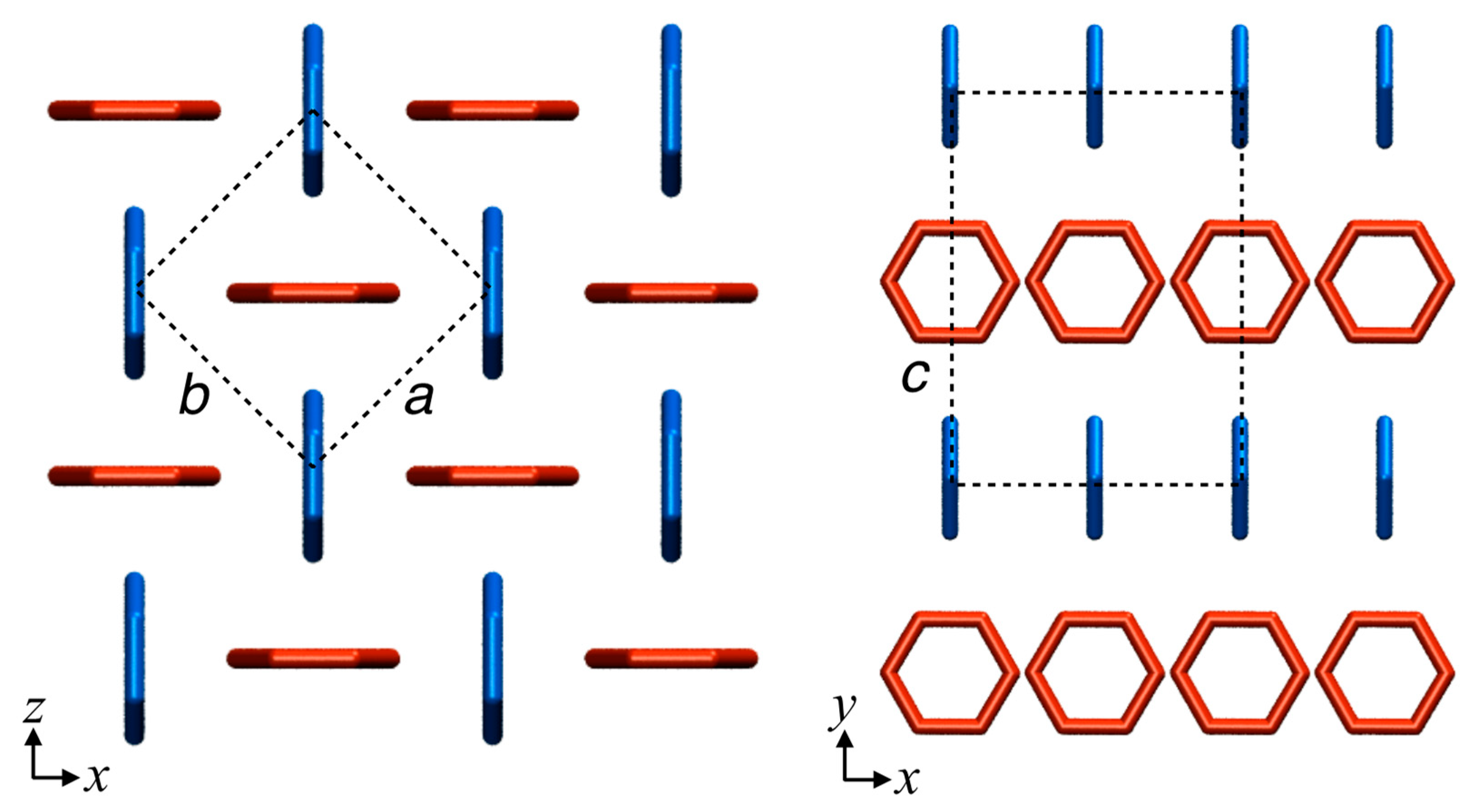
2.3. Crystals
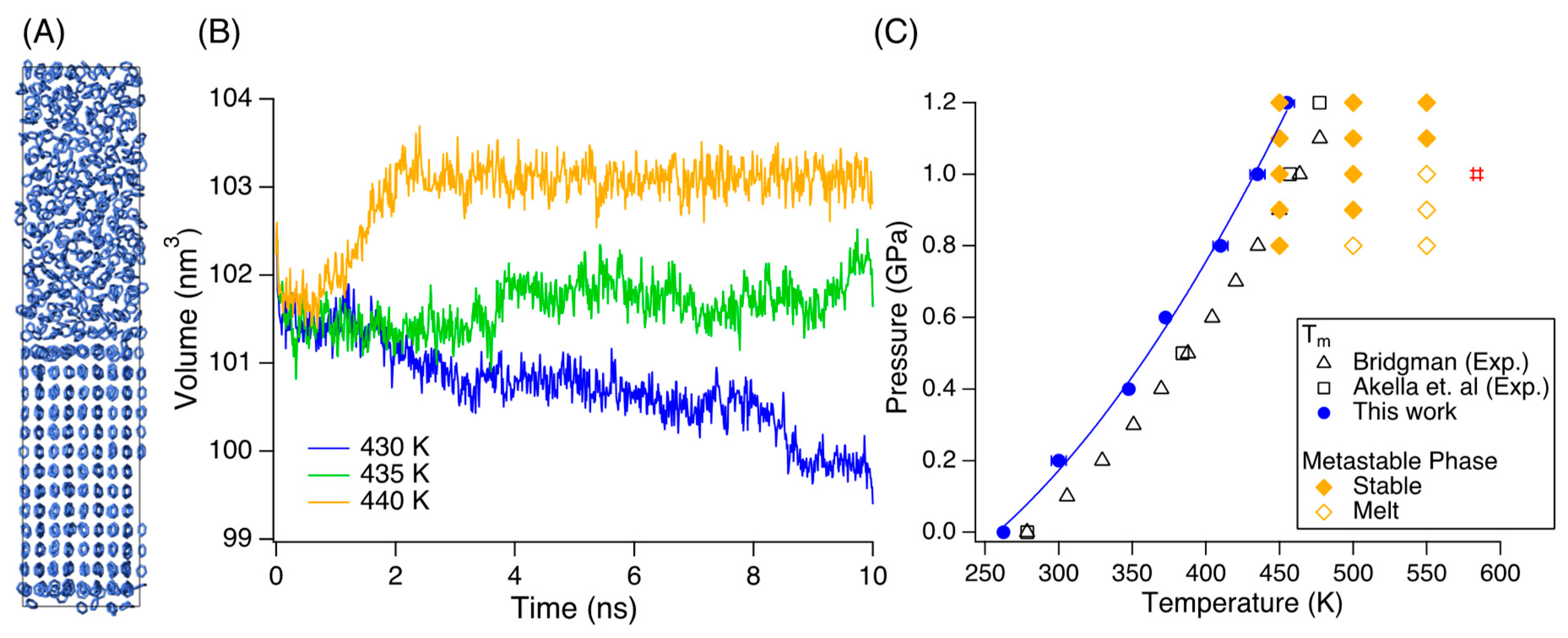
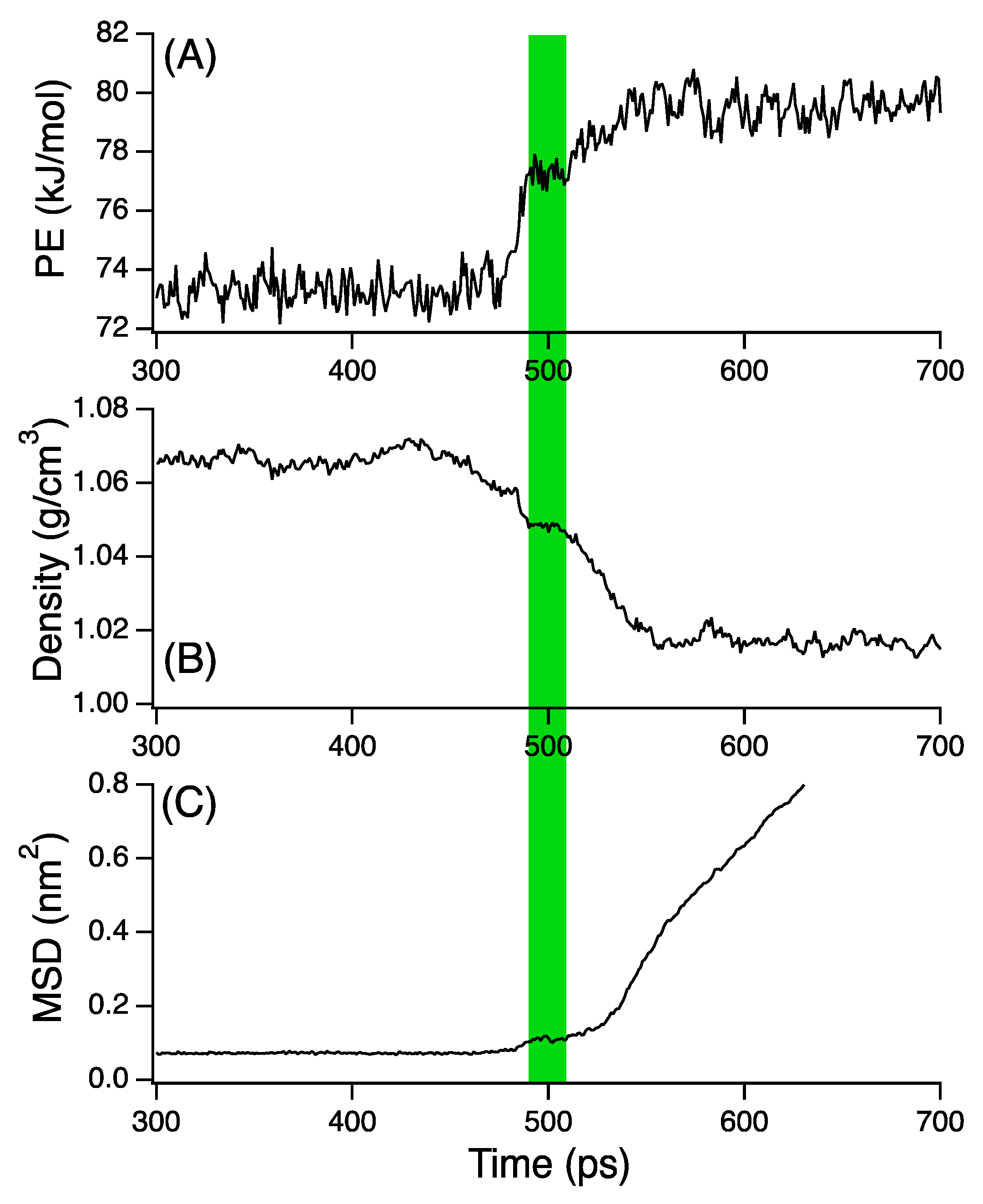
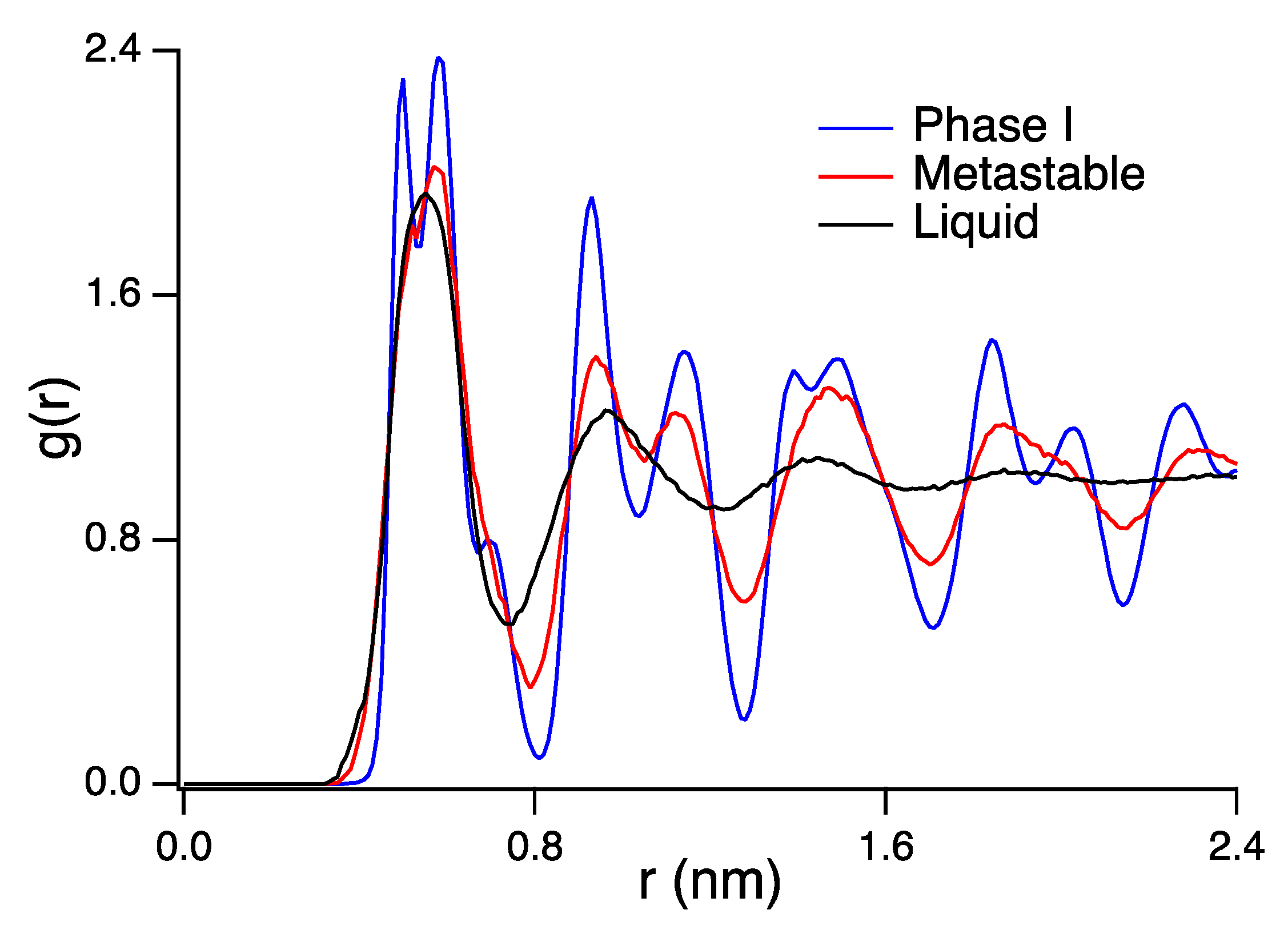
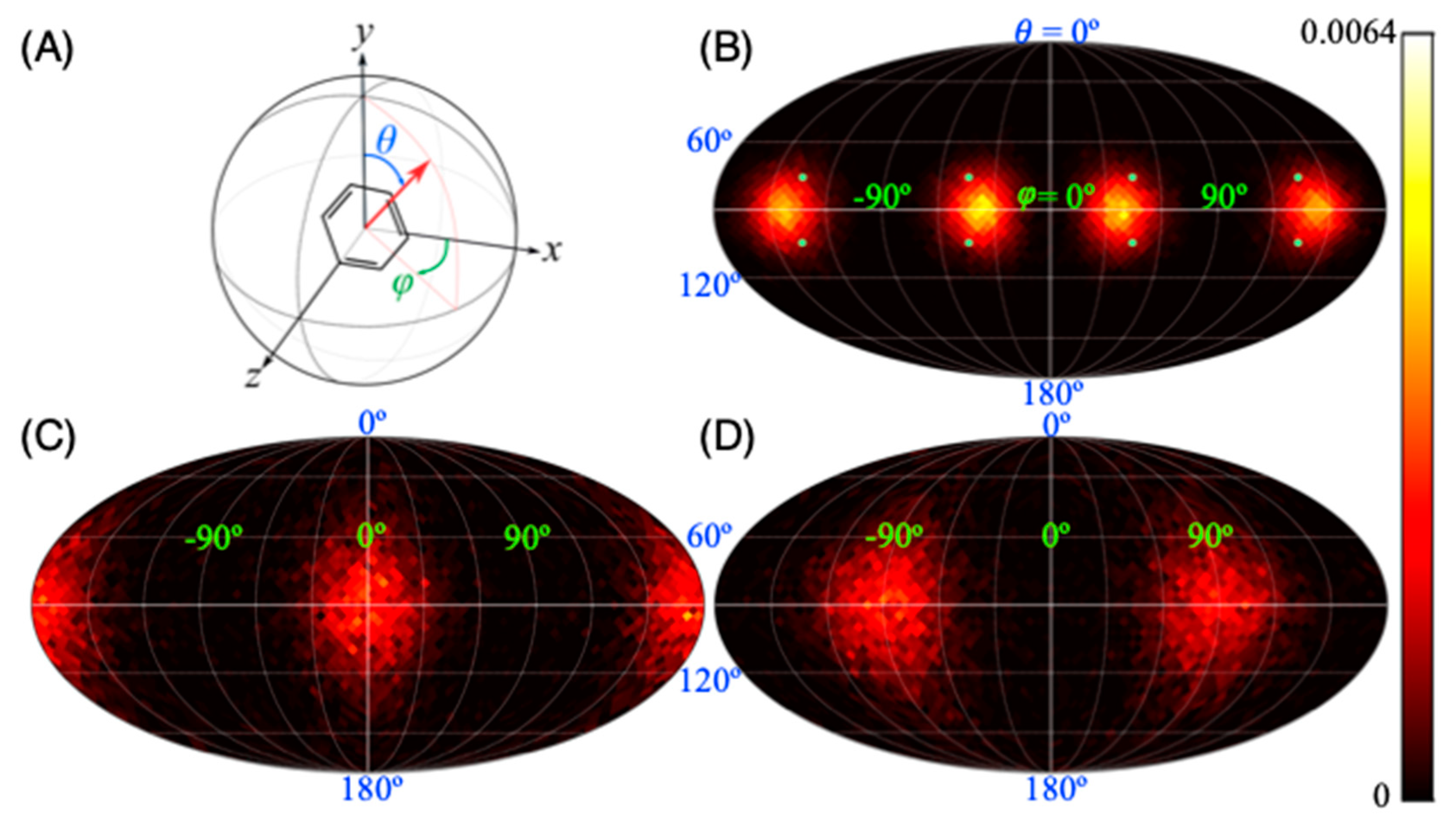
3. Results and Discussion
4. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Raiteri, P.; Martoňák, R.; Parrinello, M. Exploring Polymorphism: The Case of Benzene. Angew. Chem. Int. Ed. 2005, 44, 3769–3773. [Google Scholar] [CrossRef] [PubMed]
- Chanyshev, A.D.; Litasov, K.D.; Rashchenko, S.V.; Sano-Furukawa, A.; Kagi, H.; Hattori, T.; Shatskiy, A.F.; Dymshits, A.M.; Sharygin, I.S.; Higo, Y. High-Pressure–High-Temperature Study of Benzene: Refined Crystal Structure and New Phase Diagram up to 8 GPa and 923 K. Cryst. Growth Des. 2018, 18, 3016–3026. [Google Scholar] [CrossRef]
- Wen, X.-D.; Hoffmann, R.; Ashcroft, N.W. Benzene under High Pressure: a Story of Molecular Crystals Transforming to Saturated Networks, with a Possible Intermediate Metallic Phase. J. Am. Chem. Soc. 2011, 133, 9023–9035. [Google Scholar] [CrossRef]
- Headen, T.F.; Howard, C.A.; Skipper, N.T.; Wilkinson, M.A.; Bowron, D.T.; Soper, A.K. Structure of pi-pi interactions in aromatic liquids. J. Am. Chem. Soc. 2010, 132, 5735–5742. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, K.; Fukuyama, N.; Yamaguchi, T.; Hosokawa, S.; Uchiyama, H.; Tsutsui, S.; Baron, A.Q.R. Inelastic X-ray scattering on liquid benzene analyzed using a generalized Langevin equation. Chem. Phys. Lett. 2017, 680, 1–5. [Google Scholar] [CrossRef]
- Nagasaka, M.; Yuzawa, H.; Mochizuki, K.; Rühl, E.; Kosugi, N. Temperature-Dependent Structural Changes in Liquid Benzene. J. Phys. Chem. Lett. 2018, 9, 5827–5832. [Google Scholar] [CrossRef]
- Pravica, M.; Grubor-Urosevic, O.; Hu, M.; Chow, P.; Yulga, B.; Liermann, P. X-ray Raman Spectroscopic Study of Benzene at High Pressure. J. Phys. Chem. B 2007, 111, 11635–11637. [Google Scholar] [CrossRef]
- Piermarini, G.J.; Mighell, A.D.; Weir, C.E.; Block, S. Crystal Structure of Benzene II at 25 Kilobars. Science 1969, 165, 1250–1255. [Google Scholar] [CrossRef]
- Akella, J.; Kennedy, G.C. Phase Diagram of Benzene to 35 kbar. J. Chem. Phys. 1971, 55, 793–796. [Google Scholar] [CrossRef]
- Block, S.; Weir, C.E.; Piermarini, G.J. Polymorphism in benzene, naphthalene, and anthracene at high pressure. Science 1970, 169, 586–587. [Google Scholar] [CrossRef] [PubMed]
- Cox, E.G.; Smith, J.A.S. Crystal Structure of Benzene at −3 °C. Nature 1954, 173, 75. [Google Scholar] [CrossRef]
- Cansell, F.; Fabre, D.; Petitet, J. Phase transitions and chemical transformations of benzene up to 550 °C and 30 GPa. J. Chem. Phys. 1993, 99, 7300–7304. [Google Scholar] [CrossRef]
- Ciabini, L.; Santoro, M.; Bini, R.; Schettino, V. High pressure crystal phases of benzene probed by infrared spectroscopy. J. Chem. Phys. 2001, 115, 3742–3749. [Google Scholar] [CrossRef]
- Thiéry, M.M.; Léger, J.M. High pressure solid phases of benzene. I. Raman and x-ray studies of C6H6 at 294 K up to 25 GPa. J. Chem. Phys. 1988, 89, 4255–4271. [Google Scholar] [CrossRef]
- Schneider, E.; Vogt, L.; Tuckerman, M.E. Exploring polymorphism of benzene and naphthalene with free energy based enhanced molecular dynamics. Acta Crystallogr. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 542–550. [Google Scholar] [CrossRef]
- Yu, T.-Q.; Tuckerman, M.E. Temperature-accelerated method for exploring polymorphism in molecular crystals based on free energy. Phys. Rev. Lett. 2011, 107, 015701. [Google Scholar] [CrossRef] [PubMed]
- Van Eijck, B.P.; Spek, A.L.; Mooij, W.T.M.; Kroon, J. Hypothetical Crystal Structures of Benzene at 0 and 30 kbar. Acta Crystallogr. B 1998, 54, 291–299. [Google Scholar] [CrossRef]
- Shoda, T.; Yamahara, K.; Okazaki, K.; Williams, D.E. Molecular packing analysis: prediction of experimental crystal structures of benzene starting from unreasonable initial structures. J. Mol. Struct. THEOCHEM 1994, 313, 321–334. [Google Scholar] [CrossRef]
- Yagasaki, T.; Matsumoto, M.; Tanaka, H. Phase Diagrams of TIP4P/2005, SPC/E, and TIP5P Water at High Pressure. J. Phys. Chem. B 2018, 122, 7718–7725. [Google Scholar] [CrossRef] [PubMed]
- Jacobson, L.C.; Hujo, W.; Molinero, V. Amorphous precursors in the nucleation of clathrate hydrates. J. Am. Chem. Soc. 2010, 132, 11806–11811. [Google Scholar] [CrossRef]
- Wolde, P.R.T.; Frenkel, D. Enhancement of Protein Crystal Nucleation by Critical Density Fluctuations. Science 1997, 277, 1975–1978. [Google Scholar] [CrossRef]
- Hirata, M.; Yagasaki, T.; Matsumoto, M.; Tanaka, H. Phase Diagram of TIP4P/2005 Water at High Pressure. Langmuir 2017, 33, 11561–11569. [Google Scholar] [CrossRef]
- Mochizuki, K.; Himoto, K.; Matsumoto, M. Diversity of transition pathways in the course of crystallization into ice VII. Phys. Chem. Chem. Phys. 2014, 16, 16419–16425. [Google Scholar] [CrossRef]
- Ostwald, W. Studien über die Bildung und Umwandlung fester Körper. Z. Phys. Chem. 1897, 22, 289. [Google Scholar] [CrossRef]
- Karthika, S.; Radhakrishnan, T.K.; Kalaichelvi, P. A Review of Classical and Nonclassical Nucleation Theories. Cryst. Growth Des. 2016, 16, 6663–6681. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, F.; Peng, Y.; Zheng, Z.; Han, Y. Imaging the homogeneous nucleation during the melting of superheated colloidal crystals. Science 2012, 338, 87–90. [Google Scholar] [CrossRef]
- Samanta, A.; Tuckerman, M.E.; Yu, T.-Q.; Weinan, E. Microscopic mechanisms of equilibrium melting of a solid. Science 2014, 346, 729–732. [Google Scholar] [CrossRef]
- Mochizuki, K.; Matsumoto, M.; Ohmine, I. Defect pair separation as the controlling step in homogeneous ice melting. Nature 2013, 498, 350–354. [Google Scholar] [CrossRef]
- Shah, M.; Santiso, E.E.; Trout, B.L. Computer simulations of homogeneous nucleation of benzene from the melt. J. Phys. Chem. B 2011, 115, 10400–10412. [Google Scholar] [CrossRef]
- Tohji, K.; Murata, Y. X-Ray Diffraction Study of the Melting of Benzene. Jpn. J. Appl. Phys. 1982, 21, 1199–1204. [Google Scholar] [CrossRef]
- Craven, C.J.; Hatton, P.D.; Howard, C.J.; Pawley, G.S. The structure and dynamics of solid benzene. I. A neutron powder diffraction study of deuterated benzene from 4 K to the melting point. J. Chem. Phys. 1993, 98, 8236–8243. [Google Scholar] [CrossRef]
- Mochizuki, K. Computational Study on Homogeneous Melting of Benzene Phase I. Crystals 2019, 9, 84. [Google Scholar] [CrossRef]
- MacKerell, A.D.; Bashford, D.; Bellott, M.; Dunbrack, R.L.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef]
- MacKerell, A.D.; Wiorkiewicz-Kuczera, J.; Karplus, M. An all-atom empirical energy function for the simulation of nucleic acids. J. Am. Chem. Soc. 1995, 117, 11946–11975. [Google Scholar] [CrossRef]
- Nemkevich, A.; Bürgi, H.-B.; Spackman, M.A.; Corry, B. Molecular dynamics simulations of structure and dynamics of organic molecular crystals. Phys. Chem. Chem. Phys. 2010, 12, 14916–14929. [Google Scholar] [CrossRef] [PubMed]
- Fu, C.-F.; Tian, S.X. A Comparative Study for Molecular Dynamics Simulations of Liquid Benzene. J. Chem. Theory Comput. 2011, 7, 2240–2252. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; van der Spoel, D.; van Drunen, R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A Gen. Phys. 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 2002, 100, 191–198. [Google Scholar] [CrossRef]
- Bacon, G.E.; Curry, N.A.; Wilson, S.A. A crystallographic study of solid benzene by neutron diffraction. Proc. R. Soc. Lon. A. 1964, 279, 98–110. [Google Scholar]
- Fernández, R.G.; Abascal, J.L.F.; Vega, C. The melting point of ice Ih for common water models calculated from direct coexistence of the solid-liquid interface. J. Chem. Phys. 2006, 124, 144506. [Google Scholar] [CrossRef]
- Belonoshko, A.B. Molecular Dynamics of MgSiO3 perovskite at high pressures: Equation of state, structure, and melting transition. Geochim. Chosmochim. Acta 1994, 58, 4039–4047. [Google Scholar] [CrossRef]
- Belonoshko, A.B.; Ahuja, R.; Johansson, B. Quasi-Ab initio molecular dynamic study of Fe melting. Phys. Rev. Lett. 2000, 84, 3638–3641. [Google Scholar] [CrossRef] [PubMed]
- Belonoshko, A.B.; Arapan, S.; Martonak, R.; Rosengen, A. MgO phase diagram from first principles in a wide pressure-temperature range. Phys. Rev. B 2010, 81. [Google Scholar] [CrossRef]
- Bridgman, P.W. The Technique of High Pressure Experimenting. Proc. Am. Acad. Arts Sci. 1914, 49, 627. [Google Scholar] [CrossRef]
- Mo, M.Z.; Chen, Z.; Li, R.K.; Dunning, M.; Witte, B.B.L.; Baldwin, J.K.; Fletcher, L.B.; Kim, J.B.; Ng, A.; Redmer, R.; et al. Heterogeneous to homogeneous melting transition visualized with ultrafast electron diffraction. Science 2018, 360, 1451–1455. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Zhou, D.; Han, Y. Melting of Colloidal Crystals. Adv. Funct. Mater. 2016, 26, 8903–8919. [Google Scholar] [CrossRef]
- Bai, X.-M.; Li, M. Nature and extent of melting in superheated solids: Liquid-solid coexistence model. Phys. Rev. B 2005, 72. [Google Scholar] [CrossRef]
- Stegailov, V. Homogeneous and heterogeneous mechanisms of superheated solid melting and decay. Comput. Phys. Commun. 2005, 169, 247–250. [Google Scholar] [CrossRef]
- Delogu, F. Mechanistic Aspects of Homogeneous and Heterogeneous Melting Processes. J. Phys. Chem. B 2006, 110, 12645–12652. [Google Scholar] [CrossRef] [PubMed]
- Burakovsky, L.; Burakovsky, N.; Cawkwell, M.J.; Preston, D.L.; Errandonea, D.; Simak, S.I. Ab initio phase diagram of iridium. Phys. Rev. B 2016, 94. [Google Scholar]
- Errandonea, D.; MacLeod, S.G.; Ruiz-Fuertes, J.; Burakovsky, L.; McMahon, M.I.; Wilson, C.W.; Ibañez, J.; Daisenberger, D.; Popescu, C. High-pressure/high-temperature phase diagram of zinc. J. Phys. Condens. Matter 2018, 30, 295402. [Google Scholar] [CrossRef]
- Burakovsky, L.; Burakovsky, N.; Preston, D.; Simak, S. Systematics of the Third Row Transition Metal Melting: The HCP Metals Rhenium and Osmium. Crystals 2018, 8, 243. [Google Scholar] [CrossRef]
- Gorski, K.M.; Hivon, E.; Banday, A.J.; Wandelt, B.D.; Hansen, F.K.; Reinecke, M.; Bartelmann, M. HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere. Astrophys. J. 2005, 622, 759–771. [Google Scholar] [CrossRef]
- Kovačević, T.; Reinhold, A.; Briesen, H. Identifying Faceted Crystal Shape from Three-Dimensional Tomography Data. Cryst. Growth Des. 2014, 14, 1666–1675. [Google Scholar] [CrossRef]
- Wise, P.K.; Ben-Amotz, D. Interfacial Adsorption of Neutral and Ionic Solutes in a Water Droplet. J. Phys. Chem. B 2018, 122, 3447–3453. [Google Scholar] [CrossRef] [PubMed]
- Alexeev, A.D.; Revva, V.N.; Alyshev, N.A.; Zhitlyonok, D.M. True triaxial loading apparatus and its application to coal outburst prediction. Int. J. Coal Geol. 2004, 58, 245–250. [Google Scholar] [CrossRef]
- Jonsson, H.; Gråsjö, J.; Nordström, J.; Johansson, N.; Frenning, G. An apparatus for confined triaxial testing of single particles. Powder Technol. 2015, 270, 121–127. [Google Scholar] [CrossRef]
- Jonsson, H.; Frenning, G. Investigations of single microcrystalline cellulose-based granules subjected to confined triaxial compression. Powder Technol. 2016, 289, 79–87. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahesta, R.; Mochizuki, K. Stepwise Homogeneous Melting of Benzene Phase I at High Pressure. Crystals 2019, 9, 279. https://doi.org/10.3390/cryst9060279
Mahesta R, Mochizuki K. Stepwise Homogeneous Melting of Benzene Phase I at High Pressure. Crystals. 2019; 9(6):279. https://doi.org/10.3390/cryst9060279
Chicago/Turabian StyleMahesta, Ravi, and Kenji Mochizuki. 2019. "Stepwise Homogeneous Melting of Benzene Phase I at High Pressure" Crystals 9, no. 6: 279. https://doi.org/10.3390/cryst9060279
APA StyleMahesta, R., & Mochizuki, K. (2019). Stepwise Homogeneous Melting of Benzene Phase I at High Pressure. Crystals, 9(6), 279. https://doi.org/10.3390/cryst9060279