Peculiarities in the Director Reorientation and the NMR Spectra Evolution in a Nematic Liquid Crystals under the Effect of Crossed Electric and Magnetic Fields
Abstract
1. Introduction
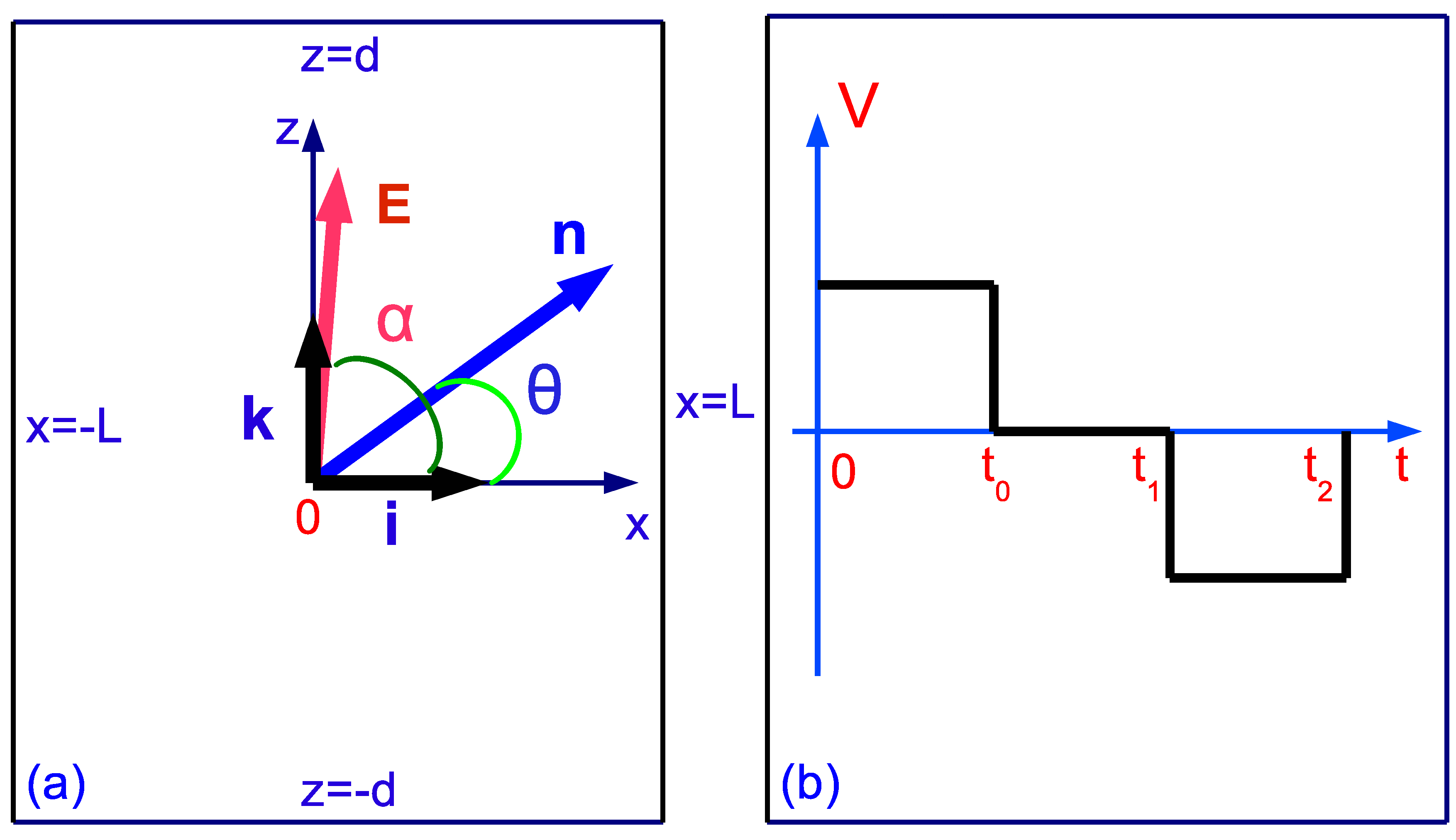
2. Theoretical Treatment of the Orientational Dynamics of Nematics under the Effect of the Crossed Electric and Magnetic Fields
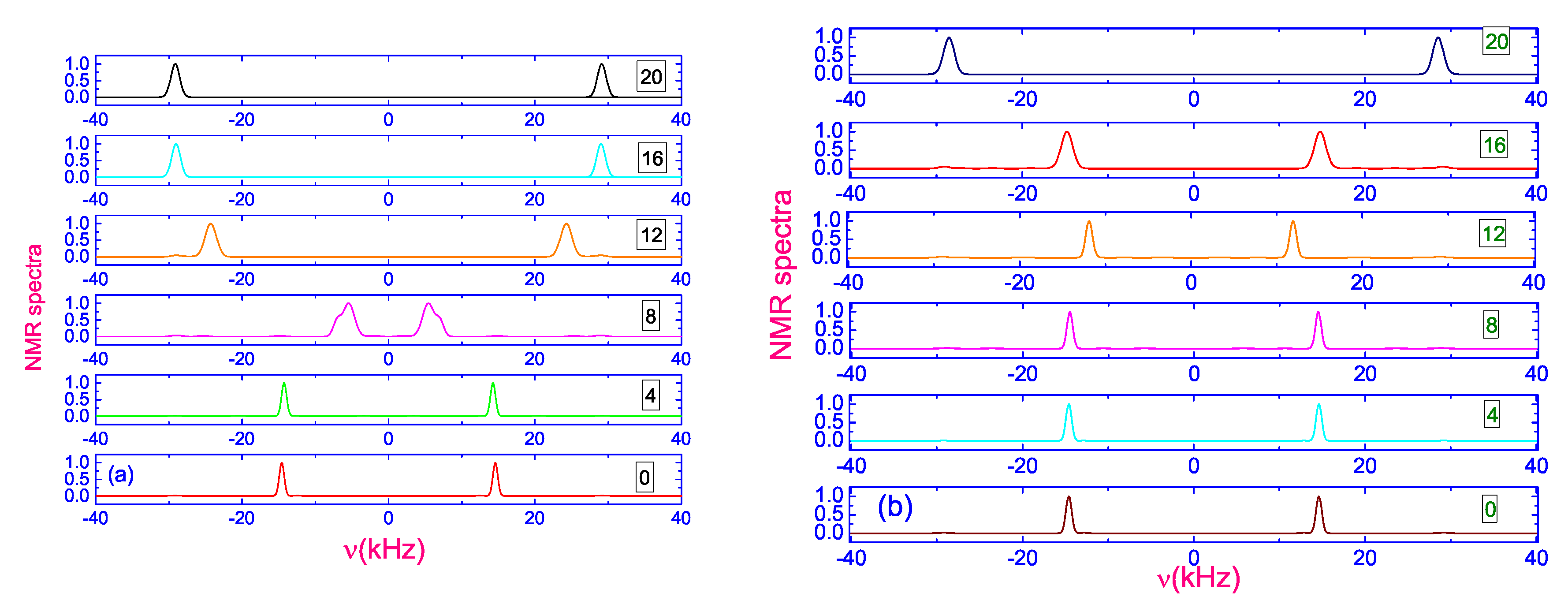
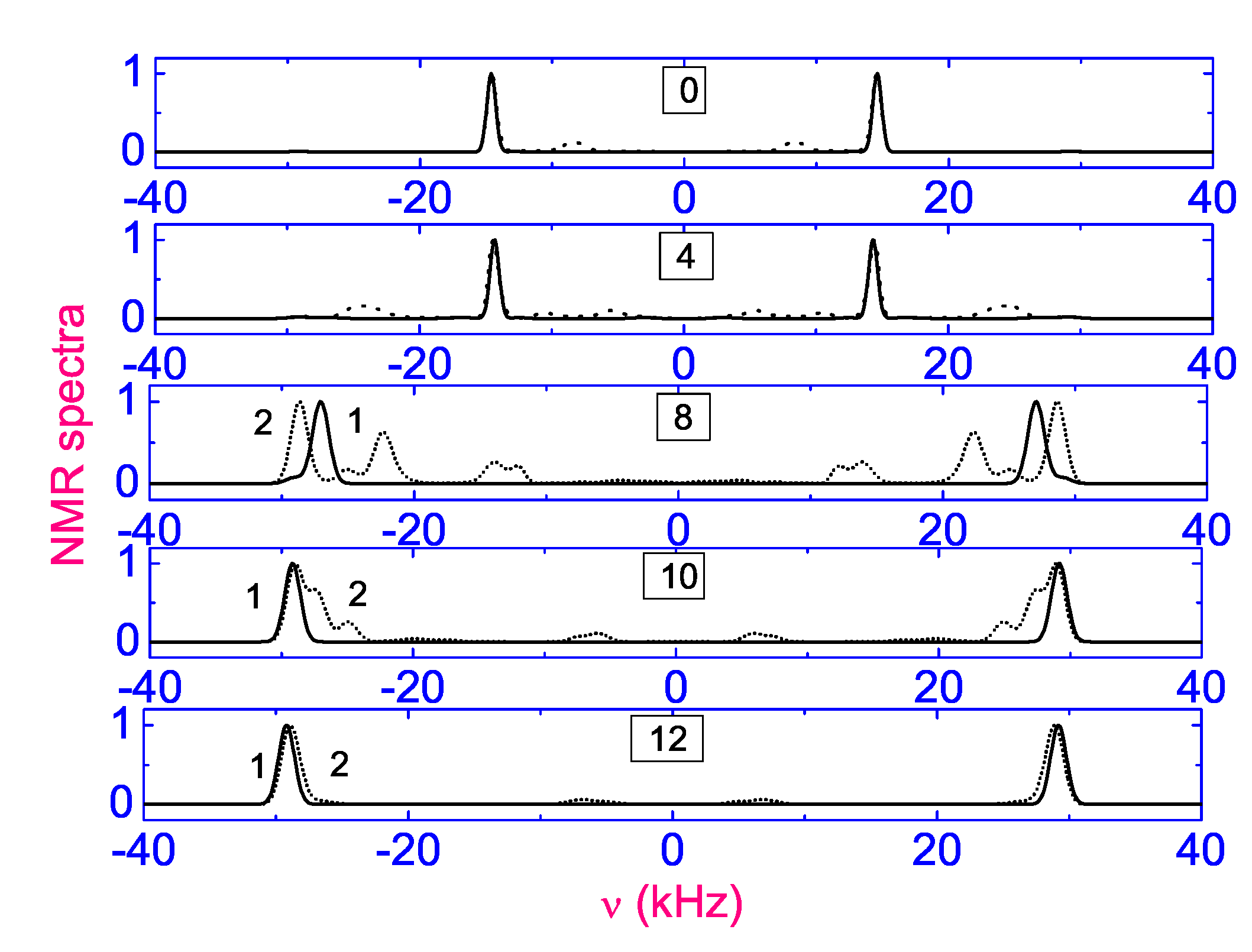
2.1. Deuterium Nuclear Magnetic Resonance Study
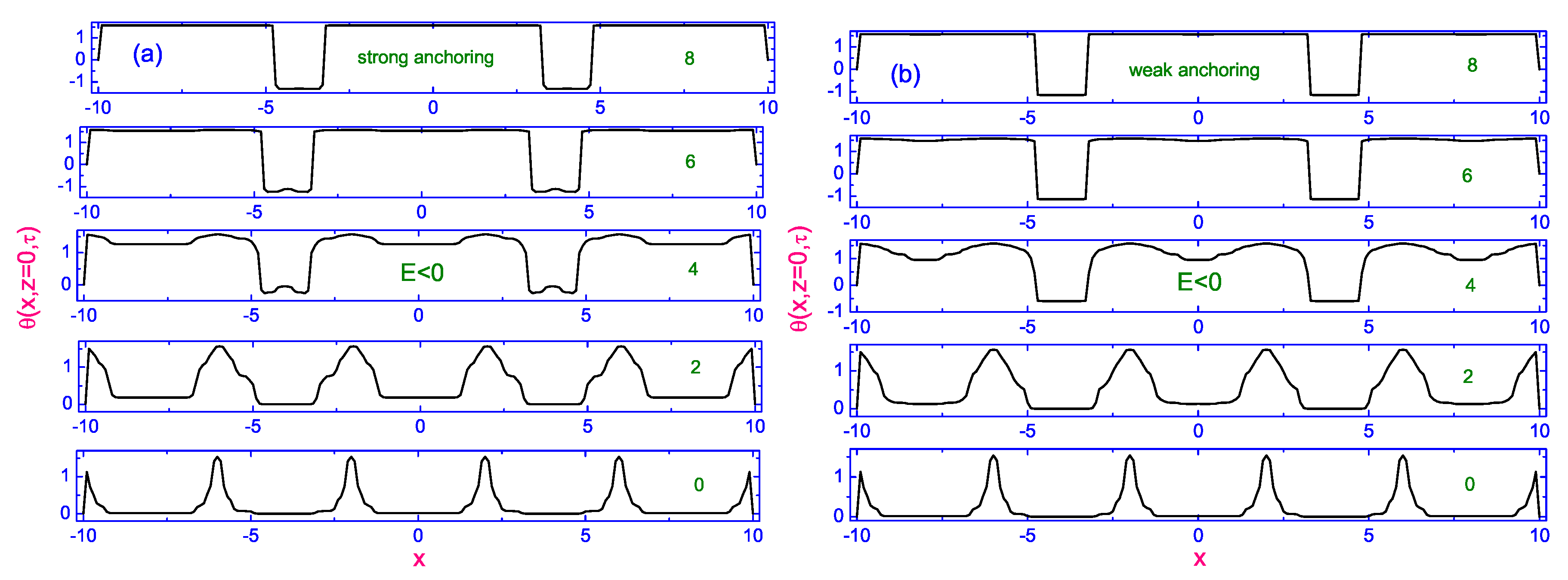
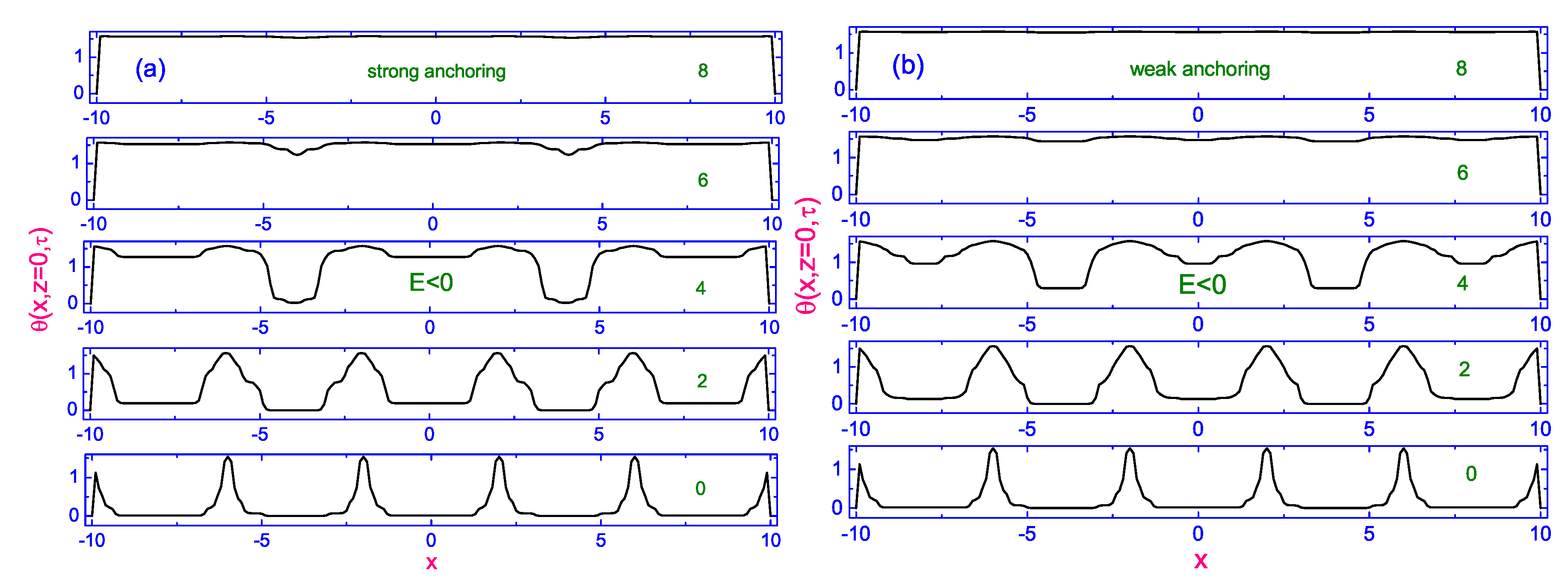
2.2. Peculiarities in the Director Reorientation under the Effect of Crossed Electric and Magnetic Fields
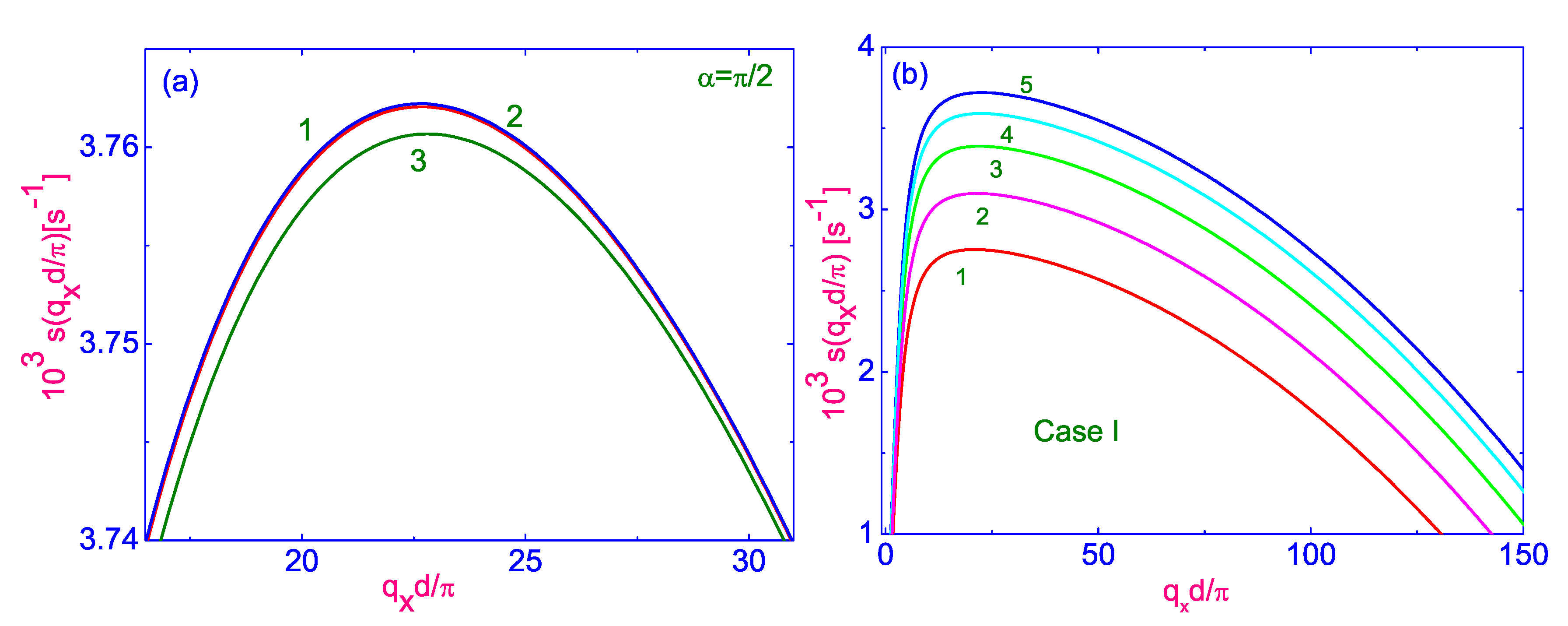
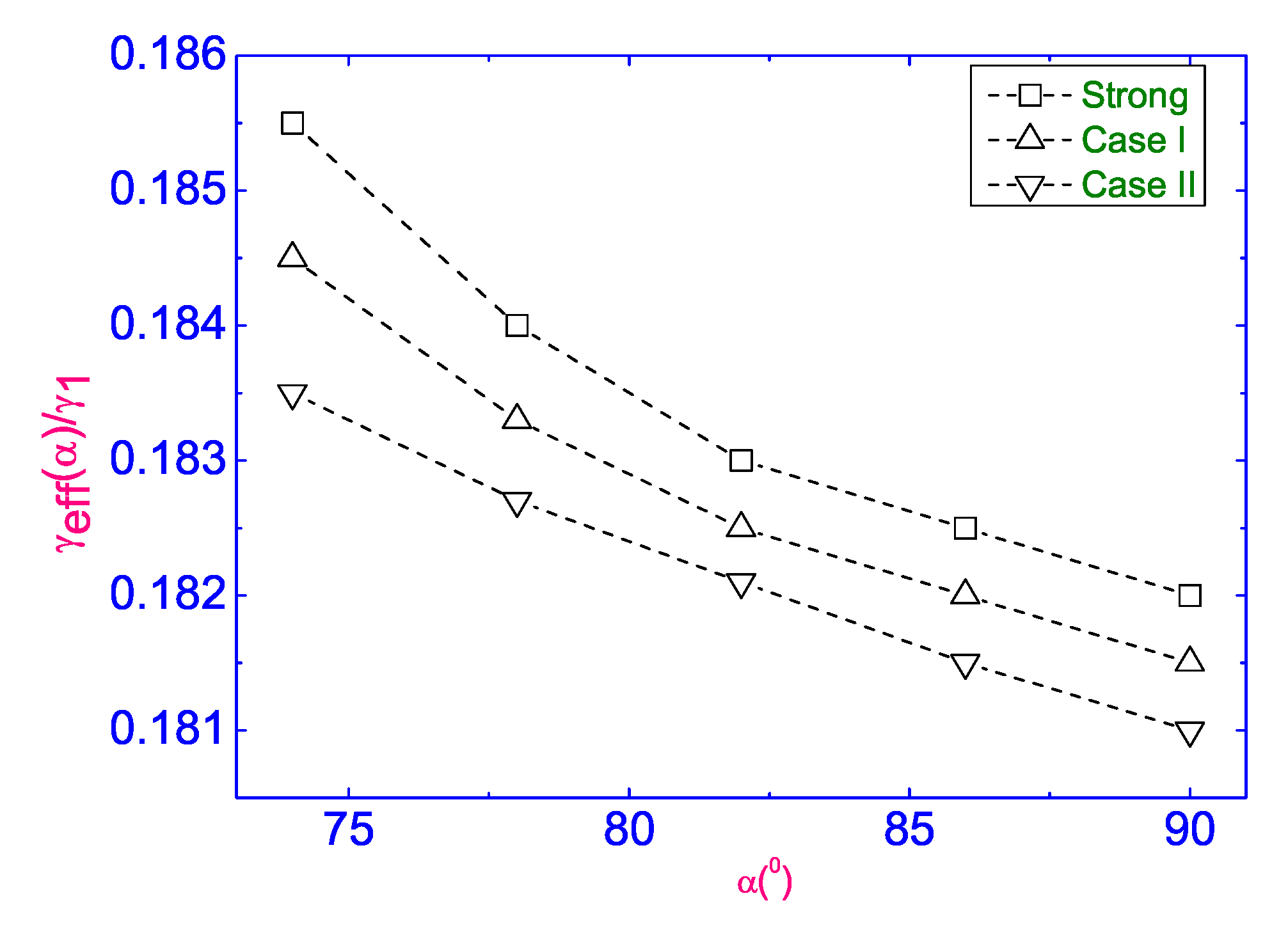
2.2.1. Theoretical Analysis in Case of the Linear Balance Equations
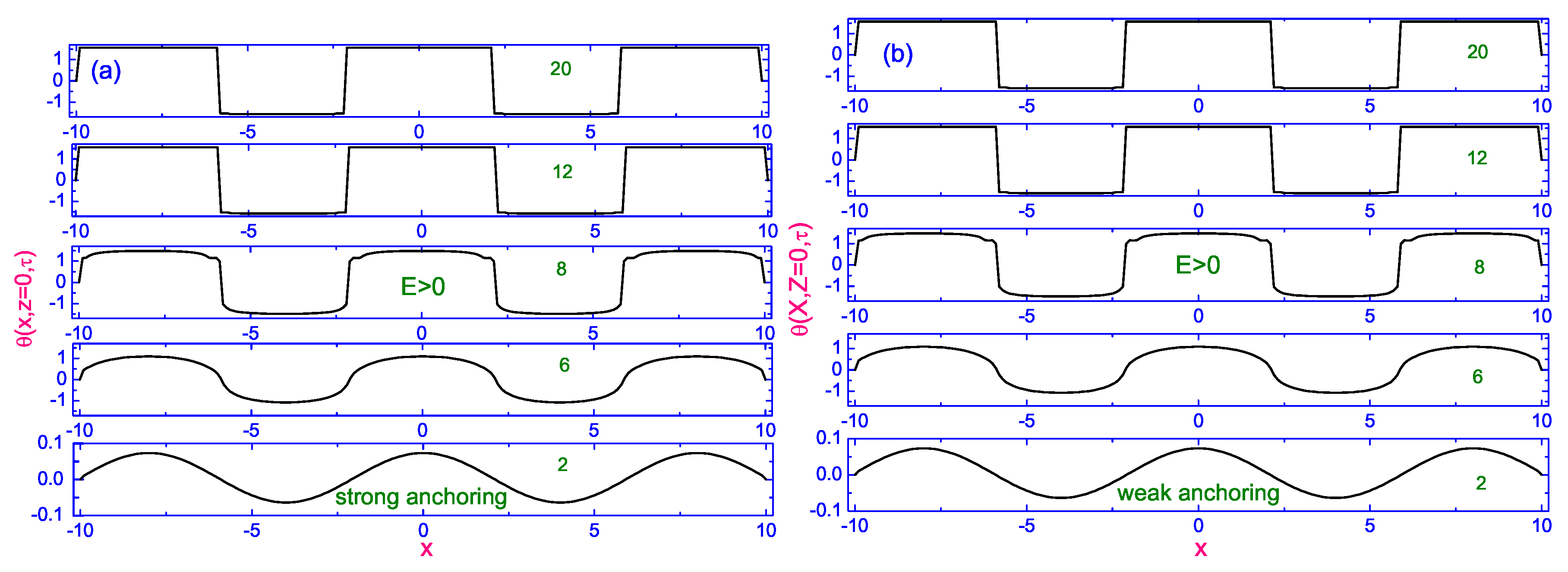
2.2.2. Theoretical Analysis in Case of the Nonlinear Balance Equations
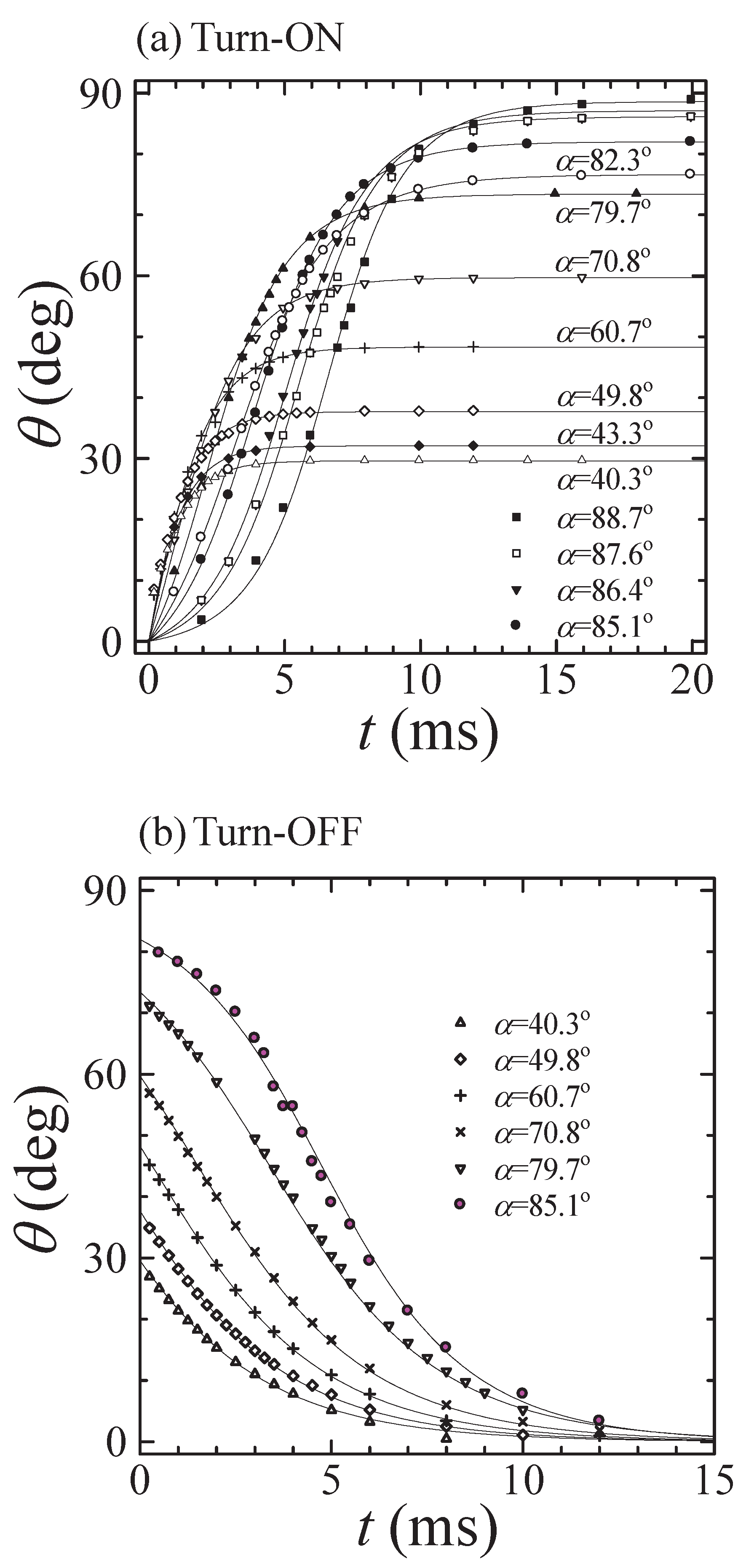
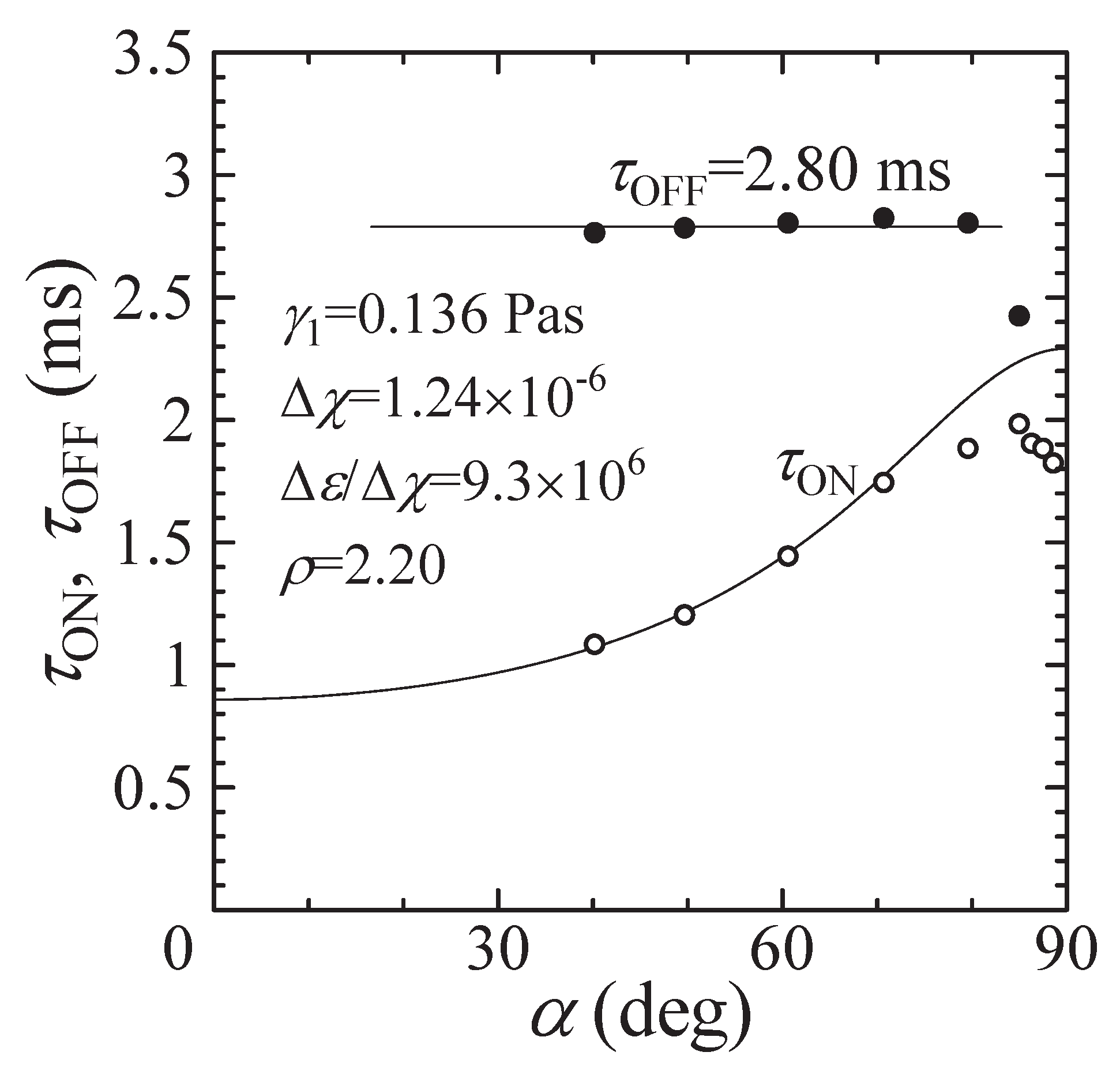
Switched-on Process in the Positive Sense
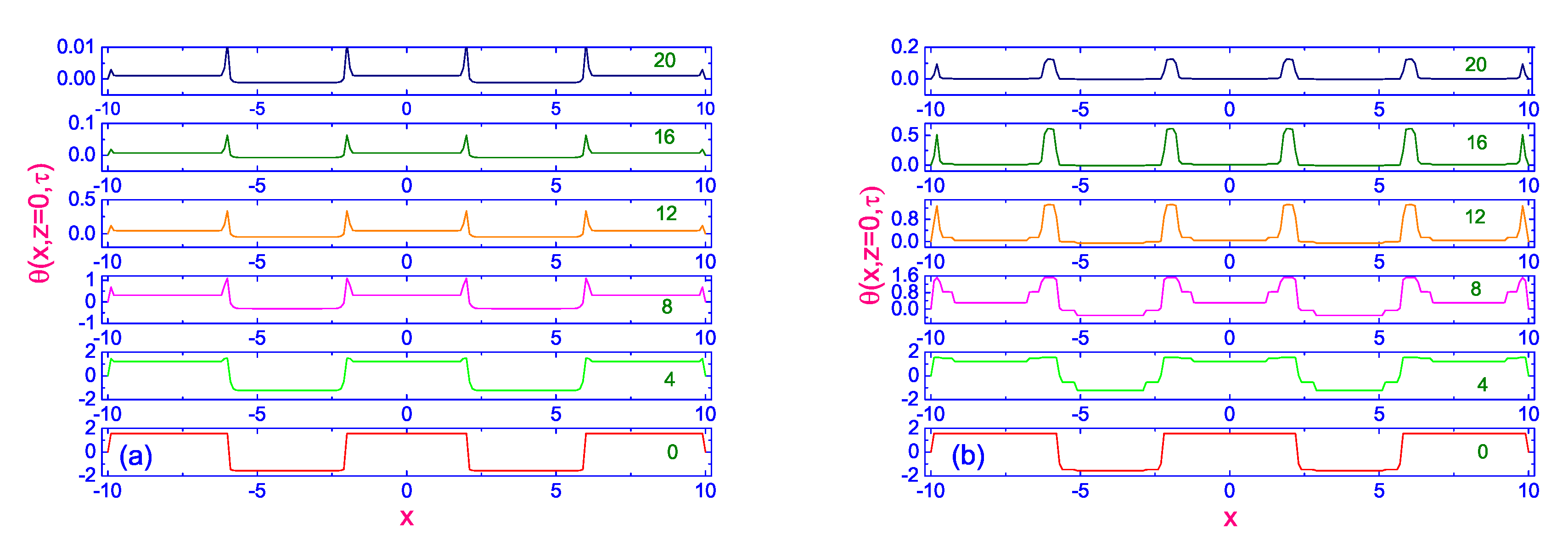
Switched-off Process
Switched-on Process in the Negative Sense
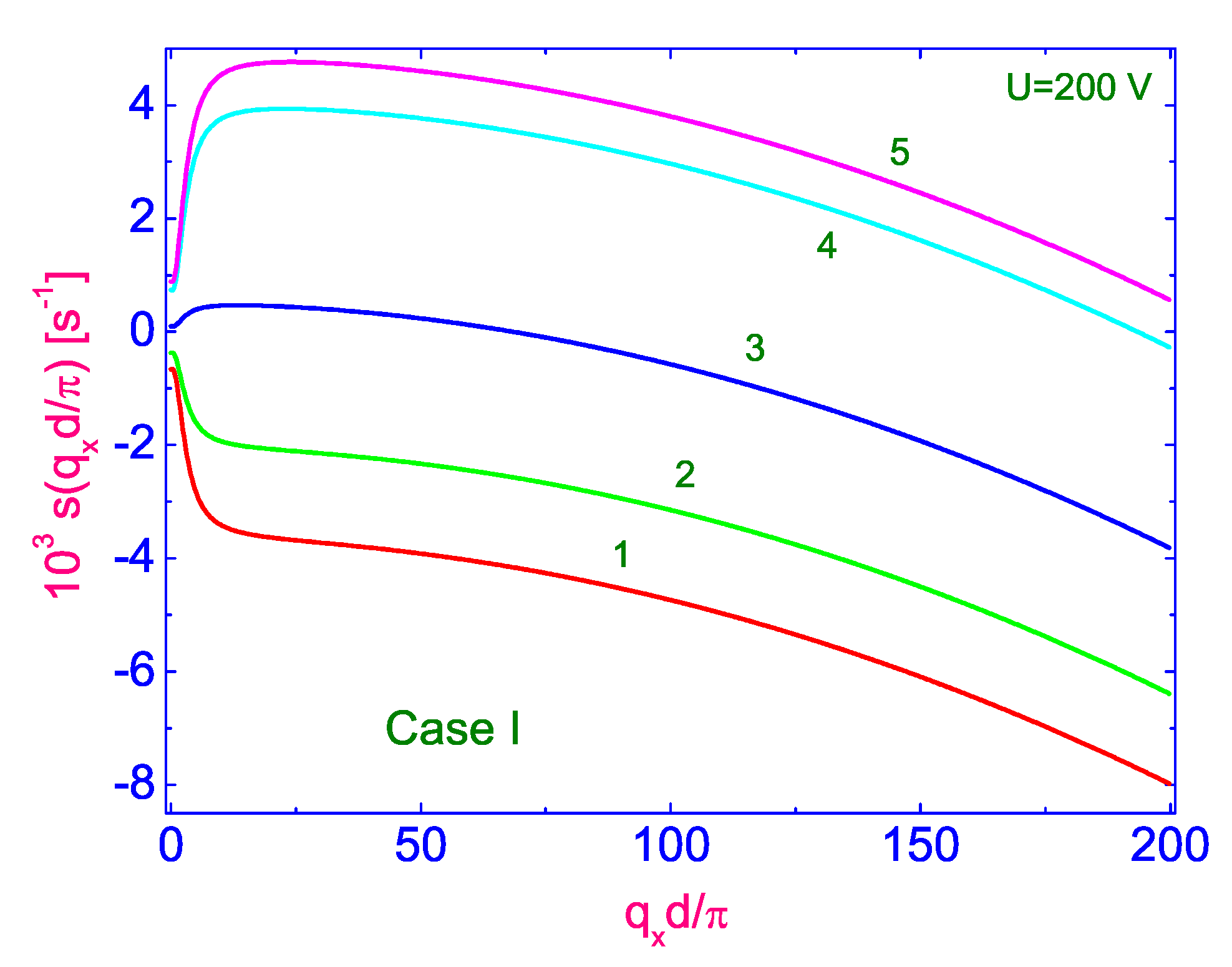
2.3. Simulation of the Time-Resolved H Spectra
3. Conclusions
Funding
Conflicts of Interest
References
- Dong, R.Y. Nuclear Magnetic Resonance of Liquid Crystals, 2nd ed.; Springer-Verlag: New York, NY, USA, 1997. [Google Scholar]
- Domenici, V.; Geppi, M.; Veracini, C. NMR in chiral and achiral smectic phases: Structure, orientational order and dynamics. Prog. Nucl. Mag. Res. Spectr. 2007, 50, 1–50. [Google Scholar] [CrossRef]
- Sugimura, A.; Luckhurst, G.R. Nuclear Magnetic Resonance Spectroscopy of Liquid Crystals; Dong, R.Y., Ed.; World Scientific Publishing Co.: Singapore, 2009; Chapter 10. [Google Scholar]
- Sugimura, A.; Luckhurst, G.R. Deuterium NMR investigations of field-induced director alignment in nematic liquid crystals. Prog. Nucl. Mag. Res. Spectr. 2016, 94–95, 37–74. [Google Scholar] [CrossRef] [PubMed]
- Fan, S.M.; Luckhurst, G.R.; Picken, S.J. A deuterium nuclear magnetic resonance investigation of orientational order and director kinetics in aramid solutions. J. Chem. Phys. 1994, 101, 3255–3267. [Google Scholar] [CrossRef]
- Luckhurst, G.R.; Miyamoto, T.; Sugimura, A.; Timimi, B.A. Director reorientation processes in a monodomain thin nematic liquid crystal film: A deuterium NMR spectroscopy study. J. Chem. Phys. 2002, 117, 5899–5907. [Google Scholar] [CrossRef]
- Luckhurst, G.R.; Sugimura, A.; Timimi, B.A.; Zimmermann, H. NMR determination of the physical properties of nematics. Liq. Cryst. 2005, 32, 1389–1396. [Google Scholar] [CrossRef]
- Hamasuna, D.; Luckhurst, G.R.; Sugimura, A.; Timimi, B.A.; Usami, K.; Zimmermann, H. Deuterium NMR spectra of a monodomain nematic: Angular dependence of the linewidths. Thin Solid Films 2008, 517, 1394–1401. [Google Scholar] [CrossRef]
- Cifelli, M.; Frezzato, D.; Luckhurst, G.R.; Moro, G.J.; Sugimura, A.; Veracini, C. Angular dependence of 2H-NMR longitudinal spin relaxation in aligned nematic 4-n-pentyl-4′- cyanobiphenyl: Molecular rotation and director fluctuations. Liq. Cryst. 2010, 37, 773–784. [Google Scholar] [CrossRef]
- Martins, A.F.; Veron, A. Theory and numerical simulation of field-induced director dynamics in confined nematics investigated by nuclear magnetic resonance. Liq. Cryst. 2010, 37, 747–771. [Google Scholar] [CrossRef]
- Sugimura, A.; Zakharov, A.V. Field-induced periodic distortions in a nematic liquid crystal: Deuterium NMR study and theoretical analysis. Phys. Rev. 2011, E84, 021703. [Google Scholar] [CrossRef] [PubMed]
- Sugimura, A.; Vakulenko, A.A.; Zakharov, A.V. The effect of backflow on the field-induced director alignment process: Nuclear Magnetic Resonance study and theoretical analysis. Phys. Procedia 2011, 14, 102–114. [Google Scholar] [CrossRef]
- Kantola, A.M.; Luckhurst, G.R.; Sugimura, A.; Tanaka, T.; Timimi, B.A. Field-induced alignment of the nematic director: Studies of nuclear magnetic resonance spectral oscillations in the limit of fast director rotation. J. Chem. Phys. 2011, 135, 044501. [Google Scholar] [CrossRef]
- Hamasuna, D.; Luckhurst, G.R.; Sugimura, A.; Timimi, B.A.; Zimmermann, H. Director alignment by crossed electric and magnetic fields: A deuterium NMR study. Phys. Rev. 2011, E84, 011705. [Google Scholar] [CrossRef]
- Veron, A.; Sugimura, A.; Luckhurst, G.R.; Martins, A.F. Properties of the static NMR response of a confined thin nematic film of 5CB-d2 under crossed electric and magnetic fields: Theory and experiments. Phys. Rev. 2012, E86, 051708. [Google Scholar] [CrossRef]
- Hamasuna, D.; Hashim, R.; Luckhurst, G.R.; Sugimura, A.; Timimi, B.A.; Zimmermann, H. Macroscopic order in a nematic liquid crystal: Perturbation by spontaneous director fluctuations. Phys. Rev. E 2015, 91, 062502. [Google Scholar] [CrossRef]
- Zakharov, A.V.; Vakulenko, A.A. Field-induced director dynamics in confined nematic liquid crystals imposed by a strong orthogonal electric field. Phys. Rev. E 2013, 88, 022505. [Google Scholar] [CrossRef]
- Zakharov, A.V.; Maslennikov, P.V. Field-induced peculiarities in the dynamics of the director reorientation in confined nematic liquid crystals. Chem. Phys. Lett. 2018, 692, 285–290. [Google Scholar] [CrossRef]
- Zakharov, A.V.; Vakulenko, A.A. Dynamics of the periodic distortions in confined nematic liquid crystals imposed by a strong orthogonal electric field. J. Non-Newton. Fluid Mech. 2015, 217, 23–31. [Google Scholar] [CrossRef]
- Ericksen, J.L. Anisotropic Fluids. Arch. Ration. Mech. Anal. 1960, 4, 231–237. [Google Scholar] [CrossRef]
- Leslie, F.M. Some constitutive equations for liquid crystals. Arch. Ration. Mech. Anal. 1968, 28, 265–283. [Google Scholar] [CrossRef]
- Guyon, E.; Meyer, R.B.; Salan, J. Domain Structure in the Nematic Freedericksz Transition. Mol. Cryst. Liq. Cryst. 1979, 54, 261–273. [Google Scholar] [CrossRef]
- Lonberg, F.; Fraden, S.; Hurd, A.J.; Meyer, R.B. Field-Induced Transient Periodic Structures in Nematic Liquid Crystals: The Twist-Freedericksz Transition. Phys. Rev. Lett. 1984, 52, 1903–1906. [Google Scholar] [CrossRef]
- Martins, A.F.; Esnault, P.; Volino, F. Measurement of the Viscoelastic Coefficients of Main-Chain Nematic Polymers by an NMR Technique. Phys. Rev. Lett. 1986, 57, 1745–1748. [Google Scholar] [CrossRef] [PubMed]
- Zakharov, A.V.; Vakulenko, A.A. Dynamics of the modulated distortions in confined nematic liquid crystals. J. Chem. Phys. 2013, 139, 244904. [Google Scholar] [CrossRef] [PubMed]
- Zakharov, A.V.; Maslennikov, P.V. Field-induced stress response of nematics encapsulated in microsized volumes. Chem. Phys. Lett. 2017, 684, 212–218. [Google Scholar] [CrossRef]
- Sugimura, A.; Vakulenko, A.A.; Zakharov, A.V. Field-induced non-uniform director reorientation for a low molar mass nematic imposed by a strong orthogonal electric field. Thin Solid Films 2014, 554, 64–68. [Google Scholar] [CrossRef]
- Berezin, I.S.; Zhidkov, N.P. Computing Methods, 4th ed.; Clarendon: Oxford, UK, 1965. [Google Scholar]
- Samarskij, A.A.; Nikolaev, E.S. Numerical Method for Grid Equations; Birkhauser: Basel, Switzerland, 1988. [Google Scholar]



| 74 | |||
| 78 | |||
| 82 | |||
| 86 | |||
| 90 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zakharov, A.V.; Sliwa, I. Peculiarities in the Director Reorientation and the NMR Spectra Evolution in a Nematic Liquid Crystals under the Effect of Crossed Electric and Magnetic Fields. Crystals 2019, 9, 262. https://doi.org/10.3390/cryst9050262
Zakharov AV, Sliwa I. Peculiarities in the Director Reorientation and the NMR Spectra Evolution in a Nematic Liquid Crystals under the Effect of Crossed Electric and Magnetic Fields. Crystals. 2019; 9(5):262. https://doi.org/10.3390/cryst9050262
Chicago/Turabian StyleZakharov, Alex V., and Izabela Sliwa. 2019. "Peculiarities in the Director Reorientation and the NMR Spectra Evolution in a Nematic Liquid Crystals under the Effect of Crossed Electric and Magnetic Fields" Crystals 9, no. 5: 262. https://doi.org/10.3390/cryst9050262
APA StyleZakharov, A. V., & Sliwa, I. (2019). Peculiarities in the Director Reorientation and the NMR Spectra Evolution in a Nematic Liquid Crystals under the Effect of Crossed Electric and Magnetic Fields. Crystals, 9(5), 262. https://doi.org/10.3390/cryst9050262




