Van der Waals Density Functional Theory vdW-DFq for Semihard Materials
Abstract
1. Introduction
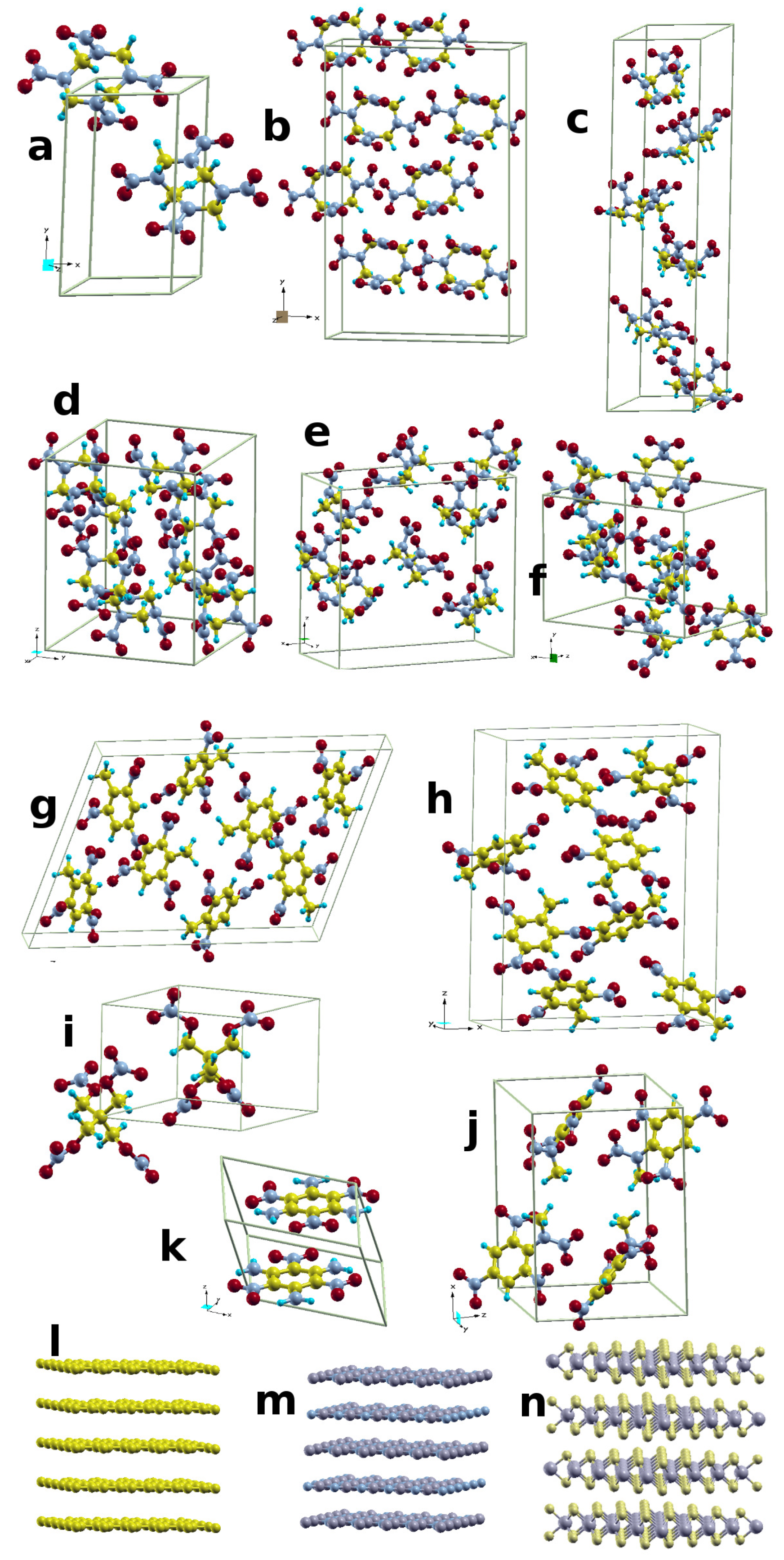
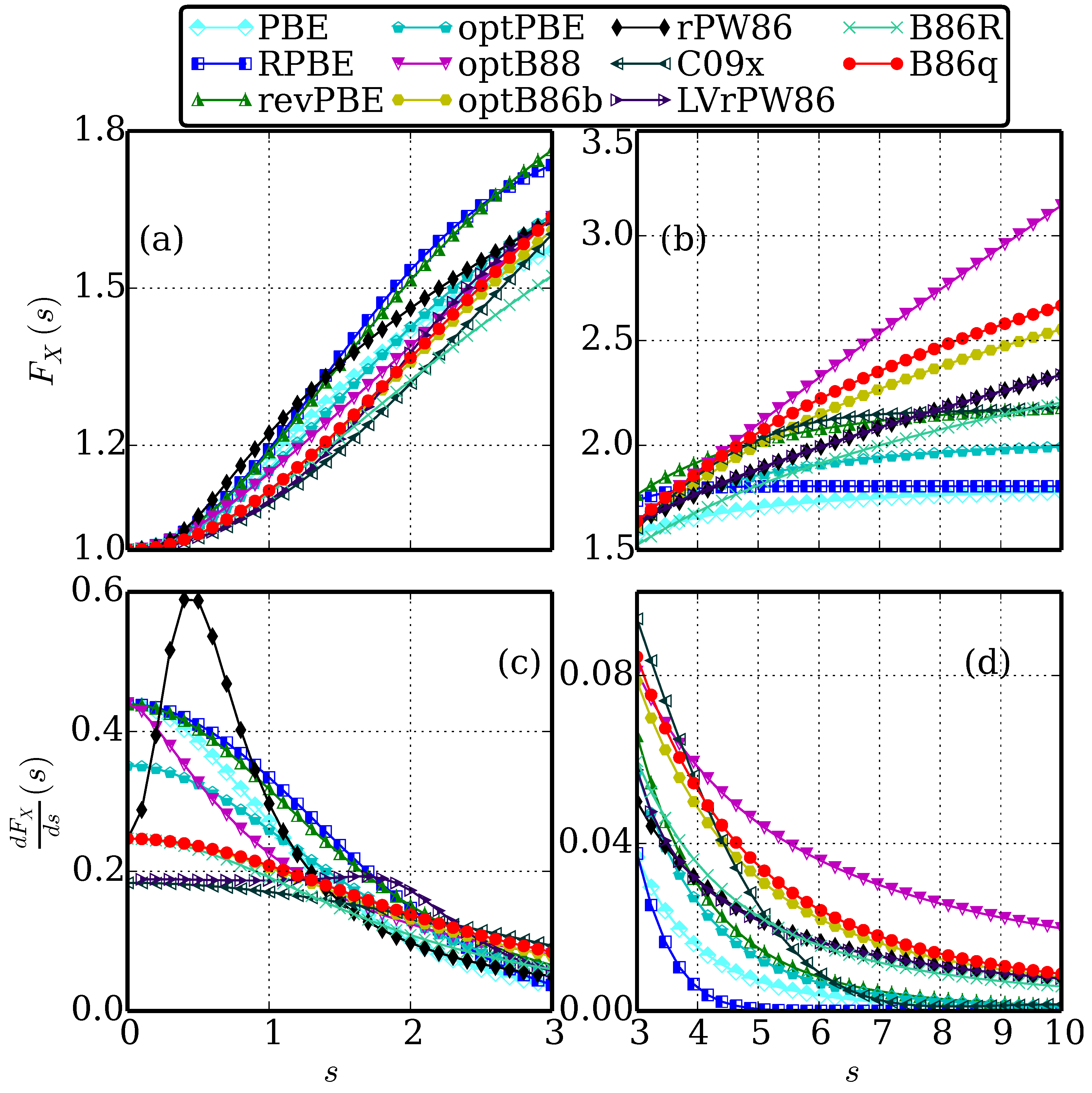
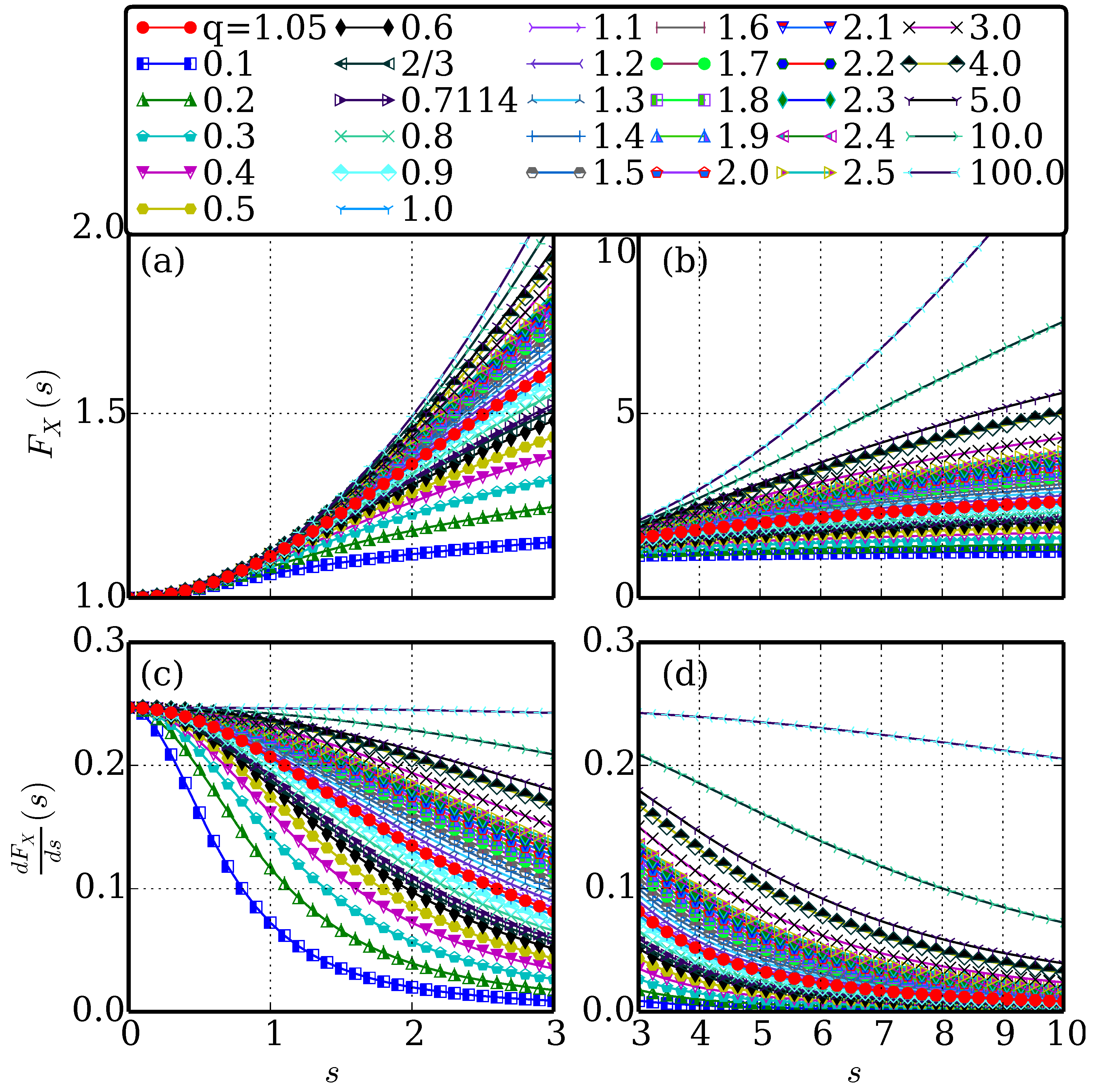
2. Methodology
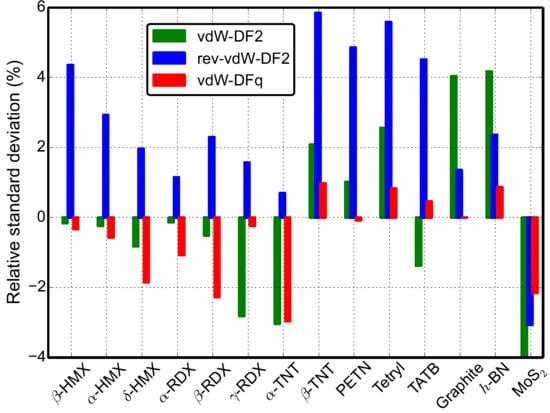
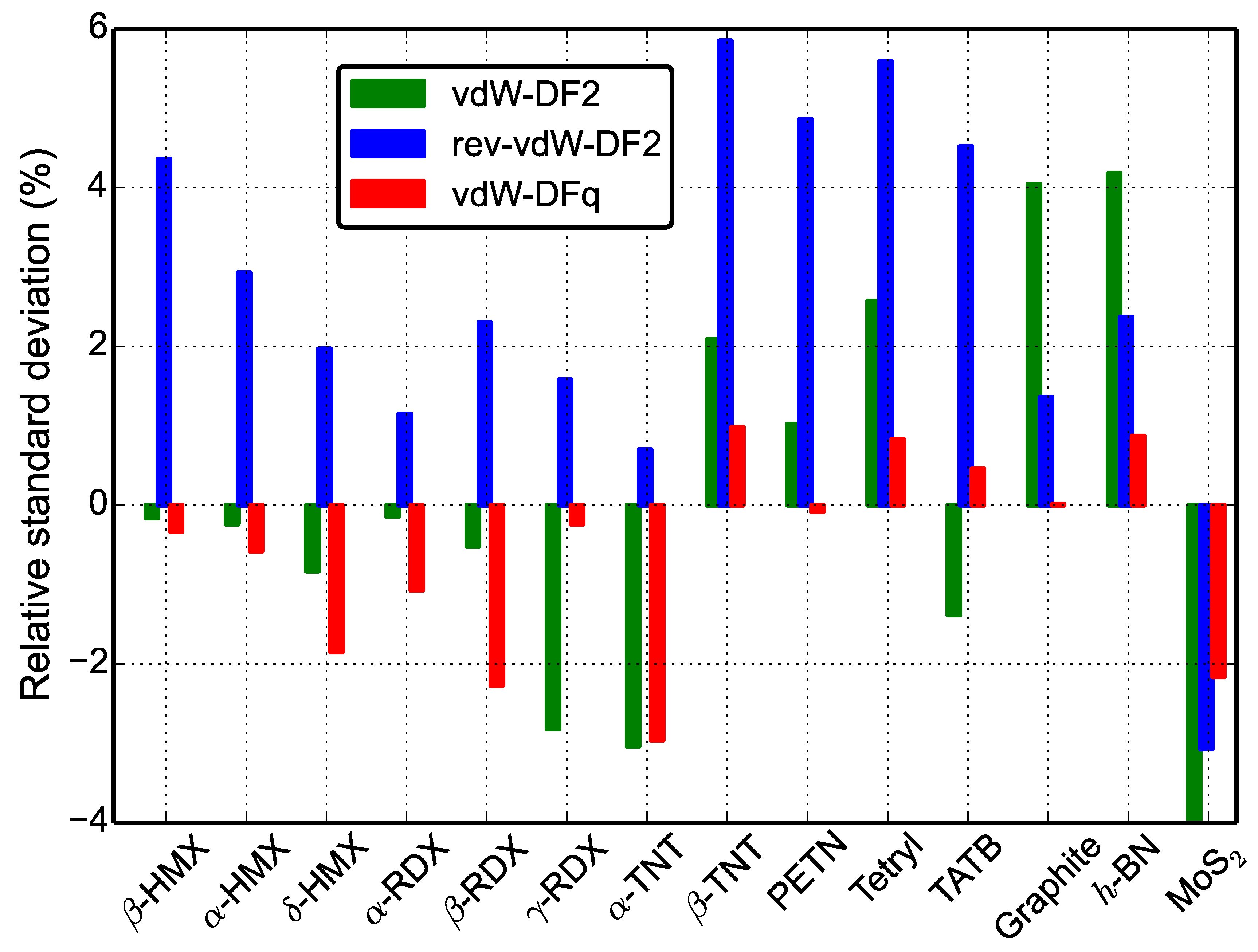
3. Results and Analysis
4. Conclusions
5. Computational Method
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Hermann, J.; DiStasio, R.A., Jr.; Tkatchenko, A. First-Principles Models for van der Waals Interactions in Molecules and Materials: Concepts, Theory, and Applications. Chem. Rev. 2017, 117, 4714–4758. [Google Scholar] [CrossRef]
- Klimes, J.; Michaelides, A. Perspective: Advances and challenges in treating van der waals dispersion forces in density functional theory. J. Chem. Phys. 2012, 137, 120901. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Comput. Chem. 2004, 25, 1463–1473. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Goerigk, L.; Grimme, S. A thorough benchmark of density functional methods for general main group thermochemistry, kinetics, and noncovalent interactions. Phys. Chem. Chem. Phys. 2011, 13, 6670–6688. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Caldeweyher, E.; Bannwarth, C.; Grimme, S. Extension of the D3 dispersion coefficient model. J. Chem. Phys. 2017, 147, 034112. [Google Scholar] [CrossRef] [PubMed]
- Tkatchenko, A.; Scheffler, M. Accurate molecular van der waals interactions from ground-state electron density and free-atom reference data. Phys. Rev. Lett. 2009, 102, 073005. [Google Scholar] [CrossRef]
- Tkatchenko, A.; DiStasio, R.A.; Car, R.; Scheffler, M. Accurate and efficient method for many-body van der waals interactions. Phys. Rev. Lett. 2012, 108, 236402. [Google Scholar] [CrossRef]
- Ruiz, V.G.; Liu, W.; Tkatchenko, A. Density-functional theory with screened van der waals interactions applied to atomic and molecular adsorbates on close-packed and non-close-packed surfaces. Phys. Rev. B 2016, 93, 035118. [Google Scholar] [CrossRef]
- Dion, M.; Rydberg, H.; Schröder, E.; Langreth, D.C.; Lundqvist, B.I. Van der waals density functional for general geometries. Phys. Rev. Lett. 2004, 92, 246401. [Google Scholar] [CrossRef]
- Lee, K.; Murray, Ḋ.; Kong, L.; Lundqvist, B.I.; Langreth, D.C. Higher-accuracy van der waals density functional. Phys. Rev. B 2010, 82, 081101. [Google Scholar] [CrossRef]
- Hyldgaard, P.; Berland, K.; Schröder, E. Interpretation of van der waals density functionals. Phys. Rev. B 2014, 90, 075148. [Google Scholar] [CrossRef]
- Berland, K.; Cooper, V.R.; Lee, K.; Schroeder, E.; Thonhauser, T.; Hyldgaard, P.; Lundqvist, B.I. Van der Waals forces in density functional theory: A review of the vdW-DF method. Rep. Prog. Phys. 2015, 78, 066501. [Google Scholar] [CrossRef] [PubMed]
- Klimeš, J.; Bowler, D.R.; Michaelides, A. Chemical accuracy for the van der waals density functional. J. Phys. Condens. Matter 2010, 22, 022201. [Google Scholar] [CrossRef]
- Klimeš, J.; Bowler, D.R.; Michaelides, A. Van der waals density functionals applied to solids. Phys. Rev. B 2011, 83, 195131. [Google Scholar] [CrossRef]
- Cooper, V.R. Van der waals density functional: An appropriate exchange functional. Phys. Rev. B 2010, 81, 161104. [Google Scholar] [CrossRef]
- Berland, K.; Hyldgaard, P. Exchange functional that tests the robustness of the plasmon description of the van der waals density functional. Phys. Rev. B 2014, 89, 035412. [Google Scholar] [CrossRef]
- Hamada, I. van der waals density functional made accurate. Phys. Rev. B 2014, 89, 121103. [Google Scholar] [CrossRef]
- Peng, H.; Perdew, J.P. Rehabilitation of the perdew-burke-ernzerhof generalized gradient approximation for layered materials. Phys. Rev. B 2017, 95, 081105. [Google Scholar] [CrossRef]
- Terentjev, A.V.; Constantin, L.A.; Pitarke, J.M. Dispersion-corrected pbesol exchange-correlation functional. Phys. Rev. B 2018, 98, 214108. [Google Scholar] [CrossRef]
- Peng, H.; Yang, Z.; Perdew, J.P.; Sun, J. Versatile van der waals density functional based on a meta-generalized gradient approximation. Phys. Rev. X 2016, 6, 041005. [Google Scholar] [CrossRef]
- Terentjev, A.V.; Cortona, P.; Constantin, L.A.; Pitarke, J.M.; Sala, F.D.; Fabiano, E. Solid-state testing of a van-der-waals-corrected exchange-correlation functional based on the semiclassical atom theory. Computation 2018, 6, 7. [Google Scholar] [CrossRef]
- Csonka, G.I.; Perdew, J.P.; Ruzsinszky, A.; Philipsen, P.H.T.; Lebègue, S.; Paier, J.; Vydrov, O.A.; Ángyán, J.G. Assessing the performance of recent density functionals for bulk solids. Phys. Rev. B 2009, 79, 155107. [Google Scholar] [CrossRef]
- Conroy, M.W.; Oleynik, I.I.; Zybin, S.V.; White, C.T. First-principles anisotropic constitutive relationships in beta-cyclotetramethylene tetranitramine (beta-HMX). J. Appl. Phys. 2008, 104, 053506. [Google Scholar] [CrossRef]
- Landerville, A.C.; Conroy, M.W.; Budzevich, M.M.; Lin, Y.; White, C.T.; Oleynik, I.I. Equations of state for energetic materials from density functional theory with van der Waals, thermal, and zero-point energy corrections. Appl. Phys. Lett. 2010, 97, 251908. [Google Scholar] [CrossRef]
- Cui, H.-L.; Ji, G.-F.; Chen, X.-R.; Zhang, Q.-M.; Wei, D.-W.; Zhao, F. Phase transitions and mechanical properties of octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine in different crystal phases by molecular dynamics simulation. J. Chem. Eng. Data 2010, 5, 3121–3129. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Ceperley, D.M.; Alder, B.J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 1980, 45, 566–569. [Google Scholar] [CrossRef]
- Gulans, A.; Puska, M.J.; Nieminen, R.M. Linear-scaling self-consistent implementation of the van der waals density functional. Phys. Rev. B 2009, 79, 201105. [Google Scholar] [CrossRef]
- Román-Pérez, G.; Soler, J.M. Efficient implementation of a van der waals density functional: Application to double-wall carbon nanotubes. Phys. Rev. Lett. 2009, 103, 096102. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Gygi, F. A simplified implementation of van der waals density functionals for first-principles molecular dynamics applications. J. Chem. Phys. 2012, 136, 224107. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Yang, W. Comment on “generalized gradient approximation made simple”. Phys. Rev. Lett. 1998, 80, 890. [Google Scholar] [CrossRef]
- Puzder, A.; Dion, M.; Langreth, D.C. Binding energies in benzene dimers: Nonlocal density functional calculations. J. Chem. Phys. 2006, 124, 164105. [Google Scholar] [CrossRef]
- Jurecka, P.; Sponer, J.; Cerny, J.; Hobza, P. Benchmark database of accurate (mp2 and ccsd(t) complete basis set limit) interaction energies of small model complexes, dna base pairs, and amino acid pairs. Phys. Chem. Chem. Phys. 2006, 8, 1985–1993. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Voorhis, T.V. Nonlocal van der waals density functional: The simpler the better. J. Chem. Phys. 2010, 133, 244103. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Voorhis, T.V. Nonlocal van der waals density functional made simple. Phys. Rev. Lett. 2009, 103, 063004. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Voorhis, T.V. Implementation and assessment of a simple nonlocal van der waals density functional. J. Chem. Phys. 2010, 13, 164113. [Google Scholar] [CrossRef]
- Sabatini, R.; Gorni, T.; de Gironcoli, S. Nonlocal van der waals density functional made simple and efficient. Phys. Rev. B 2013, 87, 041108. [Google Scholar] [CrossRef]
- Wellendorff, J.; Lundgaard, K.T.; Møgelhøj, A.; Petzold, V.; Landis, D.D.; Nørskov, J.K.; Bligaard, T.; Jacobsen, K.W. Density functionals for surface science: Exchange-correlation model development with bayesian error estimation. Phys. Rev. B 2012, 85, 23514. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Murray, E.D.; Lee, K.; Langreth, D.C. Investigation of exchange energy density functional accuracy for interacting molecules. J. Chem. Theory Comput. 2009, 5, 2754–2762. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Wang, Y. Accurate and simple density functional for the electronic exchange energy: Generalized gradient approximation. Phys. Rev. B 1986, 33, 8800–8802. [Google Scholar] [CrossRef]
- Becke, A.D. On the large-gradient behavior of the density functional exchange energy. J. Chem. Phys. 1986, 85, 7184–7187. [Google Scholar] [CrossRef]
- Hamada, I.; Otani, M. Comparative van der waals density-functional study of graphene on metal surfaces. Phys. Rev. B 2010, 82, 153412. [Google Scholar] [CrossRef]
- Choi, C.S.; Boutin, H.P. A study of crystal structure of beta-cyclotetramethylene tetranitramine by neutron diffraction. Acta Crystallogr. Sect. B Struct. Sci. 1970, B 26, 1235. [Google Scholar] [CrossRef]
- Herrmann, M.; Engel, W.; Eisenreich, N. Thermal-analysis of the phases of hmx using X-ray diffraction. Z. Krist. 1993, 204, 121–128. [Google Scholar]
- Peng, Q.; Rahul; Wang, G.; Liu, G.R.; De, S. Structures, mechanical properties, equations of state, and electronic properties of β-hmx under hydrostatic pressures: A dft-d2 study. Phys. Chem. Chem. Phys. 2014, 16, 19972–19983. [Google Scholar] [CrossRef]
- Tao, J.; Zheng, F.; Gebhardt, J.; Perdew, J.P.; Rappe, A.M. Screened van der waals correction to density functional theory for solids. Phys. Rev. Mater. 2017, 1, 020802. [Google Scholar] [CrossRef]
- Cady, H.H.; Larson, A.C.; Cromer, D.T. The crystal structure of α-HMX and a refinement of the structure of β-HMX. Acta Crystallogr. 1963, 16, 617–623. [Google Scholar] [CrossRef]
- Choi, C.S.; Prince, E. The crystal structure of cyclotrimethylenetrinitramine. Acta Crystallogr. Sect. B Struct. Sci. 1972, B28, 2857–2862. [Google Scholar] [CrossRef]
- Millar, D.I.A.; Oswald, I.D.H.; Francis, D.J.; Marshall, W.G.; Pulham, C.R.; Cumming, A.S. The crystal structure of beta-rdx-an elusive form of an explosive revealed. Chem. Commun. 2009, 562–564. [Google Scholar] [CrossRef] [PubMed]
- Olinger, B.; Roof, B.; Cady, H.H. The linear and volume compression of beta-hmx and rdx to 9 gpa. In Symposium (Int) on High Dynamic Pressures; S INT COMP MIL DENS: Paris, France, 1978; pp. 3–8. [Google Scholar]
- Golovina, N.I.; Titkov, A.N.; Raevskii, A.V.; Atovmyan, L.O. Kinetics and mechanism of phase transitions in the crystals of 2,4,6-trinitrotoluene and benzotrifuroxane. J. Solid State Chem. 1994, 113, 229–238. [Google Scholar] [CrossRef]
- Cady, H.H.; Larson, A.C. Pentaerythritol tetranitrate II: Its crystal structure and transformation to PETN I: An algorithm for refinement of crystal structures with poor data. Acta Crystallogr. Sect. 1975, 31, 1864–1869. [Google Scholar] [CrossRef]
- Cady, H.H. The crystal structure of N-methyl-N-2,4,6-tetranitroaniline (tetryl). Acta Crystallogr. 1967, 23, 601–609. [Google Scholar] [CrossRef]
- Cady, H.H.; Larson, A.C. The crystal structure of 1,3,5-triamino-2,4,6-trinitrobenzene. Acta Crystallogr. 1965, 18, 485–496. [Google Scholar] [CrossRef]
- Björkman, T.; Gulans, A.; Krasheninnikov, A.V.; Nieminen, R.M. Van der waals bonding in layered compounds from advanced density-functional first-principles calculations. Phys. Rev. Lett. 2012, 108, 235502. [Google Scholar] [CrossRef]
- Geim, A.K.; Grigorieva, I.V. Van der Waals heterostructures. Nature 2013, 499, 419–425. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Ferri, N.; DiStasio, R.A.; Tkatchenko, A. Wavelike charge density fluctuations and van der waals interactions at the nanoscale. Science 2016, 351, 1171–1176. [Google Scholar] [CrossRef]
- Peng, Q.; Rahul; Wang, G.; Liu, G.R.; Grimme, S.; De, S. Predicting Elastic Properties of β-HMX from First-principles calculations. J. Phys. Chem. B 2015, 119, 5896–5903. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef]
- Hammer, B.; Hansen, L.B.; Nørskov, J.K. Improved adsorption energetics within density-functional theory using revised perdew-burke-ernzerhof functionals. Phys. Rev. B 1999, 59, 7413–7421. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Jones, R.O.; Gunnarsson, O. The density functional formalism, its applications and prospects. Rev. Mod. Phys. 1989, 61, 689–746. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Alfè, D.; DiStasio, R.A.; Tkatchenko, A. Hard numbers for large molecules: Toward exact energetics for supramolecular systems. J. Phys. Chem. Lett. 2014, 5, 849–855. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Reilly, A.M.; DiStasio, R.A.; Tkatchenko, A. Long-range correlation energy calculated from coupled atomic response functions. J. Chem. Phys. 2014, 140, 18A508. [Google Scholar] [CrossRef]
- Reilly, A.M.; Tkatchenko, A. Seamless and accurate modeling of organic molecular materials. J. Phys. Chem. Lett. 2013, 4, 1028–1033. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Silvestrelli, P.L. Hidden by graphene—Towards effective screening of interface van der waals interactions via monolayer coating. Carbon 2018, 139, 486–491. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Silvestrelli, P.L. Faraday-like screening by two-dimensional nanomaterials: A scale-dependent tunable effect. J. Phys. Chem. Lett. 2019, 10, 2044–2050. [Google Scholar] [CrossRef] [PubMed]

| a(Å) | b(Å) | c(Å) | V(Å) | RSD | ||
|---|---|---|---|---|---|---|
| Expt. | 6.537 | 11.054 | 8.7018 | 124.443 | 518.558 | |
| PBE | 6.673 | 11.312 | 8.894 | 124.395 | 553.99 | 6.8 |
| PBE-D2 | 6.542 | 10.842 | 8.745 | 124.41 | 511.73 | −1.4 |
| PBE-D3 | 6.541 | 10.894 | 8.748 | 124.38 | 514.488 | −0.8 |
| PBE-TS | 6.530 | 10.985 | 8.770 | 124.572 | 517.992 | −0.1 |
| RPBE-D3 | 6.580 | 11.061 | 8.762 | 124.357 | 526.501 | 1.5 |
| PBEsol | 6.603 | 10.928 | 8.709 | 124.002 | 520.949 | 0.5 |
| vdW-DF | 6.653 | 10.096 | 8.901 | 124.756 | 539.880 | 4.1 |
| vdW-DF2 | 6.575 | 10.946 | 8.765 | 124.579 | 519.387 | 0.2 |
| optB88-vdW | 6.476 | 10.662 | 8.680 | 124.735 | 492.535 | −5.0 |
| optB86b-vdW | 6.481 | 10.635 | 8.700 | 124.749 | 492.710 | −5.0 |
| optPBE-vdW | 6.550 | 10.877 | 8.760 | 124.703 | 513.088 | −1.1 |
| vdW-DF-C09 | 6.435 | 10.494 | 8.650 | 124.807 | 479.676 | −7.5 |
| vdW-DF-cx | 6.556 | 10.787 | 8.779 | 124.557 | 511.324 | −1.4 |
| rev-vdW-DF2 | 6.504 | 10.696 | 8.685 | 124.670 | 496.905 | −4.2 |
| vdW-DFq e | 6.569 | 10.921 | 8.737 | 124.316 | 517.742 | −0.16 |
| optB86q | 6.922 | 11.773 | 8.985 | 121.986 | 620.991 | 19.8 |
| vdW-DFk’ | 6.486 | 10.636 | 8.694 | 124.713 | 493.013 | −4.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Q.; Wang, G.; Liu, G.-R.; De, S. Van der Waals Density Functional Theory vdW-DFq for Semihard Materials. Crystals 2019, 9, 243. https://doi.org/10.3390/cryst9050243
Peng Q, Wang G, Liu G-R, De S. Van der Waals Density Functional Theory vdW-DFq for Semihard Materials. Crystals. 2019; 9(5):243. https://doi.org/10.3390/cryst9050243
Chicago/Turabian StylePeng, Qing, Guangyu Wang, Gui-Rong Liu, and Suvranu De. 2019. "Van der Waals Density Functional Theory vdW-DFq for Semihard Materials" Crystals 9, no. 5: 243. https://doi.org/10.3390/cryst9050243
APA StylePeng, Q., Wang, G., Liu, G.-R., & De, S. (2019). Van der Waals Density Functional Theory vdW-DFq for Semihard Materials. Crystals, 9(5), 243. https://doi.org/10.3390/cryst9050243