1. Introduction
Quasicrystal is a new structure as well as a novel material that has presented an important application prospect in engineering [
1]. Quasicrystals are brittle at low and intermediate temperature, and the structural integrity requires materials to have a sufficient strength and toughness for engineering applications. Hence, the study of the crack and fracture problems of the material is significant. It is well-known that the deformation of quasicrystals is governed by two different displacement fields: one is the phonon field, which is similar to the conventional displacement field
under the long-wave length approximation; and the other is the phason field
, which is an unusual physical quantity compared to the traditional condensed matter physics and materials science [
2,
3,
4,
5,
6,
7,
8,
9]. The elasticity of quasicrystals is more difficult to determine than the elasticity of crystals or classical elasticity [
2,
3,
4,
5,
6,
7,
8,
9]. To investigate the notch/crack and fracture problems of the material, Fan introduced a mathematical theory of the elasticity of quasicrystals, where one of the mathematical theories can be found in his recently published monograph [
10]. In the over 200 individual quasicrystals observed to date, there are about 70 individual quasicrystals belonging to two-dimensional decagonal quasicrystals. Therefore, these kinds of quasicrystals are very important from a fundamental point and from their applications. In this study, we focused on the discussion of this class of quasicrystal. In order to measure some of the fracture parameters of the material, some scientists have acquired the fracture parameters by using the experimental specimens [
4,
5,
6,
7,
8]. Recently, Mariano and his co-workers, on the basis of first invariance principles and within the framework of the (both finite and small strain) continuum mechanics of quasicrystals, have discussed the steady crack propagation and dislocation of the quasicrystals [
11,
12,
13]. In addition, Wang et al. studied quasicrystals by experimental observation and pointed out that the long-period structure in magnesium alloys as well as the precipitation of the quasicrystalline phase were very important areas of this research [
14]. Li et al. [
15,
16], Gao [
17], Li et al. [
18], and Li [
19,
20] studied many cracked quasicrystals by adopting a variety of methods. Of course, many studies on quasicrystals can be found in [
21,
22,
23,
24,
25,
26,
27], amongst others.
Notch/crack problems for conventional structural materials were studied by Muskhelishvili [
28] in terms of complex analysis. In the present case, we studied the problem for quasicrystals governed by the quadruple harmonic equation. Therefore, the mathematical solution is much more complicated than for conventional structural and foam materials. Later, we introduce the complex analysis developed in monograph [
10]. Here, we further developed the complex analysis for so-called Saint-Venant problems of quasicrystalline materials, which may extend the methodology to more worthwhile engineering applications.
2. Governing Equations of Elasticity of Decagonal Quasicrystals
Consider a plane in two-dimensional quasicrystals, and assume that it is perpendicular to the periodic symmetrical axis (e.g., axis
). In this case, the phonon and phason fields are respectively:
The strain field associated with the phonon displacement field and phason field is respectively defined by [
7]:
Here, we considered only the plane problem. It was assumed that all variables were independent of , i.e., the deformation is limited in a plane perpendicular to the z-axis, and this leads to . Furthermore, we can obtain the strains .
If we denote
as the stress tensor associated to the strain tensor
and
as the stress tensor associated with the strain tensor
, then the generalized Hooke’s law for decagonal quasicrystals with
point groups can be expressed by [
7]:
where
;
represents the phonon elastic constants;
represents the phason elastic constants; and
is the phonon–phason coupling elastic constant. In addition, the equilibrium equations are as follows:
Equations (2)–(4) are the basic equations describing the elasticity of decagonal quasicrystals under plane deformation, and this is an equation made of 18 field equations.
Based on the deformation compatibility equations,
If we introduce the three functions
,
, and
, as follows:
Equation (5) can be transformed into the following simple forms:
where
is the two-dimensional Laplacian operator, and
,
. When we let the three functions
,
, and
, so that:
then the Equation (7) set can be reduced to a unique equation of a higher order, i.e., the potential function
satisfies the quadruple harmonic equation as follows [
10]:
where the constant is defined by
.
By introducing a complex variable, the solution of Equation (9) can be expressed as [
10]:
where
are four analytic functions of a single complex variable
. The bar denotes the complex conjugate hereinafter, i.e.,
These analytic functions will be determined by the boundary conditions of practical problems. It is easy to prove that
has no contribution to the stress and displacement fields, so
.
From the fundamental solution of Equation (10), we can find the complex representation of the stresses as given below [
10]:
and
where the prime, two prime, three prime, and superscript (
) denote the first to fourth order differentiation of
to the variable
in addition to
, and it is evident that
and
are not analytic functions.
By some derivation from Equation (11), we have the complex representation of the displacements, as follows:
and the constants can be expressed by
,
,
; and
has been listed in the above expression.
If we introduce the new functions for convenience, such that:
All the stress and displacement components can be rewritten by
, based on these new functions. In order not to change the stresses and displacements, the analytic functions
can be replaced by
, and
can be replaced by
[
10]. Therefore, we can obtain the complex function written in the following form:
where
,
,
,
, and
are real constants, and
,
,
,
, and
can be expressed as:
and
where
are principal stresses at infinity, and
is the angle of
and the
-direction. Let
, we have
, and yields
, where
are the generalized principal stresses at infinity, and
is the angle of
and the
-direction.
As is widely-known, Muskhelishvili [
28] provided two kinds rational conformal mapping for solving plane problems of elastic materials for some complicated configurations, and the first kind of rational conformal mapping reads
. This mapping can transform the exterior of the unit circle in the
-plane into the exterior of the material with defects in the physical plane. As a result of the transformation, we can obtain the series expansion of the logarithmic item
. As
outside the unit circle was noted, we can obtain
and also have
, where
is analytic outside the unit circle. In light of a similar analysis, it is very easy to obtain the following formula for each of the items
,
, and
of two dimensional decagonal quasicrystals, for example, the series expansion
, and so on. Substituting these results into Equation (15), we have:
where
,
, and
are single valued analytical functions of
. The other kind of rational conformal mapping reads
. This can transform the interior of the unit circle in the mapping plane into the exterior of the material with defects in the physical plane. Through a similar analysis with the first kind of mapping, we have:
where
,
, and
are single valued analytical functions of
.
Considering the stress boundary conditions for the plane elasticity of decagonal quasicrystals in the following, we can express them as:
where the point
represents an arbitrary boundary point of a multi-connected quasicrystalline material; meanwhile, we need to consider
and
. Here,
and
represent the surface tractions and generalized surface tractions, respectively, and
denotes the outer unit normal vector of an arbitrary boundary point.
According to Equations (11) and (15) and the boundary conditions in Equation (18), we can write the boundary conditions based on our analytic functions:
3. An Arc of Elliptic Notch Inner Surface in a Decagonal Quasicrystal
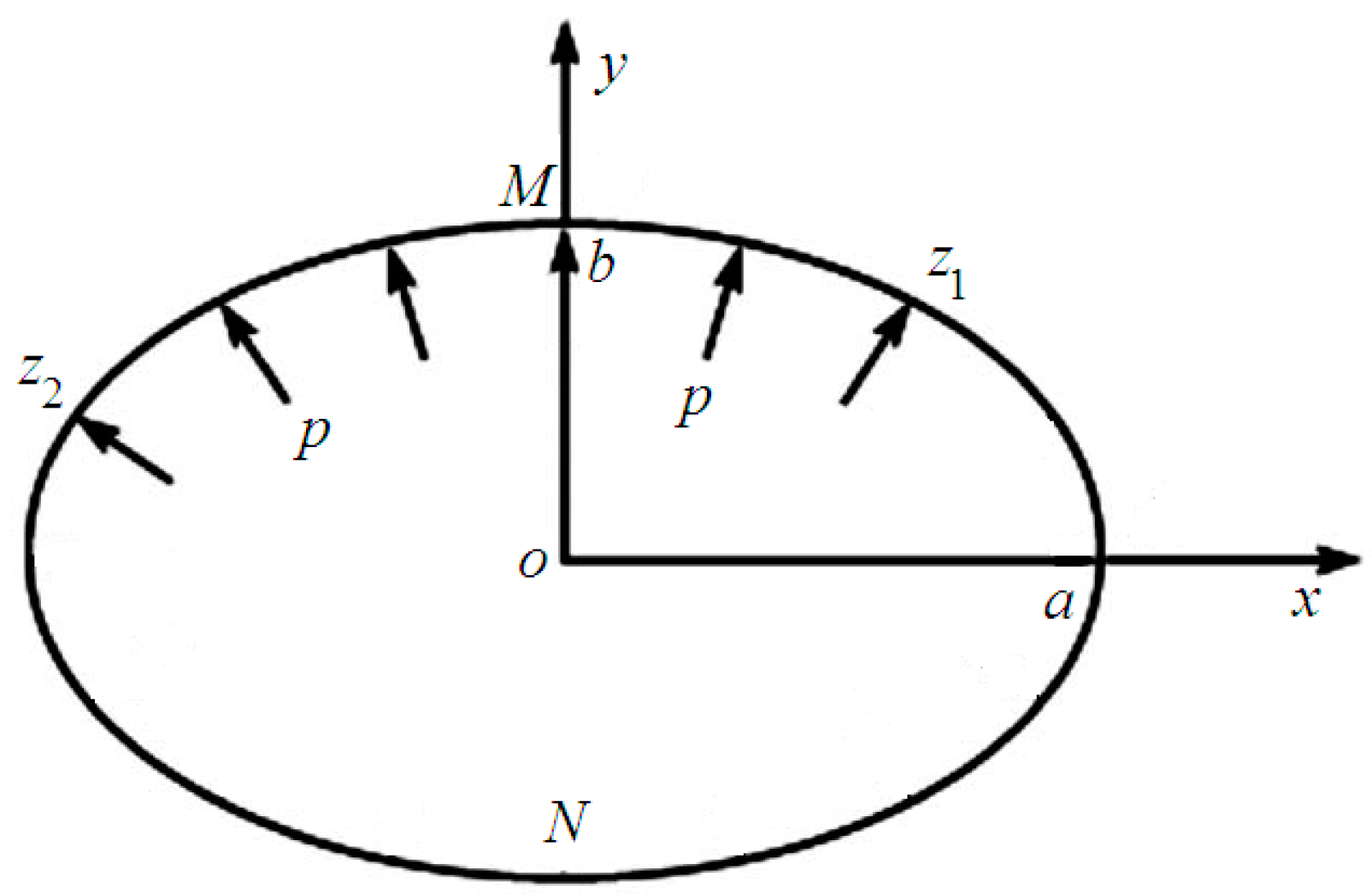
We assumed a two dimensional decagonal quasicrystal weakened by an elliptic notch
(see
Figure 1), in which the arc
of the elliptic notch was subjected to a uniform pressure
. For this configuration and based on the above mappings, we can obtain the simplified form of the conformal mapping:
This can transform the exterior of the unit circle in the -plane into the exterior of the ellipse in the z-plane, where and the constants can be expressed by , .
In the boundary of the unit circle, we introduce
and can obtain:
where
Take the conjugate on both sides of Equation (21), and it will yield:
If we multiply both sides of Equation (21) by
, and integrate around the unit circle, then we obtain:
When we give the same treatment to Equation (12), we can obtain:
Meanwhile, according to the mapping equation
, we can obtain these formulas based on the above mapping, i.e.,
,
,
, and
. Now, we can solve Equation (23), and because
is a single valued analytical function of
, we can obtain:
where
is an analytical function of
, and we have
. Therefore, Equation (23) becomes
, where the constants are omitted. Based on the Cauchy integral basic formula for Equation (24), we have
and
. Meanwhile, we find that
is a single valued analytical function of
, and we have
. Therefore, Equation (24) becomes
, where the constants are omitted. If we assume that the material is not subjected to force at infinity, it will lead to
and
. So, we have:
where
As
is a single valued analytic function of
, we have
. For
, let
, and we can obtain:
where
. Therefore, we have
.
Calculating the sum of the above results, and noting Equation (17), we have:
Similarly, by solving Equation (24), one gets:
where
4. Solutions to a Decagonal Quasicrystalline Strip Containing a Centric Crack
It is difficult to determine the solutions to a decagonal quasicrystalline strip containing a crack because of its essential complexity. To avoid this difficulty, we performed a step to determine the conformal mapping from the interior of the unit circle to the exterior of the given crack. Here, we present a new approach for finding the wanted conformal transformation. We constructed a conformal mapping from the physical plane to the complex plane, where a conformal map maps the exterior of the crack in the physical plane to the interior of the unit circle in the plane.
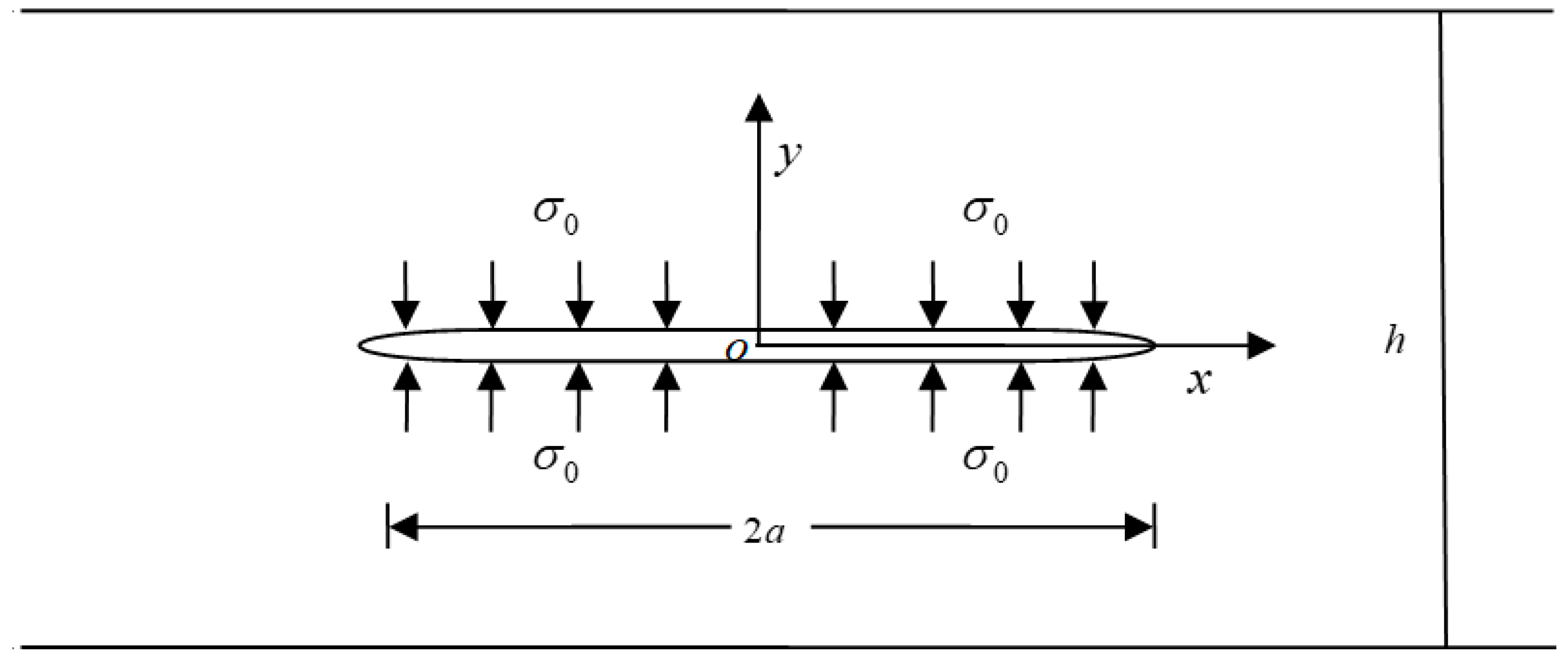
Figure 2 shows a schematic of a decagonal quasicrystalline strip containing a centric crack. There was a Griffith crack with a length of
along the
axis embedded at the mid plane of a decagonal quasicrystalline strip with a height of
. The surfaces of the crack can be denoted by two coincident lines, namely
and
, respectively. The portion
of the crack surfaces were assumed to be subject to the action of uniform loadings
,
. Meanwhile, we adopted
to simulate the crack length of the strip.
The boundary conditions for this problem can be described as follows:
The essential building block in the present application as well as in all of the applications of the method of conformal mappings, is the fundamental mapping
that maps the interior circle onto a Griffith crack with the length of
in the
plane:
Second, we introduced some transformations, so that:
The conformal map was constructed as described in the foregoing section. For the discussion below, we will denote simply
as follows:
The point position
in the mathematical domain was mapped by
onto the point position
in the physical domain. Of course, we could not obtain the solution immediately by means of this transformation. We maintained that Equation (19) holds on and began by writing the unknown functions
and
by means of the conformal mapping:
We can clearly rewrite the boundary condition for the unit circle in the
plane. If we denote
in the unit circle
, the boundary conditions can result in:
Considering that the phason field can be discussed similarly in the above analysis process, we omit the procedure of the phason field here. In the calculation below, we affirmed that the coefficients
and
according to the free stresses at infinity, and meanwhile the circumference of the resultant force was zero:
where
and
denote the generalized surface tractions in the
-direction and
-direction, respectively. Multiplying both sides of Equation (34) and its conjugate equation by
and then calculating the Cauchy integration results in:
where
represents the value of
at the boundary of
in the mapping plane and
and
are single valued analytic functions in
. It is necessary to analyze the functions
and
in the mathematical domain to compute these integrations. This is the most expensive step in our solution. Using the last two equations together with the conformal map in Equation (32), we obtain:
It is very easy to prove that Equation (36) can determine the functions
and
together when these series and function sets of linear equations are posed distinctly. This has been proved with some generality, and the fact can be seen in [
10], where the result
, related to the stress intensity factor, is directly given:
where
denotes the action of uniform loading, and
can be seen in the preceding sections respectively.
When inverse conformal mapping is rarely at hand, it is difficult to calculate the expression of the stress field in terms of the inverse conformal mapping. However, for this problem, if we substitute these expressions into Equation (11), it is very easy to calculate the full stress field for a crack. On the other hand, the stress intensity factor can be seen as the most important quantities, which can be characterized by the universal near-tip fields. Now, we calculate the stress intensity factors from our solution. In fact, the calculation can be completed directly from the solution based on the conformal map as described above. Previous authors derived the following expression for the complex combination (of the real) stress intensity factor [
10]:
This result can be extended to mode
of decagonal quasicrystals. Due to its similarity, the process was omitted. In particular, this special result (Equation (41)) can be converted into the results obtained in [
10]. If we let
or
, the expression (Equation (41)) can be converted into:
which is the stress intensity factor of the decagonal point group 10 mm quasicrystals of the infinite plate weakened by a Griffith crack [
10].