Improvement of Growth Interface Stability for 4-Inch Silicon Carbide Crystal Growth in TSSG
Abstract
1. Introduction
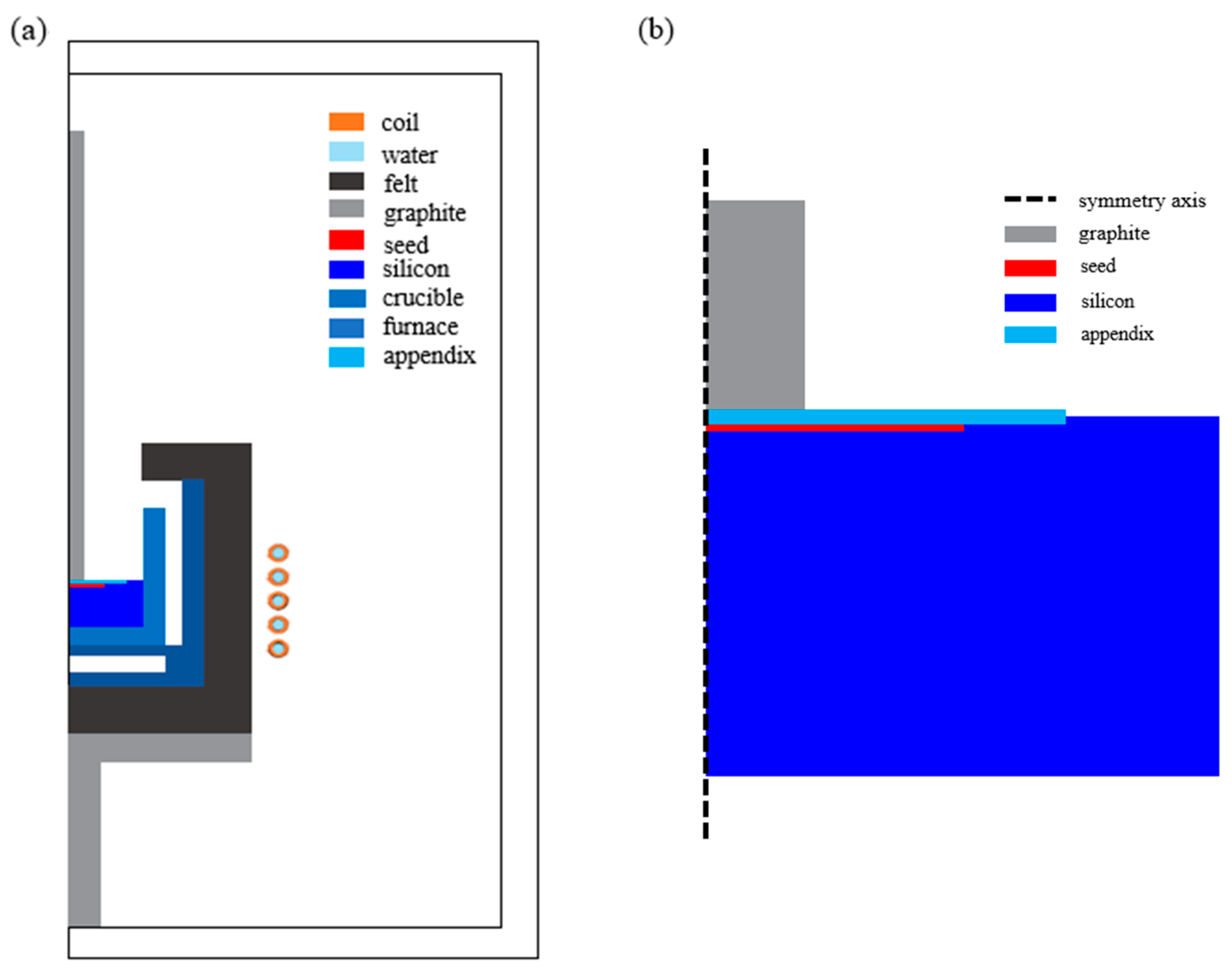
2. Numerical Analysis
2.1. Electromagnetic Field
2.2. Heat Field
2.3. Fluid Flow in the Si Solution
2.4. Numerical Method
3. Results and Discussion
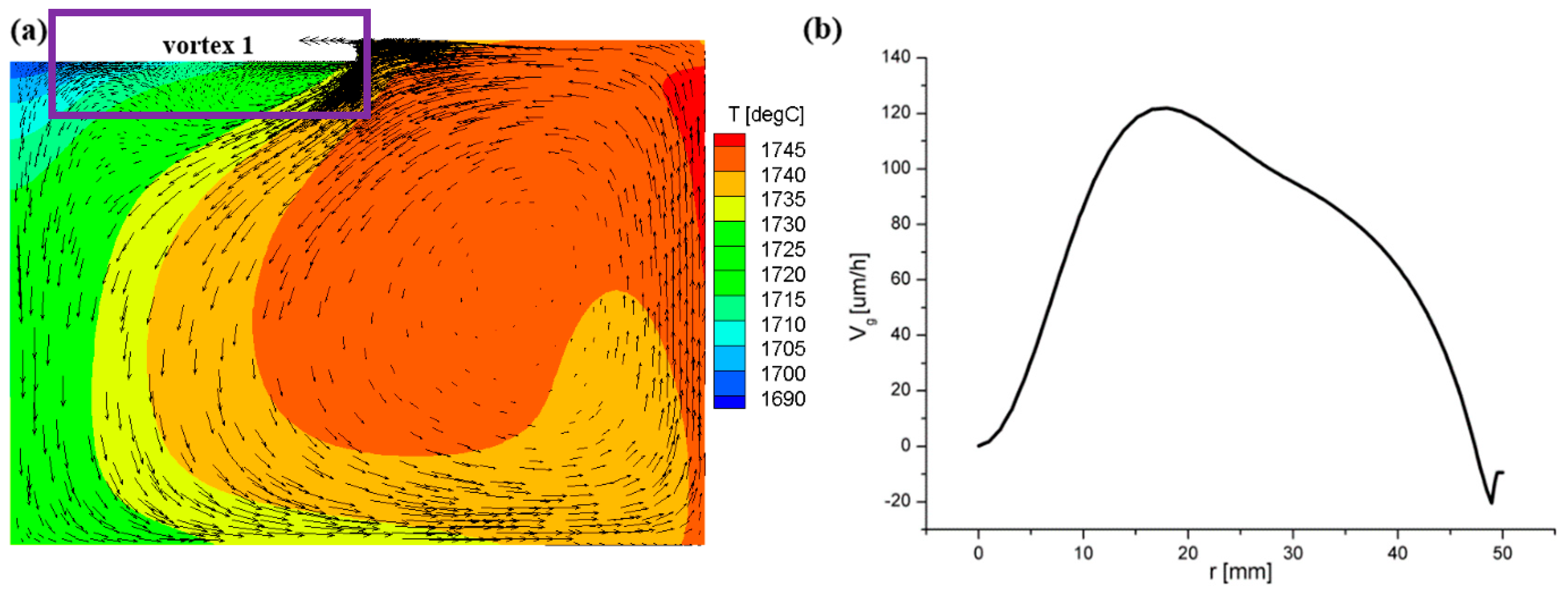
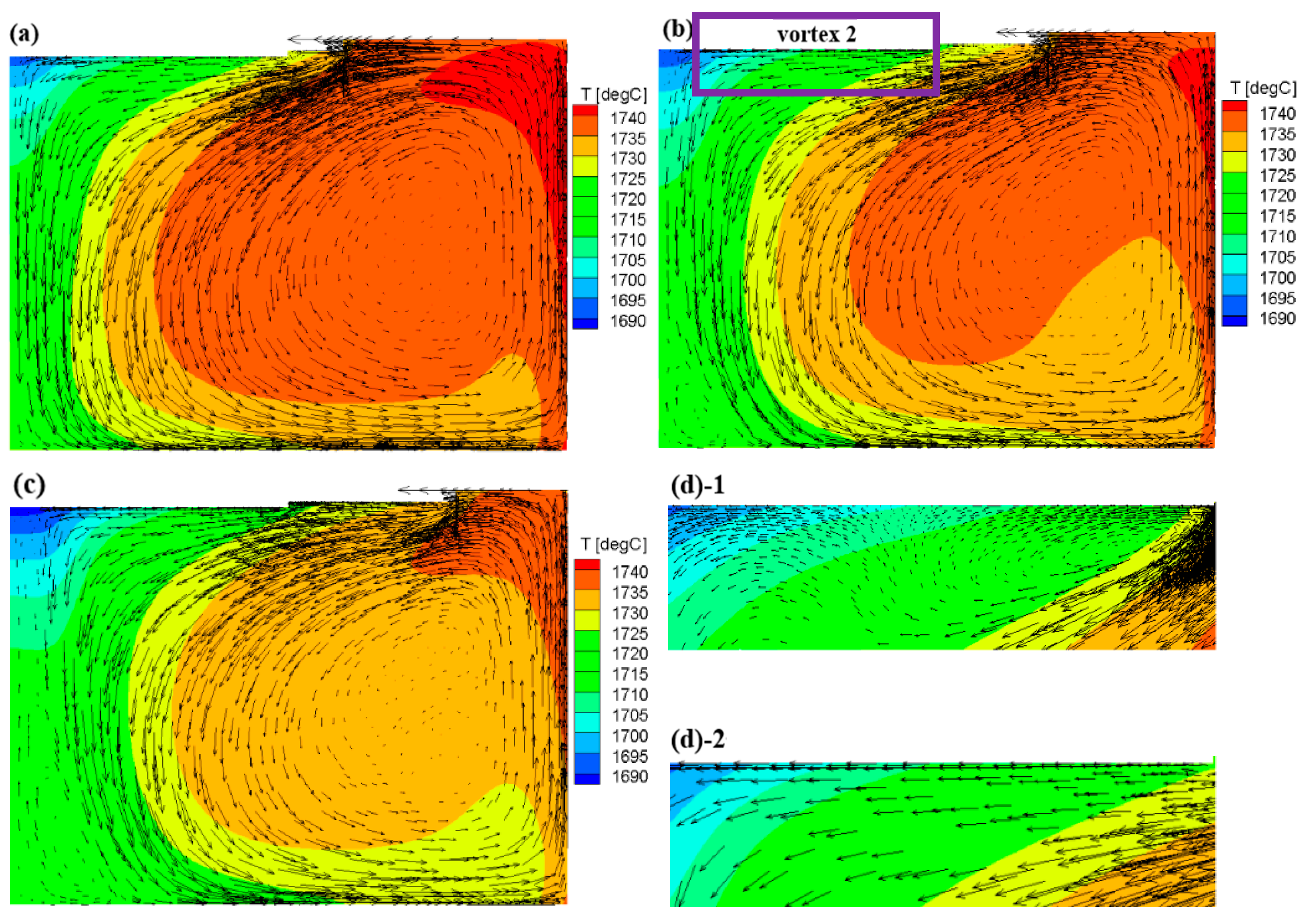
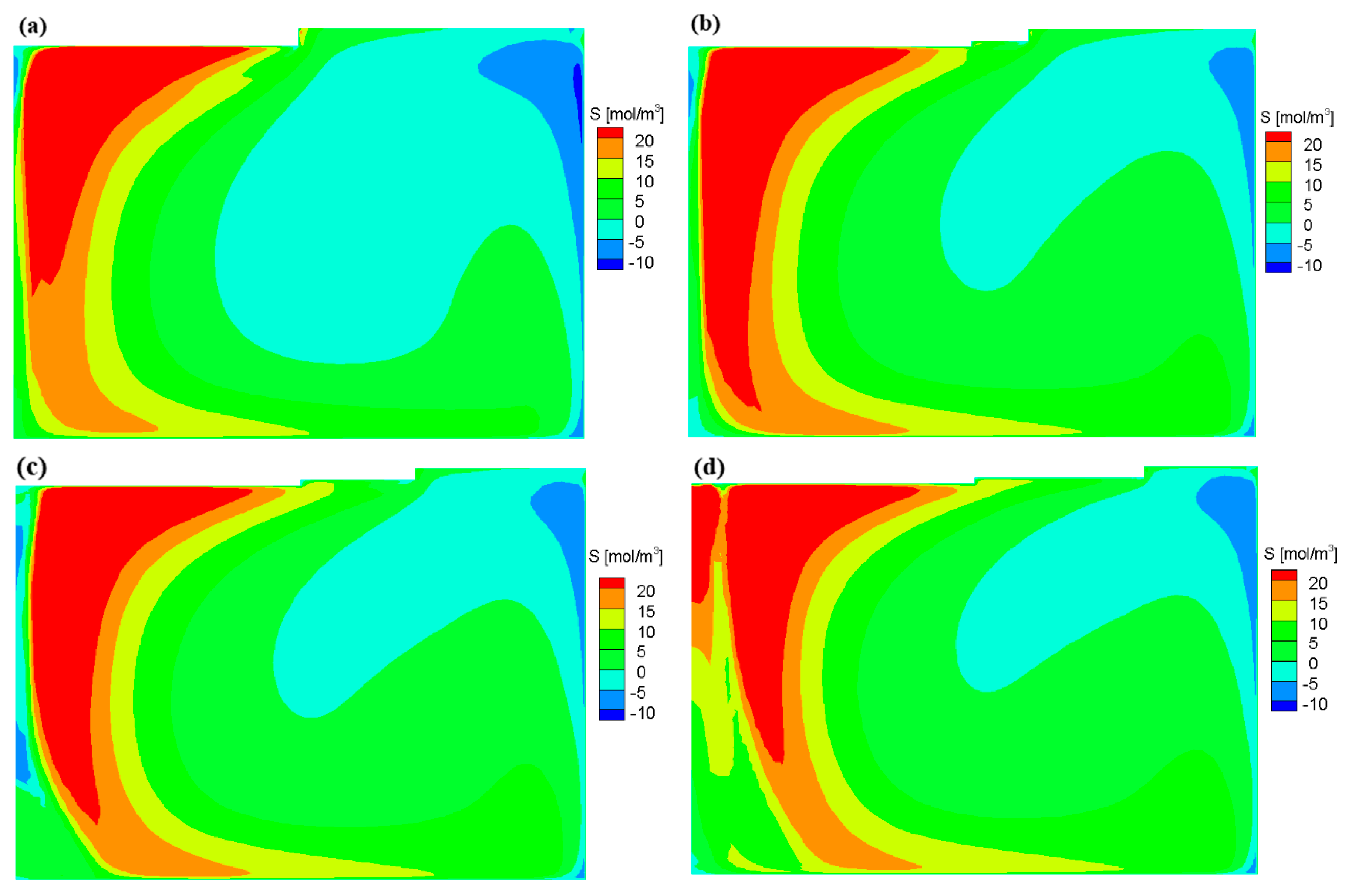
3.1. Flow Field and Growth Rate without the Appendix
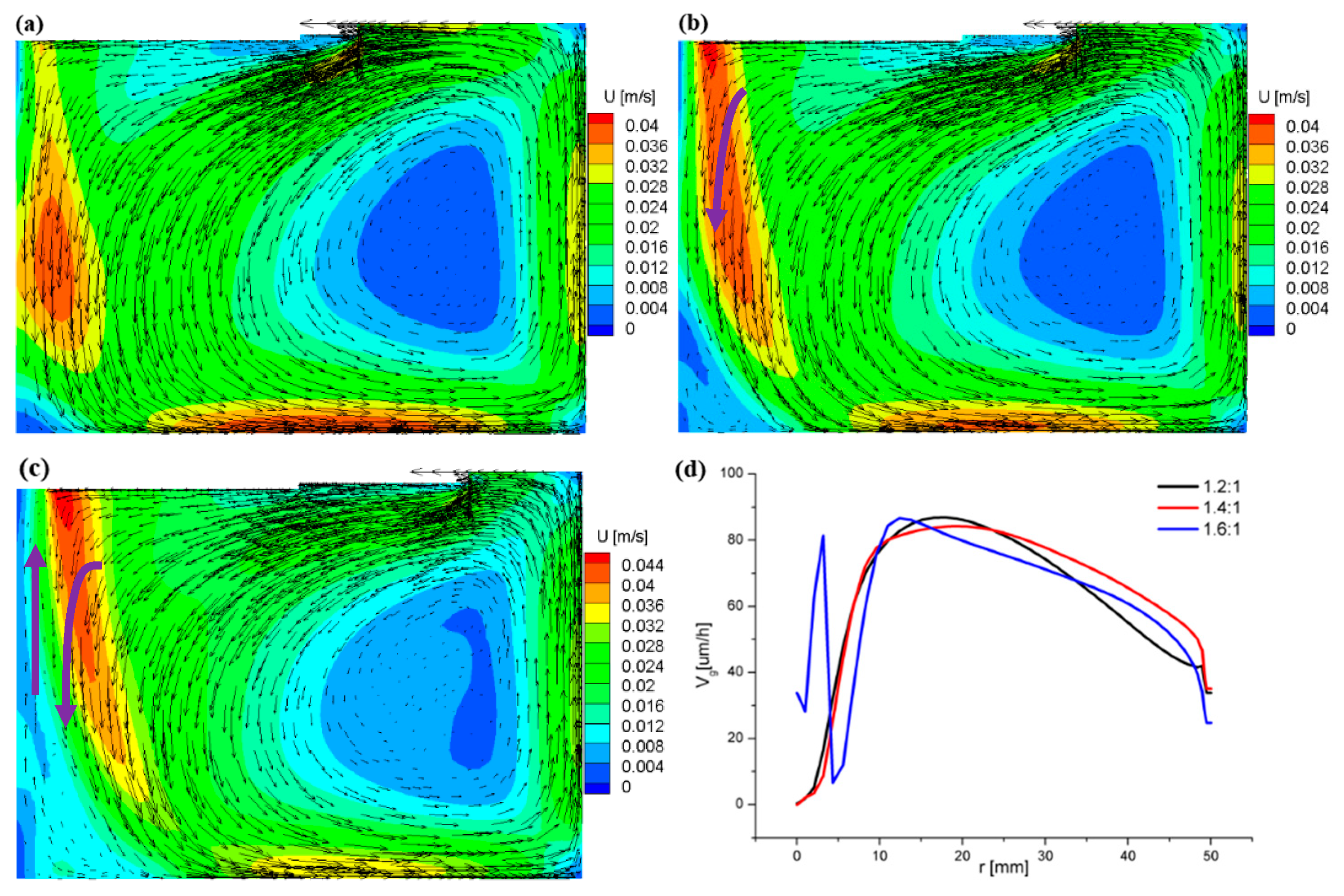
3.2. Flow Field and Growth Rate with the Appendix
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nee, H.P.; Rabkowski, J. High-efficiency power conversion using silicon carbide power electronics. Mater. Sci. Forum. 2014, 1083, 778–780. [Google Scholar]
- Biela, J.; Schweizer, M.; Waffler, S.; Kolar, J.W. SiC versus Si—Evaluation of potentials for performance improvement of inverter and DC–DC converter systems by SiC power semiconductors. IEEE Trans. Ind. Electron. 2011, 58, 2872. [Google Scholar] [CrossRef]
- Tairov, Y.M.; Tsvetkov, V.F. Investigation of growth processes of ingots of silicon carbide single crystals. J. Cryst. Growth 1978, 43, 209–212. [Google Scholar] [CrossRef]
- Powell, A.R.; Sumakeris, J.J.; Khlebnikov, Y.; Paisley, M.J.; Leonard, R.T.; Deyneka, E.; Gangwal, S.; Ambati, J.; Tsevtkov, V.; Seaman, J.; et al. Bulk Growth of Large Area SiC Crystals. Mater. Sci. Forum. 2016, 858, 5–10. [Google Scholar] [CrossRef]
- Hofmann, D.H.; Muller, M.H. Prospects of the use of liquid phase techniques for the growth of bulk silicon carbide crystals. Mater. Sci. Eng. B 1999, 61, 29–39. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Harada, S. Low-dislocation-density 4H-SiC crystal growth utilizing dislocation conversion during solution method. Appl. Phys. Express. 2014, 7, 065501. [Google Scholar] [CrossRef]
- Mercier, F.; Dedulle, J.M.; Chaussende, D.; Pons, M. Coupled heat transfer and fluid dynamics modeling of high-temperature SiC solution growth. J. Cryst. Growth 2010, 312, 155–163. [Google Scholar] [CrossRef]
- Yamamoto, T.; Adkar, N.; Okano, Y.; Ujihara, T.; Dost, S. Numerical investigation of the transport phenomena occurring in the growth of SiC by the induction heating TSSG method. J. Cryst. Growth 2017, 474, 50–54. [Google Scholar] [CrossRef]
- Yamamoto, T.; Okano, Y.; Ujihara, T.; Dost, S. Global simulation of the induction heating TSSG process of SiC for the effects of Marangoni convection, free surface deformation and seed rotation. J. Cryst. Growth 2017, 470, 75–88. [Google Scholar] [CrossRef]
- Liu, B.; Yu, Y.; Tang, X.; Gao, B. Influence of silicon melt convection on interface instability in large-size silicon carbide solution growth. J. Cryst. Growth 2019, 527, 125248. [Google Scholar] [CrossRef]
- Mercier, F.; Nishizawa, S. Numerical Investigation of the Growth Rate Enhancement of SiC Crystal Growth from Silicon Melts. Jpn. J. Appl. Phys. 2011, 50, 035603. [Google Scholar] [CrossRef]
- Lefebure, J.; Dedulle, J.M.; Ouisse, T.; Chaussende, D. Modeling of the growth rate during top seeded solution growth of SiC using pure silicon as a solvent. Cryst. Growth Des. 2011, 12, 909–913. [Google Scholar] [CrossRef]
- Ha, M.T.; Yu, Y.J.; Shin, Y.J.; Bae, S.Y.; Lee, M.H.; Kim, C.J.; Jeong, S.M. Flow modification enhancing the growth rate in top seeded solution growth of SiC crystals. RSC Adv. 2019, 9, 26327–26337. [Google Scholar] [CrossRef]
- Kusunoki, K.; Okada, N.; Kamei, K.; Moriguchi, K.; Daikoku, H.; Kado, M.; Sakamoto, T.; Ujihara, T. Top-seeded solution growth of three-inch-diameter 4H-SiC using convection control technique. J. Cryst. Growth 2014, 395, 68–73. [Google Scholar] [CrossRef]
- Tsunooka, Y.; Kokubo, N.; Hatasa, G.; Harada, S.; Tagawa, M.; Ujihara, T. High-speed prediction of computational fluid dynamics simulation in crystal growth. CrystEngComm 2018, 20, 6546–6550. [Google Scholar] [CrossRef]
- Muller, G.; Neumann, G.; Weber, W. Natural convection in vertical Bridgman configurations. J. Cryst. Growth 1984, 70, 78–93. [Google Scholar] [CrossRef]
- Touihri, R.; Hadid, H.B.; Henry, D. On the onset of convective instabilities in cylindrical cavities heated from below. Phys. Fluids. 1999, 11, 2078. [Google Scholar] [CrossRef]
| Materials | Property (Symbol) | Value | Unit |
|---|---|---|---|
| Silicon | Density (ρ) | 2550 | kg m−3 |
| Viscosity (μ) | 8.0 × 10−4 | Pa s | |
| Electrical conductivity (σe) | 1.2 × 106 | S m−1 | |
| Thermal conductivity (k) | 65 | W m−1 K−1 | |
| Specific heat (Cp) | 1.0 × 103 | J kg−1 K−1 | |
| Surface tension | −2.5 × 10−4 | N m−1 K−1 | |
| coefficient of | |||
| temperature (σT) | |||
| Thermal expansion coefficient (β) | 1.4 × 10−4 | K−1 | |
| Emissivity(ε) | 0.3 | ||
| Graphite | Electrical conductivity (σe) | 75.4 × 104 | S m−1 |
| Thermal conductivity (k) | 150 × 300/T | W m−1 K−1 | |
| Emissivity(ε) | 0.6 | ||
| Felt | Electrical conductivity (σe) | 430 | S m−1 |
| Thermal conductivity (k) | 0.336 | W m−1 K−1 | |
| Emissivity (ε) | 0.6 | ||
| Seed | Specific heat (Cp) | 1290 | J kg−1 K−1 |
| Density (ρ) | 3216 | kg m−3 | |
| Thermal conductivity (k) | 30 | W m−1 K−1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Yu, Y.; Tang, X.; Gao, B. Improvement of Growth Interface Stability for 4-Inch Silicon Carbide Crystal Growth in TSSG. Crystals 2019, 9, 653. https://doi.org/10.3390/cryst9120653
Liu B, Yu Y, Tang X, Gao B. Improvement of Growth Interface Stability for 4-Inch Silicon Carbide Crystal Growth in TSSG. Crystals. 2019; 9(12):653. https://doi.org/10.3390/cryst9120653
Chicago/Turabian StyleLiu, Botao, Yue Yu, Xia Tang, and Bing Gao. 2019. "Improvement of Growth Interface Stability for 4-Inch Silicon Carbide Crystal Growth in TSSG" Crystals 9, no. 12: 653. https://doi.org/10.3390/cryst9120653
APA StyleLiu, B., Yu, Y., Tang, X., & Gao, B. (2019). Improvement of Growth Interface Stability for 4-Inch Silicon Carbide Crystal Growth in TSSG. Crystals, 9(12), 653. https://doi.org/10.3390/cryst9120653





