Thermo-Optical Generation of Particle-Like Structures in Frustrated Chiral Nematic Film
Abstract
1. Introduction
2. Results
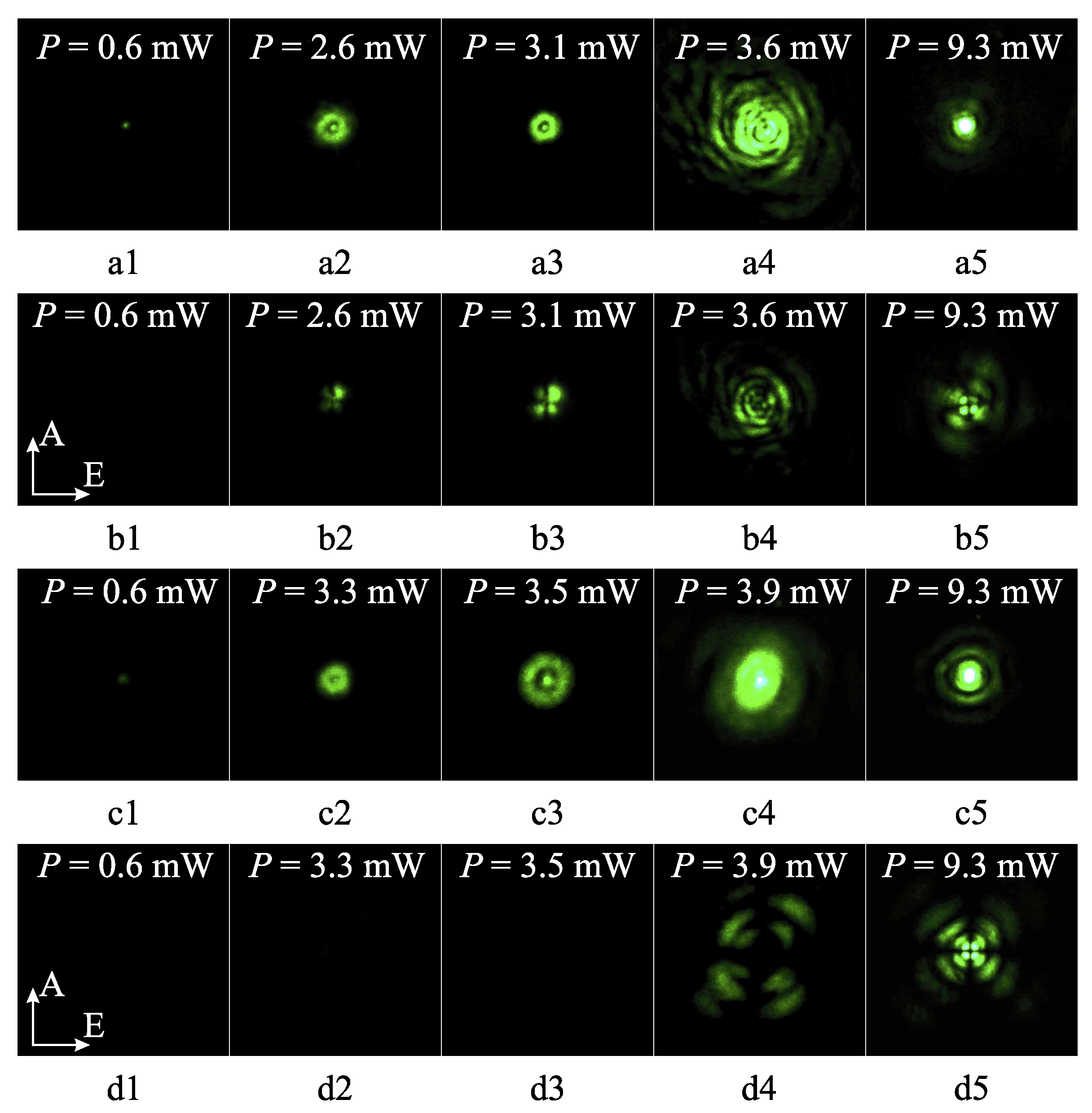
2.1. The Effect of Light Beam Exposure
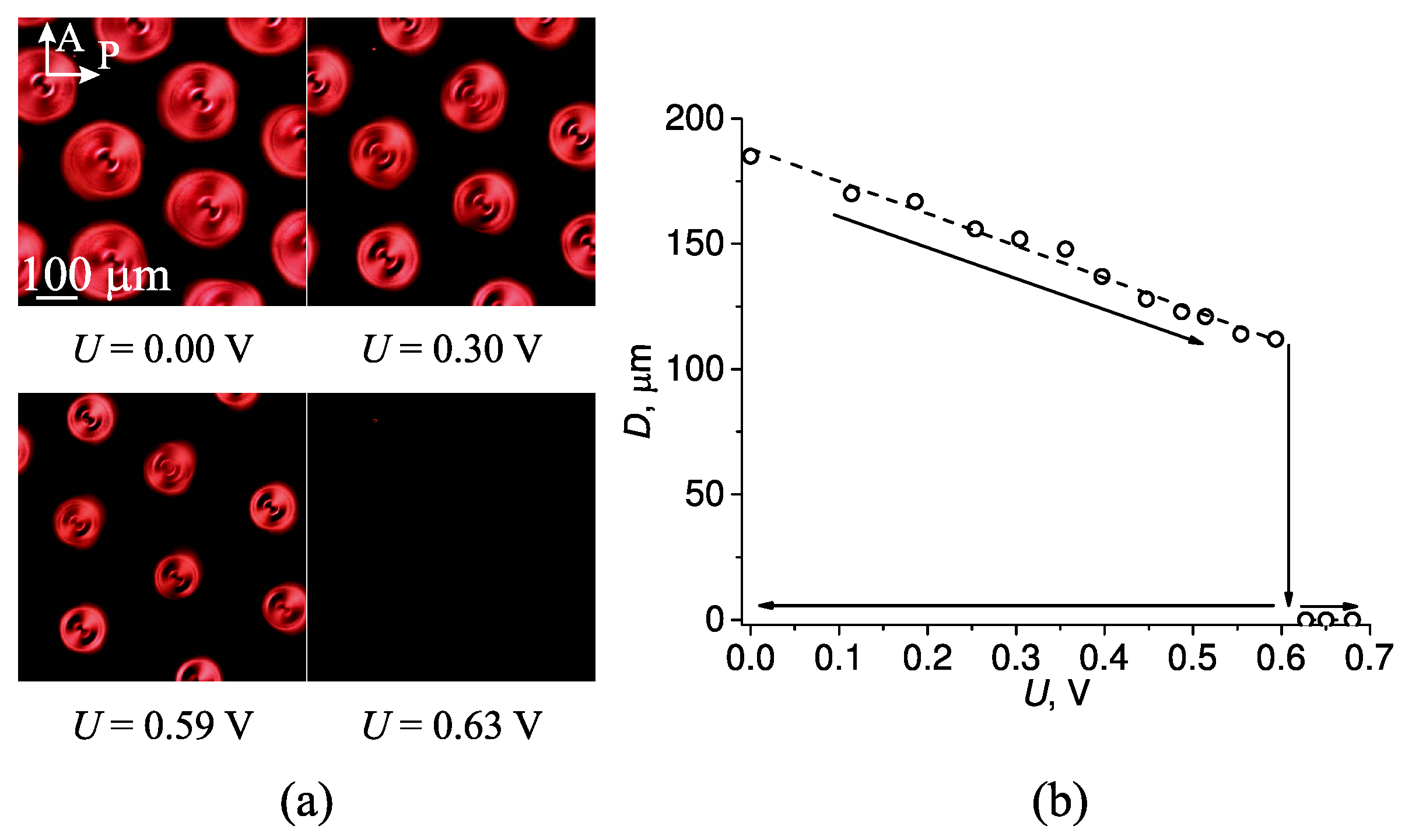
2.2. The Effect of Uniform Thermal and AC Electric Fields
3. Discussion
4. Materials and Methods
4.1. Sample Preparation
4.2. Optical Setup
4.3. Optical Microscopy
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CLC | Cholesteric liquid crystal |
| NLC | Nematic liquid crystal |
| LC | Liquid crystalline |
| BA | Benzoic Acid |
| ITO | Indium tin oxide |
Appendix A
References
- Kurik, M.V.; Lavrentovich, O.D. Defects in liquid crystals: homotopy theory and experimental studies. Sov. Phys. Uspekhi 1988, 31, 196–224. [Google Scholar] [CrossRef]
- Kleman, M.; Lavrentovich, O.D. Topological point defects in nematic liquid crystals. Philos. Mag. 2006, 86, 4117–4137. [Google Scholar] [CrossRef]
- Nych, A.; Ognysta, U.; Muševič, I.; Seč, D.; Ravnik, M.; Žumer, S. Chiral bipolar colloids from nonchiral chromonic liquid crystals. Phys. Rev. E 2014, 89, 062502. [Google Scholar] [CrossRef]
- Ackerman, P.J.; Smalyukh, I.I. Diversity of Knot Solitons in Liquid Crystals Manifested by Linking of Preimages in Torons and Hopfions. Phys. Rev. X 2017, 7, 011006. [Google Scholar] [CrossRef]
- Orlova, T.; Aßhoff, S.J.; Yamaguchi, T.; Katsonis, N.; Brasselet, E. Creation and manipulation of topological states in chiral nematic microspheres. Nat. Commun. 2015, 6, 7603. [Google Scholar] [CrossRef]
- Oswald, P.; Pieranski, P. Nematic and Cholesteric Liquid Crystals; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar] [CrossRef]
- Oswald, P.; Baudry, J.; Pirkl, S. Static and dynamic properties of cholesteric fingers in electric field. Phys. Rep. 2000, 337, 67–96. [Google Scholar] [CrossRef]
- Smalyukh, I.I.; Senyuk, B.I.; Palffy-Muhoray, P.; Lavrentovich, O.D.; Huang, H.; Gartland, E.C.; Bodnar, V.H.; Kosa, T.; Taheri, B. Electric-field-induced nematic-cholesteric transition and three-dimensional director structures in homeotropic cells. Phys. Rev. E 2005, 72, 061707. [Google Scholar] [CrossRef]
- Dierking, I. Textures of Liquid Crystals; Wiley-VCH: Hoboken, NJ, USA, 2003. [Google Scholar] [CrossRef]
- Zeldovich, B.; Tabiryan, N. Freedericksz transition in cholesteric liquid-crystals without external fields. JETP Lett. 1981, 34, 406–408. [Google Scholar]
- Tabiryan, N.V.; Zeldovich, B.Y. Equilibrium structure of a cholesteric with homeotropic orientation on the walls. J. Exp. Theor. Phys. 1982, 56, 563–566. [Google Scholar]
- Nawa, N.; Nakamura, K. Observation of Forming Process of Bubble Domain Texture in Liquid Crystals. Jpn. J. Appl. Phys. 1978, 17, 219–225. [Google Scholar] [CrossRef]
- Pirkl, S.; Ribière, P.; Oswald, P. Forming process and stability of bubble domains in dielectrically positive cholesteric liquid crystals. Liq. Cryst. 1993, 13, 413–425. [Google Scholar] [CrossRef]
- Bhide, V.G.; Chandra, S.; Jain, S.C.; Medhekar, R.K. Structure and properties of bubble domains in cholesteric-nematic mixtures. J. Appl. Phys. 1976, 47, 120–126. [Google Scholar] [CrossRef]
- Gilli, J.M.; Thiberge, S.; Manaila-Maximean, D. New Aspect of the Voltage/Confinement Ratio Phase Diagram for a Confined Homeotropic Cholesteric. Mol. Cryst. Liq. Cryst. 2004, 417, 207–213. [Google Scholar] [CrossRef]
- Ackerman, P.J.; van de Lagemaat, J.; Smalyukh, I.I. Self-assembly and electrostriction of arrays and chains of hopfion particles in chiral liquid crystals. Nat. Commun. 2015, 6, 6012. [Google Scholar] [CrossRef]
- Varanytsia, A.; Posnjak, G.; Mur, U.; Joshi, V.; Darrah, K.; Muševič, I.; Čopar, S.; Chien, L.C. Topology-commanded optical properties of bistable electric-field-induced torons in cholesteric bubble domains. Sci. Rep. 2017, 7, 16149. [Google Scholar] [CrossRef]
- Carboni, C.; Al-Lawati, A.; George, A.K.; Al-Harthi, S.H.; Al-Barwani, M. Observation of a Bubble Texture At the Cholesteric To Homeotropic-Nematic Transition In a Confined Chiral Nematic Liquid Crystal. Mol. Cryst. Liq. Cryst. 2004, 410, 239–245. [Google Scholar] [CrossRef]
- Smalyukh, I.I.; Lansac, Y.; Clark, N.A.; Trivedi, R.P. Three-dimensional structure and multistable optical switching of triple-twisted particle-like excitations in anisotropic fluids. Nat. Mater. 2010, 9, 139–145. [Google Scholar] [CrossRef]
- Smalyukh, I.I.; Kaputa, D.; Kachynski, A.V.; Kuzmin, A.N.; Ackerman, P.J.; Twombly, C.W.; Lee, T.; Trivedi, R.P.; Prasad, P.N. Optically generated reconfigurable photonic structures of elastic quasiparticles in frustrated cholesteric liquid crystals. Opt. Express 2012, 20, 6870. [Google Scholar] [CrossRef]
- Ackerman, P.J.; Qi, Z.; Smalyukh, I.I. Optical generation of crystalline, quasicrystalline, and arbitrary arrays of torons in confined cholesteric liquid crystals for patterning of optical vortices in laser beams. Phys. Rev. E 2012, 86, 021703. [Google Scholar] [CrossRef]
- Ackerman, P.J.; Trivedi, R.P.; Senyuk, B.; van de Lagemaat, J.; Smalyukh, I.I. Two-dimensional skyrmions and other solitonic structures in confinement-frustrated chiral nematics. Phys. Rev. E 2014, 90, 012505. [Google Scholar] [CrossRef]
- Loussert, C.; Brasselet, E. Multiple chiral topological states in liquid crystals from unstructured light beams. Appl. Phys. Lett. 2014, 104, 051911. [Google Scholar] [CrossRef]
- Loussert, C.; Iamsaard, S.; Katsonis, N.; Brasselet, E. Subnanowatt Opto-Molecular Generation of Localized Defects in Chiral Liquid Crystals. Adv. Mater. 2014, 26, 4242–4246. [Google Scholar] [CrossRef]
- Orlova, T.; Lancia, F.; Loussert, C.; Iamsaard, S.; Katsonis, N.; Brasselet, E. Revolving supramolecular chiral structures powered by light in nanomotor-doped liquid crystals. Nat. Nanotechnol. 2018, 13, 304–308. [Google Scholar] [CrossRef]
- Darmon, A.; Benzaquen, M.; Seč, D.; Čopar, S.; Dauchot, O.; Lopez-Leon, T. Waltzing route toward double-helix formation in cholesteric shells. Proc. Natl. Acad. Sci. USA 2016, 113, 9469–9474. [Google Scholar] [CrossRef]
- Krakhalev, M.N.; Rudyak, V.Y.; Gardymova, A.P.; Zyryanov, V.Y. Toroidal Configuration of a Cholesteric Liquid Crystal in Droplets with Homeotropic Anchoring. JETP Lett. 2019, 109, 478–481. [Google Scholar] [CrossRef]
- Krakhalev, M.N.; Rudyak, V.Y.; Prishchepa, O.O.; Gardymova, A.P.; Emelyanenko, A.V.; Liu, J.H.; Zyryanov, V.Y. Orientational structures in cholesteric droplets with homeotropic surface anchoring. Soft Matter 2019, 15, 5554–5561. [Google Scholar] [CrossRef]
- Posnjak, G.; Čopar, S.; Muševič, I. Points, skyrmions and torons in chiral nematic droplets. Sci. Rep. 2016, 6, 26361. [Google Scholar] [CrossRef]
- Kim, Y.H.; Gim, M.J.; Jung, H.T.; Yoon, D.K. Periodic arrays of liquid crystalline torons in microchannels. RSC Adv. 2015, 5, 19279–19283. [Google Scholar] [CrossRef]
- Pandey, M.B.; Ackerman, P.J.; Burkart, A.; Porenta, T.; Žumer, S.; Smalyukh, I.I. Topology and self-assembly of defect-colloidal superstructure in confined chiral nematic liquid crystals. Phys. Rev. E 2015, 91, 012501. [Google Scholar] [CrossRef]
- Volterra, V.; Wiener-Avnear, E. Cw thermal lens effect in thin layer of nematic liquid crystal. Opt. Commun. 1974, 12, 194–197. [Google Scholar] [CrossRef]
- Zeldovich, B.Y.; Akopyan, R. Thermomechanical effects in deformed nematlcs. J. Exp. Theor. Phys. 1984, 60, 953–958. [Google Scholar]
- Barnik, M.I.; Zolot’ko, A.S.; Kitaeva, V.F. Interaction of light with a dye-doped nematic liquid crystal. J. Exp. Theor. Phys. 1997, 84, 1122–1130. [Google Scholar] [CrossRef]
- Budagovsky, I.A.; Zolot’ko, A.S.; Korshunov, D.L.; Smayev, M.P.; Shvetsov, S.A.; Barnik, M.I. Generation of spiral dislocation of wave front in absorbing nematic liquid crystal. Opt. Spectrosc. 2015, 119, 280–285. [Google Scholar] [CrossRef]
- Cui, M.; Kelly, J.R. Temperature Dependence of Visco-Elastic Properties of 5CB. Mol. Cryst. Liq. Cryst. Sci. Technol. Sec. A Mol. Cryst. Liq. Cryst. 1999, 331, 49–57. [Google Scholar] [CrossRef]
- Faetti, S.; Palleschi, V. Nematic-isotropic interface of some members of the homologous series of 4-cyano-4′-(n-alkyl)biphenyl liquid crystals. Phys. Rev. A 1984, 30, 3241–3251. [Google Scholar] [CrossRef]
- Holyst, R.; Poniewierski, A. Orientation of Liquid-Crystal Molecules at the Nematic-Isotropic Interface and the Nematic Free Surface. Mol. Cryst. Liq. Cryst. Inc. Nonlinear Opt. 1990, 192, 65–67. [Google Scholar] [CrossRef]
- Hamdi, R.; Petriashvili, G.; Lombardo, G.; De Santo, M.P.; Barberi, R. Liquid crystal bubbles forming a tunable micro-lenses array. J. Appl. Phys. 2011, 110, 074902. [Google Scholar] [CrossRef]
- Haas, W.E.L.; Adams, J.E. Electrically variable diffraction in spherulitic liquid crystals. Appl. Phys. Lett. 1974, 25, 263–264. [Google Scholar] [CrossRef]
- Yaroshchuk, O.; Reznikov, Y. Photoalignment of liquid crystals: basics and current trends. J. Mater. Chem. 2012, 22, 286–300. [Google Scholar] [CrossRef]
- Janossy, I.; Lloyd, A.D. Low-Power Optical Reorientation in Dyed Nematics. Mol. Cryst. Liq. Cryst. 1991, 203, 77–84. [Google Scholar] [CrossRef]
- Loussert, C.; Kushnir, K.; Brasselet, E. Q-plates micro-arrays for parallel processing of the photon orbital angular momentum. Appl. Phys. Lett. 2014, 105, 121108. [Google Scholar] [CrossRef]
- Yang, B.; Brasselet, E. Arbitrary vortex arrays realized from optical winding of frustrated chiral liquid crystals. J. Opt. 2013, 15, 044021. [Google Scholar] [CrossRef]
- Janossy, I.; Kosa, T. Laser-Induced Effects in Dyed Nematics. Mol. Cryst. Liq. Cryst. 1991, 207, 189–197. [Google Scholar] [CrossRef]
- Ahlers, G.; Cannell, D.S.; Berge, L.I.; Sakurai, S. Thermal conductivity of the nematic liquid crystal 4- n -pentyl-4’-cyanobiphenyl. Phys. Rev. E 1994, 49, 545–553. [Google Scholar] [CrossRef] [PubMed]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shvetsov, S.; Orlova, T.; Emelyanenko, A.V.; Zolot’ko, A. Thermo-Optical Generation of Particle-Like Structures in Frustrated Chiral Nematic Film. Crystals 2019, 9, 574. https://doi.org/10.3390/cryst9110574
Shvetsov S, Orlova T, Emelyanenko AV, Zolot’ko A. Thermo-Optical Generation of Particle-Like Structures in Frustrated Chiral Nematic Film. Crystals. 2019; 9(11):574. https://doi.org/10.3390/cryst9110574
Chicago/Turabian StyleShvetsov, Sergey, Tetiana Orlova, Alexander V. Emelyanenko, and Alexander Zolot’ko. 2019. "Thermo-Optical Generation of Particle-Like Structures in Frustrated Chiral Nematic Film" Crystals 9, no. 11: 574. https://doi.org/10.3390/cryst9110574
APA StyleShvetsov, S., Orlova, T., Emelyanenko, A. V., & Zolot’ko, A. (2019). Thermo-Optical Generation of Particle-Like Structures in Frustrated Chiral Nematic Film. Crystals, 9(11), 574. https://doi.org/10.3390/cryst9110574





