Crystal Structure, Raman Spectroscopy and Dielectric Properties of New Semiorganic Crystals Based on 2-Methylbenzimidazole
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Single Crystal XRD
3.2. Powder XRD
3.3. Elemental Analysis
3.4. Raman Spectroscopy
3.5. Dielectric Measurements
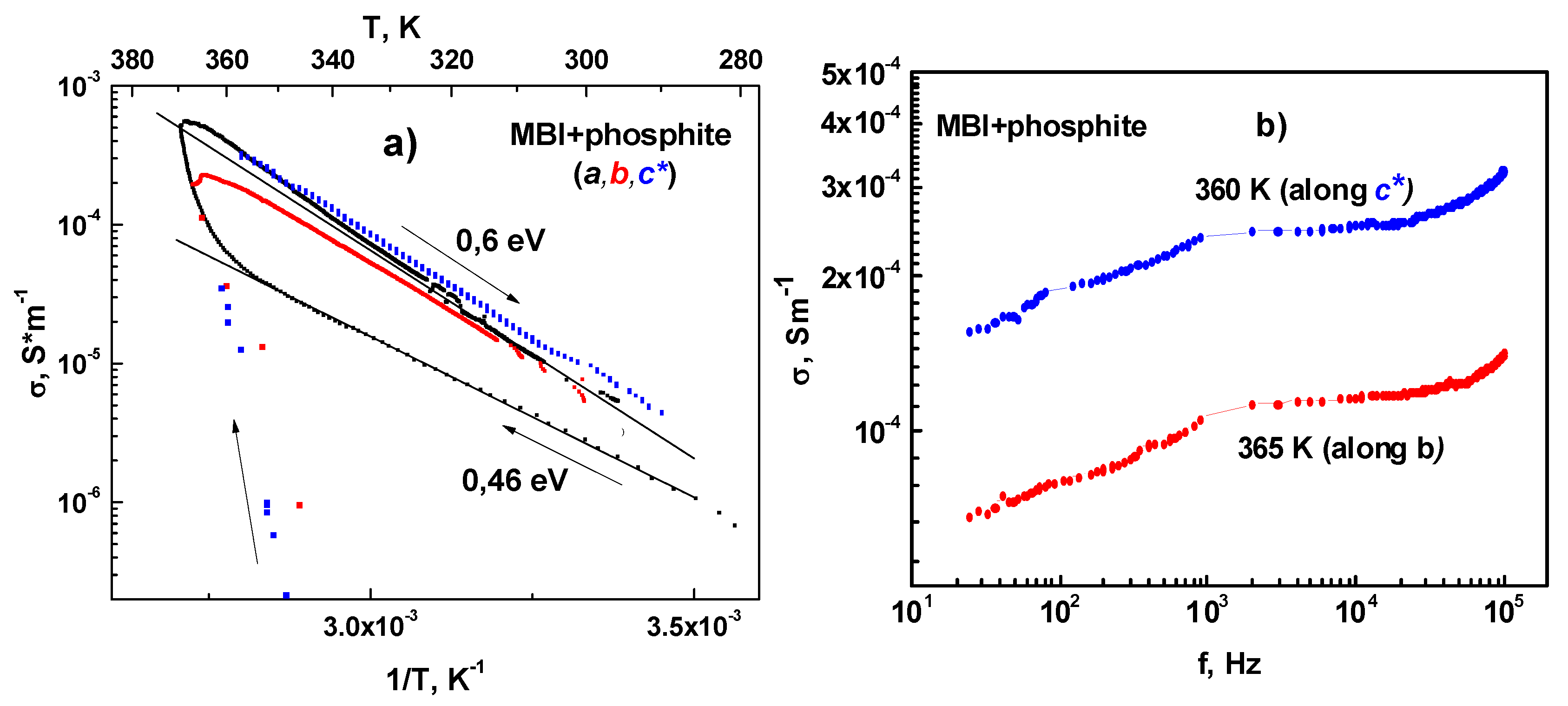
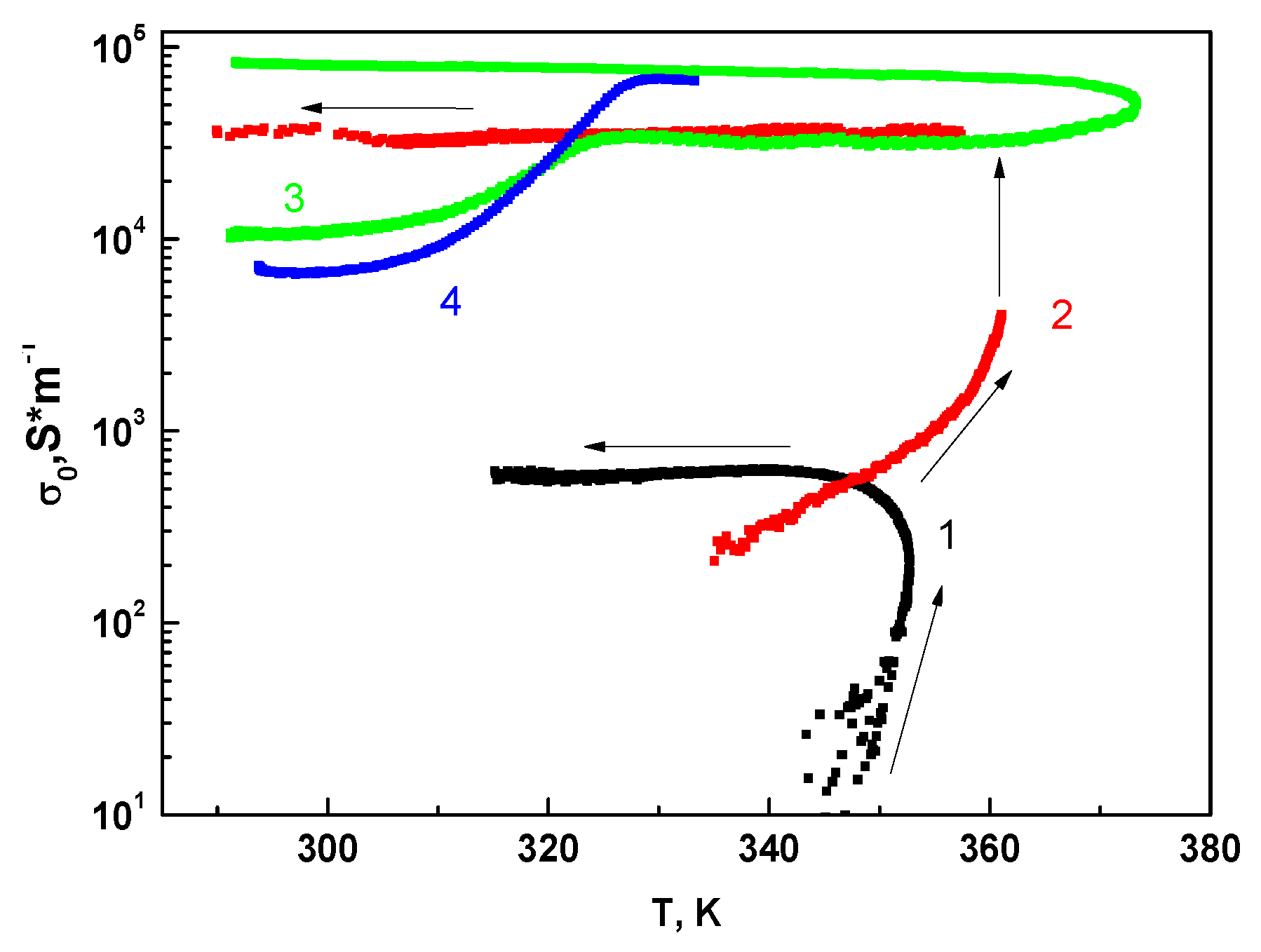
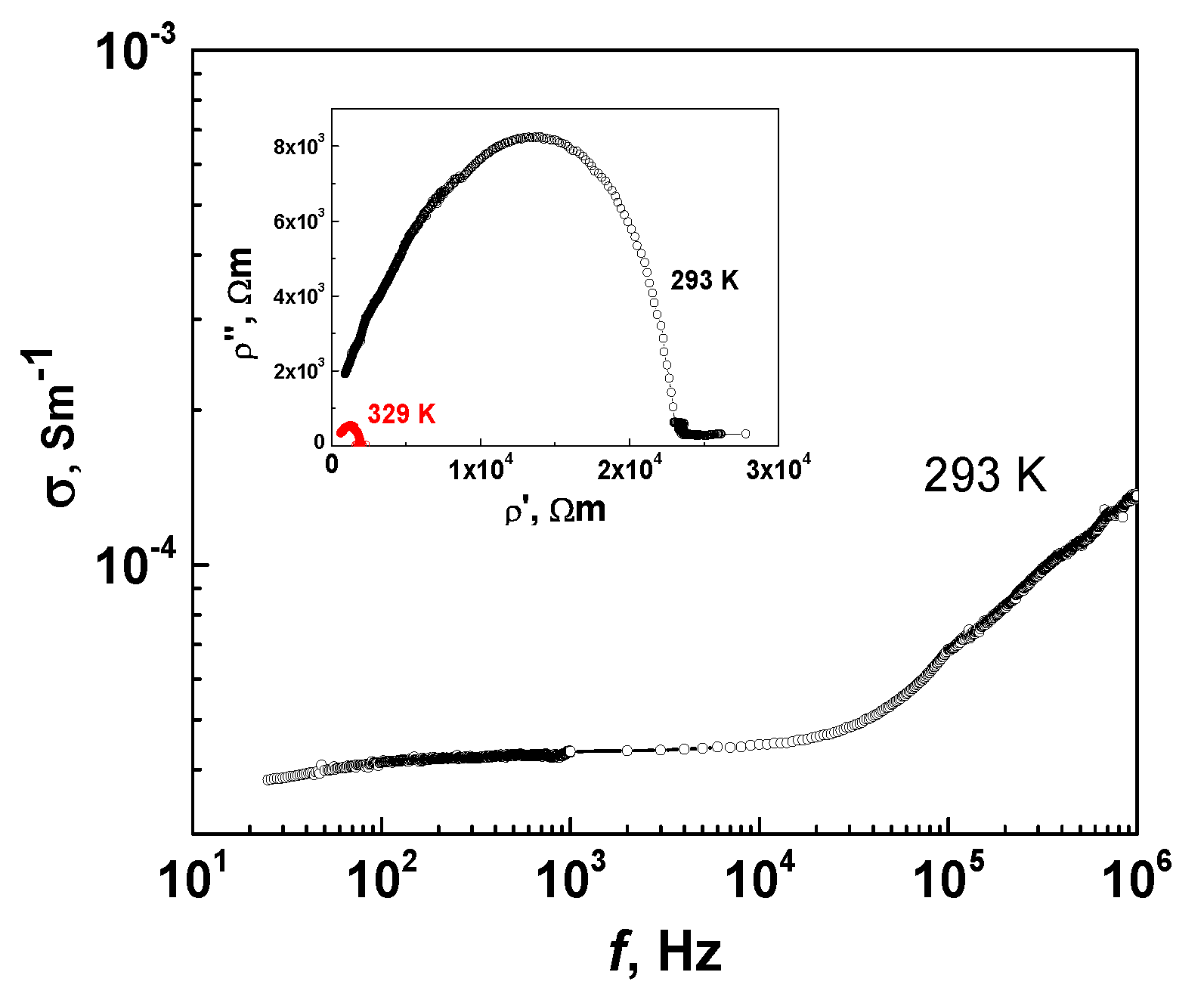
3.5.1. MBI-Phosphite
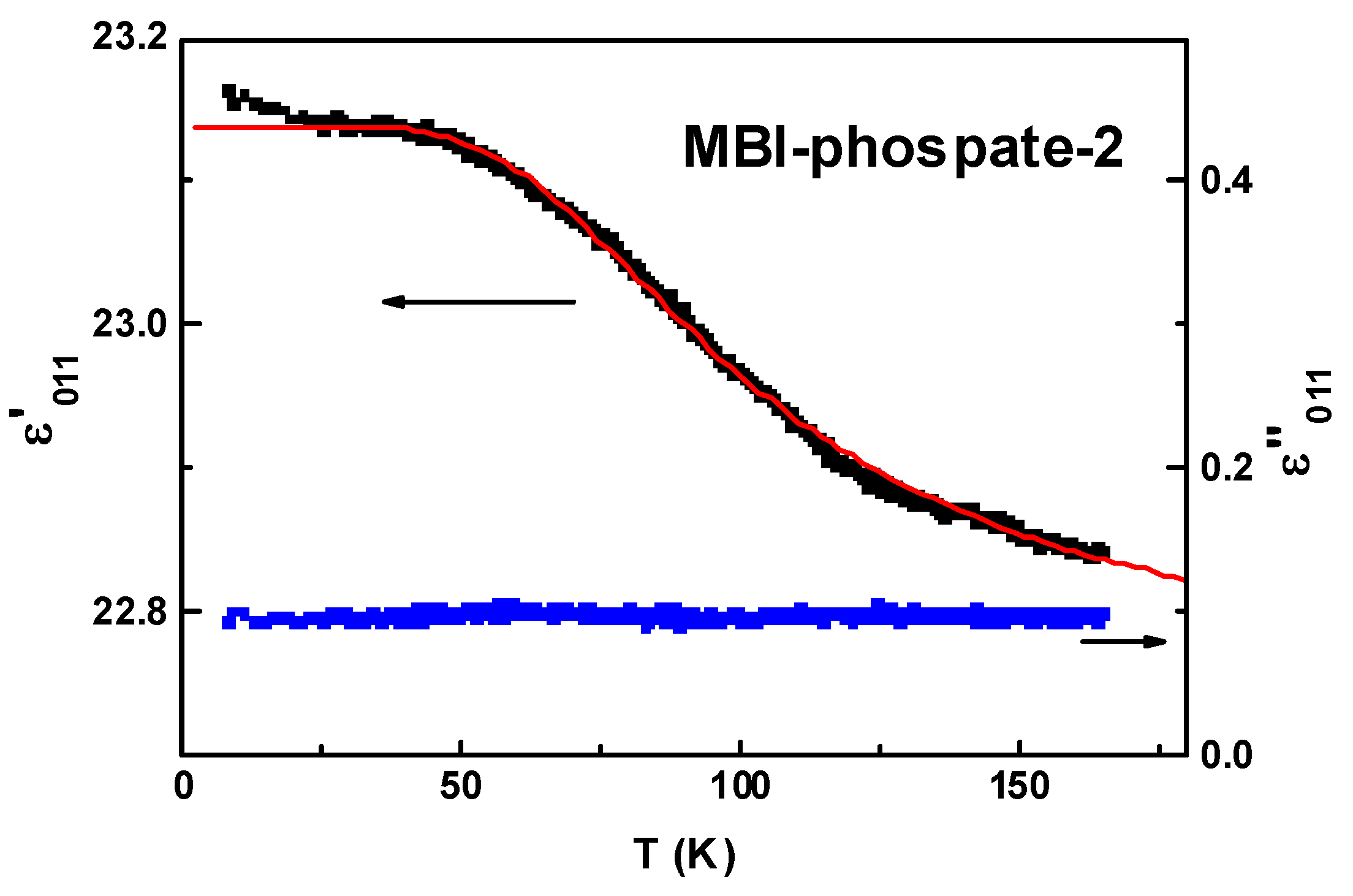
3.5.2. MBI-Phosphate-2
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Horiuchi, S.; Tokura, J. Organic ferroelectrics. Nat. Mater. 2008, 7, 357–366. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Liu, Y.; Zhang, Y.; Cai, H.-L.; Xiong, R.-G. Molecular ferroelectrics: Where electronics meet biology. Phys. Chem. Chem. Phys. 2013, 15, 20786–20796. [Google Scholar] [CrossRef] [PubMed]
- Tayi, A.S.; Kaeser, A.; Matsumoto, M.; Aida, T.; Stupp, S.I. Supramolecular ferroelectrics. Nat. Chem. 2015, 7, 281–294. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Luo, J.; Zhang, S.H.; Ji, C.H.; Zhou, L.; Li, S.H.; Deng, F.; Hong, M. Solid-State Reversible Quadratic Nonlinear Optical Molecular Switch with an Exceptionally Large Contrast. Adv. Mater. 2013, 25, 4159–4163. [Google Scholar] [CrossRef]
- Ghazaryan, V.V.; Zakharov, B.A.; Petrosyan, A.M.; Boldyreva, E.V. L-Argininiumphosphite—A new candidate for NLO materials. Acta Cryst. 2015, C71, 415–421. [Google Scholar] [CrossRef]
- Haile, S.M.; Boysen, D.A.; Chisholm, C.R.I.; Merle, R.B. Solid acids as fuel cell electrolytes. Nature 2001, 410, 910–913. [Google Scholar] [CrossRef]
- Blazcues-Kastro, A.; Garcia-Kabanes, A.; Carracosa, M. Biological applications of ferroelectric materials. Appl. Phys. Rev. 2018, 5, 041101. [Google Scholar] [CrossRef]
- Horiuchi, S.; Kobayashi, K.; Kumai, R.; Ishibashi, S.H. Proton tautomerism for strong polarization switching. Nat. Comm. 2017, 8, 14426. Available online: www.nature.com/naturecommunications (accessed on 16 February 2017). [CrossRef]
- Chen, S.H.; Zeng, X.C. Design of ferroelectric organic molecular crystals with ultrahigh polarization. J. Am. Chem. Soc. 2014, 136, 6428–6436. [Google Scholar] [CrossRef]
- Samara, G.A.; Semmingsen, D. Effects of pressure on the dielectric properties and phase transitions of the 2-D antiferroelectric squaric acid (H2C4O4 and D2C4O4). J. Chem. Phys. 1979, 71, 1401–1407. [Google Scholar] [CrossRef]
- Albers, J. Betaine compounds – a new family with ferroelectric and uncommensurate phases. Ferroelectrics 1988, 78, 3–10. [Google Scholar] [CrossRef]
- Horiuchi, S.; Tokunaga, Y.; Giovannetti, G.; Picozzi, S.; Itoh, H.; Shimano, R.; Kumai, R.; Tokura, Y. Above-room-temperature ferroelectricity in a single-component molecular crystal. Nature 2010, 463, 789–793. [Google Scholar] [CrossRef] [PubMed]
- Kagawa, F.; Hatahara, K.; Horiuchi, S.; Tokura, Y. Domain-wall dynamics coupled to proton motion in a hydrogen-bonded organic ferroelectric. Phys. Rev. B 2012, 85, 220101(R). [Google Scholar] [CrossRef]
- Mochida, T.; Izuoka, A.; Sugawara, T. Organic hydrogen-bonded dielectrics: Quantum paraelectricity based on tautomerization of 9-hydroxyphenalenone derivatives. J. Chem. Phys. 1994, 101, 7971–7974. [Google Scholar] [CrossRef]
- Takasu, I.; Izuoka, A.; Sugawara, T.; Mochida, T. Observation of Quantum paraelectricity in an intermolecular ionic hydrogen-bonded crystal of a squaric acid derivative. J. Phys. Chem. B 2004, 108, 5527–5531. [Google Scholar] [CrossRef]
- Horiuchi, S.; Kobayashi, K.; Kumai, R.; Minami, N.; Kagawa, F.; Tokura, Y. Quantum ferroelectricity in charge-transfer complex crystals. Nat. Comm. 2015, 6, 7469. [Google Scholar] [CrossRef]
- Saripalli, R.K.; Swain, D.; Prasad, S.; Nhalil, H.; Bhat, H.L.; Guru Row, T.N.; Elizabeth, S. Observation of ferroelectric phase and large spontaneous electric polarization in organic salt of diisopropylammonium iodide. J. Appl. Phys. 2017, 121, 114101. [Google Scholar] [CrossRef]
- Horiuchi, S.; Kagawa, F.; Hatahara, K.; Kobayashi, K.; Kumai, R.; Murakami, Y.; Tokura, Y. Above-room-temperature ferroelectricity and antiferroelectricity in benzimidazoles. Nat. Comm. 2012, 3, 1308. [Google Scholar] [CrossRef]
- Horiuchi, S.; Ishibashi, S.H.; Inada, S.; Aoyagi, S.H. Hydrogen-Bonded Architectures and Field-Induced Polarization Switching in Bridged Bis(benzimidazole) Crystals. Cryst. Growth Des. 2019, 19, 328–335. [Google Scholar] [CrossRef]
- Baran, J.; Bator, G.; Jakubas, R.; Sledz, M. Dielectric dispersion and vibrational studies of a new ferroelectric, glyciniumphosphite crystal. J. Phys. Condens. Matter 1996, 8, 10647–10658. [Google Scholar] [CrossRef]
- Balashova, E.V.; Lemanov, V.V.; Albers, J.; Klöpperpieper, A. Ultrasonic study of betaine compounds. Ferroelectrics 1998, 208–209, 63–81. [Google Scholar] [CrossRef]
- Bauch, J.; Banys, R.; Böttcher, A.; Pöppl, A.; Völkel, G.; Klimm, C.; Klöpperpieper, A. Structural phase transitions in partially deuterated betaine phosphite crystals studied by dielectric and electron paramagnetic resonance methods. Ferroelectrics 1995, 163, 59. [Google Scholar] [CrossRef]
- Balashova, E.V.; Krichevtsov, B.B.; Yurko, E.I.; Svinarev, F.B.; Pankova, G.A. Dielectric Properties of Ferroelectric Betaine Phosphite Crystals with a High Degree of Deuteration. Phys. Solid State 2015, 57, 2382–2388. [Google Scholar] [CrossRef]
- Averbuch-Pouchot, M.T. Crystal structure of L-histidinium phosphite and a structure reinvestigation of the monoclinic form of L-histidine. Z. Krist. 1993, 207, 111–120. [Google Scholar] [CrossRef]
- Balashova, E.V.; Krichevtsov, B.B.; Popov, S.N.; Brunkov, P.N.; Pankova, G.A.; Zolotarev, A.A. Elastic and Piezoelectric Parameters of the Crystals of Histidine Phosphite L-Hist ⋅H3РО3 Measured by the Method of Electromechanical Resonance. Tech. Phys. Lett. 2018, 44, 118–122. [Google Scholar] [CrossRef]
- Sheldrick, G.M. A short history of SHELX. Acta Cryst. A 2008, 64, 112–122. [Google Scholar] [CrossRef]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Cryst. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Bruker-AXS. APEX2; Version 2014.11-0; Bruker-AXS: Madison, WI, USA, 2014. [Google Scholar]
- Sheldrick, G.M. Sadabs; University of Goettingen: Goettingen, Germany, 2007. [Google Scholar]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Bruker AXS. TOPAS5 Technical Reference; Brucker AXS: Karlsruhe, Germany, 2014. [Google Scholar]
- Thompson, P.; Cox, D.E.; Hastings, J.B. Rietveld refinement of Debye-Scherrer synchrotron X-ray data from Al2O3. J. Appl. Crystallogr. 1987, 20, 79–83. [Google Scholar] [CrossRef]
- Young, R.A. Introduction to the Rietveld Method. In The Rietveld Method; IUCr Book Series Oxford Uni. Press: Oxford, UK, 1993; pp. 1–39. [Google Scholar]
- Berger, H. Study of the K alpha emission spectrum of copper. X-ray Spectrom. 1986, 15, 241–243. [Google Scholar] [CrossRef]
- Rietveld, H.M. Line profiles of neutron powder-diffraction peaks for structure Refinement. Acta Cryst. 1967, 22, 151–152. [Google Scholar] [CrossRef]
- Le Bail, A.; Duroy, H.; Fourquet, J.L. Ab-initio structure determination of LiSbWO6 by X-ray powder diffraction. Mat. Res. Bull. 1988, 23, 447–452. [Google Scholar] [CrossRef]
- March, A. Mathematische Theorie der Regelung nach der Korngestalt bei affiner Deformation. Z. Krist. 1932, 81, 285–297. [Google Scholar]
- Järvinen, M. Application of symmetrized harmonics expansion to correction of the preferred orientation effect. J. Appl. Cryst. 1993, 26, 525–531. [Google Scholar] [CrossRef]
- Bérar, J.-F.; Lelann, P.J. E.s.d.’s and estimated probable error obtained in Rietveld refinements with local correlations. J. Appl. Crystallogr. 1991, 2, 1–5. [Google Scholar]
- Levin, A.A.; Filatov, S.K.; Paufler, P.; Bubnova, R.S.; Krzhizhanovskaya, M.; Meyer, D.C. Temperature-dependent evolution of RbBSi2O6 glass into crystalline Rb-boroleucite according to X-ray diffraction data. Z. Kristallogr. Cryst. Mater. 2013, 228, 259–270. [Google Scholar] [CrossRef]
- Walba, H.; Isensee, R.W. Acidity Constants of Some Arylimidazoles and Their Cations. J. Org. Chem. 1961, 26, 2789–2791. [Google Scholar] [CrossRef]
- Obodovskaya, A.E.; Starikova, Z.A.; Belous, S.N.; Pokrovskaya, I.E. Crystal and molecular structure of 2-methylbenzimidazole. J. Struct. Chem. 1991, 32, 421–422. [Google Scholar] [CrossRef]
- Wächtler, M.; Bräutigam, M.; Poppaband, J.; Dietzek, B. Mechanism of protonation induced changes in Raman spectra of a trisheteroleptic ruthenium complex revealed by DFT calculations. RSC Adv. 2013, 3, 5597–5606. [Google Scholar] [CrossRef]
- Güllüoglu, M.T.; Özduran, M.; Kurt, M.; Kalaichelvan, S.; Sundaraganesan, N. Molecular structure and vibrational spectra of 2- and 5-methylbenzimidazole molecules by density functional theory. Spectrochim. Acta Part A 2010, 76, 107–114. [Google Scholar] [CrossRef]
- Tsuboi, M. Vibrational Spectra of Phosphite and Hypophosphite Anions, and the Characteristic Frequencies of PO32− and PO2− Groups. J. Am. Chem. Soc. 1957, 79, 1351–1354. [Google Scholar] [CrossRef]
- Baran, J.; Czapla, Z.; Drozd, M.K.; Ilczyszyn, M.M.; Marchewka, M.; Ratajczak, H. Polarised FTIR and Raman spectra of betainephosphite single crystal I. Paraelectric phase. J. Mol. Struct. 1997, 403, 17–37. [Google Scholar] [CrossRef]
- Fleck, M.; Ghazaryan, V.V.; Petrosyan, A.M. Growth and characterization of L-proliniumphosphite. J. Mol. Struct. 2015, 1079, 460–464. [Google Scholar] [CrossRef]
- Carey, D.M.; Korenowski, G.M. Measurement of the Raman spectrum of liquid water. J. Chem. Phys. 1998, 108, 7. [Google Scholar] [CrossRef]
- Frost, R.L.; Xi, Y.; Scholz, R.; Belotti, F.M.; Lopez, A. Infrared and Raman spectroscopic characterization of the phosphate mineral fairfieldite—Ca2(Mn2+,Fe2+)2(PO4)2•2(H2O). Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2013, 106, 216–223. [Google Scholar] [CrossRef] [PubMed]
- Frost, R.L.; Scholz, R.; Belotti, F.M.; Lopez, A.; Theiss, F.L. A vibrational spectroscopic study of the phosphate mineral vantasselite Al4(PO4)3(OH)3•9H2O. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2015, 147, 185–192. [Google Scholar] [CrossRef]
- Mita, Y.; Takebe, K.; Kobayashi, M.; Endo, S.; Tominaga, Y. Temperature and pressure studies of Raman peaks related to hydrogen modes in KDP. J. Phys. Condens. Matter 2006, 18, 5185. [Google Scholar] [CrossRef]
- Litasov, K.D.; Podgornykh, N.M. Raman spectroscopy of various phosphate minerals and occurrence of tuite in the Elga IIE iron meteorite. J. Raman Spectrosc. 2017, 48, 1518–1527. [Google Scholar] [CrossRef]
- Lu, G.W.; Sun, X. Raman Study of Lattice Vibration Modes and Growth Mechanism of KDP Single Crystals. Cryst. Res. Technol. 2002, 37, 93–99. [Google Scholar] [CrossRef]
- Baran, J.; Ilczyszyn, M.M.; Sledz, M.; Ratajczak, H. Polarised vibrational spectra of KH2PO3 single crystal. J. Mol. Struct. 2000, 526, 235–254. [Google Scholar] [CrossRef]
- Venkateswaran, C.S. The Raman spectra of ortho-phosphoric acid and some phosphates. Proc. Indian Acad. Sci. 1936, 3, 25. [Google Scholar] [CrossRef]
- Pawlig, O.; Schellenschlager, V.; Lutz, H.D.; Trettin, R. Vibrational analysis of iron and zinc phosphate conversion coating constituents. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2001, 57, 581–590. [Google Scholar] [CrossRef]
- Poulet, H.; Mathieu, J.-P. Spectres de Vibration et Syme’trie des Cristaux; Gordon & Breach: Paris, France, 1970; Chapter 9. [Google Scholar]
- Totz, J.; Michel, D.; Banys, J.; Klöpperpieper, A. Conductivity processes in deuterated betaine phosphate (1−x) betaine phosphite (x) mixed crystals. J. Phys. Condens. Matter 1998, 10, 9281–9292. [Google Scholar] [CrossRef]
- Balashova, E.V.; Svinarev, F.B.; Ankudinov, A.V.; Pankova, G.A.; Lityagin, G.A.; Kunkel, T.S.; Krichevtsov, B.B. Polarization switching, dielectric, structural and elastic properties of 2-Methylbenzimidazole crystals and films. Ferroelectrics 2019, 538, 74–82. [Google Scholar] [CrossRef]
- Jonscher, A.K. Dielectric relaxation in solids. J. Phys. D Appl. Phys. 1999, 32, R57–R70. [Google Scholar] [CrossRef]
- Pradhan, D.K.; Choudhary, R.N.P.; Samantaray, B.K. Studies of Dielectric Relaxation and AC Conductivity Behavior of Plasticized Polymer Nanocomposite Electrolytes. Int. J. Electrochem. Sci. 2008, 3, 597–608. [Google Scholar]
- Seliger, J.; Žagar, V. Nuclear Quadrupole Resonance Study of Hydrogen Bonds in Solid 2−Methylbenzimidazole and 5,6-Dimethylbenzimidazole. J. Phys. Chem. C 2013, 117, 20193–20200. [Google Scholar] [CrossRef]
- Ponomareva, V.G.; Bagryantseva, I.N. Proton Conductivity, Structural and Thermal Properties of (1–x) CsH2PO4−xBa(H2PO4)2. Phys. Sol. State 2017, 59, 1829–1835. [Google Scholar] [CrossRef]
- Barrett, J.H. Dielectric Constant in Perovskite Type Crystals. Phys. Rev. 1952, 86, 118. [Google Scholar] [CrossRef]
- Parker, R.A. Static Dielectric Constant of Rutile (TiO2), 1.6-1060 K. Phys. Rev. 1961, 124, 1719. [Google Scholar] [CrossRef]
- Rowley, S.E.; Hadjimichael, M.; Ali, M.N.; Durmaz, Y.C.; Lashley, J.C.; Cava, R.J.; Scott, J.F. Quantum criticality in a uniaxial organic ferroelectric. J. Phys. Condens. Matter 2015, 27, 395901. [Google Scholar] [CrossRef] [PubMed]

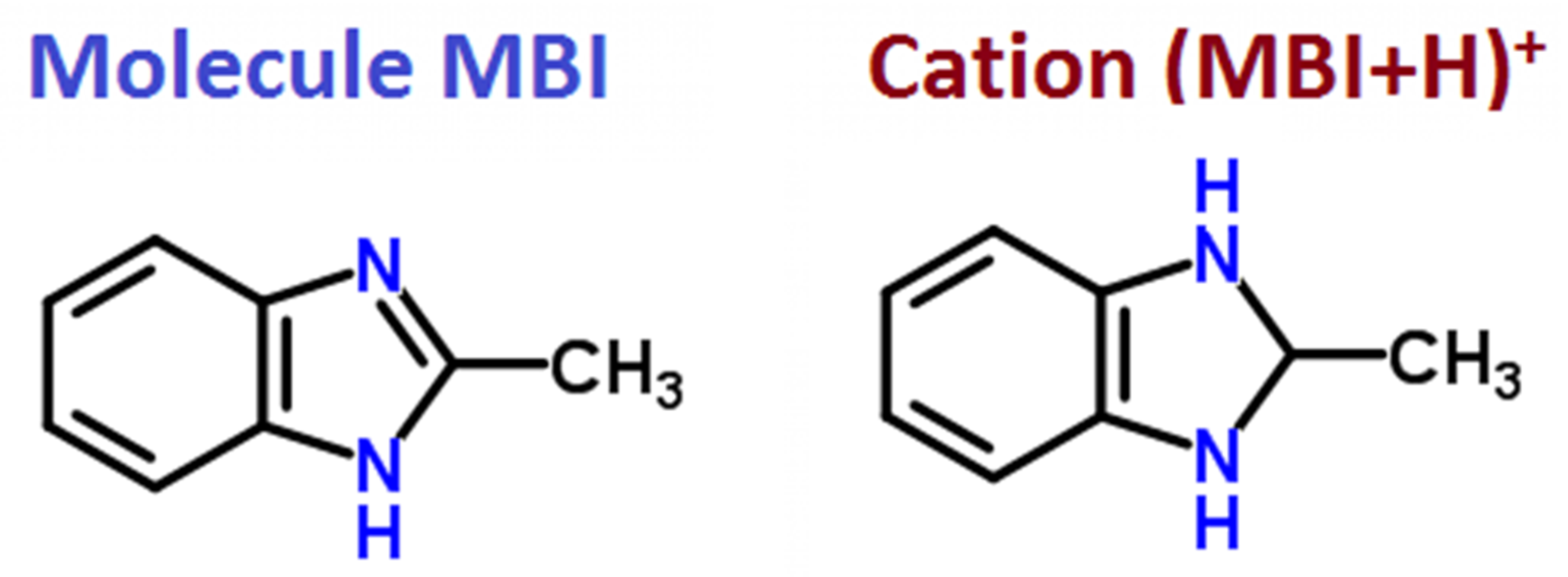

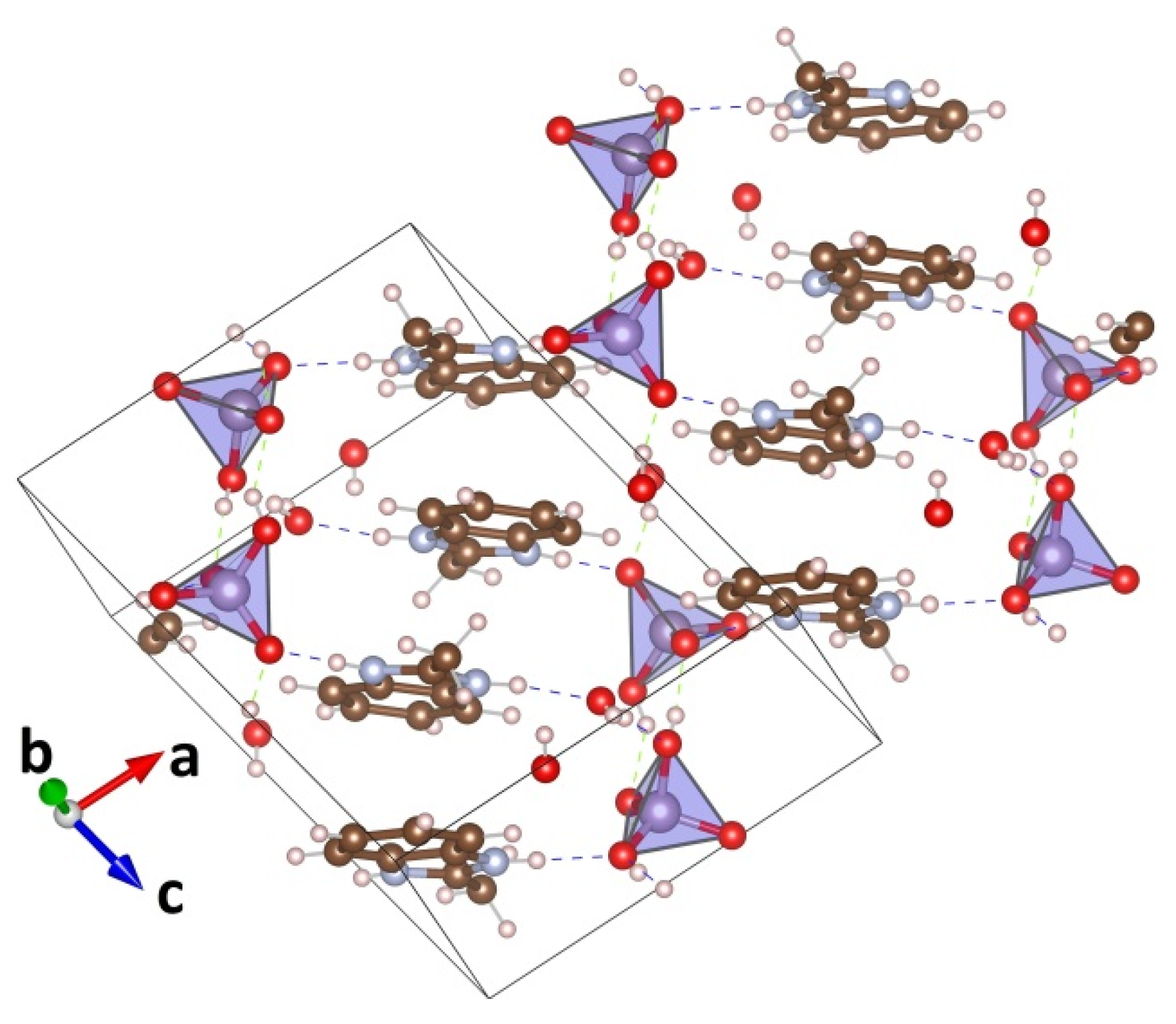
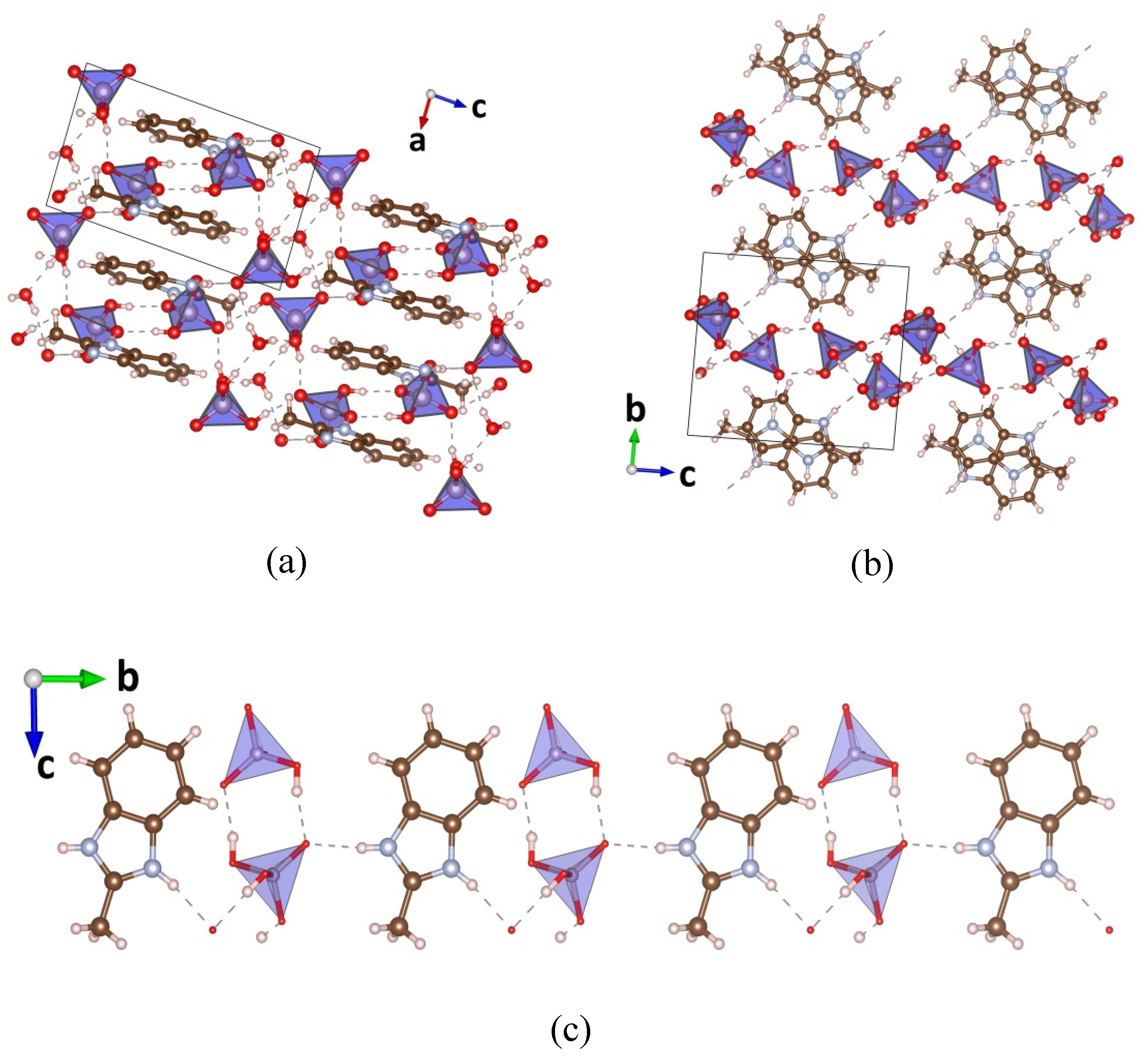
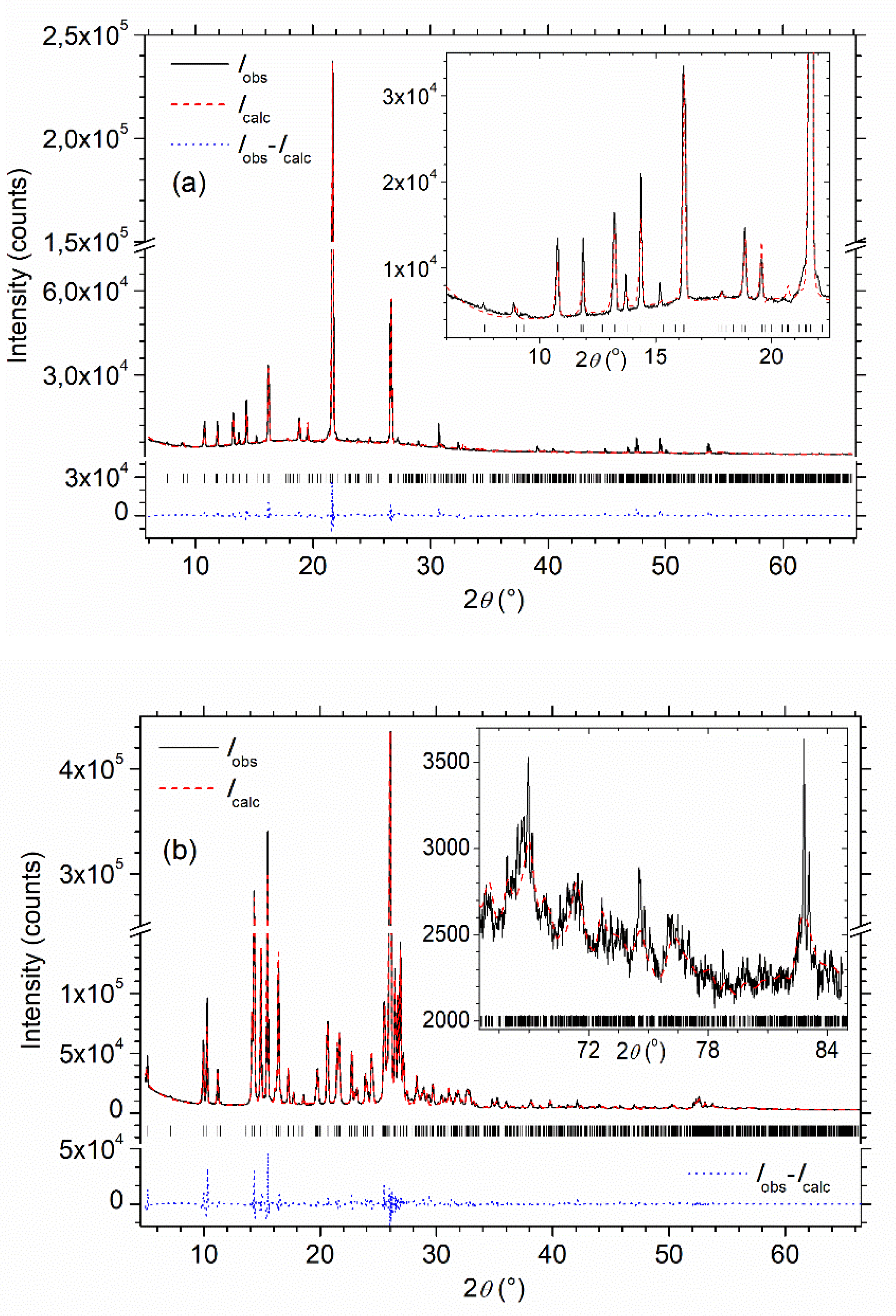
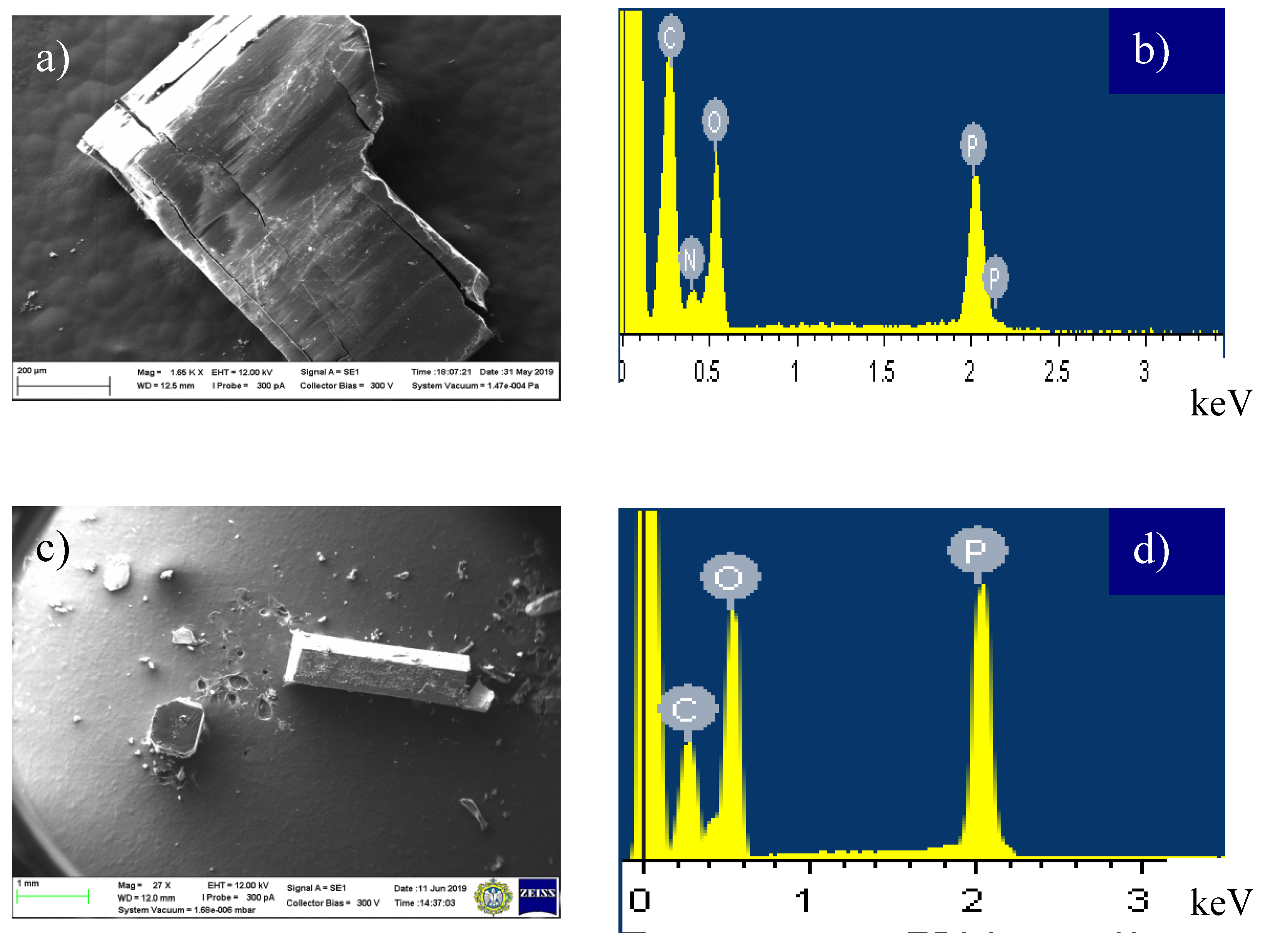
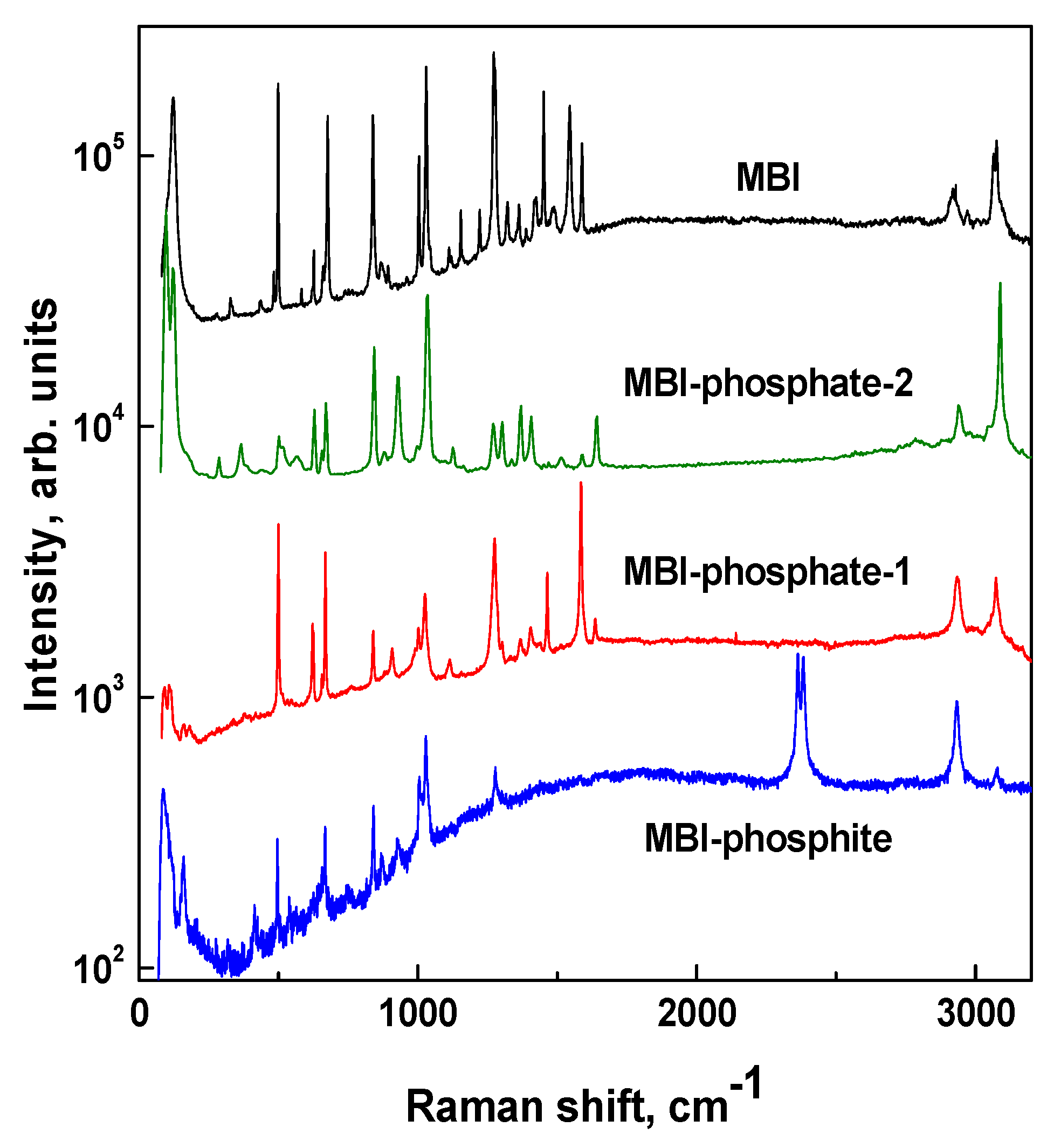
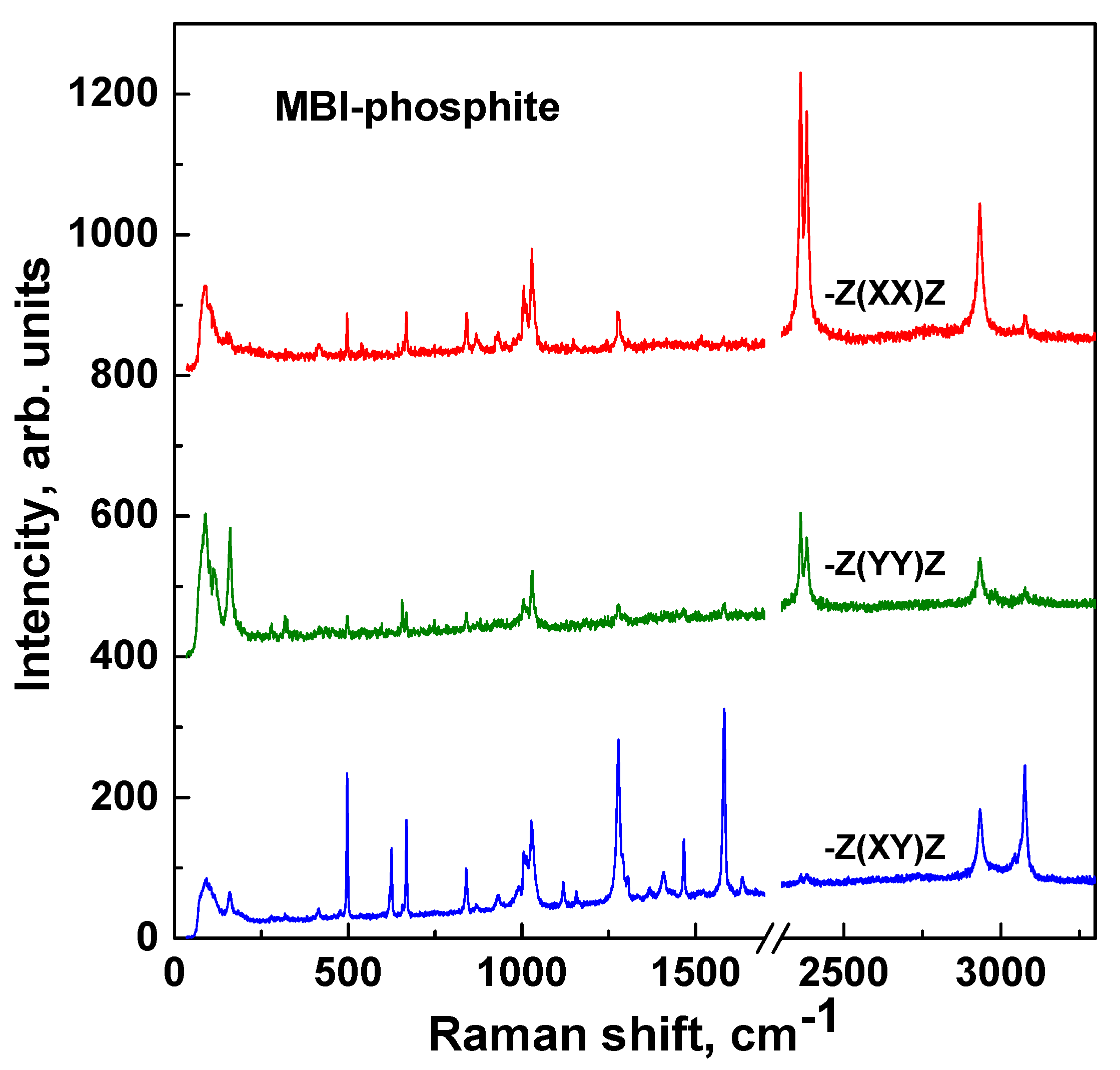
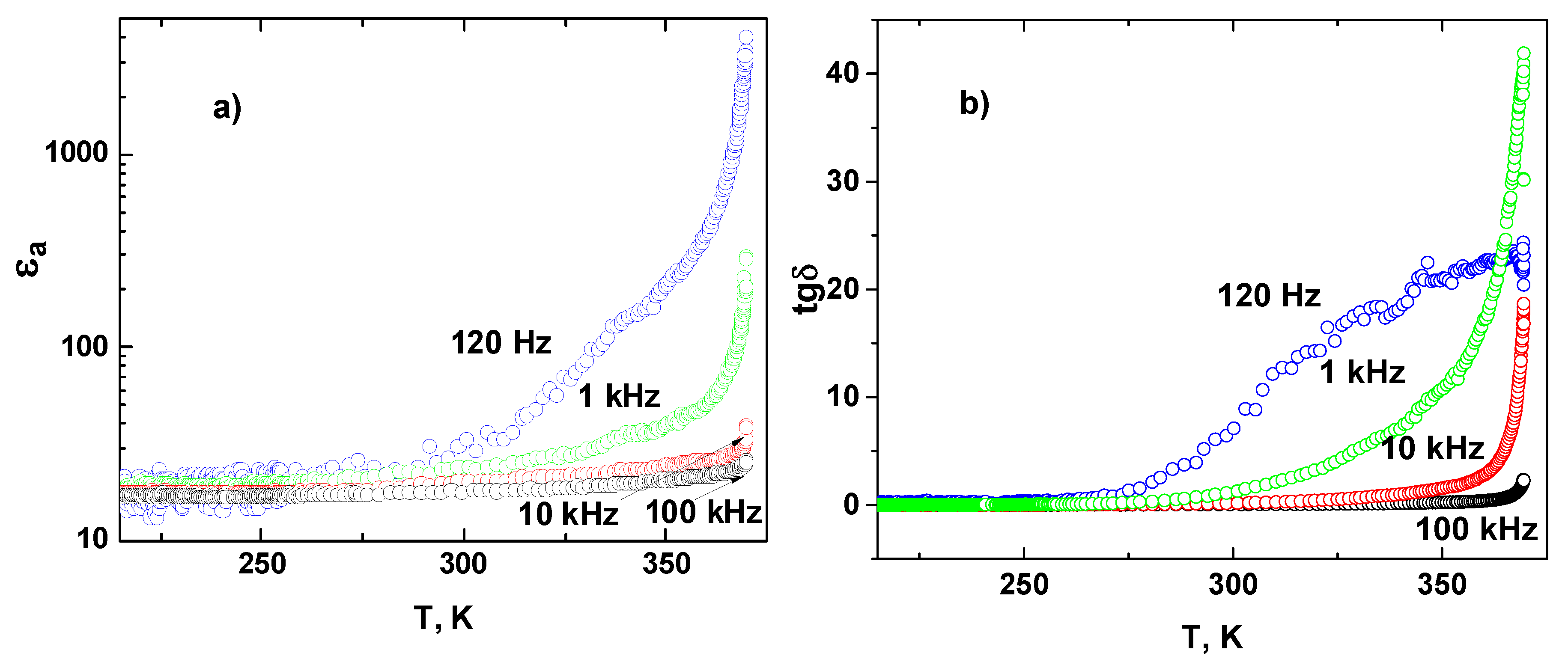
| MBI-Phosphite | MBI-Phosphate-1 | MBI-Phosphate-2 | |
|---|---|---|---|
| Chemical Formula | C16H24N4O7P2 | C16H24N4O9P2 | C8H16N2O9P2 |
| Temperature, K | 293 | 293 | 296 |
| Formula Weight | 446.33 | 478.33 | 345.16 |
| Crystal System | Monoclinic | Triclinic | Triclinic |
| Space Group | P21/c (N 14) | P(N 2) | P (N 2) |
| a, Å | 17.1966(6) | 9.574(9) | 6.8476(3) |
| b, Å | 17.7098(7) | 9.779(9) | 10.1778(4) |
| c, Å | 6.9992(4) | 11.796(10) | 11.0834(5) |
| α, ° | 90 | 88.294(18) | 87.953(1) |
| β, ° | 94.963(4) | 78.07(2) | 85.546(1) |
| γ, ° | 90 | 87.646(19) | 74.760(1) |
| V, Å3 | 2123.60(17) | 1079.3(17) | 742.93(6) |
| Z | 4 | 2 | 2 |
| Dcalc, g cm−3 | 1.396 | 1.472 | 1.548 |
| F(000) | 936.0 | 500.0 | 358.0 |
| μ, mm−1 | 0.250 | 0.258 | 0.337 |
| Crystal Size, mm3 | 0.22 × 0.18 × 0.12 | 0.25 × 0.14 × 0.10 | 0.22 × 0.16 × 0.11 |
| Radiation | Mo-Kα (λ = 0.71073 Å) | Mo-Kα (λ = 0.71073 Å) | Mo-Kα (λ = 0.71073 Å) |
| 2θ Range for Data Collection | 4.600 to 54.998° | 3.530 to 51.992° | 3.686 to 73.350 ° |
| Miller Indices | −22 ≤ h ≤ 22, −23 ≤ k ≤ 22, −9 ≤ l ≤ 8 | −11 ≤ h ≤ 11, −12 ≤ k ≤ 12, −14 ≤ l ≤ 14 | −5 ≤ h ≤ 11, −17 ≤ k ≤ 17, −18 ≤ l ≤ 18 |
| Reflections Collected | 26288 | 15284 | 20949 |
| Independent Reflections | 4857 [Rint = 0.0644, Rsigma = 0.0554] | 4131[Rint = 0.0545, Rsigma = 0.0495] | 6792[Rint = 0.0223, Rsigma = 0.0231] |
| Data/restraints/Parameters | 4857/4/288 | 4131/6/306 | 6792/7/219 |
| GoF | 1.035 | 1.025 | 1.034 |
| Final R Factors [I ≥2σ (I)] | R1 = 0.0605, wR2 = 0.1426 | R1 = 0.0461, wR2 = 0.1149 | R1 = 0.0358, wR2 = 0.1059 |
| Final R Factors [All Data] | R1 = 0.1174, wR2 = 0.1701 | R1 = 0.0609, wR2 = 0.1250 | R1 = 0.0462, wR2 = 0.1138 |
| Largest Diff. Peak/Hole, eÅ−3 | 0.29/−0.27 | 0.45/−0.41 | 0.37/−0.51 |
| № | MBI | MBI-Phosphite | MBI-Phosphate-1 | MBI-Phosphate-2 | Assignment |
|---|---|---|---|---|---|
| 1 | 3065m 3075m | 3076s | 3073s 3085s | 3086s | MBI: νCH |
| 2 | 2968m | 2984w | MBI: M νCH | ||
| 3 | 2919m 2929m | 2934s | 2933s 2940s | 2938s | MBI: M νCH |
| 4 | 2363s, 2382s | H3PO3: νPH [5,20,45,46,47] | |||
| 5 | 1637m | 1637m | 1637s | δH2O [48,49,50] | |
| 6 | 1589m | 1583s | 1585s | 1584m | MBI: νCC |
| 7 | 1545s | MBI: νCN (double bond) + νCC | |||
| 8 | 1517w | 1515w | 1512m | δH2O [48,49,50] | |
| 9 | 1472w 1488m | MBI: MδCH2+ΓCCCN + δCCH | |||
| 10 | 1438m 1452s | 1466s | 1436w 1464s | 1466s | MBI: δCCH+ νCC |
| 11 | 1425m | *MBI: δCNH +νCN +νCC+ δCCH | |||
| 12 | 1418w | 1408s | 1405m | 1403s | MBI: MδCH2 + δCCH |
| 13 | 1363m | 1369m | 1368w | 1364s | MBI: νCC+ νCN+ MδCH2 |
| 14 | 1322m | 1332w | 1337m | MBI: δCCH+ νCN | |
| 15 | 1303w | 1302s | δOH…O [51] | ||
| 16 | 1272s | 1276s | 1276s | 1266s | MBI: νCN+ νCC+ δCCH |
| 17 | 1222m | 1224w | MBI: δCCH+ νCN + νCC | ||
| 18 | 1155m | 1157m | 1156w | 1160m | *MBI: δCCH |
| 19 | 1113m 1120m | 1119s | 1115m | 1121s | MBI: δCCH+ νCC |
| 20 | 1044m | MBI: δCCH + ΓNCCH | |||
| 21 | 1030s | 1028s | 1026s | 1028vs | MBI: νCC+ νCN |
| 22 | 1004s | 1006s | 1002m | 1004w | MBI: νCC+ δCCH |
| 23 | 991m | 990w | 991w | νOPO [45,52] | |
| 24 | 960w | *MBI: ΓHCCH + ΓCCCH | |||
| 25 | 933m | 908m | 924s | νOPO [5,47,49,53] | |
| 26 | 921w | MBI: ΓHCCH + ΓCCCH | |||
| 27 | 893m | 897w | MBI: δCCC + δCCH | ||
| 28 | 868m | 867m | 878w | *MBI: ΓCCCH + ΓHCCN + ΓHCCH + ΓCCCH | |
| 29 | 839s | 840s | 840s | 839s | MBI: νCC |
| 30 | 764w | 761w | 768w | MBI: ΓCCCH + ΓCCCC | |
| 31 | 741m | 745w | MBI: ΓCCCH + ΓHCCN | ||
| 32 | 677s | 667s | 669s | 667s | MBI: νCC + δCCC + δCCN |
| 33 | 657m | 656m | 656w | 652s | *MBI: ΓCNCN + ΓHCCN + ΓCCCN + ΓHNCN |
| 34 | 623w 628m | 624s | 623m | 624s | MBI: δCCN + δCCC + νCC |
| 35 | 582s | 581w | *MBI: ΓCCCC + ΓCCCN + ΓCCCH | ||
| 36 | 546w | 546w 566m | H3PO4: PO4 bending (ν4) [49;52] | ||
| 37 | 537m | H3PO3: PO3 asym. bending [5,54] | |||
| 38 | 516w | 513sb | H3PO4 [53,55] | ||
| 39 | 499s | 497s | 500s | 497s | MBI: δCCC + νCC + νCN |
| 40 | 483m | 483w | 483w | *MBI: δCCN + δCCC + νCC | |
| 41 | 435m | 435w | 435w | MBI: ΓCCCC + ΓCCCH + ΓCCNH + ΓCCNC | |
| 42 | 415m | 419w | Water libration? lattice modes? | ||
| 43 | 379w | 364s 383mb | H3PO4:PO4 sym. bending [53,56] | ||
| 44 | 329w 334m | 318m | 339w | 324w | MBI: ΓCCCN + ΓCCNH |
| 45 | 274m | 279m | 288w | 285s | MBI: δCCN |
| 46 | 123vs | 115w 160s | 114w 159w | 122vs | MBI: ΓCCCN + ΓHCCN lattice modes? |
| 47 | 89sb | 90m, 108m | 96vs | *MBI: ΓHCCN? lattice modes? |
| Wavenumber, cm−1 | -Z(XX)Z | -Z(YY)Z | -Z(XY)Z | Powder | Assignment | Sym. |
|---|---|---|---|---|---|---|
| 3076 | m | w | s | sb | MBI: νCH (A′) | Bg |
| 2934 | s | m | s | s | MBI: MνCH (A″) | Ag, Bg |
| 2363 2382 | vs vs | vs vs | w w | vs vs | H3PO3: νPH (А1) | Ag |
| 1637 | m | w | δH2O | Bg | ||
| 1583 | w | mb | vs | MBI: νCC (A′) | Bg | |
| 1517 | w | w | δH2O | Ag, Bg | ||
| 1466 | s | MBI: δCCH + νCC (A′) | Bg | |||
| 1408 | s | MBI: MδCH2 + δCCH (A′) | Bg | |||
| 1369 | m | MBI: νCC + νCN + MδCH2 (A′) | Bg | |||
| 1276 | m | w | vs | s | MBI: νCN + νCC + δCCH (A′) | Bg |
| 1157 | m | MBI: δCCH (A′) | Bg | |||
| 1119 | m | MBI: δCCH + νCC (A′) | Bg | |||
| 1028 | s | s | s | s | MBI: νCC + νCN (A′) | Ag, (Bg) |
| 1006 | m | m | s | s | MBI: νCC + δCCH (A′) | Ag, Bg |
| 991 | m | νOPO (А1) | Bg | |||
| 930 | w | mb | sb | νOPO (А1) | Bg, (Ag) | |
| 867 | m | mb | s | MBI: ΓCCCH + ΓHCCN + ΓHCCH + ΓCCCH (A″) | Ag, (Bg) | |
| 840 | m | m | s | s | MBI: νCC (A′) | Bg, (Ag) |
| 745 | w | w | MBI: ΓCCCH + ΓHCCN (A″) | Ag | ||
| 667 | m | w | s | s | MBI: νCC + δCCC + δCCN (A′) | Bg, (Ag) |
| 656 | m | m | w | w | MBI: ΓCNCN + ΓHCCN + ΓCCCN + ΓHNCN (A″) | Ag, (Bg) |
| 624 | s | w | MBI: δCCN + δCCC + νCC (A′) | Bg | ||
| 537 | m | w | H3PO3: HPO3 asym. bending (E) | Ag | ||
| 497 | m | m | vs | s | MBI: δCCC + νCC + νCN (A′) | Bg, (Ag) |
| 415 | mb | m | m | lattice modes? Water libration? ΓCCNH | Ag, (Bg) | |
| 318 | m | m | MBI: ΓCCCN + ΓCCNH (A″) | Ag, (Bg) | ||
| 279 | w | w | MBI: δCCN (A′) | Ag, (Bg) | ||
| 160 | mb | s | s | s | MBI: ΓCCCN + ΓHCCN (A″) | Ag, (Bg) |
| 89 | sb | sb | sb | sb | MBI: ΓHCCN (A″)? lattice mode? | Ag, (Bg) |
| C2h | N | A | T | L | Internal Modes | Hydrogen Bonds between HPO32− Vibrations | Selection Rules | ||
|---|---|---|---|---|---|---|---|---|---|
| (MBI+H)+ | HPO32− | H2O | |||||||
| Ag | 159 | 0 | 15 | 15 | 102 | 18 | 3 | 6 | XX,YY |
| Bg | 159 | 0 | 15 | 15 | 102 | 18 | 3 | 6 | XY |
| Au | 159 | 1 | 14 | 15 | 102 | 18 | 3 | 6 | i |
| Bu | 159 | 2 | 13 | 15 | 102 | 18 | 3 | 6 | i |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balashova, E.V.; Svinarev, F.B.; Zolotarev, A.A.; Levin, A.A.; Brunkov, P.N.; Davydov, V.Y.; Smirnov, A.N.; Redkov, A.V.; Pankova, G.A.; Krichevtsov, B.B. Crystal Structure, Raman Spectroscopy and Dielectric Properties of New Semiorganic Crystals Based on 2-Methylbenzimidazole. Crystals 2019, 9, 573. https://doi.org/10.3390/cryst9110573
Balashova EV, Svinarev FB, Zolotarev AA, Levin AA, Brunkov PN, Davydov VY, Smirnov AN, Redkov AV, Pankova GA, Krichevtsov BB. Crystal Structure, Raman Spectroscopy and Dielectric Properties of New Semiorganic Crystals Based on 2-Methylbenzimidazole. Crystals. 2019; 9(11):573. https://doi.org/10.3390/cryst9110573
Chicago/Turabian StyleBalashova, E. V., F. B. Svinarev, A. A. Zolotarev, A. A. Levin, P. N. Brunkov, V. Yu. Davydov, A. N. Smirnov, A. V. Redkov, G. A. Pankova, and B. B. Krichevtsov. 2019. "Crystal Structure, Raman Spectroscopy and Dielectric Properties of New Semiorganic Crystals Based on 2-Methylbenzimidazole" Crystals 9, no. 11: 573. https://doi.org/10.3390/cryst9110573
APA StyleBalashova, E. V., Svinarev, F. B., Zolotarev, A. A., Levin, A. A., Brunkov, P. N., Davydov, V. Y., Smirnov, A. N., Redkov, A. V., Pankova, G. A., & Krichevtsov, B. B. (2019). Crystal Structure, Raman Spectroscopy and Dielectric Properties of New Semiorganic Crystals Based on 2-Methylbenzimidazole. Crystals, 9(11), 573. https://doi.org/10.3390/cryst9110573






