Galloping Reduction of Transmission Lines by Using Phononic Crystal
Abstract
:1. Introduction
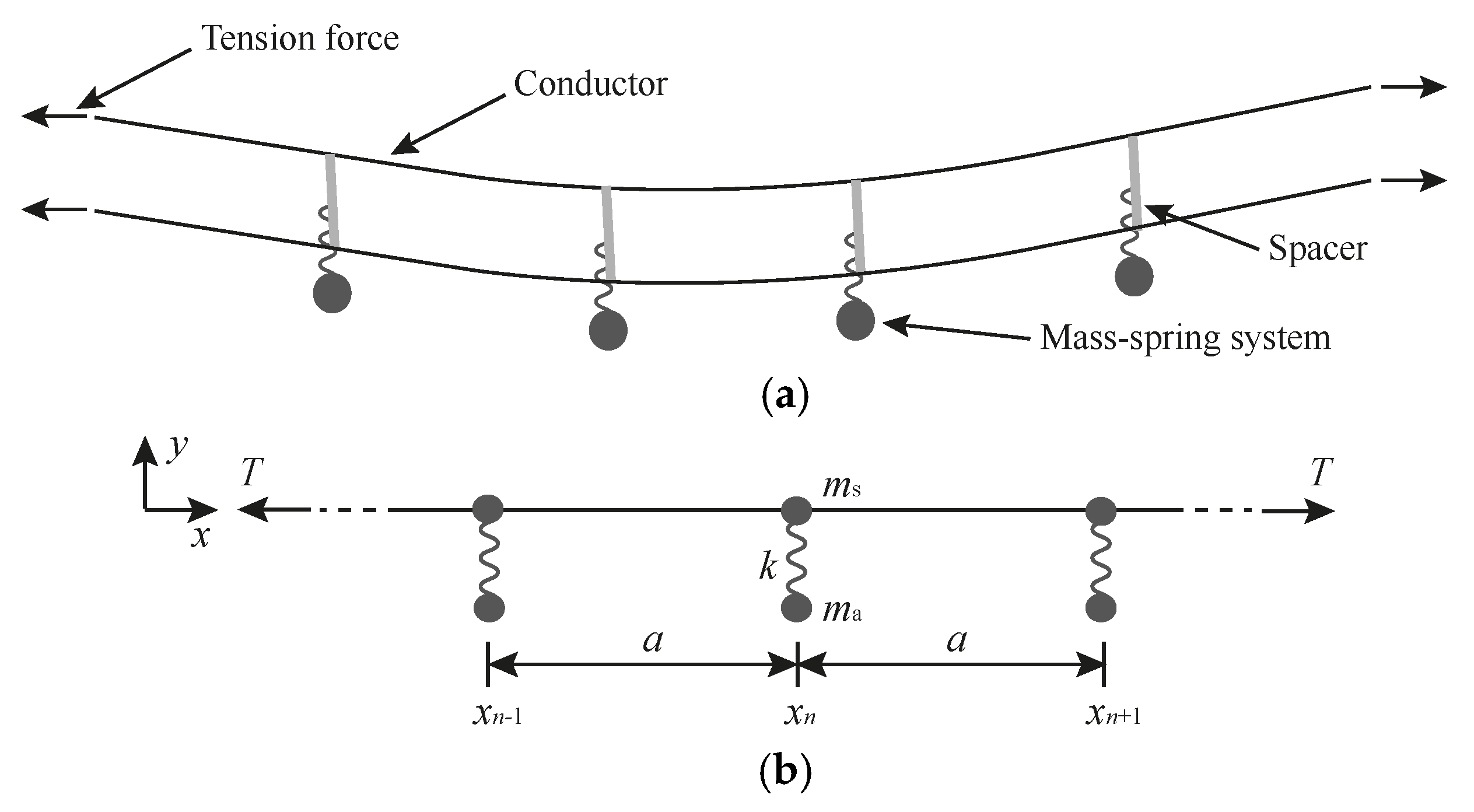
2. Model and BG Calculation Method
3. Results and Discussion
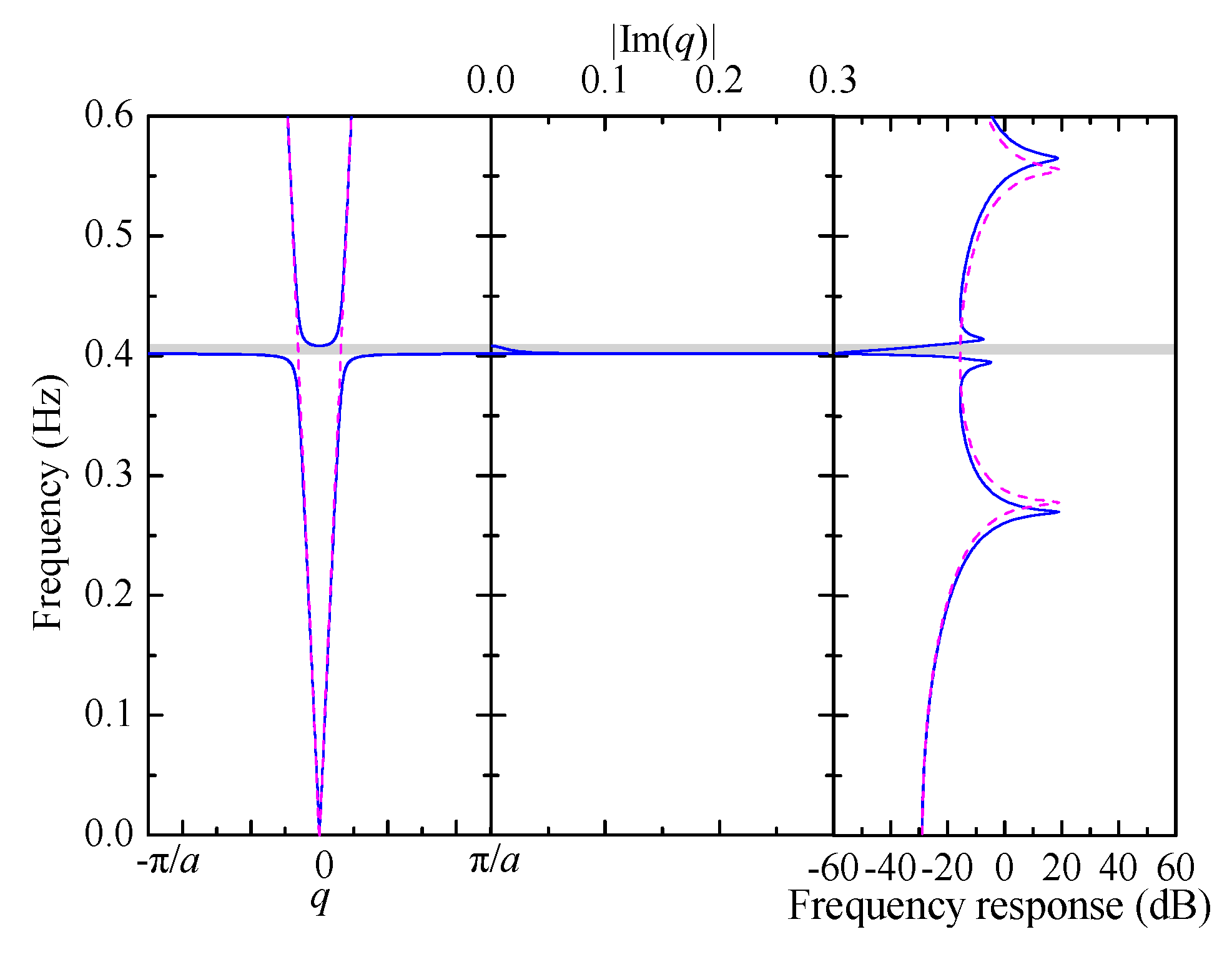
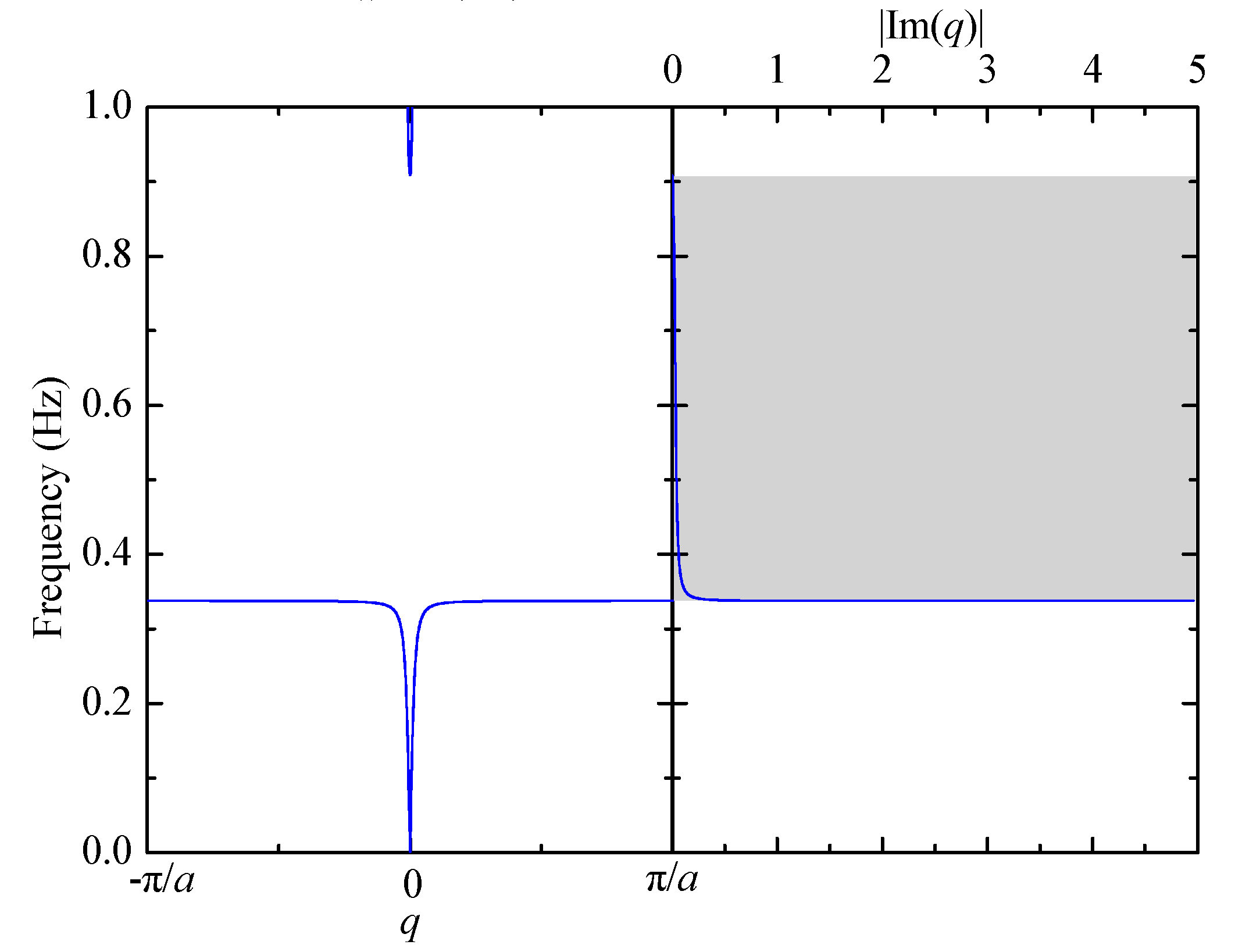
3.1. Existence of BGs in Galloping Frequency Range
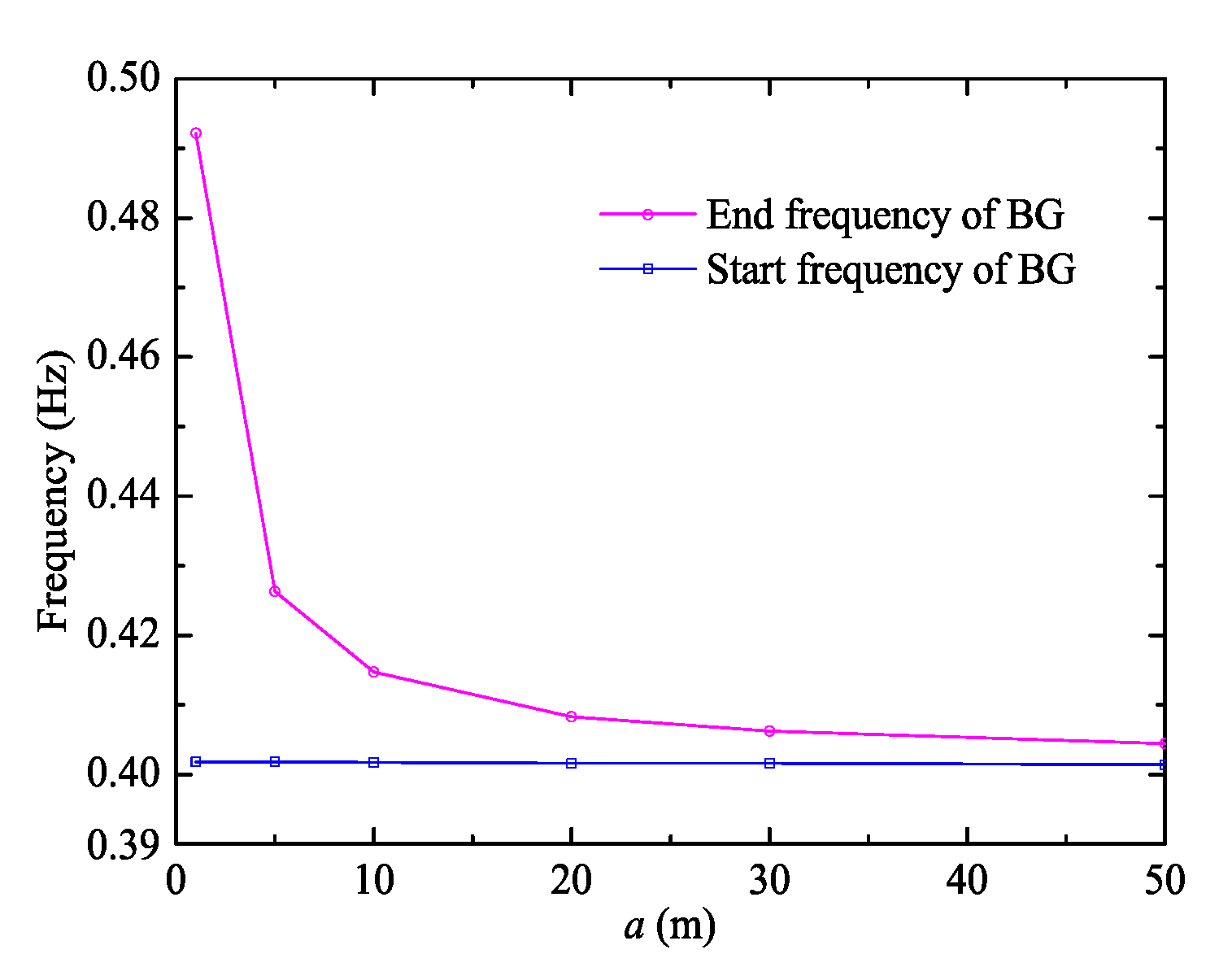
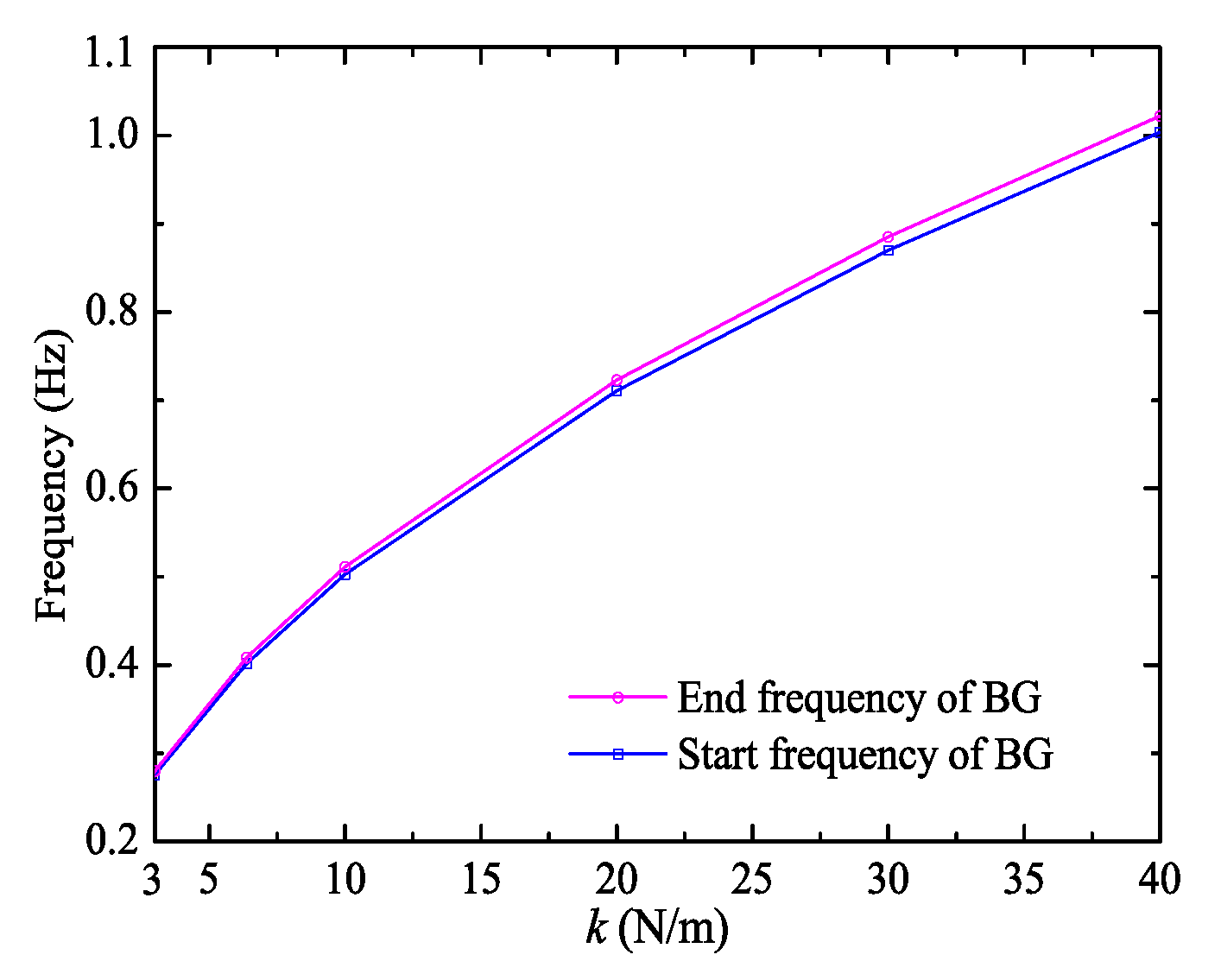
3.2. Effect of the Spacer on BG
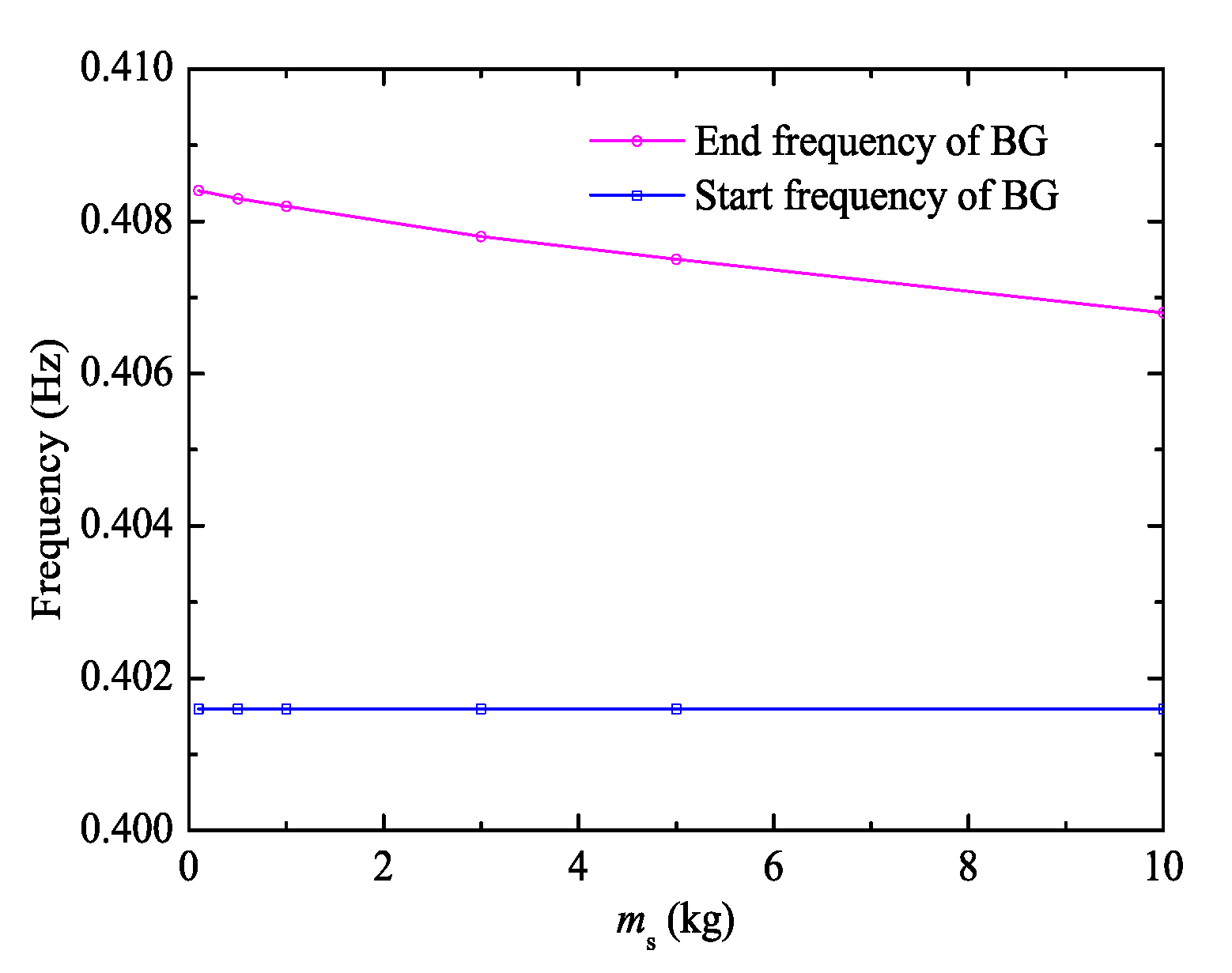
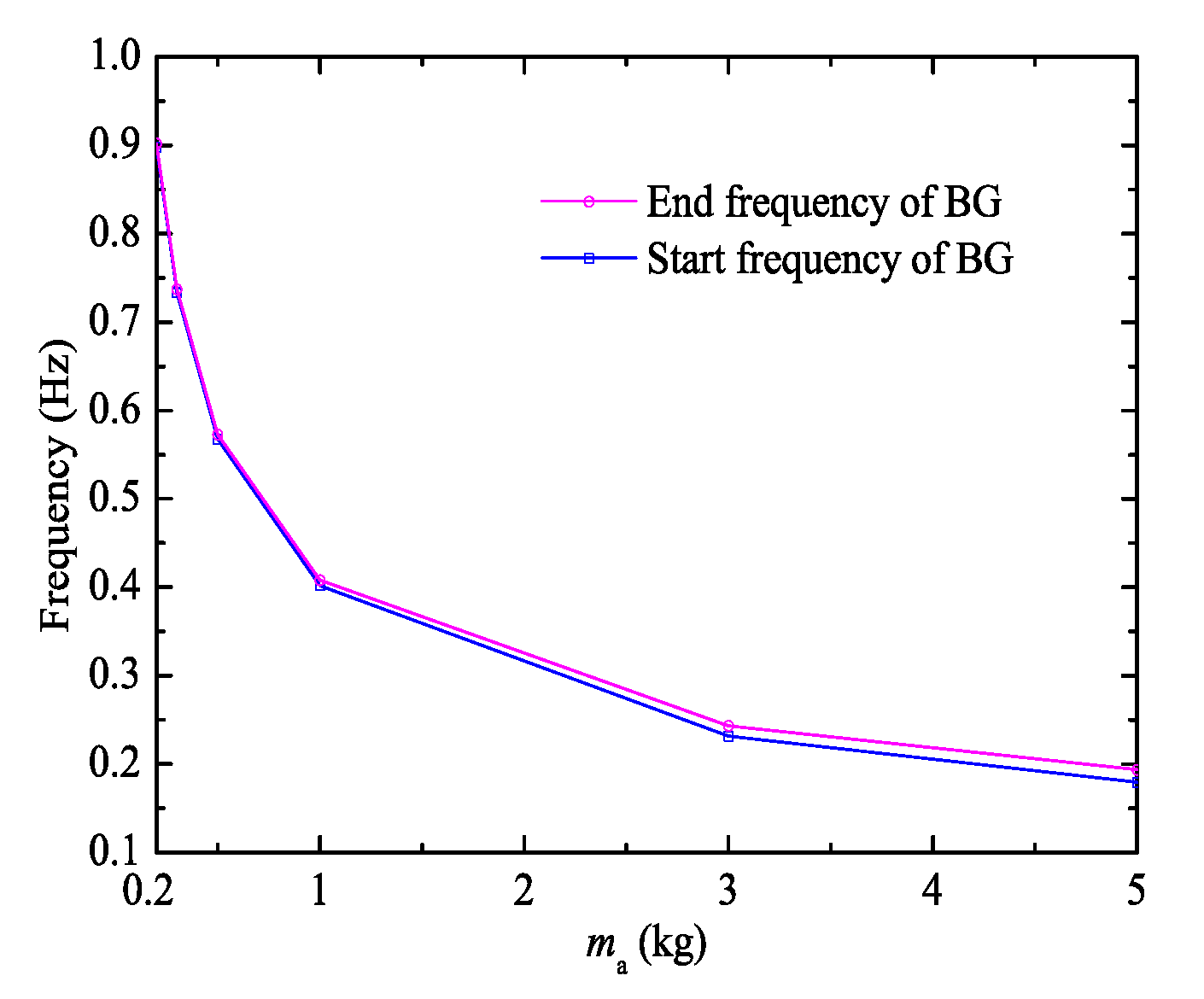
3.3. Effect of Attached Mass-Spring System on BG
3.4. Remark
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fu, X.; Li, H.; Li, J.; Zhang, P. A pounding spacer damper and its application on transmission line subjected to fluctuating wind load. Struct. Control Health Monit. 2017, 24, e1950. [Google Scholar] [CrossRef]
- Lu, M.L.; Popplewell, N.; Shah, A.H.; Chan, J.K. Hybrid nutation damper for controlling galloping power lines. IEEE Trans. Power Deliv. 2007, 22, 450–456. [Google Scholar] [CrossRef]
- Loredo-Souza, A.M.; Davenport, A.G. A novel approach for wind tunnel modelling of transmission lines. J. Wind Eng. Ind. Aerod. 2001, 89, 1017–1029. [Google Scholar] [CrossRef]
- Zhou, L.; Yan, B.; Zhang, L.; Zhou, S. Study on galloping behavior of iced eight bundle conductor transmission lines. J. Sound Vib. 2016, 362, 85–110. [Google Scholar] [CrossRef]
- Van Dyke, P.; Laneville, A. Galloping of a single conductor covered with a D-section on a high-voltage overhead test line. J. Wind Eng. Ind. Aerod. 2008, 96, 1141–1151. [Google Scholar] [CrossRef]
- Gurung, C.B.; Yamaguchi, H.; Yukino, T. Identification of large amplitude wind-induced vibration of ice-accreted transmission lines based on field observed data. Eng. Struct. 2002, 24, 179–188. [Google Scholar] [CrossRef]
- Fu, G.; Wang, L.; Guan, Z.; Hou, L.; Meng, X.; Macalpine, M. Simulations of the controlling effect of interphase spacers on conductor galloping. IEEE Trans. Dielect. Electr. Insul. 2012, 19, 1325–1334. [Google Scholar] [CrossRef]
- Yan, B.; Liu, X.; Lv, X.; Zhou, L. Investigation into galloping characteristics of iced quad bundle conductors. J. Vib. Control 2016, 22, 965–987. [Google Scholar] [CrossRef]
- Qin, Z.; Chen, Y.; Zhan, X.; Liu, B.; Zhu, K. Research on the galloping and anti-galloping of the transmission line. Int. J. Bifurcat. Chaos 2012, 22, 1250038. [Google Scholar] [CrossRef]
- Keutgen, R.; Lilien, J.L. A new damper to solve galloping on bundled lines. Theoretical background, laboratory and field results. IEEE Trans. Power Deliv. 1998, 13, 260–265. [Google Scholar] [CrossRef]
- Denhartog, J.P. Transmission line vibration due to sleet. Trans. Am. Inst. Electr. Eng. 1932, 51, 1074–1086. [Google Scholar] [CrossRef]
- Nigol, O.; Buchan, P.G. Conductor galloping part II Torsional mechanism. IEEE Trans. Power Appar. Syst. 1981, 708–720. [Google Scholar] [CrossRef]
- Luongo, A.; Piccardo, G. Linear instability mechanisms for coupled translational galloping. J. Sound Vib. 2005, 288, 1027–1047. [Google Scholar] [CrossRef]
- Wang, J.; Lilien, J.L. Overhead electrical transmission line galloping. A full multi-span 3-DOF model, some applications and design recommendations. IEEE Trans. Power Deliv. 1998, 13, 909–916. [Google Scholar] [CrossRef]
- Jones, K.F. Coupled vertical and horizontal galloping. J. Eng. Mech. 1992, 118, 92–107. [Google Scholar] [CrossRef]
- Havard, D.G.; Pohlman, J.C. Five years' field trials of detuning pendulums for galloping control. IEEE Trans. Power Appar. Syst. 1984, 318–327. [Google Scholar] [CrossRef]
- Xu, Z.D.; Xu, L.Z.; Xu, F.H. Study on the iced quad-bundle transmission lines incorporated with viscoelastic antigalloping devices. J. Dyn. Sys. Meas. Control 2015, 137, 61009. [Google Scholar] [CrossRef]
- Hunt, J.C.R.; Richards, D.J.W. Overhead-line oscillations and the effect of aerodynamic dampers. Proc. Inst. Electr. Eng. 1969, 116, 1869–1874. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Pennec, Y.; Pan, Y.; Djafari-Rouhani, B. Phononic crystal plate with hollow pillars actively controlled by fluid filling. Crystals 2016, 6, 64. [Google Scholar] [CrossRef]
- Maldovan, M. Sound and heat revolutions in phononics. Nature 2013, 503, 209–217. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Wu, T. Vibration reduction in a periodic truss beam carrying locally resonant oscillators. J. Vib. Control 2015, 22, 270–285. [Google Scholar] [CrossRef]
- Yan, Y.; Laskar, A.; Cheng, Z.; Menq, F.; Tang, Y.; Mo, Y.L.; Shi, Z. Seismic isolation of two dimensional periodic foundations. J. Appl. Phys. 2014, 116, 44908. [Google Scholar] [CrossRef]
- Sanchez-Dehesa, J.; Garcia-Chocano, V.M.; Torrent, D.; Cervera, F.; Cabrera, S.; Simon, F. Noise control by sonic crystal barriers made of recycled materials. J. Acoust. Soc. Am. 2011, 129, 1173–1183. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, S.; Eftekhar, A.A.; Hunt, W.D.; Adibi, A. High-Q micromechanical resonators in a two-dimensional phononic crystal slab. Appl. Phys. Lett. 2009, 94, 51906. [Google Scholar] [CrossRef]
- Wang, Y.; Maznev, A.; Laude, V. Formation of Bragg band gaps in anisotropic phononic crystals analyzed with the empty lattice model. Crystals 2016, 6, 52. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Han, L.; Zhang, Y.; Jiang, L.; Zhang, Z. Free transverse vibration in periodically hinged identical beams on elastic foundations: A single material phononic crystal. Phys. Status Solidi-RRL 2013, 7, 514–517. [Google Scholar] [CrossRef]
- Yu, D.; Wen, J.; Zhao, H.; Liu, Y.; Wen, X. Flexural vibration band gap in a periodic fluid-conveying pipe system based on the Timoshenko beam theory. J. Vib. Acoust. 2011, 133, 14502. [Google Scholar] [CrossRef]
- Wang, Y.F.; Wang, Y.S.; Laude, V. Wave propagation in two-dimensional viscoelastic metamaterials. Phys. Rev. B 2015, 92, 104110. [Google Scholar] [CrossRef]
- Graczykowski, B.; Sledzinska, M.; Alzina, F.; Gomis-Bresco, J.; Reparaz, J.S.; Wagner, M.R.; Sotomayor, C.M. Phonon dispersion in hypersonic two-dimensional phononic crystal membranes. Phys. Rev. B 2015, 91, 95414. [Google Scholar] [CrossRef]
- Delpero, T.; Schoenwald, S.; Zemp, A.; Bergamini, A. Structural engineering of three-dimensional phononic crystals. J. Sound Vib. 2015, 363, 156–165. [Google Scholar] [CrossRef]
- Shi, Z.; Huang, J. Feasibility of reducing three-dimensional wave energy by introducing periodic foundations. Soil Dyn. Earthq. Eng. 2013, 50, 204–212. [Google Scholar] [CrossRef]
- Sharma, B.; Sun, C.T. Local resonance and Bragg bandgaps in sandwich beams containing periodically inserted resonators. J. Sound Vib. 2016, 364, 133–146. [Google Scholar] [CrossRef]
- Xiao, Y.; Mace, B.R.; Wen, J.; Wen, X. Formation and coupling of band gaps in a locally resonant elastic system comprising a string with attached resonators. Phys. Lett. A 2011, 375, 1485–1491. [Google Scholar] [CrossRef]
- Wang, T.; Sheng, M.; Qin, Q. Multi-flexural band gaps in an Euler–Bernoulli beam with lateral local resonators. Phys. Lett. A 2016, 380, 525–529. [Google Scholar] [CrossRef]
- Ding, L.; Zhu, H.P.; Luo, H.; Yin, T. Flexural wave propagation and localization in periodic jointed tunnels subjected to moving loads. J. Vib. Control 2016, 22, 2788–2804. [Google Scholar] [CrossRef]
- Shu, H.; Shi, X.; Li, S.; Liu, S.; Wang, W.; Shi, D. Numerical research on dynamic stress of phononic crystal ROD in longitudinal wave band gap. Int. J. Mod. Phys. B 2014, 28, 1450231. [Google Scholar] [CrossRef]
- Xiao, Y.; Wen, J.H.; Wen, X.S. Longitudinal wave band gaps in metamaterial-based elastic rods containing multi-degree-of-freedom resonators. New J. Phys. 2012, 14, 33042. [Google Scholar] [CrossRef]
- Yu, D.; Liu, Y.; Wang, G.; Cai, L.; Qiu, J. Low frequency torsional vibration gaps in the shaft with locally resonant structures. Phys. Lett. A 2006, 348, 410–415. [Google Scholar] [CrossRef]
- Zhu, D.L.; Ma, C. Study on sub-span oscillation of bundle conductor for transmission line. Adv. Mater. Res. 2012, 594–597, 2815–2818. [Google Scholar] [CrossRef]
- Han, L.; Zhang, Y.; Ni, Z.; Zhang, Z.; Jiang, L. A modified transfer matrix method for the study of the bending vibration band structure in phononic crystal Euler beams. Physica B 2012, 407, 4579–4583. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics; Wiley: New York, NY, USA, 2005. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, L.; Zhang, Y.; Li, X.; Jiang, L.; Chen, D. Galloping Reduction of Transmission Lines by Using Phononic Crystal. Crystals 2017, 7, 346. https://doi.org/10.3390/cryst7110346
Han L, Zhang Y, Li X, Jiang L, Chen D. Galloping Reduction of Transmission Lines by Using Phononic Crystal. Crystals. 2017; 7(11):346. https://doi.org/10.3390/cryst7110346
Chicago/Turabian StyleHan, Lin, Yan Zhang, Xiaomei Li, Linhua Jiang, and Da Chen. 2017. "Galloping Reduction of Transmission Lines by Using Phononic Crystal" Crystals 7, no. 11: 346. https://doi.org/10.3390/cryst7110346
APA StyleHan, L., Zhang, Y., Li, X., Jiang, L., & Chen, D. (2017). Galloping Reduction of Transmission Lines by Using Phononic Crystal. Crystals, 7(11), 346. https://doi.org/10.3390/cryst7110346





