Abstract
The crack geometry and associated strain field around Berkovich and Vickers indents on silicon have been studied by X-ray diffraction imaging and micro-Raman spectroscopy scanning. The techniques are complementary; the Raman data come from within a few micrometres of the indentation, whereas the X-ray image probes the strain field at a distance of typically tens of micrometres. For example, Raman data provide an explanation for the central contrast feature in the X-ray images of an indent. Strain relaxation from breakout and high temperature annealing are examined and it is demonstrated that millimetre length cracks, similar to those produced by mechanical damage from misaligned handling tools, can be generated in a controlled fashion by indentation within 75 micrometres of the bevel edge of 200 mm diameter wafers.
1. Introduction
The work described in this paper arose from a detailed study of cracks associated with robotic handling damage in silicon wafers. Catastrophic wafer fracture [1,2] during high temperature processing is a major problem in semiconductor manufacturing with multi-million dollar associated costs on a single production line [3]. At the beginning of our research programme, it was believed that the fracture was associated with cracks introduced by mechanical damage but the location of such damage was not clear. Subsequently the origin of such failure has been shown to be cracks produced at the wafer bevel edge [4,5] due to handling tool misalignment. These cracks can be millimetres in length. Some result in high temperature wafer shattering, while some are benign. As an outcome of our project, commercial X-ray diffraction imaging tools are now available, together with associated analytical software to predict the probability of failure and hence make appropriate decisions relating to the manufacturing process.
As part of the research programme, we used nano-indentation at room temperature to generate cracks in a controlled manner and determine whether such artificially induced cracks could lead to wafer fracture during rapid thermal annealing (RTA). We used scanning electron microscopy (SEM), X-ray Diffraction Imaging (XRDI), also known as X-ray topography, and micro-Raman spectroscopy to study the detailed crack geometry and associated strain fields around Berkovich and Vickers indents. The crack geometry and associated strain fields were studied as a function of indenter load, using a Berkovich tip from 100 mN to 600 mN and a Vickers tip from there up to 5 N. As will become apparent from the results presented below, the cracks generated had high symmetry and in no case were we able to induce wafer fracture during RTA from indents generated away from the wafer edge. Only when the indentation was with a high load and within approximately 75 μm of the bevel edge could millimetre length cracks, such as those now known to induce catastrophic fracture during processing, be produced. Such indentation-generated cracks sometimes initiated catastrophic fracture during RTA. In this paper, we present results of the study of the strain fields around various indentations and explain how the low symmetry bevel edge cracks are generated.
2. Results
In all of the indentation experiments, both with Berkovich and Vickers tips, median surface-breaking cracks were observed to originate at the indenter apices (Figure 1), as was the case in the experiments of Yan et al. [6] for Vickers indents of typically 300–500 mN load on InP. Unlike the indentation of InP, however, the crack projections on the surface did not correspond to the intersection of the low surface energy planes which are {111} or {110} in the case of silicon [7]. Rotation of the Bervovich indenter apices with respect to the in-plane crystallographic directions had almost no effect on the crack geometry, the median cracks still emerging almost parallel to the projection of the indenter apices on the surface. For constant indenter load of less than 200 mN, the total crack length in the surface remained constant as the indenter was rotated.

Figure 1.
Scanning electron microscope image of surface-breaking cracks and associated directions from a 150 mN Berkovich indent with the indenter apex parallel to [011].
Despite the crack extension being only a few microns beyond the indenter impression, the X-ray diffraction images (topographs) [8] were often over 100 μm in extent (Figure 2a), demonstrating that the strain field from the defective region is long range. In transmission, the images consisted of two half lobes, with the line of no contrast perpendicular to the projection of the diffraction vector, and a dark central region. The contrast differs from that in the reflection (Bragg) geometry, in which the images consist of a light central region with a complete dark circle at the edge of the contrast area [9]. Although the three images of Figure 2a are all from the same 600 mN indenter load, the image length varies significantly for the three images from 139 to 96 μm. Such a large dispersion in image size is not observed for loads below about 200 mN. On rotation of the indenter tip about the [100] axis, no change in average image dimension was observed (Figure 2b). (Note that because of the superposition of the three-fold symmetry of the indenter and the four-fold symmetry of the crystal structure, only a limited range of angle is required to cover all possible angles of rotation.)
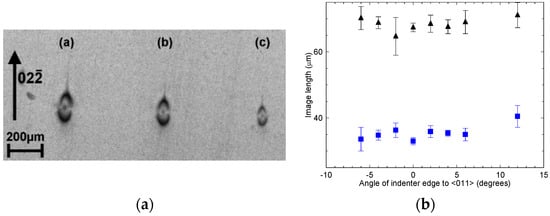
Figure 2.
(a) X-ray diffraction image taken in white beam mode of 600 mN indents with the indenter tip rotated by 6° with respect to the [011] direction. (b) Extent of the X-ray diffraction contrast for 100 mN indents as a function of rotation of the Berkovich tip apex from the [011] direction. Triangles represent image extent in the direction parallel to the diffraction vector, while squares represent the extent perpendicular to the diffraction vector.
The magnitude of the strain field close to the indenter could be imaged in detail using micro-Raman spectroscopy mapping (Figure 3). The medium range strain field is compressive with a maximum value of −0.23 GPa for a 400 mN load indent and −0.85 GPa for a 600 mN load. Close to the centre of the indent, there is tensile strain, which has a maximum value immediately below the indent. For a 400 mN indent its maximum value was 0.75 GPa, while for a 600 mN indent it was 1.2 GPa. For indenter loads above 200 mN, although there is still evidence of a three-fold symmetry in the strain field associated with the indent apex directions, the complete symmetry is lost. This behaviour is found for all indent loads above 200 mN. Annealing of the sample for 30 min at 1000 °C results in a reduction in the magnitude of the compressive strain field by a factor of about four (Figure 4). The tensile stress below the indenter tip and the quasi-three-fold symmetry is completely lost upon annealing.
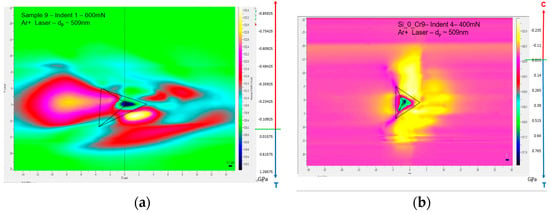
Figure 3.
Two-dimensional maps of the stress as a function of position around: (a) a 600 mN; and (b) a 400 mN indent measured by micro-Raman spectroscopy profiling. The Raman spectroscopy map covers a region whose extent is 30 µm (X) by 50 µm (Y). Step size 0.5 μm. The red and blue arrows indicate whether the stress is compressive (C) or tensile (T). The highest compressive stress is indicated by the yellow regions, while the greatest tensile strain is indicated by the black/blue regions. (Figure 3a is reproduced from ref. [9]) The Raman figures and the stress figures do not correspond directly. These scans took approximately 40 h to complete so the stress figures were calculated by compensating for environmental drift using the plasma peak.
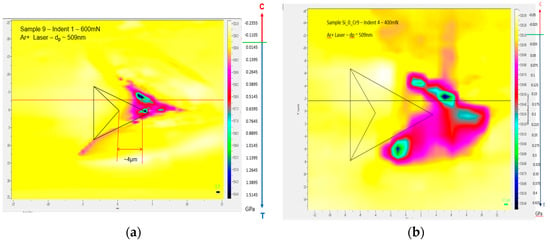
Figure 4.
Micro-Raman maps of the stress around the indents shown in Figure 3 after annealing for 30 min at 1000 °C. The Raman spectroscopy maps covers regions whose extent is: 30 µm (X) by 50 µm (Y) (a); and 30 µm (X) by 32 µm (Y) (b). Step size 0.5 μm. The red and blue arrows indicate whether the stress is compressive (C) or tensile (T). The highest compressive stress is indicated by the yellow regions, while the greatest tensile strain is indicated by the black/blue regions.
The origin of the loss, in the micro-Raman image maps, of three-fold symmetry, seen in the surface-breaking crack geometry, lies in the presence of breakout above 200 mN indent load. An example of such breakout around a 500 mN indent is shown in Figure 5. There are two areas of breakout around the three edges of the indenter footprint, as is also the case for the 600 mN imprint shown in Figure 3a.

Figure 5.
SEM micrograph of a 500 mN Berkovich indent, showing chipping flaws at the edges of the imprint.
Recalling that our objective was to use nanoindentation to generate macroscopic cracks which would lead to wafer fracture during subsequent high temperature processing, we continued to increase the indenter load, switching to a Vickers tip for loads above 600 mN. Due to the omnipresent breakout, we were never able to generate macroscopic length cracks, despite the symmetry breaking. We were, however, able to use the bevel edge and the breakout process to achieve this successfully. With a 5 N Vickers indent within 75 μm of the bevel at the edge of the wafer, commonly we found that two of the breakout regions propagated right through the thin bevel of the wafer as shown schematically in Figure 6a. One long crack (a of type 1) then propagated from the apex of the Vickers tip which pointed inwards from the edge, there sometimes being macroscopic cracks (b in Figure 6a) of type 2 generated from the intersection of the bevel edge with the breakout line. As shown in the white beam X-ray topographs of Figure 6b, long cracks, which again did not propagate on the low surface energy surfaces, could be generated by such an indentation technique. Here, both cracks appear of type 2, originating from the intersection of the break-out with the bevel edge. Residual stress from the indent itself can be seen between the cracks. The curved image of the wafer edge arises because of long range lattice strain associated with the indent changing the local diffraction conditions. Macroscopic crack generation was achieved at a typically 50% success level, it being sensitive to the exact distance of the indent from the bevel edge. These cracks were similar to those generated by repetitive mechanical damage from misaligned wafer handling tools.

Figure 6.
(a) Schematic diagram of the type 1 and type 2 macroscopic cracks generated by Vickers indentation within 75 μm of the bevel edge. (b) Composite of white beam X-ray topographs of a pair of such cracks in reflection. (The break-out dimensions α and β are not discussed here.)
3. Discussion
As was evident from a systematic series of experiments with increasing indenter loads, it proved impossible to generate macroscopic cracks in silicon when the indent was far from the wafer edge. In all cases, the crack lengths were limited to several micrometres, the median surface breaking cracks always being initiated at the indenter apex. Unlike conical indents [10,11], where it was found that {110} cracks were mainly introduced from the indent, indicating that fracture occurs most easily along the {110} planes among the crystallographic planes of the <001> zone, with Berkovich indents, we found no association of the crack geometry with the low surface energy planes. Indeed, ultra-fast X-ray diffraction imaging of fracture in silicon has recently shown that even when cracks are apparently following low energy {110} surfaces, there is a continual jumping between {110} and various high indexed {hkl} planes [12].
The limit on the length of crack is primarily determined by breakout associated with lateral cracks intersecting the surface. When breakout occurs, the strain is relaxed and further crack propagation does not occur. We have noted elsewhere that there is strong asterism in X-ray topographs when breakout is about to occur [9]. Lateral cracks were always found to be present even at low indenter loads when breakout did not occur. An example is shown in Figure 7a in the case of a 120 mN load indent where breakout did not occur. This is a three-dimensional reconstruction from a sequence of images taken during focused ion beam milling of the sample. Further examples can be found in reference [13]. We have shown that finite element (FE) modelling reproduces the shape of the main median crack rather well [9] when cohesive elements are included to represent the relaxation from cracking. The presence of varying length lateral cracks, explains the breaking of the symmetry in Raman strain maps of low load indents even when breakout does not occur. Without the stochastic nature of the lateral cracking process, the FE simulations always show three-fold symmetry, even to the highest loads. An example is shown in Figure 7b, which is a simulation that does not include cohesive elements. We note that the simulation shows stress concentration at the tips of the indenter, which is where the median cracks are initiated. However, in contrast to the experimental data of Figure 3, the stress at those points is tensile and a compressive strain is predicted directly below the indenter apex. The experimental Raman results of Figure 3 and Figure 4 show tensile stresses under the indenter apex with the Ar+ laser (where the penetration depth is 565 nm) but with the UV laser (where the penetration depth is only 9 nm), compressive stresses were observed. Development of tensile stresses implies the presence of lateral cracks and this is captured by the Raman data using the Ar+ laser but not with the UV laser. The Raman map simulated from FE stresses should be compared with results from the UV laser as the simulated stresses are from the surface.
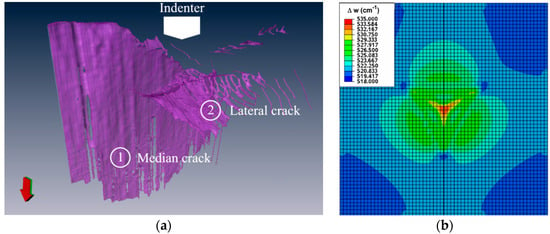
Figure 7.
(a) 3D reconstruction of subsurface cracks corresponding to a 120 mN Berkovich indent, showing: one of the three median cracks (1); and a lateral crack (2). (b) Simulation of the shift of the UV Raman TO phonon line for a 150 mN indent without cohesive elements.
Due to the high strain sensitivity of X-ray diffraction imaging, the localized symmetry breaking is not reflected in the geometry of the X-ray images of the strain fields around the indents. The X-ray images form at typically 30 μm distance from the indent where the strain level is relatively low and the long range strain field is still nearly symmetric. When breakout occurs, the long range strain field falls in magnitude and the X-ray contrast begins to occur at a smaller distance from the indent. It does not, however, significantly change its symmetry (Figure 2a). The line of zero contrast, perpendicular to the diffraction vector direction, arises because the contrast only arises from displacement components in the diffraction vector direction. Along the horizontal line through the centre of the indent, the strain field is entirely in the horizontal direction; there is no component in the diffraction vector direction. There is thus no contrast along this line, giving rise to the two lobes in the image. The difference between the image widths parallel and perpendicular to the diffraction vector arises from a diffraction contrast effect. The diffraction vector lies in the incidence plane, which also includes the entrance and exit beams. So-called “direct” or “kinematical” contrast [14], such as seen here, forms at a point when the effective misorientation of the deformed lattice exceeds the perfect crystal diffraction, or Darwin, width. For deformation greater than this, the region selects a slightly different wavelength which diffracts kinematically and additional intensity appears locally in the image. However, the X-ray beams from this region have a different Bragg angle and the diffracted wave therefore travels in a different direction in space. Due to the large distance, typically 300–400 mm, between the sample and detector, the image is spread out as the propagation distance increases. No such magnification takes place in the direction perpendicular to the incidence plane (or diffraction vector) and hence there is a difference in the width in the two directions. The absence of change in the dimensions of the image as the indenter orientation is changed confirms the symmetry of this long range strain field. The magnitude of the strain field at the edge of the image is determined by the perfect crystal reflecting range. For a wavelength of 0.0506 nm and the 220 reflection, the Darwin width Δθ is 1.58 arc seconds, i.e., 7.6 × 10−6 radians. At the point of high symmetry parallel to the diffraction vector the lattice plane tilt is zero and the strain e is given by
where θB is the Bragg angle, d is the crystal lattice spacing and Δd is the lattice displacement. Thus, the X-ray diffraction images show quantitatively that, at a distance of typically some 20 μm from the indent, the associated strain is 6 × 10−5.
An interesting feature in all three diffraction images of Figure 2a is the central dark circular region. This does not have a line of no contrast perpendicular to the diffraction vector, indicating that the strain displacement field is not radial, as at larger distance from the indent. We have already noted that, in the micro-Raman images close to the indent (Figure 3), the strain field switches from tensile to compressive as a function of distance from the indent centre. There must therefore be a region of zero displacement around the indent and this gives rise to the circle of zero contrast between the outer dark lobes and the inner dark circular disc in the X-ray image. As the X-ray beam passes through the region of intense tensile strain, which is almost twice the magnitude of the maximum compressive strain, it must experience components of displacement in the diffraction vector direction along the central line, thus giving no line of zero contrast in this central part of the image. The central component of the image is not seen in the reflection geometry [9] due to the low penetration of the X-ray beam below the surface and hence not being scattered by the tensile strained region.
As was pointed out by Tang et al. [15], discontinuity in the unloading curve referred to as pop-out, does not signify the appearance of cracks and the 3D reconstructions from all samples studied showed the presence of lateral as well as median cracks (Figure 7a). During the loading stage, below the indenter, normal diamond cubic structure Si-I phase material is transformed to the metallic β-Sn phase Si-II. On subsequent unloading, the transformation of the Si-II phase to body centre cubic (bc8) Si-III and rhombohedral (r8) Si-XII phases is associated with the pop-out phenomenon, though the size and position of the discontinuity is related to the maximum load and the unloading rate [16]. In all indents at and above 150 mN load, below which the stress level was apparently not sufficient to transform Si-I to Si-II on loading, micro-Raman spectra taken after indentation reveal lines attributable to the Si-III and Si-XII phases. Our loading/unloading data are entirely consistent with previous work [17,18]. Further, in all samples thinned and studied by scanning transmission electron microscopy, we have observed a region of plastic deformation below the indent [9] such as has been associated [19,20] with the pop-in discontinuities which we also observed during loading.
The factor of four reduction in the maximum compressive stress and the loss of the tensile stress below the indenter point, following high temperature annealing, is associated with nucleation of dislocation loops from the indentation site at temperatures where Si is ductile [21]. As illustrated in the X-ray section topograph in Figure 8a, taken with a 15 μm wide entrance slit, the dislocation loops lie on the inclined {111} slip planes and propagate right through the 750 μm thick wafer. Depending on the profile of the temperature gradients within the annealing furnace, the loops propagate in one or both of the two orthogonal <011> directions in the wafer plane. The loops subsequently thicken into slip bands by a process of cross-slip, the early stages of which are illustrated in Figure 8b. Dislocation nucleation and propagation relieves the short range stress around the indent, imaged in the micro-Raman profiles.
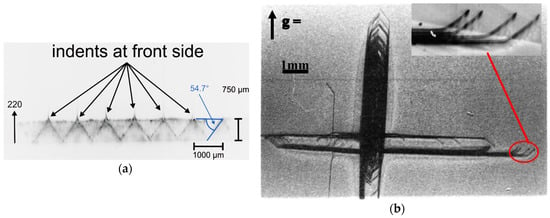
Figure 8.
(a) X-ray section topograph of slip dislocations generated on {111} glide planes from surface indentations upon annealing. (b) X-ray diffraction image of the early stages of cross slip leading to thickening of the dislocation loops into a slip band and nucleation of the orthogonal slip systems.
An example of how very quickly the individual X-ray diffraction images of dislocations become indistinguishable during the process of slip band development is given in Figure 9. This shows two indents of the same load of 500 mN, close to the bevel edge, following an anneal for 60 s at 1000 °C. (The varying thickness on the bevel gives rise to the almost horizontal thickness fringes at the top of the image, this being a well-known dynamical X-ray diffraction effect.) The indent A on the left, probably having experienced a stronger temperature gradient, has a well-developed slip band within which, although some dislocations can still just be resolved, most dislocation images cannot be individually distinguished. In contrast, the slip band development in the right hand image B is much less developed and the operation of a source of dislocation loops can be identified. As the loop expands, driven by the stress around the indent and the thermal gradient in the furnace, the 60° segment parallel to the interface glides out of the crystal and the screw and other 60° segments glide on the inclined {111} slip planes. The dislocation images are narrow where the dislocation intersects the exit surface of the wafer with respect to the X-ray beam and the elegant interference fringes that decorate the broadening image of the dislocation towards the X-ray entrance surface constitute the so-called intermediary image. This is a dynamical diffraction effect sometimes seen under conditions of moderate absorption, such as here. The dislocation loop originating from C, and interfering with the development of the slip band from indent B, arises from handling damage on the wafer surface. It has very similar characteristics to the effect of the indents, generating its own loop system that is developing into a slip band.

Figure 9.
X-ray diffraction image of early stage slip band generation from two adjacent indents close to the bevel edge of the wafer.
Breakout results from the intersection of the lateral cracks with the surface and exploitation of the symmetry-breaking of the bevel edge enabled us to generate millimetre length cracks into the 200 mm wafers in a controlled manner. These cracks resembled those produced by misaligned handling tools [4] and we have shown elsewhere how analysis of the ratio of the crack length to the width of the X-ray image at the crack tip provides a predictor of the probability of failure during subsequent high temperature processing [4]. The near-edge indentation technique has proven to be a satisfactory method for generating such cracks, an example of which is shown in Figure 10. This is a full X-ray diffraction image of a 200 mm wafer which was indented at both the left and right edges through the centre line of the wafer. The left hand indent did not generate a macroscopic crack, as full breakout did not occur, and the strain field in the X-ray image is localized. The right hand indent, also a 5 N Vickers indent, generated a crack of length 15 mm and the strain image extends over a similarly large radius. It is of interest to note that, because the ratio κ of the crack length (L) to the width of the X-ray image at the crack tip (D) is small, this particular crack was benign. We have shown elsewhere that, by modelling the crack as a super-dislocation, the width of the X-ray image provides a quantitative measure of the back stress which counters the opening and propagation of a crack [4]. A narrow image width D indicates a small back stress, potentially leading to an unstable crack. Using the Griffith criterion, it is straightforward to show that when κ exceeds a critical value κc, i.e., when
the crack will propagate during processing at high temperatures. Whether a particular crack is, or is not, benign depends on the temperature profile of the specific furnace and calibration is necessary to determine relevant κc in order to use the model predictively.
κ = L/D > κc

Figure 10.
X-ray diffraction image, taken on a prototype of the Bruker/Jordan Valley QCTT wafer imaging tool, of two edge indents, one (A) of which generated a macroscopic crack in the 200 mm diameter wafer (right) and one (B, arrowed) which did not nucleate such a crack (left).
The upper crack shown in Figure 6b was similarly benign due to its low κ value, but the lower and longer of the two cracks resulted in wafer fracture. Although not shown here, the image of the tip of the lower crack is very narrow and as the crack is long, the κ value is high. Under the particular annealing conditions, κ > κc and the wafer fractured.
4. Materials and Methods
All experiments were performed on (100) oriented, integrated circuit quality, dislocation-free, 200 mm diameter silicon wafers purchased from Y Mart Inc, Palm Beach Gardens, FL, USA. Wafers were within 0.2° of (100) orientation. The nominally defect-free, double side polished, p-type wafers had resistivity below 10 ohm mm, and were of thickness 725 (±25) μm. No edge defects were visible either under optical inspection or in X-ray diffraction images of the as-received wafers, which had been packed and shipped in standard cassettes.
Two pieces of indentation equipment were used to generate controlled damage on silicon. The first was a Nanoindenter® II from Agilent (formerly Nano Instruments Inc., Oak Ridge, TN, USA), used to indent at low loads (100 mN to 600 mN), and the second was a Mitutoyo AVK-C2 hardness tester (Mitutoyo, Kawasaki, Japan) used for application of heavier loads from 500 mN up to 50 N. A Berkovich tip, was used with the Nanoindenter® II. It was a three-sided diamond pyramid with each face making an angle of 65.35° with the indenter axis, with a total included angle of 142.3°. The Mitutoyo AVK-C2 had a Vickers tip which was a four sided diamond pyramid, with a total included angle of 136°, but the same projected area-to-depth as the Berkovich indenter. All indents were performed at room temperature.
Micro-Raman spectroscopy was used to measure the strain and crystalline damage as well as high pressure phase transformations produced by the nano-indentation. The system used in this study was a Horiba Jobin-Yvon HR800® system (Horiba, Kyoto, Japan) running LabSpec 5 software (Horiba, Kyoto, Japan) and integrated with a microscope coupled confocally to an 800 mm focal length spectrometer (Figure 11a). Samples were mounted on a high precision table capable of x-y and z translation. An autofocusing system was incorporated. A diffraction grating of 1800 groves per millimetre was used to split the Raman signal into individual wavelengths, which were then directed onto a CCD detector. The HR800 uses two different CCD detectors; an air cooled Synapse CCD system and a liquid nitrogen cooled CCD3000 system used for acquisition times of greater than 120 s. Three lasers are connected to the Raman system through a periscope: a Uniphase 2014 488 nm Argon ion (Ar+) visible laser with a maximum output power of 20 mW, a Spectra-Physics Stablite 2017 364 nm Ar+ UV laser with a max. output power of 100 mW and a Kimmon Koha IK3201IR-F 325 nm Helium Cadmium (He-Cd) ultraviolet (UV) laser with a max. output power of 22.4 mW. The output light was linearly polarized.

Figure 11.
(a) Microscope lenses attached to the LabRam® HR800 System. The sample under test typically sits on a glass microscope slide below the objective lens. (b) Internal light paths for LabRam® HR800 System. The red line shows the path of the laser beam, while the green line shows the path of the Raman scattered beam.
For the μRS measurements, a backscattering geometry was used. In this configuration, a microscope objective is used to focus the beam onto the sample surface and the system is equipped with a number of lenses allowing different optical magnifications and can produce spot sizes as small as 1–3 µm in diameter (Figure 11a). Scattered light is collected through the same objective and passes through a beam splitter and is focused on to the entrance slit of the spectrometer which disperses the light onto one of the CCD detectors (Figure 11b). The use of a flip mirror enables the specimen under the microscope objective to be visualised using a small camera, which is particularly useful for precise positioning of the laser beam onto the area of interest.
The spectrometer was centred on the Raman line of the TO Raman phonon peak shift for unstrained silicon at 520.07 cm−1 [22]. There was no detectable asymmetry in the unstressed Si lineshapes. Assuming the strain in the indented silicon to be biaxial, the stress components σxx and σyy are equal and related to the spectral line shift by [22]
where is the wavenumber (in cm−1) of the unstrained Raman spectral line of the Si-Si transverse optical (TO) phonon and is that of the measured Raman spectral line of the sample. Long scans required for 2D Raman maps can take from a number of hours to a number of days to complete. To compensate for temperature and laser stability, the plasma lines of the laser were recorded as fidiucal markers over the entire duration of the scan. The laser plasma lines are Rayleigh scattered and thus are insensitive to any strain in the sample [22]. The Ar+ laser was used to create the maps of Figure 3 and Figure 4.
In addition, as the laser is focused to a spot of ~1–3 µm in diameter, localised heating can arise. Any associated thermal expansion in the silicon can cause the Raman TO phonon to shift to move to a lower energy (at a rate of ~0.025 cm−1/K), erroneously implying the presence of a tensile strain. However, this shift [23] is smaller than the resolution of the spectrometer used in this study, which was ~0.3 cm−1.
X-ray diffraction imaging was performed in white beam mode at the TOPO-TOMO beamline at the ANKA synchrotron radiation source at Karlsruhe, Germany and at beamline B16 of the Diamond Light Source at Didcot, Oxford, U.K. At ANKA, transmission images were recorded on a CCD camera optically coupled to a macroscope and with a Lu3Al5O12 scintillator. The effective pixel size of the detection system was 2.5 × 2.5 μm. At the Diamond Light Source, transmission images were recorded with a CCD camera manufactured by PCO. Imaging GmbH, Kelheim, Germany, which has 4008 × 2672 pixels and a 14 bit dynamic range. Scintillators and objective lenses were chosen such that the pixel size effective (binned) was 2 μm. Data acquisition times were between 10 and 40 s. All transmission diffraction images were taken with the 022 reflection, oriented such that there was a principal wavelength of 0.0506 nm. Further details of the ANKA instrumentation can be found in reference [24].
Scanning electron microscopy (SEM) was performed on a field emission electron microscope (LEO 1525, Leo Electron Microscopy Inc., Thornwood, NY, USA) with an in-lens secondary electron backscattering detector. A Quanta 3D dual beam FIB (focused ion beam) from FEI, Hillsboro, OR, USA, which incorporates FEGSEM (field emission gun scanning electron microscopy) and FIB cannons, was used to make microscopic observations of cracks around indents as the specimen was FIB milled down. The electron and ion beam cannons form an angle of 52° to each other. The instrument incorporated SE (secondary electron), BS (backscattered electron) and STEM (scanning transmission). From the FIB cross sections, three-dimensional reconstruction of the cracks was achieved using Amira reconstruction software. Simulation of the crack geometry was performed using the commercial software ABAQUS (version 6.8-3, Dassault Systemes, Vélizy-Villacoublay, France). The code incorporates a cohesive zone model and a simple triangular relation between stress and crack face separation was used. Conversion of stress to Raman shift was done using Equation (3).
5. Conclusions
Micro-Raman and X-ray diffraction imaging both provide maps of the strain field around indentations but on substantially different length scales. In particular, the symmetry associated with the indenter profile is lost in the X-ray images whereas the micro-Raman maps reveal in detail not only the magnitude and sense of the strain field but also its detailed symmetry. This is particularly revealing when breakout occurs. On annealing, the strain field maximum moves away from the site of the indent due to the formation of a series of dislocation loops, which are the precursors of slip bands. By exploiting the symmetry breaking of the bevelled edge of the wafer, i.e., by indentation close to the wafer edge, we have been able to generate macroscopic cracks in 200 mm wafer in a controlled, though not always predictable, manner.
Acknowledgments
Financial support was provided through the European Community FP7 STREP project SIDAM (Grant No. FP7-ICT-216382). Technical support from Kawal Sawhney, Igor Dolbnya and Andrew Malandain at beamline B16 of the Diamond Light Source and P. Vagovic, T. dos Santos Rolo and H. Schade at ANKA (Angströmquelle Karlsruhe) is gratefully acknowledged. Thanks are extended to Keith Bowen for valuable discussions and initially conceiving the SIDAM project. Funds for open access publication came from Dublin City University.
Author Contributions
Brian K. Tanner, Reyes M. Elizalde, Patrick J. McNally and Andreas N. Danilewsky collaboratively conceived and supervised the experiments within the research programme framework, which was coordinated by Brian K. Tanner; Jorge Garagorri performed most of the indentations; David Allen undertook micro-Raman analysis; Eider Gorostegui-Colinas made finite element simulations of the strain fields; Brian K. Tanner, Patrick J. McNally, Andreas N. Danilewsky, David Allen and Jochen Wittge undertook X-ray diffraction imaging experiments; and Brian K. Tanner wrote the first draft of the paper.
Conflicts of Interest
The authors declare that there are no conflicts of interest.
References
- Chen, P.Y.; Tsai, M.H.; Yeh, W.K.; Jing, M.H.; Chang, Y. Investigation of the relationship between whole-wafer strength and control of its edge engineering. Jpn. J. Appl. Phys. 2009, 48, 126503. [Google Scholar] [CrossRef]
- Chen, P.Y.; Tsai, M.H.; Yeh, W.K.; Jing, M.H.; Chang, Y. Relationship between wafer edge design and its ultimate mechanical strength. Microelectron. Eng. 2010, 87, 2065–2070. [Google Scholar] [CrossRef]
- Atrash, F.; Meshi, I.; Krokhmal, A.; Ryan, P.; Wormington, M.; Sherman, D. Crystalline damage in silicon wafers and ‘rare event’ failure introduced by low-energy mechanical impact. Mater. Sci. Semicond. Process. 2017, 63, 40–44. [Google Scholar] [CrossRef]
- Tanner, B.K.; Fossati, M.C.; Garagorri, J.; Elizalde, M.R.; Allen, D.; McNally, P.J.; Jacques, D.; Wittge, J.; Danilewsky, A.N. Prediction of the propagation probability of individual cracks in brittle single crystal materials. Appl. Phys. Lett. 2012, 101, 041903. [Google Scholar] [CrossRef]
- Tanner, B.K.; Garagorri, J.; Gorostegui-Colinas, E.; Elizalde, M.R.; Bytheway, R.; McNally, P.J.; Danilewsky, A.N. The geometry of catastrophic fracture during high temperature processing of silicon. Int. J. Fract. 2015, 195, 79–85. [Google Scholar] [CrossRef]
- Yan, J.; Tamaki, J.; Zhao, H.W.; Kuriyagawa, T. Surface and subsurface damages in nanoindentation tests of compound semiconductor InP. J. Micromech. Microeng. 2008, 18, 105018. [Google Scholar] [CrossRef]
- Tanaka, M.; Higashida, K.; Nakashima, H.; Takagi, H.; Fujiwara, M. Orientation dependence of fracture toughness measured by indentation methods and its relation to surface energy in single crystal silicon. Int. J. Fract. 2006, 139, 383–394. [Google Scholar] [CrossRef]
- Bowen, D.K.; Tanner, B.K. X-ray Metrology in Semiconductor Manufacturing; CRC Press: Boca Raton, FL, USA, 2006; pp. 279–290. [Google Scholar]
- Tanner, B.K.; Garagorri, J.; Gorostegui-Colinas, E.; Elizalde, M.R.; Allen, D.; McNally, P.J.; Wittge, J.; Ehlers, C.; Danilewsky, A.N. X-ray asterism and the structure of cracks from indentations in silicon. J. Appl. Cryst. 2016, 49, 250–259. [Google Scholar] [CrossRef]
- Tanaka, M.; Higashida, K.; Nakashima, H.; Takagi, H.; Fujiwara, M. Fracture toughness evaluated by indentation methods and its relation to surface energy in silicon single crystals. Mater. Trans. 2003, 44, 681–684. [Google Scholar] [CrossRef][Green Version]
- Tanaka, M.; Higashida, K.; Nakashima, H.; Takagi, H.; Fujiwara, M. Orientation dependence of fracture toughness and its relation to surface energy in Si crystals. J. Jpn. Inst. Met. 2004, 68, 787–791. [Google Scholar] [CrossRef]
- Rack, A.; Scheel, M.; Danilewsky, A.N. Real-time direct and diffraction X-ray imaging of irregular silicon wafer breakage. IUCrJ 2016, 3, 108–114. [Google Scholar] [CrossRef] [PubMed]
- Garagorri, J. Prediction of Critical Damage in Silicon Wafer during Rapid Thermal Processing. Ph.D. Thesis, University of Navarra, San Sebastian, Spain, 2014. [Google Scholar]
- Bowen, D.K.; Tanner, B.K. High Resolution X-ray Diffraction and Topography; Taylor and Francis: London, UK, 1998; pp. 252–262. [Google Scholar]
- Tang, Y.; Yonezu, A.; Ogasawara, N.; Chiba, N.; Chen, X. On radial crack and half-penny crack induced by Vickers indentation. Proc. R. Soc. Lond. A 2008, 464, 2967–2984. [Google Scholar] [CrossRef]
- Chang, L.; Zhang, L.C. Deformation mechanisms at pop-out in monocrystalline silicon under nanoindentation. Acta Mater. 2009, 57, 2148–2153. [Google Scholar] [CrossRef]
- Bradby, J.E.; Williams, J.S.; Wong-Leung, J. Transmission electron microscopy observation of deformation microstructure under spherical indentation in silicon. Appl. Phys. Lett. 2000, 77, 3749–3751. [Google Scholar] [CrossRef]
- Gerbig, Y.B.; Stranick, S.J.; Morris, D.J.; Vaudin, M.D.; Cook, R.F. Effect of crystallographic orientation on phase transformations during indentation of silicon. J. Mater. Res. 2009, 24, 1172–1183. [Google Scholar] [CrossRef][Green Version]
- Bradby, J.E.; Williams, J.S.; Wong-Leung, J.; Swain, M.V.; Munroe, P. Mechanical deformation in Silicon by micro-indentation. J. Mater. Res. 2001, 16, 1500–1507. [Google Scholar] [CrossRef]
- Bradby, J.E.; Williams, J.S.; Swain, M.V. In situ electrical characterization of phase transformations in Si during indentation. Phys. Rev. B 2003, 67, 085205. [Google Scholar] [CrossRef]
- Wittge, J.; Danilewsky, A.N.; Allen, D.; McNally, P.; Li, Z.; Baumbach, T.; Gorostegui-Colinas, E.; Garagorri, J.; Elizalde, M.R.; Jacques, D.; Fossati, M.C.; et al. Dislocation sources and slip band nucleation from indents on silicon wafers. J. Appl. Cryst. 2010, 43, 1036–1039. [Google Scholar] [CrossRef]
- De Wolf, I. Micro-Raman spectroscopy to study local mechanical stress in silicon integrated circuits. Semicond. Sci. Technol. 1996, 11, 139–154. [Google Scholar] [CrossRef]
- Dombrowski, K.F. Micro-Raman Investigation of Mechanical Stress in Si Device Structures and Phonons in SiGe. Ph.D. Thesis, Brandenburg University of Technology, Cottbus-Senftenburg, Germany, 2000; p. 24. [Google Scholar]
- Danilewsky, A.N.; Wittge, J.; Hess, A.; Cröll, A.; Rack, A.; Allen, D.; McNally, P.J.; dos Santos Rolo, T.; Vagovic, P.; Baumbach, T.; et al. Real-time X-ray diffraction imaging for semiconductor wafer metrology and high temperature in situ experiments. Phys. Stat. Sol. A 2011, 208, 2499–2504. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).