Longitudinal Near-Field Coupling between Acoustic Resonators Grafted onto a Waveguide
Abstract
1. Introduction
2. Experimental and Numerical Methods
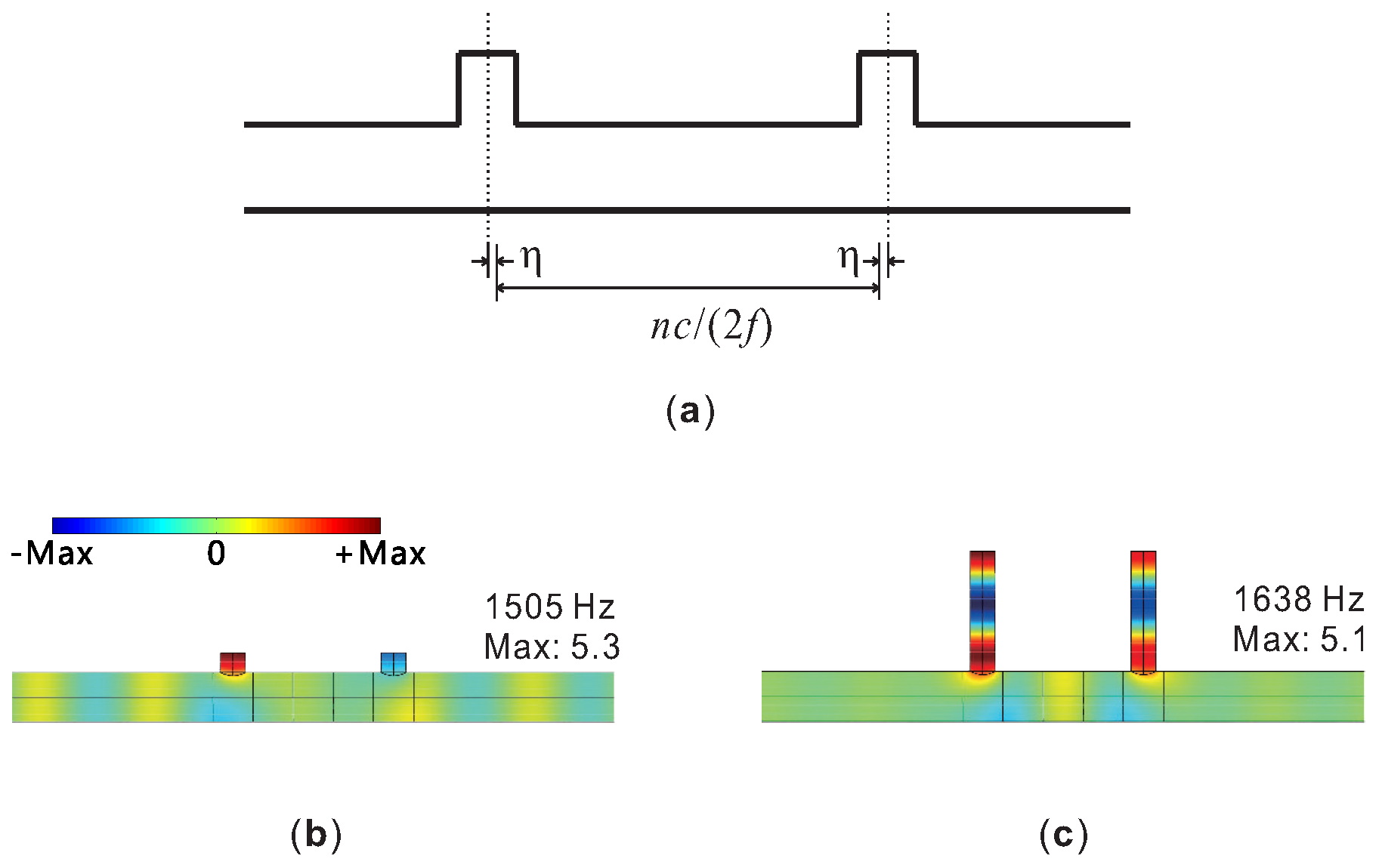
3. Evanescent Waves Originating from a Grafting Point
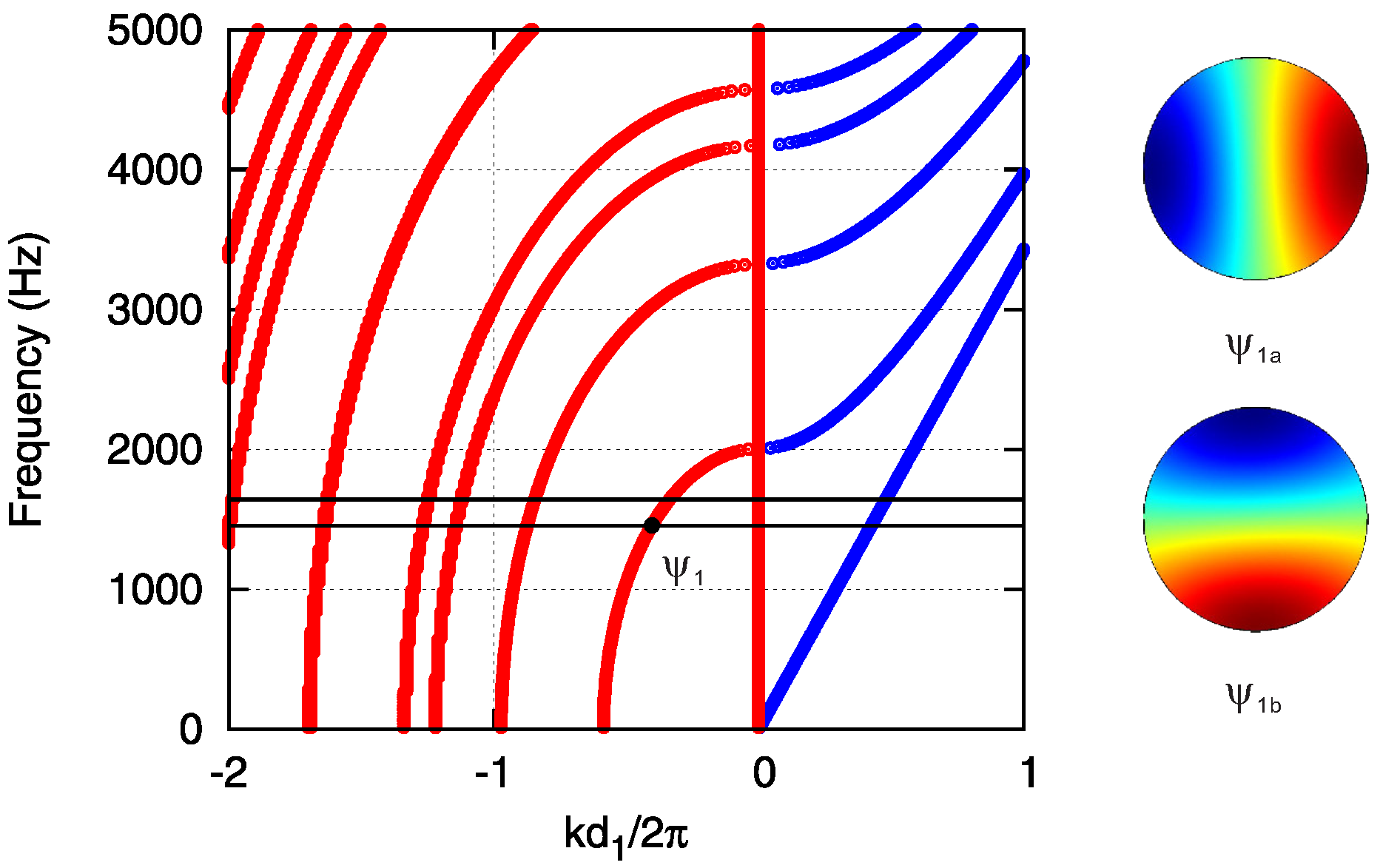
3.1. Guided Evanescent Waves
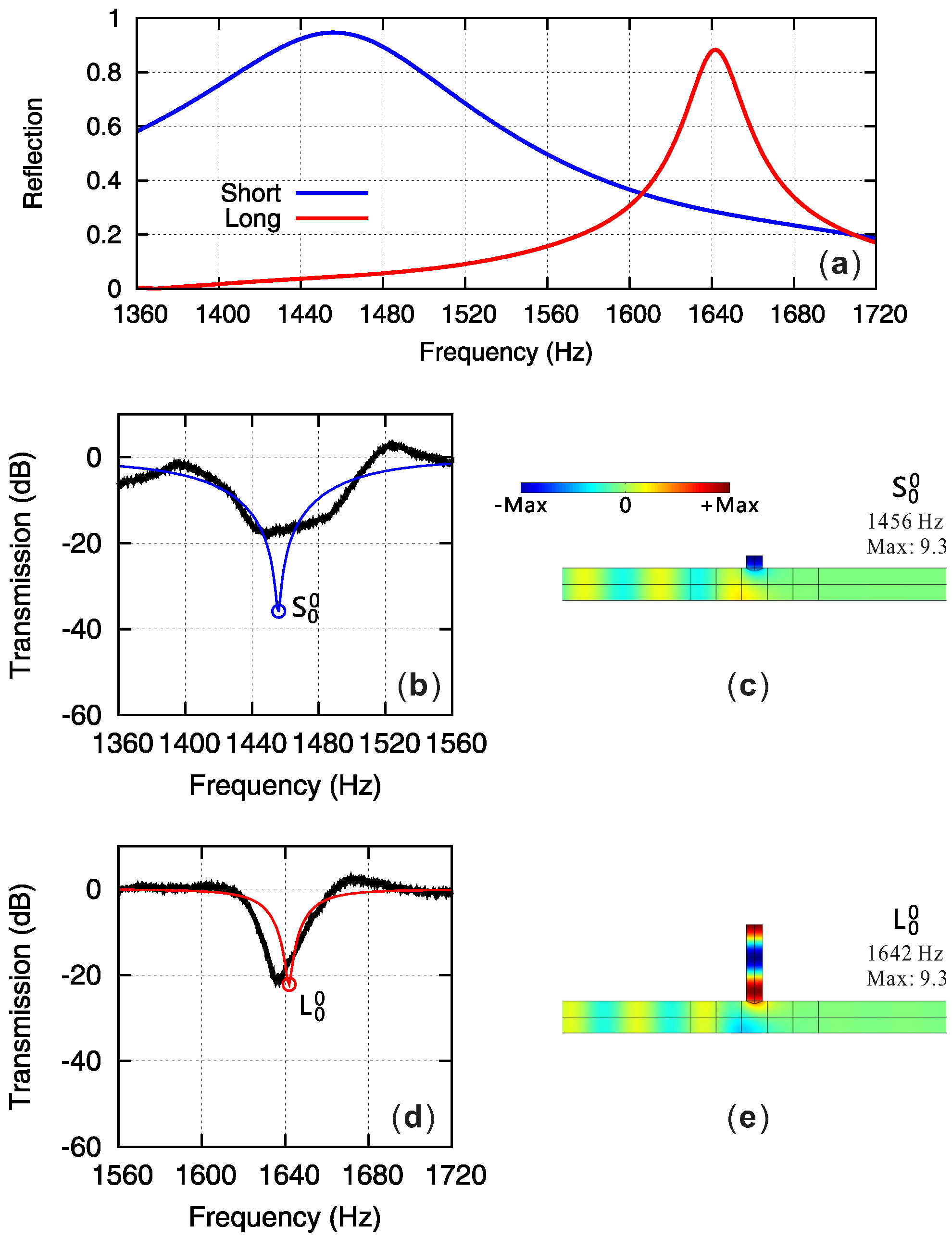
3.2. Single Grafted Tube
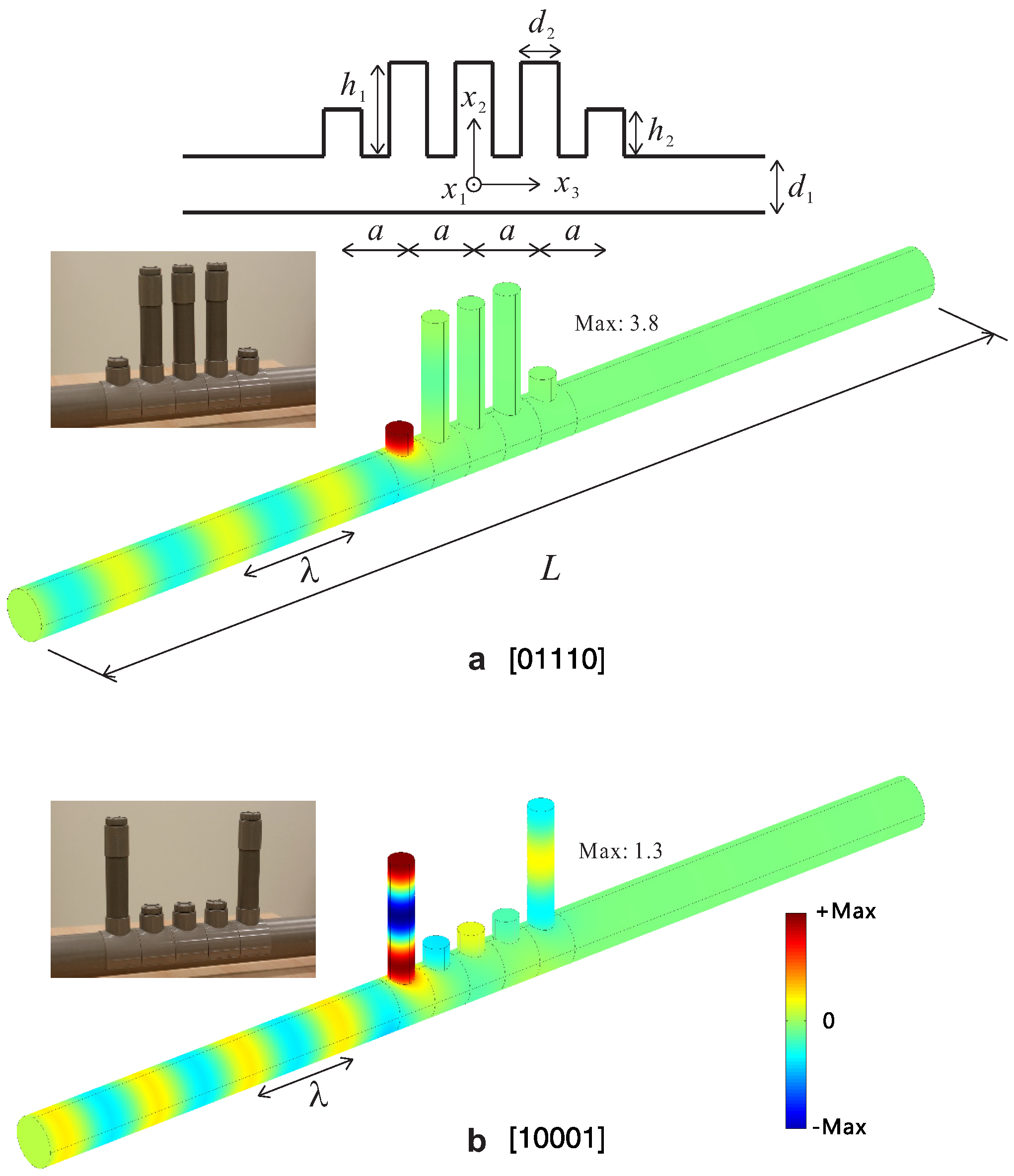
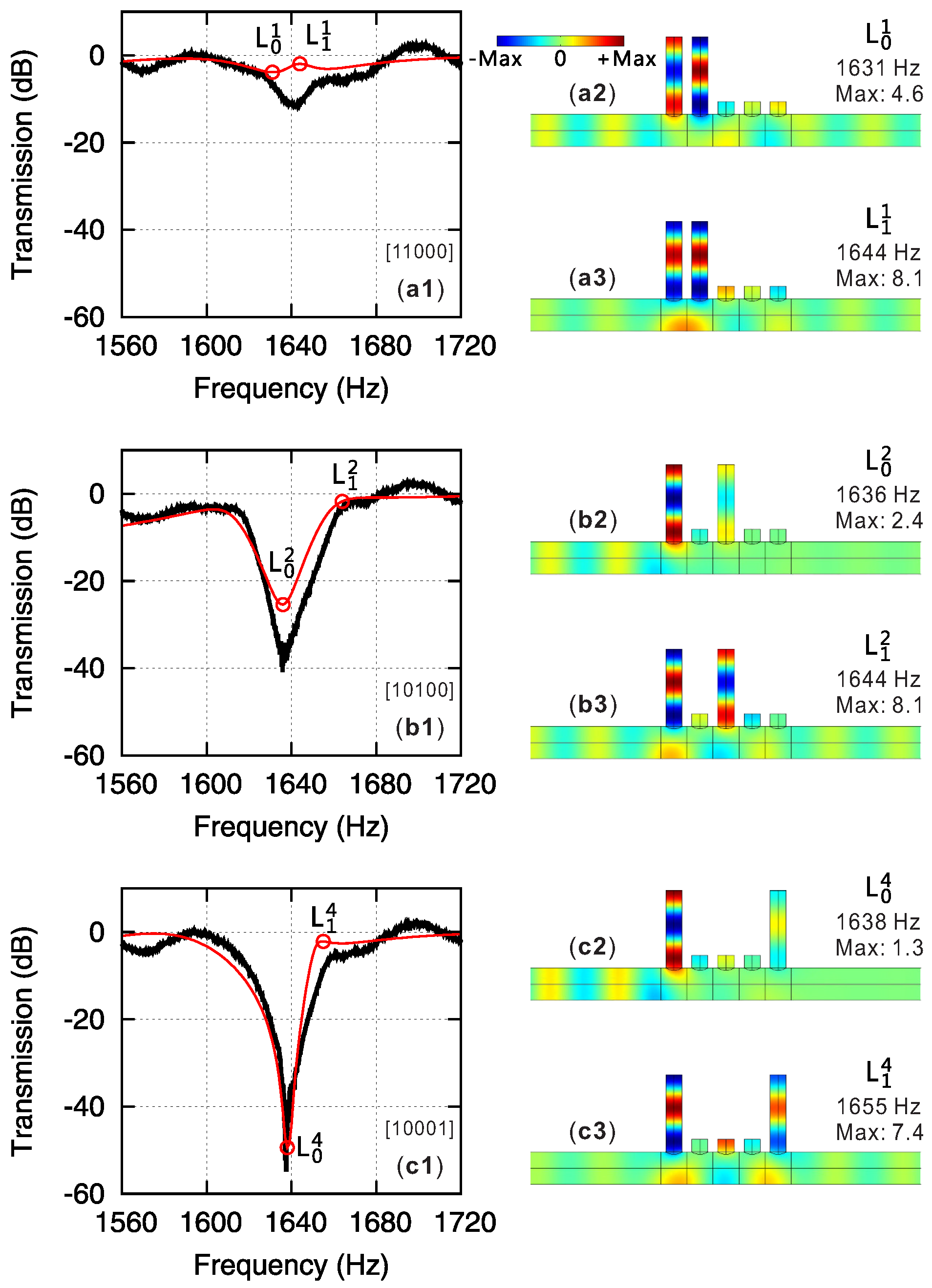
4. Aperiodic Sequences of Resonators
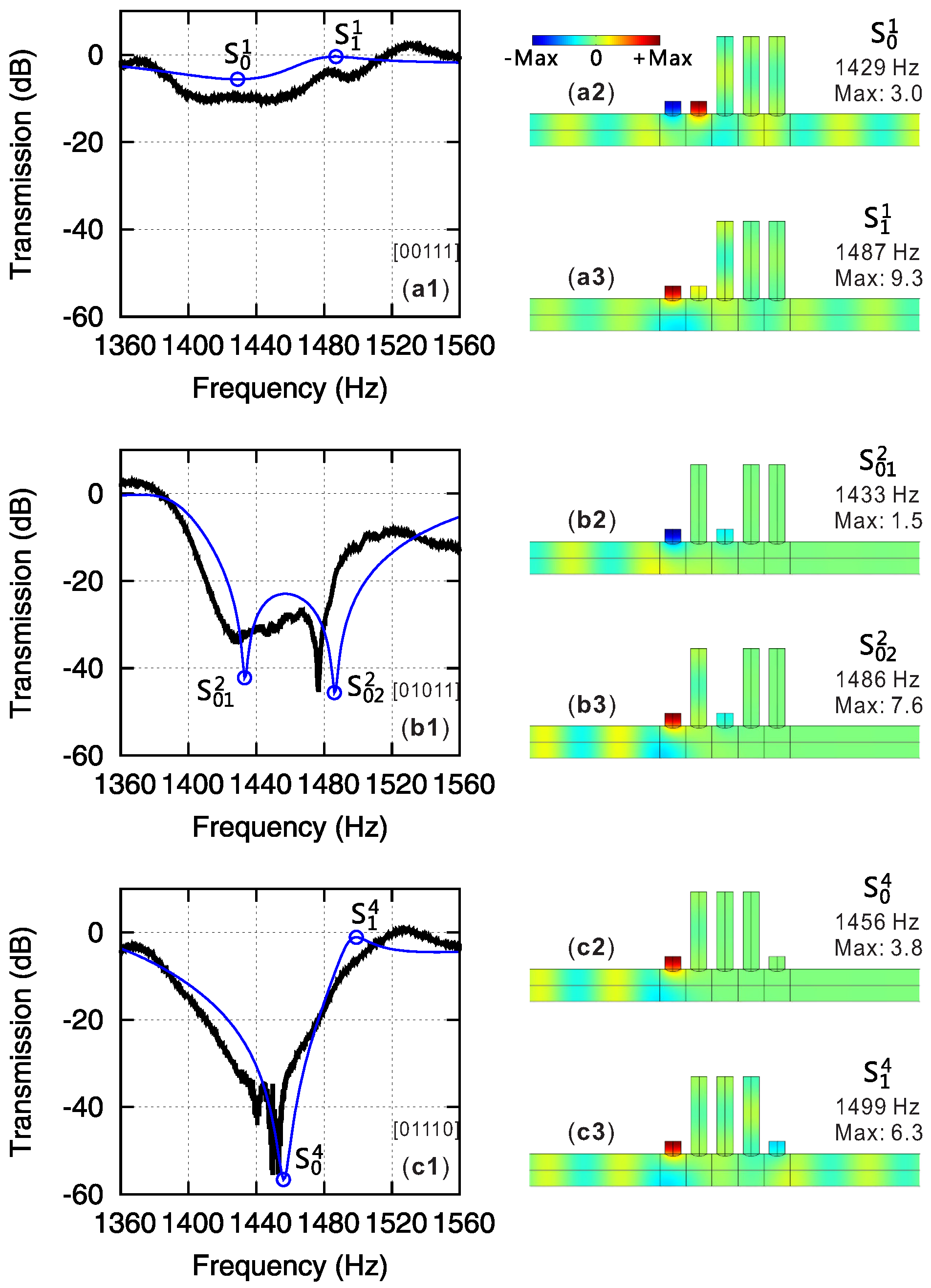
4.1. Near-Field Coupling Regime
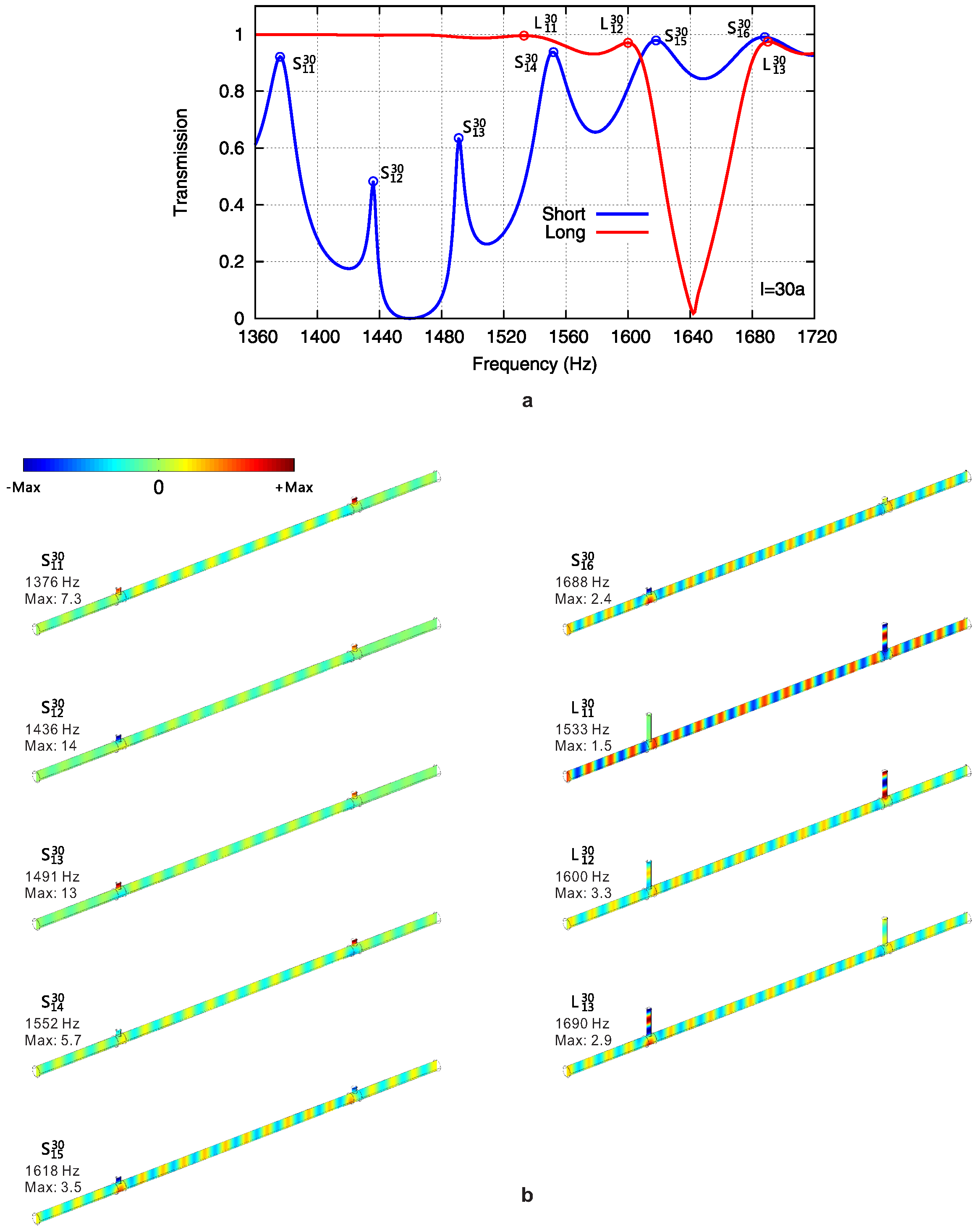
4.2. Locally-Resonant Fabry–Perot Interferometers
4.3. Two Identical Resonators Grafted onto the Waveguide with a Large Separation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Deymier, P.A. (Ed.) Acoustic Metamaterials and Phononic Crystals; Springer: Berlin, Germany, 2013. [Google Scholar]
- Hussein, M.; Leamy, M.; Ruzzene, M. Dynamics of phononic material and structures: Historical origins, recent progess, and future outlook. Appl. Mech. Rev. 2014, 66. [Google Scholar] [CrossRef]
- Popa, B.I.; Cummer, S.A. Non-reciprocal and highly nonlinear active acoustic metamaterials. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef] [PubMed]
- Khelif, A.; Adibi, A. (Eds.) Phononic Crystals; Springer: Berlin, Germany, 2015. [Google Scholar]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.; Yang, Z.; Chan, C.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Lai, Y.; Wu, Y.; Sheng, P.; Zhang, Z. Hybrid elastic solids. Nat. Mater. 2011, 10, 620–624. [Google Scholar] [CrossRef] [PubMed]
- Zhu, R.; Liu, X.; Hu, G.; Sun, C.; Huang, G. Negative refraction of elastic waves at the deep-subwavelength scale in a single-phase metamaterial. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.F.; Wang, Y.S.; Su, X.X. Large bandgaps of two-dimensional phononic crystals with cross-like holes. J. Appl. Phys. 2011, 110. [Google Scholar] [CrossRef]
- Wang, G.; Wen, X.; Wen, J.; Shao, L.; Liu, Y. Two-dimensional locally resonant phononic crystals with binary structures. Phys. Rev. Lett. 2004, 93. [Google Scholar] [CrossRef] [PubMed]
- Elford, D.; Chalmers, L.; Kusmartsev, F.; Swallowe, G. Matryoshka locally resonant sonic crystal. J. Acoust. Soc. Am. 2011, 130, 2746–2755. [Google Scholar] [CrossRef] [PubMed]
- Yilmaz, C.; Hulbert, G.; Kikuchi, N. Phononic band gaps induced by inertial amplification in periodic media. Phys. Rev. B 2007, 76. [Google Scholar] [CrossRef]
- Ma, T.X.; Wang, Y.S.; Wang, Y.F.; Su, X.X. Three-dimensional dielectric phoxonic crystals with network topology. Opt. Express 2013, 21, 2727–2732. [Google Scholar] [CrossRef] [PubMed]
- Pennec, Y.; Djafari-Rouhani, B.; Larabi, H.; Vasseur, J.; Hladky-Hennion, A. Low-frequency gaps in a phononic crystal constituted of cylindrical dots deposited on a thin homogeneous plate. Phys. Rev. B 2008, 78. [Google Scholar] [CrossRef]
- Achaoui, Y.; Khelif, A.; Benchabane, S.; Robert, L.; Laude, V. Experimental observation of locally-resonant and Bragg band gaps for surface guided waves in a phononic crystal of pillars. Phys. Rev. B 2011, 83. [Google Scholar] [CrossRef]
- Fang, N.; Xi, D.; Xu, J.; Ambati, M.; Srituravanich, W.; Sun, C.; Zhang, X. Ultrasonic metamaterials with negative modulus. Nat. Mater. 2006, 5, 452–456. [Google Scholar] [CrossRef] [PubMed]
- Lemoult, F.; Fink, M.; Lerosey, G. Acoustic resonators for far-field control of sound on a subwavelength scale. Phys. Rev. Lett. 2011, 107. [Google Scholar] [CrossRef] [PubMed]
- Feng, T.; Lajnef, N.; Chakrabartty, S. Design of a CMOS system-on-chip for passive, near-field ultrasonic energy harvesting and back-telemetry. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2016, 24, 544–554. [Google Scholar] [CrossRef]
- Mehdizadeh, E.; Piazza, G. Chip-Scale Near-Field Resonant Power Transfer via Elastic Waves. J. Microelectromech. Syst. 2017, 26, 1155–1164. [Google Scholar] [CrossRef]
- Fu, Y.; Liu, A.; Zhu, W.; Zhang, X.; Tsai, D.; Zhang, J.; Mei, T.; Tao, J.; Guo, H.; Zhang, X.; et al. A Micromachined reconfigurable metamaterial via reconfiguration of asymmetric split-Ring resonators. Adv. Funct. Mater. 2011, 21, 3589–3594. [Google Scholar] [CrossRef]
- Liu, N.; Liu, H.; Zhu, S.; Giessen, H. Stereometamaterials. Nat. Photon. 2009, 3, 157–162. [Google Scholar] [CrossRef]
- Powell, D.; Hannam, K.; Shadrivov, I.; Kivshar, Y. Near-field interaction of twisted split-ring resonators. Phys. Rev. B 2011, 83. [Google Scholar] [CrossRef]
- Wang, Y.F.; Laude, V.; Wang, Y.S. Coupling of evanescent and propagating guided modes in locally resonant phononic crystals. J. Phys. D Appl. Phys. 2014, 47. [Google Scholar] [CrossRef]
- Goffaux, C.; Sánchez-Dehesa, J.; Yeyati, A.; Lambin, P.; Khelif, A.; Vasseur, J.; Djafari-Rouhani, B. Evidence of fano-like interference phenomena in locally resonant materials. Phys. Rev. Lett. 2002, 88. [Google Scholar] [CrossRef] [PubMed]
- Miroshnichenko, A.; Flach, S.; Kivshar, Y. Fano resonances in nanoscale structures. Rev. Mod. Phys. 2010, 82, 2257–2298. [Google Scholar] [CrossRef]
- Driscoll, T.; Kim, H.; Chae, B.; Kim, B.; Lee, Y.; Jokerst, N.; Palit, S.; Smith, D.; Di Ventra, M.; Basov, D. Memory metamaterials. Science 2009, 325, 1518–1521. [Google Scholar] [CrossRef] [PubMed]
- Tao, H.; Strikwerda, A.; Fan, K.; Padilla, W.; Zhang, X.; Averitt, R. Reconfigurable terahertz metamaterials. Phys. Rev. Lett. 2009, 103. [Google Scholar] [CrossRef] [PubMed]
- Ou, J.; Plum, E.; Jiang, L.; Zheludev, N. Reconfigurable photonic metamaterials. Nano Lett. 2011, 11, 2142–2144. [Google Scholar] [CrossRef] [PubMed]
- Caleap, M.; Drinkwater, B. Acoustically trapped colloidal crystals that are reconfigurable in real time. Proc. Natl. Acad. Sci. USA 2014, 111, 6226–6230. [Google Scholar] [CrossRef] [PubMed]
| () | n | |||
|---|---|---|---|---|
| 0 | 1 | 2 | 4 | |
| 21.1 @ 1456 Hz | 1 | 0.18 | 0.034 | 0.0012 |
| 25.3 @ 1642 Hz | 1 | 0.13 | 0.017 | 0.0003 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.-F.; Laude, V. Longitudinal Near-Field Coupling between Acoustic Resonators Grafted onto a Waveguide. Crystals 2017, 7, 323. https://doi.org/10.3390/cryst7110323
Wang Y-F, Laude V. Longitudinal Near-Field Coupling between Acoustic Resonators Grafted onto a Waveguide. Crystals. 2017; 7(11):323. https://doi.org/10.3390/cryst7110323
Chicago/Turabian StyleWang, Yan-Feng, and Vincent Laude. 2017. "Longitudinal Near-Field Coupling between Acoustic Resonators Grafted onto a Waveguide" Crystals 7, no. 11: 323. https://doi.org/10.3390/cryst7110323
APA StyleWang, Y.-F., & Laude, V. (2017). Longitudinal Near-Field Coupling between Acoustic Resonators Grafted onto a Waveguide. Crystals, 7(11), 323. https://doi.org/10.3390/cryst7110323








