3.1.1. Three-Dimensional Structure
We first consider the case of a 3D simple cubic (
sc) crystal made of touching D5N35 spheres, with lattice parameter
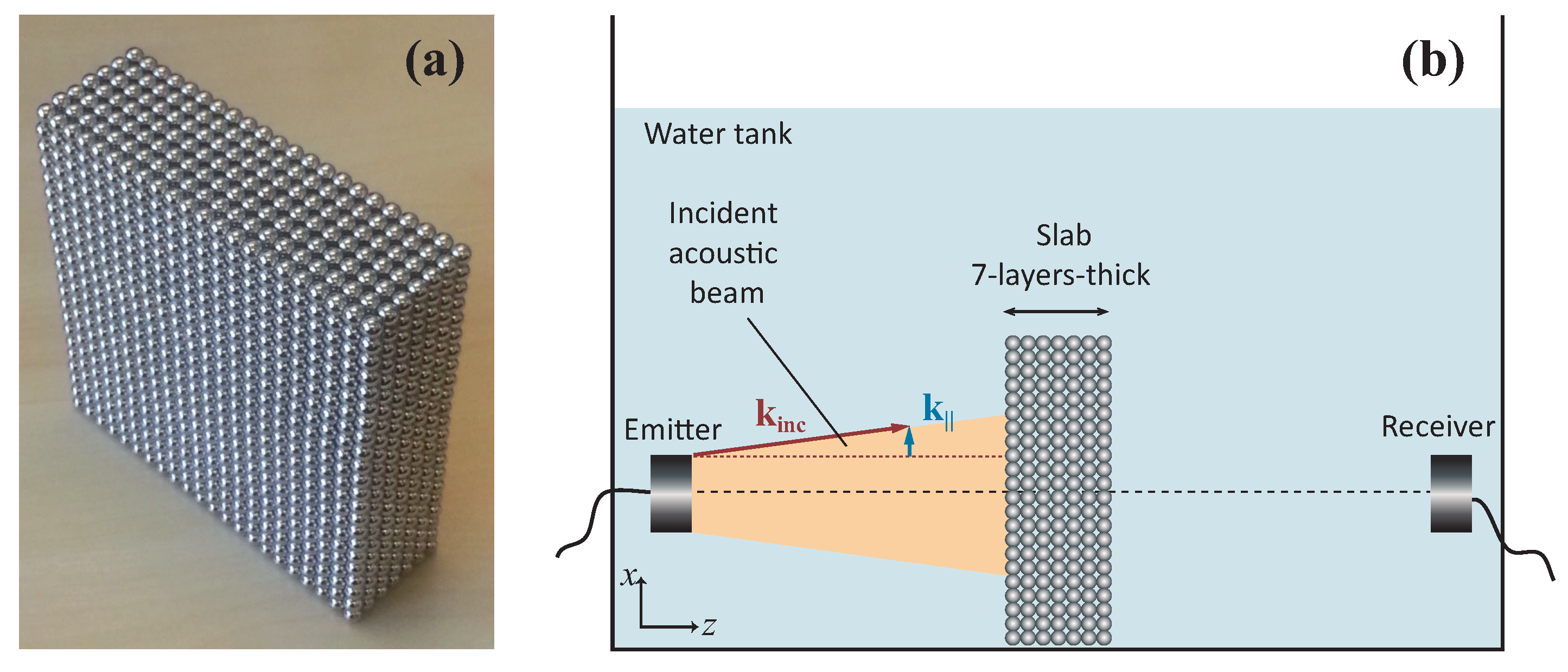
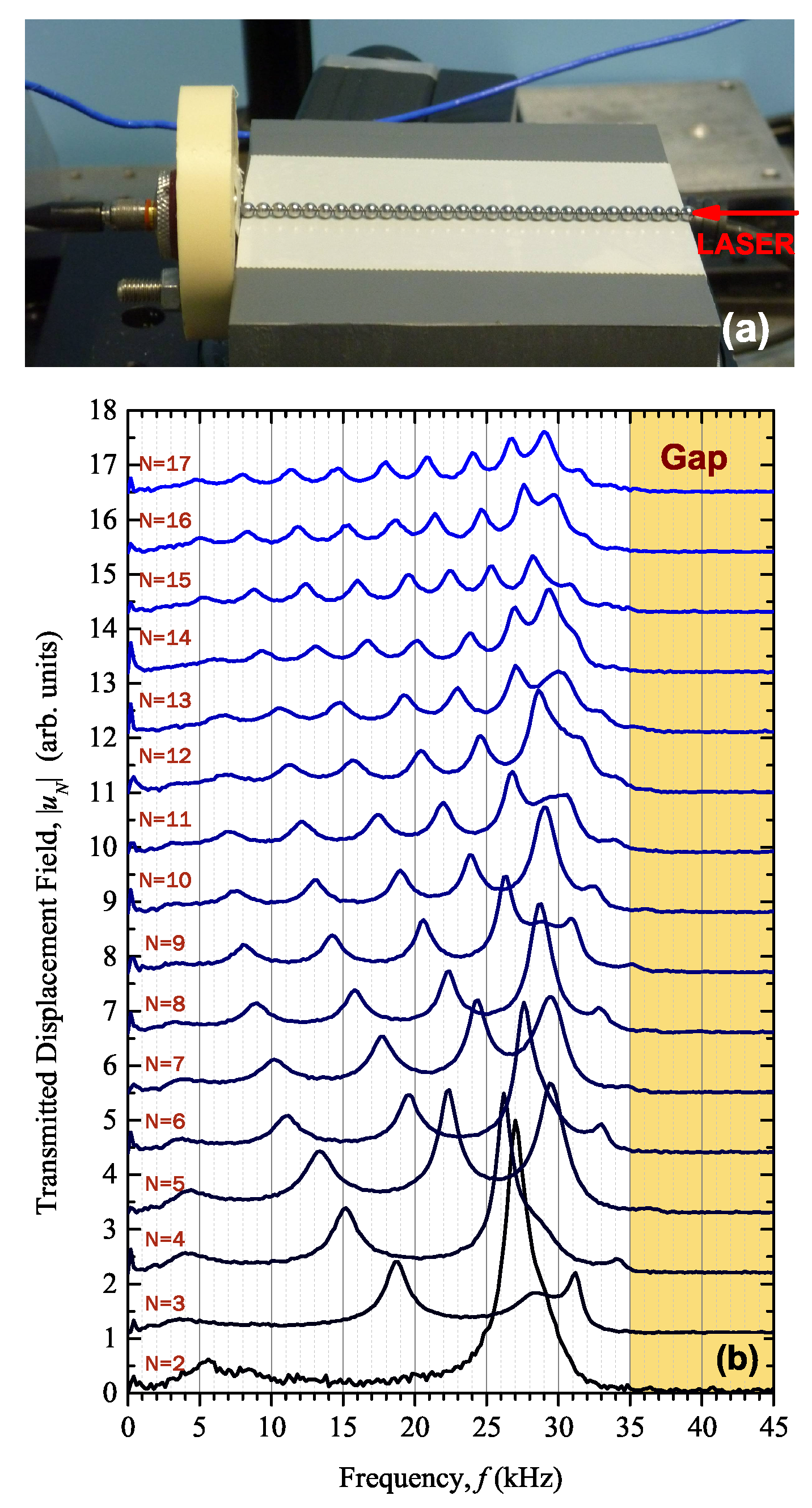
. The finite-size fabricated array, shown in
Figure 1a, is a succession of seven (001)
sc layers of spheres, each one consisting of a square array of
spheres. Magnetic attractive force is used to keep spheres in touch.
To analyze the frequency response of this structure, a standard underwater transmission measurement technique is used in the first stage. The corresponding experimental setup is shown in
Figure 1b. The sample is immersed in water and placed at the bottom of a sufficiently big water tank to optimally delay side-wall reflections. Both emitting and receiving transducers are
broadband
-centered Panametrics immersion transducers (
diameter) (Panametrics, Tokyo, Japan). Each one is located at
from the (001) surface side of the sample, their mean-beam axis passing at the center of the slab and coinciding with the
z-axis, i.e., the incidence is, apart from a symmetric angular spreading, assumed to be in the first order normal to the (001) surface. The emitter transducer is excited by a 5058PR Olympus pulse generator/receiver (Olympus, Tokyo, Japan), providing a
high and
wide electric pulse. The generator acts also as a trigger for a Yokogawa Numeric Oscilloscope (Yokogawa, Tokyo, Japan) recording signals measured by the receiver transducer and amplified by the 5058PR. The transmitted signals, sampled at
and captured within a
duration window, are next averaged using 512 acquisitions in order to minimize noise.
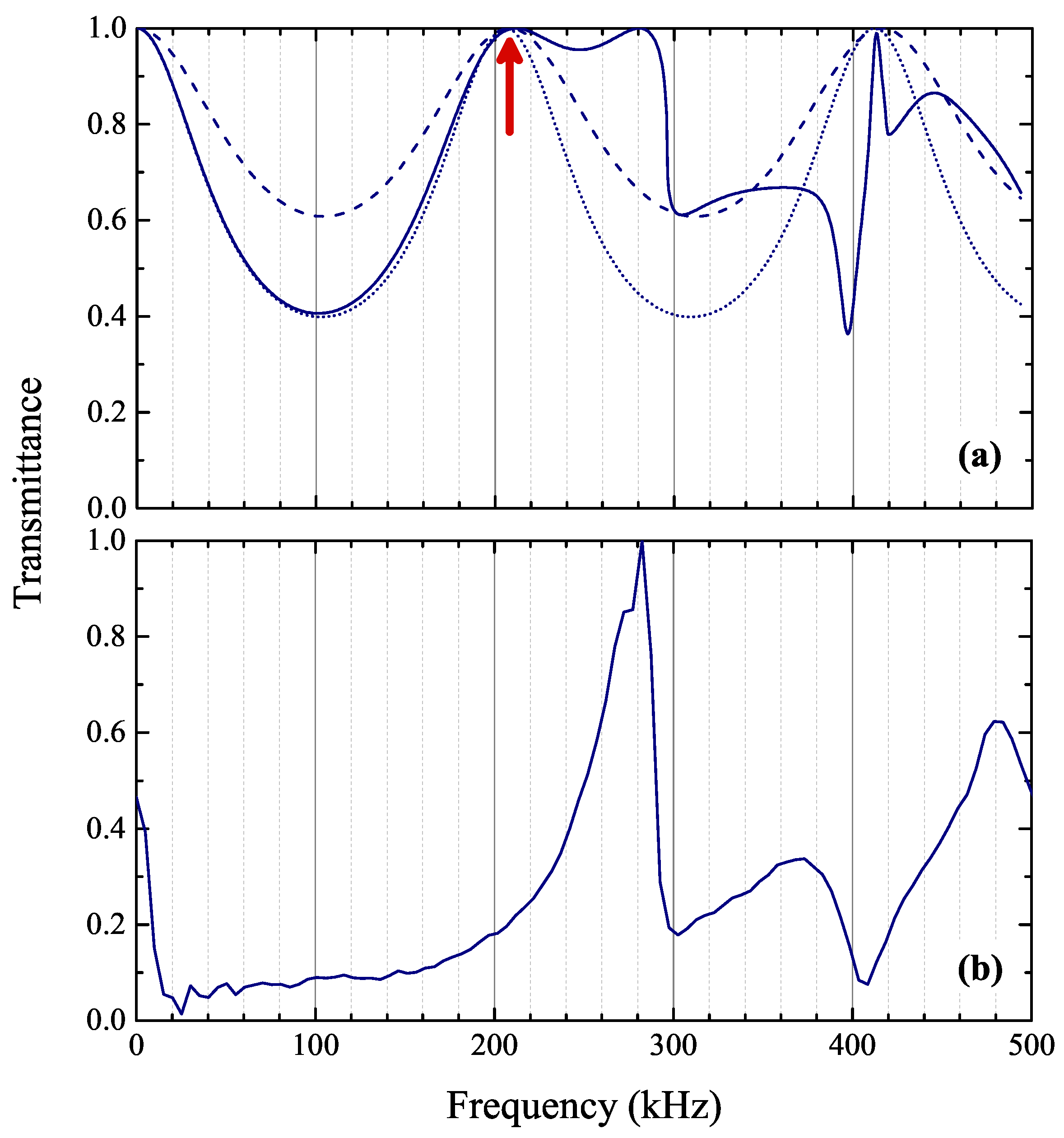
The ratio between the Fast Fourier transforms (using eventually zero-padded data in order to decrease the Fourier transform frequency step, and consequently increase the accuracy of the obtained spectra) of the signal transmitted through the slab and the signal transmitted without the slab, i.e., directly from the emitter transducer to the receiver, is formed to obtain a pseudo-transmission coefficient. The corresponding experimental transmittance spectrum is presented in
Figure 2a. One observes three pass-band frequency regions separated by relatively large forbidden bands (transmission-gaps) extending from
to
, from
to
, and from
to
, these limits are found if a
transmittance level is imposed. These are, in general, in accordance with multiple-scattering theoretical predictions [
22], shown in
Figure 2b. In the theoretical calculations, the
sc (001) planes extend to infinity and a longitudinal acoustic plane wave is considered to be incident normally (
) on the structure. The main difference when comparing the plots (a) and (b) of
Figure 2 is the absence of well constructed Fabry–Perot (FP) resonances in the experimental spectrum within the first transmission band extending up to
. Additionally, the experimental gaps are slightly narrower and the whole transmittance spectrum is slightly shifted towards higher frequencies, with the first and second transmission bands leaking within the gap regions, as predicted from the theoretical calculations at normal incidence (
Figure 2b). A possible explanation could be the simultaneous generation of several incident waves with different
components and amplitudes, due to the angular spreading of the emitter transducer beam, as schematically displayed in
Figure 1b. An attempt to reproduce this behavior, theoretically, is given in
Figure 2c. We sum the transmittances corresponding to several
components along the
direction, precisely over
, where
q varies from 0 to
with a step of
. Next, we normalize the total-sum curve with respect to its maximum value within the frequency window of interest. The obtained curve mimics quite successfully the behavior of the experimental spectrum at the edges of the two first transmission-gaps. As we move towards higher frequencies, the effect of the transducer-beam angular spreading should weaken, the angular spreading being proportional to the emitted wavelength. This approach does not constitute of course a rigorous proof, especially that the sum should be performed by integrating over the whole irreducible part of the surface Brillouin zone (see
Figure 3). Here, we used for simplicity only a part of the
direction to match the upper frequency limit of the first transmission band. A complete picture of the transmittance along the whole
direction is given in
Figure 3.
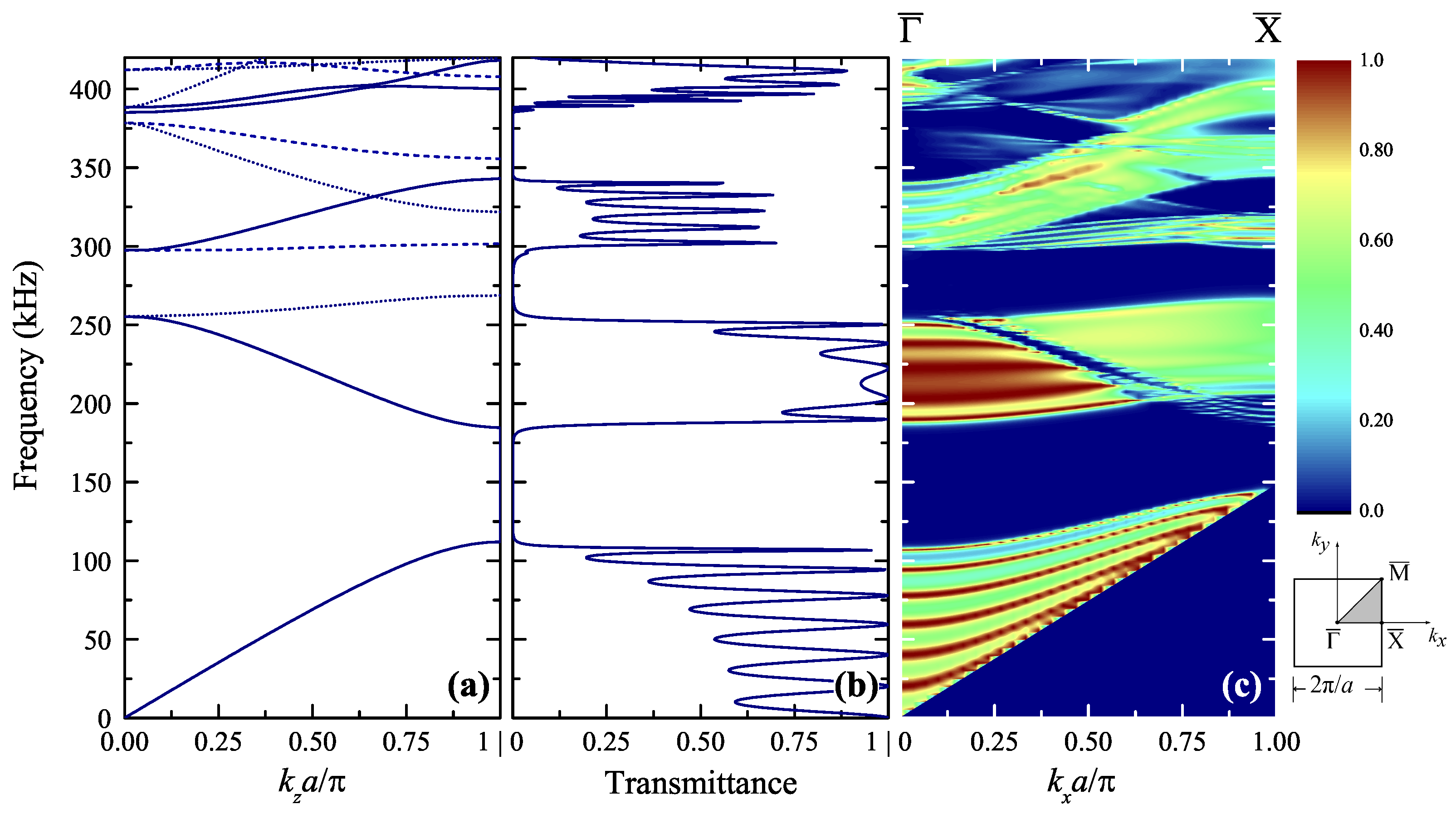
For a deeper understanding of the behavior of this 3D system and of the origin of the transmission-bands, we calculate the frequency band structure for the
sc crystal along the [001] direction (we consider a (001) plane to be the unit cell for the infinite structure and put
). The results are displayed in
Figure 3a together with the calculated transmittance of a normally incident plane acoustic wave through a finite slab of seven (001) planes of spheres (see
Figure 3b), the same curve as the one of
Figure 2b to facilitate comparison. The analysis of the band structure reveals some active bands of symmetry
, which represent modes that couple with an external acoustic plane wave, incident normally on a finite (001) slab of the crystal; indeed, perfect agreement exists between these bands and the corresponding transmittance. Additionally, we observe the existence of several inactive (deaf) bands, of symmetry
,
,
, and
, which represent modes that do not couple with the above-mentioned external wave incident on the same finite slab. These bands transform into active ones (though, usually, with a weak transmission level) at off-normal incidence (
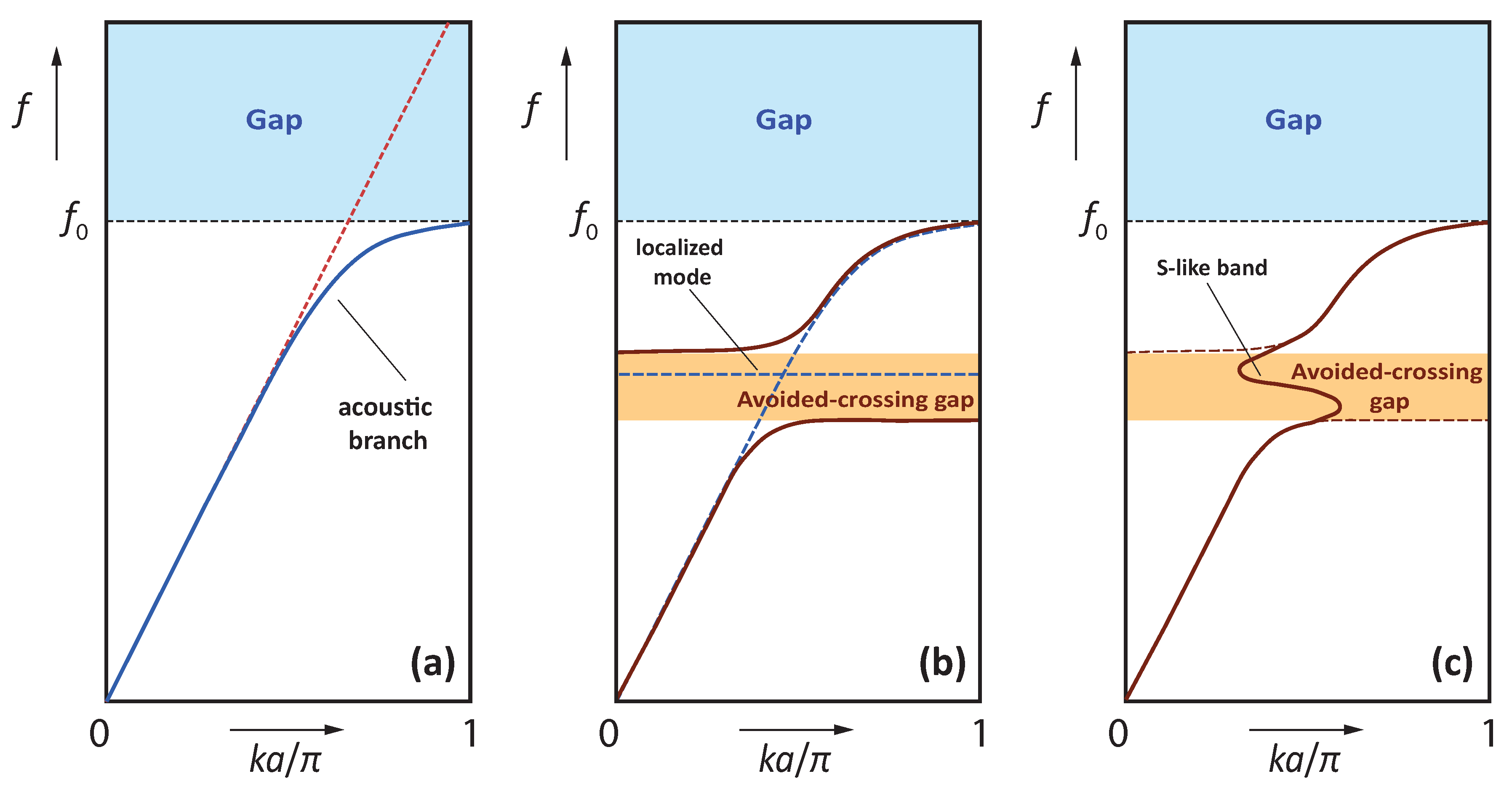
). The first two gaps are
Bragg gaps and vary slightly along
(see
Figure 3c); the third one, around
, is a
hybridization (or avoided-crossing) gap originating from the existence of some localized modes at this frequency region for the system under study and closes quickly along
(see
Figure 3c). The role of the symmetry of these bands will become clearer in the following.
As a first remark, we can say that the magnetic character of the spheres does not seem to influence their elastic behavior, as described by the classical theory of elasticity used in the calculation method. The magnetic force which keeps spheres in contact, is not apparent when the experimental results are compared to the corresponding calculations, at least at these frequency scales and with the given degree of accuracy in the obtained spectra. The next step is to study closer the elastodynamic properties of a single sc (001) layer of spheres (i.e., a square array) for two principal reasons. First, the plane, being the unit cell of the 3D crystal, contains by its own, some fundamental properties useful for the analysis of the behaviour of the structure. Often, localized resonances have their origin in the single plane or in the single sphere, whose separate study can illuminate the physical origin of the phenomena. Second, such a plane can offer a lower-dimension structure than the corresponding 3D case. In addition, the question to answer is: does the main conclusion of this part concerning the magnetic character of the spheres still remain valid? For these reasons, we will focus next on the corresponding 2D case: a single sc (001) plane of touching magnetic spheres, immersed in water.
3.1.2. Two-Dimensional Structure
In this part, we present some experiments concerning the single square array of touching D5N35 spheres (lattice constant ), immersed in water, together with the theoretical analysis of the underlying physical mechanisms. Precisely, two different experiments have been realized: transmission at normal incidence and guided-wave detection, both involving the same transducers, electronics and time signal processing, as for the case of the measured, at normal incidence, transmittance through the slab of the 3D crystal of spheres.
We begin with the study of the transmission properties of the monolayer of spheres. We compute the corresponding transmittance of an acoustic plane wave through the array for the case of normal incidence (
). The results are shown in
Figure 4a. We observe a transmission resonance peak at
, which corresponds to the first FP resonance of an equivalent homogeneous fluid plate of effective thickness
D and whose effective elastic parameters, mass density
and longitudinal propagation velocity
, can be estimated as follows. Applying theoretical developments for disordered arrays of spherical particles, with a 3D spatial distribution, embedded in a host medium [
30], for the case of the 3D
sc crystal with
, the volume filling fraction occupied by the spheres, we find that the crystal can be described, at the long-wavelength limit, by an equivalent effective medium with parameters
and
. The latter is in very good agreement with the corresponding slope, as calculated from the band structure diagram (
) given in
Figure 3a. However, we expect that when the dimensions of the system become lower, going from the 3D cubic crystal to the single 2D square array, the assumption of isotropic 3D spatial distribution of the spheres is not valid anymore and these effective parameters cannot describe the behaviour of the array at low frequencies. We calculate the transmittance of an acoustic plane wave through a fluid plate of thickness
and with elastic parameters
and
(dashed line in
Figure 4a), where the thickness has been adjusted in order to produce the FP at the same frequency position (
). Of course, the pair (
D,
) is not unique. For instance, putting
and
(i.e., with constant
) reproduces perfectly the low-frequency behaviour of the array, with only a slight adjustment of
(dotted line in
Figure 4a). At higher than the FP frequencies, this effective picture fails to describe the response of the composite layer. Other phenomena such as resonances originating from the spheres and/or lattice effects will appear, giving a more complex structure in the calculated transmittance of the square array. We observe some prominent peaks at
and
and two clear dips at
and
, which occur slightly below the cut-off frequencies for the generation of the first two non-zero orders of the diffracted beams,
and
(corresponding to reciprocal-lattice vectors
, i.e., with
, and
, i.e., with
, respectively). These dips are, in other words, associated to lattice resonances, localized in the plane passing at the center of the spheres, the first of them corresponding to the first lattice resonance along
, i.e., with wavelength
, and the second to the first lattice resonance along
, i.e., with wavelength
. The same phenomenology has been observed for monolayers of solid spherical particles embedded in a solid matrix [
31].
Following the same experimental procedure as that described in the previous section, we obtain the transmitted pressure through a
sc (001) plane of spheres excited by the transducer’s acoustic central beam incident normally on the plane. The results, normalized to their maximum value in the frequency window
, are plotted in
Figure 4b. Apart from the low frequency region (i.e., below
) where the transducers sensibility vanishes, most of the features predicted by the theoretical curve are present. We observe a sharp transition about 280–300
and a transmission dip at
. The main difference seems to be the absence of the FP peak at about
. In fact, the very strong narrow peak at
obscures the FP resonance that is hidden in the background. We verified this hypothesis by calculating the transmitted pressure through the square array, where the FP peak is found to be relatively weakened in amplitude, in accordance with the picture obtained experimentally.
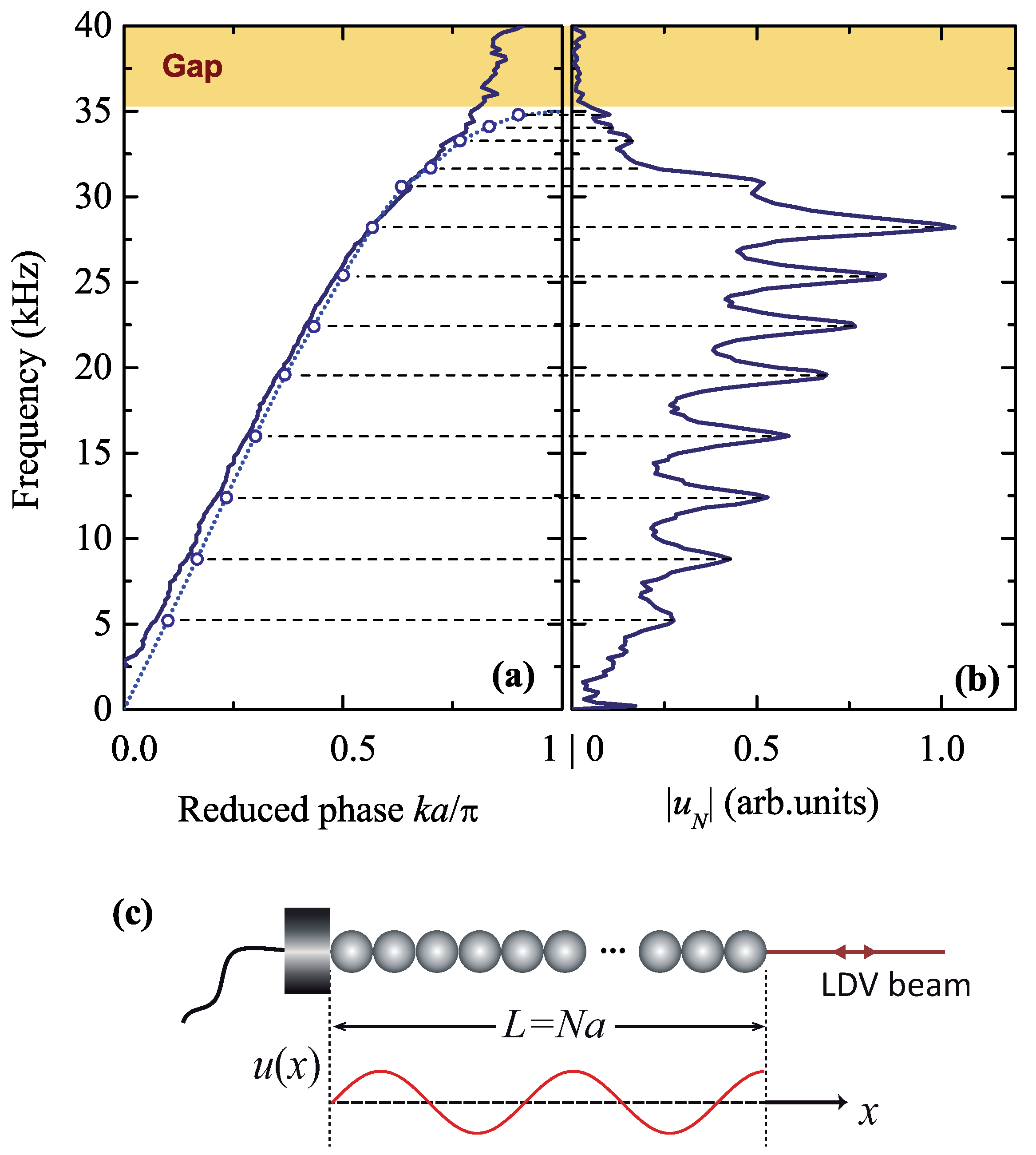
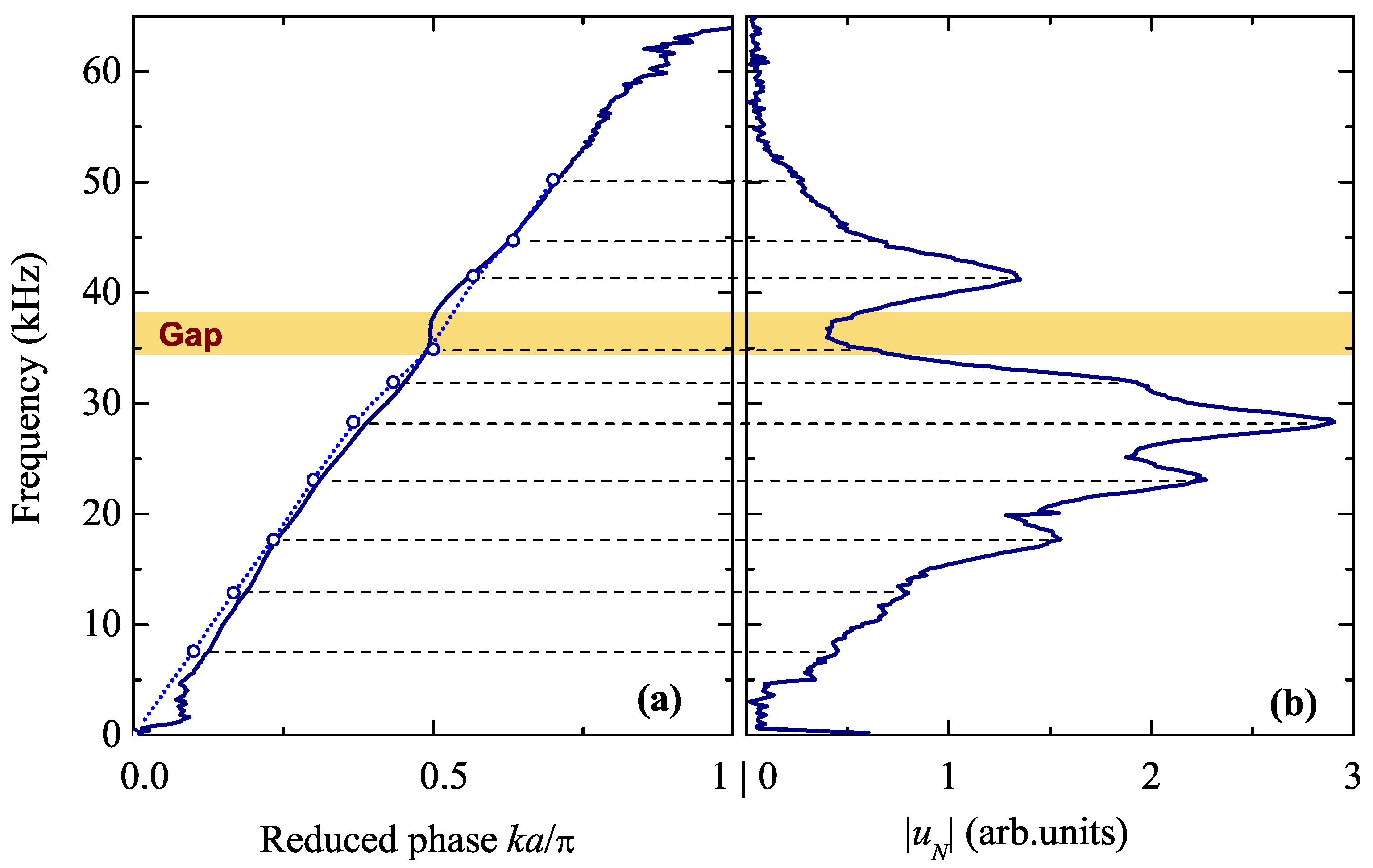
Next, we focus on the study of the guided wave response of the monolayer. We proceed to its experimental characterization by measuring the transmitted pressure through the layer, adopting for the transducers a transmission configuration, as the one shown in
Figure 5a, i.e., with their axis making an angle of
with the normal to the plane, in order to probe elastic modes propagating along the layer and being localized in it with respect to the
z-direction. We note in passing that the choice of the angle ensures that guided waves will be excited and thus observed in the frequency region of interest, without completely losing the symmetry advantages of the normal incidence. Both transducers’ mean beams belong to the same plane as the normal to the plane; the projection of the wavevector component parallel to the layer lies on the
direction of the surface Brillouin zone (see inset of
Figure 3),
,
q varying from 0 to
. The receiver is translated parallel to the layer (
x-axis), and the pressure scattered by the plate is captured every
, from
to
(we set
at the location of maximal forced transmission regime). After a double time-space FFT in the free time and space regime of the signal, we obtain the transmitted pressure in the frequency-wavenumber space,
, whose modulus is plotted in
Figure 5b. We observe a more or less continuous transmission band of relatively weak amplitude, extending up to ∼300
, interrupted by two transmission-gap regions, from 140 to
and from 225 to
. This physical picture is in accordance with the one shown in the transmission plot along
direction (
Figure 3c), for
. The nature of these modes is of FP type; in this frequency region, i.e., below
, no localized modes exist originating from the spheres or from one plane of spheres, and the behaviour of the real system is practically the same to that of an array of rigid (impenetrable) scatterers. Acoustic waves hardly penetrate within the sphere and its interior is not seen. The most important feature of the guided-response plot of
Figure 5b is the appearance of three isolated, well-defined, and relatively high-amplitude spots centered at 308, 394, and
. We note here that the peak level of the second spot (the strongest one) has been saturated in order to better visualize the two others.
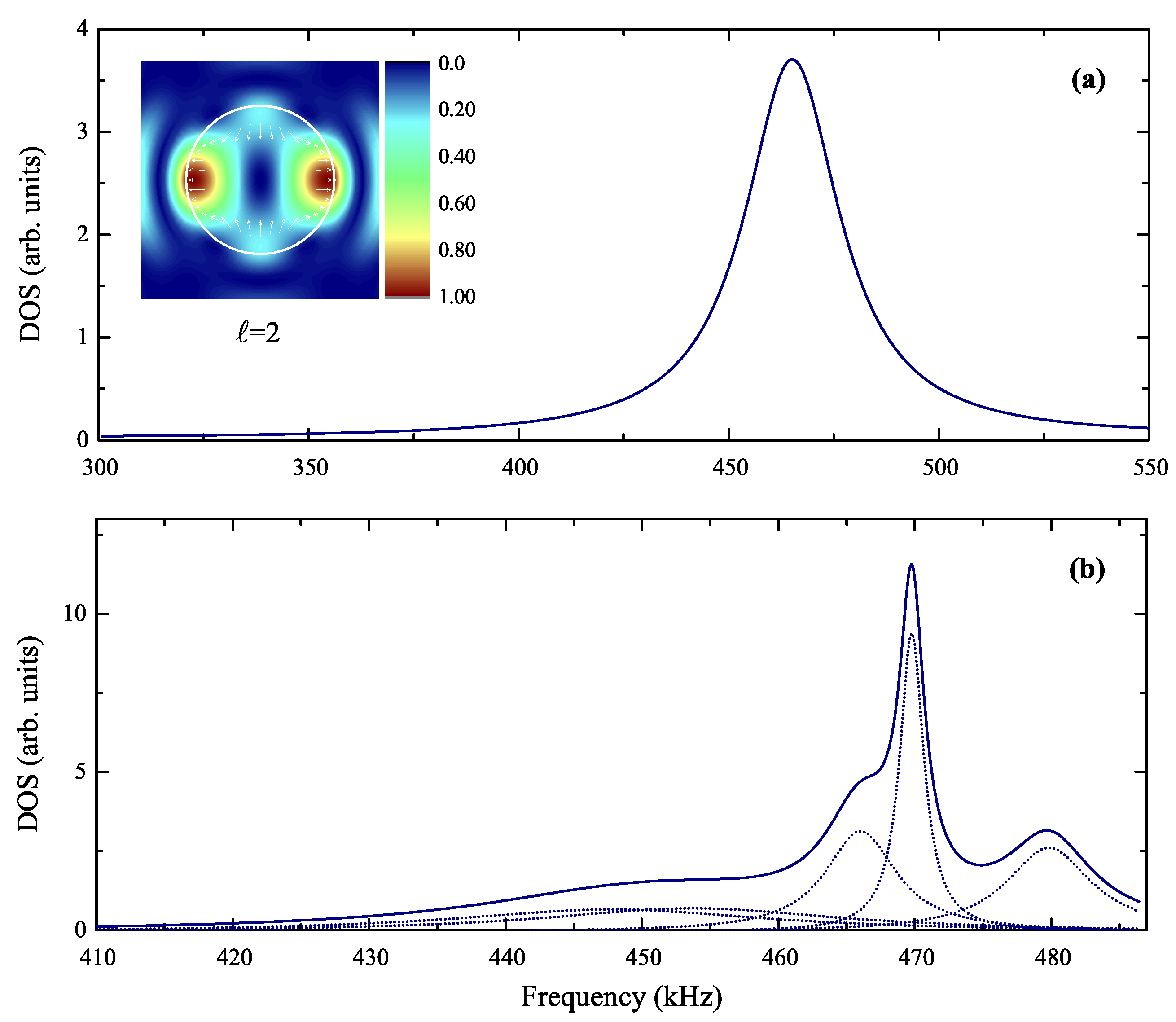
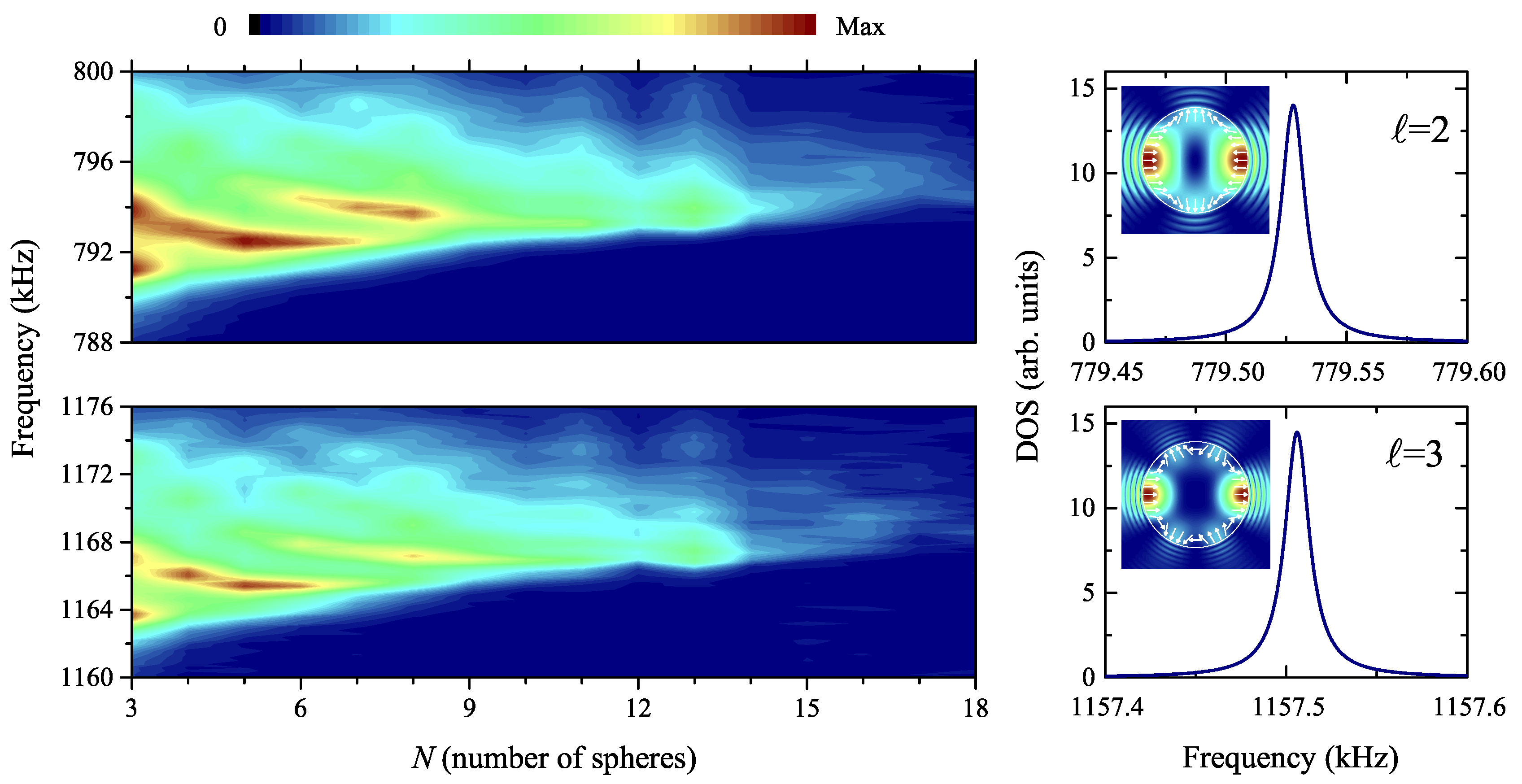
In order to clarify the origin of these three observed peaks, we need to analyze theoretically the resonant behaviour of one single sphere and of a square-array monolayer of such touching spheres. In
Figure 6a, we show the calculated change in the density-of-states of the elastic field (Equation (
5)) for a D5N35 sphere (
) immersed in water, with respect to the infinitely extended water. In the frequency window that interests us here,
, there is only an
(quadrupole-like) five-fold spheroidal mode at about
, manifested as a Lorentzian-shape peak in the DOS spectrum and whose elastic field spatial distribution (see inset plot in
Figure 6a) reveals a
-like orbital form corresponding to
angular momentum numbers. When bringing spheres close to form a 2D square array of spheres, the high, spherical symmetry of the system lowers, and we expect that the five-fold degeneracy (
, for
) splits up to five non-degenerated modes. Indeed, for a
lying, for instance, on the
direction, we obtain five non-degenerate modes, corresponding to five Lorentzian peaks, each of them of different height and width, as shown in
Figure 6b for
, through DOS calculations for the monolayer (Equations (
5) and (
6)).
The physical meaning of these modes can become clearer if we go back to a high-symmetry point in the
-space. Following group theory basic arguments, we can show [
32] that an
, five-fold, spherical mode at the Γ point,
, splits into a double-degenerated mode of symmetry
and a triple-degenerated mode of symmetry
. Considering now
along the [001] direction, lowers further the symmetry of the system to the
symmetry, and these modes split as
and
. In other words, flat localized bands originating from an
resonant mode of the sphere will split along the [001] direction to three non-degenerate bands of symmetry
,
, and
and one double-degenerate band of symmetry
. We remember, at this point, the connection between these symmetries and the
d-orbitals.
transforms like a
orbital (angular momentum numbers
,
), and it has a spatial distribution along the
z-axis, perpendicular to the (001) plane of spheres. This mode couples with a longitudinal wave incident normally on the plane.
and
transform like
and
orbitals (
,
), respectively, lying both on the
-plane. The former has its lobes aligned along
x- and
y-axes and can thus be excited by a incident wave with a
component along the
direction; the latter has its lobes aligned along the
lines and can thus be excited by an incident wave with a
component along
direction. Finally,
transforms like a
or
orbital (
,
), both having their lobes on the planes
and
at
with respect to the
z-axis. From the above, it is thus evident that only modes with
symmetry will be localized on the (001) plane along the
direction. After analysis of the eigenmodes for the band structure of
Figure 3a, we find that there exists a flat mode of
symmetry at about
originating from the
mode of the individual sphere. This mode corresponds to the one bright experimental spot at
.
The other two bright experimental spots, at 308 and
, do not originate from resonant modes of the individual sphere. They correspond to lattice resonances, and both of them constitute the evolution with
of the first dip at about
, observed in the transmission spectrum of the monolayer at normal incidence (
) shown in
Figure 4a. We remember that this dip is associated with a lattice resonance corresponding to reciprocal lattice vectors
with
. The dispersion relation
of these lattice resonances can be approximately described by setting the
z-component of the wavevector (Equation (
1)) equal to zero, i.e.,
. For
lying along
,
, and
we have
. The first bright spot, at
, is very close to the value of
obtained from this dispersion relation for
and
. In other words, this spot corresponds to the first lattice resonances along
and
whose dispersion relation varies very little with
along
. Of course, this double-degenerated mode, lying outside
should not be observed; however, it produces a weak spot due to some angular spreading of the emitter transducer, thus exciting slightly modes out of the
. The second bright spot, at
, is very close to the value of
obtained from this dispersion relation for
and
. In other words, this spot corresponds to the first lattice resonance along
and its dispersion relation varies significantly with
along
. This mode produces a high-amplitude spot since the corresponding lattice resonance is naturally aligned along
. We note in passing that, following similar analysis, close to the third experimental spot at about
, there exists a branch corresponding to a
lattice resonance: for
, we obtain
, which could probably interfere with the mode originating from the sphere resonance.