Abstract
We have successfully synthesized niobium monophosphide and tantalum monophosphide crystals by a chemical vapor transport technique. We report resistivity vs. temperature of both materials in the temperature range from 2 K to 300 K. We have also performed electronic structure calculations and present the band structure and density of states of these two compounds. The calculations show that both compounds are semimetals, as their conduction and valence bands overlap near the Fermi energy.
1. Introduction
The discovery and growth of new materials that exhibit unique physical properties, such as high temperature superconductivity, topological phases, exotic magnetism, etc., is one of the challenging but promising fields in materials science and condensed matter physics. These “quantum materials” are drivers of technological innovation as well as intellectual challenge. Recently, the concept of Weyl fermions [1]—first discussed in the context of high energy physics—has been applied to condensed matter systems [2,3].
A crystal whose low energy excitations are Weyl fermions is called a Weyl semimetal. A necessary condition for Weyl semimetal formation is a lack of either inversion symmetry or time reversal symmetry. A Weyl semimetal is analogous to a 3D version of graphene, since both share similar electronic band dispersion near the Fermi energy. A key property of a Weyl semimetal is that the surface states possesses “Fermi arcs” connecting the projection of bulk nodes in the surface Brillouin zone [4,5].
The first experimental evidence of a Weyl semimetal phase was observed in a single crystal of TaAs [6] which belongs to nonsymmorphic space group and lacks inversion symmetry. Angle resolved photoemission spectroscopy (ARPES) experiments revealed Fermi arcs on the surface and Weyl fermion cones and Weyl nodes in the bulk of the sample [5,7,8]. Furthermore, TaAs exhibits gigantic magnetoresitance of at 10 K upon application of a 9 T magnetic field, and a large mobility of ·· [9]. Similar properties have also been reported in NbP, with magnetoresistance of at 2 K and 9 T, and mobility of ·· [10]. Other transition metal monopnictides that are Weyl semimetals and belong to nonsymmorphic space group are TaP [4] and NbAs [7,11].
In this paper, we will discuss the crystal growth of two transition metal monophosphides (NbP and TaP), discuss their crystal chemistry, and report transport measurements on the two compounds. We also report electronic structure calculations on these materials that demonstrate the critical role of spin–orbit coupling in determining their physical properties. Though a detailed crystal growth recipe has been mentioned in Reference [5], here we use a slightly different method which helps to improve the size of crystals. It is also a fact that a larger crystal plays an important role in physical measurements, and we have obtained relatively larger crystals than that reported elsewhere [5,12,13,14].
2. Experimental Details
We synthesized single crystals of NbP and TaP by chemical vapor transport method. First, polycrystalline samples of NbP and TaP were prepared by heating stoichiometric amounts of Ta/Nb (99.99% Alfa-Aesar) and P (99.99% Alfa-Aesar) at 900 °C for four days, and subsequently the samples were cooled slowly to room temperature over 24 h. To avoid explosion of the silica tubes, the temperature was raised slowly so that the reaction could occur without building up an excessive vapor pressure of phosphorous in the tubes. Polycrystalline samples thus obtained were finely ground inside a glove box under inert atmosphere. Phase purity of the polycrystalline samples was checked using powder X-ray diffraction (XRD). A single phase of TaP/NbP was confirmed, and no impurity phases were observed. About 3 g of the polycrystalline sample and 0.5 g of iodine were loaded in a quartz tube, and the tube was subsequently sealed under vacuum. For these growths, short (about 110 mm) and large diameter (19 mm) tubes were used, since transport rate is inversely proportional to length and proportional to tube diameter [15]. The sealed tube was placed horizontally in a tube furnace, with one end at 1000 °C and the other at 900 °C. After one week, the furnace was cooled slowly to room temperature at a rate of 1 °C/min, and most of the polycrystalline powder had transported to the hotter end of the tube. Many tetrahedral crystals with shiny surfaces were obtained. Typical crystal dimensions were ; large diameter tubes, a small temperature gradient, and long cooking hours are the factors for obtaining bigger crystals.
The resistivity measurements were performed in a Physical Properties Measurement System from Quantum Design from 2 K to 300 K. The resistivity was measured using a conventional four probe technique. Contacts to the sample were made with gold wires and silver epoxy. The electronic structure calculations were carried out using the WIEN2k [16] package.
3. Results and Discussion
3.1. Crystal Chemistry
The crystal structure of NbP (TaP) illustrated in Figure 1 is a conventional unit cell of NbP (TaP) viewed along the (111) direction. These compounds belong to non-symmorphic space group (# 109), and they crystallize in a body-centered tetragonal structure. One conventional unit cell of TaP (NbP) contains four Ta(Nb) atoms and four P atoms; a primitive unit cell contains two Nb (Ta) and two P atoms. The structure of Nb(Ta)P is formed by and trigonal prisms extended on the -plane and stacked along the c-axis by the four-fold screw axis. Ta/Nb and P both occupy the 4a Wyckoff position, and the atomic coordinates of Nb/Ta and P are (0,0,0) and (0,0,0.416) [17], respectively. This lattice system lacks a horizontal mirror plane, and hence inversion symmetry is broken, which leads to a realization of unusual physical phenomenon such as Weyl semimetallic behavior. Powder XRD patterns of NbP and TaP are shown in Figure 2, and match well with previously reported work by J. Xu et al. [12]. The experimental values of lattice parameters are Å and Å.
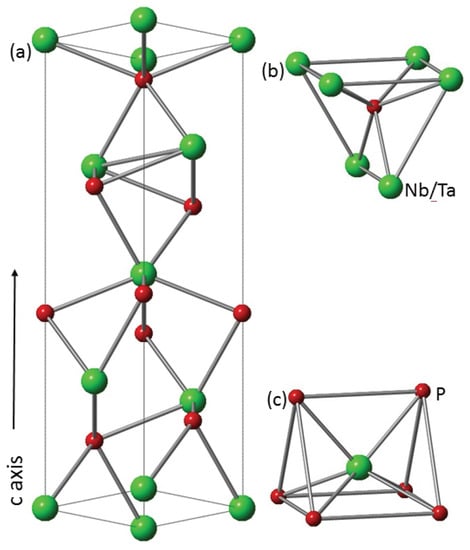
Figure 1.
Conventional unit cell of NbP or TaP (a); Trigonal prismatic environment of P (b) and Nb/Ta (c).
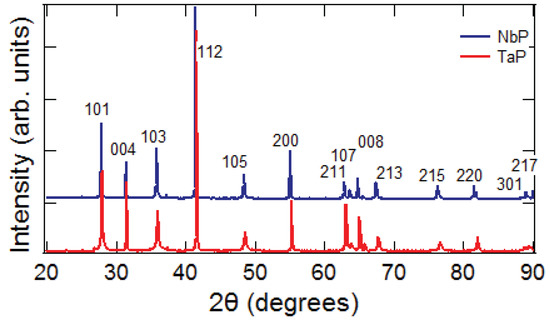
Figure 2.
Room temperature X-ray diffraction pattern of NbP and TaP with reflections indicated.
3.2. Resistivity
The temperature-dependent resistivities, ρ(T), of NbP and TaP are plotted in Figure 3 and Figure 4, respectively. The resistivities were measured on unoriented crystals. Residual resistivity ratios, , of NbP and TaP were 15.13 and 12.33, respectively, indicating that the crystals are of good quality, though these values are smaller than previously reported values [10,13,14]. The resistivities of both samples increase with temperature, as expected for a metallic system. No change in the resistivities were observed with temperature cycling. The room temperature resistivities of NbP and TaP were Ω·cm and Ω·cm, respectively. We fit the low temperature resistivity data to power law and found a deviation from the famous Bloch law, which correctly describes the temperature dependence resistivity of simple metals (non-correlated systems like Cu); rather, we found that resistivities follow the power law (Figure 5), suggesting that these systems may be moderately correlated. In the temperature range from 100–220 K, the resistivities vary linearly with temperature, suggesting that electron–phonon scattering is dominant. Above 220 K, their temperature dependence is sublinear, perhaps due to the Fermi level changing with temperature in a region of small density of states.
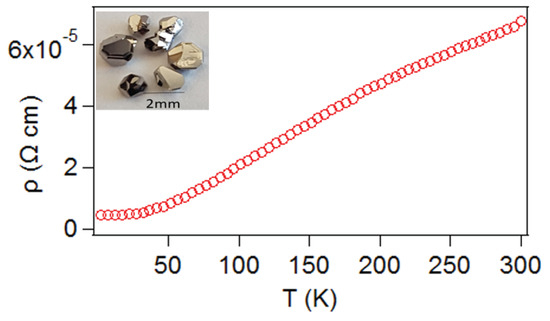
Figure 3.
Resistivity vs. temperature of an unoriented crystal of NbP. Single crystals of NbP are shown in the inset.
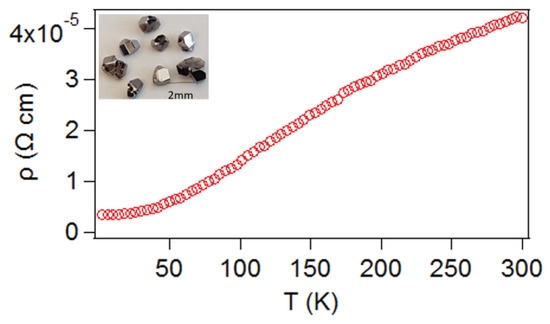
Figure 4.
Resistivity vs. temperature of an unoriented crystal of TaP. Single crystals of TaP are shown in the inset.
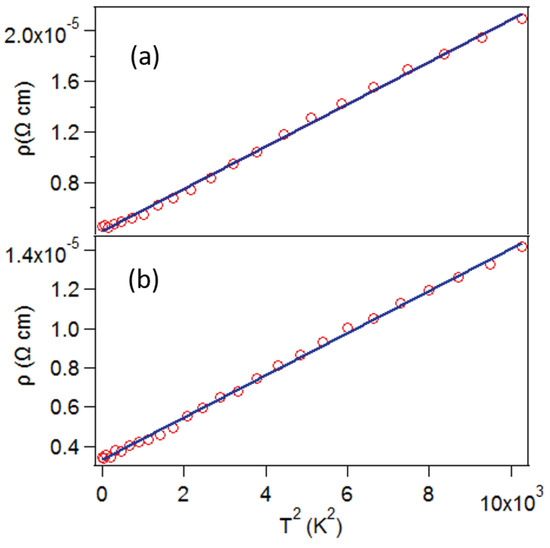
Figure 5.
power law fit of low temperature resistivity of (a) NbP and (b) TaP .
3.3. Electronic Structure Calculations
First principles calculations of both monophosphide compounds were performed within a density functional theory (DFT) approach using the linear augmented plane wave (LAPW) method as implemented in the WIEN2k package. We used the experimental lattice parameters Å and Å. Muffin-tin radii of 2.5 for Ta and Nb and 2.14 a.u. for P were used, where is the Bohr radius. The number of k points in the whole Brillouin zone was taken as 1000. We used the exchange correlation potential GGA by Perdew, Burke, and Ernzerof (PBE) 96 [18] and conduction and valence band separation energy of Ry. The plane wave cut off is specified by = 7, where and are the smallest muffin-tin radius in a unit cell and largest wave vector, respectively.
We performed non-spin-polarized calculations for both compounds. The band structures of NbP and TaP with and without the inclusion of spin orbit coupling (SOC) are shown in Figure 6 and Figure 7, respectively. The electronic density of states of NbP and TaP with including SOC are shown in Figure 8. Bands near the Fermi level are mainly dominated by Nb/Ta d orbitals and P p orbitals, and there is strong hybridization between these two orbitals. The conduction and valence bands are not well separated, which leads to semimetallic character. The lower two bands between eV and eV are constructed from P s orbitals. Bands between eV and eV are admixtures of Nb d and Nb p states. Without SOC, the bands are crossing the Fermi level along Γ – Σ, Σ – N, and Σ – Z. When we include SOC, a band gap opens up at the Weyl point, and the bands are linearly dispersive. The double degeneracy of bands is lifted in the presence of SOC, and Weyl nodes appear at band crossing points as a result of time reversal or inversion symmetry breaking. These results are consistent with recent calculations [17,19,20]. Furthermore, recent angle resolved photoemission spectroscopy (ARPES) results [4,5,13,21] show the linear bulk band dispersion across the Weyl points, in agreement with the theoretical calculations.
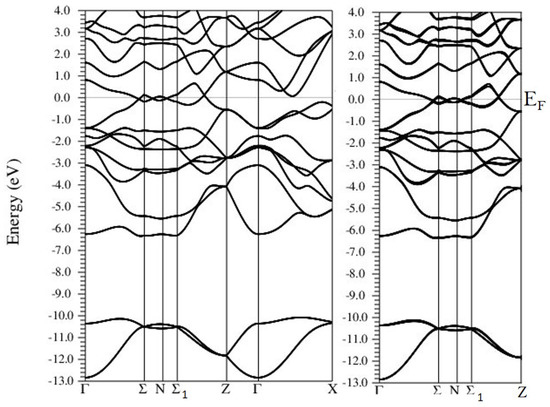
Figure 6.
The band structure of NbP. The left panel does not include spin orbit coupling (SOC); the right panel includes SOC.
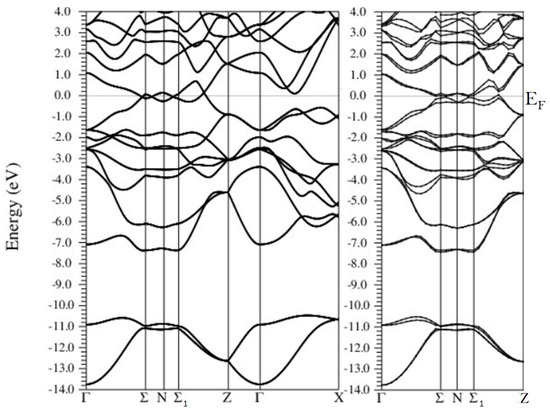
Figure 7.
The band structure of TaP. The left panel does not include SOC; the right panel includes SOC.
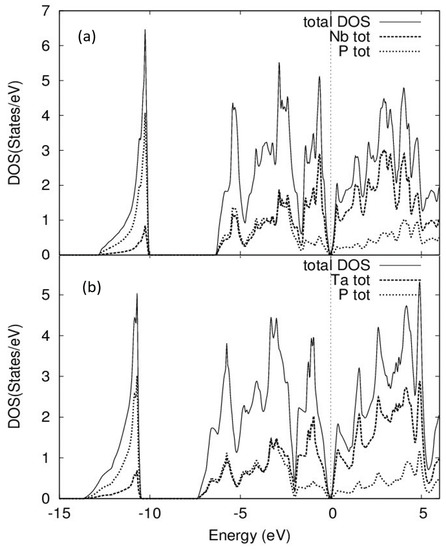
Figure 8.
Non-spin polarised electronic density of states of (a) NbP and (b) TaP including SOC.
The electronic density of states plot shows a minimum value at the Fermi level. The density of states near the Fermi level mainly comprises Nb/Ta orbitals and P p orbitals. Lower states in between eV and eV are mainly derived from P s states, as explained previously in band structure. We infer a very small Sommerfeld coefficient value— mJ·· and mJ·· for NbP and TaP, respectively. Such a small value of γ is due to the very low density of states at Fermi level. The density of states at Fermi level for NbP and TaP are 0.0323 states/eV and 0.0036 states/eV, respectively.
4. Conclusions
In conclusion, we report the successful growth of good quality single crystals of the Weyl semimetals NbP and TaP. The phases were confirmed by powder X-ray diffraction. We also performed resistivity measurements on both samples, and they showed metallic behavior with dependence from 2–100 K. First principles calculations were performed using the WIEN2k package. The band structure calculations show conduction and valence bands crossing the Fermi level without including spin–orbit coupling, but a band gap opens up at the Weyl point when spin–orbit coupling is included. A very small value for the Sommerfeld coefficient was inferred because of the negligible density of states at the Fermi level.
Acknowledgments
This work was supported by the National Science Foundation under grant NSF-EFRI-1433496.
Author Contributions
Deepak Sapkota and David Mandrus conceived and designed the experiments; Deepak Sapkota and Rupam Mukherjee performed the experiments; Deepak Sapkota performed the first principles calculations; Deepak Sapkota and David Mandrus analyzed the data; Deepak Sapkota wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Weyl, H. Elektron und Gravitation. I. Zeitschrift für Physik A Hadrons and Nuclei 1929, 56, 330–352. [Google Scholar] [CrossRef]
- Wan, X.; Turner, A.M.; Vishwanath, A.; Savrasov, S.Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 2011, 83, 205101. [Google Scholar] [CrossRef]
- Wilczek, F. Why are there analogies between condensed matter and particle theory? Phys. Today 1998, 51, 11–13. [Google Scholar] [CrossRef]
- Xu, S.Y.; Belopolski, I.; Sanchez, D.S.; Zhang, C.; Chang, G.; Guo, C.; Bian, G.; Yuan, Z.; Lu, H.; Chang, T.-R.; et al. Experimental discovery of a topological Weyl semimetal state in TaP. Sci. Adv. 2015, 1, e1501092. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.K.; Yang, L.X.; Sun, Y.; Zhang, T.; Peng, H.; Yang, H.F.; Chen, C.; Zhang, Y.; Guo, Y.F.; Prabhakaran, D.; et al. Evolution of the Fermi surface of Weyl semimetals in the transition metal pnictide family. Nat. Mater. 2016, 15, 27–31. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.-Y.; Belopolski, I.; Alidoust, N.; Neupane, M.; Bian, G.; Zhang, C.; Sankar, R.; Chang, G.; Yuan, Z.; Lee, C.-C. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 2015, 349, 613–617. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.-Y.; Alidoust, N.; Belopolski, I.; Yuan, Z.; Bian, G.; Chang, T.-R.; Zheng, H.; Strocov, V.-N.; Sanchez, D.-S.; Chang, G. Discovery of a Weyl fermion state with Fermi arcs in niobium arsenide. Nat. Phys. 2015, 11, 748–754. [Google Scholar] [CrossRef]
- Lv, B.-Q.; Weng, H.-M.; Fu, B.-B.; Wang, X.-P.; Miao, H.; Ma, J.; Richard, P.; Huang, X.-C.; Zhao, L.-X.; Chen, G.F.; et al. Experimental Discovery of Weyl Semimetal TaAs. Phys. Rev. X 2015, 5, 031013. [Google Scholar] [CrossRef]
- Zhang, C.; Yuan, Z.; Xu, S.; Lin, Z.; Tong, B.; Hasan, M.Z.; Wang, J.C.; Zhang, C.; Jia, S. Tantalum Monoarsenide: An Exotic Compensated Semimetal. arXiv, 2015; arXiv:1502.00251. [Google Scholar]
- Shekhar, C.; Nayak, A.K.; Sun, Y.; Schmidt, M.; Nicklas, M.; Leermakers, I.; Zeitler, U.; Skourski, Y.; Wosnitza, J.; Liu, Z.; et al. Extremely large magnetoresistance and ultrahigh mobility in the topological Weyl semimetal candidate NbP. Nat. Phys. 2015, 11. [Google Scholar] [CrossRef]
- Ghimire, N. J.; Luo, Y.; Neupane, M.; Williams, D.; Bauer, E.; Ronning, F. Magnetotransport of single crystalline NbAs. J. Phys. Condens. Matter. 2015, 27, 152201. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Greenblatt, M.; Emge, T.; Höhn, P.; Hughbanks, T.; Tian, Y. Crystal Structure, Electrical Transport, and Magnetic Properties of Niobium Monophosphide. Inorg. Chem. 1996, 35, 845–849. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.-F.; Du, Y.-P.; Wang, Z.; Li, Y.-P.; Niu, X.-H.; Yao, Q.; Dudin, P.; Xu, Z.-A.; Wan, X.-G.; Feng, D.-L. Observation of Fermi Arcs in Non-Centrosymmetric Weyl Semi-Metal Candidate NbP. Chin. Phys. Lett. 2015, 32, 107101. [Google Scholar] [CrossRef]
- Wang, Z.; Zheng, Y.; Shen, Z.; Lu, Y.; Fang, H.; Sheng, F.; Zhou, Y.; Yang, X.; Li, Y.; Feng, C.; Xu, Z.-A. Helicity-protected ultrahigh mobility Weyl fermions in NbP. Phys. Rev. B 2016, 93, 121112. [Google Scholar] [CrossRef]
- Binnewies, M.; Glaum, R.; Schmidt, M.; Schmidt, P. Chemical Vapor Transport Reactions; Walter de Gruyter: Berlin, Germany, 2012. [Google Scholar]
- Blaha, P.; Schwarz, K.; Madsen, G.; Kvasnicka, D.; Luitz, J. WIEN2k: An Augmented Plane Wave+ Local Orbitals Program for Calculating Crystal Properties; Vienna University of Technology: Vienna, Austria, 2001. [Google Scholar]
- Weng, H.; Fang, C.; Fang, Z.; Bernevig, B.A.; Dai, X. Weyl Semimetal Phase in Noncentrosymmetric Transition-Metal Monophosphides. Phys. Rev. X 2015, 5, 011029. [Google Scholar] [CrossRef]
- Perdew, J.-P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 011029. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Wu, S.-C.; Yan, B. Topological surface states and Fermi arcs of the noncentrosymmetric Weyl semimetals TaAs, TaP, NbAs, and NbP. Phys. Rev. B 2015, 92, 115428. [Google Scholar] [CrossRef]
- Huang, S.-M.; Xu, S.-Y.; Belopolski, I.; Lee, C.-C.; Chang, G.; Wang, B.; Alidoust, N.; Bian, G.; Neupane, M.; Bansil, A.; et al. Theoretical Discovery/Prediction: Weyl Semimetal states in the TaAs material (TaAs, NbAs, NbP, TaP) class. arXiv, 2015; arXiv:1501.00755. [Google Scholar]
- Belopolski, I.; Xu, S.-Y.; Sanchez, D.; Chang, G.; Guo, C.; Neupane, M.; Zheng, H.; Lee, C.-C.; Huang, S.-M.; Bian, G.; et al. Observation of surface states derived from topological Fermi arcs in the Weyl semimetal NbP. arXiv, 2015; arXiv:1509.07465. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).