1. Introduction
A substantial amount of work has been devoted in the past few years to better understand transport, localization, and wave phenomena in disordered media [
1,
2,
3,
4,
5]. These activities unveiled fascinating analogies between the behavior of electronic and optical wave excitations, such as disorder-induced Anderson light localization [
1,
6,
7]. However, the applications of random media to optical engineering are presently quite limited. In fact, random structures, while providing a convenient path to field localization and lasing [
8,
9,
10], are not reproducible and lack simple design rules for deterministic optimization. On the other hand, aperiodic optical media generated by mathematical rules, known as deterministic aperiodic structures, have recently attracted significant attention in the optics and electronics communities due to their simplicity of design, fabrication, and compatibility with current material deposition and device fabrication technologies [
11,
12,
13,
14,
15,
16,
17]. In particular, recent experimental and theoretical studies in the fields of nanophotonics, plasmonic and metamaterials have focused on optical nanostructures that exploit deterministic aperiodic order as an emerging strategy to demonstrate novel optical functions [
18,
19,
20,
21,
22,
23,
24,
25].
Deterministic aperiodic structures manifest distinctive optical responses that cannot be found in either periodic or random systems, such as fractal transmission spectra and anomalous transport properties [
26,
27,
28,
29,
30,
31,
32,
33]. Also, they support a rich spectrum of optical modes with various degrees of spatial localization, known as critical modes [
34,
35,
36,
37]. Critical modes manifest a power-law localization scaling with highly fragmented multifractal envelopes that were recently employed in multi-mode aperiodic lasing and optical sensing devices [
36,
38,
39,
40,
41]. The characteristic features that result from the richer optical phase space spanned by deterministic aperiodic designs found engineering applications to optical sensing, light emission and lasing, photo-detection, optical imaging and nonlinear optical devices [
17,
24,
42,
43,
44]. In addition to their importance for key technological applications, the study of deterministic aperiodic nanostructures (DANS) is a highly interdisciplinary and fascinating research field conceptually rooted in several branches of pure and applied mathematics, such as number theory [
45,
46], symbolic dynamics [
47,
48], and computational geometry (i.e., tiling and tessellation theory, point patterns and graph theory) [
49,
50,
51,
52]. As a result, the optics of deterministic aperiodic media can stimulate numerous cross-disciplinary and exciting research opportunities that only recently began to be actively pursued in the engineering disciplines.
The goal of our paper is to provide a comprehensive discussion of the relationship between structural and spectral properties that governs the distinctive optical behavior of large arrays of scattering particles with controllable degree of aperiodic order. In particular, we apply the interdisciplinary methods of spatial point pattern analysis [
51] and spectral graph theory [
53,
54] to gain information on the characteristic geometrical and connectivity properties of deterministic aperiodic arrays that determine their resonant scattering behavior. Based on this knowledge, we show how it is possible to predict general features of the scattering resonances including their complex mode structures. Our work, which is primarily concerned with the fundamental structure-property relationships in deterministic aperiodic systems, unveils the importance of spectral geometry and graph connectivity methods for the engineering of scattering arrays with various degrees of aperiodic order. We then systematically investigate, using the rigorous Green’s matrix spectral method [
55,
56,
57], the specific electromagnetic scattering resonances of quasiperiodic Penrose arrays, Vogel spiral arrays as well as periodic and random systems that serve as a reference benchmark widely characterized in the optics and electronics literature. We focus on planar structures as two-dimensional aperiodic and quasiperiodic optical structures are the most relevant case for experiments and applications. The Green’s matrix spectral method provides important physical information about light transport in open scattering systems that cannot be easily accessed via other numerical methods, such as Finite Difference Time Domain (FDTD) or Finite Elements (FEM) [
58]. Indeed, in contrast to purely numerical methods, the Green’s matrix spectral method allows one not only to obtain the frequency positions and lifetimes (the inverse of the resonance width) of scattering resonances, but also to correlate them to the spatial distribution of optical quasi-modes (i.e., the modes of open systems) and explore their spectral statistics. Hence, this method permits efficient access to the full spectral information of deterministic aperiodic arrays, which has not been explored in previous studies that primarily relied on purely numerical methods. Based on the complete knowledge of the complex eigenvalues and eigenvectors of the Green’s matrix, we quantify the degree of spatial localization of scattering resonances by numerically computing their
Inverse Participation Ratio (IPR) and introduce a simple criterion that permits to identify critical modes in the spectra of aperiodic structures.
Finally we address the spectral fluctuations of deterministic aperiodic optical media and investigate the statistics of their complex eigenvalues and level spacing distributions for the first time. This analysis is performed for different structures as a function of their optical density , where S is the areal density of particles in the arrays and λ the optical wavelength. The optical density measures the number of particles distributed within an area of lateral dimension equal to the wavelength and it is indicative of the scattering strength in a system of particles.
Our results demonstrate very rich and novel spectral properties that cannot be obtained with either periodic or random systems, and stimulate the development of novel theoretical approaches capable to account for the spectral fluctuations of aperiodically ordered media beyond the traditional methods of random matrix theory. By focusing on a number of deterministic aperiodic systems of current interest to basic optical science and technology, the ideas and computational work presented in this paper aim to introduce a broader set of interdisciplinary tools that contribute to clarify the fundamental connections among the geometrical, spectral and optical properties of deterministic aperiodic media.
2. Spectral Measures of Aperiodic Arrays
Let us first review some basic notions that are important in the discussion of light scattering by general arrays of point scatterers. A very powerful model for the study of the geometry of point patterns has been introduced in the metric theory of discrete sets. In particular, deterministic aperiodic arrays of scattering dipoles in the two dimensional Euclidean plane are examples of Delaunay, or Delone sets (These sets are also known as Delone sets from the Russian mathematician Boris Nikolaevich Delaunay or Delone, which is a transliteration from Cyrillic. Delaunay is the French version of his name that was used in his early French and German publications. Delone largely contributed to the development of modern mathematical crystallography and invented what is now called Delaunay triangulation, which became a fundamental tool to generate discrete meshes for numerical computations. In the mathematical literature his geometrical work is almost exclusively referred to as Delone sets theory). Delone sets are discrete set of points characterized by the following two properties: (a) there is a minimum separation distance between any two distinct points and half of this distance is called the packing radius
r of the set; (b) there is a positive real number, called the covering radius
R, such that every disk (or ball) of radius greater than
R contains in its interior at least one point of the set [
49,
50]. This implies that
R is the smallest radius such that closed disks of that radius centered at the points of the set covers all of it as their union. A set of points is considered uniformly discrete if it has a nonzero packing radius, and relatively dense if it has a finite covering radius. As a result, a Delone set
can be simply characterized as a point set that is both uniformly discrete and relatively dense. Notice that according to this rigorous definition a crystal is just a special Delone set with ‘sufficient order’ to produce diffraction patterns with bright spots, or delta-peaks. As it is now well-known, this diffraction condition does not require translational symmetry (i.e., periodicity) in the crystal, since it can be satisfied in aperiodic structures such as quasicrystals. Quasicrystals feature diffraction patterns with rotational symmetry axes of order
(pentagonal symmetry) or higher, which are forbidden (except the case
) by the classical crystallographic restriction theorem [
15,
50,
59]. This theorem states that the combination of translation and rotation operations restricts the total number of rotational symmetries to only the ones compatible with the periodicity of the array. We say that a structure possesses an
n-fold rotational symmetry if it is left unchanged when rotated by an angle
, and we call the integer
n the order of the rotational symmetry (or the order of the symmetry axis). Only rotational symmetries of order
and 6 match the translational symmetry of 2D and 3D periodic arrays in Euclidean space.
Traditionally, optical media have been classified as either periodic or aperiodic, without the need of further distinctions. However, the word ‘aperiodic’ encompasses a very broad range of different concepts that are useful to characterize complex structures with varying degrees of order and spatial correlations, ranging from quasiperiodic crystals to more disordered amorphous materials with diffuse diffraction spectra. A key question in the theory of aperiodic patterns regards the relationship between their structural order, determined by a given aperiodic density function and the physical properties that originate from the structure. In the case of a general point pattern (i.e., a Delone set
) with points located at position vectors
, the density function can be expressed as:
where
δ denotes the Dirac delta function associated to the position of the points in the pattern. Of particular interest is the gap-labeling theorem [
60], which provides a relationship between spatial Fourier or diffraction spectra and Hamiltonian energy spectra. This theorem, which originates within the tight-binding theory of aperiodic electronic systems, relates the positions and number of electronic energy gaps to the singularities of the spatial Fourier transform of the structure itself [
61].
The Fourier
spatial spectrum (i.e., the array factor) of a general point pattern is provided by:
It is interesting to notice that the above trigonometric sum contains in principle all the information on the nature of diffraction from an arbitrary point set. Moreover, Equation (
2) establishes a fundamental link between the diffraction geometry of Delone sets and number theory, as originally noticed by Senechal [
50]. In fact, Equation (
2) can be viewed as a generalized Dirichlet series restricted to its line of convergence, on which the delicate question of the convergence of the series still remains open.
A diffraction spectral measure (We remind that a measure on a set is a function that assigns a non-negative real number to each suitable subset of that set, intuitively interpreted as its size. The measure function must satisfy certain axioms such as countable additivity and null empty set (i.e., being zero for an empty set). As a result, a measure is a generalization of the usual concepts of length, area, and volume.)
can now be naturally associated to the power spectrum
, which is proportional to the static
structure factor and the diffraction intensity. The power spectrum
can be alternatively obtained via the Fourier transform of the autocorrelation function
of the array density, known as the autocorrelation measure in mathematical crystallography. Since
is a positive measure, according to the well-known Lebesgue’s decomposition theorem it can be uniquely decomposed in terms of three kinds of primitive spectral components, or mixtures of them, namely [
48]: pure-point (
), singular continuous (
), and absolutely continuous spectra (
), such that:
. More explicitly, we can decompose the Fourier power spectrum of a Delone set as [
50]:
where
are real numbers,
δ denotes the Dirac delta function associated to the discrete (pure-point) spectral components of the measure and
represents the continuous components (singular and absolutely continuous). From a more physical standpoint, pure-point spectral components give rise to sharp diffraction peaks while absolutely continuous measures are responsible for diffuse scattering. The remaining singular continuous component does not have a simple physical interpretation. A similar decomposition applies to the spectral measure associated to the optical transmission or energy spectra of the considered structures. Note that the support
of the pure-point spectrum is always countable and that a Delone set will diffract if it contains a countable infinity of delta functions (i.e., a so-called “Dirac comb”). Therefore a (generally aperiodic) Delone set behaves as a diffracting crystal when there is a countably infinite discrete component in its spectrum. This diffraction condition is normally satisfied by both periodic point lattices as well as by special aperiodic Delone sets known as
quasicrystals [
62,
63].
4. Structural Properties of Aperiodic Arrays
The diffraction spectra of quasicrystals consist of a countably infinite series of discrete (pure-point) components. However, it is important to realize that the diffraction q-vectors of the aperiodic Fourier space cannot be regarded as reciprocal (or dual) lattice vectors but merely as the locally varying spatial frequency (spectral) components of the point pattern.
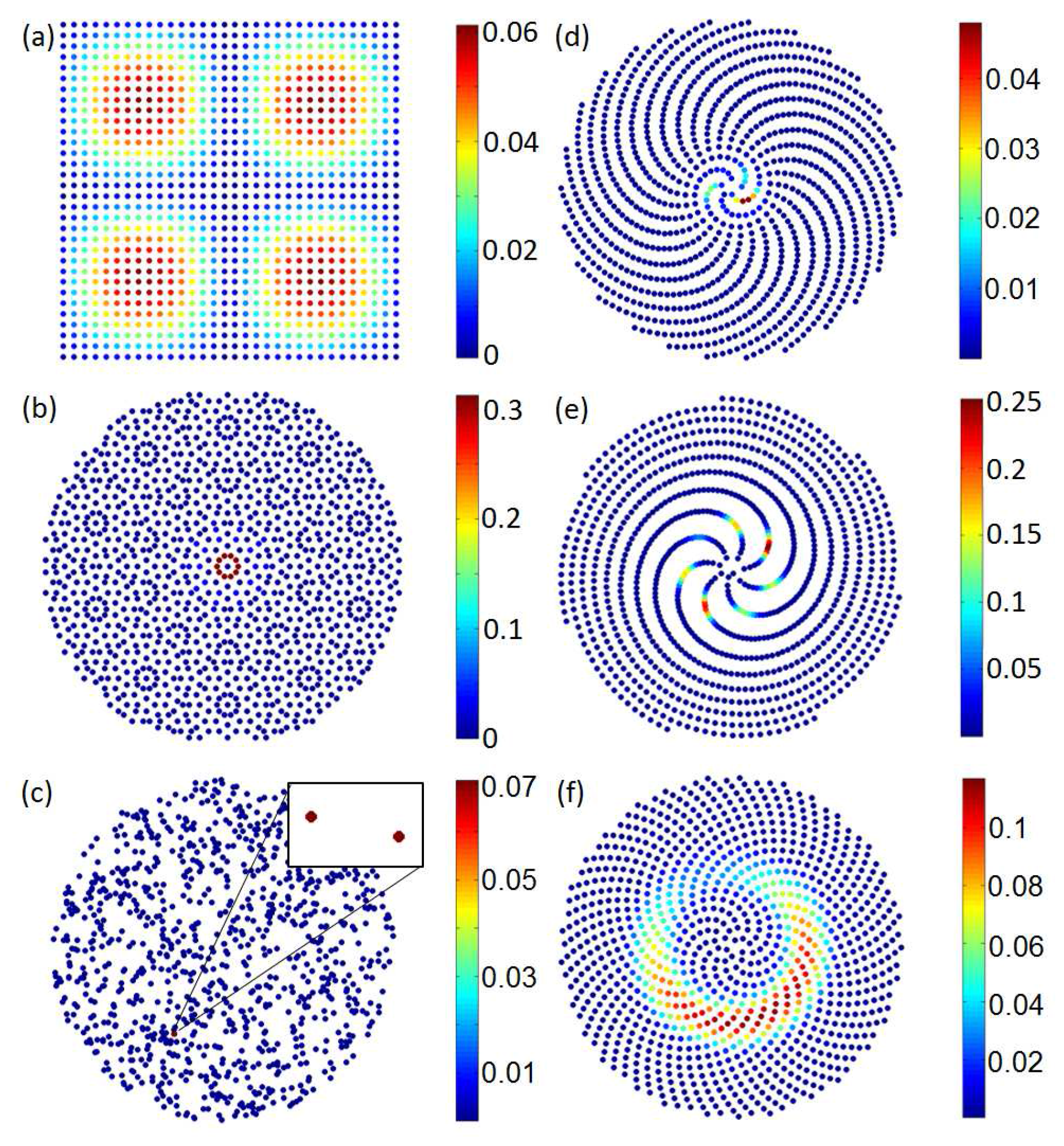
Examples are illustrated in
Figure 1a–d where we show the arrays and the corresponding structure factors for a regular square lattice and for a quasiperiodic Penrose point pattern with decagonal rotational symmetry [
66,
67]. This situation is contrasted by the scenario of a random point pattern consisting of uniformly distributed dipoles (without overlaps) in
Figure 1e. The corresponding structure factor is display in
Figure 1f, which demonstrates its structureless or absolutely continuous spectral measure. Notice that aperiodic point patterns can be designed to accommodate arbitrary rotational symmetries as well as more abstract types of group symmetries, making the study of their aperiodic Fourier space particularly attractive to optical engineering applications where isotropic and polarization insensitive responses are of great interest. In our paper, we will additionally address the structural and spectral properties of aperiodic spiral arrays.
Spiral point patterns are interesting examples of long-range ordered systems where both translational and orientational symmetries are missing. In particular, we focus on the properties of the so-called Vogel spiral arrays, which have been investigated by mathematicians, botanists, and theoretical biologists in relation to the fascinating geometrical problems of phyllotaxis [
68,
69]. Phyllotaxis (from the Greek
phullon, leaf, and
taxis, arrangement) is concerned with understanding the spatial patterns of leaves, bracts, and florets on plant stems (e.g., the spiral arrangement of florets in the
capituli of sunflowers and daisies). The field of phyllotaxis goes back to Leonardo Da Vinci (1452–1519), who described the spiral arrangements of leaves, and Kepler (1571–1639), who observed the frequent occurrence of the number 5 in plants. The history of mathematical phyllotaxis started in the first half of the nineteenth century when the brothers Auguste and Louis Bravais presented the first quantitative treatment of the phenomenon and recognized the relevance of the theory of continued fractions in this area (i.e., in the so-called cylindrical representation of phyllotaxis) [
70]. Aperiodic Vogel spiral arrays of nanoparticles are rapidly emerging as a powerful nanophotonics platform with distinctive optical properties of interest to a number of engineering applications [
42,
58,
71,
72,
73,
74,
75,
76,
77,
78]. This fascinating category of deterministic aperiodic media features circularly symmetric scattering rings in Fourier space entirely controlled by simple generation rules that induce a very rich structural complexity.
Vogel spiral point patterns are defined in polar coordinates (
) by the following equations:
where
is an integer,
is a positive constant called scaling factor, and
α is an irrational number known as the divergence angle. This angle specifies the constant aperture between successive point particles in the array. Since
α is irrational, Vogel spiral point patterns lack both translational and rotational symmetry. Any irrational number (
ξ) can be used to produce the divergence angle (
, in degrees) according to the relationship
where
denotes the fractional part of
ξ. When
ξ is equal to the golden mean (
), the resulting divergence angle
α∼
is called the ’golden angle’ while the resulting Vogel spiral structure is called the golden angle spiral, or GA spiral. This structure can be decomposed into clockwise (CW) and counterclockwise (CCW) families of out-spiraling particles lines, known as
parastichies, which stretch out from the center of the structure. Remarkable, the number of spiral arms in each family of parastichies is given by consecutive Fibonacci numbers.
Trevino et al. [
76] described the structure of a large number of Vogel spiral arrays using multifractal geometry and discovered that such structures feature a degree of local order in between short-range correlated amorphous/liquid systems and uncorrelated random systems. Moreover, it has been recently demonstrated that Vogel spiral arrays of metallic nanoparticles feature distinctive structural resonances and produce polarization insensitive, planar light diffraction across a broad spectral range, referred to as circular light scattering [
72]. The planar diffraction property of Vogel spirals is ideally suited to enhance light-matter interactions on planar substrates and recently led to the demonstration of thin-film solar cell absorption enhancement, light emission, and second harmonic generation enhancement using metal-dielectric arrays [
42,
77,
78]. Another fascinating feature of Vogel spiral diffracting elements is their ability to support distinctive scattering resonances encoding well-defined numerical sequences in the orbital angular momentum (OAM) of light [
72,
73,
74,
75], potentially leading to novel applications to singular optics and optical cryptography [
79]. Interestingly, Vogel spirals of scattering particles give rise to characteristic band-gap regions with a fractal distribution of localized band-edge modes, despite the lack of diffraction peaks in their diffraction spectra [
73,
76].
In this paper we focus on the structural properties and resonant modes of the Vogel spirals shown in
Figure 2 along with their corresponding diffraction spectra. These structures, which have been introduced in our prior publications [
74,
75]. They are named
μ-,
π- and
τ-spiral and are generated considering
,
and
, respectively. We can appreciate in
Figure 2b,d,f that all the diffraction spectra lack Bragg peaks and display diffuse circular rings instead (It is interesting to mention that disordered hyperuniform optical media exhibit similar diffraction spectra [
80]). Interestingly, despite the lack of rotational symmetry of Vogel spirals, their Fourier spectra are highly isotropic (approaching circular symmetry) as a consequence of a large degree of statistical isotropy.
Using analytical Fourier-Hankel decomposition (FHD) Dal Negro et al. [
74] recently derived closed-form expressions for the scattered (scalar) far-field and for the point pattern geometry of an arbitrary Vogel spiral arrays with divergence angle
α. In particular, it was found that the Fourier-Hankel transform of the Vogel spiral density:
can be written as:
where
is the radial wave vector associated to the radial spatial frequency
and
is the
m-th order cylindrical Bessel function of the first kind. The important thing to notice in the previous equation is that the exponential factor will contribute with azimuthal peaks when the product
is an integer. Since
α is an irrational number, this will never happen exactly but the situation can approximated by fractions that are called the convergents of the continued fraction expansion:
It is clear that for spirals generated using an arbitrary irrational number
ξ azimuthal peaks of order
m (i.e., Bessel order
m) will appear in the FHD due to the denominators
of the rational approximations (i.e., the convergents) of
. In fact, for all integer Bessel orders
the exponential sum in Equation (
6) will produce in-phase contributions in the FHD that result in strong azimuthal peaks. The number-theoretic prediction of distinctive azimuthal peaks that appear in the geometry of Vogel spirals’point-patterns is of great importance because the geometry of the pattern encodes its symmetries on the resonant states of the system, as we will confirm with our analysis later in this paper. An identical azimuthal structure carries over the solution for the diffracted far-field of Vogel spirals, which can be written as:
This result enables to “encode” well-defined values of discrete OAM uniquely determined by the rational approximations of the irrational divergence angles (or of
ξ) that appear in simple exponential sums. The superposition of many OAM modes characteristic of Vogel spirals scattered fields can provide exciting opportunities for secure optical communication and it has been actively investigated for classical and quantum cryptography [
79].
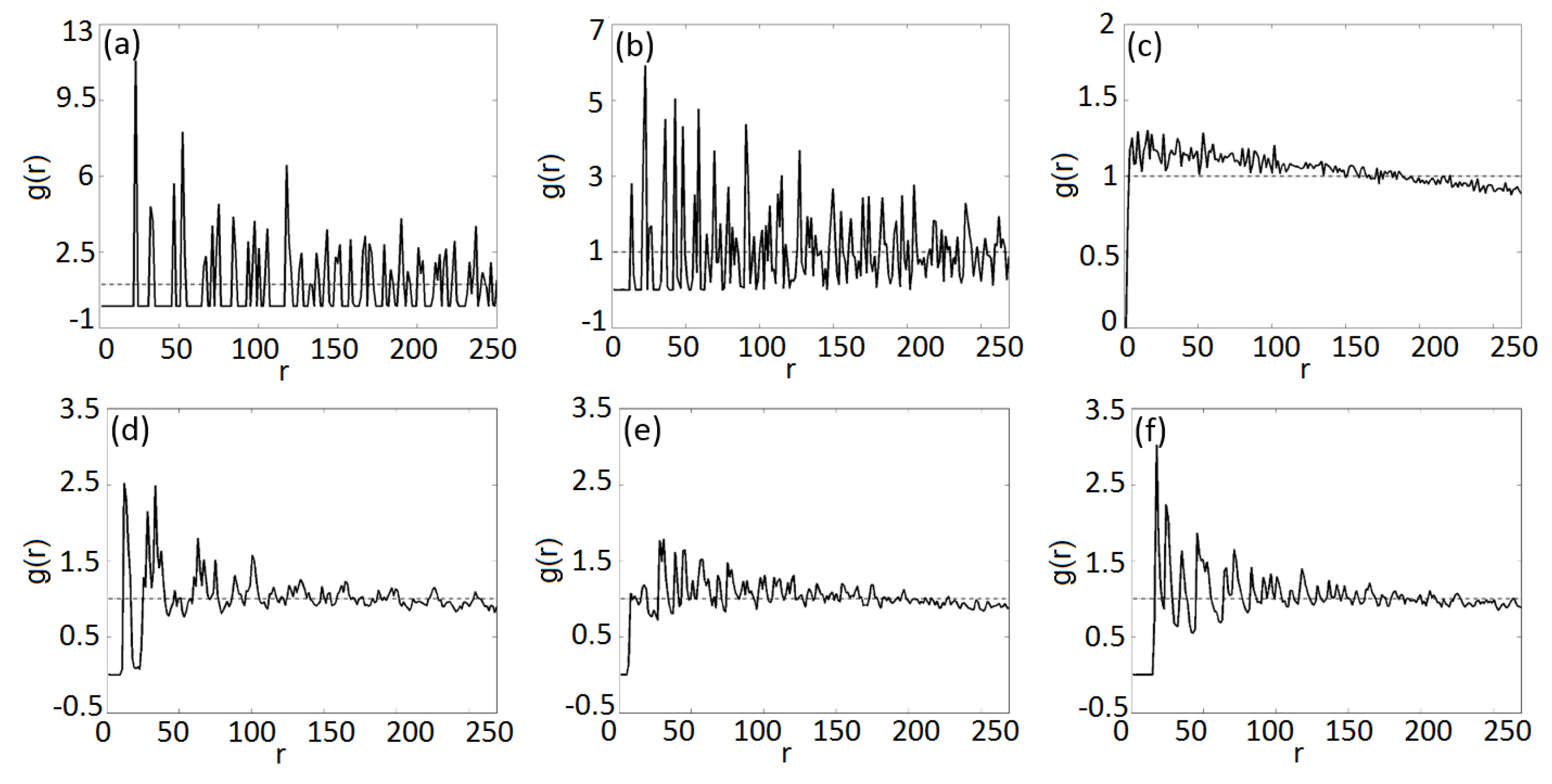
In order to extract important information on the degree of local order of aperiodic point patterns it is also important to study their radial distribution function
, which is proportional to the probability of finding two particles separated by a given distance
r. In
Figure 3 we summarize our results for all the arrays considered in the paper, which have been computed using the macro RDF for the freely available image processing and analysis software ImageJ [
81].
Clear peaks can be observed for the periodic lattice and for the Penrose quasicrystal pattern, corresponding to local coordination shells where it is more likely to find particles in the array. On the other hand for the random point pattern the is almost constant and equal to one, with minor deviations attributed to the lack of ensemble averaging (only single-realization results are shown here) and the non-overlapping point condition. In strike contrast, the of the investigated Vogel spirals reveals an intriguing structure that is somewhat intermediate between random and quasicrystalline systems. Interestingly we find that the π-spiral geometry exhibits the lowest degree of structural order, followed by the μ-spiral and by the τ-spiral, which is visibly the most “regular” of among the three. This ordering reflects the smallest number of fractional approximations that are sufficient to represent the number π compared to μ and τ, at any level of accuracy. The smaller this number the smaller will be the number of azimuthal spectral peak components in the Fourier-Hankel coefficients, thus reducing the local order in the structure. This exact criterion is also consistent with the visibly richer structure of the diffraction spectrum of the π-spiral. Differently from the case of Penrose patterns, our results demonstrate that the degree of local order in Vogel spiral structures can be deterministically tuned between amorphous and almost completely uncorrelated random systems by controlling the divergence angle α, which controls the aperiodic geometry of the structures.
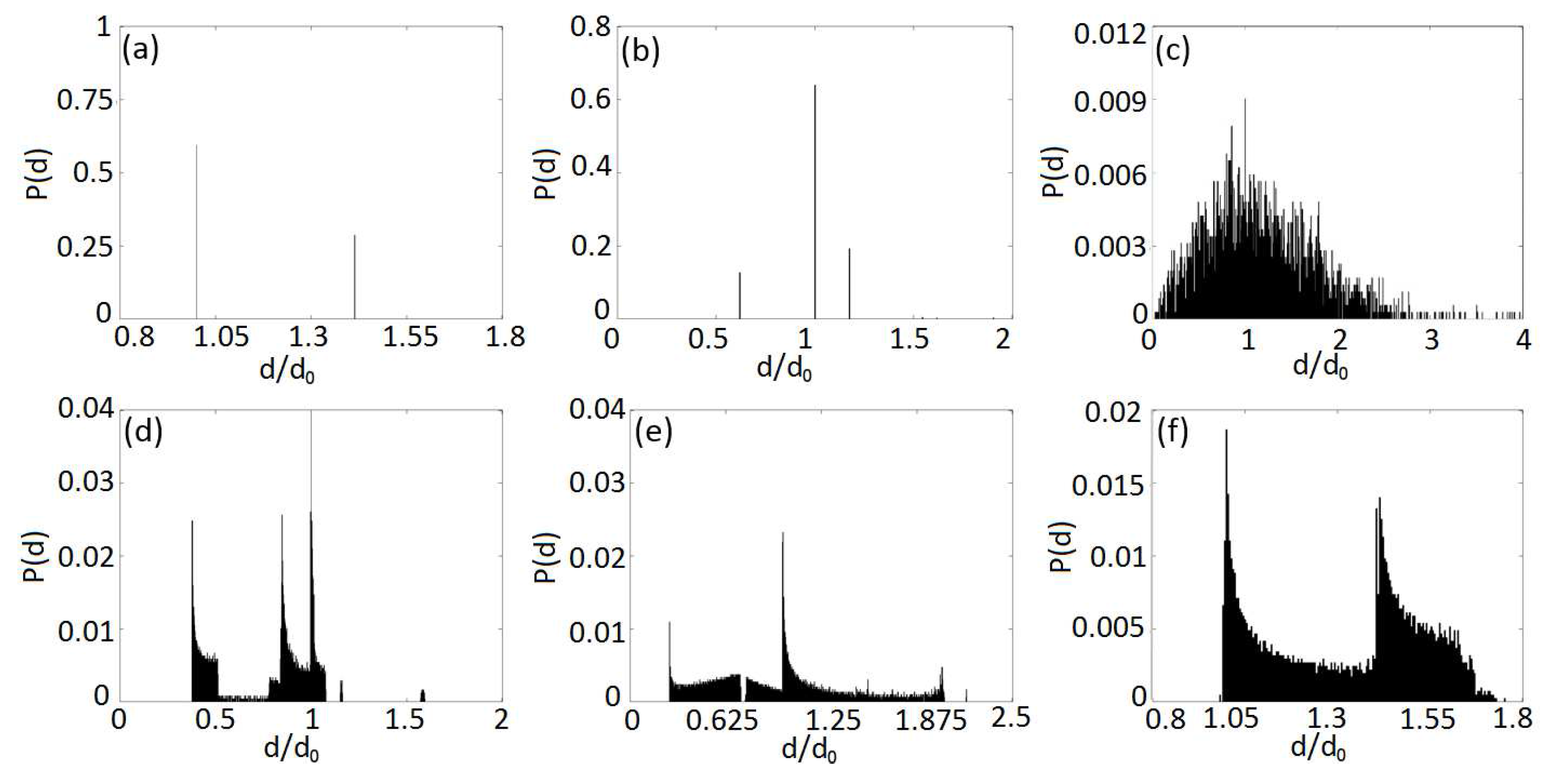
We have also investigated the geometrical properties of our structures by considering the spatial distribution of the distance
d between neighboring particles that can be obtained by performing a Delaunay triangulation of the point patterns. This spatial pattern analysis technique provides information on the statistical distribution of the first neighbor distance and measures the spatial uniformity of a given point pattern. In
Figure 4 we show the calculated statistical distributions of the spacing parameter
d normalized by
, which corresponds to the most probable value (where the distributions are peaked). In the case of homogeneous aperiodic structures the most probable value
was generally found to be close to the average inter-particle separation. For the square lattice in
Figure 4a only two values of
d can be detected, corresponding to the vertices of the Delaunay triangulation connected by straight or by diagonal edges. Interestingly, in the case of the triangulated Penrose point-pattern (
Figure 4b) only three separations are dominant, while additional contributions have negligible intensity. The random point pattern in
Figure 4c feature a very broad and almost symmetric distribution of distances, as expected in a uniform structure. In sharp contrast, the probability distributions obtained for the three Vogel spiral arrays, shown in
Figure 4d–f, present large fluctuations and are distinctively non-Gaussian with slowly decaying tails.
These characteristic geometrical fluctuations are very broad for the π-spiral while they are less severe in the case of the more regular μ- and τ-spirals, in agreement with the picture established by the radial correlation function analysis. It is also striking to observe clear gaps in the distance statistics of Vogel spirals separated by regions of almost uniform fluctuations.
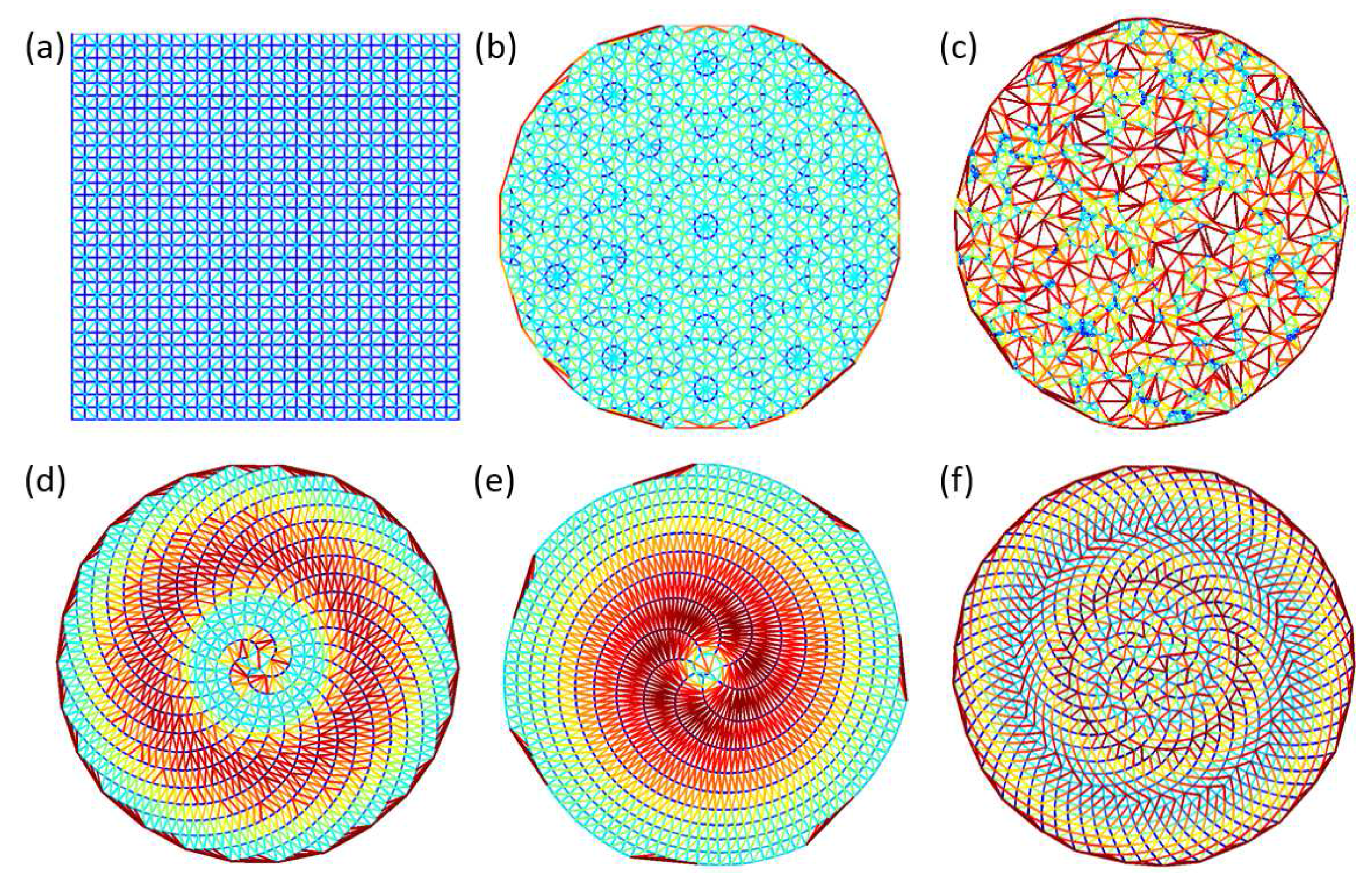
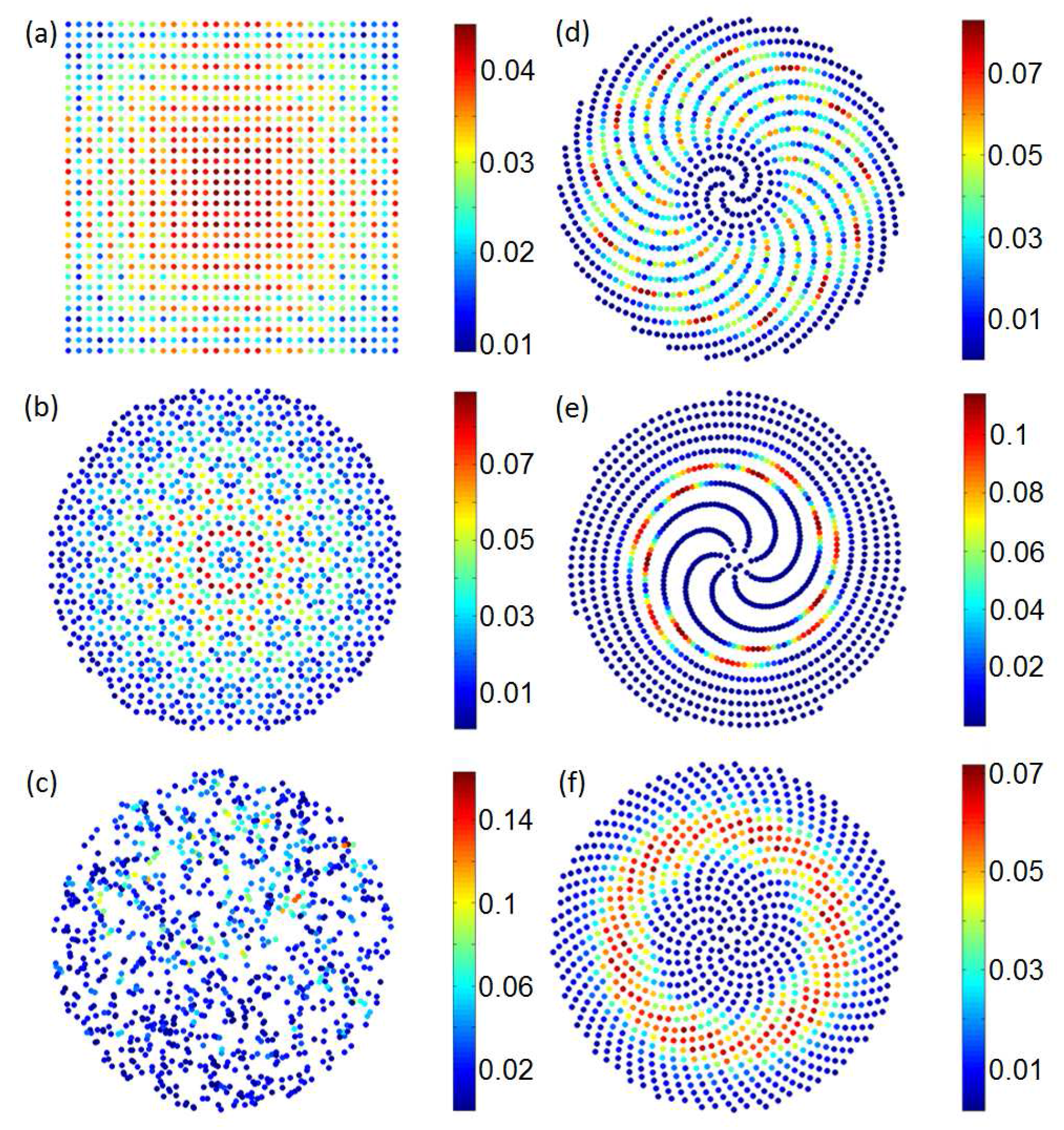
In order to better understand the unique features of the Vogel’s spiral geometry, it is very instructive to perform spatial Delaunay triangulation analysis using the color-coded edge length in order to visualize the distribution of neighboring distances in the different structures [
73,
76]. This method identifies very clearly the spatial regions of the structures where the values of neighboring lengths appear more frequently. In
Figure 5 we summarize our results for all the investigated structures. Each line segment in the Delaunay triangulations connects two neighboring particles on the array and the edge length
d is color-coded with increasing numerical values from blue to red color. In this analysis, simple periodic (
Figure 5a) or quasiperiodic structures (
Figure 5b) appear uniform in color while random arrays (
Figure 5c) contain a wide gamut of colors due to their broader distribution of distances. Moreover, it is evident that the color-coded triangulation unveils the quasi-crystallographic rotational symmetry of the Penrose array. On the other hand, the distinctive spatial order of Vogel spirals is manifested by the presence of circularly symmetric bands of similar edge lengths. The more diffuse and broader central region visible in
Figure 5e for the
π-spiral is consistent with its irregular structure characterized by more significant spatial fluctuations with respect to the Vogel spirals in
Figure 5d,f. Azimuthally symmetric regions of Vogel spirals with almost constant values of the separation
d alternate radially across the structures, creating effective ‘radial heterostructures’ that can, similarly to circular gratings, spatially localize radiation in the radial direction. The formation of the distinctive radially localized resonances of Vogel spirals, which will be rigorously investigated using the spectral Green’s matrix method later in the manuscript, can be qualitatively understood based on this characteristic geometrical feature. The point patterns analysis methods introduced in this section unveil subtle structural correlations that enable to quantitatively compare the geometry of different aperiodic structures. In order to extend our geometrical approach, we will introduce in the next section additional metrics that deepen our understanding of the salient geometrical features of complex aperiodic structures. In this context we propose a robust methodology, originally developed in the context of graph and network theory, that can even capture relevant characteristics of the localized optical modes supported by aperiodic arrays uniquely based on their local connectivity.
5. Aperiodic Arrays and Spectral Graph Theory
The primary objects of graph theory are graphs, which are mathematical structures used to model pairwise relations between objects. Graphs, initially conceived as convenient tools for the study of molecular structures in chemistry, are now among the primary concepts of discrete mathematics and found numerous applications to physics (e.g., tight-binding models), neuroscience, linguistics and computer science where they model networks flows and communication streams, data structures, etc. [
53,
54]. In what follows we apply graph theory to better analyze the distinctive geometry of aperiodic patterns. This is achieved by studying the graph structure of the Delaunay triangulation associated to each point pattern. In addition, we will investigate the spectral properties of Laplacian operator defined on graphs. Before we proceed with our discussion, let us introduce some basic notions of graph theory.
A graph is composed of vertices (nodes, or points) that are connected by line segments called edges. More precisely, a simple (In this context the adjective ’simple’ means that the graph is unweighted (each edge has the same unit length), undirected and it does not contain loops or multiple edges connecting the same pair of vertices.) graph is an ordered pair comprising a set V of vertices together with a set E of edges such that each edge is associated with two vertices. A weighted graph is a graph in which a numerical weight (a real number w) has been assigned to every edge. The degree of a vertex in an unweighted graph is the number of edges in which it is involved. Simple graphs are named regular if every vertex has the same degree d. When dealing with weighted graphs, we should consider the weighted degree of a vertex, which is the sum of the weights of the attached edges.
The key idea of spectral graph theory is to study graphs through the spectral properties (i.e., eigenvalues, and eigenvectors) of symmetric matrices associated to them, such as the adjacency matrix or the graph Laplacian matrix. In short, graph spectral theory addresses the relationship between structural and spectral properties of graphs. Since we can associate a graph to any aperiodic point patter via its Delaunay triangulation, we propose here to apply spectral graph theory methods in order to investigate the structure-property relationships of the aperiodic graphs associated to deterministic aperiodic arrays.
The first operator that is typically associated to a graph
G is represented by the
adjacency matrix defined by:
For a graph with n vertices, is an symmetric matrix (The adjacency matrix is always symmetric because we are considering only simple graphs and simple graph are undirected.) that associates to each pair of connected vertices in the graph the weight of their connecting edge. If the graph is unweighted, then the weight for connected vertices and otherwise. Clearly the elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph. In our study the weights of the vertices of the graphs are simply the lengths of edges of the Delaunay triangulation corresponding to the aperiodic point patterns. The adjacency matrix of undirected simple graphs is symmetric and therefore it has a complete set of real eigenvalues and an orthogonal eigenvector basis. The set of eigenvalues of a graph is the spectrum of the graph. Many important structural properties of a graph are ‘encoded’ in its spectrum.
We then consider the the
degree matrix that is a diagonal matrix stores along its diagonal all the values of the degrees of each vertices in the graph:
where
is a vector containing the (weighted) degrees of all the nodes.
Based on the adjacency and degree matrices we can define the
graph Laplacian matrix as:
and the
random walk Laplacian (or ‘diffusion matrix’) as:
The Laplacian matrices of weighted graphs arise in many different applications. For example, they appear when applying the finite difference discretization schemes to solve Laplace equation with Neumann boundary conditions. They also arise in the modeling of diffusion through networks, where a quantity ϕ diffuses over time through a graph G. Given the initial values for the diffusing quantity ϕ, as time progresses they diffuse smoothly to their neighbors via the edge connections and eventually the whole system settles to the same value at equilibrium. This process is called graph diffusion. In the case of a simple path (A path in a graph is a finite sequence of edges which connect a sequence of vertices that are all distinct from one another), the eigenvalues and eigenvectors of the graph Laplacian corresponds to the oscillation frequencies and vibrational modes of the corresponding discretized string. For simple graphs the Laplacian matrix has non-negative eigenvalues and stores the degree of each node of the graph along its diagonal. We will see in this section that the eigenvectors of the graph Laplacian associated to the edge-weighted Delaunay triangulation of aperiodic arrays allows to identify distinctive geometrical resonances in aperiodic arrays.
The smallest non-zero eigenvalue of is called the spectral gap. The second smallest eigenvalue of is the algebraic connectivity of the graph G. This eigenvalue is greater than 0 if and only if G is a connected graph. The magnitude of reflects how well connected is the graph G overall. The connectivity of a graph is defined as the minimum number of elements (nodes or edges) that need to be removed in order to disconnect the remaining nodes. The algebraic connectivity is bounded above by the vertex connectivity of the graph. Finally we mention an important variant of the graph Laplacian that is known as the random walk Laplacian. The random walk Laplacian of G encodes the dynamics of a random walk on the graph. The random walk on a weighted graph moves from a vertex a to its neighbor b with probability proportional to . The walk matrix is used to study the evolution of the probability distribution of a random walk. As the eigenvalues and eigenvectors of provide information about the behavior of a random walk on G, they also provide information about the graph itself. We will not consider random walks on graphs in this paper.
In
Table 1 we summarize the important graph-based topological parameters associated to the unweighted Delaunay triangulations of each array, all considering
. We can observe that all the arrays have comparable average inter-article separation (scaled by the wavelength)
but vary in their minimum inter-particle distance
significantly. Due to the its homogeneously disordered nature the random array features the smallest
. In order to deepen our understanding of geometrical structures we also computed their average node degree
, which is the average number of links per node.
can readily be obtained from the diagonal entries of the graph Laplacian matrix. We notice that the average node degree does not vary significantly across the different structures due to the homogeneous nature of their Delaunay graph. However, significant differences can be observed by considering the Pearson correlation coefficient
R, also known in graph theory as the
assortativity coefficient. This parameter measures the spatial correlations between nodes of similar degree and it can be computed as [
54]:
where
is the node degree of the
j-th node,
and
is the standard deviation of the node distribution
. In general,
R lies between
and 1. Positive values of
R indicate a spatial correlation between nodes of similar degree, while negative values indicate relationships between nodes of different degree (non-assortativity). Typical social networks are assortative as opposed to biological networks that, due to their tendendy towards a disassortative equilibrium state, are often found to be disassortative [
54]. Interestingly, the graph topology of all our structures is disassortative except the
τ-spiral, which is assortative. This property reflects the more regular and homogeneous geometry of this structure.
Next we calculated the
Newman global clustering coefficient C of the graphs, which measures to what extent nodes in a graph tend to cluster together. This metric is based on cluster triplets, which are three connected nodes. The global clustering coefficient is defined as [
53,
54]:
where
is the number of triangles (A triangle is formed by three closed triplets, one centered at each node.) and
is the number of paths of length 2 in the network that can be obtained by the formula
. The number of triangles can be obtained directly by using the spectral property of the adjacency matrix as
. Only small differences can be detected in the global clustering behavior of the graphs. Furthermore, it is of interest to consider the local clustering properties of the graphs, that are captured by their Watts-Strogatz index
, where
N is the total number of nodes.
We will now study more in detail the spectral properties of the graph Laplacian
. The algebraic connectivity AC of each graphs, which indicates how well connected is a given graph G overall, is listed in
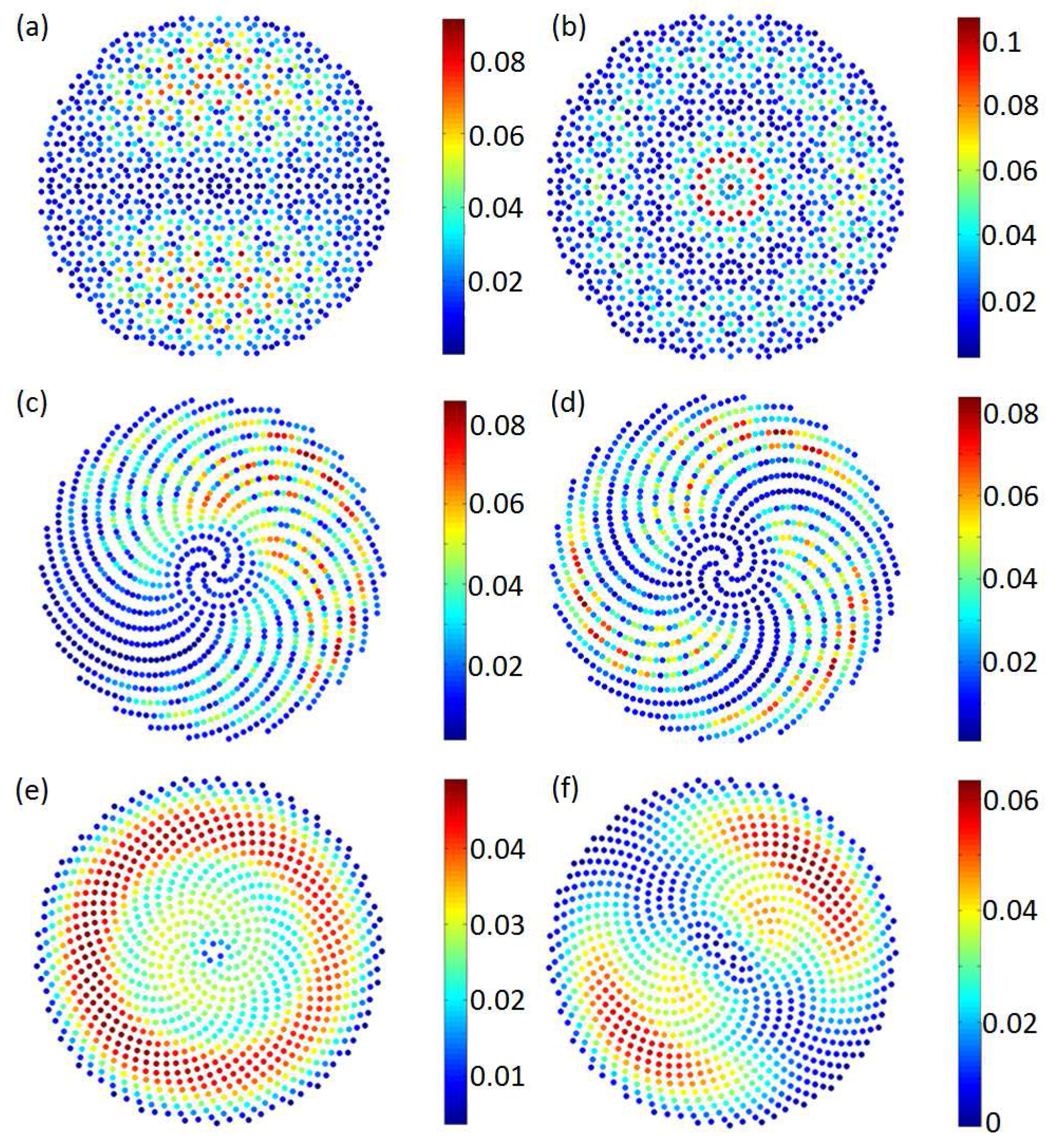
Table 1. We then turn our attentions to the eigenvectors of the graph Laplacian, which form an expansion base for the characterization of the graph geometry of the array. We consider here the weighted graph Laplacian with weights equal to the edge lengths of the Delaunay triangulation. In
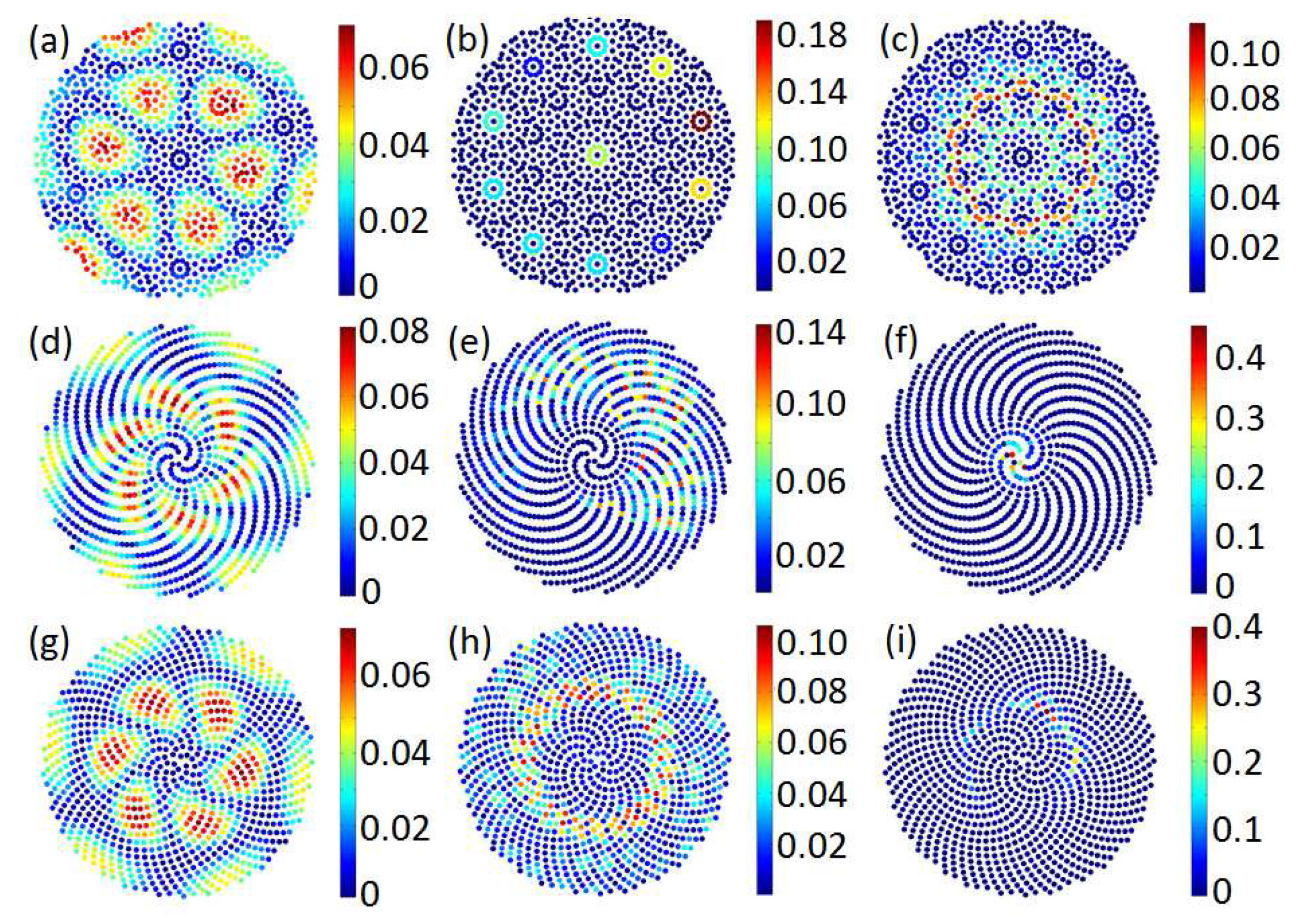
Figure 6 we show some representative eigenvectors of the weighted graph Laplacian. Their spatial structures correspond to what we call the
geometrical resonances of deterministic aperiodic arrays. We notice that the spatial distributions of the geometrical resonances with the smallest eigenvalues are similar to the (scalar) resonant modes of a cylindrical cavity described by a wavefunction
characterized by radial and azimuthal mode indices. However, due to the non-homogeneous nature of the underlying aperiodic graph, these resonances are not perfectly circularly symmetric, as it can be easily appreciated in the case of the Vogel spirals (
Figure 6d,g).
By investigating the geometrical resonances with larger eigevalues we discovered that spatial distributions that are very similar to the most localized electromagnetic field resonances of the vector point patterns can be obtained. This close correspondence is highly remarkable since the modes of the graph Laplacian originate from purely topological/interconnectivity properties of aperiodic graphs, and do not have a direct physical meaning outside the scalar theory of diffusion on graphs. Nevertheless, as shown by the results in
Figure 6 and the comparison with the electromagnetic modes discussed later in the paper (see Figures 18–20), our graph theory approach to aperiodic structures not only help to quantitatively capture their structural properties but it also reveals, at minimal computational cost, essential features of the resulting optical resonances.
In order to study the optical resonances of our arrays and their spectral statistics we will now turn our attention to the electromagnetic spectral Green’s matrix method that provides a rigorous solution to the multiple scattering problem for arrays of vector point scatterers.
6. The Green’s Matrix Method
The Green’s matrix method (The Green’s matrix method should not be confounded with the coupled-dipole method as the latter term is often used when an external excitation is included while treating light propagation in an assembly of discrete dipoles.) is a powerful tool that has been primarily applied to the study of wave propagation in random media. The method relies on the analysis of the spectra of the Green’s matrix, which is an important class of the so-called Euclidean random matrices that appear in Random Matrix Theory (RMT) [
82]. In general terms, the elements of an Euclidean random matrix are determined by a function of the positions of pairs of randomly distributed points in the Euclidean space. In particular, Hermitian Euclidean random matrices have important applications in disordered superconductors [
83], supercooled liquids [
84], diffusion of particles, and scalar phonon localization [
85]. In recent years, however, the interest on non-Hermitian random matrices such as the Green’s matrix has significantly increased due their applications in the theoretical description of open and dissipative systems. In particular, the study of the spectra of Green’s matrices unveiled important information about structural resonances in disordered systems. Indeed, the numerical analysis of Green’s matrices has been successfully employed to address different aspects of light propagation in open random media, such as Anderson localization of light [
55,
86,
87,
88,
89] and matter waves [
90], random lasing [
91,
92,
93], light transport in nonlinear media [
94], and superradiance in atomic random systems [
95,
96,
97,
98]. An analytical theory has also been developed for the eigenvalue density of random Green’s matrices, providing fundamental insights into light-matter interactions in disordered media [
93,
99,
100]. However, the applications of the Green’s matrix method has been mostly confined to random media so far. In our work we apply this approach to random as well as deterministic arrays and shed some light on their unique spectral properties. Before discussing our results, we will first review the Green’s matrix method in the general context of the electromagnetic multiple scattering formulation for discrete media (i.e., point patterns).
The Green’s matrix method describes the vector light propagation in a system of identical, point-like dipoles arbitrarily positioned inside a homogeneous medium (typically in vacuum). This approach is perfectly suitable to investigate the electromagnetic scattering properties of both random and deterministic point patterns. The
T-matrix
describes light scattering by one particle and exhibits a scattering resonance at frequency
with linewidth
[
56]. The total
T matrix of an assembly of
N scatterers at the positions
is given by:
where
is the unit matrix,
and
are, respectively, the incident and the scattered wave vectors, and in the far field
. The elements of the
-matrix represent the general electromagnetic dyadic Green’s function that is calculated from the relative positions of the
N dipoles [
57] as:
It is important to emphasize that multiple scattering contributions (i.e., all scattering orders) are treated exactly within the Green’s matrix method in Equation (
15) and the only approximation involved is the description of the scatterers as vector point dipoles. Hence this method is particularly suited to treat light propagation in cold atomic clouds, where it has been extensively applied [
95,
96,
97,
98], but it also provides fundamental insights into the complex optical physics of aperiodic scattering systems with a large number of components.
Equation (
15) contains all the information on the electric field scattered by the ensemble of dipoles, and it requires the diagonalization of the
scattering matrix:
The
T-matrix describing one single scatterer
can be expressed as a Neumann-Born series [
101]:
where
is the optical scattering potential for a point scatterer and
is the return Green’s function, i.e., the dyadic Green’s function
evaluated at
. In contrast to the analogous scattering formulation for quantum mechanical waves, the optical scattering potential is frequency-dependent and for a point dipole at position
takes the form:
where
is the polarizability of the scatterer [
101].
Equation (
16) shows that the matrix elements of the Green’s function
exhibit singularities at
. However, this feature can be easily handled by regularisation [
101]:
where the inverse length scale parameter
provides the resonance position
and resonance width
of a single dipole by the relations
and
, respectively. Using Equations (
20) and (
18), we can write:
where Equation (
19) has been used. Assuming that
(for an atom, typically
we can consider, close to the resonance,
and introduce the detuning parameter
. We can then rewrite the total scattering matrix
in (Equation (
17)) as:
Notice that the only frequency dependence of the total scattering matrix (
22) near resonance is contained in Δ. Very importantly we can now realize from Equation (
22) that in order to obtain the global
T-matrix in Equation (
15) we need to diagonalize the Green’s matrix
, which is
independent of the frequency detuning Δ. Notice that Equation (
22) crucially depends on the geometric structure of the scattering system, which makes the Green’s matrix method ideally suited to investigate structure-property relationships in aperiodic structures.
The Green’s matrix Equation (
16) fully takes into account the vector character of light, but its scalar approximation
has been frequently used to simplify the problem [
55,
99]. Although the scalar version of the Green’s matrix method has been successfully applied to describe several aspects of light propagation in disordered media, it seems to fail to treat the regime of Anderson localization, when light diffusion comes to a halt due interference effects. Indeed, there is numerical evidence of absence of Anderson localization for vector waves in three dimensions for ensemble of point scatterers at the same optical densities where Anderson localization is expected to occur for scalar waves [
86]. This result is related to the near-field coupling between scatterers that becomes important at high optical densities, and which is more relevant for vector waves. Indeed, note that in the vectorial case, the Green’s function Equation (
16) has a
singularity for
related to the intrinsic transverse nature of electromagnetic waves. In contrast, in the scalar case the singularity of the Green’s function (
23) at
is weaker, a fact that may play a crucial role at high optical densities, where Anderson localization is expected to occur [
86]. Interestingly, this near-field dipole-dipole coupling was shown to be suppressed by the application of an external magnetic field, which can induce a transition from extended to localized states for light in an ensemble of point scatterers [
98].
7. Spectral Properties of Aperiodic Arrays
It is possible to extract important physical information on scattering arrays from the distribution of eigenvalues Λ of the Green’s matrix in the complex plane. Indeed, the real and imaginary parts of Λ are related to the relative widths
and frequency positions
of the scattering resonances of the arrays, respectively [
55]:
From Equation (
24) we can see that a clustering of eigenvalues around the value Re
evidences the formation of a band of long-lived modes (i.e., with very small Γ). This situation is very well understood for random systems of point scatterers where analytical random matrix theory can often be applied, but it remains to be investigated for deterministic aperiodic systems. We address this issue in the present paper, where we systematically explore the characteristic resonances and complex eigenvalue distributions of the Green’s matrix for periodic, quasiperiodic, random, and deterministic aperiodic systems of point particles on the plane.
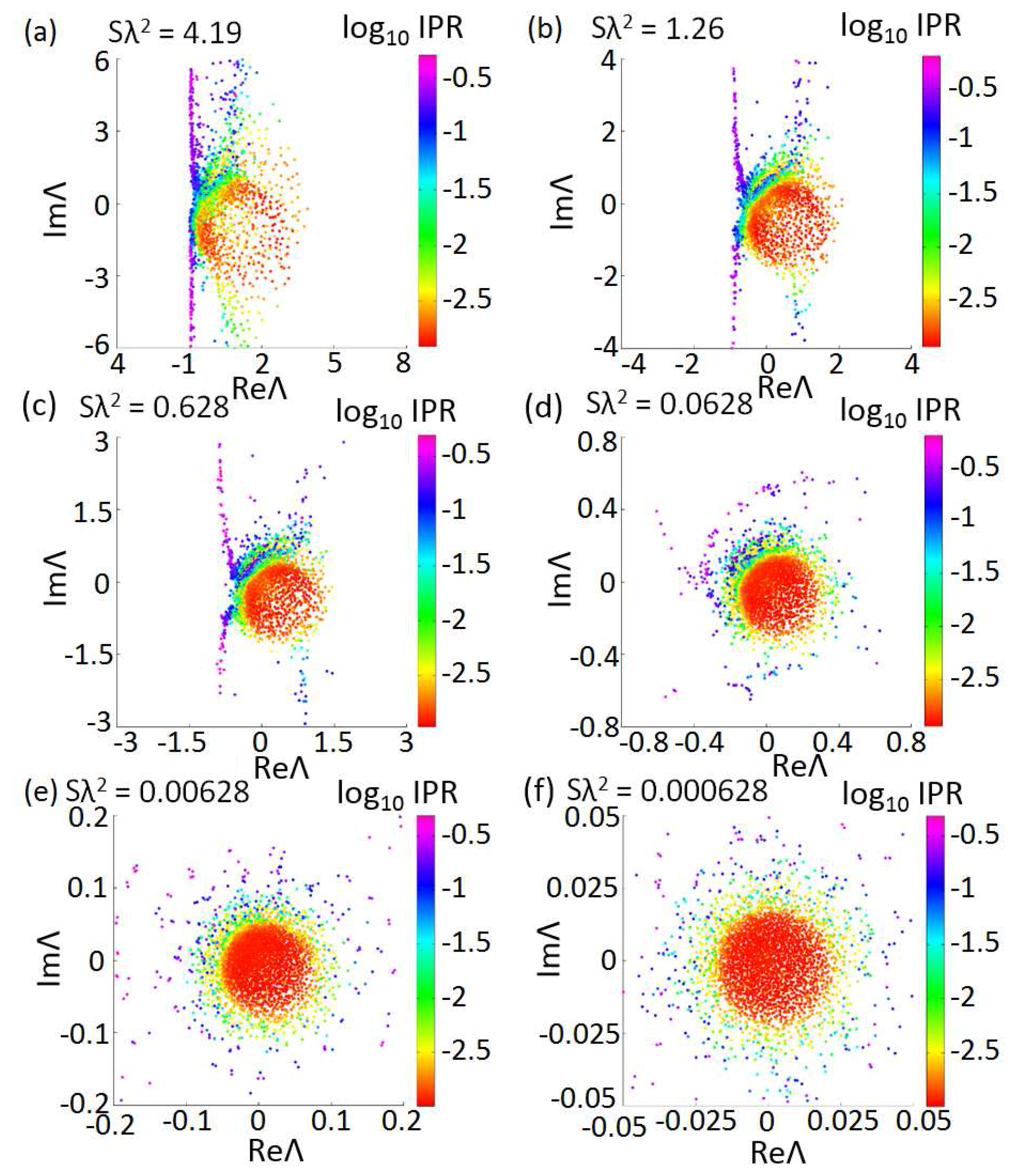
In
Figure 7 we show our results for the distributions of complex eigenvalues Λ of the Green’s matrix (
16) that correspond to a periodic square array of
dipoles. In our analysis we consider different values of the optical density, which measures the number of scatterers in the array per wavelength squared and can be interpreted as a measure of the ’scattering strength’ in the system. All the eigenvalues are color-coded with respect to the IPR value of the corresponding eigenvectors, so that their spatial localization character becomes immediately apparent. The IPR of a given state is defined as:
where
is the (unit) eigenvector of the Green’s matrix for the mode of frequency
. The eigenvectors are normalized so that the obey the condition
. The IPR measures the degree of spatial localization of the eigenvectors of the system. An eigenvector extended over all the
N scatterers is characterized by
, whereas an eigenvector localized on a single point has
.
The results in
Figure 7 clearly show the presence of appreciable spectral gaps in the eigenvalue distributions that are the result of the periodicity of the structure. Contrary to the case of homogeneous random systems, we can appreciate that the complex eigenvalues of the periodic array are non uniformly distributed in the complex plane. This is the consequence of the periodic spatial correlations that are present in the square array. Moreover, the finite size of the array also introduce additional resonances that are strongly influenced by the square shape of the array for small values of the optical density as sown in
Figure 7e,f. These resonances are similar to the optical modes of supported by a homogeneous square cavity and are not significantly affected by the the optical density of the array (granted that it remains small enough). It is ultimately the complex interplay between the array periodicity, size and its overall shape that determines the rich features observed in its spectral distributions.
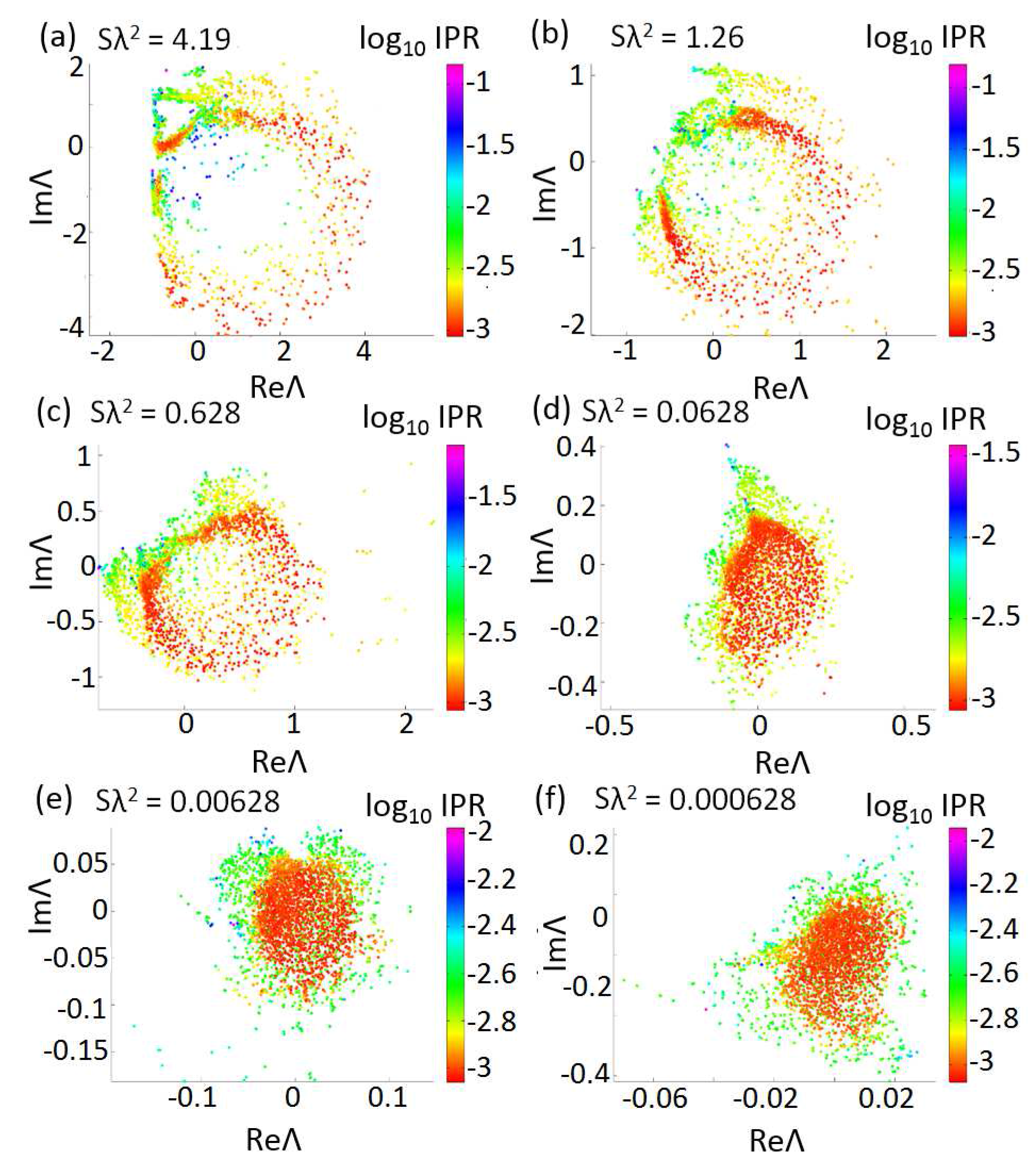
Figure 8 shows our results for the quasiperiodic Penrose array with
point s scatterers. Interestingly, we can clearly appreciate that despite the lack of global periodicity the Penrose array supports spectral gap regions for large enough values of the optical density, corresponding to the strong resonant scattering regime. It is also worth noticing that the spectral gaps suddenly disappear as the values of the optical density are reduced. This behavior is indicative of a characteristic threshold for band gap formation in quasiperiodic structures, which has indeed been discovered experimentally for Penrose quasicrystals [
102]. Moreover, differently from the periodic square array, the distribution of the complex eigenvalues of the Penrose array approaches a homogeneous circular disk for small values of the optical density (i.e., weak scattering). This behavior is clearly associated to the circular shape of array that resonates similarly to a homogeneous disk in the limit of very small optical density. The highly structured complex distributions observed at larger densities betrays the correlated nature of the Penrose structure but cannot presently be described by the conventional theoretical models based on random matrix theory [
82].
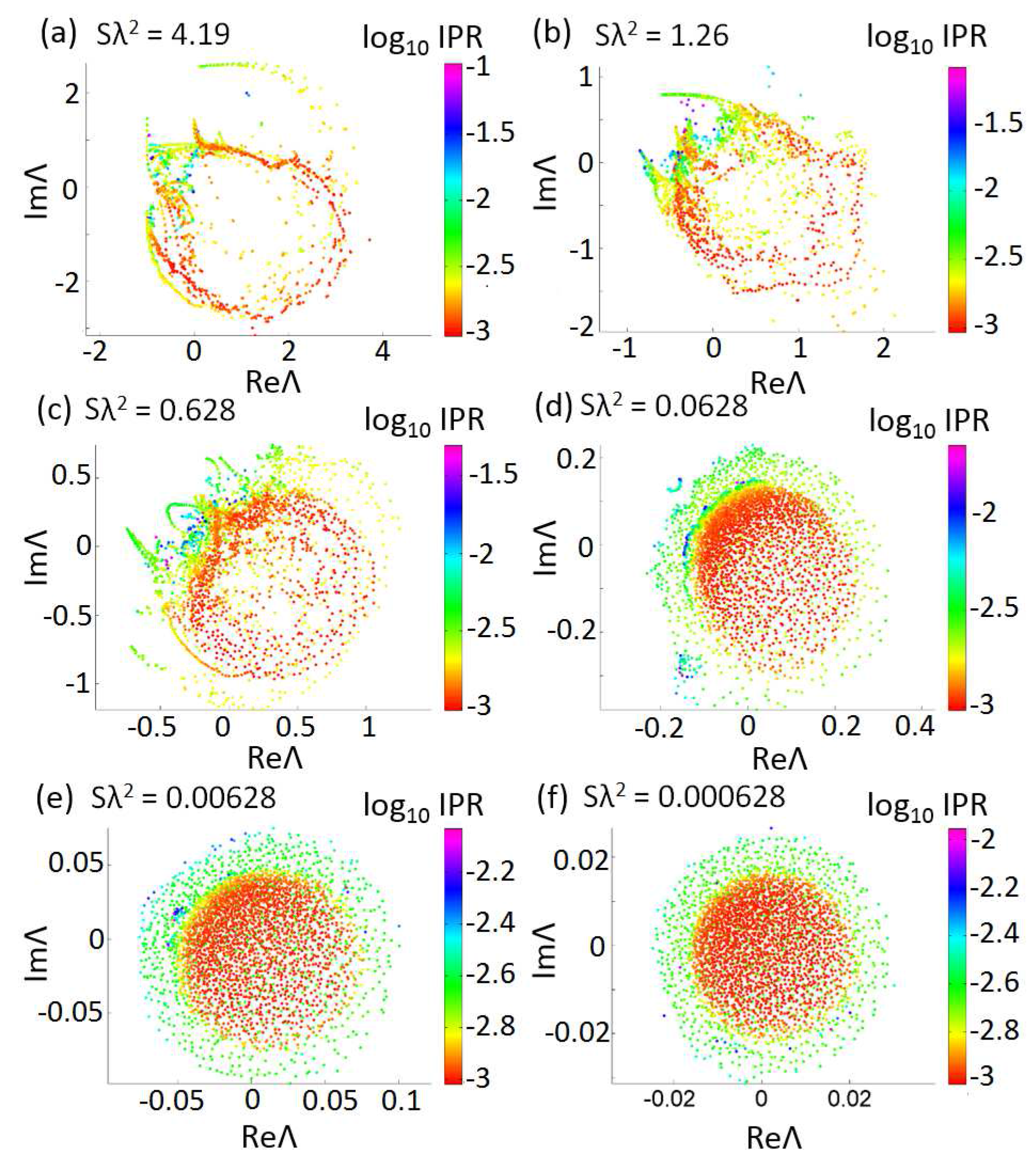
Figure 9 shows the eigenvalue Λ distribution of the Green’s matrix (
16) for a typical configuration of
scatterers randomly located inside a circular region for different values of the optical density. Generally speaking, we observe that these distributions converge to circular disks and become highly uniform. However, it is interesting to note the presence of distinctive spiral arms that are visible even at low values of the optical density. For random systems that these spectral regions are typically populated by long-lived resonances, localized over a small number of scatterers, down to only two particles. It is known that already for systems of only two scatterers randomly placed within the wavelength of the scattered wave field extremely narrow resonances can appear [
55]. Furthermore, in the case of three or few scatterers collective resonances may appear in the spectrum in close analogy to the quantum mechanical Efimov’s effect [
103]. Simulations based on the scalar Green’s function approximation has shown that even for a large system of many particles such electromagnetic resonances can occur [
55]. These subradiant quasi-modes are called
proximity resonances. Importantly, they are not related to Anderson wave localization because they do not require multiple scattering in order to occur [
55,
99].
At very small optical density (
Figure 9e–f) we notice that the circular distributions of complex eigenvalues become more uniform but the spiral branches are not completely suppressed even if the scattering strength in the system becomes very weak in the limit of small optical density. Unfortunately, in the absence of analytical results for
open two-dimensional systems with aperiodic order we cannot account for the details of the distribution of complex eigenvalues. However, physical information can be gained by studying the corresponding eigenvectors of the system.
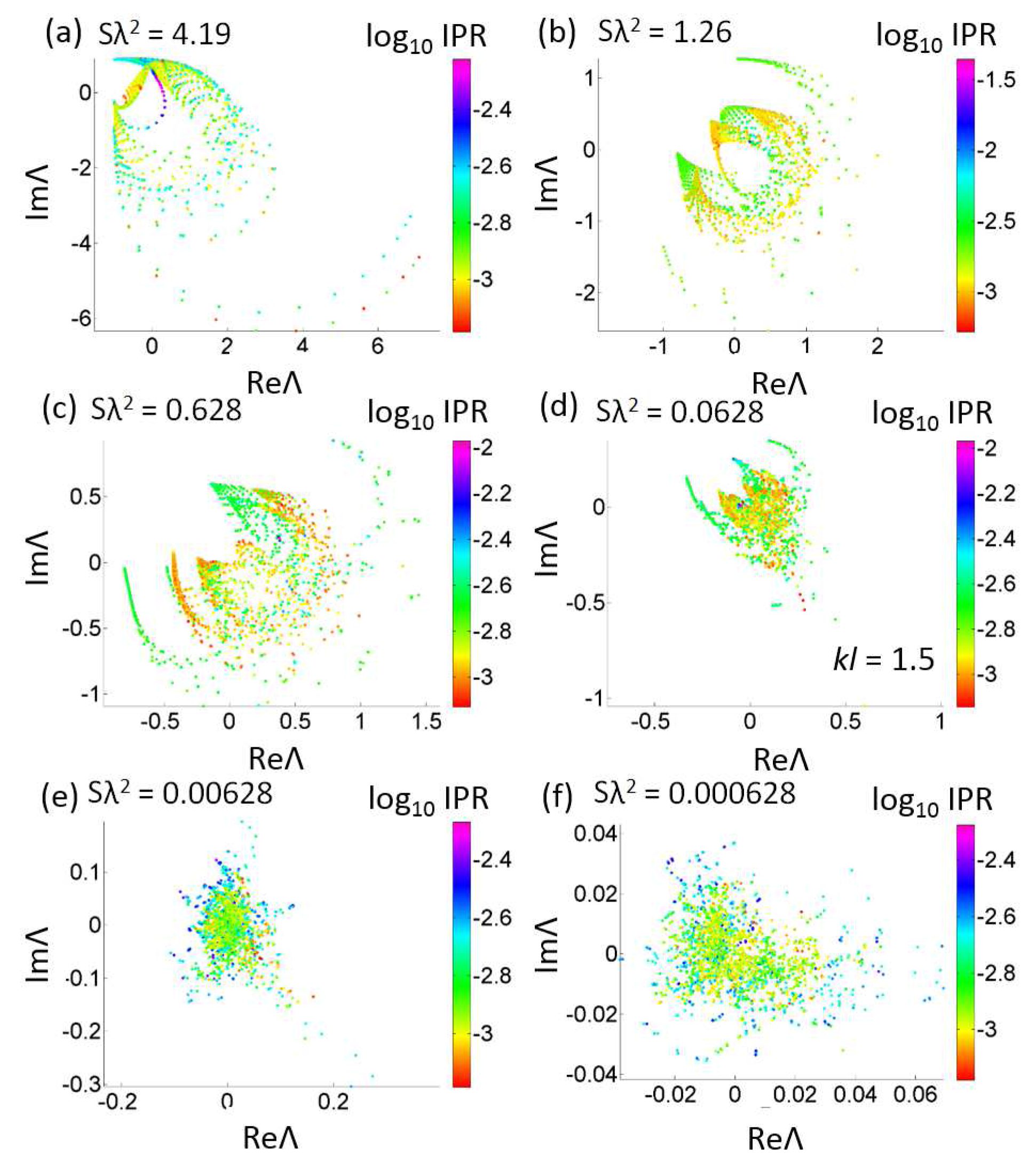
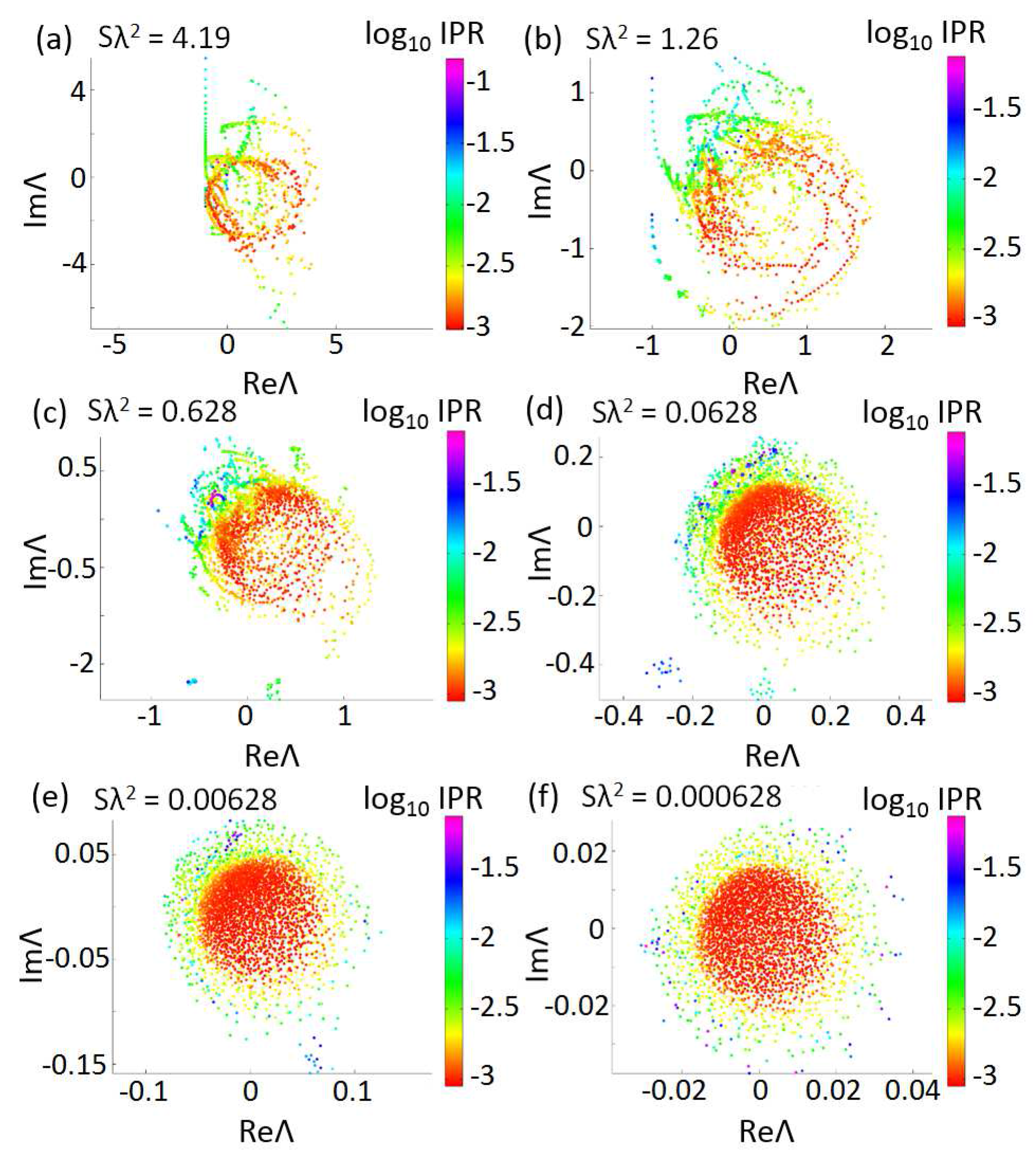
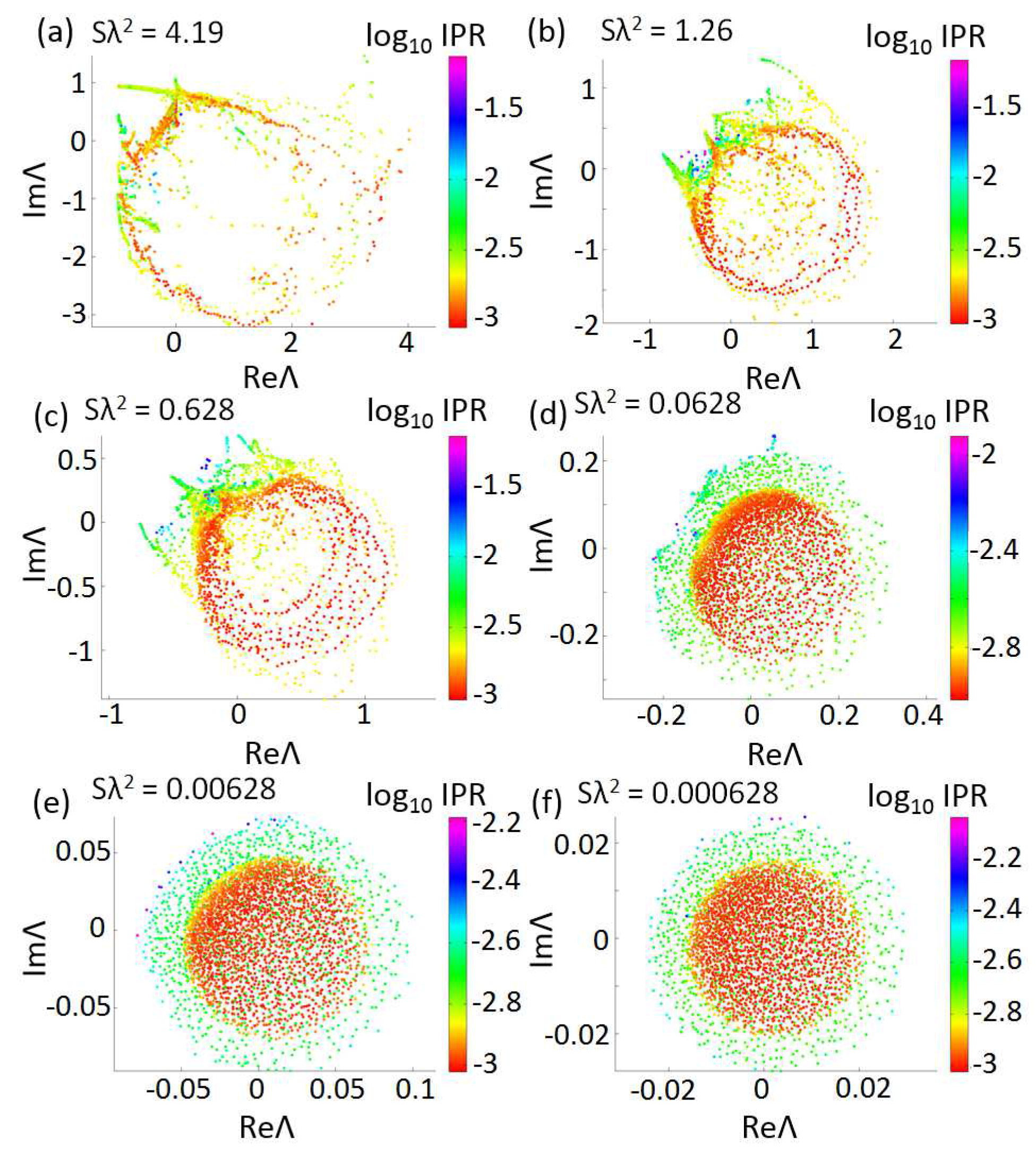
Let us now discuss the spectral distributions of the complex eigenvalues of the Vogel spiral arrays considered in this paper. Our results are displayed in
Figure 10,
Figure 11 and
Figure 12. All the spirals have the same number of particles
and are investigated for different values of the optical density. Few tentative conclusions that be drawn from our study. At large values of the optical density, all the Vogel spiral data feature highly structured eigenvalue distributions supporting clearly defined spectral gap regions that are manifested by ‘open eye’ patterns in the eigenvalue distributions. The size of the gap regions increases with the degree of geometrical order that in turn increases from the
π-spiral to the
τ-spiral. This behavior is consistent with our previous numerical investigations of two-dimensional Vogel spirals of dielectric pillars that we modeled using the FEM. In those studies, by focusing on the local density of states of Vogel spirals we demonstrated the presence of large band gap regions with a multifractal scaling of localized band-edge modes [
73,
76]. Here, by systematically studying their complete distribution of eigenvalues, we demonstrate a remarkable series of spiral branches that we associate to the distinctive proximity resonances of Vogel structures.
This interpretation is confirmed by the analysis of the associated eigenvectors of the Green’s matrix. In fact, we discovered that the quasi-modes associated to the spiral branches are extremely localized in between several particles that are located along the parastichies of the Vogel spiral. The parastichies are families of out-spiraling particles lines that stretch out from the center of the structure. Similarly to the case of the random systems, when the scattering is weakened by lowering the optical density, all the eigenvalue distributions converge to a circular disk region containing modes with low IPR values. However, differently from the random case, the central disk of the Vogel spiral’s distribution is surrounded by a very well-defined band of modes with higher IPR values. This very striking ‘bipartition’ of the population of eigenvalues reflects the specific aperiodic order of Vogel spirals and it becomes more pronounced as their degree of order is increased from the π-spiral to the τ-spiral.
In
Figure 10 we summarize our results for the
μ-spiral. The results for the
π-spiral are displayed in
Figure 11. Consistently with the more ‘disordered’ nature of this structure (see
Figure 3e again), its distribution of eigenvalues resembles very closely the one of random systems even for larger values of the optical density. However, due to the formation of large spectral gap regions the eigenvalues are forced to ‘wrap around’ the gaps giving rise to very rich spectral sub-structures that cannot be found in random media.
The results obtained for the
τ-spiral, shown in
Figure 12, deserve additional consideration. In fact consistently with its more ordered geometrical structure, at the largest value of the optical density there appear the widest spectral gap around which ’band-edge eigenvalues’ cluster forming a very complex nested structure. This phenomenon reflects the intricate multifractal scaling of band-edge modes that is characteristic of Vogel structures [
73,
76]. By decreasing the optical density the eigenvalue distributions become more circularly symmetric and uniform. At very small values of optical density the eigenvalues are orderly arranged in a bipartite disk structure. We attribute this features to the more uniform nature of the
τ-spiral geometry that supports distinctive geometrical resonances (quasi-modes) akin to the circularly symmetric modes of a homogeneous cylindrical cavity. Such resonances are indexed by a radial and an azimuthal index and can already be inferred by studying the spectrum of the graph Laplacian as we previously discussed. We have referred to such modes as ‘geometrical resonances’ of the array. However, it is important to point out that while similar ‘cavity resonances’ can be found in all the Vogel spiral geometries at large enough optical density (i.e., the homogeneous limit), their detailed spatial distribution reflects the specific geometrical structure of each Vogel spiral. In particular, perfect rotationally symmetric modes cannot be achieved because the Vogel spiral geometry does not exhibit rotational symmetry. We believe that further investigations should address quantitatively the unique interplay between symmetry, chirality and aperiodic order in Vogel spirals in order to understand the complex spatial patterns that can be exhibited by their localized quasi-modes.
Our comprehensive analysis of the eigenvalue distributions and the scattering resonances of Vogel spirals, made possible by the efficient Green’s matrix method, unveils the nature of geometrical resonances in the spectrum of aperiodic systems and addresses the structure-property relationships that are manifested in the eigenvalue distributions.
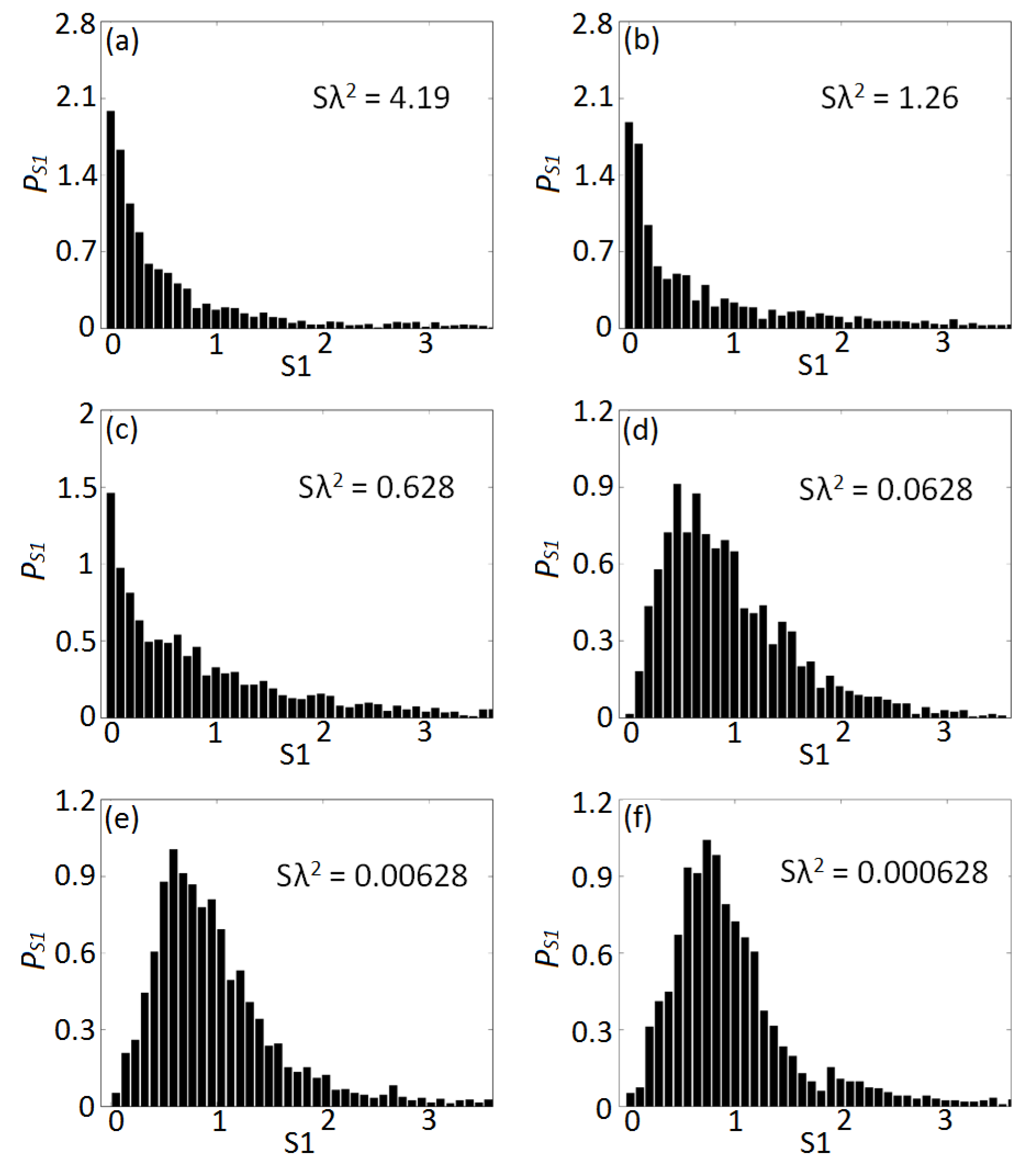
8. Level Statistics
The knowledge of the positions and widths of scattering resonances (Equation (
24)) allows one to investigate level statistics of a disordered medium via the Green’s matrix method. Level statistics provides important information about electromagnetic propagation in both closed and open systems. Indeed, from RMT it is possible to identify the presence of localized and extended states by investigating level statistics in closed systems.
In closed systems, a well-known result of RMT in the extended regime of wave transport, where almost all modes overlap in space, is the existence of level repulsion [
82]. This means that the probability density function for the spacing between adjacent energy levels
and
,
, tends to zero for
[
104]. This fact results in the following expression for the probability density function of normalized energy spacings
(for systems with time reversal symmetry) [
104]:
In contrast, for closed systems level repulsion does not occur in the localized regime. In this case two spatially distant, exponentially localized states hardly influence each other, resulting in a Poissonian level spacing distribution [
104]:
so that two states with infinitely close energies are possible.
On the other hand, in
open systems the eigen-energies are complex with a finite decay rate, as specified by Equation (
24). The concept of level repulsion for extended states can be generalized to this case [
104]. Indeed, for each complex energy
the nearest quasi-mode (In our terminology we use the term ’quasi-mode’ to denote an eigevector of the Green’s matrix with complex eigenvalue.)
is the one that minimizes the Euclidean distance between two quasi-modes in the complex plane
. For non-Hermitian matrices belonging to the Ginibre’s ensemble of random matrices,
reads [
104]:
so that
, which means that two adjacent quasi-modes repeal each other in the complex plane. This generalized level repulsion rule for open disordered systems has been recently verified for vectorial waves in the extended regime [
98]. As in the case of closed systems, the appearance of localized modes due to increasing disorder leads to the suppression of the (generalized) level repulsion [
98]. Our results on the spectral statistics of the complex eigenvalues of random systems fully support this picture and even suggest its generalization to the more general deterministic aperiodic structures.
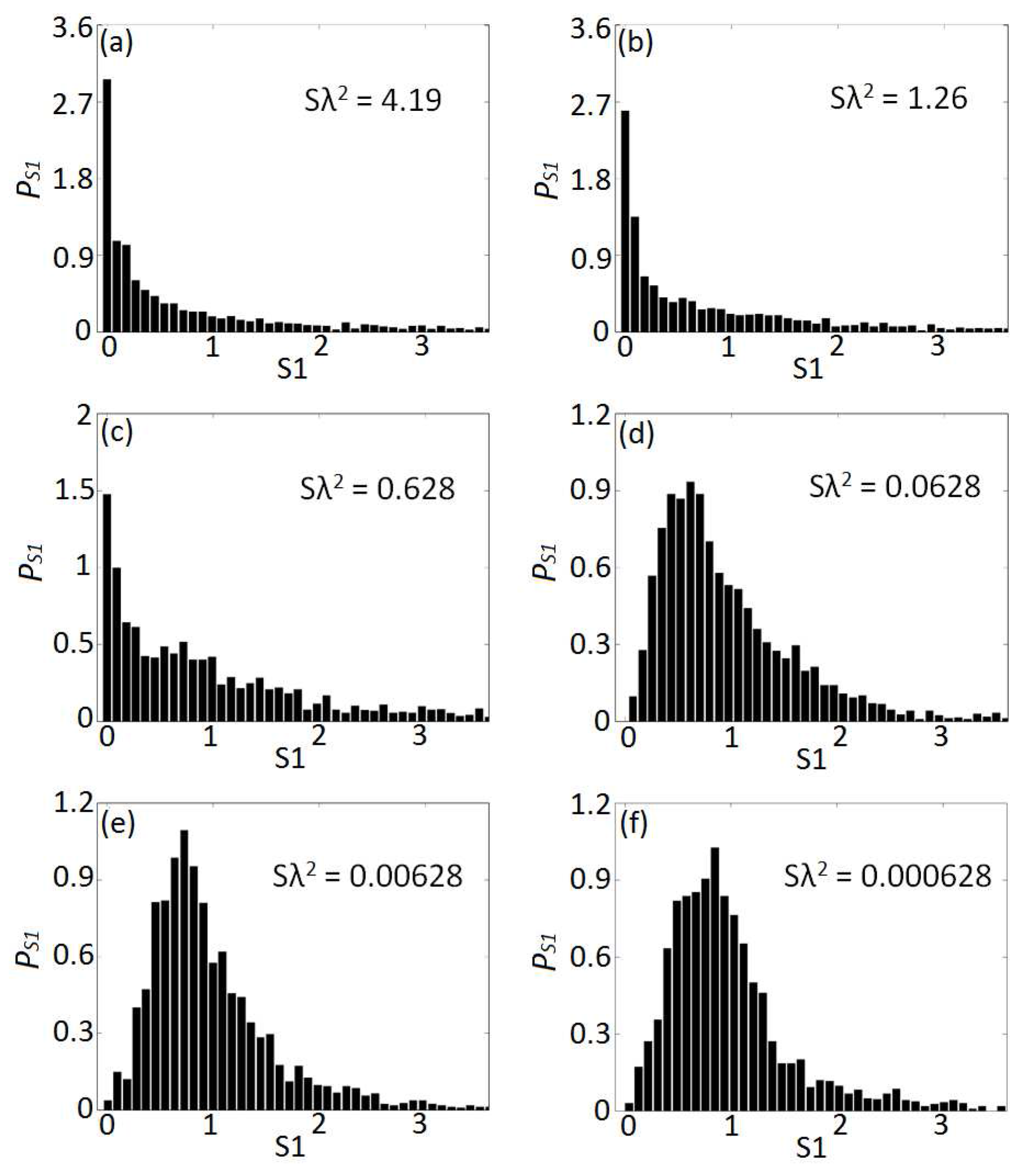
Figure 13 summarizes our results for the level spacing statistics of the Penrose array considering different values of the optical density. In particular, the data show the computed probability density function (pdf) of the level spacing
in the complex plane.
A clear transition can be observed between the absence of level repulsion at large optical densities and the level repulsion behavior at small optical densities. To the best of our knowledge this transition, which is analogous to the case of an open random system as recently demonstrated in Ref. [
98], has not been previously reported in deterministic structures.
It is also very interesting to notice that the probability distributions of the level spacing in the Penrose quasicrystal display extreme heavy tails that are markedly non-Gaussian. This behavior is consistent with the deterministic fractal nature of the Penrose array and cannot be observed in uniform random media. Moreover, our results show that at the largest optical density the statistical distribution of level spacing ‘flattens’ and appears to oscillate around a slowly decreasing probability value. We attribute this distinctive behavior to the deterministic spatial structure of the Penrose structure that establish persistent correlations in the level statistics that ’survive’ even at large optical density. This scenario cannot be observed in random systems where the level spacing are uncorrelated and the corresponding probability decays very quickly. Finally we note that the absence of level repulsion in the Penrose array persists up to relatively small values of the array’s optical density ().
In order to compare directly our findings obtained for deterministic aperiodic structures with a well-established reference situation, we summarize in
Figure 14 the results obtained using the same computational approach when considering a single realization of a uniform random array with
particles. We have ensured by performing additional simulations (not shown here) that the overall size of this random system is large enough so that an ensemble averaging procedure that considers different realizations will not alter in any relevant way our main conclusions. As a result, it suffices to consider a single realization of a large enough random system. As expected for random media, the transition towards the level repulsion regime can be distinctly observed by increasing the optical density of the array. In fact, the level statistics of open random systems has been studied in great detail using random matrix theory in recent years, fully supporting this physical picture. However, in our paper we establish a direct comparison among the level spacing statistics of deterministic aperiodic structures and random media for the first time.
While reflecting on these results, it is important to keep in mind that a comprehensive theory of level statistics in random open systems of vector point scatterers is currently not available for arbitrary values of the optical density. As a result, our extensive numerical results are intended to stimulate a broader interest in the yet-unknown spectral fluctuation properties of aperiodically ordered media and additionally provide new vistas for future theoretical developments. In the context of the present paper our interest is to point to the relationships between the aperiodic order and spectral statistics.
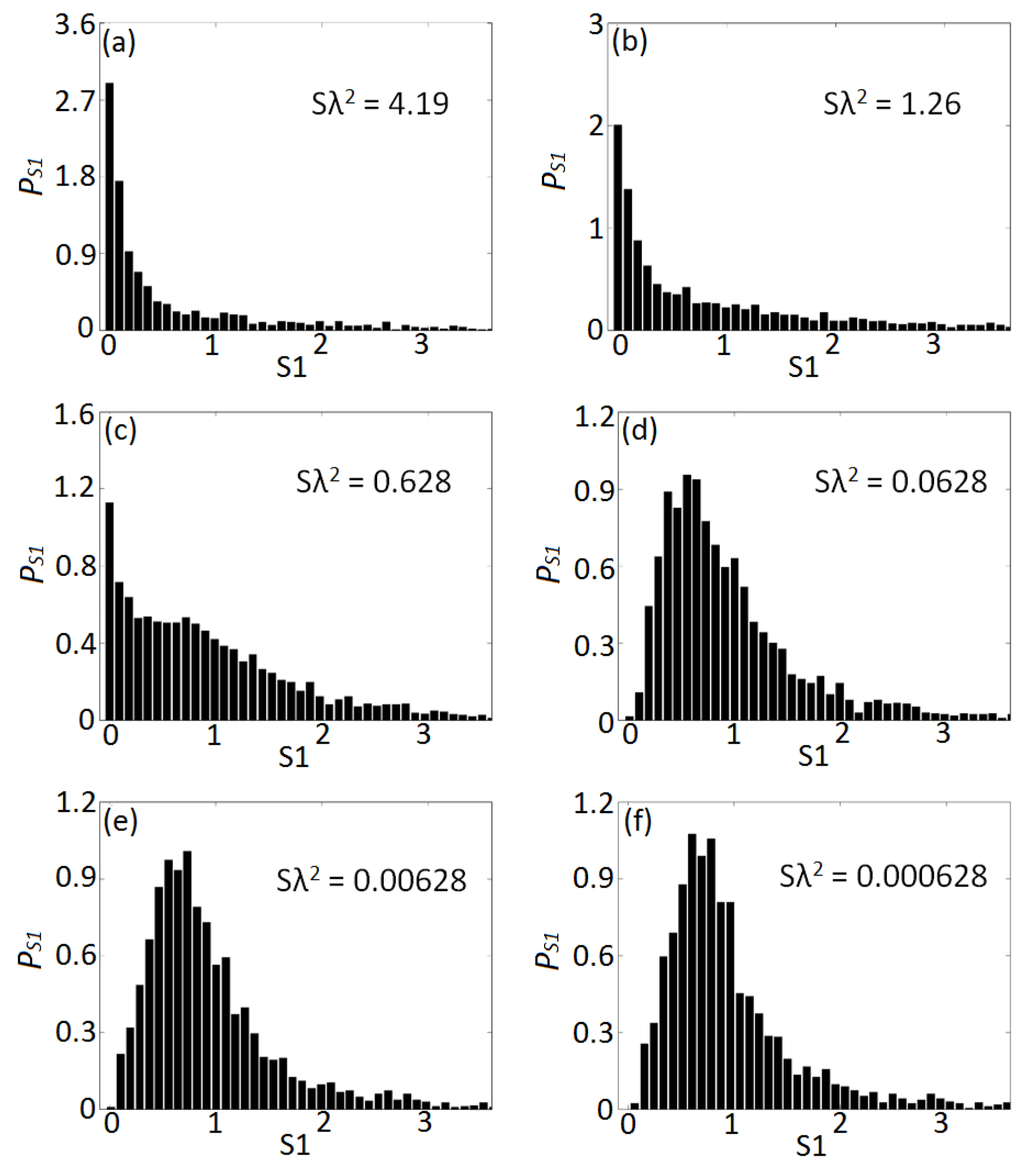
In order to extend the scope of our analysis we also investigate the spectral statistics of the Vogel spirals and summarize our results in
Figure 15,
Figure 16 and
Figure 17. Similarly to the Penrose structure, a transition to a level repulsion regime is visible at
. All the probability density functions exhibit long tails with slow decay and a distinctive oscillatory behavior.
Oscillations in the density of states of fractal and multifractal structures have been recently explained based on the analytic theory of spectral zeta functions on fractals [
105,
106]. Physically, they can be interpreted as the manifestation of resonant scattering phenomena between neighboring lattice clusters that share similar local geometrical structures in fractal environments. For instance, the existence of a hierarchy of resonance oscillations with different time scales in quasicrystalline systems can be understood from the celebrated Conway’s theorem [
107]. This important result of mathematical crystallography states that if one selects a cluster of length
L within a quasi-crystal such as a Penrose structure, then it is possible to find an identical copy of the selected cluster within a distance of the same order
L. Therefore, resonant oscillations develop at every length scale in quasi-periodic structures. This intriguing phenomenon was also discussed in the context of the electron transport across Fibonacci chains using the renormalization group arguments. Indeed, what determines spectral oscillations is the fractal dimension of the energy spectrum of the structures. This parameters do not vary significantly across the different Vogel’s spirals. As a result, the overall characteristics of the level statistics do not appear to be strongly influenced by the different geometries of the Vogel’s spirals. We remind the reader that the
π-spiral is significantly more ’disordered’ than the other spirals and it exhibits a radial correlation function that is very similar to the one of a random gas model. Nevertheless, the spectral fluctuations shown in
Figure 16 do not significantly differ from the results obtained when considering the other Vogel’s structures. We have extended our numerical analysis to additional Vogel’s spirals (not shown here) and consistently found level spacing distributions with very similar characteristics.
The results for the
μ-spiral are summarized in
Figure 15 while the results obtained on the
τ-spiral are summarized in
Figure 17. The general resemblance o the level statistics distributions of Vogel’s spirals points towards a possible universality behavior for these class of aperiodic structures that is induced by the distinctive type of Vogel’s aperiodic order. In particular, we remind that all aperiodic Vogel’s spirals lack both translational and rotational symmetry. Moreover, differently from periodic and quasiperiodic arrays, Vogel spiral arrays support circularly symmetric scattering rings in Fourier space that are entirely controlled by the same deterministic generation rule. Our previous work has demonstrated that all spirals exhibit clear multifractal behavior with singularity spectra of characteristic downward concavity, demonstrating the multifractal nature of their geometrical structure and energy spectra (i.e., local density of states LDOS) [
76]. The connection between the multifractality of geometrical structures and the corresponding energy or LDOS spectra is far from trivial in general. In fact, multifractal energy spectra have been discovered for deterministic quasiperiodic and aperiodic systems that do not display any fractality in their spatial geometry, despite the fact that they are generated by fractal recursion rules. Typical examples are Fibonacci optical quasicrystals and Thue-Morse structures.
In our opinion it is very important to establish the connection between multifractal spectra and level statistics in aperiodic structures. This is very relevant to a number of device applications that rely on the unique properties of critical modes. In fact, optical structures with multifractal eigenmode density (or energy spectra) display a rich and fascinating behavior, leading to the formation of a hierarchy of satellite pseudogaps, called fractal gaps, and of critically localized eigenmodes with anomalous transport properties. In general, dynamical excitations with characteristic fractal or multifractal wavefunctions originate in aperiodic environments with multiscale local correlations, which are well described by multifractal geometry. However, it is not clear which condition should be satisfied by the aperiodic geometry of deterministic structures in order for them to support critical modes with fractal distributions. The study of the associated spectral statistics may suggest an alternative approach to attack this difficult problem. In the next section we will address the scattering resonances of deterministic aperiodic structures and propose a simple criterion to identify critical modes in the complex eigenvalue spectrum of aperiodic systems.
9. Critical Modes and Resonances of Aperiodic Systems
A relevant problem in the study of aperiodically ordered structures is related to understanding the nature of their critical modes and scattering resonances. To this regard, it is important to realize that once the eigenvectors of the Green’s matrix have been computed, the corresponding optical modes at the positions of every scatterer can be obtained by multiplication with the dyadic Green’s matrix. Keeping this in mind, we can understand the spatial structure of the optical modes of aperiodic systems by studying the corresponding Green’s matrix eigenvectors.
Presently, for general aperiodic structures there is no clear definition of the notion of critical modes, leading to somewhat confusing situations. However, critical modes are believed to exhibit general characteristics [
15]. In particular, in contrast with the fully disordered case, where exponentially (Anderson) localized modes can occur, critically localized states decay weaker than exponentially, most likely by a power law, and have a rich self-similar structure described by fractal or multifractal scaling laws. The spatial oscillations of critical modes originate through a series of tunneling events involving the overlap of different sub-structures that repeat over different length scales. However, the notion of a slowly decaying envelope function is clearly inadequate to describe the scattering resonances and the strongly the fluctuating wavefunctions of critical modes. More precise criteria need to be developed in order to better capture their distinctive properties.
The rich physical behavior of critical states, including the presence of extended fractal wavefunctions at the band-edge energy of the Fibonacci spectrum, and their relation to optical transport have been analytically studied by Kohmoto [
34] and Macía Barber [
108] using the tight binding method and a transfer matrix renormalization technique, respectively.
In this final section of the paper we show that the Green’s matrix method can provide essential insights into this problem. The key question that is made possible by the Green’s spectral method is how to classify the quasi-modes of aperiodic systems based on the full knowledge of the distributions of their complex eigenvalues. In order to address this problem we have computed all the Green’s matrix eigenvectors and the corresponding IPR values. Based on our extensive numerical analysis we have been able to generally distinguish among three main types of eigenvectors. The first type corresponds to long-lived scattering resonances with
and large IPR values, which feature strong spatial localization. It is known that in random systems proximity resonances involving two particles, which correspond to
, do exist as shown in
Figure 18c. On the other hand, the long-lived resonances of the periodic square array are spatially extended and have small IPR, as shown in
Figure 18a. A representative long-lived resonance of a Penrose structure with one of the largest possible IPR is shown in
Figure 18b. The resonance is strongly localized within few groups of particles and manifest the decagonal rotational symmetry of the array. Remarkably, similar geometrical resonances were also previously identified using the graph Laplacian method (compare with
Figure 6b).
The long-lived resonances of Vogel’s spirals, shown in
Figure 18d,e, are also very interesting. Generally speaking they are strongly localized within the central region of the array where they spread across only few neighboring particles along the parastichies (spiral arms). These distinctively localized resonances are the analogue for the Vogel spiral geometry of the Efimov’s few-body resonances that occur in random systems. To the best of our knowledge Efimov-like resonances of deterministic aperiodic structures have not been previously demonstrated and deserved to be systematically investigated in future studies. On the other hand, our analysis shows that proximity resonances between two particles only cannot be obtained for the Vogel spirals within the range of optical density that we have considered.
We have additionally discovered a class of long-lived resonances that are extended azimuthally but localized in the radial direction. An example is shown in
Figure 18f. Again, these resonances correspond to geometrical resonances and can be predicted based on the graph Laplacian approach introduced earlier in the paper. However, it is important to realize that none of these strongly localized resonances display any fractality in space.
In order to identify long-lived critical modes in aperiodically ordered structures we confine our attention to a different area of the complex eigenvalue distribution. In particular, since critical modes are technically extended, we focus our search to regions of long-lived resonances with low IPR values. In the case of periodic systems such a requirement simply selects extended band-edge modes (see as an example the profile in
Figure 19a) while for random systems (see as an example the profile in
Figure 19c) it singles out extended modes that rapidly leak out through the boundary of the array. However, for Penrose and Vogel’s spirals arrays the constraint
with small IPR values unveils long-lived resonant modes with a very rich spatial structure. In particular, the resonances of the Penrose structure displayed in
Figure 19b as well as
Figure 20a,b reveal the distinctive fractal nature of critical modes.
We emphasize the similarity between the Green’s matrix eigenvectors and the eigenvectors of the graph Laplacian associated to the Penrose array. In the case of Penrose systems, this interesting correspondence reveals very clearly how the fractality of such resonances is a direct manifestation of the fractality of the underlying geometry of the pattern. On the other hand, the long-lived modes of Vogel spirals with low IPR values spread over extended clusters of coupled particles that are distributed along the spiral’s parastichies arms, as shown in
Figure 20c,d. Finally, purely geometrical resonances such as the ones in
Figure 20e,f with spatial distributions that are very similar to the graph Laplacian eigenvectors of
Figure 6 can be readily found when considering eigenvectors that satisfy the condition ‘
and small IPR values’ simultaneously. Based on our extensive numerical analysis we now appreciate that critical modes in quasiperiodic fractal structures correspond to long-lived resonances with low IPR and that their physical origin can be traced back to the geometrical resonances of a fractal structure. Following the same procedure we were not able to detect ant clear self-similarity in the quasi-modes of the considered Vogel’s spirals. Therefore, a complex multifractal geometry such as the one of Volge’s spirals point patterns does not directly imply fractality of the modes. In the absence of a general theory for this class of systems, based on our numerical studies it is tempting to attribute this anomalous behavior to the absence of discrete components in the Vogel’s spirals spectra.