Retrieval of Effective Parameters of Subwavelength Periodic Photonic Structures
Abstract
: We revisit the standard Nicolson–Ross–Weir method of effective permittivity and permeability restoration of photonic structures for the case of subwavelength metal-dielectric multilayers. We show that the direct application of the standard method yields a false zero-epsilon point and an associated spurious permeability resonance. We show how this artifact can be worked around by the use of the cycle shift operator to the periodic multilayer in question.1. Introduction
Determining the effective macroscopic parameters of a slab containing a photonic structure is often both highly relevant both from a practical and from a fundamental point of view, providing a link between the actual microscopic composition of the structure and its macroscopic optical response. The most common ways to accomplish this task are various types of ellipsometry [1,2] or reflectance and transmittance measurements [3].
However, there are two major issues with such parameter restoration techniques. One is the fundamental applicability limit of the effective medium approximation approach. It is normally mitigated by considering photonic structures with feature sizes much smaller than the wavelength (deeply subwavelength structures), although an exception exist in special cases, such as hyperbolic metamaterials [4]. The other issue is related to the artifacts of the restoration procedure itself. For example, it is known that the constitutive parameters of a slab are hard to obtain nearby the total transmission frequency or when we approach the magnetic or electric resonances of a structure [5]. These difficulties can be overcome with a modified extraction procedure, based upon a generalized homogenization technique [6].
In this work, we address another difficulty arising when extraction is to be carried out at the point of total reflection. It is shown that application of the widely used standard Nicolson–Ross–Weir procedure [7] results in spurious features near this point, such as false zero-epsilon points and permeability poles. In the optics of subwavelength structures, total reflection is often associated with the true ε-near-zero regime [8]. Therefore, being able to make a correction for artifacts in such a regime becomes of particular importance to determine the correct operational wavelengths of epsilon-near-zero behavior and the optical mechanism of subwavelength photonic structures.
The rest of the paper is organized as follows. In Section 2, we demonstrate the artifacts associated with the application of the standard restoration procedure to subwavelength metal-dielectric periodic photonic multilayers. In Section 3, we trace these artifacts to the total reflection from a photonic metamaterial slab at the point where artifacts are observed. In Section 4, we show how to amend the artifact behavior and ensure correct parameter restoration by applying the cycle shift operator to the multilayer in question. Finally, in Section 5, we summarize the results.
2. Spurious Features in the Nicolson–Ross–Weir Restoration Procedure
We consider periodic layered structures formed by alternating layers of metal and dielectric. It was shown previously that the nonlocal permittivity tensor of such plasmonic multilayers generally possesses off-diagonal components [9,10], which only vanish when light propagates normal to layer interfaces. Furthermore, in this case, no more than one eigenmode corresponds to each frequency. Hence, we will consider the normal incidence of light throughout the paper and will aim at the restoration of the longitudinal component of the permittivity tensor from the reflection r and transmission t coefficients.
We apply the standard Nicolson–Ross–Weir extraction method [7] to a finite multilayer slab of thickness D and calculate its effective permittivity ε and permeability μ as follows. First, the impedance Z and the refraction index n are given by:
It can be seen that there is a singular point in Equation (1) where . Therefore:
If we suppose that R = 1 and T = 0, then Equation (1) results in Z = ±∞. Since , it follows that infinite Z implies either that μ must approach infinity or that ε must approach zero. On the other hand, the refractive index remains finite as per Equation (1); therefore, we see both μ → ∞ and ε → 0 at the same time.
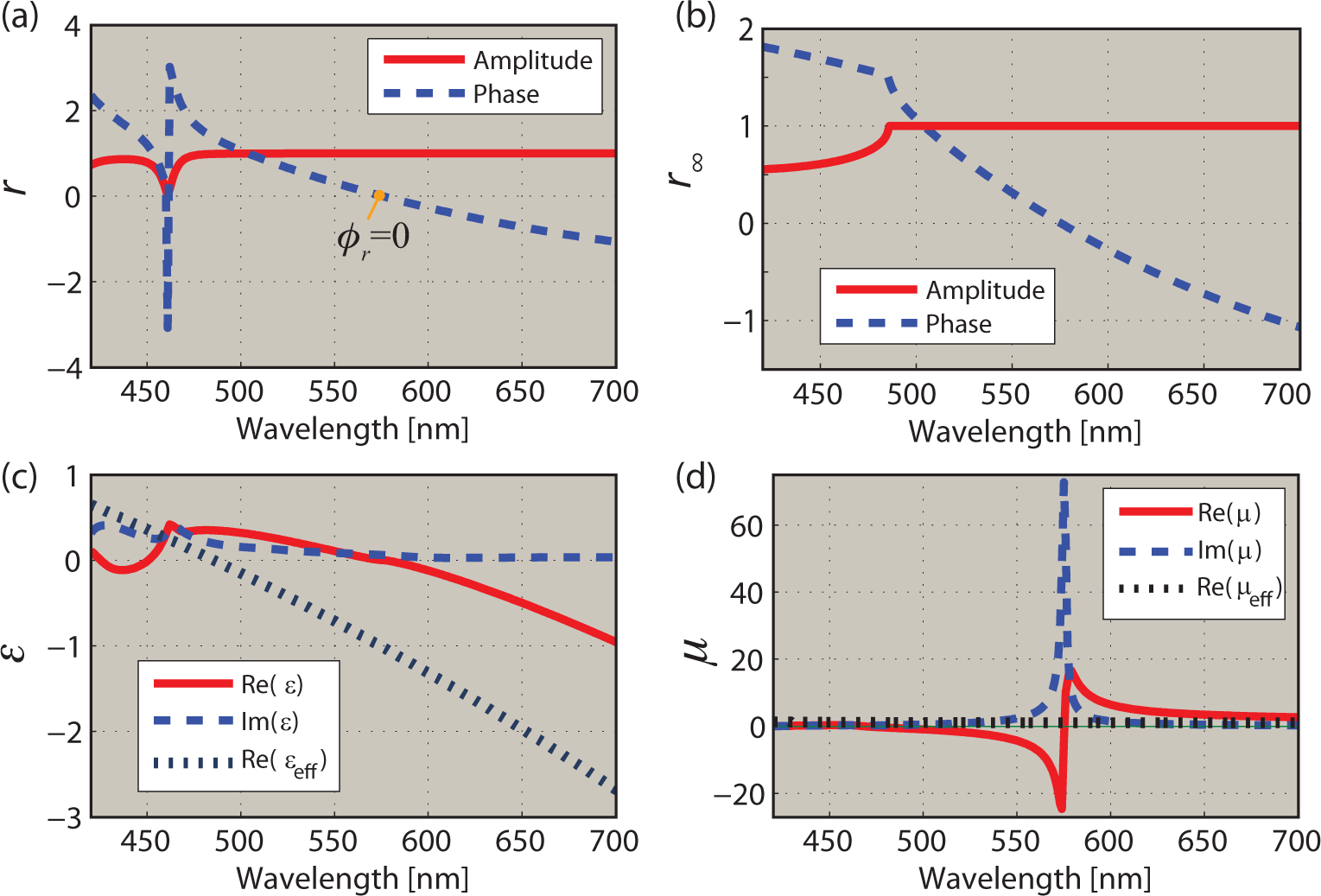
Therefore, at first glance, there should always be an epsilon-near-zero, mu-near-pole response for the case of total reflection. Figure 1 shows an example of such a situation, where we observe a spurious permeability resonance. We also see a poor match between the correct effective parameters εeff, μeff and extracted ε.
Because of this apparent extraction artifact, which can be easily misinterpreted as optical magnetism in plasmonic multilayers, special care should be taken in applying the simple extraction procedure described above. In what follows, we address the subject in detail and show how the artifacts can be worked around using a cycle shift geometrical transformation on the multilayer structure.
3. Detailed Analysis of the Total-Reflection Point in Multilayers
We can characterize an arbitrary multilayer by the 2 × 2 transfer matrix M = mjk that connects the tangential components of propagating electric and magnetic fields. Let us place one unit cell of multilayer having thickness L = lm + ld (ld,m are the thicknesses of the dielectric and metal layers) between input and output host media having impedances of . Knowing M and assuming normal incidence, the reflection (H−) and incident (H+) magnetic fields in the case of normal incidence [13]:
Eigenmodes of M provide us with the Bloch wave numbers of the structure. Based on the knowledge of M’s eigenmodes, we can calculate the transfer matrix for a slab composed of N unit cells (with the total thickness D = NL) simply by raising M to the N-th power. Taking into account that M is a unimodular matrix, we have [14]:
Now, we are ready to write down the reflection coefficient for a semi-infinite multilayer. It can be noticed that for complex kx:
If we put N → ∞, then and . Finally:
In the case of a semi-infinite structure, we are not interested in the output interface, and it can be assumed that ξi = ξo = ξh. Then,
We see that the total reflection occurs when:
If the host medium is free space, then:
Here, we are concerned with multilayers formed by periodically alternating layers of two types, one made of a dielectric and the other made of metal. For this case, M is of the following form:
Based on Equations (13) and (14), we see that m11 is always real, while m12 is imaginary for a wave propagating across the layers. Separating the real and imaginary parts in Equation (11), we immediately obtain that. As a result,
We note that since |r|2 + |t|2 = 1 in the case of total reflection, there is no transmission through the structure, regardless of whether the structure is infinite or finite. Consequently, we will obtain false material parameters for a finite structure at this point, as can be seen from Figure 1.
4. Obtaining Correct ε and μ Using the Cycle Shift Operator
However, there is a way to correct permittivity εeff, and permeability μeff can be obtained from reflection and transmission coefficients. We recall that multilayered metal-dielectric structures have a strong inherent spatial dispersion and are typically described by a nonlocal dielectric permittivity tensor [9]. However, as we only consider the normal incidence of light, we can move from the spatial dispersion framework to a ε(ω) − μ(ω) description of the system [15,16]. In such a paradigm, we can write the following expressions for the effective permittivity and permeability [17], valid for the case of normal incidence:
We see that the two artifacts in the parameter retrieval seen in Figure 1 are connected. It is the mismatch in the retrieved ε that causes the faulty point where ε = 0 appears in the spectrum, which is where the pole in the effective μ appears. Calculations show that it can be traced to the mismatch in the retrieved impedance, Z, with respect to the Bloch impedance in the structure [18].
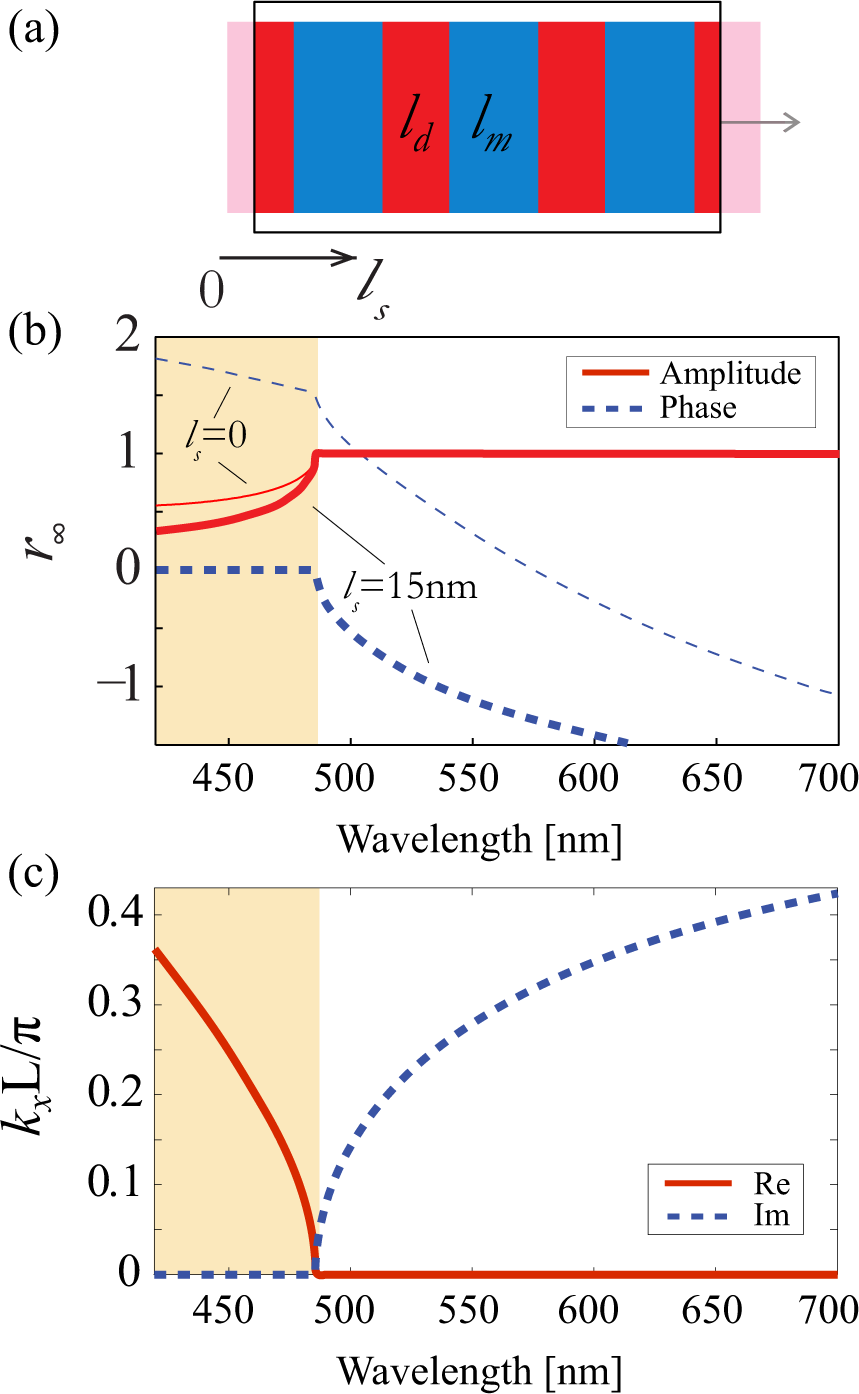
The method to avoid the appearance of the artifact features is based on a cycle shift operator applied to the multilayer structure. Taking a finite multilayer composed of N periods, this operator acts like a frame of length NL, moving across an infinite multilayer and cutting out the region that it covers, as depicted in Figure 2a.
As can be seen in Figure 2b, different values of frame shift cause a significant difference in the phase of the reflection coefficient for a semi-infinite structure, corresponding to changing of the retrieved impedance to match the Bloch impedance. This, in turn, makes it possible to pick the value of the phase that would result in correct values of the extracted parameters.
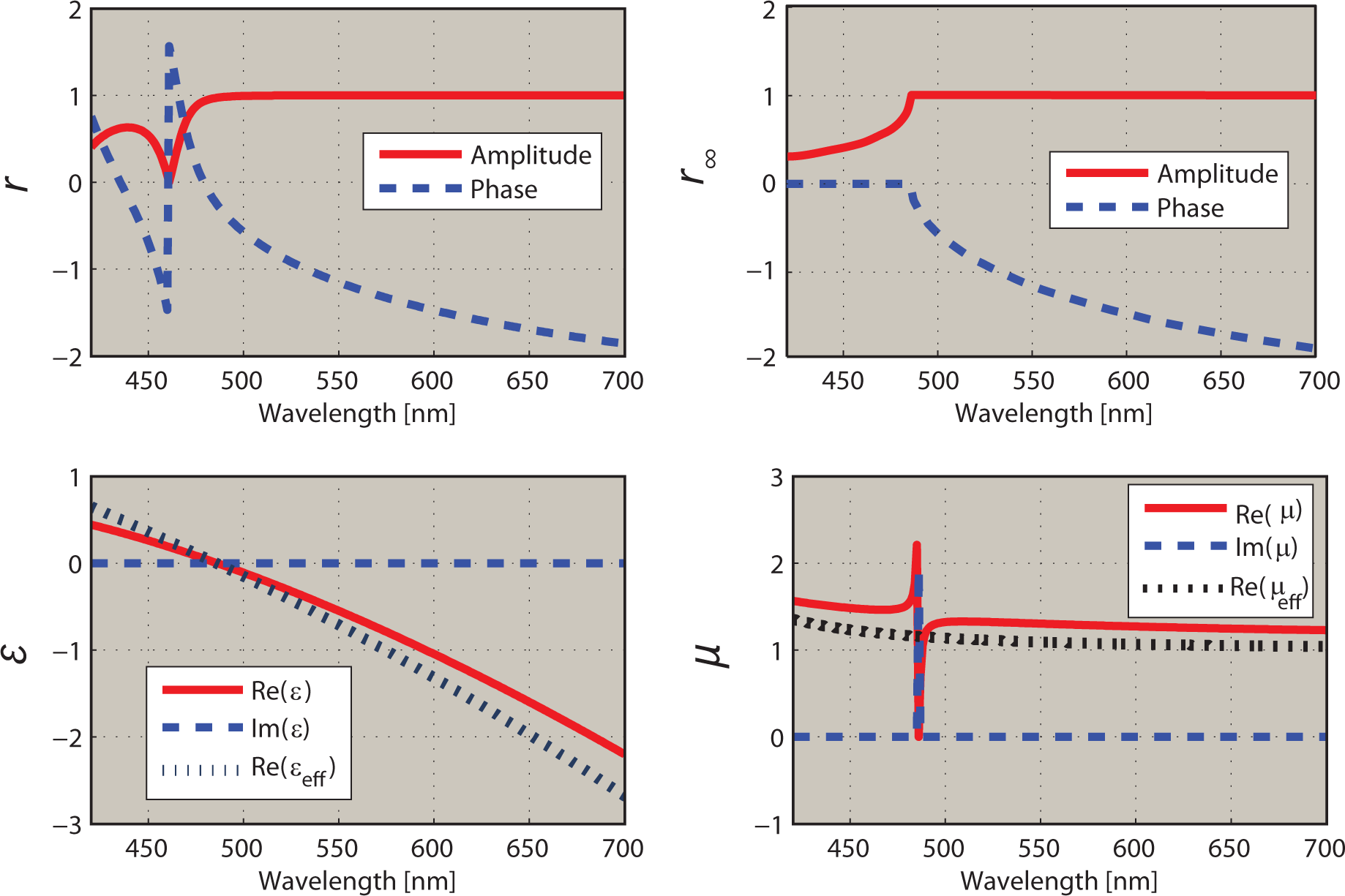
For our example with ld = 30 nm and lm = 60 nm and for the structure containing five periods, we start from the dielectric layer and apply the cycle shift operator, shifting the frame with a step of 1 nm. Calculating r and t at each step and extracting material parameters, we find that the best correspondence of the extracted ε and μ with the accurate values εeff and μeff is achieved when the frame is shifted by 15 nm or 60 nm, making the unit cell symmetric. Figure 3 demonstrates the extraction procedure for a 15-nm frame shift, showing a much better matching with the theoretically calculated values, as well as the disappearance of the artifact features in comparison with the extraction without the frame shift operator application (Figure 1).
Physically, the “magic” value of the shift corresponds to positioning the point where r = 1 (implying that ϕr = ±2πm, m ∈ ℤ) at the edge of the stop band shown in Figure 2c. One can also explain why the cycle shift operator restores the validity of the extraction procedure by noting that the impedance mismatch (the difference between the wave impedance, which enters the extraction procedure, and the Bloch impedance, which is an attribute of the infinite periodic multilayer) can result from a poorly chosen termination of the multilayer. Namely, poor termination causes high impedance mismatch between the outer space and the multilayer and, accordingly, the associated strong reflection, leading to artifacts. Applying the cycle shift operator effectively cycles through all possible terminations, and the best correspondence in parameter extraction happens when a good impedance matching between the multilayer and the outer space is achieved. Our results agree with previous accounts [19,20], where it was shown that a symmetric unit cell facilitates a good matching between the effective medium and extracted parameters.
5. Conclusions
We have demonstrated that the singularity in impedance originating from r = 1 and the zero value of its phase leads to artifacts in the retrieval of constitutive parameters of subwavelength photonic metal-dielectric multilayers, namely spurious magnetic resonance and a large mismatch of effective permittivity. We have shown that these artifacts can be worked around by applying the cycle shift operator to the multilayer. The obtained results are useful for accurate experimental determination of effective macroscopic parameters of photonic multilayers and metamaterials, especially those that work in the epsilon-near-zero regime and those that are designed to exhibit artificial optical magnetism. The proposed procedure is applicable to lossless and lossy systems within the limits assessed by the standard Nicolson–Ross–Weir technique. These results can also be used to better understand why some metamaterial geometries lend themselves to homogenization and extraction-based parameter retrieval much more readily than some others [21].
Acknowledgments
We acknowledge financial support from the People Programme (Marie Curie Actions) of the European Union’s 7th Framework Programme FP7-PEOPLE-2011-IIF under REAGrant Agreement No. 302009 (Project HyPHONE), the President of the Russian Federation (Grant SP-2154.2012.1), the Government of the Russian Federation (Grant 074-U01), the Ministry of Science and Education of the Russian Federation (GOSZADANIE2014/190) and the Russian Fund for Basic Research (Project 14-02-31720).
Author Contributions
Alexey A. Orlov is the main author of the present paper. Elizaveta A. Yankovskaya carried out initial numerical calculations. Sergei V. Zhukovsky contributed to writing and revising the text of the paper. Viktoriia E. Babicheva and Ivan V. Iorsh verified all calculations and proof-read the manuscript. The work had been inspired and was conducted by Pavel A. Belov.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vedam, K. Spectroscopic ellipsometry: A historical overview. Thin Solid Films 1998, 313–314, 1–9. [Google Scholar]
- Losurdo, M. Ellipsometry at the Nanoscale; Springer: Berlin, Germany, 2013. [Google Scholar]
- Sarabandi, K.; Ulaby, F.T. Technique for measuring the dielectric constant of thin materials. IEEE Trans. Instrum. Measur. 1988, 37, 631–636. [Google Scholar]
- Kidwai, O.; Zhukovsky, S.V.; Sipe, J.E. Effective-medium approach to planar multilayer hyperbolic metamaterials: Strengths and limitations. Phys. Rev. A 2012, 85. [Google Scholar] [CrossRef]
- Alù, A. Restoring the physical meaning of metamaterial constitutive parameters. Phys. Rev. B 2011, 83. [Google Scholar] [CrossRef]
- Liu, X.X.; Alù, A. Generalized retrieval method for metamaterial constitutive parameters based on a physically driven homogenization approach. Phys. Rev. B 2013, 87. [Google Scholar] [CrossRef]
- Nicolson, A.M.; Ross, G.F. Measurement of the intrinsic properties of materials by time-domain techniques. IEEE Trans. Instrum. Meas. 1970, 19, 377–382. [Google Scholar]
- Subramania, G.; Fischer, A.J.; Luk, T.S. Optical properties of metal-dielectric based epsilon near zero metamaterials. Appl. Phys. Lett. 2012, 101. [Google Scholar] [CrossRef]
- Chebykin, A.V.; Orlov, A.A.; Vozianova, A.V.; Maslovski, S.I.; Kivshar, Y.S.; Belov, P.A. Nonlocal effective medium model for multilayered metal-dielectric metamaterials. Phys. Rev. B 2011, 84. [Google Scholar] [CrossRef]
- Chebykin, A.V.; Orlov, A.A.; Simovski, C.R.; Kivshar, Y.S.; Belov, P.A. Nonlocal effective parameters of multilayered metal-dielectric metamaterials. Phys. Rev. B 2012, 86. [Google Scholar] [CrossRef]
- Luukkonen, O.; Maslovski, S.I.; Tretyakov, S. An approach to Finding the Correct Branch from the Forest of Possible Solutions for Extracted Effective Material Parameters, Proceedings of the 2011 XXXth URSI General Assembly and Scientific Symposium, Istanbul, Turkey, 13–20 August 2011.
- Luukkonen, O.; Maslovski, S.I.; Tretyakov, S. A. Stepwise Nicolson–Ross–Weir-based Material Parameter Extraction Method. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 1295–1298. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Pergamon Press: Oxford, UK, 1964. [Google Scholar]
- Yeh, P. Optical Waves in Layered Media, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2005. [Google Scholar]
- Agranovich, V.; Gartstein, Y. Electrodynamics of metamaterials and the Landau-Lifshitz approach to the magnetic permeability. Metamaterials 2009, 3, 1–9. [Google Scholar]
- Rukhadze, A.A.; Silin, V.P. Electrodynamics of media with spatial dispersion. Soviet Phys. Uspekhi 1961, 4, 459–484. [Google Scholar]
- Silveirinha, M.G. Metamaterial homogenization approach with application to the characterization of microstructured composites with negative parameters. Phys. Rev. B 2007, 75. [Google Scholar] [CrossRef]
- Simovski, C.R.; Tretyakov, S.A. Local constitutive parameters of metamaterials from an effective-medium perspective. Phys. Rev. B 2007, 75. [Google Scholar] [CrossRef]
- Mattiucci, N.; D’Aguanno, G.; Akozbek, N.; Scalora, M.; Bloemer, M.J. Homogenization procedure for a metamaterial and local violation of the second principle of thermodynamics. Opt. Commun. 2010, 283, 1613–1620. [Google Scholar]
- Mattiucci, N.; Bloemer, M.J.; Akozbek, N.; D’Aguanno, G. Impedance matched thin metamaterials make metals absorbing. Sci. Rep. 2013, 3. [Google Scholar] [CrossRef]
- Andryieuski, A.; Ha, S.; Sukhorukov, A.; Kivshar, Y.; Lavrinenko, A. Bloch-mode analysis for retrieving effective parameters of metamaterials. Phys. Rev. B 2012, 86. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Orlov, A.A.; Yankovskaya, E.A.; Zhukovsky, S.V.; Babicheva, V.E.; Iorsh, I.V.; Belov, P.A. Retrieval of Effective Parameters of Subwavelength Periodic Photonic Structures. Crystals 2014, 4, 417-426. https://doi.org/10.3390/cryst4030417
Orlov AA, Yankovskaya EA, Zhukovsky SV, Babicheva VE, Iorsh IV, Belov PA. Retrieval of Effective Parameters of Subwavelength Periodic Photonic Structures. Crystals. 2014; 4(3):417-426. https://doi.org/10.3390/cryst4030417
Chicago/Turabian StyleOrlov, Alexey A., Elizaveta A. Yankovskaya, Sergei V. Zhukovsky, Viktoriia E. Babicheva, Ivan V. Iorsh, and Pavel A. Belov. 2014. "Retrieval of Effective Parameters of Subwavelength Periodic Photonic Structures" Crystals 4, no. 3: 417-426. https://doi.org/10.3390/cryst4030417
APA StyleOrlov, A. A., Yankovskaya, E. A., Zhukovsky, S. V., Babicheva, V. E., Iorsh, I. V., & Belov, P. A. (2014). Retrieval of Effective Parameters of Subwavelength Periodic Photonic Structures. Crystals, 4(3), 417-426. https://doi.org/10.3390/cryst4030417



