2.1. The SAW Propagation in GaPO4
The SAW propagating along the
x direction of a semi-infinite
y-rotated GaPO
4 substrate is a generalized SAW (GSAW) as it has three particle displacement components (the longitudinal
U1, the shear horizontal and vertical,
U2 and
U3) that rapidly decrease in depth. The GSAW phase velocity is strongly affected by the cut angle, as shown in
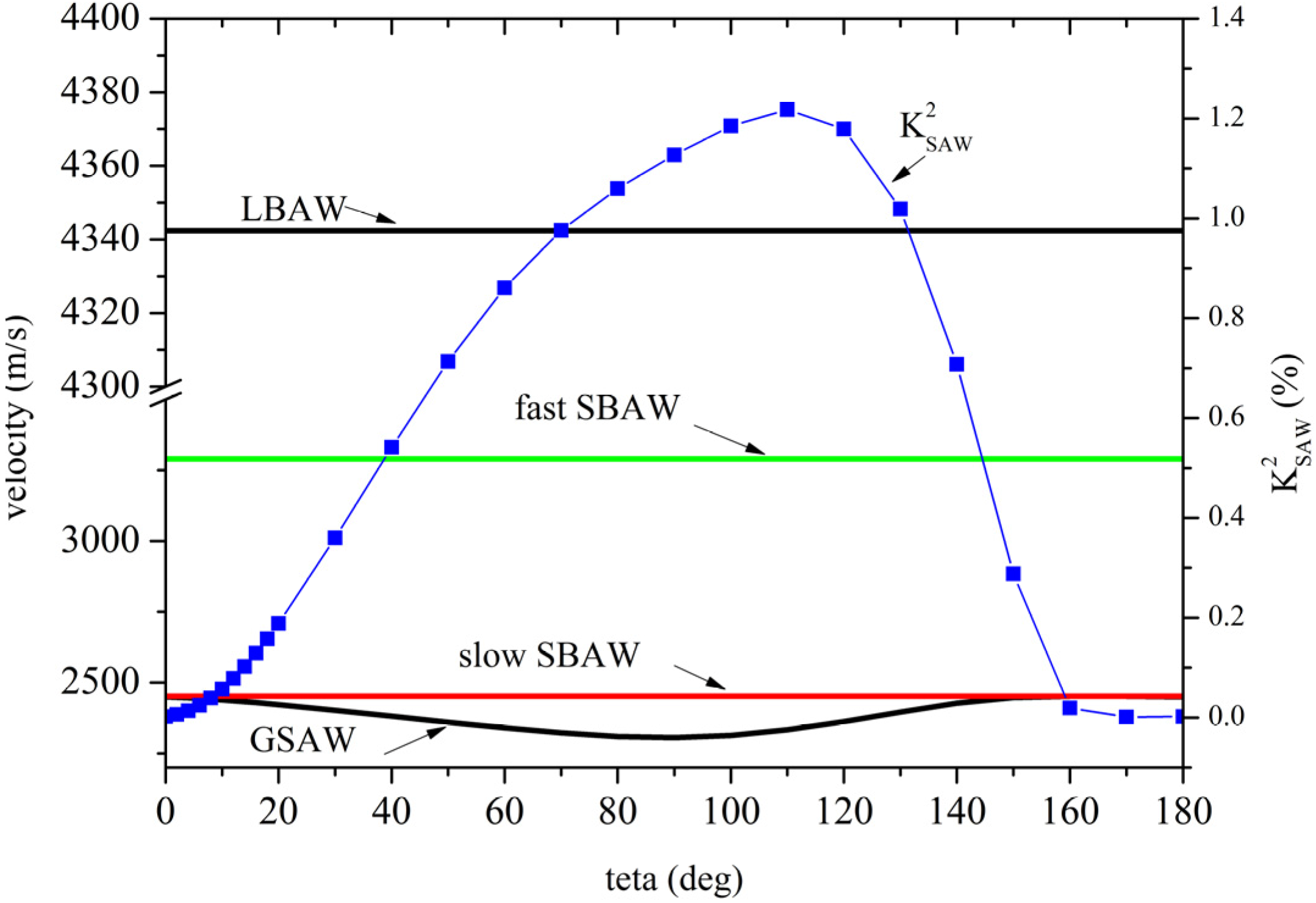
Figure 1 where the angular dispersion velocity curves of the SAW and BAW (the longitudinal BAW, LBAW, and the two transverse BAW, the fast shear, FSBAW, and the slow shear, SSBAW, having velocity equal to 4342.35, 3289.78 and 2451.96 m/s, respectively) are reported.
Figure 1.
The bulk acoustic wave (BAW) and generalized surface acoustic wave (GSAW) angular dispersion curves, and the GSAW K2 angular dispersion curves along (0° θ 0°) GaPO4 substrate.
Figure 1.
The bulk acoustic wave (BAW) and generalized surface acoustic wave (GSAW) angular dispersion curves, and the GSAW K2 angular dispersion curves along (0° θ 0°) GaPO4 substrate.
In
Figure 1, the angle θ means the amount of rotation around the crystal
x axes of a
y-cut GaPO
4 plate and is expressed in the Euler notation. The GSAW phase velocity along (0° θ 0°) GaPO
4 is lower than that of the SSBAW except for the 162° ≤ θ ≤ 169° range. While varying the cut angle and the velocity moving toward the SSBAW velocity, the shear horizontal amplitude U
2 of the GSAW decreases more and more slowly in the depth and the GSAW loses energy into the bulk. The electromechanical coupling coefficient,
K2, is a measure of the electrical to acoustic energy conversion efficiency and it was calculated as 2 × (
vf −
vm)/
vf, being
vf and
vm the GSAW velocity along the free surface and the surface covered by a infinitesimally thin conductive film. The
K2 angular dispersion curve is also shown in
Figure 1. The highest
K2 value is equal to 1.22% and it is reached at θ = 110°; while the velocity moving toward the SBAW velocity, the GSAW
K2 approaches the zero value, in accordance with the increased
U2 contribution in the depth. The acoustic waves velocity calculations along GaPO
4 were performed by using Matlab and the software from McGill University [
8] in the lossless approximation; the GaPO
4 material data (the mass density, the elastic, piezoelectric, dielectric constants) as well as the thermal expansion coefficients and the third order temperature coefficients of the elastic constants, valid in the −50 °C <
T < 700 °C temperature range, are referred to [
7,
9,
10], and are those provided by Piezocryst Advanced Sensorics GmbH, which is an European GaPO
4 wafers suppliers.
2.2. The Flexural Plate Waves (FPWs) Propagation in GaPO4
The FPWs propagating along a thin plate consist in two sets of infinite modes: the symmetric waves, whose particle displacements are symmetric about the central plane of the plate, and the antisymmetric waves, whose displacements have odd symmetry about the central plane of the plate. For sufficiently thin plate, only the first symmetric and antisymmetric modes, S
0 and A
0, propagate:
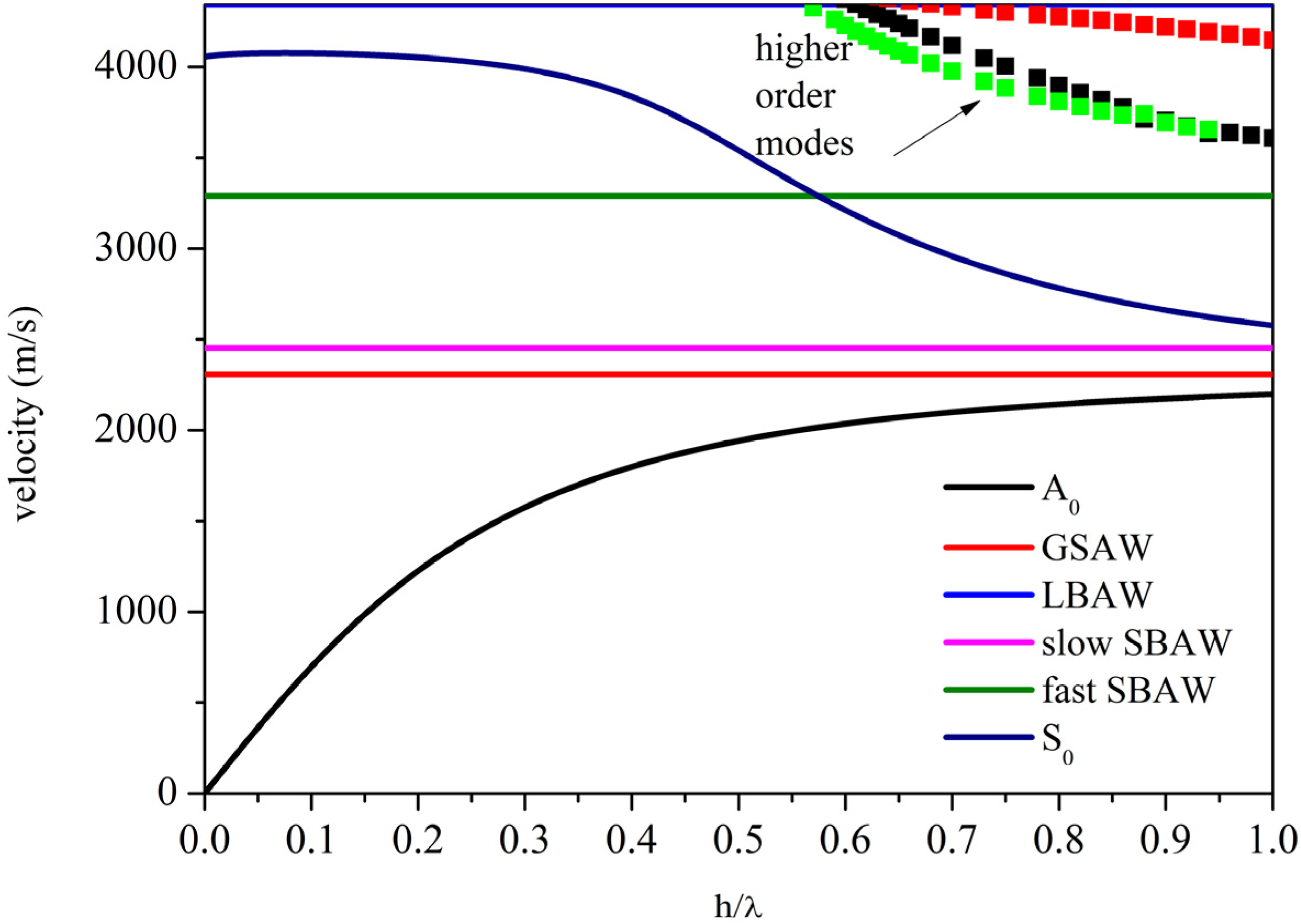
Figure 2 shows the dispersion curves of a few modes propagating along (0° 90° 0°) GaPO
4 plate as an example.
Figure 2.
Dispersion curves of the fundamental and higher order modes propagating along (0° 90° 0°) GaPO4 plate.
Figure 2.
Dispersion curves of the fundamental and higher order modes propagating along (0° 90° 0°) GaPO4 plate.
The A
0 mode is clearly identified by its reducing velocity as the plate thickness approaches zero. On the contrary, the dispersion curve of the S
0 mode is characterized by a low dispersion region, where itsvelocity is almost constant and
v ≈
vLBAW, followed by a drop in velocity. The magnitude of the flat zone of the dispersion curve depends on the rotation angle θ, as can be seen in
Figure 3 where the S
0 velocity dispersion curves are shown for different rotating angles and for plate thickness normalized to the acoustic wavelength,
h/λ, up to 0.5. The low dispersion region reaches its largest amplitude for θ = 40°.
Figure 3.
S0 velocity dispersion curves for different rotating angles.
Figure 3.
S0 velocity dispersion curves for different rotating angles.
For very small thicknesses, h/λ << 0.1, the S0 velocity increases slowly and reaches a plateau where the velocity is close to the LBAW velocity. In this flat region, for plate thicknesses up to a value that depends on θ, hereafter mentioned h/λAM, the S0 mode transforms for first to the AM counterpart with constant and dominant longitudinal displacement. Subsequently, the mode transforms to the QL counterpart for increasing the plate thicknesses up to h/λQLM: The longitudinal displacement component is no longer constant through the thickness of the plate and is dominant over the other two components. For higher plate thicknesses, the S0 mode is characterized by three particle displacement components and, when the velocity approaches the shear horizontal BAW velocity, the U2 component largely dominates over U1 and U3. For large h/λ > 1, the mode begins to act as a Rayleigh wave propagating on the surface of the plate: The mode is confined to the surface of the plate to a depth of a few wavelengths and the plate acts as a semi-infinite half space.
In the present paper, the S
0 and A
0 modes propagation along GaPO
4 plates is studied for two different coupling structures as depicted in
Figure 4. The configurations called Substrate/Transducer (ST) and Metal/Substrate/Transducer (MST) refer to a plate with one surface that sustain the excitation and detection of the acoustic waves through the interdigital transducers (IDTs), while the opposite surface is free or covered by a ground metal electrode. The FPWs
K2 depends very strongly on θ, on the electrical boundary conditions and on the plate thickness. With increasing the plate thickness, for
h/λ >> 1, the
K2 moves toward the
K2 of the GSAW that propagates along the
x direction of the
y-rotated cut GaPO
4 semi-infinite substrate.
Figure 4.
The Substrate/Transducer (ST) and Metal/Substrate/Transducer (MST) coupling configurations.
Figure 4.
The Substrate/Transducer (ST) and Metal/Substrate/Transducer (MST) coupling configurations.
The
K2 dispersion curves of the S
0 and A
0 modes were studied for the ST and MST structures by calculating the perturbation of the phase velocity when the tangential electric field component is shorted out at the plate surface. For each configuration
K2 was approximated to be 2 × [(
vf −
vm)/
vf], where
vm and
vf are the phase velocities along the structures with and without the IDTs, under the assumption that a perfect conductor is placed at both the IDT and the ground electrode position. The
K2 dispersion curves of each configuration were calculated for different plate thicknesses normalized to the acoustic wavelength,
h/λ, in the range 0.0001 to 2, with 0.0001
h/λ step, in the approximation of infinitesimally-thin perfectly-conductive grounded electrode and IDTs.
K2 values much higher than that of the SAW travelling in the same direction and crystal plane can be reached in thin plates (
h/λ << 1), for both S
0 and A
0 modes, even for that cut angles for which the SAW has a
K2 = 0%. The
K2 angular dispersion curves of the S
0 mode in both the ST and MST configurations have similar behavior: The
K2 reaches a peak for small plate thickness (at about
h/λ ~ 0.1 and 0.4, respectively), then it resets and increases again, and finally it asymptotically reaches the
K2 of the SAW.
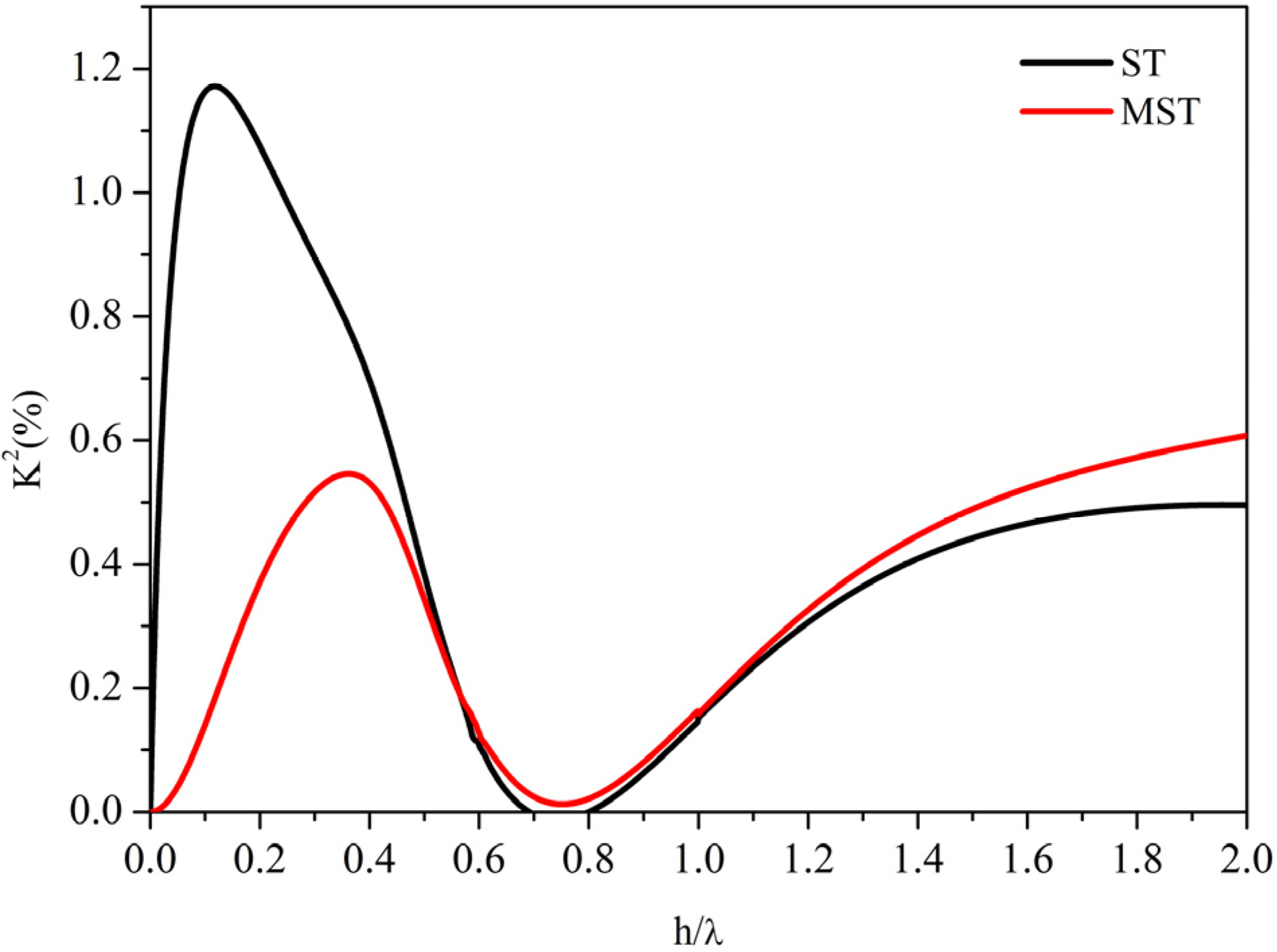
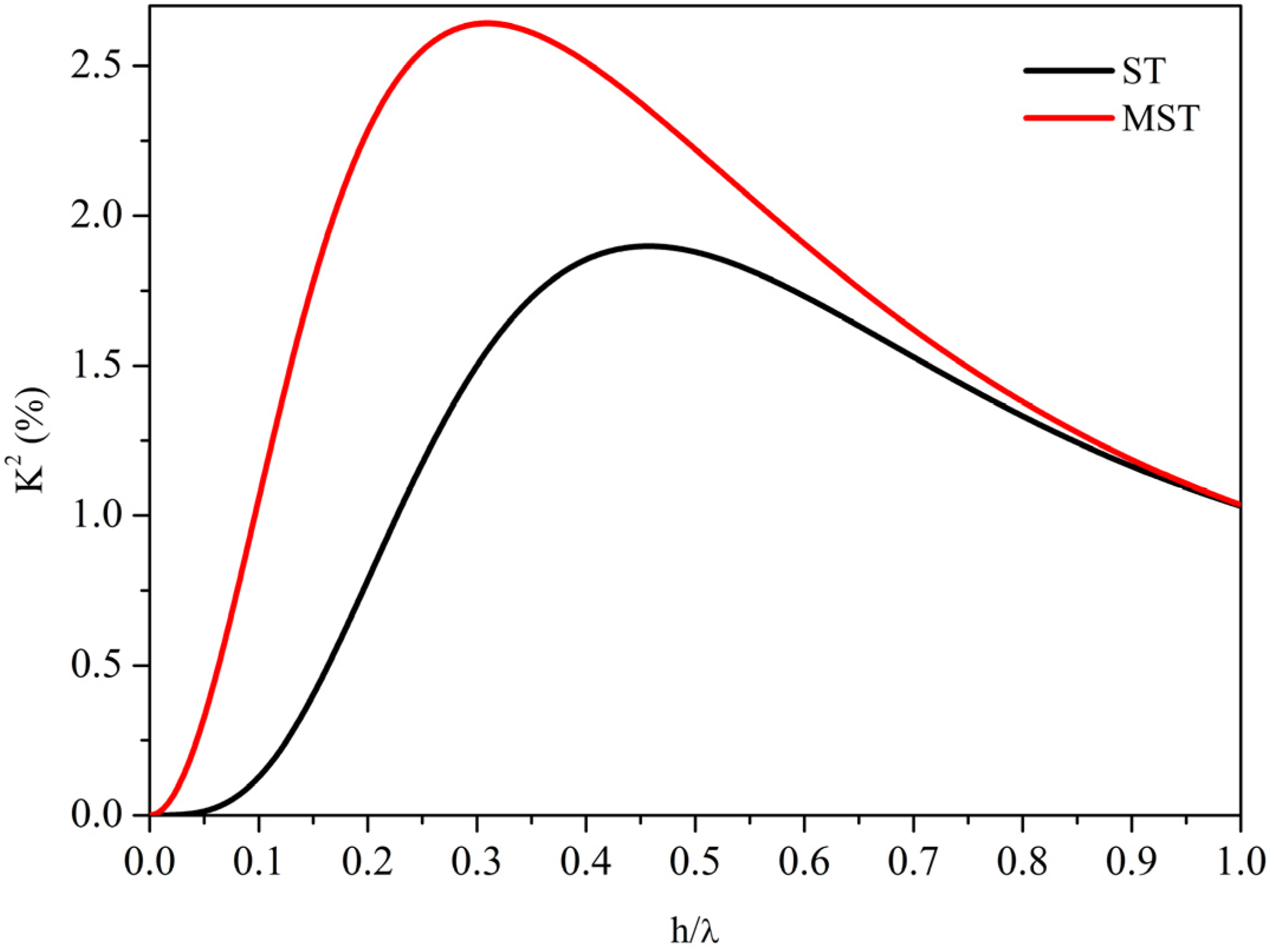
Figure 5 shows, as an example, the S
0 mode
K2 dispersion curves of the two configurations in (0° 85° 0°)
x-GaPO
4. The
K2 dispersion curve of the MST configuration has a second broad peak at
h/λ ~ 2 that is higher than the
K2 of the SAW: With increasing the plate thickness, the
K2 decreases and then, for
h/λ >> 1, it asymptotically reaches the
K2 of the SAW travelling on the free surface of the plate.
Figure 5.
The S0 mode K2 dispersion of the two configurations in (0° 85° 0°) x-GaPO4.
Figure 5.
The S0 mode K2 dispersion of the two configurations in (0° 85° 0°) x-GaPO4.
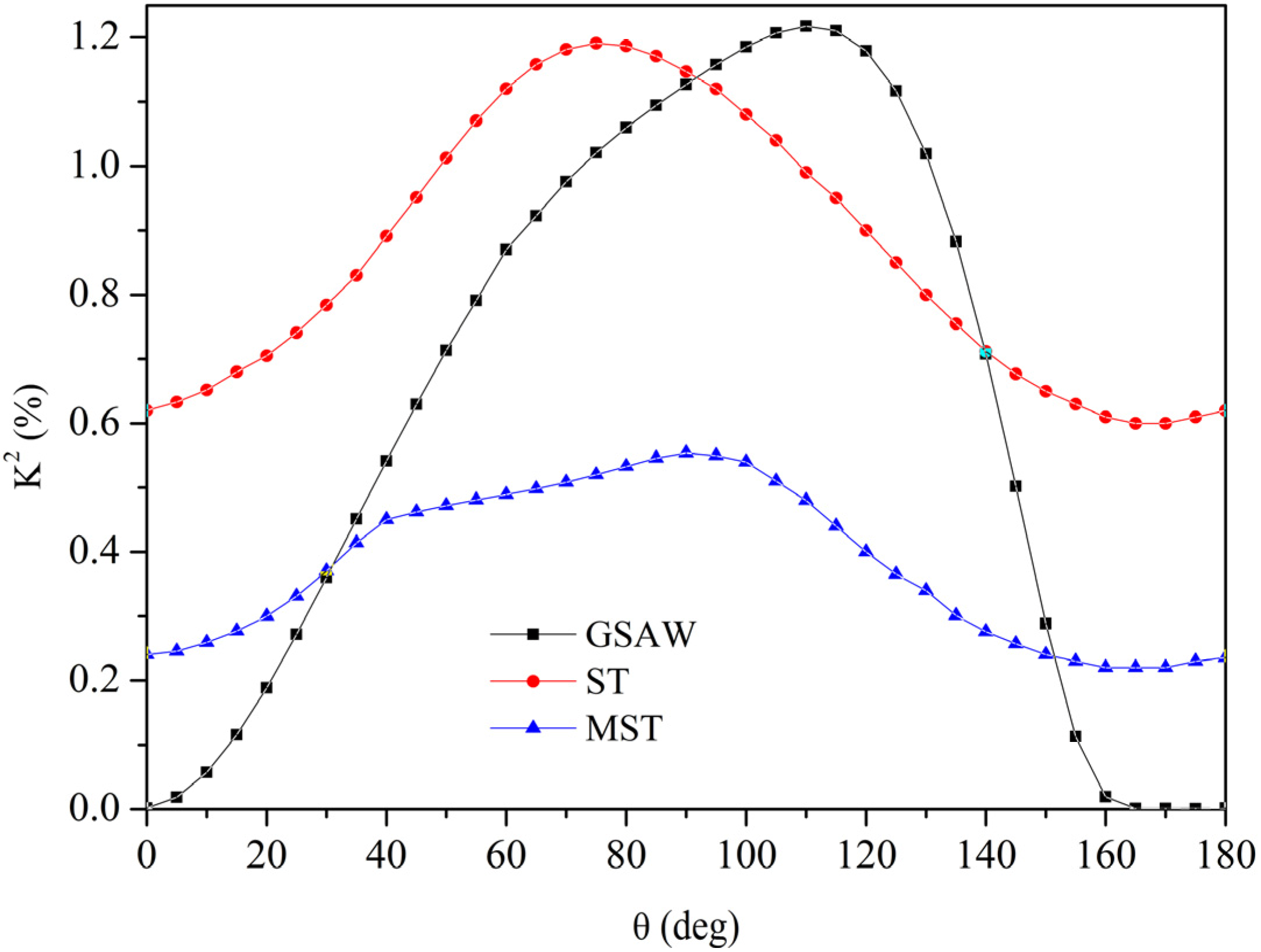
Figure 6 shows the
K2 angular dispersion curve of the SAW travelling along the free plate surface, and the angular dispersion curves of the maximum
K2 value achievable by the S
0 mode for the two coupling configurations. The
K2 peak value of the ST configuration is higher than the
K2 of the SAW for θ ≤ 90° and >150°, while that of the MST configuration is higher only for θ ranging from 0° to 30° and θ >140°.
Figure 6.
The angular dispersion curves of the maximum K2 value achievable with the two S0 mode coupling configurations and the SAW K2 angular dispersion.
Figure 6.
The angular dispersion curves of the maximum K2 value achievable with the two S0 mode coupling configurations and the SAW K2 angular dispersion.
The highest coupling efficiency of the S0 mode is around 1.2%, and it is reached by the ST configuration at h/λ ~ 0.11.
As an example,
Figure 7 shows the field profile of the shear mode propagating at
v = 3300 m/s along the (0° 75° 0°)
x-GaPO
4 plate with
h/λ = 0.11, for which the conditions U
2 >> U
1, U
3 across the depth are satisfied, and
v ~
vSHBAW. This type of mode is largely applied for sensing applications in liquid environments [
11,
12,
13] thanks to its right polarization, but it is disadvantageous compared to the AMs or QLMs as it travels at a lower velocity.
Figure 7.
The field profile of the shear horizontal (SH) wave travelling along (0° 75° 0°) x-GaPO4 plate with h/λ = 0.7.
Figure 7.
The field profile of the shear horizontal (SH) wave travelling along (0° 75° 0°) x-GaPO4 plate with h/λ = 0.7.
The A
0 mode is far more efficient than the S
0 and its most efficient of the two configurations is the MST for all the θ values from 0° to 180°. The
K2 dispersion curves of the A
0 mode depends on θ, on the electrical boundary conditions and on the plate thickness: These curves have a peak value at
h/λ << 1, and then asymptotically reach the
K2 of the SAW with increasing the plate thickness. As an example,
Figure 8 shows the
K2 dispersion curves of the two A
0-based configurations on (0° 95° 0°)
x-GaPO
4.
Figure 8.
The K2 of the two A0 coupling configurations on (0° 95° 0°) x-GaPO4.
Figure 8.
The K2 of the two A0 coupling configurations on (0° 95° 0°) x-GaPO4.
Figure 9 shows the angular dispersion of the
K2 peaks of the A
0 mode for the two coupling configurations.
K2 as high as 1.9% and 2.64% can be reached by the ST and MST configurations for θ = 95°, and for plate thickness equal to
h/λ = 0.458 and 0.31.
Figure 9.
The angular dispersion of the K2 peaks of the A0 mode for the two coupling configurations.
Figure 9.
The angular dispersion of the K2 peaks of the A0 mode for the two coupling configurations.
The A0 mode, while being elliptically polarized, can travel along thin membranes that are in contact with a liquid as a consequence of its dispersive phase velocity that can be designed to be lower than the liquid medium compressional velocity, at the proper plate thickness. The phase velocity corresponding to the K2 peak values is 1888 and 1583 m/s for the ST and MST configurations, respectively. Thus, a little decrease in K2 has to be accepted to reduce the velocity of the A0 mode up to a value lower than the velocity of the fluid environment (about 1500 m/s for water). Another benefit of the low-velocity A0 mode is that it allows for inexpensive signal processing equipment to be used, due to its low resonant frequency f = v/λ.
2.3. The Anisimkin Jr. Modes
In references [
14,
15] the peculiarities of the AMs are so defined: they have a velocity very close to that of the longitudinal BAW and have a dominant longitudinal displacement component
U1 with constant amplitude along the whole depth of the plate, being the shear components,
U2 and
U3, at least 10 times less than
U1 at any plate depth. The propagation of the AMs was investigated by studying the field profile of the modes that propagate along the plate with a phase velocity close to that of the LBAW: Plate thicknesses up to
h/λ = 2 were studied. As an example,
Figure 10 shows the field profile (the three displacement components normalized to the U
1 surface value
vs. the plate depth) of the AM propagating along the (0° 60° 0°)
x-GaPO
4 plate with
h/λ = 0.11.
Figure 10.
The field profile of the Anisimkin Jr. mode (AM) propagating at velocity v = 4191 m/s along a (0° 60° 0°) x-GaPO4 plate h/λ = 0.11 thick.
Figure 10.
The field profile of the Anisimkin Jr. mode (AM) propagating at velocity v = 4191 m/s along a (0° 60° 0°) x-GaPO4 plate h/λ = 0.11 thick.
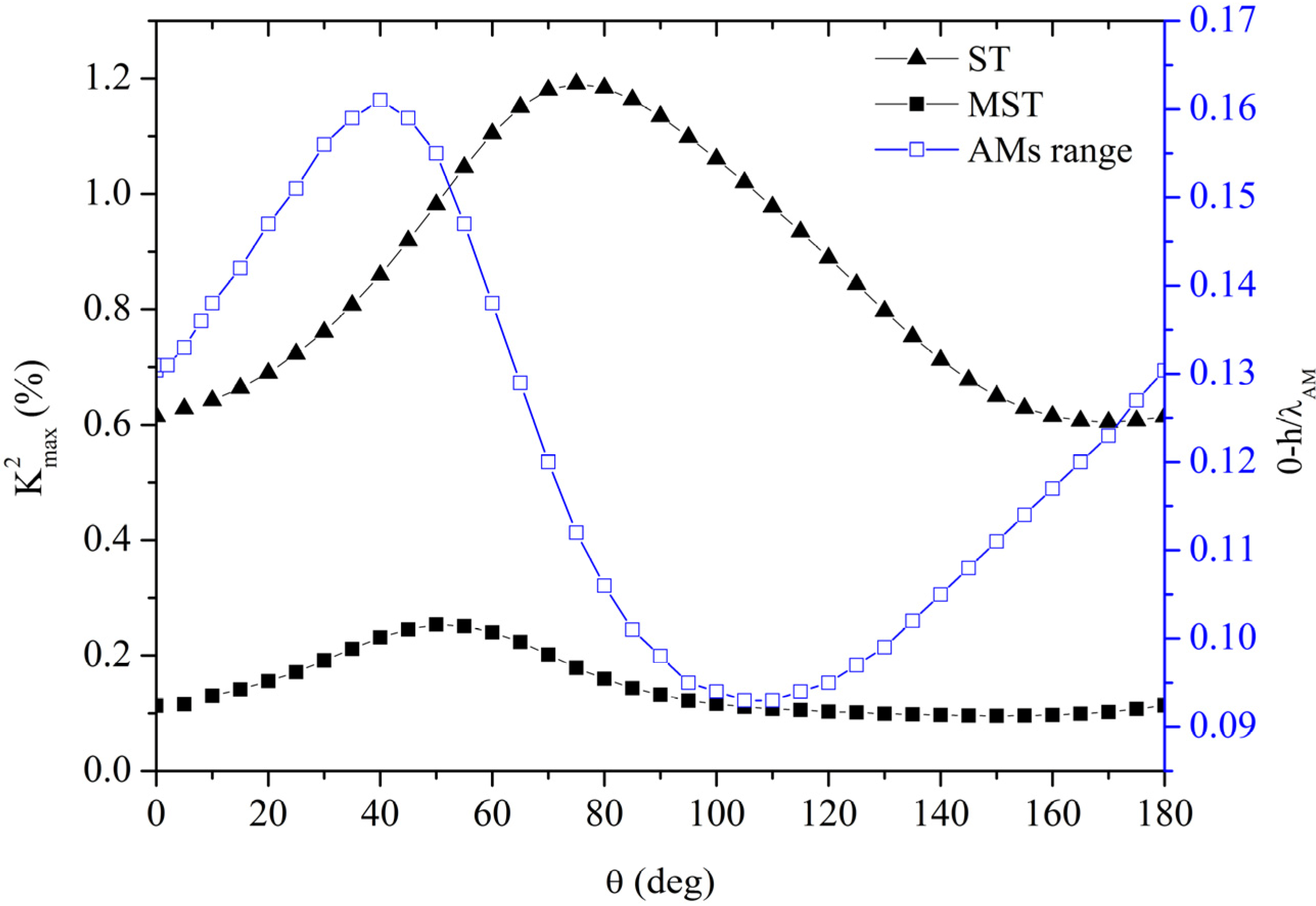
Figure 11 shows the normalized plate thicknesses for which both the conditions
U1 = 1,
U2,
U3 ≤ 0.1 across the plate depth and
v ~
vLBAW are satisfied and the maximum
K2 value achievable in this thickness range, for the ST and MST configurations, as a function of the substrate
y-rotation angle. No other plate thickness range suitable for the AMs propagation was found in the 0 to 2 range of
h/λ.
As can be seen, the ST configuration is the most favorable as it ensures the highest K2 at the largest plate thickness: the latter characteristic is particularly important as it is difficult to fabricate and handle a device implemented on a thin and fragile plate.
Figure 11.
The AMs plate thickness range, 0–h/λAM, and the peak K2 of the two configurations vs. the rotation angle.
Figure 11.
The AMs plate thickness range, 0–h/λAM, and the peak K2 of the two configurations vs. the rotation angle.
The temperature coefficient of velocity (
TCV),
TCV = (1/
T °C)(
vT °C −
v20 °C)/v
20 °C, that is linked to the
TCD by the relation
TCD = α −
TCV, being α the thermal expansion coefficient of the plate, was calculated over the plate thickness range, 0.001–
h/λ
AMs, over which the AMs propagate. The calculated
TCV is referred to 20 °C, being
vT °C and
v20 °C the wave velocity at a certain temperature value between −20 and 420 °C, and at 20°C, respectively. The relative velocity shift (
vT °C −
v20 °C)/
v20 °C vs. temperature curves, calculated for different
h/λ values in the 0.001–
h/λ
AMs range for each
y-rotation angle, were then fitted by a quadratic function.
Figure 12 shows the first and second order coefficients A
1 and A
2 of the quadratic fit: The bar centered on each point refers to the coefficient evaluated at the upper (
h/λ
AMs) and lower (0.001) plate thickness range. As can be seen in
Figure 12, for θ ≥ 55°, the two coefficients are poorly affected by the plate thickness change over the 0.001–
h/λ
AMs.
Figure 12.
The first and second order coefficients, A1 and A2, of the temperature coefficient of velocity (TCV) quadratic fit.
Figure 12.
The first and second order coefficients, A1 and A2, of the temperature coefficient of velocity (TCV) quadratic fit.
In the 60° to 90° range, the two coefficients A1 and A2 reach very small values, hence zero or very low TCD structures based on the AMs propagation can be fabricated.
The PFA is related to the incremental slope of the inverse velocity surface. The PFA of the AMs propagating along the x-axis of the unmetallized and metallized surface of the GaPO4 plates was theoretically investigated in order to evaluate the effect of an electrical shorting layer on the plate surface on the PFA. In both the two cases the PFA is very small, in the 0 to 0.09 range, and it is poorly affected by the presence of a shorting layer on one plate surface.
2.4. The Quasi Longitudinal Modes
In the present paper, a mode is attributed to the QL-family if
U1 is not constant through the plate, and
U2 and
U3 are less than 20% of
U1 at any depth. As an example,
Figure 13 shows the field profile of the QLM propagating along the (0° 0° 0°)
x-GaPO
4 plate at
v = 4097 m/s, being the plate thickness equal to
h/λ = 0.22.
Figure 13.
The field profile of the quasi longitudinal mode (QLM) propagating along the (0° 0° 0°) x-GaPO4 plate with h/λ = 0.22 at v = 4097 m/s.
Figure 13.
The field profile of the quasi longitudinal mode (QLM) propagating along the (0° 0° 0°) x-GaPO4 plate with h/λ = 0.22 at v = 4097 m/s.
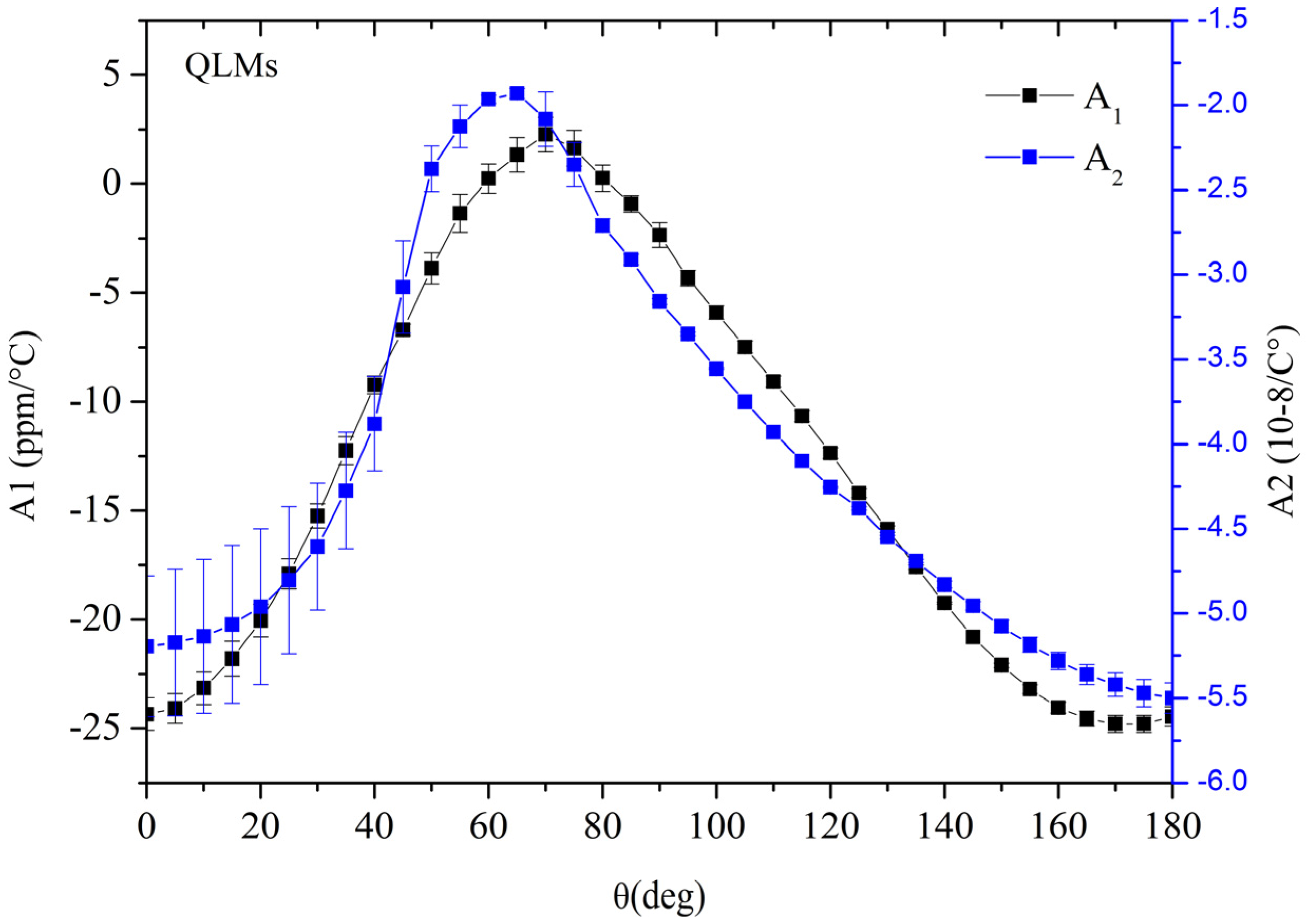
In
Figure 14, the first and second order coefficients of the quadratic fit of the
TCV vs. T °C of the QLMs are shown, being these coefficients calculated over the
h/λ
AMs–
h/λ
QLM range, for each y rotation angle.
As compared with the AMs, the coefficients A1 and A2 of the QLMs are a little bit more temperature sensitive than those of the AMs.
As for the AMs, the PFA of the QLMs propagating along the x axis of y rotated GaPO4 plates is very small, in the 0 to 0.09 deg range, and poorly affected by the presence of a metal shorting layer on the plate surface.
Figure 14.
The first and second order coefficients of the quadratic fit of the TCV of the QLMs propagating along the (0° θ 0°) GaPO4 plate.
Figure 14.
The first and second order coefficients of the quadratic fit of the TCV of the QLMs propagating along the (0° θ 0°) GaPO4 plate.