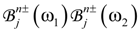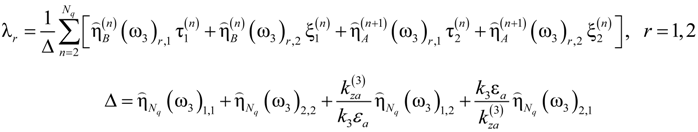Combinatorial Frequency Generation in Quasi-Periodic Stacks of Nonlinear Dielectric Layers
Abstract
:1. Introduction
2. Problem Statement and Methodology
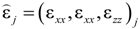 and nonlinear susceptibility
and nonlinear susceptibility 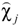 where j = A, B:
where j = A, B:

- (a)
- Fibonacci type QPS (Figure 1a) of order q ≥ 2 is defined recursively by the recurrence relation: Sq = {Sq−1 ◡ Sq−2}, where S0 = {B}, S1 = {A}; the number of layers in a stack Sq equals Fibonacci number Фq+1 and the corresponding stack thickness is Lq = Lq−1 + Lq−2 with L0 = dB; L1 = dA;
- (b)
- Thue-Morse type QPS (Figure 1b) of order q ≥ 1 is defined recursively by the recurrence relations: Qq = {Qq-1 ◡ Q'q-1} and Q'q = {Q'q-1 ◡ Qq-1}, where Qq and Q'q are complementary to each other and Q0 = {A}, Q'0 = {B}; the stacks Qq and Q'q contain 2 q layers and have thicknesses Lq = L'q = (dA + dB)q at q > 0 and L0 = dA, L'0 = dB.
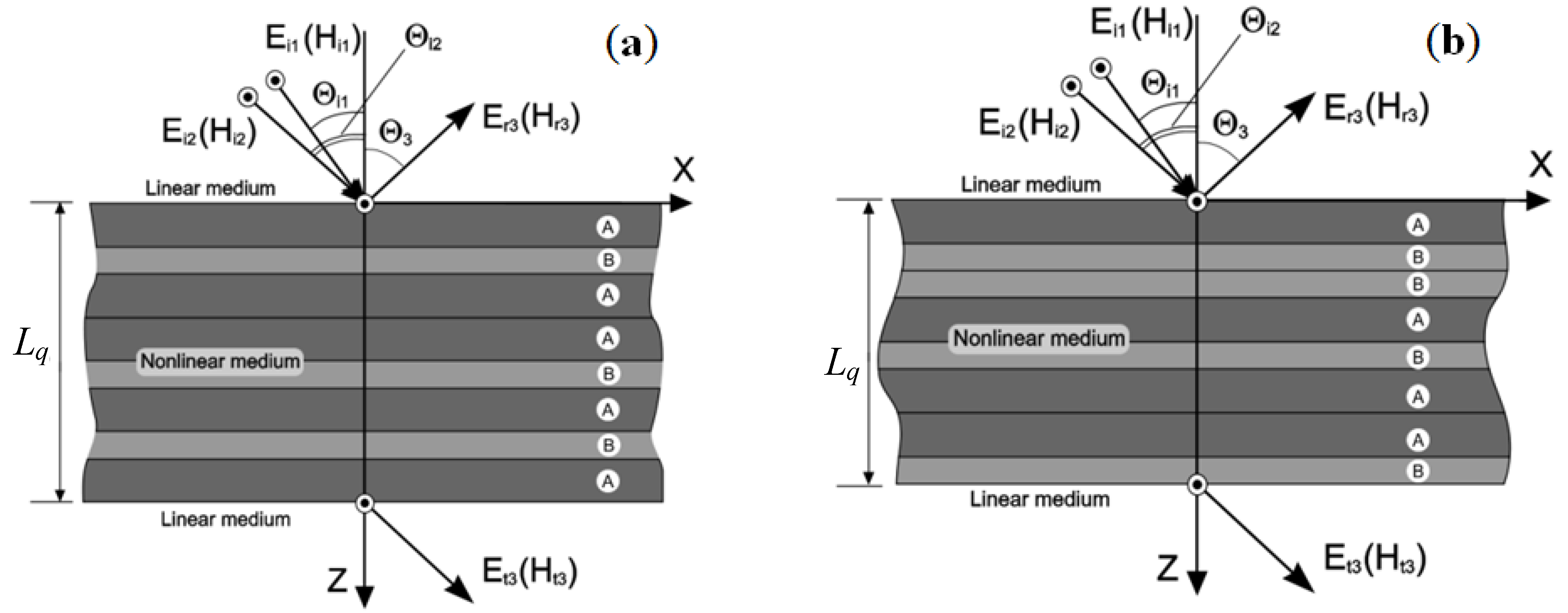
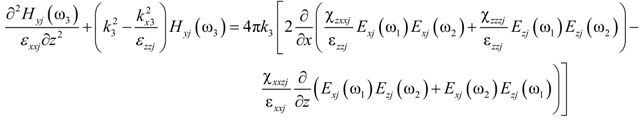
 ; angle Θ3 defines the emission direction from the stacks at frequency ω3, which is determined by the phase synchronism condition in the three-wave mixing process [39]:
; angle Θ3 defines the emission direction from the stacks at frequency ω3, which is determined by the phase synchronism condition in the three-wave mixing process [39]:
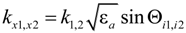 , k1,2 = ω1,2/c
, k1,2 = ω1,2/c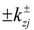 and
and 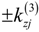 .
.
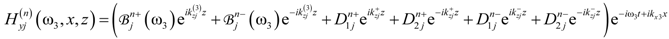
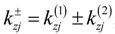 ,
, 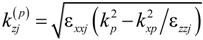 , p = 1,2,3 and superscript n is a serial number of a primitive cell, which identifies the position of a jth type layer in the stack.
, p = 1,2,3 and superscript n is a serial number of a primitive cell, which identifies the position of a jth type layer in the stack. 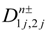 are amplitudes of the waves of frequency ω3, generated inside this layer, which depend on amplitudes
are amplitudes of the waves of frequency ω3, generated inside this layer, which depend on amplitudes 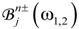 of the pump waves refracted into this layer [40].
of the pump waves refracted into this layer [40]. 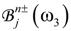 are amplitudes of the waves of frequency ω3 generated outside the layer and refracted into it.
are amplitudes of the waves of frequency ω3 generated outside the layer and refracted into it. 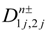 and
and  in Equation (4) for Fibonacci and Thue-Morse QPSs as detailed in Appendix 1.
in Equation (4) for Fibonacci and Thue-Morse QPSs as detailed in Appendix 1. 3. Simulation Results and Discussion
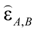 and nonlinear susceptibility
and nonlinear susceptibility 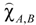 (the
(the 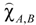 units [m/V] are omitted below for brevity) [45]:
units [m/V] are omitted below for brevity) [45]:
Layer B (ZnO) εxxB = 1.4, εzzB = 2.6, χxxzB = 2.82 × 10−8, χzxxB = 2.58 × 10−8, χzzzB = 8.58 × 10−8.
 .
.3.1. Spectral Efficiency of Frequency Mixing
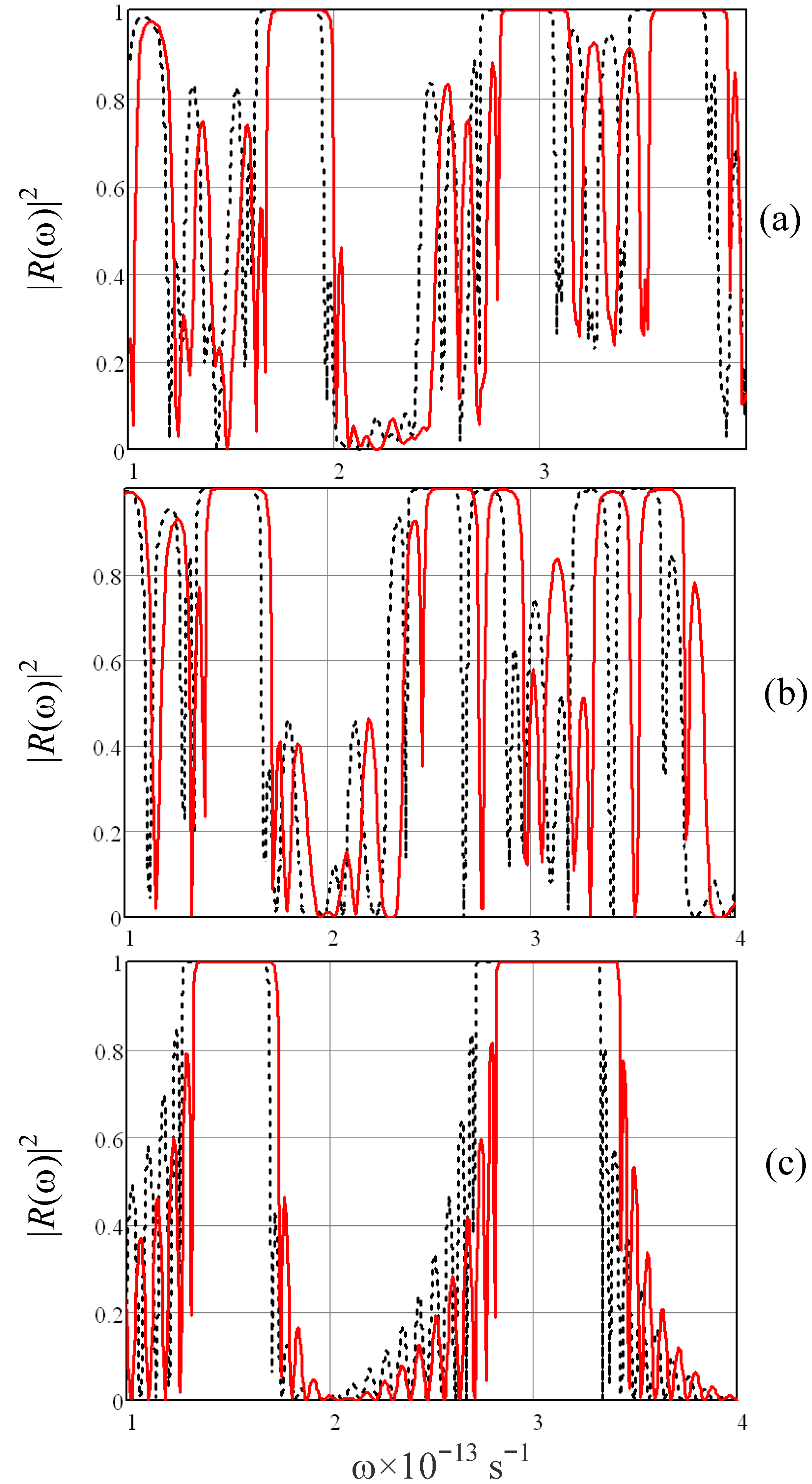
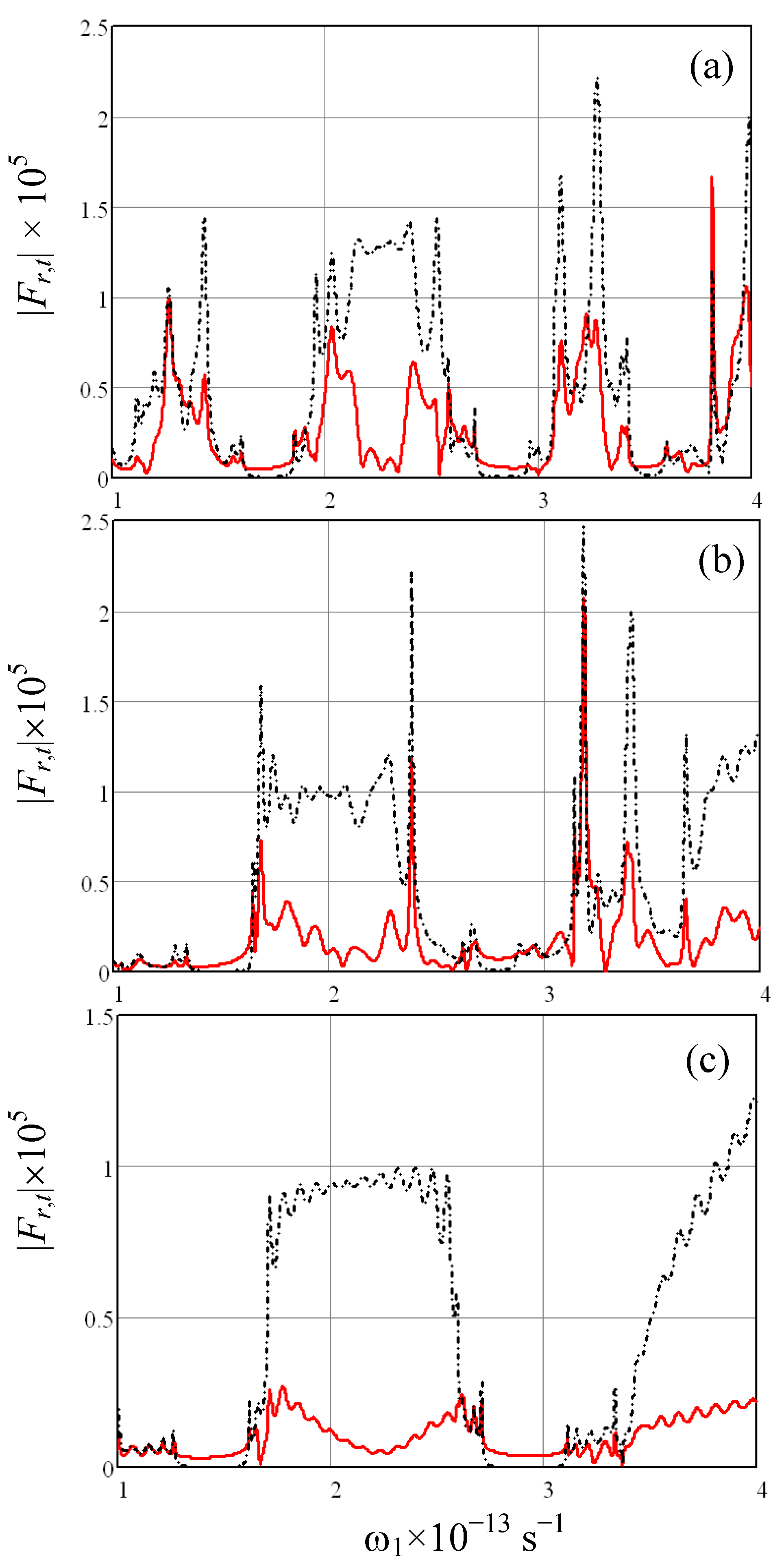
3.2. Effect of Stack Composition and Layer Anisotropy

3.3. Effect of Loss
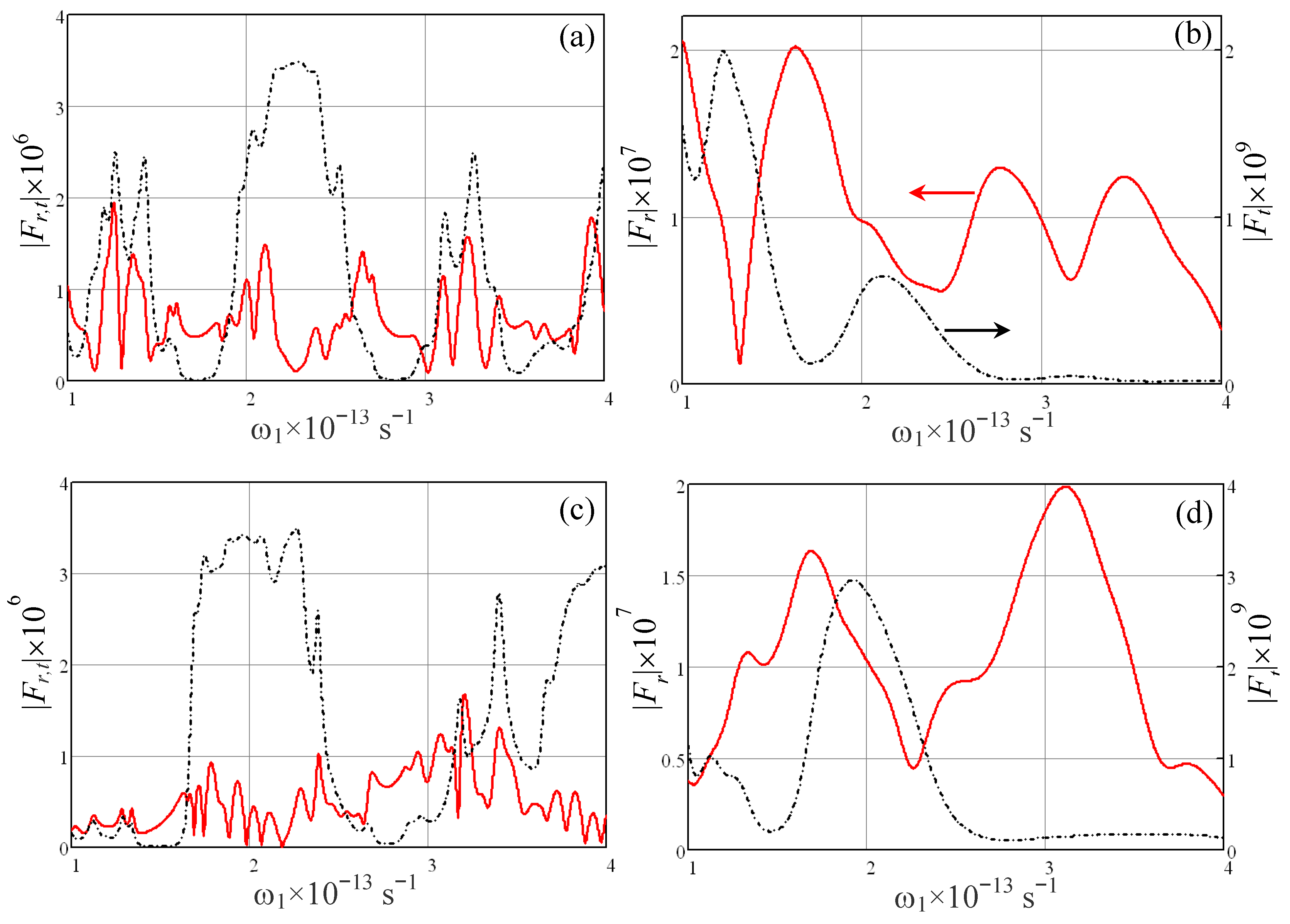
4. Conclusions
Acknowledgments
Author Contributions
Appendix 1
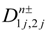 in Equation (4) for the waves generated inside each constituent layer of QPS. In the non-depleting wave approximation, this is accomplished by the harmonic balance method, which allows
in Equation (4) for the waves generated inside each constituent layer of QPS. In the non-depleting wave approximation, this is accomplished by the harmonic balance method, which allows 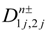 (ω1, ω2) to be explicitly related to amplitudes
(ω1, ω2) to be explicitly related to amplitudes 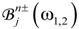 of the pump waves of frequencies ω1 and ω2 refracted into each layer [40]. In contrast to regular periodic stacks, evaluation of
of the pump waves of frequencies ω1 and ω2 refracted into each layer [40]. In contrast to regular periodic stacks, evaluation of  in QPSs is not straightforward and usually requires direct multiplication of the transfer matrices of all layers one by one. An alternative approach, based upon the QPS decomposition in “regular” and “defective” unit cells, is outlined in Section 2 and further elaborated here.
in QPSs is not straightforward and usually requires direct multiplication of the transfer matrices of all layers one by one. An alternative approach, based upon the QPS decomposition in “regular” and “defective” unit cells, is outlined in Section 2 and further elaborated here. 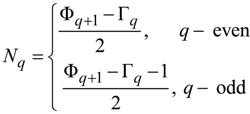
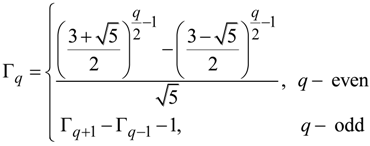
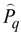 of length Φq+1, composed of 0’s and 1’s. The 1’s are located only in the columns corresponding to the first A layer of the doublets. At q ≥ 4,
of length Φq+1, composed of 0’s and 1’s. The 1’s are located only in the columns corresponding to the first A layer of the doublets. At q ≥ 4, 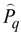 is defined by the recurrence relations:
is defined by the recurrence relations:
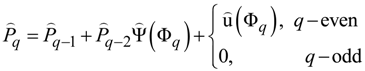
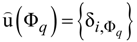 is a row-matrix with 1’s in the Φq column only, δi,i' is Kronecker delta;
is a row-matrix with 1’s in the Φq column only, δi,i' is Kronecker delta; 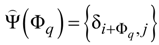 is a square Toeplitz matrix with 1’s only at the secondary diagonal offset for Φq from the main diagonal. Then the serial number νi(q), i = 1,2, … Γq of each defective cell in the stack can be deduced from
is a square Toeplitz matrix with 1’s only at the secondary diagonal offset for Φq from the main diagonal. Then the serial number νi(q), i = 1,2, … Γq of each defective cell in the stack can be deduced from 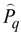 evaluated recursively in Equation (A3) for Fibonacci QPS of arbitrary order q:
evaluated recursively in Equation (A3) for Fibonacci QPS of arbitrary order q:
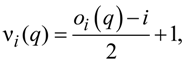
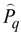 .
.
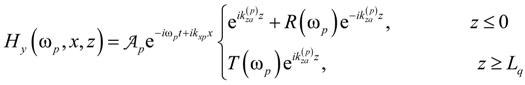

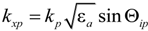 ,
, 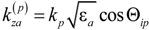 and
and 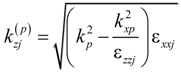 are the transverse and longitudinal wavenumbers outside the stack and inside the layers at frequencies ωp, p = 1,2,3; kp = ωp/c, c is the speed of light; Ap are amplitudes of the incident waves.
are the transverse and longitudinal wavenumbers outside the stack and inside the layers at frequencies ωp, p = 1,2,3; kp = ωp/c, c is the speed of light; Ap are amplitudes of the incident waves. 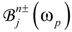 are amplitude coefficients of the field in individual layers.
are amplitude coefficients of the field in individual layers. 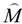 q(ωp):
q(ωp):
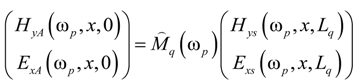


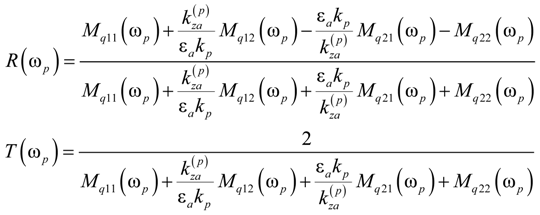
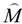 q(ωp) are evaluated by TMM at each frequency ωp. For Fibonacci QPS,
q(ωp) are evaluated by TMM at each frequency ωp. For Fibonacci QPS, 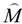 q(ωp) is defined recursively at q ≥ 2.
q(ωp) is defined recursively at q ≥ 2.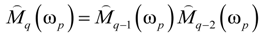
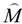 0(ωp) =
0(ωp) = 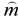 LB(dB, ωp),
LB(dB, ωp), 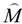 1(ωp) =
1(ωp) = 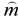 LA(dA, ωp);
LA(dA, ωp); 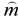 LA(dA, ωp) and
LA(dA, ωp) and 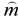 LB(dB, ωp) are the transfer matrices of layers A and B, respectively.
LB(dB, ωp) are the transfer matrices of layers A and B, respectively. 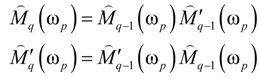
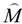 0(ωp) =
0(ωp) = 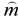 LA(dA, ωp),
LA(dA, ωp), 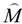 '0(ωp) =
'0(ωp) = 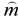 LB(dB, ωp).
LB(dB, ωp).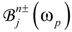 can be progressively deduced for each layer using the transfer matrices. In contrast to regular periodic structures, the direct evaluation of
can be progressively deduced for each layer using the transfer matrices. In contrast to regular periodic structures, the direct evaluation of 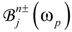 for QPS is rather involved. The approach developed in this paper, where the QPSs are formed by cascading the regular and defective primitive cells, dramatically simplifies the analysis. The conventional procedure utilised for the periodic stacks can be adopted here as long as the positions of the defective cells are determined. Then the field amplitudes
for QPS is rather involved. The approach developed in this paper, where the QPSs are formed by cascading the regular and defective primitive cells, dramatically simplifies the analysis. The conventional procedure utilised for the periodic stacks can be adopted here as long as the positions of the defective cells are determined. Then the field amplitudes 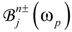 in each layer can be expressed in the following form
in each layer can be expressed in the following form
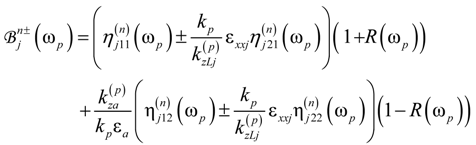
 are the transfer matrices of a subset of (n − 1) primitive cells preceding the layer of type j = A, B in the nth primitive cell:
are the transfer matrices of a subset of (n − 1) primitive cells preceding the layer of type j = A, B in the nth primitive cell:
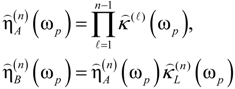


Appendix 2
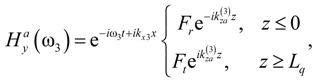
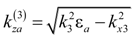 is the longitudinal wave number in the surrounding homogeneous media. To evaluate the field amplitudes Fr,t in Equation (A12), it is necessary to relate the fields of the nonlinear products generated inside the stack to the field emitted from the QPS. This is accomplished by enforcing the tangential field continuity at the stack external interfaces and applying the modified TMM [40] to find the fields inside the stack. The fields at the stack outer interfaces of Fibonacci QPS are related as follows
is the longitudinal wave number in the surrounding homogeneous media. To evaluate the field amplitudes Fr,t in Equation (A12), it is necessary to relate the fields of the nonlinear products generated inside the stack to the field emitted from the QPS. This is accomplished by enforcing the tangential field continuity at the stack external interfaces and applying the modified TMM [40] to find the fields inside the stack. The fields at the stack outer interfaces of Fibonacci QPS are related as follows
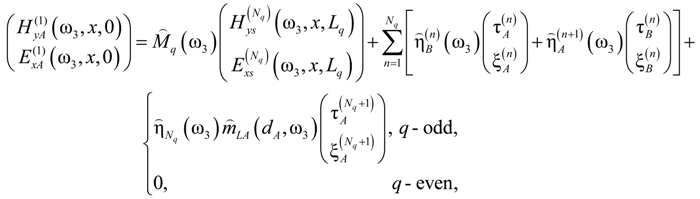
 and
and  (ω3) are defined in (A1.11);
(ω3) are defined in (A1.11);  and
and 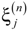 at j = A, B are:
at j = A, B are:
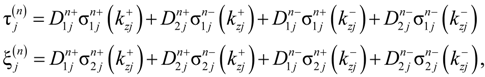
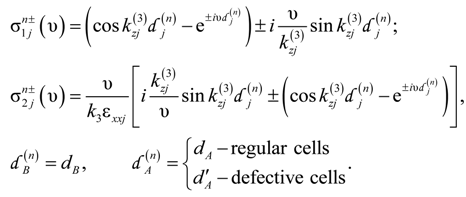
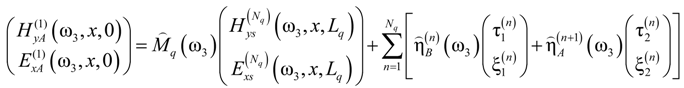
 (ω3) are defined in Equation (A11);
(ω3) are defined in Equation (A11); 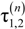 and
and 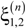 are as follows
are as follows

 and
and 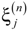 , j = A, B have the form of Equation (A14) except the layer A thickness remaining the same in both regular and defective cells, i.e.,
, j = A, B have the form of Equation (A14) except the layer A thickness remaining the same in both regular and defective cells, i.e., 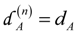 .
. 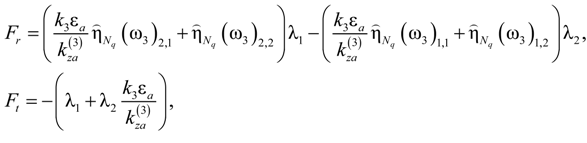
 (ω3) are defined in (A.11) and λ1,2 are
(ω3) are defined in (A.11) and λ1,2 are
- -
- for Fibonacci QPS:
- -
- for Thue-Morse QPS:
Conflicts of Interest
References and Notes
- Valy Vardeny, Z.; Nahata, A.; Agrawal, A. Optics of photonic quasicrystals. Nat. Photon. 2013, 7, 177–187. [Google Scholar] [CrossRef]
- Merlin, R.; Bajema, K.; Clarke, R.; Juang, F.-Y.; Bhattacharya, P.K. Quasiperiodic GaAs-AlAs Heterostructures. Phys. Rev. Lett. 1985, 55, 1768–1770. [Google Scholar] [CrossRef]
- Pelster, R.; Gasparian, V.; Nimtz, G. Propagation of plane waves and of waveguide modes in quasiperiodic dielectric heterostructures. Phys. Rev. E 1997, 55, 7645–7655. [Google Scholar] [CrossRef]
- Liu, N. Propagation of light waves in Thue-Morse dielectric multilayers. Phys. Rev. B 1997, 55, 3543–3547. [Google Scholar] [CrossRef]
- Maciá, E. Hierarchical description of phonon dynamics on finite Fibonacci superlattices. Phys. Rev. B 2006, 73. [Google Scholar] [CrossRef]
- Albuquerque, E.L.; Cottam, M.G. Polaritons in Periodic and Quasiperiodic Structures; Elsevier: Amsterdam, The Netherland, 2004. [Google Scholar]
- Zoorob, M.E.; Chariton, M.D.B.; Parker, G.J.; Baumberg, J.J.; Netti, M.C. Complete photonic bandgaps in 12-fold symmetric quasicrystals. Nature 2000, 404, 740–743. [Google Scholar]
- Cojocaru, E. Omnidirectional reflection from finite periodic and Fibonacci quasi-periodic multilayers of alternating isotropic and birefringent thin films. Appl. Opt. 2002, 41, 747–755. [Google Scholar]
- Barriuso, A.; Monzón, J.; Sánchez-Soto, L.; Felipe, A. Comparing omnidirectional reflection from periodic and quasiperiodic one-dimensional photonic crystals. Opt. Exp. 2005, 13, 3913–3920. [Google Scholar]
- Freedman, B.; Bartal, G.; Segev, M.; Lifshitz, R.; Christoet, D.N. Wave and defect dynamics in nonlinear photonic quasicrystals. Nature 2006, 440, 1166–1169. [Google Scholar] [CrossRef]
- El Hassouani, Y.; Aynaou, H.; El Boudouti, E.H.; Djafari-Rouhani, B.; Akjouj, A.; Velasco, V.R. Surface electromagnetic waves in Fibonacci superlattices: Theoretical and experimental results. Phys. Rev. B 2006, 74. [Google Scholar] [CrossRef]
- Moretti, L.; Rea, I.; Rotiroti, L.; Rendina, I.; Abbate, G.; Marino, A.; de Stefano, L. Photonic band gaps analysis of Thue-Morse multilayers made of porous silicon. Opt. Exp. 2006, 14, 6264–6272. [Google Scholar]
- Makarava, L.N.; Nazarov, M.M.; Ozheredov, I.A.; Shkurinov, A.P.; Smirnov, A.G.; Zhukovsky, S.V. Fibonacci-like photonic structure for femtosecond pulse compression. Phys. Rev. E 2007, 75. [Google Scholar] [CrossRef]
- Tuz, V. Optical properties of a quasi-periodic generalized Fibonacci structure of chiral and material layers. JOSA B 2009, 26, 627–632. [Google Scholar] [CrossRef]
- Reyes-Gómez, E.; Raigoza, N.; Cavalcanti, S.B.; de Carvalho, C.A.A.; Oliveira, L.E. Plasmon polaritons in photonic metamaterial Fibonacci superlattices. Phys. Rev. B 2010, 81. [Google Scholar] [CrossRef]
- Pang, X.-N.; Dong, J.-W.; Wang, H.-Z. Photonic localization of interface modes at the boundary between metal and Fibonacci quasiperiodic structure. JOSA B 2010, 27, 2009–2013. [Google Scholar] [CrossRef]
- Olkhovskiy, Y.A.; Shramkova, O.V. Electromagnetic wave transmission and reflection by a quasiperiodic layered semiconductor structure. Phys. B Condens. Matter 2011, 406, 1415–1419. [Google Scholar] [CrossRef]
- Dolev, I.; Volodarsky, M.; Porat, G.; Arie, A. Multiple coupling of surface plasmons in quasiperiodic gratings. Opt. Lett. 2011, 36, 1584–1586. [Google Scholar]
- Hsueh, W.J.; Wun, S.J.; Lin, Z.J.; Cheng, Y.H. Features of the perfect transmission in Thue-Morse dielectric multilayers. J. Opt. Soc. Am. B 2011, 28, 2584–2591. [Google Scholar] [CrossRef]
- Hsueh, W.J.; Chang, C.H.; Cheng, Y.H.; Wun, S.J. Effective Bragg conditions in a one-dimensional quasicrystal. Opt. Expr. 2012, 20, 26618–26623. [Google Scholar] [CrossRef]
- Kruk, S.S.; Helgert, C.; Decker, M.; Staude, I.; Menzel, C.; Etrich, C.; Rockstuhl, C.; Jagadish, C.; Pertsch, T.; Neshev, D.N.; et al. Optical metamaterials with quasicrystalline symmetry: Symmetry-induced optical isotropy. Phys. Rev. B 2013, 88. [Google Scholar] [CrossRef]
- Savoia, S.; Castaldi, G.; Galdi, V. Optical nonlocality in multilayered hyperbolic metamaterials based on Thue-Morse superlattices. Phys. Rev. B 2013, 87. [Google Scholar] [CrossRef]
- Xu, S.; Zhu, Y.; Wang, L.; Yang, P.; Chu, P.K. Passband and defective bands in photonic and quasi-crystals. J. Opt. Soc. Am. B 2014, 31, 664–671. [Google Scholar] [CrossRef]
- Gong, Y.; Liu, X.; Wang, L.; Lu, H.; Wang, G. Multiple responses of TPP-assisted near-perfect absorption in metal/Fibonacci quasiperiodic photonic crystal. Opt. Expr. 2011, 19, 9759–9769. [Google Scholar] [CrossRef]
- Feng, J.; Zhu, Y.; Ming, N. Harmonic generations in an optical Fibonacci superlattice. Phys. Rev. B 1990, 41, 5578–5582. [Google Scholar] [CrossRef]
- Zhu, S.; Zhu, Y.; Ming, N. Quasi-phase-matched third-harmonic generation in a quasi-periodic optical superlattice. Science 1997, 278, 843–846. [Google Scholar] [CrossRef]
- Fradkin-Kashi, K.; Arie, A. Multiple-wavelength quasi-phase-matched nonlinear interactions. IEEE J. Quant. Electron. 1999, 35, 1649–1656. [Google Scholar] [CrossRef]
- Chern, G.-W.; Chang, J.-F.; Wang, L.A. Modeling of nonlinear pulse propagation in periodic and quasi-periodic binary long-period fiber gratings. JOSA B 2002, 19, 1497–1508. [Google Scholar] [CrossRef]
- Huang, T.; Huang, D. Interplay between optical nonlinearity and localization in a finite disordered Fibonacci chain. Phys. Rev. B 2007, 76. [Google Scholar] [CrossRef]
- Lifshitz, R.; Arie, A.; Bahabad, A. Photonic quasicrystals for nonlinear optical frequency conversion. Phys. Rev. Lett. 2005, 95. [Google Scholar] [CrossRef]
- Werchner, M.; Schafer, M.; Kira, M.; Koch, S.W.; Sweet, J.; Olitzky, J.D.; Hendrickson, J.; Richards, B.C.; Khitrova, G.; Gibbs, H.M.; et al. One dimensional resonant Fibonacci quasicrystals: Noncanonical linear and canonical nonlinear effects. Opt. Expr. 2009, 17, 6813–6828. [Google Scholar] [CrossRef]
- Vasconcelos, M.S.; Mauriz, P.W.; Albuquerque, E.L. Optical filters based in quasiperiodic photonic crystal. Microelectron. J. 2009, 40, 851–853. [Google Scholar] [CrossRef]
- Grigoriev, V.; Biancalana, F. Bistability, multistability and non-reciprocal light propagation in Thue-Morse multilayered structures. New J. Phys. 2010, 12. [Google Scholar] [CrossRef]
- Zhukovsky, S.V.; Smirnov, A.G. All-optical diode action in asymmetric nonlinear photonic multilayers with perfect transmission resonances. Phys. Rev. A 2011, 83. [Google Scholar] [CrossRef]
- Lotfi, E.; Jamshidi-Ghaleh, K.; Moslemi, F.; Masalehdan, H. Optical multistability in 1D photonic crystals with nonlinear Thue-Morse structure. Appl. Phys. A 2011, 103, 669–672. [Google Scholar]
- Zhu, S.N.; Zhu, Y.Y.; Qin, Y.Q.; Wang, H.F.; Ge, C.Z.; Ming, N.B. Experimental realization of second harmonic generation in a Fibonacci optical superlattice of LiTaO3. Phys. Rev. Lett. 1997, 78, 2752–2755. [Google Scholar] [CrossRef]
- Chen, Y.B.; Zhang, C.; Zhu, Y.Y.; Zhu, S.N.; Wang, H.T.; Ming, N.B. Optical harmonic generation in a quasi-phase-matched three-component Fibonacci superlattice LiTaO3. Appl. Phys. Lett. 2001, 78, 577–579. [Google Scholar] [CrossRef]
- Sheng, Y.; Koynov, K.; Zhang, D. Collinear second harmonic generation of 20 wavelengths in a single two-dimensional decagonal nonlinear photonic quasi-crystal. Opt. Commun. 2009, 282, 3602–3606. [Google Scholar] [CrossRef]
- Blombergen, N. Nonlinear Optics: A Lecture Note; Benjamin: New York, NY, USA & Amsterdam, The Netherland, 1965. [Google Scholar]
- Shramkova, O.V.; Schuchinsky, A.G. Nonlinear scattering by anisotropic dielectric periodic structures. Adv. OptoElectron. 2012. [Google Scholar] [CrossRef]
- Jeong, Y.; Lee, B. Matrix analysis for layered quasi-phase-matched media considering multiple reflection and pump wave depletion. IEEE J. Quant. Electron. 1999, 35, 162–172. [Google Scholar] [CrossRef]
- Li, J.-J.; Li, Z.-Y.; Zhang, D.-Z. Second harmonic generation in one-dimensional nonlinear photonic crystals solved by the transfer matrix method. Phys. Rev. E 2007, 75. [Google Scholar] [CrossRef]
- Szczepański, P.; Osuch, T.; Jaroszewicz, Z. Modeling of amplification and light generation in one-dimensional photonic crystal using a multiwavelength transfer matrix approach. Appl. Opt. 2010, 48, 5401–5406. [Google Scholar]
- Li, J.-J.; Li, Z.-Y.; Zhang, D.-Z. Nonlinear frequency conversion in two-dimensional nonlinear photonic crystals solved by a plane-wave-based transfer-matrix method. Phys. Rev. B 2008, 77. [Google Scholar] [CrossRef]
- Yariv, A.; Yeh, P. Optical Waves in Crystals: Propagation and Control of Laser Radiation; Wiley: New York, NY, USA, 1984. [Google Scholar]
- The approximation of the non-depleting nonlinear process is used here. Therefore extinction of pump waves is caused by the dissipative losses only.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Shramkova, O.; Schuchinsky, A. Combinatorial Frequency Generation in Quasi-Periodic Stacks of Nonlinear Dielectric Layers. Crystals 2014, 4, 209-227. https://doi.org/10.3390/cryst4030209
Shramkova O, Schuchinsky A. Combinatorial Frequency Generation in Quasi-Periodic Stacks of Nonlinear Dielectric Layers. Crystals. 2014; 4(3):209-227. https://doi.org/10.3390/cryst4030209
Chicago/Turabian StyleShramkova, Oksana, and Alexander Schuchinsky. 2014. "Combinatorial Frequency Generation in Quasi-Periodic Stacks of Nonlinear Dielectric Layers" Crystals 4, no. 3: 209-227. https://doi.org/10.3390/cryst4030209
APA StyleShramkova, O., & Schuchinsky, A. (2014). Combinatorial Frequency Generation in Quasi-Periodic Stacks of Nonlinear Dielectric Layers. Crystals, 4(3), 209-227. https://doi.org/10.3390/cryst4030209