Study on Modifying Mechanical Properties and Electronic Structure of Aerospace Material γ-TiAl Alloy
Abstract
1. Introduction
2. Model Construction and Computational Methods
3. Results and Discussion
3.1. Geometric Structure
3.2. Phonon Spectrum
3.3. Mechanical Properties
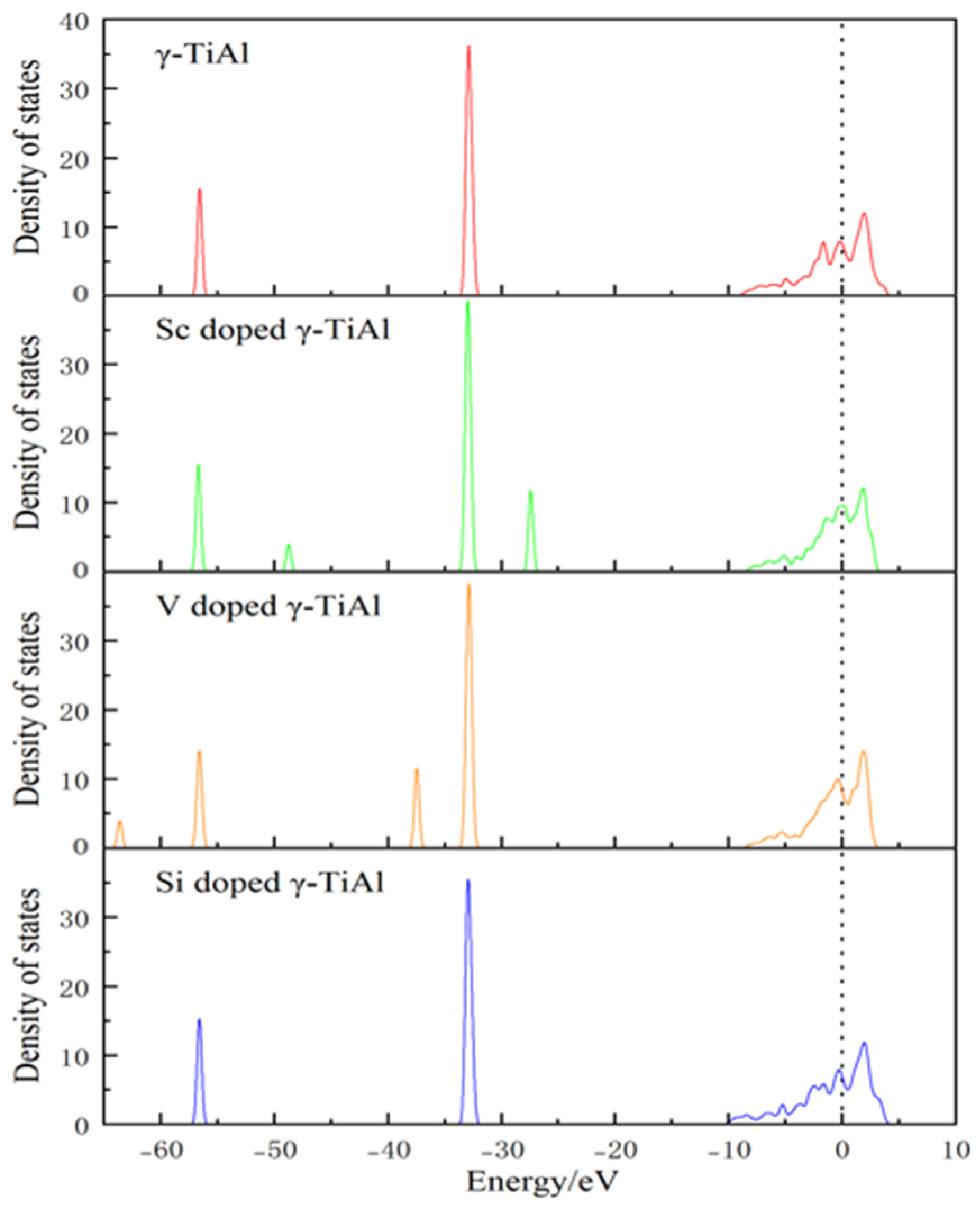
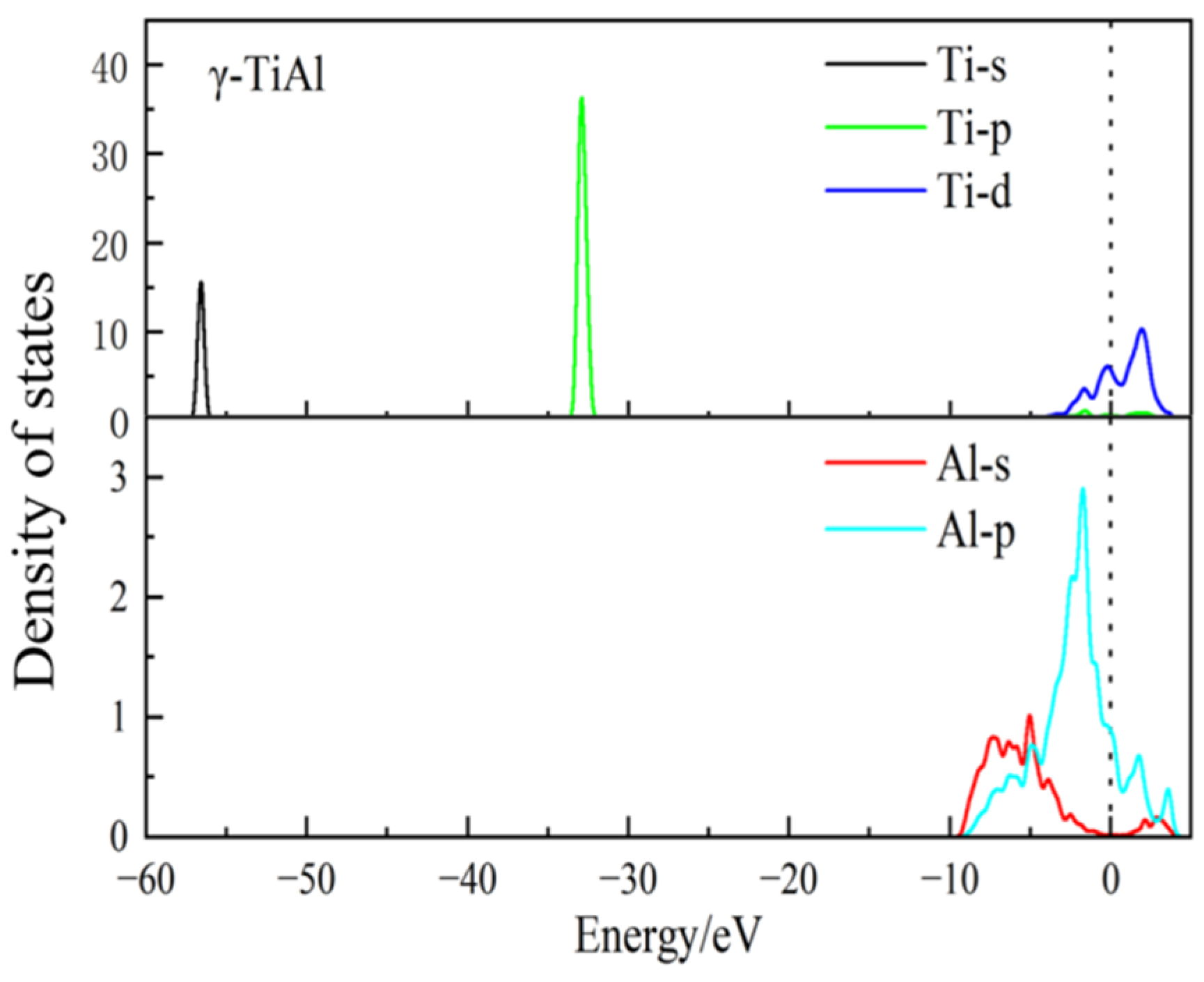
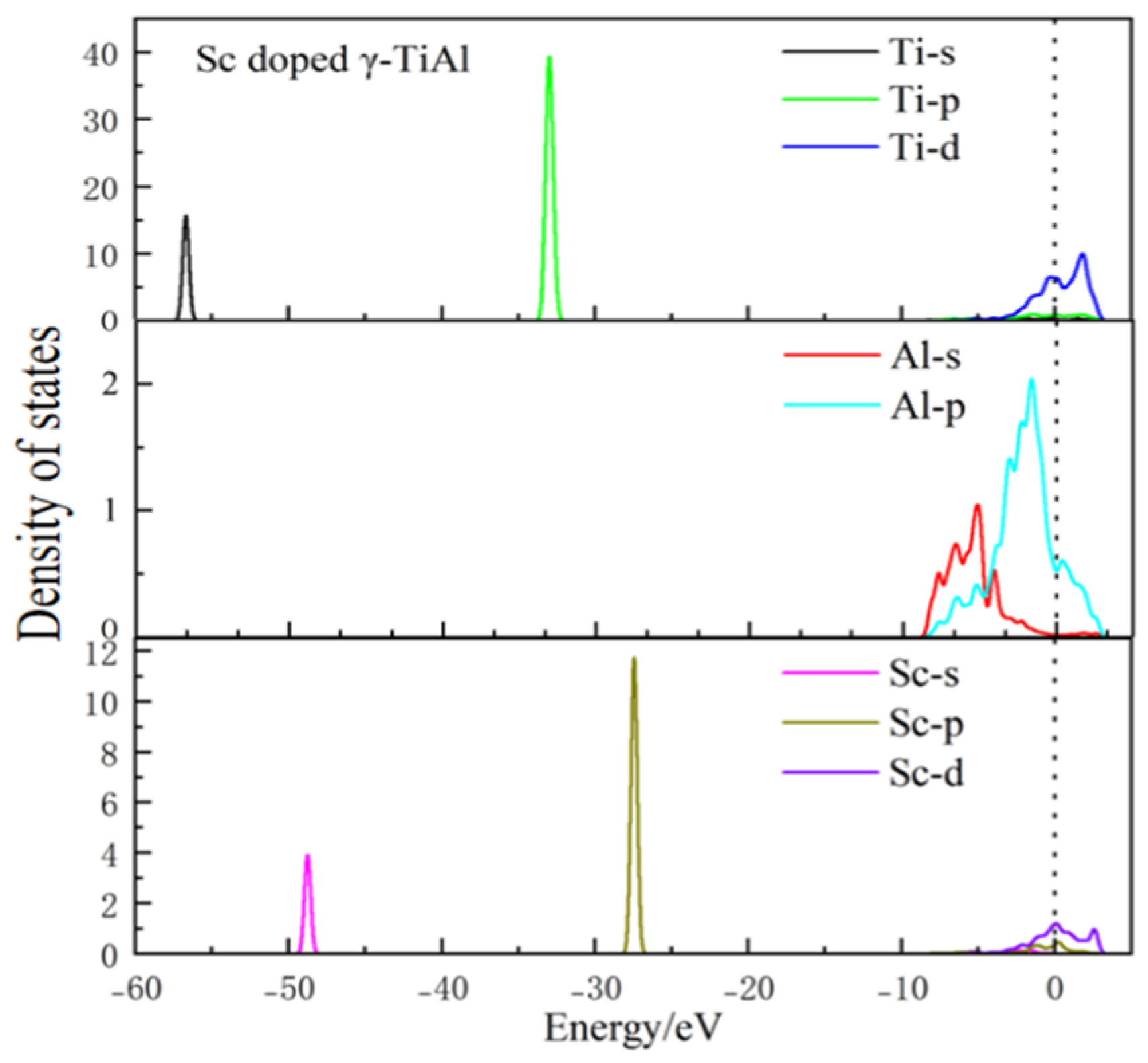
3.4. Electronic Density of States
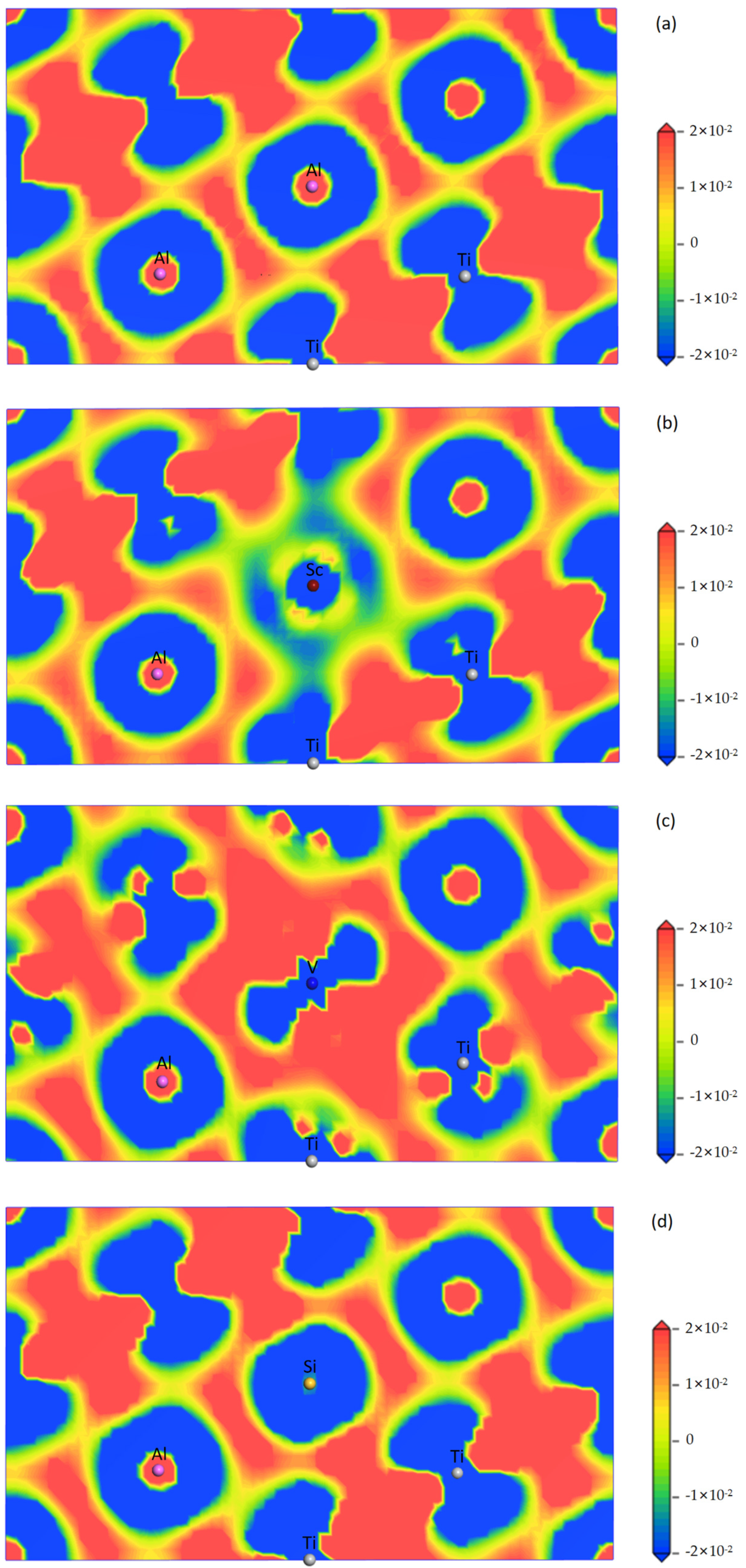
3.5. Mulliken Population Analysis and Differential Charge Density
4. Conclusions
- (1)
- Structural stability: After the incorporation of Sc, V, and Si, due to the difference in atomic radius, the structural parameters of γ-TiAl change significantly. The calculation results of the phonon spectrum show that all branches of the phonon spectrum before and after doping are located above the zero value of the frequency axis, with no imaginary frequency phenomenon, indicating that the calculation model in this paper has specific thermodynamic stability. Meanwhile, according to the criterion of mechanical stability—the Bonn criterion, it is concluded that the structure of γ-TiAl is stable before and after doping.
- (2)
- Mechanical property transformation: After doping, the bulk elastic modulus B, shear modulus G, and Young’s modulus E of γ-TiAl all significantly decreased, while the Poisson’s ratio υ and B/G value increased. The doped system underwent a transformation from brittleness to toughness.
- (3)
- Anisotropic enhancement: The AU, Acomp, Ashear, and A1 values of the doped system all increased, indicating that doping can significantly enhance the anisotropy of the material’s mechanical behavior.
- (4)
- Conductor properties: The electron density of states near the Fermi level is not zero before and after doping, indicating that γ-TiAl possesses conductor properties. Moreover, the electronic density of states at this location slightly increases after doping, indicating that doping can enhance the electrical conductivity of γ-TiAl alloys.
- (5)
- Bonding characteristics: The internal mechanism by which doped atoms affect the electron density of states was reasonably analyzed through the partial wave density of states diagrams of each atom before and after doping. According to the Mulliken population analysis and the differential charge density diagram, incorporating Sc and V enhances the covalent interaction of the Al-Ti bond. However, the incorporation of Si weakens the covalent interaction of the Al-Ti bond while shortening the bond lengths and increasing the bond strength.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pan, D.; Wang, X.; Qiao, Y.; Niu, J.T.; Wang, S.R.; Guo, P.Q. Review on Cutting of γ-TiAl Alloy. Tool Eng. 2021, 55, 3–11. [Google Scholar]
- Xia, J.J.; Liang, W.P.; Miao, Q.; Ren, B.L.; Han, P.D. First-principles Study on Electronic Structure of γ-TiAl Alloy Doped with Y. Rare Met. Mater. Eng. 2017, 46, 421–426. [Google Scholar]
- Greenberg, B.A.; Anisimov, V.I.; Gornostirev, Y.N.; Taluts, G.G. Possible factors affecting the brittleness of the intermetallic compound TiAl. Scr. Metall. 1988, 22, 859–864. [Google Scholar] [CrossRef]
- Morinaga, M.; Saito, J.; Yukawa, N.; Adachi, H. Electronic effect on the ductility of alloyed TiAl compound. Acta Metall. Mater. 1990, 38, 25–29. [Google Scholar] [CrossRef]
- Hussain, A.; Hayat, S.S.; Choudhry, M.A. Ab-initio calculations of electronic structure and optical properties of TiAl alloy. Phys. B Condens. Matter 2011, 406, 1961–1965. [Google Scholar] [CrossRef]
- Shi, L.; Wang, T.; Wang, L.; Liu, E. Research on Johnson–Cook Constitutive Model of γ-TiAl Alloy with Improved Parameters. Materials 2023, 16, 6715. [Google Scholar] [CrossRef]
- Song, J.; Zhao, B.; Ding, W.; Zhao, Y.; Zhu, J.; Cui, H. Wear mechanism of aggregated cBN grains during single-grain ultrasonic vibration-assisted grinding of γ-TiAl alloys. Int. J. Adv. Manuf. Technol. 2024, 135, 4749–4764. [Google Scholar] [CrossRef]
- Luo, Y.Y.; Yang, H.Y.; Yin, Y.F.; Mao, X.N. Effect of Temperature on Tensile Properties and Fracture Mechanism of γ-TiAl Alloy Bars. Rare Met. Mater. Eng. 2022, 51, 3716–3721. [Google Scholar]
- Wang, W.Y.; Xu, Y.; Tian, B.; Gan, X.Z.; Wang, Z.G.; Liang, Y.F.; Lin, J.P. Research on stability and phase relation of TiAl-Nb intermetallic compounds based on first-principles and thermodynamic calculations. J. At. Mol. Phys. 2025, 42, 151–162. [Google Scholar]
- Huang, Z.X.; Zhou, L.X.; Zhang, Y.F.; Li, J.; Tian, A.M. Electronic Structure Factors Affecting the Ductility of TiAl Alloy. Chin. J. Struct. Chem. 1999, 18, 442–446. [Google Scholar]
- Liu, Q.; Zhang, M.; Fu, L.Q.; Yang, Z.W.; Wang, Y.; Wang, D.P. Microstructure and Properties of γ-TiAl Fabricated by In-situ Alloying Assisted Double-wire Arc Additive Manufacturing. Rare Met. Mater. Eng. 2020, 49, 3919–3924. [Google Scholar]
- Dang, H.L.; Wang, C.Y.; Yu, T. First-principles investigation on alloying effect of Nb and Mo in γ-TiAl. Acta Phys. Sin. 2007, 56, 2838–2844. [Google Scholar] [CrossRef]
- Shao, Y.; Xu, L.J.; Xiao, S.L.; Tian, J.; Chen, Y.Y. Creep Behavior of As-cast Ti-43Al-6Nb-1Mo-1Cr-0.2TiB2 Alloy at Elevated Temperature. Spec. Cast. Nonferrous Alloys 2024, 44, 203–211. [Google Scholar]
- Han, J.D.; Wu, Z.E.; Zhang, F.; Dang, X.H. Effect of boron addition on the microstructure of high Nb-containing TiAl alloy. J. Baoji Univ. Arts Sci. (Nat. Sci. Ed.) 2022, 42, 37–40. [Google Scholar]
- Imayev, V.M.; Parkhimovich, N.Y.; Trofimov, D.M.; Imayev, R.M. The Influence of Nb, Zr, and Zr+Hf on the Lattice Parameters and Creep Behavior of β-Solidifying γ-TiAl Alloys. J. Mater. Eng. Perform. 2022, 31, 5706–5711. [Google Scholar] [CrossRef]
- He, Q.; Zhao, C.; Song, W.; Zhang, S.; Shi, Z.; Ren, X.; Yang, Q. Insight into the interface properties of γ-TiAl/α2-Ti3Al with La doping obtained by first-principles calculations. Phys. Chem. Chem. Phys. 2025, 27, 5683–5693. [Google Scholar] [CrossRef]
- Lin, Z. Effect of Element Doping on High Temperature Properties of Mm(NiCoMnZrTiAl)5.15 Hydrogen Storage Alloy. Fujian Metall. 2023, 52, 19–23. [Google Scholar]
- Li, D.; Zhang, G.Y.; Liang, T.; Chu, R.; Zhu, S.L. First-principles study on the influence of alloying when oxygen absorption on the surface of γ-TiAl(111). J. Shenyang Norm. Univ. (Nat. Sci. Ed.) 2011, 29, 199–203. [Google Scholar]
- Song, Q.G.; Jiang, Q.J.; Gu, W.F.; Hu, X.L. Effects of impurity concentration on ductility of Mn-doped γ-TiAl alloys. J. Civ. Aviat. Univ. China 2017, 35, 60–64. [Google Scholar]
- Liu, X.K.; Zheng, Z.; Liu, C.; Lan, X.H.; Yin, W. First-principles Investigation on Site Substitution of 5d Transition Metals in γ-TiAl Alloy. Mater. Rep. 2012, 26, 115–119. [Google Scholar]
- Yu, Q.; Gu, G.C.; Gao, X.; Li, Z.N.; Jiao, Z.B.; Xu, W.W. Theoretically probing intrinsic properties of γ′ phase in FeCoNiTiAl high-entropy alloys. Rare Met. 2025, 44, 2720–2734. [Google Scholar] [CrossRef]
- Song, L.L.; Fu, G.S.; Wang, H.S. Effect of Ce on the heterogeneous nucleation interface of TiAl3/α-Al by first-principles. J. Ningde Norm. Univ. (Nat. Sci.) 2024, 36, 360–366. [Google Scholar]
- Chen, Z.; Wang, Z. First-principles Calculation for Site Substitution of Sc Elements in L10-TiAl Intermetallic Compound. J. Chang. Aeronaut. Vocat. Tech. Coll. 2006, 6, 46–49. [Google Scholar]
- Yin, S.B.; Huang, B.Y.; He, Y.H.; Yin, Z.M. Influence of minor Sc addition on high temperature mechanical properties and microstructure of TiAl base alloys. Chin. J. Nonferrous Met. 1999, 9, 253–258. [Google Scholar]
- Song, Q.G.; Zhu, Y.X.; Wang, L.J.; Gu, W.F.; Hu, X.L.; Kang, J.H. Effects of Ce and V Co-doping on Plasticity and Electronic Structures of γ-TiAl Based Alloys. Chin. J. Rare Met. 2019, 43, 942–951. [Google Scholar]
- Song, Q.G.; Gu, W.F.; Zhen, D.D.; Guo, Y.R.; Hu, X.L. Effect of Mo(or Cr, V) substitution doping on energy, ductility and electronic properties of dual-phase γ-TiAl/α2-Ti3Al interface. Chin. J. Nonferrous Met. 2019, 29, 370–379. [Google Scholar]
- Song, Q.G.; Wang, L.J.; Zhu, Y.X.; Kang, J.H.; Gu, W.F.; Wang, M.C.; Liu, Z.F. Effects of Si and Y co-doping on stability and oxidation resistance of γ-TiAl based alloys. Acta Phys. Sin. 2019, 68, 190–200. [Google Scholar] [CrossRef]
- Dong, L.M.; Cui, Y.Y.; Yang, R.; Wang, F.H. Effects Si on oxidation resistance of TiAl alloys. Acta Metall. Sin. 2004, 40, 383–387. [Google Scholar]
- Song, Q.G.; Zhao, J.P.; Gu, W.F.; Zhen, D.D.; Guo, Y.R.; Li, Z.P. Ductile and electronic properties of La-doped γ-TiAl systems based on density functional theory. Acta Phys. Sin. 2017, 66, 066103. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-Principles Simulation: Ideas, Illustrations and the CASTEP Code. J. Phys. Condens. Matter 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft Self-Consistent Pseudopotentials in a Generalized Eigenvalue Formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Slater, J.C. Atomic radii in crystals. J. Chem. Phys. 1964, 41, 3199–3204. [Google Scholar] [CrossRef]
- Xiao, B.; Feng, J.; Zhou, C.T.; Xing, J.; Xie, X.; Chen, Y. First Principles Study on the Electronic Structures and Stability of Cr7C3 Type Multi-Component Carbides. Chem. Phys. Lett. 2008, 459, 129–132. [Google Scholar] [CrossRef]
- Dobson, P. Physical Properties of Crystals; Oxford University Press: Oxford, UK, 1985; Volume 36, p. 506. [Google Scholar]
- Reuss, A. Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle. J. Appl. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Hadi, M.A.; Kelaidis, N.; Naqib, S.H. Mechanical Behaviors, Lattice Thermal Conductivity and Vibrational Properties of a New MAX Phase Lu2SnC. J. Phys. Chem. Solids 2019, 129, 162–171. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, Z.; Xu, L.; Wang, L.M.; He, J. Novel High-Pressure Phase of RhB: First-Principles Calculations. J. Phys. Chem. C 2011, 115, 19910–19915. [Google Scholar] [CrossRef]
- Huang, B.; Duan, Y.H.; Hu, W.C.; Sun, Y.; Chen, S. Structural, anisotropic elastic and thermal properties of MB (M=Ti, Zr and Hf) monoborides. Ceram. Int. 2015, 41, 6831–6843. [Google Scholar] [CrossRef]
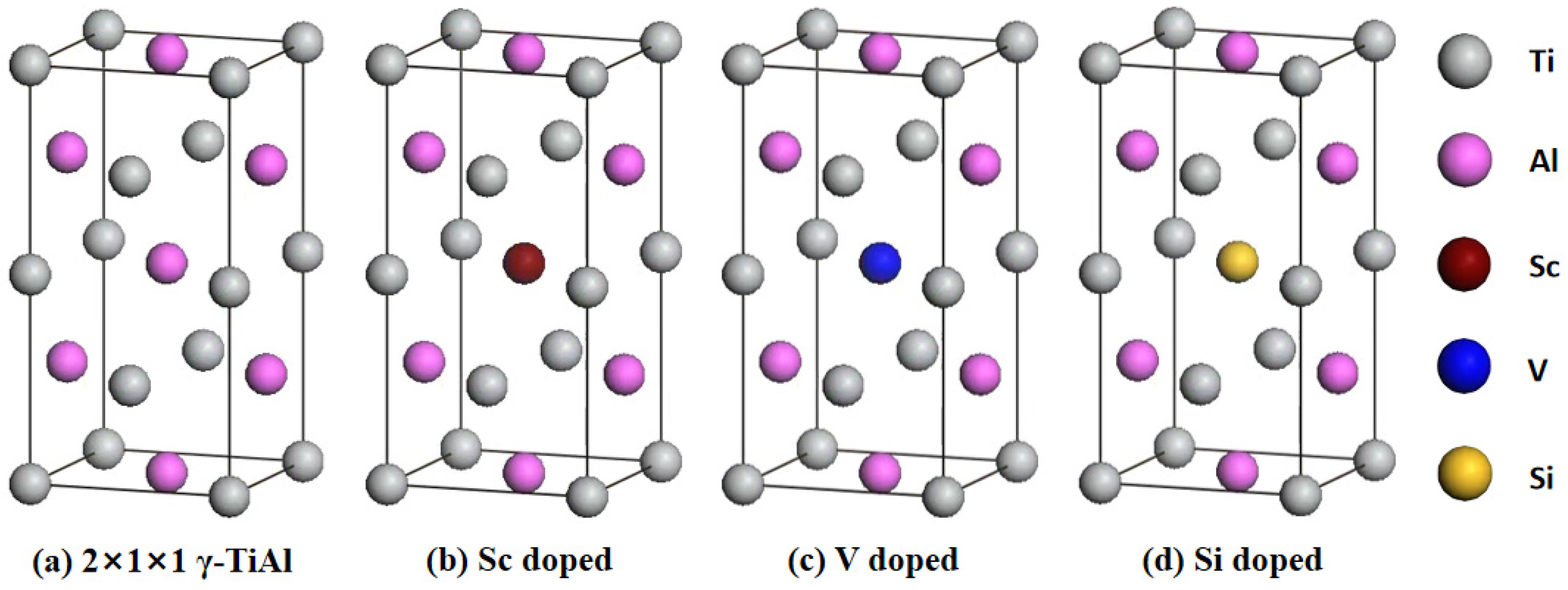
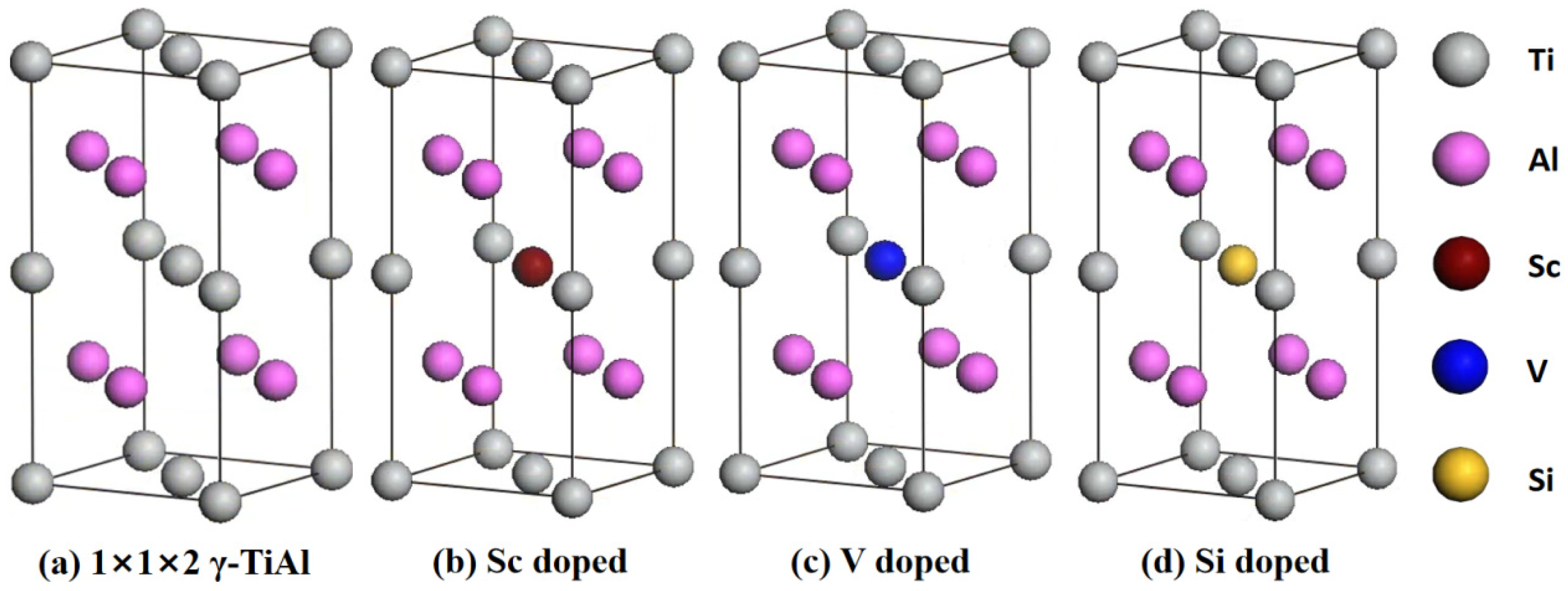



| Sample | a (nm) | b (nm) | c (nm) | V (nm3) | E (eV) | Eb (eV) | |
|---|---|---|---|---|---|---|---|
| 2 × 1 × 1 γ-TiAl | 0.7980 | 0.4003 | 0.4098 | 0.1309 | −6641.3795 | −5.4814 | |
| 1 × 1 × 2 γ-TiAl | 0.3994 | 0.3994 | 0.8213 | 0.1310 | −6641.3145 | −5.4732 | |
| Sc doped | Replace Al | 0.8310 | 0.4068 | 0.4114 | 0.1391 | −7861.0374 | −5.4268 |
| Replace Ti | 0.4087 | 0.4087 | 0.8204 | 0.1370 | −6315.3163 | −5.2140 | |
| V doped | Replace Al | 0.8475 | 0.4113 | 0.3697 | 0.1289 | −8560.5950 | −5.8125 |
| Replace Ti | 0.3951 | 0.3951 | 0.8122 | 0.1268 | −7014.4108 | −5.5418 | |
| Si doped | Replace Al | 0.7916 | 0.3963 | 0.4035 | 0.1266 | −6692.5999 | −5.6896 |
| Replace Ti | 0.3876 | 0.3876 | 0.8392 | 0.1260 | −5145.4654 | −5.3001 | |
| Sample | C11 | C12 | C13 | C33 | C44 | C66 |
|---|---|---|---|---|---|---|
| γ-TiAl | 191.3037 | 92.2742 | 81.2407 | 195.4126 | 121.6786 | 71.0021 |
| Sc-doped γ-TiAl | 139.0976 | 72.2648 | 68.4600 | 153.1293 | 85.6506 | 64.3171 |
| V-doped γ-TiAl | 186.9689 | 51.0905 | 92.5921 | 134.9768 | 112.3177 | 52.5427 |
| Si-doped γ-TiAl | 168.9596 | 90.8389 | 77.5810 | 172.6962 | 108.6766 | 64.0101 |
| Sample | B (GPa) | G (GPa) | E (GPa) | υ | B/G |
|---|---|---|---|---|---|
| γ-TiAl | 120.8216 | 79.0349 | 194.6594 | 0.2315 | 1.5287 |
| Sc-doped γ-TiAl | 94.3628 | 57.7156 | 143.8241 | 0.2460 | 1.6350 |
| V-doped γ-TiAl | 108.9627 | 63.06095 | 158.5890 | 0.2574 | 1.7279 |
| Si-doped γ-TiAl | 111.3678 | 68.2116 | 169.9394 | 0.2457 | 1.6327 |
| Sample | AU | Acomp | Ashear | A1 | A2 | A3 |
|---|---|---|---|---|---|---|
| γ-TiAl | 0.7318 | 0.0126% | 6.8172% | 2.1706 | 2.1403 | 1.3710 |
| Sc doped γ-TiAl | 0.7893 | 0.0505% | 7.3073% | 2.2060 | 1.9947 | 1.8290 |
| V doped γ-TiAl | 2.0109 | 0.0815% | 16.7309% | 3.2851 | 4.4167 | 0.8107 |
| Si doped γ-TiAl | 0.9128 | 0.0307% | 8.3594% | 2.3309 | 2.4966 | 1.6439 |
| Sample | Atom | s | p | d | Total | Charge (e) |
|---|---|---|---|---|---|---|
| γ-TiAl | Ti | 2.31 | 6.72 | 2.84 | 11.88 | 0.12 |
| Al | 0.98 | 2.14 | 0 | 3.12 | −0.12 | |
| Sc-doped | Ti | 2.39 | 6.82 | 2.78 | 11.99 | 0.01 |
| Al | 1.01 | 2.13 | 0 | 3.14 | −0.14 | |
| Sc | 2.32 | 6.77 | 1.79 | 10.87 | 0.13 | |
| V-doped | Ti | 2.33 | 6.88 | 2.77 | 11.97 | 0.03 |
| Al | 0.97 | 2.10 | 0 | 3.07 | −0.07 | |
| V | 2.41 | 6.79 | 9.85 | 13.05 | −0.05 | |
| Si-doped | Ti | 2.34 | 6.69 | 2.86 | 11.89 | 0.11 |
| Al | 0.98 | 2.10 | 0 | 3.07 | −0.07 | |
| Si | 1.33 | 2.86 | 0 | 4.19 | −0.19 |
| Sample | Bond | Population | Length (Å) |
|---|---|---|---|
| γ-TiAl | Al-Al | 0.62 | 2.81 |
| Al-Ti | 0.81 | 2.84 | |
| Sc-doped γ-TiAl | Sc-Al | 0.31 | 2.95 |
| Sc-Ti | 0.27 | 2.89 | |
| V-doped γ-TiAl | V-Al | 0.25 | 2.91 |
| V-Ti | 0.57 | 2.77 | |
| Si-doped γ-TiAl | Si-Al | 0.57 | 2.80 |
| Si-Ti | 0.78 | 2.83 |
| Sample | Bond | Population | Length (Å) |
|---|---|---|---|
| γ-TiAl | Al-Al | 0.62 | 2.81 |
| Ti-Ti | −0.35 | 2.81 | |
| Al-Ti | 0.81 | 2.84 | |
| Sc-doped γ-TiAl | Al-Al | 0.52 | 2.87 |
| Ti-Ti | 0.08 | 2.99 | |
| Al-Ti | 1.01 | 2.89 | |
| V-doped γ-TiAl | Al-Al | 0.26 | 3.00 |
| Ti-Ti | −0.69 | 2.93 | |
| Al-Ti | 1.04 | 2.77 | |
| Si-doped γ-TiAl | Al-Al | 0.64 | 2.81 |
| Ti-Ti | −0.82 | 2.75 | |
| Al-Ti | 0.74 | 2.83 |
| Bond Sample | Population Variation | Bond Length Variation | Bonding Evolution | Mechanical Behavior | |
|---|---|---|---|---|---|
| Sc-doped | Al-Al | −0.1 | +0.06 | covalent bond weakening | dislocation slip resistance ↓ → plasticity ↑ |
| Ti-Ti | +0.43 | +0.18 | anti-bond state → weak covalent/metal bond | dislocation slip resistance ↓ → plasticity ↑ | |
| Al-Ti | +0.2 | +0.05 | strong covalent bond enhancement | lattice resistance ↑ → plasticity ↓ | |
| Sc-Al | −0.31 | +0.14 | covalent bond weakening | dislocation slip resistance ↓ → plasticity ↑ | |
| Sc-Ti | −0.54 | +0.05 | covalent bond weakening | dislocation slip resistance ↓ → plasticity ↑ | |
| V-doped | Al-Al | −0.36 | +0.19 | covalent bond weakening | dislocation slip resistance ↓ → plasticity ↑ |
| Ti-Ti | −0.34 | +0.12 | enhanced anti-bond repulsion | lattice resistance ↑ →plasticity ↓ | |
| Al-Ti | +0.23 | −0.07 | strong covalent bond enhancement | lattice resistance ↑ →plasticity ↓ | |
| V-Al | −0.37 | +0.1 | covalent bond weakening | dislocation slip resistance ↓ → plasticity ↑ | |
| V-Ti | −0.24 | −0.07 | covalent bond weakening | dislocation slip resistance ↓ → plasticity ↑ | |
| Si-doped | Al-Al | +0.02 | 0 | covalent bond enhancement | lattice resistance ↑ →plasticity ↓ |
| Ti-Ti | −0.47 | −0.06 | enhanced anti-bond repulsion | lattice resistance ↑ →plasticity ↓ | |
| Al-Ti | −0.07 | −0.01 | covalent bond weakening | dislocation slip resistance ↓ → plasticity ↑ | |
| Si-Al | −0.05 | −0.01 | covalent bond weakening | dislocation slip resistance ↓ → plasticity ↑ | |
| Si-Ti | −0.03 | −0.01 | covalent bond weakening | dislocation slip resistance ↓ → plasticity ↑ | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, M.; Zhang, C.; Yan, W. Study on Modifying Mechanical Properties and Electronic Structure of Aerospace Material γ-TiAl Alloy. Crystals 2025, 15, 726. https://doi.org/10.3390/cryst15080726
Fang M, Zhang C, Yan W. Study on Modifying Mechanical Properties and Electronic Structure of Aerospace Material γ-TiAl Alloy. Crystals. 2025; 15(8):726. https://doi.org/10.3390/cryst15080726
Chicago/Turabian StyleFang, Mingji, Chunhong Zhang, and Wanjun Yan. 2025. "Study on Modifying Mechanical Properties and Electronic Structure of Aerospace Material γ-TiAl Alloy" Crystals 15, no. 8: 726. https://doi.org/10.3390/cryst15080726
APA StyleFang, M., Zhang, C., & Yan, W. (2025). Study on Modifying Mechanical Properties and Electronic Structure of Aerospace Material γ-TiAl Alloy. Crystals, 15(8), 726. https://doi.org/10.3390/cryst15080726







