A Comprehensive Investigation of the Two-Phonon Characteristics of Heat Conduction in Superlattices

Abstract

The Anderson localization of phonons in disordered superlattices has been proposed as a route to suppress thermal conductivity beyond the limits imposed by conventional scattering mechanisms. A commonly used signature of phonon localization is the emergence of the nonmonotonic dependence of thermal conductivity $\kappa$ on system length L, i.e., a $\kappa$-L maximum. However, such behavior has rarely been observed. In this work, we conduct extensive non-equilibrium molecular dynamics (NEMD) simulations, using the LAMMPS package, on both periodic superlattices (SLs) and aperiodic random multilayers (RMLs) constructed from Si/Ge and Lennard-Jones materials. By systematically varying acoustic contrast, interatomic bond strength, and average layer thickness, we examine the interplay between coherent and incoherent phonon transport in these systems. Our two-phonon model decomposition reveals that coherent phonons alone consistently exhibit a strong nonmonotonic $\kappa$-L. This localization signature is often masked by the diffusive, monotonically increasing contribution from incoherent phonons. We further extract the ballistic-limit mean free paths for both phonon types, and demonstrate that incoherent transport often dominates, thereby concealing localization effects. Our findings highlight the importance of decoupling coherent and incoherent phonon contributions in both simulations and experiments. This work provides new insights and design principles for achieving phonon Anderson localization in superlattice structures.

1. Introduction

The development of advanced thermoelectric materials, thermal barrier coatings, and materials for thermal management has sparked renewed interest in understanding and controlling phonon thermal transport [1,2,3]. Among the various mechanisms under investigation, phonon localization—particularly its strong form, known as Anderson localization—has emerged as a compelling subject of study [4,5,6,7,8,9]. This resurgence is largely motivated by experimental observations of significantly suppressed lattice thermal conductivity in aperiodic superlattices (also referred to as random multilayers) [4,7,8,10] and in periodic superlattices embedded with nanoparticles [5,6]. Of particular interest is the possibility of realizing wave localization phenomena for phonons [11,12], analogous to the well-established cases for electrons and photons [13,14,15,16], where disorder-induced interference halts wave diffusion.

A central challenge in identifying phonon localization—especially in experimental settings—is the lack of definitive and robust signatures. Mendoza et al. [5] predicted, via atomistic Green’s function simulations, a nonmonotonic dependence of thermal conductivity $\kappa$ on system length L in GaAs/AlAs superlattices embedded with ErAs nanoparticles. This behavior, attributed to a transition from diffusive to localized phonon transport, was later corroborated experimentally by the same group, who observed a peak in $\kappa$ at cryogenic temperatures ($T<50$ K) [6]. Similarly, Juntunen et al. [7] reported comparable $\kappa$-L behavior in aperiodic Si/Ge superlattices via molecular dynamics simulations, although corresponding experimental validation remains elusive.

An alternative strategy to infer phonon localization compares the thermal conductivities of periodic and aperiodic superlattices with identical average layer thicknesses. While this approach normalizes for interface density and scattering rates, it does not eliminate other factors such as altered phonon band structures and anharmonic scattering phase space. For instance, Ma et al. [17] showed that such band structure modifications alone can significantly affect thermal transport, even in the absence of localization effects.

Earlier work by Wang et al. [4] demonstrated, using classical molecular dynamics, that randomizing layer thicknesses in superlattices can drastically suppress $\kappa$. Their two-channel transport model—decomposing $\kappa$ into coherent and incoherent components—revealed that periodic superlattices support substantial coherent phonon transport, while disorder in aperiodic structures leads to localization and exponential attenuation of the coherent contribution. This coherent component exhibits a nonmonotonic L-dependence: initially increasing due to ballistic transport, then decaying due to localization. However, because incoherent phonons—dominated by interface scattering—can dominate the total $\kappa$, the overall $\kappa$-L relation may remain monotonic, thereby masking the signature of Anderson localization. Subsequent studies further emphasized the significant reductions in $\kappa$ (up to 70–99%) achieved through thickness randomness and impurity scattering [8,10,18,19,20,21], highlighting both the potential and the complexity of identifying localization effects.

To resolve modal contributions to heat transport, frequency-domain techniques such as spectral heat flux [22,23,24,25] and spectral energy density (SED) analysis [25,26,27,28,29] have been employed. Spectral heat flux quantifies contributions of phonons across frequencies and polarizations and captures their sensitivity to geometric factors like interface roughness and periodicity [24,30]. SED analysis, on the other hand, yields detailed phonon mode properties—such as dispersion relations, group velocities, lifetimes, and mean free paths (MFPs)—at finite temperatures [28,31].

Although this study focuses on superlattice systems, insights from phononic crystals such as nanomeshes are noteworthy. Nanomeshes—thin films patterned with nanoscale holes—have been widely explored for their potential to induce coherent phonon transport [32,33]. Yu et al. [34] reported a reduction of nearly an order-of-magnitude in the $\kappa$ of silicon nanomeshes, attributed to zone folding and reduced group velocities. Hopkins et al. [35] and Zen et al. [36] further demonstrated phonon coherence effects that cannot be explained by classical boundary scattering alone. Alaie et al. [37] confirmed coherence-related scattering at room temperature, while Wagner et al. [38] explored the effects of aperiodic hole distributions. However, coherence in nanomeshes remains debated: Lee et al. [39] observed no significant difference in $\kappa$ between periodic and aperiodic nanomeshes, while Maire et al. [40] found coherence-induced suppression at low temperatures but not at room temperature. Compared to superlattices, the two-dimensional nature of nanomeshes introduces additional complexity in analyzing phonon transport.

To isolate the physics of phonon localization, the present study focuses on superlattices, avoiding complications from hole-edge scattering inherent to nanomeshes. Recent studies by our group [24,25] using spectral analysis revealed that aperiodic hole patterns in nanomeshes primarily suppress low-frequency coherent phonons, while rough boundaries affect a broader spectrum.

Wave-packet simulations offer a powerful tool for directly modeling phonon wave propagation, interference, and coherence in real space [41,42,43]. Unlike particle-based models, the wave-packet method allows simultaneous control over the phonon mode, wavevector, and spatial coherence length—the latter being the key parameter that delineates coherent (wave-like) and incoherent (particle-like) transport. When the coherence length exceeds the superlattice period, phonons traverse interfaces coherently; when it is shorter, phonons undergo scattering. Wave-packet simulations by Maranets and Wang [44] provided direct evidence that incoherent phonons can mode-convert into coherent ones, aligning with the superlattice dispersion relation. This conversion process also occurs in aperiodic superlattices, leading to finite transmission and non-trivial $\kappa$, contrary to the expectation of complete suppression due to localization. Their later work [45] revealed that coherent phonons in aperiodic superlattices propagate diffusively rather than ballistically, explaining the slower increase in $\kappa$ with L. They also directly visualized Anderson localization via destructive interference in aperiodic systems [46].

Unlike photons, for which coherence can be directly measured via emission characteristics, phonon coherence lacks direct experimental observables [47]. Thermal conductivity measurements reflect ensemble-averaged properties and obscure modal-specific behaviors. Therefore, computational methods, particularly wave-packet simulations, play a critical role in advancing our understanding of phonon coherence and localization.

Despite their importance, coherent phonon transport and localization remain insufficiently understood. In particular, clear, experimentally accessible criteria for identifying and quantifying coherent phonon conduction and localization are still lacking. While the design of newer-generation thermoelectric materials or other thermal materials relies on the synergistic consideration of various material properties, and involves the interplay between morphology/bonding/microstructure and/or electronic/optical properties [48], this study focuses on evaluating the feasibility of using the nonmonotonic $\kappa$-L relation, arising from the Anderson-type localization of ballistic phonons, as a robust indicator of phonon localization. We decompose the total $\kappa$ into coherent and incoherent contributions to provide a physically grounded basis for interpreting thermal transport behavior in disordered superlattice structures.

2. Methodology

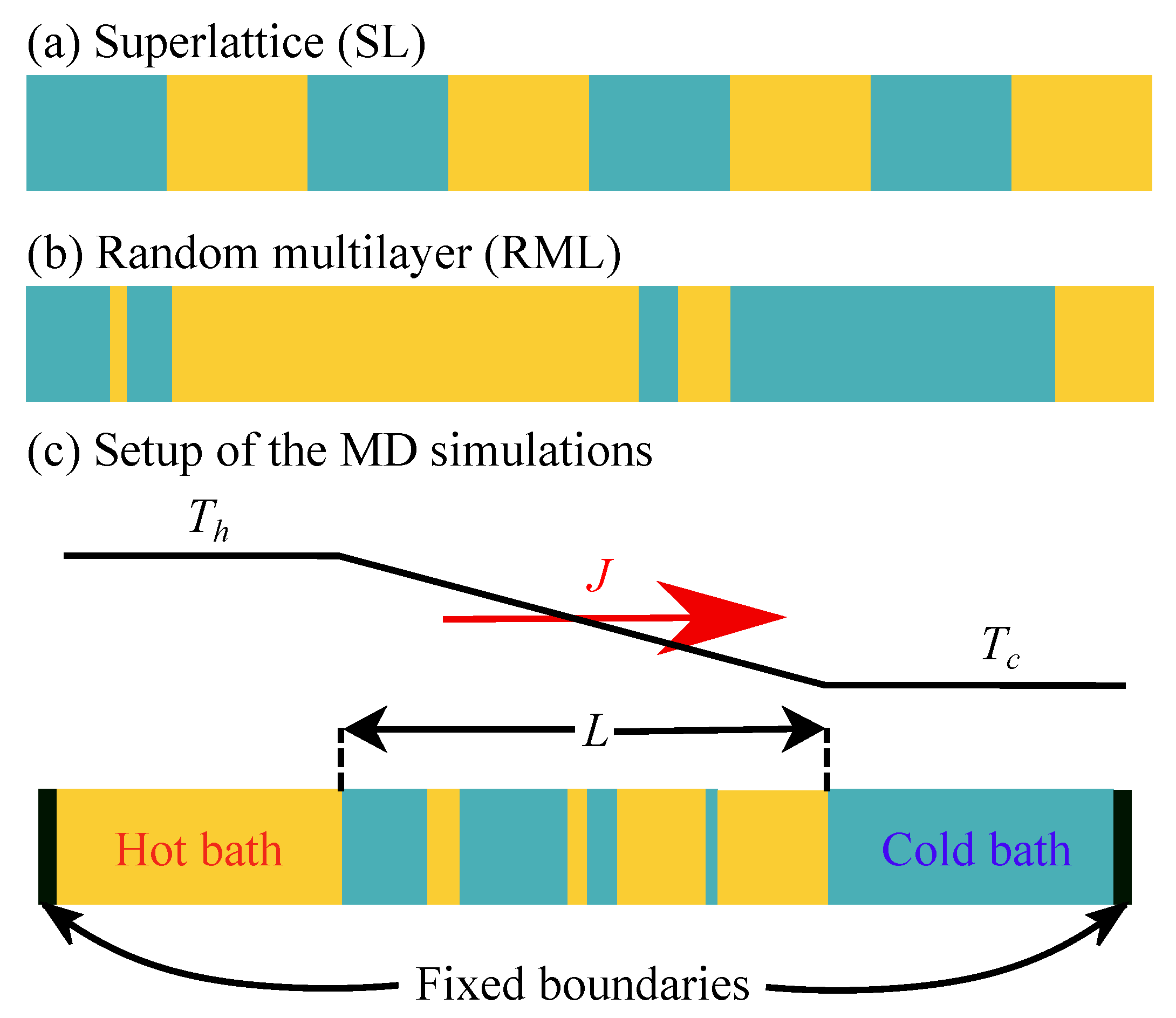
2.1. Model System

To investigate phonon transport in artificial layered materials, we performed classical molecular dynamics (MD) simulations using the LAMMPS package [49], a widely adopted tool for atomistic modeling. The primary structures considered are superlattices (SLs), composed of alternating layers of two materials with atomic masses $m_A$ and $m_B$. Each layer has equal thickness, denoted as $d_{m_A}=d_{m_B}=d$, resulting in a total period length of $L_p=2d$. When the layer thicknesses are randomized rather than periodic, the configuration is referred to as a random multilayer (RML). To ensure sufficient disorder, we employed the randomization algorithm from our previous work [4], which has been shown to produce structures that approach the minimum possible thermal conductivity [20]. For SL and RML systems with the same average d, the interface density remains constant.

Two categories of material systems were studied. The first included Si and/or Ge, modeled using the Stillinger–Weber (SW) potential [50,51], which accurately describes the covalent bonding in these group IV semiconductors. Cross-interactions between Si and Ge atoms were parameterized using the Lorentz–Berthelot mixing rule. Since Si and Ge differ in terms of both atomic mass and lattice constant (leading to interfacial stress), we also constructed a model system using Si and a fictitious “heavy Si” (hSi) with the same bonding characteristics but a larger atomic mass of 112 g/mol. This allowed us to isolate the effects of acoustic contrast by eliminating lattice mismatch.

The second class of model systems was constructed using atoms interacting via Lennard-Jones (LJ) potentials. These systems, resembling FCC solid argon, serve as a simplified model for exploring thermal transport while maintaining the essential physics of atomic bonding. The LJ potential is given by

$$\mathsf{\Phi }\left(r_{ij}\right)=4ϵ\left[{\left({\displaystyle \frac{\sigma }{r_{ij}}}\right)}^{12}-{\left({\displaystyle \frac{\sigma }{r_{ij}}}\right)}^6\right],$$

(1)

where $\Phi \left(r_{ij}\right)$ is the potential energy between atoms i and j separated by a distance of $r_{ij}$, $\sigma$ defines the length scale for zero potential energy, and $ϵ$ denotes the depth of the potential well. We set $\sigma =0.34$ nm to match the lattice constant of solid argon. The bonding strength $ϵ$ was scaled as $ϵ=n{ϵ}_{\mathrm{Ar}}$, where ${ϵ}_{\mathrm{Ar}}=0.0104$ eV and $n=16$, 32, or 64, to span a range of bonding strengths, from relatively weak to substantially stronger than that of solid argon. These values were chosen to approximate the bonding characteristics of semiconductors such as Si/Ge [52,53], GaAs/AlAs [6,54], and Bi₂Te₃/Sb₂Te₃ [55].

The use of the LJ potential provides computational efficiency while preserving the essential physics of phonon transport. While more sophisticated potentials such as Tersoff or SW offer higher fidelity for real materials, even these may fall short in capturing complex anharmonic and quantum effects. We note that the truly predictive modeling of thermal transport often requires machine-learned interatomic potentials [29,56], which are significantly more computationally intensive and beyond the scope of this study.

To assess the effect of structural parameters, we simulated SLs with two different average layer thicknesses, 4 UC and 8 UC, where UC refers to the unit cell length of FCC solid argon (approximately 5.3 Å). Each simulation domain had a cross-section of $4\mathrm{UC}\times 4\mathrm{UC}$ in the y–z plane, with heat transport occurring along the x-direction. The two alternating layers in these superlattices were modeled with identical LJ parameters (i.e., the same $ϵ$, $\sigma$, and lattice constants), differing only in terms of atomic mass: one layer contained atoms of mass 40 g/mol (m40, comparable to silicon), while the other contained atoms with masses of 90, 120, or 160 g/mol (denoted asm90, m120, and m160, respectively, analogous to heavier semiconductor elements like germanium).

Figure 1 shows schematic illustrations of the SL and RML configurations employed in this work. A summary of the material parameters used in each system is provided in

Table 1. The material systems used in the simulations and their associated parameters.

Material System	Potential	Mass_A (g/mol)	Mass_B (g/mol)	Bond Strength	Avg. Layer Thickness (d)
Lennard-Jones	Lennard-Jones	40	90	1${\epsilon }_{\mathrm{Ar}}$	4 UC
Lennard-Jones	Lennard-Jones	40	120	1${\epsilon }_{\mathrm{Ar}}$	4 UC
Lennard-Jones	Lennard-Jones	40	160	1${\epsilon }_{\mathrm{Ar}}$	4 UC
Lennard-Jones	Lennard-Jones	40	90	1${\epsilon }_{\mathrm{Ar}}$	8 UC
Lennard-Jones	Lennard-Jones	40	120	1${\epsilon }_{\mathrm{Ar}}$	8 UC
Lennard-Jones	Lennard-Jones	40	160	1${\epsilon }_{\mathrm{Ar}}$	8 UC
Lennard-Jones	Lennard-Jones	40	90	16${\epsilon }_{\mathrm{Ar}}$	4 UC
Lennard-Jones	Lennard-Jones	40	120	16${\epsilon }_{\mathrm{Ar}}$	4 UC
Lennard-Jones	Lennard-Jones	40	160	16${\epsilon }_{\mathrm{Ar}}$	4 UC
Lennard-Jones	Lennard-Jones	40	90	16${\epsilon }_{\mathrm{Ar}}$	8 UC
Lennard-Jones	Lennard-Jones	40	120	16${\epsilon }_{\mathrm{Ar}}$	8 UC
Lennard-Jones	Lennard-Jones	40	160	16${\epsilon }_{\mathrm{Ar}}$	8 UC
Lennard-Jones	Lennard-Jones	40	90	32${\epsilon }_{\mathrm{Ar}}$	4 UC
Lennard-Jones	Lennard-Jones	40	120	32${\epsilon }_{\mathrm{Ar}}$	4 UC
Lennard-Jones	Lennard-Jones	40	160	32${\epsilon }_{\mathrm{Ar}}$	4 UC
Lennard-Jones	Lennard-Jones	40	90	32${\epsilon }_{\mathrm{Ar}}$	8 UC
Lennard-Jones	Lennard-Jones	40	120	32${\epsilon }_{\mathrm{Ar}}$	8 UC
Lennard-Jones	Lennard-Jones	40	160	32${\epsilon }_{\mathrm{Ar}}$	8 UC
Lennard-Jones	Lennard-Jones	40	90	64${\epsilon }_{\mathrm{Ar}}$	4 UC
Lennard-Jones	Lennard-Jones	40	120	64${\epsilon }_{\mathrm{Ar}}$	4 UC
Lennard-Jones	Lennard-Jones	40	160	64${\epsilon }_{\mathrm{Ar}}$	4 UC
Lennard-Jones	Lennard-Jones	40	90	64${\epsilon }_{\mathrm{Ar}}$	8 UC
Lennard-Jones	Lennard-Jones	40	120	64${\epsilon }_{\mathrm{Ar}}$	8 UC
Lennard-Jones	Lennard-Jones	40	160	64${\epsilon }_{\mathrm{Ar}}$	8 UC
Si/Ge	Stillinger–Weber	28.08	72.63	Default	4 UC
Si/hSi	Stillinger–Weber	28.08	112.3	Default	4 UC
Si/hSi	Stillinger–Weber	28.08	112.3	Default	8 UC

.

2.2. Simulation Setup

A schematic of the simulation domain is shown in Figure 1c. The central region of length L, referred to as the device, is flanked by two heat baths, each of length $L_{\mathrm{bath}}$. To enforce fixed boundary conditions, approximately 1 nm of atoms at both ends of the structure are immobilized (marked as dark regions in the figure). Buffer zones of 8.4 nm are inserted between the device and each heat bath to accurately measure the temperatures at the left and right ends, denoted as $T_L$ and $T_R$, respectively. All simulations employ a time step of 1 fs.

Nonequilibrium molecular dynamics (NEMD) simulations at the target temperature T are performed using the LAMMPS software package [49]. Initially, periodic boundary conditions are applied in all three spatial directions. Each atom is assigned a velocity drawn from a Gaussian distribution corresponding to an initial temperature of 5 K.

Subsequently, the entire system undergoes equilibration in the NPT ensemble at zero pressure. During the first stage, the temperature is linearly ramped from 5 K to the target temperature T over 500 ps. A second NPT equilibration is then conducted at temperature T for another 500 ps.

After equilibration, the NEMD stage begins. The velocities of atoms in the heat baths are continuously rescaled at each time step to maintain temperatures of $T+\Delta T/2$ and $T-\Delta T/2$ at the hot and cold ends, respectively. The fixed boundary atoms remain stationary throughout. This NEMD run continues for 10 to 70 ns, depending on the system length, to ensure that a steady-state heat flux is established.

The steady-state thermal conductance G is computed using the relation:

$$G={\displaystyle \frac{J}{A(T_L-T_R)}},$$

(2)

where A is the cross-sectional area of the simulation domain, and J is the steady-state heat flux, defined as the rate of energy transferred from the hot bath to the cold bath. Once G is obtained, the thermal conductivity $\kappa$ is calculated by

$$\kappa =G·L.$$

(3)

2.3. Two-Phonon Model

Traditional models of phonon transport in SLs often assume either fully incoherent or fully coherent behavior. In the incoherent limit, phonons are treated as particles governed by properties of individual layers, whereas in the coherent limit, they are considered wave-like excitations influenced by the collective band structure of the periodic system.

In this work, we adopt a two-phonon model that captures both transport mechanisms concurrently to describe phonon thermal transport in SLs and RMLs. The model classifies phonons into two categories: (i) coherent phonons, which may undergo Anderson localization in disordered systems such as RMLs, and (ii) incoherent phonons, which scatter diffusively at interfaces in both SLs and RMLs. Coherent phonons generally correspond to long-wavelength modes with long MFPs ($\lambda$), while incoherent phonons are associated with shorter wavelengths and reduced $\lambda$.

Under the Landauer framework, the length-dependent thermal conductance $G\left(L\right)$ for either phonon type is given by

$$G\left(L\right)={\displaystyle \frac{G_0\lambda }{\lambda +L}},$$

(4)

where $G_0$ is the ballistic-limit conductance (i.e., conductance in the limit of $L\to 0$), and $\lambda$ is the effective mean free path. Correspondingly, the thermal conductivity is

$$\kappa \left(L\right)=G\left(L\right)·L={\displaystyle \frac{G_0\lambda L}{\lambda +L}}.$$

(5)

This expression captures two transport regimes: a ballistic regime where $\kappa$ scales linearly with L for $L\ll \lambda$, and a diffusive regime where $\kappa$ saturates for $L\gg \lambda$. This formalism has been successfully applied to describe phonon transport in systems such as silicon and Bi₂Te₃ [57,58,59].

For SLs, the total thermal conductance is modeled as the sum of coherent and incoherent phonon contributions:

$$G_{\mathrm{SL}}\left(L\right)=G_{\mathrm{coh}}\left(L\right)+G_{\mathrm{inc}}\left(L\right)={\displaystyle \frac{G_{\mathrm{coh},0}{\lambda }_{\mathrm{coh}}}{{\lambda }_{\mathrm{coh}}+L}}+{\displaystyle \frac{G_{\mathrm{inc},0}{\lambda }_{\mathrm{inc}}}{{\lambda }_{\mathrm{inc}}+L}}.$$

(6)

In RMLs, structural disorder causes coherent phonons to undergo Anderson localization, resulting in the exponential suppression of their contribution to thermal transport with increasing L [13]. The conductance in RMLs is therefore expressed as

$$G_{\mathrm{RML}}\left(L\right)={\displaystyle \frac{G_{\mathrm{coh},0}{\lambda }_{\mathrm{coh}}}{{\lambda }_{\mathrm{coh}}+L}}·exp\left(-{\displaystyle \frac{L}{\xi }}\right)+{\displaystyle \frac{G_{\mathrm{inc},0}{\lambda }_{\mathrm{inc}}}{{\lambda }_{\mathrm{inc}}+L}},$$

(7)

where $\xi$ is the localization length, quantifying the decay of coherent phonon transport in RMLs. All transport parameters ($G_0$, $\lambda$) for coherent and incoherent phonons are assumed to be the same as in SLs, except that coherent phonons experience localization in RMLs.

For long structures ($L\gg \xi$), the coherent term becomes negligible, and the RML conductance simplifies to

$$G_{\mathrm{RML}}\left(L\right)\approx G_{\mathrm{inc}}\left(L\right)={\displaystyle \frac{G_{\mathrm{inc},0}{\lambda }_{\mathrm{inc}}}{{\lambda }_{\mathrm{inc}}+L}}.$$

(8)

The difference in conductance between SLs and RMLs is defined as $\Delta G\left(L\right)=G_{\mathrm{SL}}\left(L\right)-G_{\mathrm{RML}}\left(L\right)$. When $L\gg \xi$, this difference approximates the coherent phonon contribution:

$$\Delta G\left(L\right)\approx G_{\mathrm{coh}}\left(L\right)={\displaystyle \frac{G_{\mathrm{coh},0}{\lambda }_{\mathrm{coh}}}{{\lambda }_{\mathrm{coh}}+L}}.$$

(9)

At smaller lengths, the coherent phonon contribution in RMLs remains non-negligible and is described by

$$G_{\mathrm{coh},\mathrm{RML}}\left(L\right)={\displaystyle \frac{G_{\mathrm{coh},0}{\lambda }_{\mathrm{coh}}}{{\lambda }_{\mathrm{coh}}+L}}·exp\left(-{\displaystyle \frac{L}{\xi }}\right).$$

(10)

Figure 2 displays a few representative $\kappa$-L relations governed by the two-phonon model discussed above, which will be discussed in detail in later sections. Moreover, we can leverage the two-phonon model to evaluate essential coherent and incoherent phonon properties. In Figure 3a–c, Equations (6)–(10) are fitted to the NEMD results for various systems. Fitting is performed through the following four steps:

1

Extraction of incoherent parameters: Equation (8) is fitted to the raw NEMD data points of $G_{\mathrm{RML}}$ for $L>200$ nm to extract $G_{\mathrm{inc},0}$ and ${\lambda }_{\mathrm{inc}}$. This yields the full $G_{\mathrm{inc}}\left(L\right)$ curve.

2

Extraction of coherent parameters: The difference $\Delta G=G_{\mathrm{SL}}-G_{\mathrm{RML}}$ (subtraction between raw NEMD data points) is fitted using Equation (9) for $L>200$ nm, yielding $G_{\mathrm{coh},0}$ and ${\lambda }_{\mathrm{coh}}$, and reconstructing $G_{\mathrm{SL},\mathrm{coh}}\left(L\right)$.

3

Determination of localization length: Subtracting $G_{\mathrm{inc}}\left(L\right)$ from $G_{\mathrm{RML}}$ provides the localized coherent contribution in RMLs, which is fitted using Equation (10) to extract $\xi$ and generate $G_{\mathrm{RML},\mathrm{coh}}\left(L\right)$.

4

Model validation: Using Equation (6), $G_{\mathrm{SL}}\left(L\right)$ is reconstructed as the sum of $G_{\mathrm{SL},\mathrm{coh}}\left(L\right)$ and $G_{\mathrm{inc}}\left(L\right)$, and can be compared to the NEMD data to validate the fitting quality and, thus, the applicability of the two-phonon model for the system being investigated.

3. Results and Discussion

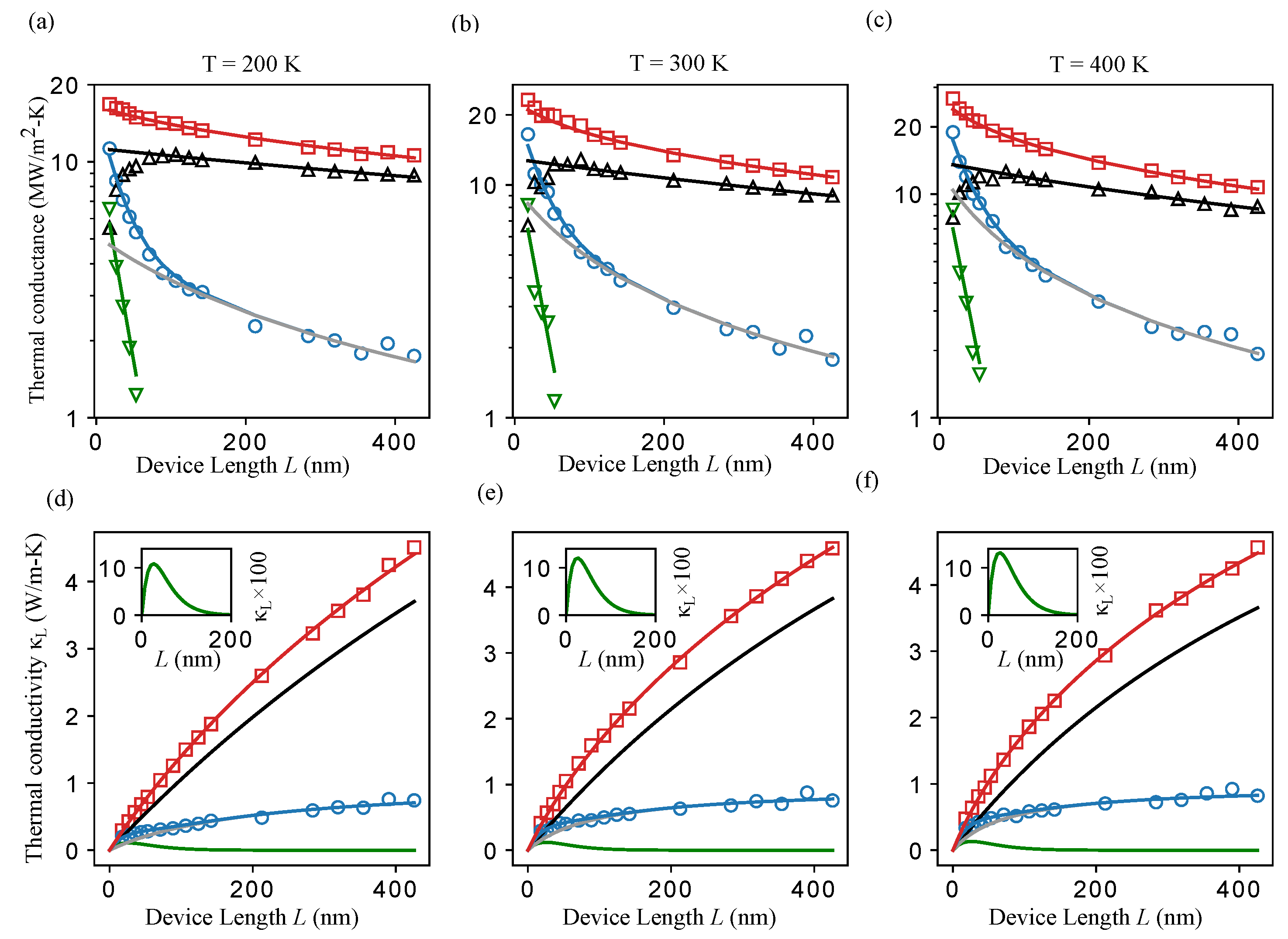
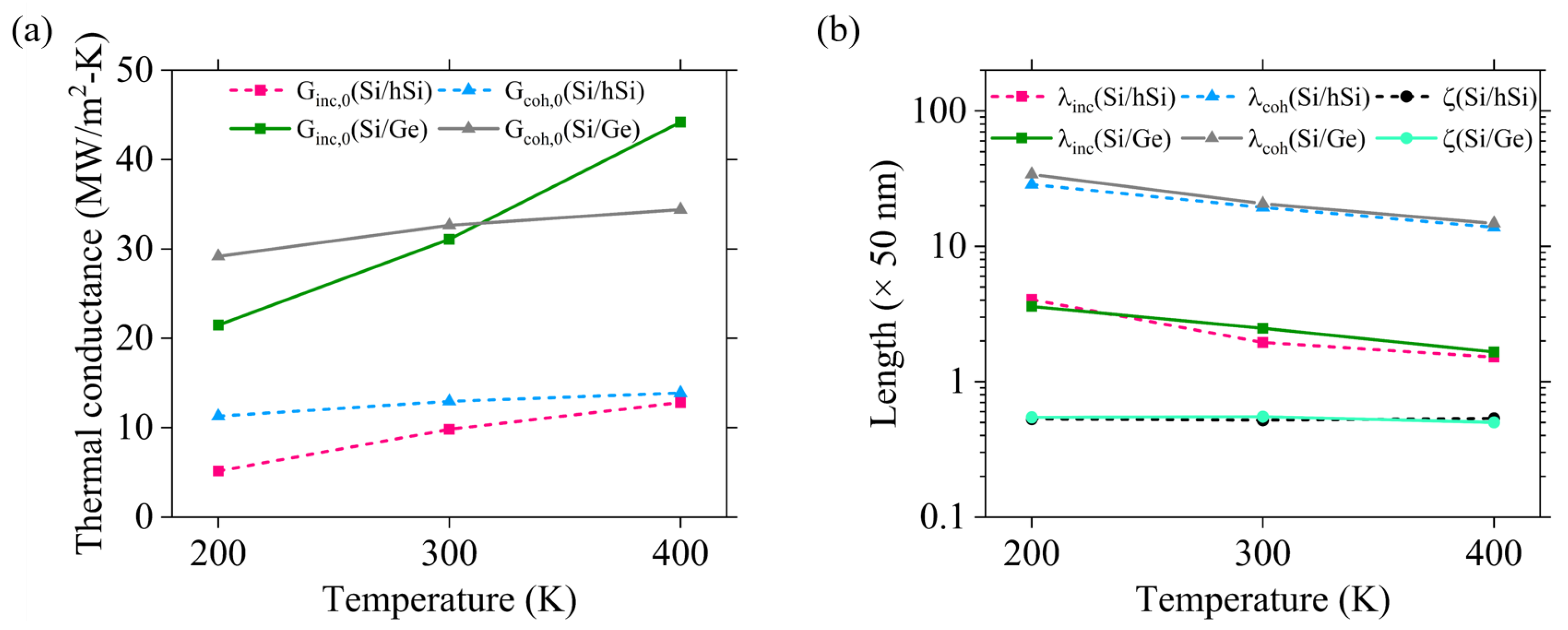
3.1. Two-Phonon Model Analysis

To develop a clear understanding of representative $\kappa$–L trends arising from different combinations of coherent and incoherent phonon properties in a superlattice, we begin with a simple yet rigorous parametric analysis based on the two-phonon model introduced in the methodology section. This analysis provides theoretical guidance on the phonon transport characteristics required for observing nonmonotonic $\kappa$–L behavior, particularly in systems where the Anderson localization of phonons may be significant.

Specifically, we employ Equation (7), which describes the total thermal conductivity $\kappa$ of an aperiodic superlattice. The first term on the right-hand side represents the contribution from coherent phonons, while the second term accounts for incoherent phonons. The exponentially decaying term within the coherent contribution captures the reduction in phonon transmission (or conductance) with increasing device length L, with the decay length $\xi$ corresponding to the phonon localization length.

It is important to clarify that the usage of “coherent” and “incoherent” in this model is somewhat qualitative. Not all coherent phonons are localized in an aperiodic superlattice, and conversely, certain incoherent phonons may exhibit partial localization due to factors such as material interfaces, impurities, or pores. In our recent studies [17,45], we demonstrated that some coherent phonons display exponential decay in transmission with increasing L, indicative of localization, while others are limited by scattering and follow a $1/L$ trend instead.

With this more nuanced understanding of phonon transport, we reinterpret the two-phonon model in Equation (7) as distinguishing between phonons that undergo localization in aperiodic superlattices and those that do not. Despite this reinterpretation, the model remains a powerful tool for analyzing thermal transport phenomena in disordered systems, as we demonstrate below.

By taking the derivative of the coherent phonon term in Equation (7) with respect to L and setting it to zero, we find that the maximum thermal conductivity of the coherent phonon contribution occurs at

$$L_{\max }={\displaystyle \frac{\xi }{\sqrt{0.25+\xi /{\lambda }_{\mathrm{coh}}}+0.5}}.$$

(11)

This implies that if the contribution of localized (coherent) phonons can be isolated, their associated thermal conductivity will initially increase with L before peaking at $L=L_{\max }$ and subsequently decreasing due to localization effects.

In practical experiments and simulations, however, it is typically not feasible to distinguish between the coherent and incoherent phonon contributions to $\kappa$. Therefore, it is essential to consider the role of the incoherent phonon component—described by the second term in Equation (7)—in shaping the overall $\kappa$–L behavior.

The incoherent contribution increases monotonically with L, suggesting that when it dominates, any nonmonotonic behavior originating from coherent phonon localization will be obscured. Since Equation (7) does not admit a simple analytical expression for the total $\kappa$ maximum, we examine several representative cases to illustrate how parameters such as $G_{0,\mathrm{coh}}$, $G_{0,\mathrm{inc}}$, ${\lambda }_{\mathrm{coh}}$, ${\lambda }_{\mathrm{inc}}$, and $\xi$ affect the shape of the resulting $\kappa$–L curves.

In Figure 2, we present the thermal conductivities of coherent and incoherent phonons in periodic and aperiodic superlattices (i.e., random multilayers or RMLs) as functions of device length L for four representative parameter sets. The thick purple curve in each panel represents the total thermal conductivity of the RML. Our goal is to identify regimes exhibiting nonmonotonic $\kappa$–L trends.

In Figure 2a, it is shown that incoherent phonons possess significantly higher ballistic-limit conductance ($G_{0,\mathrm{inc}}$) than coherent phonons ($G_{0,\mathrm{coh}}$). Although the coherent phonons alone (green dashed curve) show nonmonotonic $\kappa$–L dependence due to combined localization and scattering, the total $\kappa$ (purple curve), dominated by the incoherent contribution (blue dashed curve), increases monotonically with L. Such behavior is expected in high-temperature environments, where incoherent phonon conductance is enhanced by inelastic scattering [60], while coherent phonon transport is suppressed due to decoherence [28,30,46]. Similar behavior occurs in superlattices composed of acoustically similar materials, which promote incoherent phonon transmission across interfaces.

In Figure 2b, the coherent and incoherent phonon contributions are comparable. This condition may arise at low temperatures, where phase-breaking events are rare, or in systems with high acoustic contrast between layers, which hinders incoherent phonon transmission. As seen in the purple curve, $\kappa$ initially increases with L due to ballistic transport but decreases beyond $L_{\max }$ due to the localization of coherent phonons. The nonmonotonic feature is even more pronounced in Figure 2c, where $G_{0,\mathrm{coh}}/G_{0,\mathrm{inc}}=5$, highlighting the dominant role of coherent phonons.

Figure 2d shows the case of a large localization length $\xi$ equal to ${\lambda }_{\mathrm{coh}}$, further amplifying the nonmonotonic behavior. Here, $\kappa$ is primarily dictated by the coherent phonon component. Unlike $G_{0,\mathrm{coh}}$ and $G_{0,\mathrm{inc}}$, which can be tuned via temperature or material choice, there is currently no systematic strategy for controlling the ratio ${\lambda }_{\mathrm{coh}}/\xi$.

To summarize, the total thermal conductivity of an RML exhibits nonmonotonic $\kappa$–L dependence only when $G_{0,\mathrm{coh}}\gg G_{0,\mathrm{inc}}$, and this behavior is enhanced by a longer localization length $\xi$. Conversely, when $G_{0,\mathrm{inc}}$ is comparable to or exceeds $G_{0,\mathrm{coh}}$, the monotonic increase in the incoherent component masks any nonmonotonic signature of localization. Notably, the absence of a nonmonotonic $\kappa$–L relation does not imply the absence of phonon localization; coherent phonons may still be localized even if their contribution is overwhelmed by incoherent phonons.

Thus, we argue that the nonmonotonic $\kappa$–L feature may be too stringent as a criterion for phonon localization. In this work, we analyze a broad class of systems—including LJ crystals, Si/Ge superlattices, and graphene/hexagonal boron nitride multilayers—to search for phonon localization. We evaluate localization at three levels: (i) nonmonotonic $\kappa$–L behavior (a strict criterion) and (ii) exponential decay in the thermal conductance of the coherent phonon mode predicted by the two-phonon model. Through these analyses, we aim to establish a comprehensive and quantitative understanding of phonon localization in multilayered structures.

3.2. NEMD Simulations of Si/Ge Superlattices

We first examine a realistic SL system composed of alternating covalently bonded layers of Si and Ge, modeled using the SW potential. As shown in Figure 3a–c, the thermal conductance of SLs (red squares) consistently exceeds that of the corresponding random multilayers (RMLs, blue circles), in agreement with prior studies on Si/Ge and other superlattice systems.

The fitting curves, based on the two-phonon model, exhibit excellent agreement with the NEMD data, demonstrating the validity of a coherent–incoherent phonon transport framework for these systems, consistent with earlier findings [4,60]. Notably, the green downward-pointing triangles indicate the conductance attributed to coherent phonons in the RMLs. Their exponential decay with increasing device length strongly supports the presence of Anderson localization in the coherent phonon population.

Figure 3d–f present the thermal conductivity $\kappa$ for both SLs (red squares) and RMLs (blue circles) as a function of device length L. Importantly, the $\kappa$-L relationship for RMLs increases monotonically and saturates at longer lengths, consistent with expectations for a scattering-dominated system. However, this monotonic trend does not rule out phonon localization in RMLs. The green curves (with magnified insets) show the coherent phonon contributions to $\kappa$ extracted via two-phonon model fitting. These curves initially rise with L and then rapidly diminish, indicating the localization of coherent modes. Nevertheless, since incoherent phonons dominate heat transport in these systems (as shown by the black curves), their monotonic $\kappa$-L behavior masks the nonmonotonic characteristics of the localized coherent phonons.

To isolate the effect of lattice mismatch in the Si/Ge system, we also consider a model superlattice composed of Si and a fictitious “heavy silicon” (hSi). The hSi atoms are assigned a larger atomic mass (112 g/mol vs. 28 g/mol for Si) but retain the same interatomic potential parameters as Si, thus ensuring identical lattice constants and eliminating lattice mismatch and interfacial strain.

As shown in Figure 4, the thermal conductance G and thermal conductivity $\kappa$ of the Si/hSi SLs and RMLs exhibit trends similar to those observed in the Si/Ge systems (Figure 3). In particular, the $\kappa$-L relation for all Si/hSi RMLs is strictly monotonic, supporting the interpretation that incoherent phonons dominate transport, and that coherent phonon localization effects are masked.

Figure 5 shows the parameters obtained from fitting the two-phonon model to the NEMD simulation results. In Figure 5a, we observe that the ballistic-limit thermal conductance of coherent phonons, $G_{\mathrm{coh},0}$, is comparable to that of incoherent phonons, $G_{\mathrm{inc},0}$, in both Si/Ge and Si/hSi systems. At 200 K, $G_{\mathrm{coh},0}$ slightly exceeds $G_{\mathrm{inc},0}$ in the Si/Ge system. However, with increasing temperature, $G_{\mathrm{inc},0}$ surpasses $G_{\mathrm{coh},0}$ due to enhanced inelastic phonon transmission [60]. For the Si/hSi system, $G_{\mathrm{coh},0}$ consistently exceeds $G_{\mathrm{inc},0}$, although both remain in the same order of magnitude. This explains the absence of a pronounced nonmonotonic $\kappa$-L trend in the RMLs of both systems.

Figure 5b presents the MFPs of coherent and incoherent phonons, along with the localization lengths of coherent phonons. Coherent phonons exhibit significantly longer MFPs compared to incoherent ones, as the latter are strongly scattered by the dense interfaces in the SL structures. Our recent phonon wave-packet simulations have visually confirmed the ballistic transport of coherent phonons and strong scattering of incoherent phonons in SL systems [44,45,46].

For both types of phonons, MFPs decrease with temperature due to intensified anharmonic phonon–phonon scattering. Notably, the localization length of coherent phonons is approximately 25 nm in both Si/Ge and Si/hSi systems. At this stage, it remains unclear whether this similarity arises from coincidence or stems from the shared average layer thickness ($d=4$ unit cells of Si or Ge).

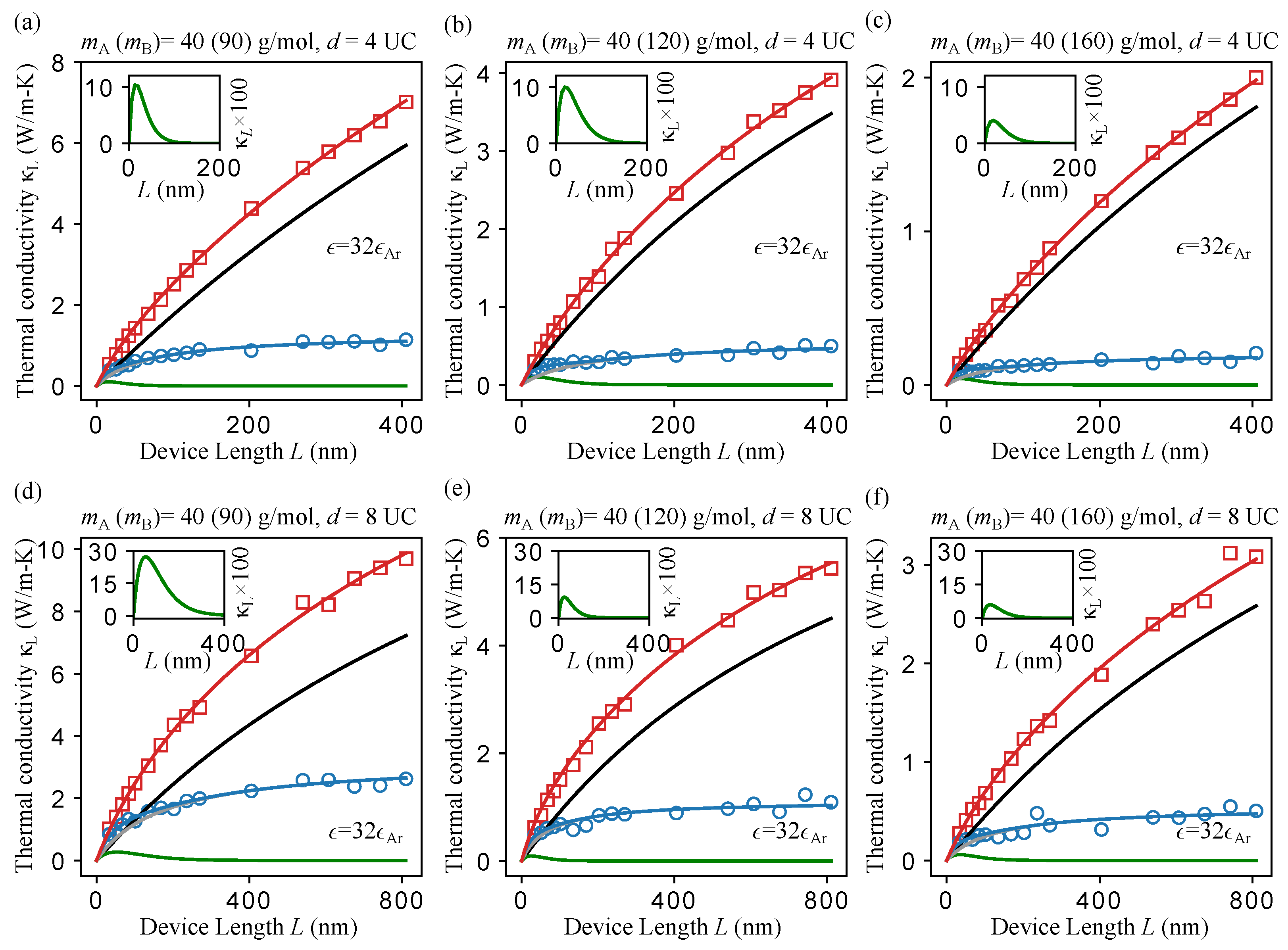
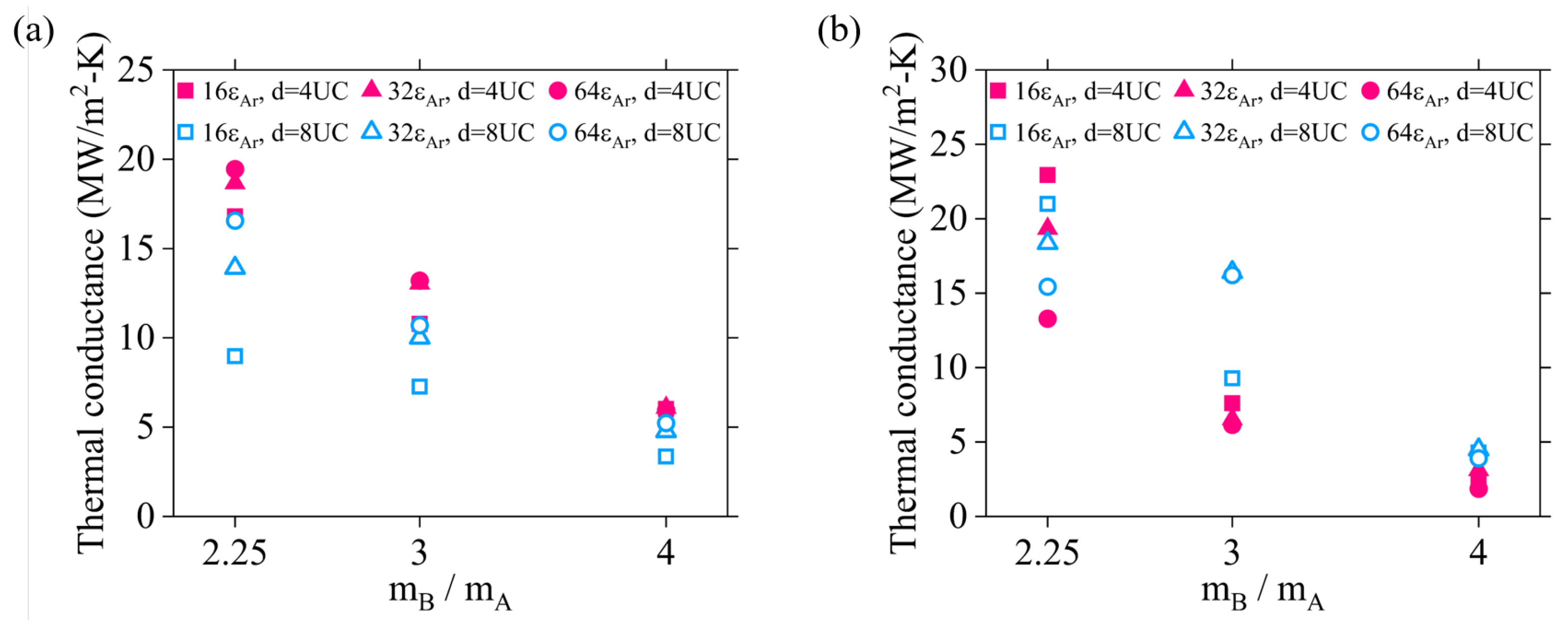
3.3. NEMD Investigation of LJ Systems with Controlled Acoustic Contrasts and Bond Strengths

In this subsection, we investigate LJ superlattice systems, which are widely used as model systems to study the impact of bond strength, bond length, and structural configuration on phonon transport. One key advantage of LJ potential is the ability to independently tune bond strength and bond length: the potential depth $ϵ$ governs the bond strength, while the parameter $\sigma$ controls the bond length. This flexibility makes LJ systems ideal for isolating the effects of individual parameters on thermal transport.

In previous studies, including our own, LJ superlattices have been extensively employed to explore phonon heat conduction in nanostructures. In particular, we study LJ superlattices composed of two types of LJ materials—one with an atomic mass of 40 g/mol (mimicking solid argon) and another with a mass of 90 g/mol—to introduce acoustic mismatch. To emulate the behavior of covalently bonded thermoelectric semiconductors, we increase the LJ potential well depth to $16{ϵ}_{\mathrm{Ar}}$, where ${ϵ}_{\mathrm{Ar}}=0.0104$ eV corresponds to the van der Waals interaction strength in solid argon. For further methodological details and prior results regarding coherent and incoherent phonon transport in LJ superlattices, we refer the reader to our earlier publications [4,19,45,46,61]. In the present work, our focus is on investigating how acoustic mismatch and bond strength affect the two-phonon transport characteristics in periodic SLs and RMLs.

We begin by examining the role of acoustic mismatch between the constituent materials. Acoustic contrast is known to reduce phonon transmission across interfaces, as described by the acoustic mismatch model and diffuse mismatch model [62,63,64]. Within the two-phonon model framework, acoustic contrast primarily impacts the transport of incoherent phonons, which undergo interface scattering [4,60]. Thus, systems with stronger acoustic contrast are expected to suppress incoherent transport more effectively, potentially allowing the signatures of coherent phonon transport—especially the nonmonotonic $\kappa$-L behavior in RMLs [7,9]—to become more visible.

To study acoustic mismatch effects, we fix the atomic mass of material A to $m_A=40$ g/mol and vary the mass of material B to $m_B=90$, 120, and 160 g/mol, corresponding to moderate to high acoustic contrast ratios ($m_B/m_A=2.25$, $3.0$, and $4.0$). We also consider two average layer thicknesses, $d=4$ UC and $d=8$ UC, since thinner layers (e.g., $d=4$ UC) increase the frequency of interface scattering and thus reduce incoherent phonon contributions.

Figure 6 shows the thermal conductivity results for systems with a relatively weak bond strength of $ϵ=16{ϵ}_{\mathrm{Ar}}$. For comparison, note that $ϵ=64{ϵ}_{\mathrm{Ar}}$ represents moderately strong bonding (e.g., a typical C–C bond is around $100{ϵ}_{\mathrm{Ar}}$). Therefore, we also study systems with $ϵ=32{ϵ}_{\mathrm{Ar}}$ and $ϵ=64{ϵ}_{\mathrm{Ar}}$, with the results shown in Figure 7 and Figure 8, respectively.

Despite examining 18 combinations (panels a, b, d, and e in Figure 6, Figure 7 and Figure 8), covering hundreds of structures, most cases exhibit a monotonic $\kappa$-L relationship. Only in systems with very high acoustic contrast ($m_B/m_A=4$) do we observe a weakly nonmonotonic trend—i.e., a thermal conductivity maximum in $\kappa$-L—a notable hallmark of the Anderson localization reported in prior studies [5,6,7,9].

However, the absence of an observable nonmonotonic $\kappa$-L trend in many systems does not imply the absence of phonon localization. In fact, the two-phonon model fitting consistently reveals a nonmonotonic length dependence in the coherent phonon contribution (green curves), confirming strong localization effects in the RMLs due to disorder-induced interference. This observation aligns with our recent phonon wave-packet studies [45]. Unfortunately, the dominant contribution from incoherent phonons, which exhibit a monotonically increasing $\kappa$ with L, masks the localization signature in total thermal conductivity.

Figure 9 presents the ballistic-limit thermal conductance of both coherent ($G_{\mathrm{coh},0}$) and incoherent ($G_{\mathrm{inc},0}$) phonons, as extracted from the two-phonon model fits to the NEMD simulation data for LJ superlattices and RMLs. These results reveal clear and physically consistent trends with respect to both material contrast and structural parameters.

As illustrated in Figure 9a, the ballistic thermal conductance of coherent phonons, $G_{\mathrm{coh},0}$, exhibits a strong inverse correlation with the mass contrast ratio $m_B/m_A$. As this ratio increases, larger phononic bandgaps are introduced into the superlattice dispersion, which suppress the group velocities of coherent phonons and thereby reduce their contribution to thermal conductance. This trend is in line with the theoretical understanding that increasing acoustic mismatch impedes wave-like phonon transport across interfaces.

A second key observation from Figure 9a is the notable decline in $G_{\mathrm{coh},0}$ with increasing layer thickness d, from 4 to 8 unit cells (UC). This finding corroborates earlier theoretical [65] and molecular dynamics studies [10,66,67] which demonstrate that longer period lengths in SLs tend to open wider mini-gaps in the phonon spectrum, leading to reduced phonon group velocities and, consequently, diminished coherent thermal transport.

Additionally, we find that $G_{\mathrm{coh},0}$ increases systematically with interatomic bond strength, as evidenced by the comparison across SLs with bonding strengths of $16{ϵ}_{\mathrm{Ar}}$, $32{ϵ}_{\mathrm{Ar}}$, and $64{ϵ}_{\mathrm{Ar}}$. This trend reflects the enhancement of group velocities in stiffer lattices, which facilitates more efficient coherent heat conduction.

Turning to the incoherent phonon contribution, Figure 9b shows that $G_{\mathrm{inc},0}$ also decreases with increasing mass contrast $m_B/m_A$. This reduction is attributed to lower interfacial phonon transmission probabilities across mass-mismatched layers, which dominantly affect short-wavelength, particle-like phonons. The sensitivity of $G_{\mathrm{inc},0}$ to interfacial properties underscores the role of interface scattering as a limiting factor in incoherent phonon transport.

Interestingly, in contrast to the coherent phonon trend, $G_{\mathrm{inc},0}$ increases with increasing layer thickness d. This behavior arises because thicker layers correspond to lower interface density within the structure, thereby reducing the frequency of phonon-interface scattering events experienced by incoherent phonons. As a result, these phonons experience fewer disruptions, enabling more effective transport.

Together, the results presented in Figure 9 highlight the contrasting dependence of coherent and incoherent phonon transport on mass contrast and structural design. These trends provide valuable insights for engineering thermal transport in nanoscale multilayered materials by tuning interfacial characteristics and structural periodicity.

In summary, this subsection shows that only LJ SLs with strong acoustic mismatch exhibit weak nonmonotonic $\kappa$-L behavior in total thermal conductivity. This is due to enhanced interface scattering suppressing incoherent transport, thus revealing the localized nature of coherent phonons. Even in systems without an observable $\kappa$-L peak, coherent phonons remain strongly localized, as confirmed by model decomposition. These results suggest that using the $\kappa$-L relation alone as an indicator of Anderson localization may overlook many relevant cases, particularly when incoherent phonon transport is substantial.

4. Conclusions

In this work, we conducted extensive NEMD simulations to investigate the length-dependent thermal conductivity of various SL structures, including periodic SLs and RMLs, composed of Si/Ge, Si/hSi, and LJ materials with systematically varied acoustic contrast, bond strength, and average layer thickness. Across all systems studied, we observed only weakly nonmonotonic $\kappa$-L behavior—namely, a thermal conductivity maximum that has been previously proposed as a hallmark of Anderson localization of phonons. Specifically, only LJ RMLs with very high acoustic contrast (mass ratio 4:1) exhibited a marginal nonmonotonic $\kappa$-L relation, while in all other cases, thermal conductivity increased monotonically with length and was saturated in the diffusive limit.

However, our two-phonon model analysis—used to decompose the total thermal conductivity into coherent and incoherent phonon contributions—revealed that inall RML systems studied, the coherent phonon contribution exhibits a significantly nonmonotonic $\kappa$-L relation. This localized behavior is consistently masked in the total $\kappa$ due to the dominant and monotonic contribution from incoherent phonons.

In addition, the model allowed us to extract the ballistic-limit MFPs of both coherent and incoherent phonons. For both Si/Ge and LJ systems, we found that the incoherent phonon contribution is comparable to, or even exceeds, that of coherent phonons. This explains why the clear localization signature in the coherent component is often obscured in the total $\kappa$. To enhance the visibility of phonon localization in thermal transport experiments, we recommend strategies that suppress incoherent phonon conduction while promoting coherent transport. Such strategies include (1) selecting materials with large acoustic contrast, (2) designing RMLs with small average layer thickness, and (3) conducting measurements at low temperatures to reduce incoherent phonon scattering.

Moreover, for strong localization effects to manifest in $\kappa$-L behavior, the localization length $\xi$ of coherent phonons must be comparable to or longer than their MFP. The factors controlling $\xi$, however, remain insufficiently understood and warrant further investigation beyond the scope of this study.

In conclusion, we recommend that experimental investigations of phonon localization in superlattices be guided by comparative studies of both SLs and RMLs using a two-phonon framework. Specifically, while the thermal conductivity measurement technique is not limited to optical approaches (e.g., time-/frequency-domain thermoreflectance or Raman-based techniques) or electrical approaches (e.g., hot wire), it is essential to measure two sets of devices, one being periodic and the other being disordered to induce phonon localization. This approach allows the total thermal conductivity to be explicitly decomposed into coherent and incoherent contributions. For atomistic simulations, spectral methods—such as phonon wave-packet simulations, spectral phonon heat flux analysis, or spectral energy density analysis—should be employed to resolve individual phonon modes and assess localization behavior. Evaluating Anderson localization based solely on the coherent component of thermal conductivity offers a more accurate and nuanced understanding of phonon transport in disordered superlattices.

This work provides a foundation for guiding both experimentalists and theorists in identifying or engineering superlattice structures that exhibit strong phonon Anderson localization, particularly pronounced $\kappa$-L dependence. Such structures hold promise for thermoelectric and thermal barrier applications where ultralow thermal conductivity is desirable.