Abstract
Crystalline products with a narrow and uniform distribution of crystals by size (CSD), characterized by a desired average size, are necessary in many practices. Therefore, extensive, but mostly experimental, research is devoted to the problem of obtaining such CSDs. Alternatively, this manuscript presents a theoretical approach for calculating CSD resulting from crystallization in unstirred solutions. First, classical equations for the rates of diffusion-controlled and kinetically controlled growth of crystals are used to discuss the size-dependent growth of the nucleated crystals and the initial CSD (which arises from the non-simultaneous nucleation of crystals). Then, applying the law of conservation of matter, it is proved that the CSD continues to expand during the growth stage. Furthermore, it is substantiated that, due to their uneven spatial distribution, crystals of the same size can grow at different rates. This depends on whether the crystals are outside the diffusion fields of other crystals or are clustered together in “nests”. Moreover, by calculating the growth rates of crystals in “nests”, an explanation is given for the observation that closely spaced crystals are smaller in size than the separately growing crystals. Finally, the CSD established during the Ostwald ripening is discussed quantitatively, step-by-step.
1. Introduction
As a relatively easy and cost-effective separation and purification technique, crystallization from solutions is widely used as an important unit operation process in the chemical, fertilizer, sucrose, food, pharmaceutical, fine chemical, and biotechnology industries. Of course, the resulting crystalline product must possess the characteristics necessary for its intended use, with crystal polydispersity and size distribution (CSD) being of paramount importance. Particularly in the pharmaceutical industry, there are strict requirements regarding CSDs [1,2]: a narrow and uniform CSD with a definite mean crystal size is obligatory; the reason is that the drug bioavailability depends on the CSD. Therefore, considerable efforts have been devoted to determining the optimal crystallization parameters, which are needed to acquire the desired CSD of medicinal substances [3,4,5,6,7,8,9,10].
CSD also affects the therapeutic drug efficiency: small crystals dissolve earlier than the larger ones, and as the number of crystals decreases, the concentration of the drug, i.e., its bioavailability, decreases. In contrast, at narrow and uniform CSD, crystals dissolve in a nearly parallel way, thus ensuring prolonged drug availability. Also in therapy, since many crystalline drugs are administered by injection, large crystals may clog the needles of the syringes, and in general, very large crystals are undesirable since they may include a solvent, thus reducing the purity of the crystalline product.
In addition, generally, CSD is of importance in determining the ease and efficiency of the solid/liquid separation steps. It is well known that small crystals affect filtration, washing, and drying, making them difficult: e.g., they clog filter pores. Thus, small crystals cause low process efficiency, low-quality products, and some product loss. That is why special attention has been devoted to their elimination. For instance, fines are removed via temperature cycling, e.g., see [4,7,11]. In addition, the suitability of crystals for further processing and storage depends on the CSD: the tendency of crystals to bind together or cake into large solid lumps during storage is reduced if the crystals are of relatively uniform size.
However, not only do medicine and technology dictate the interest in CSD. The latter is also important for laboratory studies. While relatively large and well-diffracting protein crystals are needed for X-ray crystallography, the burgeoning method of serial crystallography by X-ray free-electron lasers, XFEL, uses microjets of suspensions of microcrystals, which are irradiated with very intense X-ray beams. (XFEL determines the structures of biomolecules at room temperature, which are closer to the structures attained by biomolecules at the temperatures of the living organisms than those determined by conventional cryo-crystallography [12]; thus, XFEL offers more biologically relevant information regarding the in vivo activity of biomolecules). Moreover, to avoid blockage of the microjet injectors by large crystals, the crystals used must be highly homogeneous in size (for growing protein crystals for XFEL see [13]).
All this shows why it is necessary to know the factors determining the CSD: CSD and crystal polydispersity have been, and are, the subjects of thorough studies, e.g., [14]. The main findings in this respect can be summarized as follows:
First and foremost, methods have been developed to control the crystallization process aimed at obtaining the desired CSD of some substances; to avoid the nucleation stage of the crystallization process, which is difficult to control, seeded operation is often used in practice, e.g., [15,16,17,18]. Moreover, combined with process analytical technology (PAT) [5] and calculations performed by means of population balance equations, robust control on crystallization processes was achieved, e.g., [3]. (The most used techniques for PAT are: attenuated-total reflectance Fourier-transform infrared spectroscopy (ATR-FTIR) for solution concentration measurement, focused beam reflectance measurements (FBRMs) for monitoring changes in the number of crystals and their CSD, Raman spectroscopy for monitoring polymorphic transformation, near infrared spectroscopy, ultraviolet–visible spectroscopy, direct visualization of crystals, etc. [19].) However, protocols for obtaining desired CSDs are developed only for individual specific substances and crystallizers, while there is no generally applicable approach to the problem. Obviously, knowledge of all the factors that determine CSDs is indispensable to developing a universal procedure.
Second, it has been established that the longer the nucleation period, the greater the initial crystal polydispersity (of course, depending on the rate of crystal nucleation, not only one but several/many crystals can nucleate at the same moment). In general, crystal nucleation is not an instantaneous process but proceeds over a longer time. Consequently, the nuclei that form first have the longest time to grow, and attain the largest size, while—corresponding to shorter and shorter growing times—the later nucleated crystals attain smaller and smaller sizes; meaning that the last-born crystals are the smallest in size [20]. That is why a shorter nucleation period should decrease crystal polydispersity. In fact, using insulin crystallization as a model system, this approach has been validated experimentally [21].
As for CSD, a very important role in its shape is played by the way in which the rate of crystal nucleation changes over time. This factor determines the initial CSD, which, however, can also keep its shape during the subsequent growth of crystals. For instance, the frequently observed sigmoidal dependency of the number density of nuclei on nucleation time causes the (simplest case of) experimentally determined CSD shown in Figure 1 [22]. Moreover, the theoretical derivation, based on the sigmoidal nucleation dependency, of such bell-shaped CSDs is presented in Ref. [23].
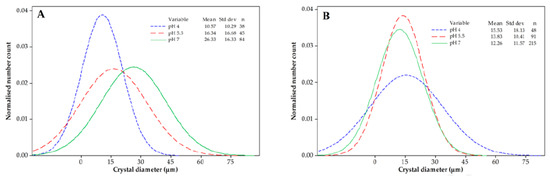
Figure 1.
Bell-shaped CSDs of lactose crystals, measured for the corresponding solution compositions (For details, see Ref. [22]). Permission for reuse: License Number 6050820639357, License date 16 June 2025. Crystal size distribution (CSD) of lactose crystallized at different pHs: (A) without whey proteins (0.63%), (B) in the presence of such proteins.
Of course, many other in situ and ex situ techniques find applications for measuring CSDs, e.g., [24,25,26].
Third, evidently, together with the moment of crystal nucleation, the growth rate determines the initial CSD; the faster the nucleated crystals grow, the more they differ in size. Therefore, to control crystallization processes aimed at obtaining crystalline products with the desired CSD, profound knowledge of crystal growth rates (respectively, growth mechanisms) is needed. Together with the growth time, the growth rates of crystals determine crystal sizes. That is why the emphasis in this article is placed on studying crystal growth rates.
Generally, there are different crystal growth rates/mechanisms: It is known from the literature that in addition to diffusion-controlled and kinetic-controlled crystal growth, there are also two other growth mechanisms, namely Growth Rate Dispersion (GRD) and size-dependent growth (SDG), and a combination of these is also possible [27]. GRD means that individual crystals of the same initial sizes do not grow at the same rate even when they are subjected to identical supersaturation and temperature levels, and hydrodynamic conditions, e.g., see [28,29]. Of course, GRD has a significant effect on the CSD from industrial crystallizers.
In addition, GRD is closely related to SDG. The two growth rates/mechanisms were compared by Srisanga et al. [30]. The authors write: “It is important to note that the extent of GRD is not an inherent property of the solute but also depends on the method of preparation of the nuclei or seed and also their subsequent growth history.” They also write: “Size-dependent crystal growth is only a real mechanism for crystals that are small enough that their surface energy has a significant effect on their thermodynamic stability—typically crystals that are smaller than approximately 1 μm in size”.
Growth Rate Dispersion and Size-Dependent Crystal Growth
Abundant experimental data of GRD for different crystalline materials can be found in review articles [31,32]. In addition, it is pointed out that crystal GRD can contribute significantly towards polydispersity in crystalline products [33]; however, no quantitative data are available. Importantly, GRD is a phenomenon that is still not understood properly. Most frequently, the surface integration step for crystal growth was thought to be the primary factor for GRD, with the role of screw dislocations emphasized as sources of growth steps [31]. Anyway, since GRD leads to an uncontrolled increase in the spread of the developing CSD, i.e., an increase in crystal polydispersity, it causes a significant decrease in product quality [34].
However, a complete theory explaining the dispersion in crystal nucleation and growth rates was developed only recently [33]. The authors suggest that this phenomenon can be related to local fluctuations in concentration and temperature—which are driven by the Brownian motion of solute molecules. (However, the consideration of GRD is beyond the scope of this article; it is discussed elsewhere, e.g., [28,29,30]).
Nevertheless, some comments are made here to the basic idea of Singh et al. [33]: Obviously, only local fluctuations in concentration, which are located close enough to the growing crystals, can affect their growth rate. However, to increase the number of molecules in some small volumes of solution, molecules from neighboring small volumes are taken out, i.e., fluctuating increases and decreases in concentration occur with almost the same probability. Therefore, fluctuations in concentration may compensate for each other, or at least be a factor of low intensity for the drastic change in the growth rate of crystals.
In the author’s opinion, an alternative to the local fluctuations in concentration and temperature [33] should be the effect expected from the consumption of solute from closely spaced larger crystals, which leads to a local decrease in concentration. In general, since the random nature of crystal nucleation leads to an uneven spatial distribution of crystals, frequently, several (or many) crystals grow clustered together in “nests”, where, inevitably, the concentration drops. However, to the best of the author’s knowledge, the effect of the uneven spatial distribution of crystals on the CSD has not been considered so far (at least not in a quantitative manner as in this paper).
The aim of this paper is to review the factors that, through the rate of crystal growth, determine CSD in unstirred solutions in which the solute concentration is not replenished. It is shown that (in contrast to GRD) SDG allows for establishing the changes in the initial CSD occurring during the nucleation stage and for the calculation of the wideness of the actual CSD. To this aim, consequences for CSDs stemming from well-established equations for diffusional and kinetically controlled crystal growth rates are pointed out; equations describing rates of growth of crystals of increasing size (i.e., growing at decreasing supersaturation) are used. (Of course, stirring the solution destroys most of the diffusion effects on CSD, but it is beyond the scope of the paper. The reason is the significant complications that arise from crystals broken by stirrers in industrial facilities). Afterwards, the law of conservation of matter is applied to calculate the wideness (i.e., the size spread) of CSD, and an expression is devised for the growth rate of crystals grouped into “nests”. It is shown that, because of the competition for a solute between closely spaced crystals, the initial CSD (arising from the non-simultaneous nucleation of crystals) widens. Then, other factors that can reshape the CSD inherited from the nucleation stage are pointed out. Finally, the course of the Ostwald ripening [35,36], which occurs because of the dissolution of small crystals in the crystallizing system, and thus, determines the final CSD, is revisited.
Importantly, looking at some theories about the Ostwald ripening, e.g., [37,38], Voorhees [39] argues that “if a small particle is located near a large particle, it will have a larger dissolution rate than when it is located at the same distance from a particle of nearly the same size, since in the former case the interfacial concentrations of the particles are quite different, whereas in the latter case the interfacial concentrations of both particles are nearly the same”. This means that, depending on the local distribution of the crystals (which is case-specific), crystals of the same size are coarsened at different rates.
2. Basic Factors That Determine Crystal Size Distribution During Crystallization in Solutions
Because of the practical importance of the CSD, we look at the factors that determine it. First, generally accepted equations for diffusion-controlled and kinetic-controlled rates of crystal growth are used for the quantitative prediction of CSD. Although due to GRD, there are significant deviations from these equations, more frequently, this is not the case. At the very least, these classical equations show average growth rates, which can be used as a starting point when discussing CSD.
2.1. CSD Resulting from the Initial Growth of Crystal Nuclei
Initially, the effect of crystal growth rate on CSD will be discussed for the case of a diffusion-controlled process (which means that the embedding of molecules in a crystal takes place much faster than their supply to it). In this case, the growth rate, expressed as the amount of mass mg deposited on the crystal surface per unit time, is [40]:
where S is the crystal surface and D [cm2/s] is the diffusion coefficient of the solute, δN [cm] is the thickness of the Nernst diffusion layer, c is the actual concentration, and ce is the equilibrium one with respect to an “infinitely” large crystal.
Importantly, due to the infinitesimal sizes of the crystal nuclei (the critical nucleus is the smallest-sized stable crystalline particle possible under the conditions present), they consume for their growth a negligible amount of solute. That is why they grow at a constant supersaturation. Equation (1) tells us that at constant the rate of increase in the crystal mass depends solely on S. The larger S, i.e., the earlier the crystal has been born, the faster it grows. So, this is an SDG case.
Of course, the increase in size of the growing crystals also depends on the growth time (meaning that the CSD established during the crystal nucleation stage is determined by these two factors). However, although the difference in size of the growing crystal nuclei expressed by the number of molecules constituting them can be significant at the nanoscale, if they were to attach the same number of molecules, the size differences would fade out of view from a macroscale perspective. Thus, all grown to macro-size crystals would be indistinguishable in size, which, of course, is not the case. Crystals grown to microscopically visible dimensions are clearly distinguishable in size. Obviously, the original CSD, established during the nucleation stage, expands as the crystal nuclei grow further.
2.2. Change of the Initial CSD Due to Diffusion-Controlled Growth of Crystals
Sooner or later, the growth of the nucleated crystals themselves causes a decrease in the overall concentration in the crystallizing system, which stops the birth of new crystals. Primary homogeneous nucleation stops first, since it requires the highest supersaturation. This happens when the growing crystals lower the supersaturation in the bulk of the solution below the supersolubility curve. (However, locally, due to the formation of nucleation exclusion zones around growing nuclei, the supersaturation can become critically low earlier—thus decreasing the volume in which homogeneous nucleation is possible). However, despite requiring lower supersaturation, heterogeneous crystal nucleation also terminates, the reason being the exhaustion of nucleation-active particles and/or centers (which is associated with the nucleation process itself). However, although insufficient for the generation of new crystals, the lowered supersaturation is sufficient for the growth of existing crystals.
Of course, with a decrease in concentration, the rate of crystal growth also decreases. Therefore, to establish quantitatively the effect of the two counteracting factors in Equation (1), namely increasing S and decreasing (c − ce), we look first at the idealized case of a uniform spatial distribution of the growing crystals: Evidently, to not compete for building material, the crystals must be located far enough from each other. In this case, the decrease in the concentration around every individual crystal is due merely to its own growth, meaning that the size of the growing crystal and the decrease in concentration around it are inversely related.
First, let us look at crystals, which, growing further, continue to stay in equilibrium with the solution like the critical nucleus of edge length l*. (Even if there are no such real crystals, their growth rate serves as a convenient benchmark in the theoretical consideration of the changes in CSD during crystal growth.)
As is well known, the lower the concentration, i.e., the supersaturation Δμ, the larger the l*, as follows:
where Ω is the volume of the crystal building block, and γc is the specific energy of the interface between the crystal and its surroundings.
According to the classical expression for the chemical potential difference, for small and medium solution supersaturations Δμ is as follows:
where kB is the Boltzmann constant and T is the absolute temperature. (That is why relatively small variations in operating temperature have little effect on the supersaturation, and thus on the CSD; see below. In addition, only for substances having temperature-dependent solubility do temperature changes affect supersaturation appreciably, which in turn evokes CSD variations.)
So, (c − ce) is as follows:
To calculate the increase in the mass of a growing (slightly larger) crystal, we substitute (c − ce) from Equation (4) in Equation (1) for a cubic crystal of edge length l, and surface S = 6l2, as follows:
Because the increase in mass with time of the crystal growth depends solely on l (all remaining parameters are constant), Equation (5) shows a case of SDG in which larger crystals engulf more mass compared with their smaller brethren. (Or to put it another way: In Equation (1), S increases with l to a power of two, i.e., faster than the decrease in , which depends on l to the power of one).
The next step is to calculate the width of the CSD due to the SDG. Denoting the size of the largest crystals by lmax and the size of the smallest crystals by lmin, we obtain the following:
Note that the coefficient in Equation (6) has dimensions of time. Moreover, because , and increases due to SDG, the width of the CSD increases during the diffusion-controlled growth of crystals obeying the Gibbs–Thomson effect, i.e., for crystals smaller than about 1 to 2 μm in size. For CSDs of larger crystals, see Section 3.
2.3. Kinetic-Controlled Growth of Crystals and the Resulting CSD
Even with unstirred solutions, the incorporation of molecules into the growing crystals can be slower than their delivery, meaning that the crystal growth is kinetically controlled. In this case, the growth rate dl/dt [cm/s] of a faceted crystal (measured in a direction perpendicular to the growing face) is related to the velocity V [cm/s] of steps on the crystal surface via the mean step density, h/d, where h is the step height and d is the characteristic distance between the steps. This distance depends on the actual supersaturation as follows [40]:
where V is the rate of tangential propagation of a step on the crystal surface as follows:
where ρ [cm3/g] is the specific crystal volume, and it is convenient to use the kinetic coefficient β in [cm/s]. The kinetic coefficient β of step propagation is measured by atomic force microscopy (AFM), laser confocal microscopy enhanced by differential interference contrast, LCM-DIM [41,42] (which enables sufficient in-depth resolution to perform in situ observation of elementary steps on protein crystal faces), and electron microscopy (using replica methods). AFM and LCM-DIM deserve special attention because they allow direct observation of growing crystals and the propagation of steps on their faces in their mother liquors. Nearly two orders of magnitude smaller β are measured for the growth of steps on the surfaces of protein crystals, compared with the corresponding β for crystals composed of small molecules, see Table 4 in Ref. [40]).
Now, substituting Equation (8) into Equation (7), we obtain the following:
As seen, Equation (9) does not reveal CSD. Therefore, to find out how much mass is deposited on the surface of a crystal growing under kinetic control, we multiply both sides of Equation (9) times l2/ρ, to obtain the following:
(Of course, the growth rate in kinetic-controlled processes depends on β, but not on the diffusivity, D).
For the initial growth of the just-born crystals, under constant , Equation (10) also shows that the deposited mass depends solely on S (in fact, h, β, and d are constants). Thus, the larger the crystal in the initial set of growing crystal nuclei, the faster it grows. So, SDG expressed by Equation (10) for kinetic-controlled crystal growth also defines the CSD established during the crystal nucleation stage. Let us derive the width of CSD in this case.
Due to the decrease in supersaturation during crystal growth, the steps on the surface of the crystal are generated by screw dislocations. For the distance between polygon-shaped steps on the surface of cubic crystals, Kaischew and Budevski [43] calculated d = 4l2D, where l2D is the edge length of the two-dimensional nucleus on the surface of a cubic crystal. Thus:
However, since for a cubic (Kossel) crystal l = 2l2D, Equation (11) transforms into the following:
Which means that CSD widens as per the following:
3. Wideness of CSD
As we have seen, SDG leads to an increase in the size spread of the CSD in a predictable way, also for crystals that are larger than the critical nucleus. However, the question remained unanswered: What are the limits of this expansion of CSD? To answer this question, we use the law of conservation of matter. Considering again cubic crystals, we arrange all of them according to their size, li. Thus, li varies from negligibly small lmin for the crystals nucleated at the end of the nucleation process, till the largest crystal(s) size, lmax—for the earliest born ones—at the start of the nucleation process. By denoting mt [gr] the mass of the solute that remains uncrystallized in the crystallizing system at any time point t of the growth process, and the solute mass initially introduced into the solution by mo, it is obvious that the mass difference and the cumulative volume of all grown crystals are related by the following equation:
where ni is the number of the crystals in the i-th category.
Considering steady-state nucleation, i.e., equal ni for all li crystal sizes, and replacing ni with a common multiplier n, we write the following:
So, for a sufficiently large number of crystals and continuous CSD, the sum in Equation (15) can be replaced by an integral as follows:
The solution to which gives the following:
However, at the beginning of the growth of the nuclei, the last-born crystals are so small that . So, the width of CSD is determined solely by lmax, which is given by the following integral:
To which the solution is as follows:
As seen, since mt decreases with the time t, i.e., increases, Equation (19) shows that the volume of the crystal nuclei increases during their further growth, i.e., that also increases and the initial CSD widens. The time course of the process can be elucidated by differentiating Equation (17) with respect to t, which, with , gives:
It is seen that, generally, SDG does not depend on the Gibbs–Thomson effect, but, although with constantly decreasing efficiency, SDG can be actual till the largest possible crystals (maximal is attained at mt, which corresponds to ce). This result (which holds true for both diffusion- and kinetic-controlled crystal growth) refutes the claim in Ref. [30] that SDG is limited to “crystals smaller than approximately 1 μm in size”.
However, the initial CSD inherited from the nucleation stage can also be changed (and very often does) because of the uneven spatial distribution of crystals in the volume of the crystallizing solution.
4. Growth of Crystals Clustered in “Nests”
As already mentioned, due to the random nature of crystal nucleation, an uneven spatial distribution of crystals and their growth in “nests” is highly probable. And obviously, the more crystals, the more they deplete the surrounding solution. Because of this, crystals in “nests” grow at a slower rate than crystals of the same size, which are located far enough apart from each other and do not compete for building material.
This idea is easy to quantify; since the diffusion is a slow process, and if a “nest” of clustered crystals is far enough away from other crystals, such a “nest” can be regarded as an isolated part of the crystallizing system. Thus, by denoting as the actual concentration in the “nest”, and the number of crystals in it is denoted by N, we calculate the supersaturation in the “nest”. Since N does not change during crystal growth, considering cubic crystals, it is evident that (in an unreplenished solution) the cumulative volume of all crystals in the “nest” totals Nλ3, where λ is the (approximate) mean crystal edge length reached at that point of crystal growth. Similar to the above, the solute mass that remains uncrystallized is denoted by [g], and thus it is obvious that, at any time point t of the growth process, the difference is the mass of solute that is consumed to grow N crystals to the mean size λ. Now, to convert the cumulative crystalline volume Nλ3 into mass, we divide Nλ3 by ρ and obtain the following:
Then, subtracting from both sides of Equation (21) the mass me (which corresponds to solubility ce), and dividing ) by the volume v of the “nest”, we obtain the supersaturation that drives the growth of the crystals in the “nest” as follows:
where co is the starting concentration. In this case, since the decrease in the concentration is due to the growth of not only one, but of several crystals, the decrease in concentration occurs faster than when the crystals are spaced far apart.
Finally, replacing the supersaturation in Equation (1) with (), for cubic crystals, we obtain the following:
Thus, the width of the CSD is determined by the following formula:
Equation (24) shows that due to SDG, the initial CSD widens also in this case.
In addition, Equation (23) confirms that decreases more quickly in the “nest”, so that the crystals clustered there must be smaller than the separately growing crystals. This corresponds to many observations. Moreover, since the growth of crystals of different sizes in “nests” leads to a different decrease in concentration around them, they grow at different rates and reshape the CSD in different ways.
Of course, the “nests” can be different in size and consist of different numbers, N, of crystals. In this case, the law of conservation of matter is expressed by Equation (25), as follows:
Evidently, the larger the “nest”, the more the solute mass mo in it, which means larger Nλ3. In addition, Equation (25) shows that in “nests” with different numbers of crystals, there is an inversely proportional relationship between N and λ; the more the crystals, the smaller their mean size, and vice versa. In addition, Equation (25) shows that the cumulative volume of all crystals increases during their growth, i.e., that also increases, and the initial CSD widens.
However, due to the relatively small number N of crystals in the “nest”, some of the i-th categories of crystals can be void, and no replacement of the sum by an integral is possible. Therefore, it is impossible to predict CSD in “nests” for the general case.
5. More Factors That May Change the CSD
Even by a regular space-positioning of crystals, in addition to the differing crystal growth rates, other factors can reshape CSD. With diffusion-controlled crystal growth, such factors are:
Convective flows (the so-called ‘plumes’) [44,45,46] arise over sufficiently large crystals. Plumes occur because the solution with lower solute concentration that surrounds a growing crystal is lighter, thus rises, and a fresh, more concentrated solution from the surroundings invades its place. The larger the growing crystal, the larger the plume formed above it, i.e., the more extensive solution replenishment. Therefore, large crystals grow faster than smaller crystals, thus widening the CSD in the direction of larger crystals (which have been nucleated earlier).
In addition, the sedimentation of large crystals, which is another gravity-evoked phenomenon, can increase CSD in diffusion-controlled growth. The reason is that, when reaching dimensions that are sufficient for their sedimentation, the first-born crystals leave areas with a decreased concentration (formed around them because of their growth) and move into a more enriched solution. Evidently, such crystals grow faster [47], and again, the CSD widens toward larger crystals.
Even in stagnant solutions, non-classical mechanisms of crystal growth, such as oriented attachment of nanocrystals (OA) [48] and crystal agglomeration [49], can modify the CSD established during the nucleation stage. (The thermodynamic driving energy for OA arises because bonding between the nanocrystals removes surface energy associated with unsatisfied bonds on the crystal surfaces and thus reduces the overall energy of the crystallizing system [48]). However, OA occurs relatively rarely, mainly by crystallization of products of chemical reactions. In such cases, the monomers are produced abruptly in very great amounts—thus creating the extremely high supersaturations that are required for nucleation of new crystal nuclei in the closest vicinity of the growing nanocrystals. Moreover, while OA produces ordinary single crystals, the agglomerated crystals are easily distinguishable as they have re-entrant portions on their surfaces.
Finally, it is worth noting that small crystals are more susceptible to random agglomeration [50].
In addition, the effect of more active step sources available on some crystal faces while missing on others [21,31] and the presence of impurities can alter the CSD established during the nucleation stage.
Finally, CSD alters drastically during the Ostwald ripening, OR, which is the natural completion of the crystallization process. OR occurs when the supersaturation is consumed.
However, obligatorily, in all cases, the change in CSD occurs in compliance with the law of conservation of matter, meaning that if some crystals remain smaller, other crystals become larger at the expense of the remaining dissolved substance.
6. CSD During Ostwald Ripening
Because the crystallizing system is striving to minimize its free energy associated with the interfaces between the two phases, crystals and solution, crystal ripening occurs spontaneously, i.e., proceeds without the need to be driven by an outside source of energy. According to the Gibbs–Thomson effect, the smaller crystals are surrounded by larger concentrations, while the larger crystals are surrounded by smaller concentrations. Therefore, the solute molecules diffuse from the areas surrounding small crystals to larger crystals. As a result, the smallest crystals dissolve, and the material released from them resumes the growth of larger crystals. Key moments in the course of the OR are consistently tracked below.
At the beginning of the OR, the dissolving small crystals are in a smaller number than the larger ones. This means that, surrounded by larger crystals, the smallest crystals dissolve relatively quickly and render enough material for the growth of the larger crystals. (Therefore, the more small crystals in the CSD, the faster the OR). That is why the simultaneous dissolution/growth of crystals keeps the solute concentration very close to the solubility, ce.
Important for the continuity of OR is the fact that crystals with the same surface S dissolve faster than they grow. This becomes evident from the comparison between Equation (1) and the Noyes–Whitney equation [51] for the rate of dissolution of a separate crystal in a diffusion-controlled process as follows:
where md is the mass of the crystal remaining undissolved at a given time t.
Although Equations (1) and (26) look the same, they differ substantially. While in Equation (1) the crystal growth rate is determined from counteracting factors, namely S and , by the same ce in Equation (26), both S and decrease in parallel. As a result, crystals with the same surface area dissolve faster than they grow. Therefore, there is enough material for the growth of the surviving crystals.
Importantly, with the dissolution of the smallest crystals, the thermodynamic driving force for OR decreases but does not disappear entirely; also, next-larger crystals are dissolved. That is why, after repeating many times this process of dissolution/growth brings about fewer and fewer, but larger and larger crystals. S Even more, all crystallizable solutes can be integrated into one crystal only—which means a minimum of the ratio surface-to-volume energy. Of course, if the crystallizing system is large and unstirred, due to the slow diffusion, several largest crystals can form in its remote parts.
To gain some insight into the intricate interaction between crystal dissolution and growth, and their combined effect on CSD, we examine the quantity of matter that is consumed by a crystal growing from an initial size Lo to the larger size L. This is conducted in the case in which the growing crystal preserves its shape. (For instance, growing a cubic crystal means filling the space between a smaller and a larger cube). Since the solute concentration is kept constant near to solubility ce, evidently, the corresponding mass m+ must be taken out of the solution:
Thus, the size of the enlarging crystal can be calculated from Equation (27) as follows:
Of course, the growth of the crystal in question is provoked by the increase in the concentration of solute in its vicinity, which is the result of the dissolution of closely spaced small crystals. Therefore, crystal growth continues until the matter released from these dissolved crystals is exhausted. In addition, if the dissolving small crystals are of the same size Ls, ns such crystals must be dissolved for the continuation of OR as follows:
So, decreasing constantly, the number of dissolving crystals becomes smaller than that of the growing crystals. However, the crystallizing system continues to strive to minimize its free energy associated with the interfaces between the crystals and the solution. That is why, finally, only one, the largest crystal, can collect all the solute, meaning the end of OR. (Incidentally, the author observed a large single lysozyme crystal, about 1.5 cm in size, grown under periodic days/nights’ temperature changes for several weeks. In addition, due to such temperature changes and an increase in solution concentration due to free evaporation of water, a single crystal of chrome alum grew to a similar size for 20 days. However, since no systematic research was conducted, these observations remained unpublished.)
So far, the idealized case of crystals that do not compete for building material has been considered. However, the dissolution of crystals grouped in “nests” (see Section 4) should be slowed down. The reason is that, due to the simultaneous dissolution of multiple small crystals clustered at one site, the solute concentration increases there to a greater extent than around a separate crystal. This means that the undersaturation, which is the driving force for dissolution, see Equation (26), decreases. On the contrary, fewer crystals located sufficiently far away from each other, whose diffusion fields do not overlap, will dissolve faster, and thus accelerate the OR. In addition, as already mentioned, depending on their case-specific distribution, crystals of the same size coarsen at different rates [39].
Because OR is a spontaneous process, it occurs unavoidably when supersaturation in the crystallizing system is exhausted. However, since the diffusive transfer of matter (by which OR takes place) is a slow process, isothermal OR proceeds slowly. That is why, although it removes small crystals, i.e., it can be potentially useful, isothermal OR is not used in practical processes. However, with substances having temperature-dependent solubility, OR is accelerated as the temperature changes. Therefore, it is possible to mitigate the effects of OR by keeping the crystallizing system at a constant temperature.
7. Discussion
Because CSD is of high interest from both scientific and practical points of view, intense intellectual effort has been dedicated to elucidating its occurrence and alteration during crystallization processes for a long time [37,38]. The central place in these studies is occupied by population balance modeling. Since this is a very fruitful approach, despite the challenges mentioned above, it continues to bring new, valuable results [52,53,54,55,56]. However, of course, these achievements do not detract from the alternative approach to determining the CSD by accounting for the SDG effect.
The purpose of this article is to reveal the impact of the factors that determine the CSD during batch crystallization in solutions. Moreover, it is pointed out that accurate knowledge of these factors can be very helpful when conducting a crystallization aimed at growing crystals with the desired CSD. To this aim, the physical chemistry of crystal nucleation and growth processes is examined. In doing so, it has been pointed out that crystal polydispersity is rooted in the process of nuclei formation, concluding that a quasi-instantaneous crystal nucleation brings about a decrease in crystal polydispersity.
In addition, the logical consequences of classical equations for the rates of diffusion-controlled and kinetically controlled growth of crystals show that the nuclei enlarge depending on their sizes, i.e., SDG is at play. Consequently, the initial CSD, arising from the non-simultaneous nucleation of crystals, widens. In addition, new equations describing the impact of crystal growth rates on CSD are derived. Importantly, applying the law of conservation of matter, it is substantiated that the CSD continues to expand during the subsequent growth stage. However, due to the uneven spatial distribution of crystals, although of the same size, some crystals can grow at different rates; this depends on whether they are outside the diffusion fields of other crystals or are clustered together in “nests”. Moreover, the observation that closely spaced crystals are smaller in size than the separately growing crystals is explained on this basis. Finally, the ultimate CSD established during Ostwald ripening is revisited.
The main advantage of the considerations presented in this paper is that they elucidate the physics behind the crystallization process in an easily comprehensible way. It is to be hoped that this study can contribute to an understanding of how it is possible to control a crystallization process to obtain the desired CSD. Since the growth of crystals leads to a constant expansion of the CSD, it is advisable to reduce the initial polydispersity, established due to the non-instantaneous nucleation of crystals. As already mentioned, this can be accomplished by shortening the duration of the crystal nucleation stage [21]. Moreover, small crystals are removed by simply dissolving them [27]. With substances having temperature-dependent solubility, this is accomplished very easily. To make CSD more homogeneous, the solubility, ce is increased for a short time (CSD is most homogeneous when the number of relatively small crystals becomes approximately equal to that of large crystals).
However, depending on the size l of the crystals to be eliminated, the appropriate dissolution time τdis must be chosen properly. For the estimation of the dissolution time, τdis, spherical crystals are more appropriate as a model because they are closer to reality compared with cubic crystals. The reason is that the vertices and edges of polyhedral crystals dissolve very quickly, and the cubic crystals are transformed into nearly spherical shapes. Consequently, within the framework of the Gibbs–Thomson effect, the crystal of radius R that stays in equilibrium with the solution obeys the following formula:
where c∞ = ce is the concentration with which the infinitely large crystal stands in equilibrium, and is the capillary length. Here, γ is the surface energy for the spherical crystal. Approximately, Equation (30) transforms into:
Since each crystal that stands in equilibrium with the solution can be considered as a critical nucleus:
So, replacing Equation (32) in Equation (31), we obtain the relationship between R and (cR − ce) in Equation (26):
However, since the rate of dissolution decreases constantly, its average value must be used (see the mathematical approach in Ref. [47]); thus, we obtain τdis:
Naturally, the larger the crystals are, the longer it takes them to dissolve. In addition, the higher the solubility ce, the sooner crystals (of a given size) dissolve. And although this effect is intuitively expected, provided that the capillary length can be determined, Equation (34) allows for accurate calculation of the time needed to remove small crystals (up to the upper limit of the Gibbs–Thomson effect).
However, strictly speaking, because of Tolman’s length correction [57], γ is no longer a constant at the end of the dissolution process. However, this does not significantly affect the calculated τdis value. Obviously, the effect of dissolving crystals clustered in nests (which increases the concentration of the solution locally) is more significant. Therefore, it is advisable to slightly extend the calculated dissolution time τdis (or slightly increase the solubility ce).
Finally, as a reminder, the effect of the size-dependent growth (SDG) becomes insignificant if seed crystals of strictly the same size are used and a sufficient supply of building material is ensured via solution flow (which, however, is beyond the scope of this consideration).
8. Conclusions
Looking at the growth of cubic crystals, we observed that, naturally, the larger the surface area of the crystal, the more substance is deposited on it. Therefore, since at the same mass non-cubic crystals have a larger surface area than cubic crystals, the former need greater diffusion mass transfer for their growth. That is why, although we are considering quiescent solutions, it is to be noted that stirring the solution, which leads to sufficient mass supply, can lead to a more homogeneous CSD.
Finaly, the author’s hope is that the approaches presented in this paper, despite some simplifying assumptions which lead to some restriction of their applicability, can contribute to a better understanding of the physical nature of the factors which determine CSD. (Or at least, provide new food for thought in this direction…).
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Abu Bakar, M.R.; Nagy, Z.K.; Saleemi, A.N.; Rielly, C.D. The impact of direct nucleation control on crystal size distribution in pharmaceutical crystallization processes. Cryst. Growth Des. 2009, 9, 1378–1384. [Google Scholar] [CrossRef]
- Shekunov, B.Y.; York, P. Crystallization processes in pharmaceutical technology and drug delivery design. J. Cryst. Growth 2000, 211, 122–136. [Google Scholar] [CrossRef]
- Nagy, Z.K. Model based robust control approach for batch crystallization product design. Comput. Chem. Eng. 2009, 33, 1685–1691. [Google Scholar] [CrossRef]
- Meng, W.; Sirota, E.; Feng, H.; McMullen, J.P.; Codan, L.; Cote, A.S. Effective control of crystal size via an integrated crystallization, wet milling, and annealing recirculation system. Org. Process Res. Dev. 2020, 24, 2639–2650. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, T.; Ma, Y.; Xue, F.; Gao, Z.; Hou, B.; Gong, J. Application of PAT-based feedback control approaches in pharmaceutical crystallization. Crystals 2021, 11, 221. [Google Scholar] [CrossRef]
- Cruz, P.; Alvarez, C.; Rocha, F.; Ferreira, A. Tailoring the crystal size distribution of an active pharmaceutical ingredient by continuous antisolvent crystallization in a planar oscillatory flow crystallizer. Chem. Eng. Res. Des. 2021, 175, 115–123. [Google Scholar] [CrossRef]
- Eren, A.; Szilagyi, B.; Quon, J.L.; Papageorgiou, C.D.; Nagy, Z.K. Experimental Investigation of an Integrated Crystallization and Wet-Milling System with Temperature Cycling to Control the Size and Aspect Ratio of Needle-Shaped Pharmaceutical Crystals. Cryst. Growth Des. 2021, 21, 3981–3993. [Google Scholar] [CrossRef]
- Acevedo, D.; Wu, W.L.; Yang, X.; Pavurala, N.; Mohammad, A.; O’Connor, T.F. Evaluation of focused beam reflectance measurement (FBRM) for monitoring and predicting the crystal size of carbamazepine in crystallization processes. CrystEngComm 2021, 23, 972–985. [Google Scholar] [CrossRef]
- He, J.; Zhou, J.; Dong, J.; Su, Z.; Huang, L. Revealing the effects of microwell sizes on the crystal growth kinetics of active pharmaceutical ingredients by deep learning. Chem. Eng. J. 2022, 428, 131986. [Google Scholar] [CrossRef]
- Pal, S.; Pankajakshan, A.; Besenhard, M.O.; Snead, N.; Almeida, J.; Abukhamees, S.; Craig, D.; Galvanin, F.; Gavriilidis, A.; Mazzei, L. Automated Continuous Crystallization Platform with Real-Time Particle Size Analysis via Laser Diffraction. Org. Process Res. Dev. 2024, 28, 2755–2764. [Google Scholar] [CrossRef]
- Trampuž, M.; Teslić, D.; Likozar, B. Process Analytical Technology-based (PAT) Model Simulations of a Combined Cooling, Seeded and Antisolvent Crystallization of an Active Pharmaceutical Ingredient (API). Powder Technol. 2020, 366, 873–890. [Google Scholar] [CrossRef]
- Nam, K.H. Comparative analysis of room temperature structures determined by macromolecular and serial crystallography. Crystals 2024, 14, 276. [Google Scholar] [CrossRef]
- Nanev, C.N.; Saridakis, E.; Chayen, N.E. Growing crystals for x-ray free-electron laser structural studies of biomolecules and their complexes. Int. J. Mol. Sci. 2023, 24, 16336. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Liu, T.; Song, B.; Fan, J.; Ni, X.; Findeisen, R. Design-of-experiments based Modeling & Optimization of LGA Cooling Crystallization via Continuous Oscillatory Baffled Crystallizer. Comput. Chem. Eng. 2025, 199, 109126. [Google Scholar] [CrossRef]
- Parambil, J.V.; Heng, J.Y.Y. Seeding in crystallisation. In Engineering Crystallography: From Molecule to Crystal to Functional form; Roberts, K., Docherty, R., Tamura, R., Eds.; NATO Science for Peace and Security Series A: Chemistry and Biology. Springer: Dordrecht, The Netherlands, 2017; pp. 235–245. [Google Scholar] [CrossRef]
- Bergfors, T. Seeds to crystals. J. Struct. Biol. 2003, 142, 66–76. [Google Scholar] [CrossRef]
- Liu, F.; Bagi, S.D.; Su, Q.; Chakrabarti, R.; Barral, R.; Gamekkanda, J.C.; Hu, C.; Mascia, S. Targeting particle size specification in pharmaceutical crystallization: A review on recent process design and development strategies and particle size measurements. Org. Process Res. Dev. 2022, 26, 3190–3203. [Google Scholar] [CrossRef]
- Trampuž, M.; Teslić, D.; Likozar, B. Crystal-size distribution-based dynamic process modelling, optimization, and scaling for seeded batch cooling crystallization of Active Pharmaceutical Ingredients (API). Chem. Eng. Res. Des. 2021, 165, 254–269. [Google Scholar] [CrossRef]
- Simone, E.; Saleemi, A.N.; Nagy, Z.K. Raman, UV, NIR, and Mid-IR Spectroscopy with Focused Beam Reflectance Measurement in Monitoring Polymorphic Transformations. Chem. Eng. Technol. 2014, 37, 1305–1313. [Google Scholar] [CrossRef]
- Turkevich, J.; Stevenson, P.C.; Hillier, J. A study of the nucleation and growth processes in the synthesis of colloidal gold. Discuss. Faraday Soc. 1951, 11, 55–75. [Google Scholar] [CrossRef]
- Nanev, C.N.; Petrov, K.P. Steering a crystallization process to reduce crystal polydispersity; case study of insulin crystallization. J. Cryst. Growth 2017, 480, 164–169. [Google Scholar] [CrossRef]
- Sánchez-García, Y.I.; Gutiérrez-Méndez, N.; Orozco-Mena, R.E.; Ramos-Sánchez, V.H.; Leal-Ramos, M.Y. Individual and combined effect of pH and whey proteins on lactose crystallization. Food Res. Int. 2019, 116, 455–461. [Google Scholar] [CrossRef]
- Nanev, C.N. Relationship between number and sizes of crystals growing in batch crystallization: Nuclei number density, nucleation kinetics and crystal polydispersity. J. Cryst. Growth 2020, 546, 125786. [Google Scholar] [CrossRef]
- Schorsch, S.; Vetter, T.; Mazzotti, M. Measuring multidimensional particle size distributions during crystallization. Chem. Eng. Sci. 2012, 77, 130–142. [Google Scholar] [CrossRef]
- Patchigolla, K.; Wilkinson, D.; Li, M. Measuring Size Distribution of Organic Crystals of Different Shapes Using Different Technologies. Part. Part. Syst. Charact. 2006, 23, 138–144. [Google Scholar] [CrossRef]
- Shukla, A.; Prakash, A.; Rohani, S. Online measurement of particle size distribution during crystallization using ultrasonic spectroscopy. Chem. Eng. Sci. 2010, 65, 3072–3079. [Google Scholar] [CrossRef]
- Nagy, Z.K.; Aamir, E.; Rielly, C.D. Internal fines removal using population balance model based control of crystal size distribution under dissolution, growth and nucleation mechanisms. Cryst. Growth Des. 2011, 11, 2205–2219. [Google Scholar] [CrossRef]
- Tavare, N.S. Growth Rate Dispersion. In Industrial Crystallization; The Springer Chemical Engineering Series; Springer: Boston, MA, USA, 1995. [Google Scholar] [CrossRef]
- Zumstein, R.C.; Rousseau, R.W. Growth Rate Dispersion by Initial Growth Rate Distributions and Growth Rate Fluctuations. AIChE J. 1987, 33, 121–129. [Google Scholar] [CrossRef]
- Srisanga, S.; Flood, A.E.; Galbraith, S.C.; Rugmai, S.; Soontaranon, S.; Ulrich, J. Crystal growth rate dispersion versus size-dependent crystal growth: Appropriate modeling for crystallization processes. Cryst. Growth Des. 2015, 15, 2330–2336. [Google Scholar] [CrossRef]
- Garside, J. Industrial crystallization from solution. Chem. Eng. Sci. 1985, 40, 3–26. [Google Scholar] [CrossRef]
- Ulrich, J. Growth rate dispersion—A review. Cryst. Res. Technol. 1989, 24, 249–257. [Google Scholar] [CrossRef]
- Singh, M.R.; Ramkrishna, D. Dispersions in crystal nucleation and growth rates: Implications of fluctuation in supersaturation. Chem. Eng. Sci. 2014, 107, 102–113. [Google Scholar] [CrossRef]
- White, E.T.; Wright, P.G. Magnitude of size dispersion effects in crystallization. Chem. Eng. Prog. Symp. Ser. 1971, 67, 81–87. [Google Scholar]
- Ostwald, W. Lehrbuch der Allgemeinen Chemie; Leipzig, W., Ed.; Engelmann: Berlin, Germany, 1896; Volume 2, Part 1. [Google Scholar]
- Ostwald, W. The formation and changes of solids. Z. Phys. Chem. 1897, 22, 289–330. [Google Scholar] [CrossRef]
- Lifshitz, I.M.; Slyozov, V.V. The kinetics of precipitation from supersaturated solid solutions. J. Phys. Chem. Solids 1961, 19, 35–50. [Google Scholar] [CrossRef]
- Wagner, C. Theorie der Alterung von Niederschlägen durch Umlösen (Ostwald-Reifung) (Theory of precipitate change by redissolution). Z. Für Elektrochem. Berichte Der Bunsenges. Für Phys. Chem. 1961, 65, 581–591. [Google Scholar] [CrossRef]
- Voorhees, P.W. Ostwald ripening of two-phase mixtures. Annu. Rev. Mater. Sci. 1992, 22, 197–215. [Google Scholar] [CrossRef]
- Chernov, A.A. Protein crystals and their growth. J. Struct. Biol. 2003, 142, 3–21. [Google Scholar] [CrossRef]
- Sazaki, G.; Matsui, T.; Tsukamoto, K.; Usami, N.; Ujihara, T.; Fujiwara, K.; Nakajima, K. In situ observation of elementary growth steps on the surface of protein crystals by laser confocal microscopy. J. Cryst. Growth 2004, 262, 536–542. [Google Scholar] [CrossRef]
- Sazaki, G.; Van Driessche, A.E.S.; Dai, G.; Okada, M.; Matsui, T.; Otalora, F.; Tsukamoto, K.; Nakajima, K. In Situ Observation Of Elementary Growth Processes Of Protein Crystals By Advanced Optical Microscopy. Protein Pept. Lett. 2012, 19, 743–760. [Google Scholar] [CrossRef]
- Kaischew, R.; Budevski, E. Surface processes in electrocrystallization. Contemp. Phys. 1967, 8, 489–516. [Google Scholar] [CrossRef]
- Onuma, K.; Tsukamoto, K.; Sunagawa, I. Role of buoyancy driven convection in aqueous solution growth; a case study of Ba(NO3)2 crystal. J. Cryst. Growth 1988, 89, 177–188. [Google Scholar] [CrossRef]
- Pusey, M.; Witherow, W.; Naumann, R. Preliminary investigations into solutal flow about growing tetragonal lysozyme crystals. J. Cryst. Growth 1988, 90, 105–111. [Google Scholar] [CrossRef]
- Qi, J.; Wakayama, N.I. Solute convection during the whole process of protein crystal growth. J. Cryst. Growth 2000, 219, 465–476. [Google Scholar] [CrossRef]
- Nanev, C.N. Thermodynamic and molecular-kinetic considerations of the initial growth of newly born crystals; crystal size distribution; dissolution of small crystals during Ostwald ripening due to temperature fluctuations. Prog. Cryst. Growth Charact. Mater. 2023, 69, 100604. [Google Scholar] [CrossRef]
- Liu, L.; Nakouzi, E.; Sushko, M.L.; Schenter, G.K.; Mundy, C.J.; Chun, J.; De Yoreo, J.J. Connecting energetics to dynamics in particle growth by oriented attachment using real-time observations. Nat. Commun. 2020, 11, 1045. [Google Scholar] [CrossRef]
- Lewis, A.; Seckler, M.; Kramer, H.; van Rosmalen, G. Agglomeration. In Industrial Crystallization Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2015; Chapter 6; pp. 130–150. [Google Scholar]
- Liu, L.X.; Marziano, I.; Bentham, A.C.; Litster, J.D.; White, E.T.; Howes, T. Effect of Particle Properties on the Flowability of Ibuprofen Powders. Int. J. Pharm. 2008, 362, 109–117. [Google Scholar] [CrossRef]
- Noyes, A.A.; Whitney, W.R. The rate of solution of solid substances in their own solutions. J. Am. Chem. Soc. 1897, 19, 930–934. [Google Scholar] [CrossRef]
- Szilágyi, B.; Nagy, Z.K. Population Balance Modeling and Optimization of an Integrated Batch Crystallizer–Wet Mill System for Crystal Size Distribution Control. Cryst. Growth Des. 2018, 18, 1415–1424. [Google Scholar] [CrossRef]
- Liu, Y.C.; Acevedo, D.; Yang, X.; Naimi, S.; Wu, W.L.; Pavurala, N.; Nagy, Z.K.; O’Connor, T.F. Population Balance Model Development Verification and Validation of Cooling Crystallization of Carbamazepine. Cryst. Growth Des. 2020, 20, 5235–5250. [Google Scholar] [CrossRef]
- Tsioufis, M.; Haloulos, I.E.; Alexopoulos, T.A.; Fytopoulos, A. Population Balance Modeling: A Framework for Optimal Design of Crystallization Processes. In Encyclopedia of Optimization; Pardalos, P.M., Prokopyev, O.A., Eds.; Springer: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]
- Barlow, D.A.; Gregus, J. Size evolution and composition of the intermediate phase during nonclassical protein crystal growth from solution. Cryst. Growth Des. 2020, 20, 4959–4966. [Google Scholar] [CrossRef]
- Barlow, D.A.; LaVoie-Ingram, E.; Bayat, J. Population-Balance Study of Protein Crystal Growth from Solution using a Hyperbolic Rate Law. J. Cryst. Growth 2022, 578, 126417. [Google Scholar] [CrossRef]
- Tolman, R.C. The effect of droplet size on surface tension. J. Chem. Phys. 1949, 17, 333–337. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).