Effect of Temperature on Adhesion Work of Model Organic Molecules on Modified Styrene–Divinylbenzene Copolymer Using Inverse Gas Chromatography
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Technique
2.2. Thermodynamic Methods
2.2.1. Surface Energy Parameters of Modified Copolymers
2.2.2. Surface Energy and Work of Adhesion
3. Results
3.1. London Dispersive Surface Energy of Modified Copolymers
3.2. Polar (Lewis Acid–Base) Surface Energy of Modified Copolymers
3.3. Polar Surface Energy of Organic Solvents
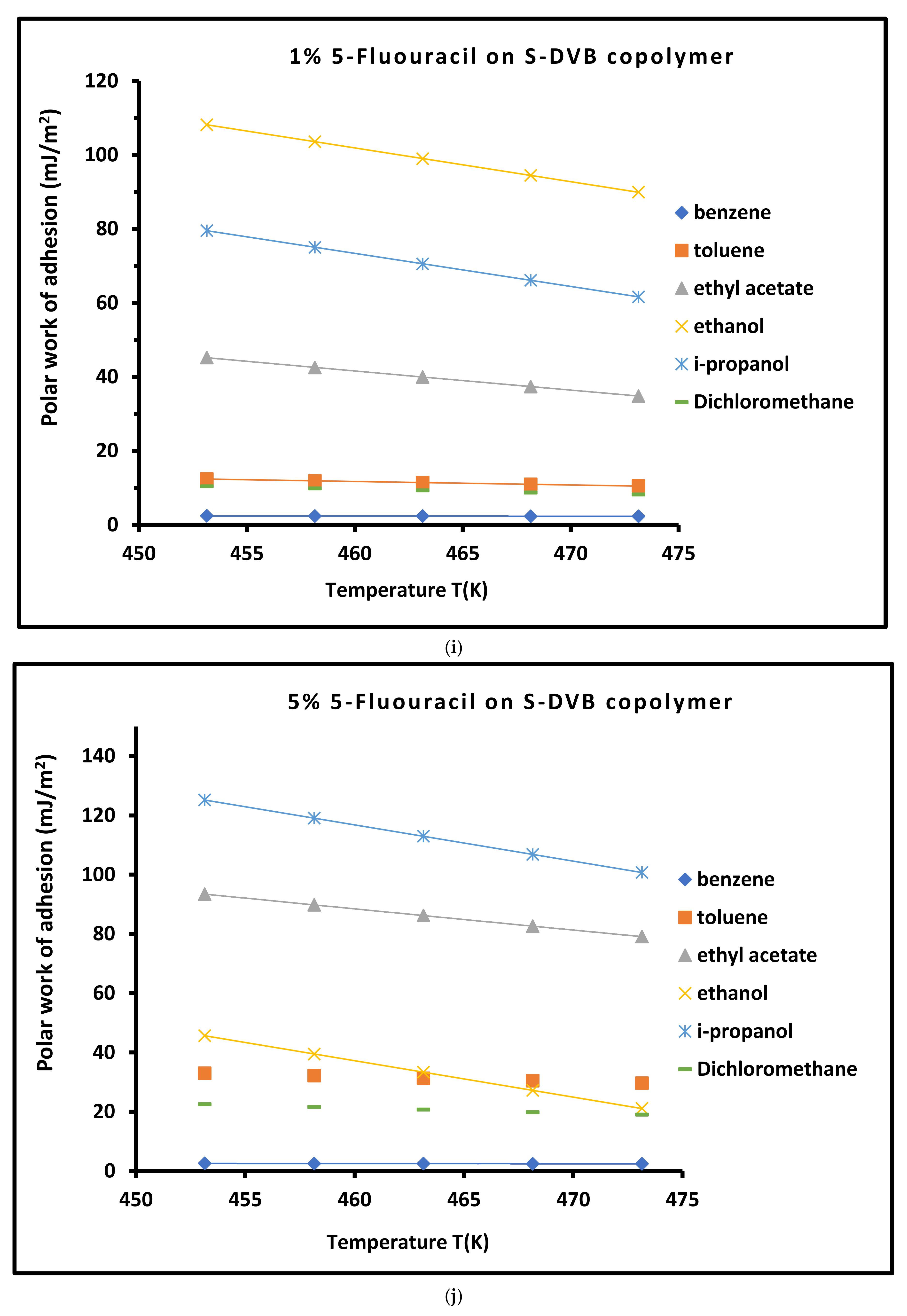
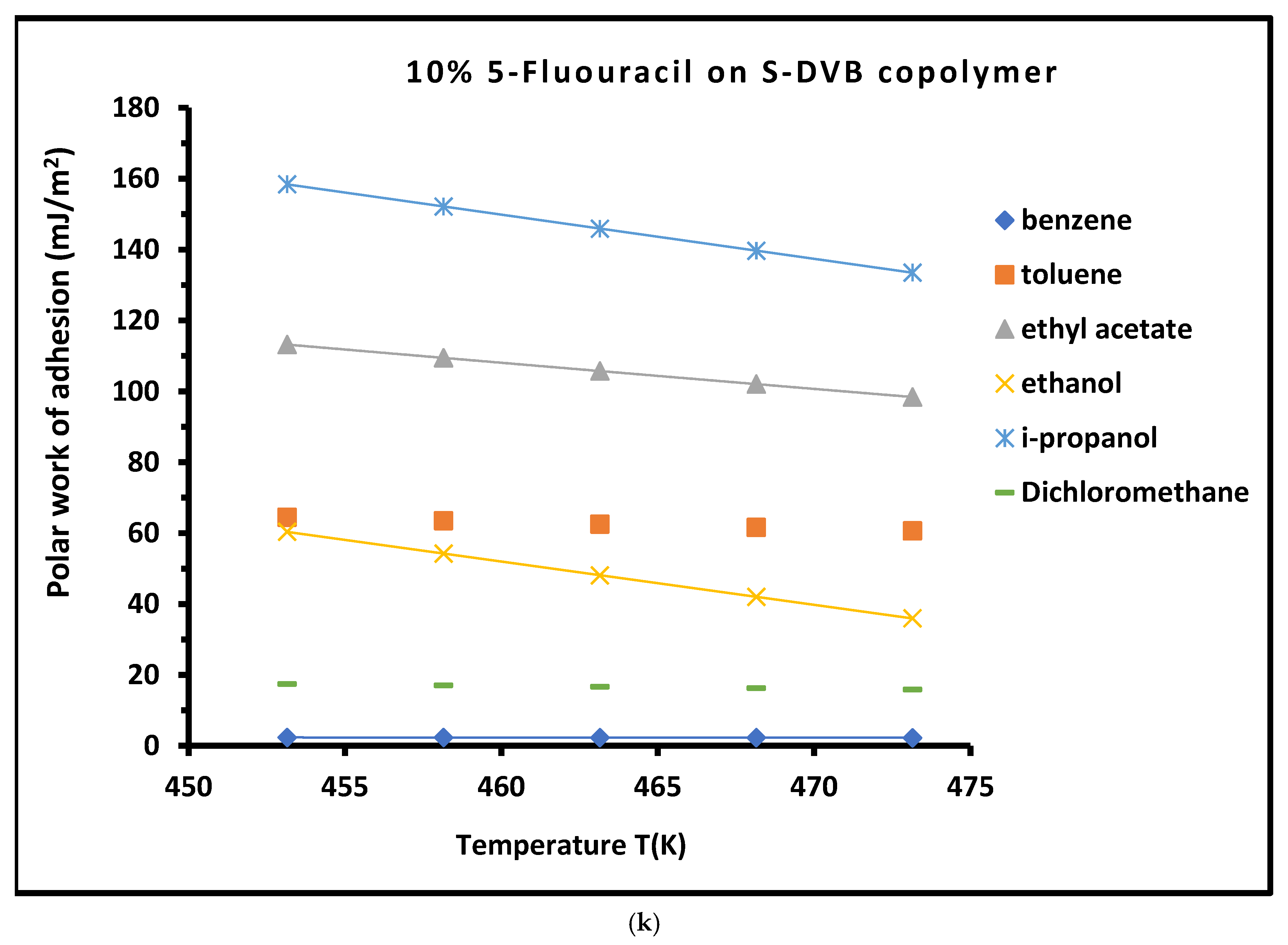
3.4. Work of Adhesion of Organic Solvents on Modified Copolymer
- Molecular features of 5-fluorouracil. 5-FU is a highly polar molecule characterized by multiple hydrogen bond donors and acceptors, particularly from its amide (C=O) and imine (N–H) groups. The presence of a fluorine atom with strong electronegativity contributed to dipole–dipole interactions and localized electron density. These features enable 5-FU to interact strongly with both the polymer backbone and the adsorbing solvents.
- Surface energy regulation by 5-FU. The incorporation of 5-FU onto the S-DVB surface increases the polar component of the surface energy through hydrogen bonding and dipole interactions. The overall surface free energy due to enhanced molecular heterogeneity also increases and leads to the increased density of functional groups. This results in stronger intermolecular forces with adsorbed molecules (e.g., polar solvents), thus increasing the work of adhesion. This was particularly observed with 5% 5-FU on S-DVB.
- Mechanism of adhesion energy enhancement. The presence of 5-FU’s amide and imide groups can lead to the formation of strong hydrogen bonds with polar solvents. These hydrogen bonding interactions are directional and cooperative, leading to stable adsorption layers. On the other hand, the C–F bond in 5-FU contributes to a high local dipole moment, enhancing van der Waals dipolar interactions with polarizable solvent molecules. The aromatic ring of 5-FU can engage in π–π stacking with aromatic solvents or even with the S-DVB backbone, stabilizing the surface architecture. The strong polar groups can induce dipoles in non-polar solvent molecules (Debye interactions), contributing further to adhesion.
- Comparison with HMU and melamine. The melamine modifier has multiple amine groups but lacks the C=O/N–H polarity balance and the electronegative substituent that 5-FU has. On the other hand, 5-HMU contains hydroxyl and carbonyl groups but is less electron-withdrawing and lacks the strong dipole moment contributed by fluorine. Thus, while all modifiers increase adhesion relative to unmodified S-DVB, 5-FU offers a unique combination of strong polar interactions and molecular alignment, leading to a higher adhesion energy.
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Su, Y.; Liu, Z.; Yang, D.; Li, W.; Ma, R.; Al Samarai, M.; Zhang, W.; Huang, H.; Fan, H.; Hu, D. High Energy Storage Under the Regulation of Polymer Phase Structure. Small 2025, 21, 2410354. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Fan, K.; Yang, J.; Liu, J.; Li, X.; Zhao, L.; He, X.; Liu, X.; Jia, S.; Li, Q. Surface modification engineering on polymer materials toward multilevel insulation properties and subsequent dielectric energy storage. Mater. Today 2024, 80, 758–823. [Google Scholar] [CrossRef]
- Zhao, H.; An, L.; Zhang, D.; Yang, X.; Yao, H.; Zhang, G.; Mu, H.; Baumeier, B. Unveiling Synergistic Interface Effects on Charge Trapping Regulation in Polymer Composite Dielectrics through Multiscale Modeling. J. Phys. Chem. B 2025, 129, 4216–4228. [Google Scholar] [CrossRef]
- Wang, T.Y.; Li, X.F.; Li, S.M.; Liu, B.X.; Liang, X.D.; Li, S.; Zhang, G.X.; Liu, J.B.; Dang, Z.M. Self-assembled wide bandgap nanocoatings enabled outstanding dielectric characteristics in the sandwich-like structure polymer composites. Nano Converg. 2022, 9, 55. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Yu, B.; Ma, S.; Ma, Y.; Zhang, G.; Hu, K.; Ma, Z.; Sheng, W.; Li, B.; Zhou, F. Engineering surface-grafted polymers for adhesion and friction control. Prog. Polym. Sci. 2024, 157, 101888. [Google Scholar] [CrossRef]
- Yi, Z.; Wang, X.; Li, W.; Qin, X.; Li, Y.; Wang, K.; Guo, Y.; Li, X.; Zhang, W. Interfacial friction at action: Interactions, regulation, and applications. Friction 2023, 11, 2153–2180. [Google Scholar] [CrossRef]
- Chen, F.; Qiu, F.; Liu, H.; Xiao, Y.; Li, X.; Gao, M.; Song, Y.; Liu, Y.; Liu, X.; Jiang, H.; et al. The importance of interface interactions in flexible sensing materials: Classification, effect, and application. Chem. Eng. J. 2025, 511, 162276. [Google Scholar] [CrossRef]
- Marić, I.; Yang, L.; Li, X.; Santiago, G.M.; Pappas, C.G.; Qiu, X.; Dijksman, J.A.; Mikhailov, K.; van Rijn, P.; Otto, S. Tailorable and Biocompatible Supramolecular-Based Hydrogels Featuring two Dynamic Covalent Chemistries. Angew. Chem. Int. Ed. Engl. 2023, 62, e202216475. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Q.; Wu, H.; Feng, X.; Jin, Z. Interfacial Engineering of Block Copolymer Nanostructures: Morphology and Solvent Stability. Langmuir 2023, 39, 9230–9238. [Google Scholar] [CrossRef]
- Al-Amiery, A.A.; Fayad, M.A.; Abdul Wahhab, H.A.; Al-Azzawi, W.K.; Mohammed, J.K.; Majdi, H.S. Interfacial Engineering for Advanced Functional Materials: Surfaces, Interfaces, and Applications. Results Eng. 2024, 22, 102125. [Google Scholar] [CrossRef]
- Wu, S. Polymer Interface and Adhesion; Marcel Dekker: New York, NY, USA, 1982. [Google Scholar] [CrossRef]
- Mittal, K.L. Polymer Surface Modification: Relevance to Adhesion, 1st ed.; CRC Press: Boca Raton, FL, USA, 2009; Volume 5. [Google Scholar] [CrossRef]
- Venkatakrishnan, A.; Kuppa, V.K. Polymer adsorption on rough surfaces. Curr. Opin. Chem. Eng. 2018, 19, 170–177. [Google Scholar] [CrossRef]
- Zdziennicka, A.; Krawczyk, J.; Jańczuk, B. Wettability and Adhesion Work Prediction in the Polymer–Aqueous Solution of Surface Active Agent Systems. Colloids Interfaces 2018, 2, 21. [Google Scholar] [CrossRef]
- Harkins, W.D. Surface energy and the orientation of molecules in surfaces as revealed by surface energy relations. Z Phys. Chem. 1928, 139, 647–691. [Google Scholar] [CrossRef]
- Young, T. An essay on the cohesion of fluids. Philos. Trans. R. Soc. Lond. 1805, 95, 65–87. [Google Scholar]
- Dupré, A. Théorie Mécanique de la Chaleur; Gauthier-Villars: Paris, France, 1869. [Google Scholar]
- Fowkes, F.M. Attractive forces at interfaces. Ind. Eng. Chem. 1964, 56, 40–52. [Google Scholar] [CrossRef]
- Owens, D.K.; Wendt, R.C. Estimation of the surface free energy of polymers. J. Appl. Polym. Sci. 1969, 13, 1741–1747. [Google Scholar] [CrossRef]
- van Oss, C.J.; Chaudhury, M.K.; Good, R.J. Interfacial Lifshitz–van der Waals and polar interactions in macroscopic systems. Chem. Rev. 1988, 88, 927–941. [Google Scholar] [CrossRef]
- Van Oss, C.J.; Good, R.J.; Chaudhury, M.K. Additive and nonadditive surface tension components and the interpretation of contact angles. Langmuir 1988, 4, 884–891. [Google Scholar] [CrossRef]
- Voelkel, A. IGC as a tool for surface characterization of polymers. J. Chromatogr. A 2004, 1037, 467–478. [Google Scholar]
- Hansen, C.M. Hansen Solubility Parameters: A User’s Handbook, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Packham, D.E. Surface energy, surface topography and adhesion. Int. J. Adhes. Adhes. 2003, 23, 437–448. [Google Scholar] [CrossRef]
- Nikkhah, S.J.; Moghbeli, M.R.; Hashemianzadeh, S.M. Investigation of the interface between polyethylene and functionalized graphene: A computer simulation study. Curr. Appl. Phys. 2015, 15, 1188–1199. [Google Scholar] [CrossRef]
- Hamieh, T. Study of the temperature effect on the surface area of model organic molecules, the dispersive surface energy and the surface properties of solids by inverse gas chromatography. J. Chromatogr. A 2020, 1627, 461372. [Google Scholar] [CrossRef] [PubMed]
- Hamieh, T. New methodology to study the dispersive component of the surface energy and acid–base properties of silica particles by inverse gas chromatography at infinite dilution. J. Chromatogr. Sci. 2022, 60, 126–142. [Google Scholar] [CrossRef]
- Hamieh, T. Inverse Gas Chromatography to Characterize the Surface Properties of Solid Materials. Chem. Mater. 2024, 36, 2231–2244. [Google Scholar] [CrossRef]
- Hamieh, T. Some Irregularities in the Evaluation of Surface Parameters of Solid Materials by Inverse Gas Chromatography. Langmuir 2023, 39, 17059–17070. [Google Scholar] [CrossRef]
- Hamieh, T. Serious irregularities and errors in the determination of the surface free energy and acido-basicity of MXene materials. Carbon 2025, 238, 120209. [Google Scholar] [CrossRef]
- Hamieh, T. New Physicochemical Methodology for the Determination of the Surface Thermodynamic Properties of Solid Particles. AppliedChem 2023, 3, 229–255. [Google Scholar] [CrossRef]
- Hamieh, T. New Progress on London Dispersive Energy, Polar Surface Interactions, and Lewis’s Acid–Base Properties of Solid Surfaces. Molecules 2024, 29, 949. [Google Scholar] [CrossRef]
- Hamieh, T. London Dispersive and Lewis Acid-Base Surface Energy of 2D Single-Crystalline and Polycrystalline Covalent Organic Frameworks. Crystals 2024, 14, 148. [Google Scholar] [CrossRef]
- Conder, J.R.; Locke, D.C.; Purnell, J.H. Concurrent solution and adsorption phenomena in chromatography. I. J. Phys. Chem. 1969, 73, 700–708. [Google Scholar] [CrossRef]
- Conder, J.R.; Purnell, J.H. Gas chromatography at finite concentrations. Part 2.—A generalized retention theory. Trans. Faraday Soc. 1968, 64, 3100–3111. [Google Scholar] [CrossRef]
- Conder, J.R.; Purnell, J.H. Gas chromatography at finite concentrations. Part 1.—Effect of gas imperfection on calculation of the activity coefficient in solution from experimental data. Trans. Faraday Soc. 1968, 64, 1505–1512. [Google Scholar] [CrossRef]
- Sawyer, D.T.; Brookman, D.J. Thermodynamically based gas chromatographic retention index for organic molecules using salt-modified aluminas and porous silica beads. Anal. Chem. 1968, 40, 1847–1850. [Google Scholar] [CrossRef]
- Saint-Flour, C.; Papirer, E. Gas-solid chromatography. A method of measuring surface free energy characteristics of short carbon fibers. 1. Through adsorption isotherms. Ind. Eng. Chem. Prod. Res. Dev. 1982, 21, 337–341. [Google Scholar] [CrossRef]
- Saint-Flour, C.; Papirer, E. Gas-solid chromatography: Method of measuring surface free energy characteristics of short fibers. 2. Through retention volumes measured near zero surface coverage. Ind. Eng. Chem. Prod. Res. Dev. 1982, 21, 666–669. [Google Scholar] [CrossRef]
- Donnet, J.-B.; Park, S.; Balard, H. Evaluation of specific interactions of solid surfaces by inverse gas chromatography. Chromatographia 1991, 31, 434–440. [Google Scholar] [CrossRef]
- Brendlé, E.; Papirer, E. A new topological index for molecular probes used in inverse gas chromatography for the surface nanorugosity evaluation, 2. Application for the Evaluation of the Solid Surface Specific Interaction Potential. J. Colloid Interface Sci. 1997, 194, 217–224. [Google Scholar] [CrossRef]
- Brendlé, E.; Papirer, E. A new topological index for molecular probes used in inverse gas chromatography for the surface nanorugosity evaluation, 1. Method of Evaluation. J. Colloid Interface Sci. 1997, 194, 207–216. [Google Scholar] [CrossRef]
- Liu, Y.; Gu, Y.; Wang, S.; Li, M. Optimization for testing conditions of inverse gas chromatography and surface energies of various carbon fiber bundles. Carbon Lett. 2023, 33, 909–920. [Google Scholar] [CrossRef]
- Pal, A.; Kondor, A.; Mitra, S.; Thua, K.; Harish, S.; Saha, B.B. On surface energy and acid–base properties of highly porous parent and surface treated activated carbons using inverse gas chromatography. J. Ind. Eng. Chem. 2019, 69, 432–443. [Google Scholar] [CrossRef]
- Hamieh, T.; Gus’kov, V.Y. Surface Thermodynamic Properties of Styrene–Divinylbenzene Copolymer Modified by Supramolecular Structure of Melamine Using Inverse Gas Chromatography. Chemistry 2024, 6, 830–851. [Google Scholar] [CrossRef]
- Hamieh, T.; Gus’kov, V.Y. London Dispersive and Polar Surface Properties of Styrene–Divinylbenzene Copolymer Modified by 5-Hydroxy-6-Methyluracil Using Inverse Gas Chromatography. Crystals 2025, 15, 438. [Google Scholar] [CrossRef]
- Hamieh, T.; Gus’kov, V.Y. Determination of Surface Physicochemical Parameters of Styrene–Divinylbenzene Copolymer Modified by 5-Fluouracil Using Inverse Gas Chromatography. Preprints 2025, 2025041864. [Google Scholar] [CrossRef]
- Young, T. Miscellaneous Works of the Late Thomas Young; John Murray: London, UK, 1855. [Google Scholar]
- Dorris, G.M.; Gray, D.G. Adsorption of n-alkanes at zero surface coverage on cellulose paper and wood fibers. J. Colloid Interface Sci. 1980, 77, 353–362. [Google Scholar] [CrossRef]
- Guo, B.Z.; Kim, S.B.; Lee, S.Y.; Park, S.J. Determination of surface free energy and acido-basicity of MXene materials measured by inverse gas chromatography at infinite dilution. Carbon 2025, 231, 119732. [Google Scholar] [CrossRef]
- Isik, B.; Bilgi, M. Investigation of physicochemical characteristics of Aspergillus Niger biomass and examination of its ability to separate butyl acetate isomers. Appl. Biochem. Biotechnol. 2024, 196, 6817–6835. [Google Scholar] [CrossRef]
- Isik, B.; Cakar, F.; Cankurtaran, O. A comparative study of surface properties of (nettle) leaves. roots, and seeds and examination of their ability to separate xylene isomers. Phytochem. Anal. 2022, 33, 886–894. [Google Scholar] [CrossRef] [PubMed]
- Arsalan, N.; Palayangoda, S.S.; Burnett, D.J.; Buiting, J.J.; Nguyen, Q.P. Surface energy characterization of carbonate rocks. Colloids Surf. A Physicochem. Eng. Asp. 2013, 436, 139–147. [Google Scholar] [CrossRef]
- Mohammadi-Jam, S.; Burnett, D.J.; Waters, K.E. Surface energy of minerals—Applications to flotation. Miner. Eng. 2014, 66, 112–118. [Google Scholar] [CrossRef]
- Grimsey, I.M.; Feeley, J.C.; York, P. Analysis of the surface energy of pharmaceutical powders by inverse gas chromatography. J. Pharm. Sci. 2002, 91, 571–583. [Google Scholar] [CrossRef]
- Das, S.C.; Stewart, P.J. Characterising surface energy of pharmaceutical powders by inverse gas chromatography at finite dilution. J. Pharm. Pharmacol. 2012, 64, 1337–1348. [Google Scholar] [CrossRef] [PubMed]
- Bilgiç, C.; Karakehya, N. Determination of Surface Energy of Natural Zeolite by Inverse Gas Chromatography. IOP Conf. Ser. Earth Environ. Sci. 2016, 44, 052048. [Google Scholar] [CrossRef]
- Schultz, J.; Lavielle, L.; Martin, C. The role of the interface in carbon fibre-epoxy composites. J. Adhes. 1987, 23, 45–60. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, W.-N.; Wang, B.; Tang, J.; Wang, Q. Surface properties of ionic liquids: A study of different calculation methods in inverse gas chromatography. J. Mol. Liq. 2020, 299, 112202. [Google Scholar] [CrossRef]
- Voelkel, A.; Strzemiecka, B.; Milczewska, K.; Adamska, K. Inverse gas chromatography fruitful and credible tool for materials characterization. J. Chromatogr. Open 2024, 6, 100177. [Google Scholar] [CrossRef]
- Yusuf, K.; Natraj, A.; Li, K.; Ateia, M.; Al Othman, Z.A.; Dichtel, W.R. Inverse Gas Chromatography Demonstrates the Crystallinity Dependent Physicochemical Properties of Two-Dimensional Covalent Organic Framework Stationary Phases. Chem. Mater. 2023, 35, 1691–1701. [Google Scholar] [CrossRef]
- Rückriem, M.; Inayat, A.; Enke, D.; Gläser, R.; Einicke, W.-D.; Rockmann, R. Inverse gas chromatography for determining the dispersive surface energy of porous silica. Colloids Surf. A Physicochem. Eng. Asp. 2010, 357, 21–26. [Google Scholar] [CrossRef]
- Peng, Y.; Gardner, D.J.; Han, Y.; Cai, Z.; Tshabalala, M.A. Influence of drying method on the surface energy of cellulose nanofibrils determined by inverse gas chromatography. J. Colloid Interface Sci. 2013, 405, 85–95. [Google Scholar] [CrossRef]
- Bauer, F.; Meyer, R.; Czihal, S.; Bertmer, M.; Decker, U.; Naumov, S.; Uhlig, H.; Steinhart, M.; Enke, D. Functionalization of porous siliceous materials, Part 2: Surface characterization by inverse gas chromatography. J. Chromatogr. A 2019, 1603, 297–310. [Google Scholar] [CrossRef]
- Przybyszewska, M.; Krzywania, A.; Zaborski, M.; Szynkowska, M.I. Surface properties of zinc oxide nanoparticles studied by inverse gas chromatography. J. Chromatogr. A 2009, 1216, 5284–5291. [Google Scholar] [CrossRef]


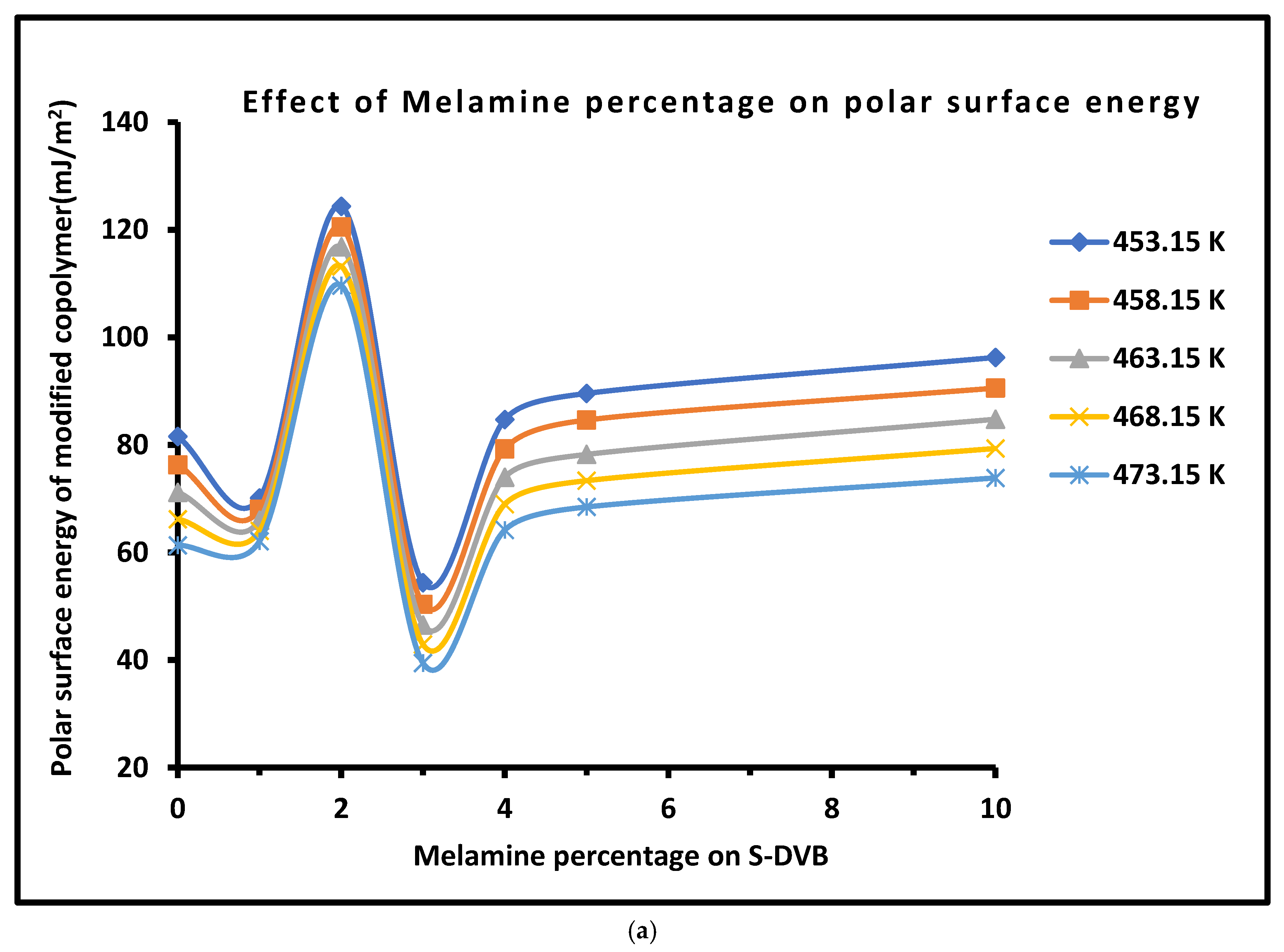

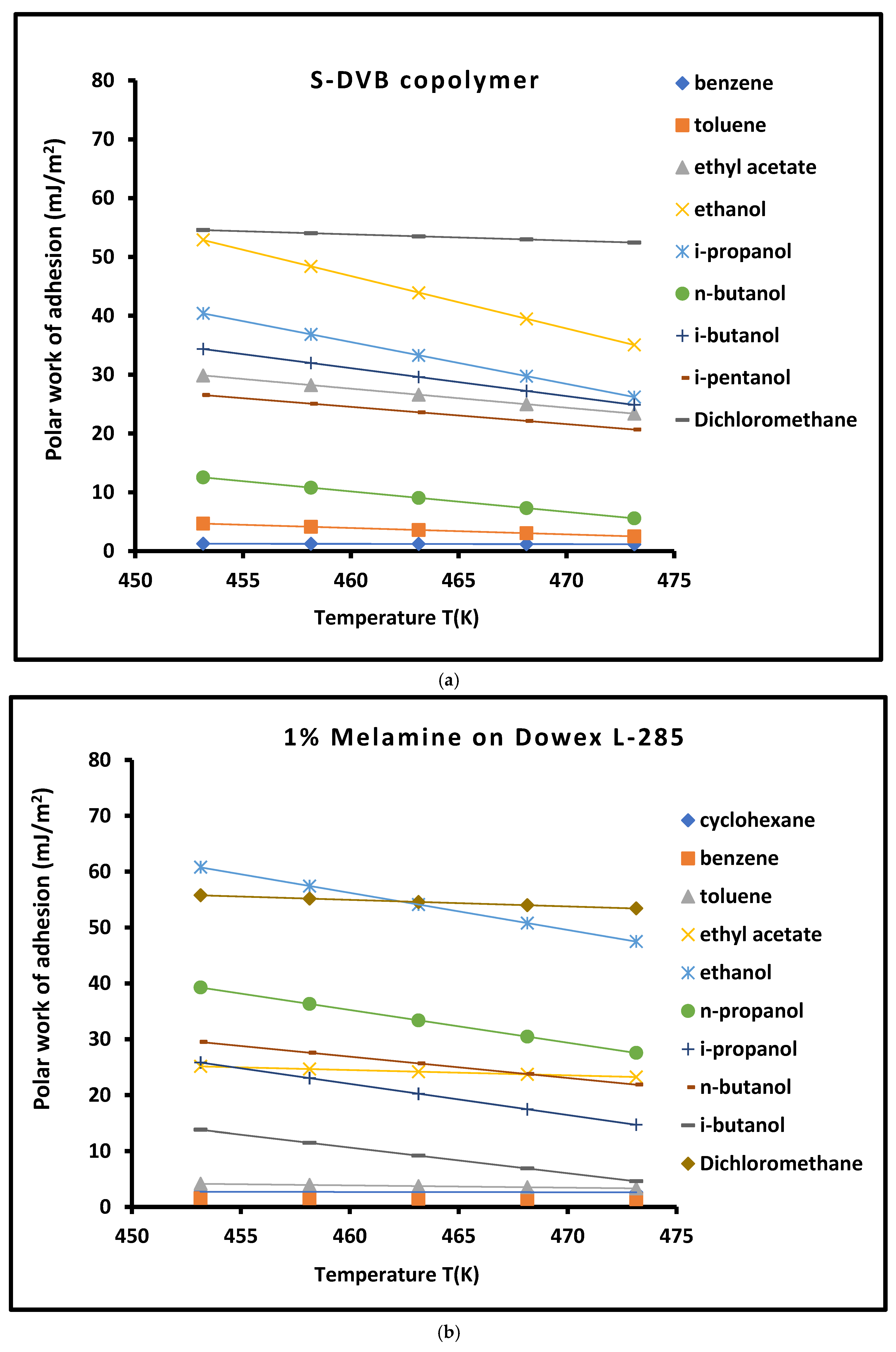
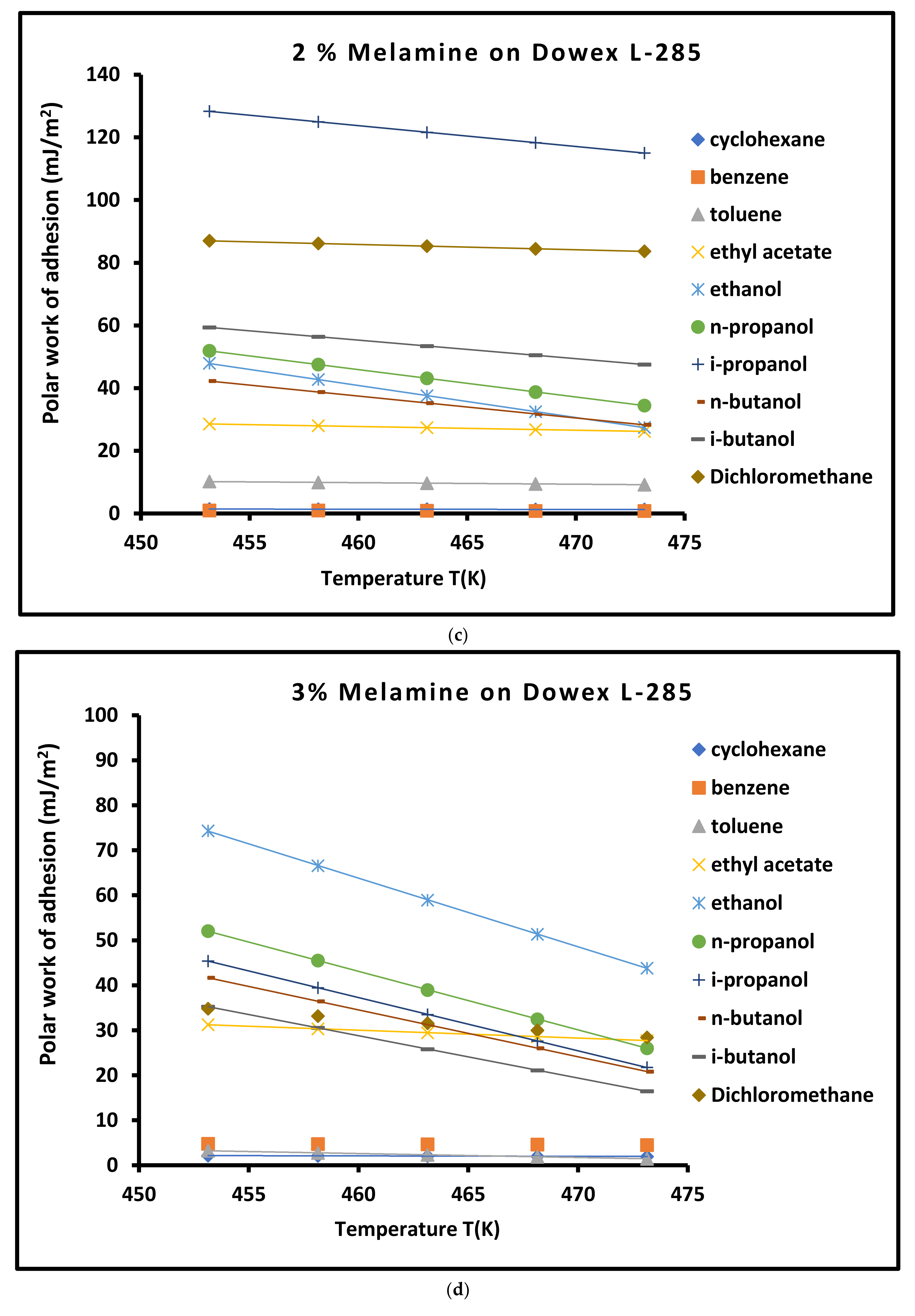
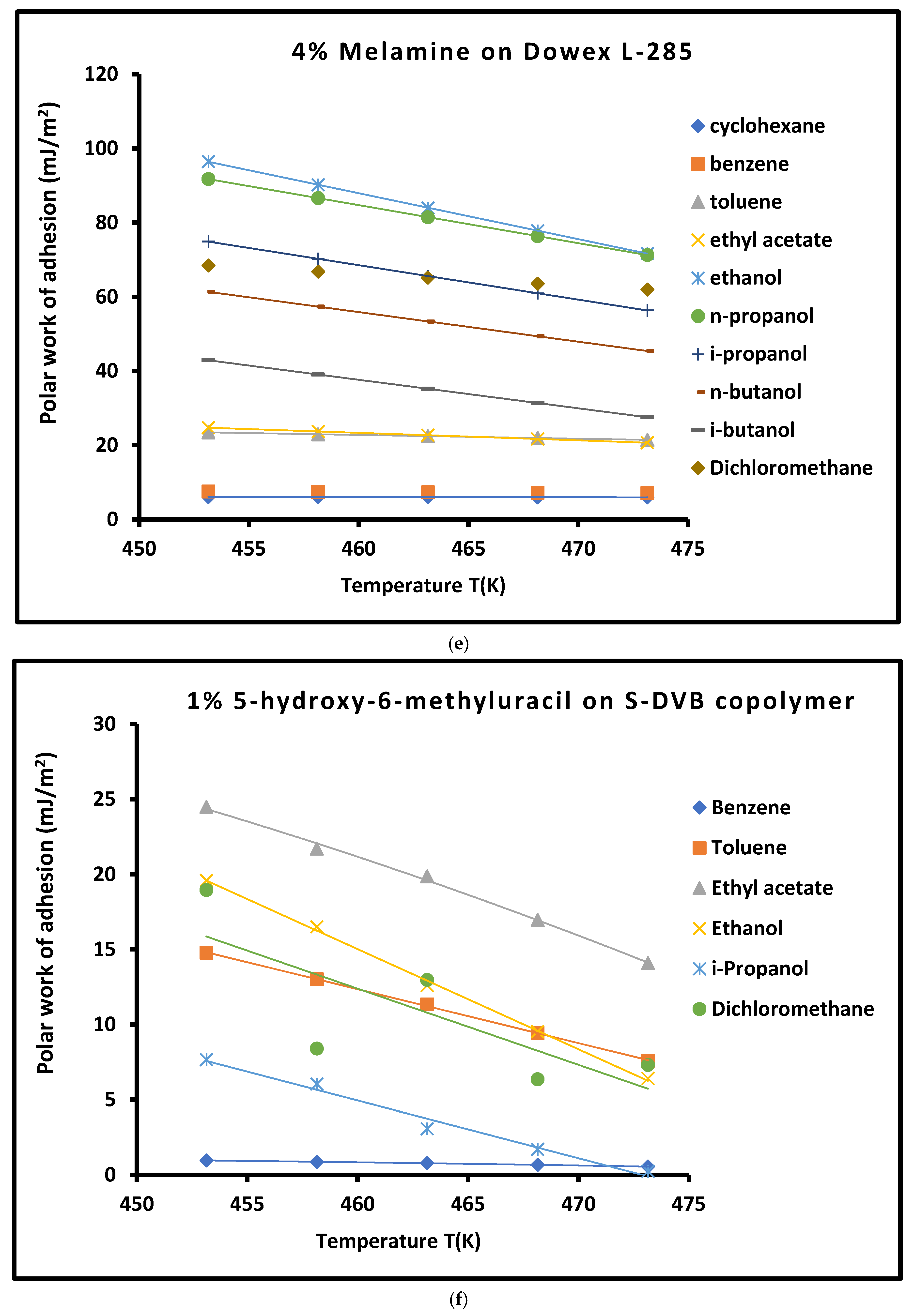
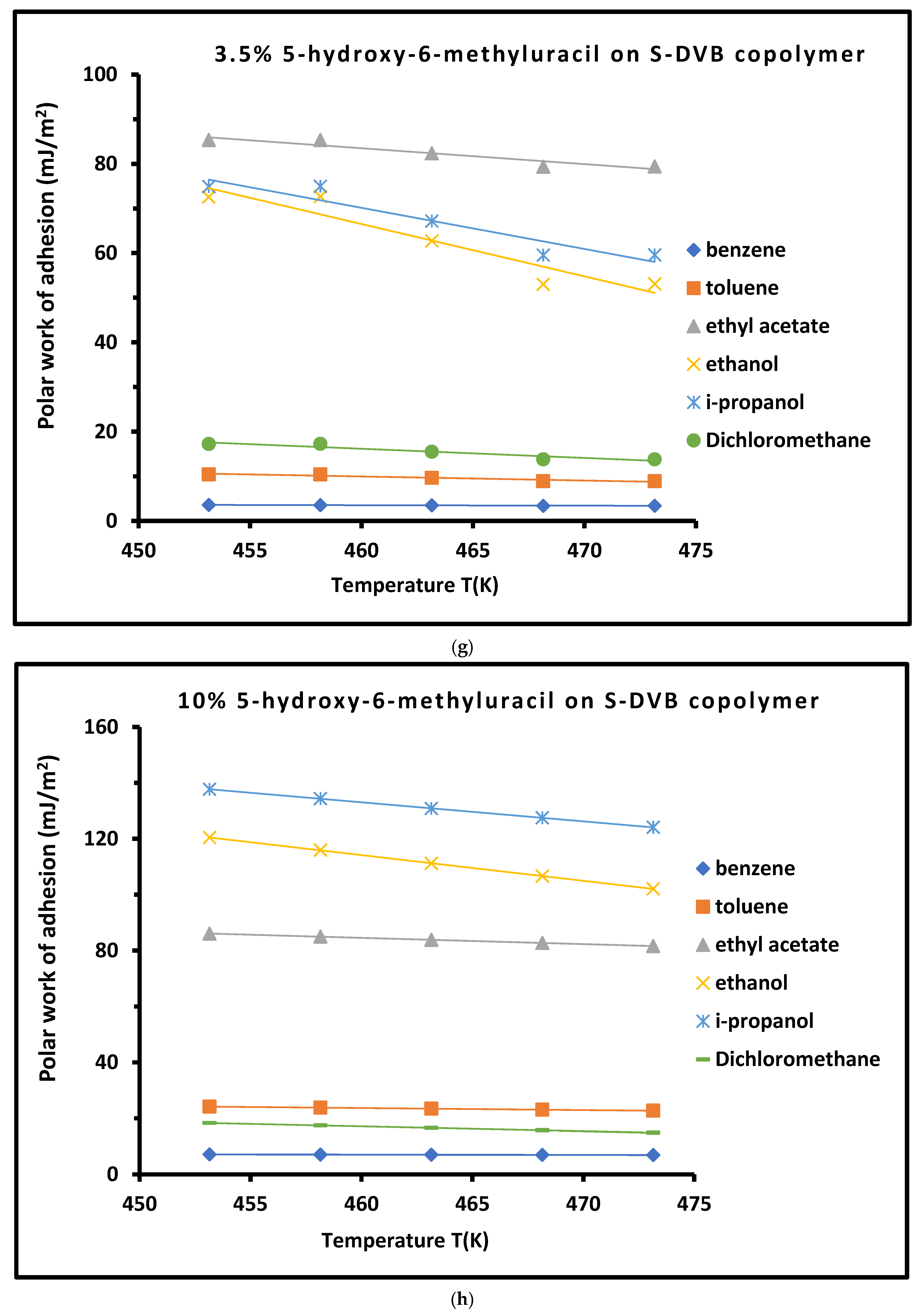
| Copolymer | (mJ/m2) | (mJ m−2 K−1) | (mJ/m2) | (mJ/m2) | (K) | |
|---|---|---|---|---|---|---|
| S-DVB | = −1.105 T + 587.13 | 0.9980 | 0.835 | 587.13 | 257.7 | 531.4 |
| 1% Melamine/S-DVB | = −0.907 T + 496.21 | 0.9972 | 0.907 | 496.21 | 225.79 | 547.1 |
| 2% Melamine/S-DVB | = −0.656 T + 341.59 | 0.9590 | 0.656 | 341.59 | 146.12 | 521.0 |
| 3% Melamine/S-DVB | = −0.827 T + 439.96 | 0.9608 | 0.827 | 439.96 | 193.51 | 532.3 |
| 4% Melamine/S-DVB | = −0.876 T + 473.64 | 0.975 | 0.876 | 473.64 | 212.40 | 540.6 |
| 5% Melamine/S-DVB | = −0.935 T + 501.23 | 0.9825 | 0.935 | 501.23 | 222.46 | 536.07 |
| 10% Melamine/S-DVB | = −1.220 T + 584.42 | 0.9915 | 1.220 | 584.42 | 220.68 | 479.03 |
| Copolymer | Equation of (mJ/m2) | (mJ m−2 K−1) | (mJ/m2) | (mJ/m2) | (K) | |
| 1% HMU/S-DVB | = −0.874 T + 444.68 | 0.9837 | 0.874 | 444.68 | 184.16 | 508.9 |
| 3.5% HMU/S-DVB | = −1.096 T + 544.23 | 0.9886 | 1.096 | 544.23 | 217.52 | 496.7 |
| 5% HMU/S-DVB | = −1.120 T + 552.77 | 0.9973 | 1.198 | 552.77 | 218.84 | 493.6 |
| 10% HMU/S-DVB | = −1.198 T + 582.13 | 0.9973 | 1.198 | 582.13 | 224.95 | 485.9 |
| Copolymer | Equation of (mJ/m2) | (mJ m−2 K−1) | (mJ/m2) | (mJ/m2) | (K) | |
| 1% 5-FU/S-DVB | = −0.497 T + 290.95 | 0.8900 | 0.497 | 290.95 | 142.77 | 585.4 |
| 5% 5-FU/S-DVB | = −0.780 T + 424.67 | 0.9800 | 0.780 | 424.67 | 192.11 | 544.4 |
| 10% 5-FU/S-DVB | = −0.913 T + 490.08 | 0.9900 | 0.913 | 490.08 | 217.87 | 536.8 |
| Temperature T (K) | 453.15 | 458.15 | 463.15 | 468.15 | 473.15 | R2 | |
|---|---|---|---|---|---|---|---|
| S-DVB copolymer | 81.54 | 76.29 | 71.17 | 66.19 | 61.33 | = −1.01 T + 539.27 | 0.9998 |
| 1% Melamine/S-DVB | 70.11 | 68.03 | 65.99 | 64 | 62.07 | = −0.40 T + 252.32 | 0.9998 |
| 2% Melamine/S-DVB | 124.35 | 120.53 | 116.81 | 113.18 | 109.63 | = −0.74 T + 457.69 | 0.9998 |
| 3% Melamine/S-DVB | 54.36 | 50.34 | 46.51 | 42.87 | 39.41 | = −0.75 T + 392.86 | 0.9991 |
| 4% Melamine/S-DVB | 84.71 | 79.24 | 73.99 | 68.97 | 64.16 | = −1.03 T + 550.05 | 0.9994 |
| Temperature T(K) | 453.15 | 458.15 | 463.15 | 468.15 | 473.15 | Equation | R2 |
| 1% 5-HMU/S-DVB | 36.89 | 35.08 | 33.04 | 31.34 | 29.61 | = −0.37 T + 202.7 | 0.9990 |
| 3.5% 5-HMU/S-DVB | 73.56 | 69.12 | 63.85 | 59.40 | 54.90 | = −0.94 T + 499.9 | 0.9992 |
| 10% 5-HMU/S-DVB | 78.82 | 74.47 | 69.42 | 65.06 | 60.66 | = −0.92 T + 493.28 | 0.9994 |
| Temperature T(K) | 453.15 | 458.15 | 463.15 | 468.15 | 473.15 | Equation | R2 |
| 1% 5-FU/S-DVB | 23.61 | 21.01 | 18.60 | 16.35 | 14.28 | = −0.47 T + 234.78 | 0.9980 |
| 5% 5-FU/S-DVB | 105.08 | 96.96 | 89.26 | 81.96 | 75.06 | = −1.50 T + 784.76 | 0.9990 |
| 10% 5-FU/S-DVB | 98.84 | 93.37 | 88.12 | 83.08 | 78.23 | = −1.03 T + 565.47 | 0.9994 |
| S-DVB | ||
|---|---|---|
| Solvents | R2 | |
| cyclohexane | = 4 × 10−4 T − 0.116 | 0.9909 |
| benzene | = 3 × 10−5 T − 0.010 | 0.9911 |
| toluene | = −0.0022 T + 1.048 | 0.9984 |
| ethyl acetate | = −0.0251 T + 14.11 | 0.9999 |
| ethanol | = −0.180 T + 90.12 | 0.9999 |
| n-propanol | = −0.063 T + 30.01 | 0.9905 |
| i-propanol | = −0.111 T + 55.49 | 0.9999 |
| n-butanol | = −0.019 T + 9.124 | 0.9958 |
| i-butanol | = −0.054 T + 28.21 | 0.9999 |
| n-pentanol | = −0.0032 T + 1.766 | 0.9995 |
| i-pentanol | = −0.020 T + 11.360 | 0.9994 |
| Pyridine | = −0.065 T + 33.38 | 1 |
| Dichloromethane | = 0.094 T − 33.51 | 0.9906 |
| 1% melamine/S-DVB | ||
| Solvents | Equation | R2 |
| cyclohexane | = 6 × 10−5 T − 0.003 | 0.9999 |
| benzene | = −6 × 10−5 T + 0.035 | 1 |
| toluene | = −8 × 10−4 T + 0.437 | 0.9999 |
| ethyl acetate | = −0.004 T + 4.024 | 0.9999 |
| ethanol | = −0.205 T + 105.85 | 0.9998 |
| n-propanol | = −0.122 T + 60.84 | 0.9992 |
| i-propanol | = −0.076 T + 36.61 | 0.9966 |
| n-butanol | = −0.059 T + 29.78 | 0.9997 |
| i-butanol | = −0.030 T + 14.080 | 0.9846 |
| Dichloromethane | = 0.020 T + 2.037 | 0.9995 |
| 2% melamine/S-DVB | ||
| Solvents | Equation | R2 |
| cyclohexane | = −2 × 10−5 T + 0.013 | 0.9999 |
| benzene | = −3 × 10−5 T + 0.016 | 0.9999 |
| toluene | = −8 × 10−4 T + 0.561 | 0.9999 |
| ethyl acetate | = −0.004 T + 3.351 | 0.9999 |
| ethanol | = −0.145 T + 70.16 | 0.9966 |
| n-propanol | = −0.136 T + 66.86 | 0.9987 |
| i-propanol | = −0.147 T + 99.70 | 0.9999 |
| n-butanol | = −0.088 T + 43.58 | 0.9989 |
| i-butanol | = −0.097 T + 50.92 | 1 |
| Dichloromethane | = 0.037 T − 1.415 | 0.9995 |
| 3% melamine/S-DVB | ||
| Solvents | Equation | R2 |
| cyclohexane | = 2 × 10−4 T − 0.050 | 0.9977 |
| benzene | = 0.0012 T − 0.452 | 0.9969 |
| toluene | = −0.0017 T + 0.825 | 0.9978 |
| ethyl acetate | = 0.020 T − 4.373 | 0.9979 |
| ethanol | = −0.662 T + 325.2 | 0.9999 |
| n-propanol | = −0.409 T + 197.56 | 0.999 |
| i-propanol | = −0.325 T + 156.67 | 0.9985 |
| n-butanol | = −0.263 T + 126.86 | 0.9991 |
| i-butanol | = −0.201 T + 96.57 | 0.9984 |
| Dichloromethane | = −0.022 T + 15.682 | 0.9996 |
| 4% melamine/S-DVB | ||
| Solvents | Equation | R2 |
| cyclohexane | = 0.002 T − 0.587 | 0.9971 |
| benzene | = 0.002 T − 0.497 | 0.9978 |
| toluene | = 0.008 T − 2.192 | 0.9983 |
| ethyl acetate | = −0.007 T + 4.91 | 0.9992 |
| ethanol | = −0.371 T + 195.72 | 0.9998 |
| n-propanol | = −0.253 T + 139.54 | 0.9995 |
| i-propanol | = −0.210 T + 111.55 | 0.9997 |
| n-butanol | = −0.154 T + 80.89 | 0.9997 |
| i-butanol | = −0.124 T + 61.62 | 1 |
| Dichloromethane | = 0.057 T − 11.874 | 0.9973 |
| 1% 5-HMU/S-DVB | ||
| Solvents | Equation | R2 |
| benzene | = 3 × 10−5 T + 0.008 | 0.9914 |
| toluene | = −0.043 T + 24.09 | 0.9891 |
| ethyl acetate | = 0.036 T − 3.586 | 0.9981 |
| ethanol | = −0.292 T + 140.76 | 0.9961 |
| i-propanol | = −0.090 T + 42.2 | 0.9287 |
| n-butanol | = −0.210 T + 103.05 | 0.9992 |
| i-butanol | = −0.124 T + 60.03 | 0.9973 |
| i-pentanol | = −0.121 T + 60.29 | 0.9998 |
| Dichloromethane | = −0.005 T + 4.348 | 0.9983 |
| 3.5% 5-HMU/S-DVB | ||
| Solvents | Equation | R2 |
| benzene | = 4 × 10−4 T − 0.156 | 0.9935 |
| toluene | = −4 × 10−4 T + 0.542 | 0.9988 |
| ethyl acetate | = 0.183 T − 58.14 | 0.9938 |
| ethanol | = −0.248 T + 130.23 | 0.9997 |
| i-propanol | = −0.139 T + 82.08 | 0.9985 |
| n-butanol | = −0.1274 T + 72.60 | 0.9983 |
| i-butanol | = −0.105 T + 62.56 | 0.998 |
| i-pentanol | = 0.047 T + 14.09 | 0.9983 |
| Dichloromethane | = −0.0070 T + 4.119 | 0.9998 |
| 10% 5-HMU/S-DVB | ||
| Solvents | Equation | R2 |
| benzene | = 0.0017 T − 0.588 | 0.9942 |
| toluene | = 0.013 T − 3.856 | 0.9949 |
| ethyl acetate | = 0.183 T − 59.09 | 0.9945 |
| ethanol | = −0.150 T + 113.86 | 0.9995 |
| i-propanol | = 0.154 T − 9.398 | 0.995 |
| n-butanol | = −0.097 T + 52.92 | 0.9993 |
| i-butanol | = 0.162 T − 21.42 | 0.996 |
| i-pentanol | = −0.074 T + 37.042 | 1 |
| Dichloromethane | = −0.008 T + 4.491 | 0.9999 |
| 1% 5-FU/S-DVB | ||
| Solvents | Equation | R2 |
| benzene | = 0.0016 T − 0.668 | 0.9905 |
| toluene | = 0.015 T − 5.243 | 0.9945 |
| ethyl acetate | = −0.020 T + 30.52 | 0.987 |
| ethanol | = 0.882 T − 276.34 | 0.9948 |
| i-propanol | = −0.021 T + 76.68 | 0.8954 |
| n-butanol | = 0.862 T − 304.64 | 0.9947 |
| i-butanol | = 0.965 T − 334.37 | 0.995 |
| i-pentanol | = −0.520 T + 259.83 | 0.9995 |
| Dichloromethane | = 0.001 T + 0.671 | 0.9858 |
| 5% 5-FU/S-DVB | ||
| Solvents | Equation | R2 |
| benzene | = 2 × 10−4 T − 0.074 | 0.9967 |
| toluene | = 0.016 T − 4.833 | 0.9979 |
| ethyl acetate | = 0.003 T + 19.418 | 0.9717 |
| ethanol | = −0.175 T + 84.021 | 0.9983 |
| i-propanol | = −0.175 T + 116.52 | 0.9974 |
| n-butanol | = −0.219 T + 121.67 | 0.9985 |
| i-butanol | = 0.160 T − 9.321 | 0.9997 |
| i-pentanol | = −0.003 T + 31.15 | 0.9386 |
| Dichloromethane | = −0.0002 T + 1.280 | 0.9714 |
| 10% 5-FU/S-DVB | ||
| Solvents | Equation | R2 |
| benzene | = 1 × 10−4 T − 0.036 | 0.9986 |
| toluene | = 0.063 T − 17.82 | 0.9988 |
| ethyl acetate | = −0.073 T + 65.639 | 0.9991 |
| ethanol | = −0.2547 T + 124.57 | 0.9992 |
| i-propanol | = −0.326 T + 211.43 | 0.9992 |
| n-butanol | = −0.318 T + 176.42 | 0.9996 |
| i-butanol | = −0.192 T + 93.24 | 0.9989 |
| i-pentanol | = −0.347 T + 213.6 | 0.9999 |
| Dichloromethane | = 0.002 T − 0.057 | 0.9981 |
| S-DVB Copolymer | |||||
|---|---|---|---|---|---|
| Solvents | (K) | R2 | |||
| n-hexane | = −1.07 T + 513.05 | 1.07 | 513.05 | 477.57 | 0.9972 |
| n-heptane | = −0.92 T + 454.45 | 0.92 | 454.45 | 495.64 | 0.9858 |
| n-octane | = −0.95 T + 475.17 | 0.95 | 475.17 | 502.61 | 0.9804 |
| n-nonane | = −0.99 T + 498.93 | 0.99 | 498.93 | 506.17 | 0.9778 |
| Benzene | = −1.10 T + 550.93 | 1.10 | 550.93 | 502.67 | 0.9812 |
| Toluene | = −1.29 T + 664.32 | 1.29 | 664.32 | 514.42 | 0.9754 |
| Ethyl acetate | = −1.29 T + 669.43 | 1.29 | 669.43 | 518.38 | 0.9859 |
| Ethanol | = −1.85 T + 945.32 | 1.85 | 945.32 | 510.21 | 0.9932 |
| i-Propanol | = −1.74 T + 891.1 | 1.74 | 891.1 | 511.04 | 0.9905 |
| Dichloromethane | = −1.23 T + 654.39 | 1.23 | 654.39 | 531.03 | 0.9921 |
| 1% Melamine/S-DVB Copolymer | |||||
| Solvents | R2 | ||||
| n-hexane | = −1.00 T + 480.8 | 1.00 | 480.8 | 479.55 | 0.9967 |
| n-heptane | = −0.66 T + 335.68 | 0.65 | 335.68 | 512.65 | 0.9999 |
| n-octane | = −0.59 T + 317.85 | 0.60 | 317.85 | 531.17 | 0.9999 |
| n-nonane | = −0.58 T + 316.17 | 0.58 | 316.17 | 542.69 | 0.9999 |
| Benzene | = −0.71 T + 375.92 | 0.71 | 375.92 | 531.94 | 0.9999 |
| Toluene | = −0.57 T + 335.24 | 0.57 | 335.24 | 585.37 | 0.9999 |
| Ethyl acetate | = −0.58 T + 319.32 | 0.58 | 319.32 | 554.47 | 0.9999 |
| Ethanol | = −0.64 T + 368.46 | 0.64 | 368.46 | 574.46 | 0.9999 |
| i-Propanol | = −1.21 T + 668.61 | 1.21 | 668.61 | 553.39 | 0.9999 |
| Dichloromethane | = −1.34 T + 662.71 | 1.34 | 662.71 | 494.38 | 0.9997 |
| 2% Melamine/S-DVB Copolymer | |||||
| Solvents | R2 | ||||
| n-hexane | = −0.78 T + 372.02 | 0.78 | 372.02 | 477.93 | 0.9946 |
| n-heptane | = −0.52 T + 265.41 | 0.52 | 265.41 | 506.89 | 0.994 |
| n-octane | = −0.50 T + 260.01 | 0.50 | 260.01 | 520.64 | 0.9894 |
| n-nonane | = −0.50 T + 263.73 | 0.50 | 263.73 | 528.73 | 0.9864 |
| Benzene | Wa = −0.59 T + 308.05 | 0.59 | 308.05 | 519.30 | 0.9904 |
| Toluene | = −0.58 T + 324.78 | 0.58 | 324.78 | 563.95 | 0.9789 |
| Ethyl acetate | = −0.59 T + 334.41 | 0.59 | 334.41 | 568.34 | 0.9892 |
| Ethanol | = −1.5 T + 764.61 | 1.50 | 764.61 | 510.52 | 0.9983 |
| i-Propanol | = −1.15 T + 694.21 | 1.15 | 694.21 | 602.30 | 0.9964 |
| Dichloromethane | = −0.85 T + 502.92 | 0.85 | 502.92 | 590.42 | 0.9978 |
| 3% Melamine/S-DVB Copolymer | |||||
| Solvents | R2 | ||||
| n-hexane | = −0.88 T + 423.69 | 0.88 | 423.69 | 479.34 | 0.9952 |
| n-heptane | = −0.60 T + 307.28 | 0.60 | 307.28 | 509.75 | 0.9954 |
| n-octane | = −0.56 T + 296.17 | 0.56 | 296.17 | 525.68 | 0.9917 |
| n-nonane | = −0.56 T + 297.66 | 0.56 | 297.66 | 535.36 | 0.9889 |
| Benzene | = −0.67 T + 355.5 | 0.67 | 355.5 | 529.33 | 0.9926 |
| Toluene | = −0.65 T + 363.83 | 0.65 | 363.83 | 557.68 | 0.9822 |
| Ethyl acetate | = −0.69 T + 392.76 | 0.69 | 392.76 | 566.75 | 0.992 |
| Ethanol | = −2.05 T + 1049.6 | 2.05 | 1049.6 | 511.88 | 0.9991 |
| i-Propanol | = −1.72 T + 875.58 | 1.72 | 875.58 | 510.42 | 0.9983 |
| Dichloromethane | = −1.12 T + 577.52 | 1.12 | 577.52 | 516.75 | 0.9985 |
| 4% Melamine/S-DVB Copolymer | |||||
| Solvents | R2 | ||||
| n-hexane | = −0.96 T + 460.73 | 0.96 | 460.73 | 479.28 | 0.9952 |
| n-heptane | = −0.63 T + 323.74 | 0.63 | 323.74 | 511.52 | 0.9969 |
| n-octane | = −0.58 T + 308.83 | 0.58 | 308.83 | 528.91 | 0.995 |
| n-nonane | = −0.57 T + 308.54 | 0.57 | 308.54 | 539.59 | 0.9934 |
| Benzene | = −0.71 T + 377.26 | 0.71 | 377.26 | 535.04 | 0.9956 |
| Toluene | = −0.67 T + 394.99 | 0.66 | 394.99 | 594.24 | 0.9896 |
| Ethyl acetate | = −0.73 T + 407.05 | 0.73 | 407.05 | 557.37 | 0.9956 |
| Ethanol | = −1.78 T + 950.98 | 1.78 | 950.98 | 535.58 | 0.9993 |
| i-Propanol | = −1.47 T + 797.06 | 1.47 | 797.06 | 543.18 | 0.9986 |
| Dichloromethane | = −1.17 T + 638 | 1.17 | 638 | 545.21 | 0.9988 |
| 1% 5-HMU/S-DVB Copolymer | |||||
| Solvents | R2 | ||||
| n-hexane | = −0.79 T + 377.09 | 0.79 | 377.09 | 478.42 | 0.9996 |
| n-heptane | = −0.59 T + 297.17 | 0.59 | 297.17 | 503.00 | 0.9969 |
| n-octane | = −0.58 T + 298.07 | 0.58 | 298.07 | 514.00 | 0.9949 |
| n-nonane | = −0.59 T + 306.26 | 0.59 | 306.26 | 520.14 | 0.9939 |
| Benzene | = −0.69 T + 355.57 | 0.69 | 355.57 | 512.20 | 0.9956 |
| Toluene | = −1.01 T + 530.27 | 1.01 | 530.27 | 523.16 | 0.9969 |
| Ethyl acetate | = −1.08 T + 552.6 | 1.08 | 552.6 | 514.14 | 0.9991 |
| Ethanol | = −1.23 T + 617.99 | 1.23 | 617.99 | 501.37 | 0.9969 |
| i-Propanol | = −0.98 T + 495.06 | 0.98 | 495.06 | 507.75 | 0.9897 |
| Dichloromethane | = −1.26 T + 619.03 | 1.26 | 619.03 | 490.52 | 0.9023 |
| 3.5% 5-HMU/S-DVB Copolymer | |||||
| Solvents | R2 | ||||
| n-hexane | = −0.80 T + 380.26 | 0.80 | 380.26 | 477.77 | 0.999 |
| n-heptane | = −0.66 T + 326.22 | 0.66 | 326.22 | 497.51 | 0.997 |
| n-octane | = −0.67 T + 337.84 | 0.67 | 337.84 | 505.37 | 0.9958 |
| n-nonane | = −0.69 T + 353 | 0.69 | 353 | 509.53 | 0.9954 |
| Benzene | = −0.78 T + 397.1 | 0.78 | 397.1 | 508.39 | 0.996 |
| Toluene | = −0.89 T + 471.28 | 0.89 | 471.28 | 526.98 | 0.9955 |
| Ethyl acetate | = −0.97 T + 567.37 | 0.97 | 567.37 | 582.46 | 0.9976 |
| Ethanol | = −1.66 T + 862.63 | 1.66 | 862.63 | 520.85 | 0.9992 |
| i-Propanol | = −1.49 T + 795.55 | 1.490 | 795.55 | 533.78 | 0.9988 |
| Dichloromethane | = −0.99 T + 495.17 | 0.986 | 495.17 | 502.00 | 0.9989 |
| 10% 5-hydroxy-6-methyluracil/S-DVB Copolymer | |||||
| Solvents | R2 | ||||
| n-hexane | = −0.76 T + 361.98 | 0.76 | 361.98 | 476.48 | 0.9998 |
| n-heptane | = −0.70 T + 344.16 | 0.70 | 344.16 | 490.89 | 0.9996 |
| n-octane | = −0.75 T + 371.62 | 0.75 | 371.62 | 495.49 | 0.9993 |
| n-nonane | = −0.80 T + 396.43 | 0.80 | 396.43 | 497.78 | 0.9991 |
| Benzene | = −0.87 T + 438.65 | 0.87 | 438.65 | 502.58 | 0.9994 |
| Toluene | = −1.08 T + 562.98 | 1.08 | 562.98 | 522.63 | 0.9979 |
| Ethyl acetate | = −1.02 T + 585.03 | 1.02 | 585.03 | 573.90 | 0.9992 |
| Ethanol | = −1.71 T + 931.89 | 1.71 | 931.89 | 544.61 | 0.9998 |
| i-Propanol | = −1.54 T + 878.5 | 1.54 | 878.5 | 569.09 | 0.9995 |
| Dichloromethane | = −1.01 T + 503.78 | 1.01 | 503.78 | 499.09 | 0.9998 |
| 1% 5-Fluouracil/S-DVB Copolymer | |||||
| Solvents | R2 | ||||
| n-hexane | = −0.85 T + 409.22 | 0.85 | 409.22 | 480.47 | 0.9991 |
| n-heptane | = −0.53 T + 276.42 | 0.53 | 276.42 | 517.25 | 0.9892 |
| n-octane | = −0.47 T + 253.35 | 0.47 | 253.35 | 540.65 | 0.9742 |
| n-nonane | = −0.44 T + 247.09 | 0.44 | 247.09 | 556.26 | 0.9622 |
| Benzene | = −0.56 T + 301.56 | 0.56 | 301.56 | 540.91 | 0.9769 |
| Toluene | = −0.48 T + 295.44 | 0.48 | 295.44 | 614.09 | 0.9325 |
| Ethyl acetate | = −0.92 T + 507.43 | 0.92 | 507.43 | 554.51 | 0.9892 |
| Ethanol | = −1.32 T + 753.74 | 1.32 | 753.74 | 569.94 | 0.9949 |
| i-Propanol | = −1.29 T + 716.03 | 1.29 | 716.03 | 556.01 | 0.9931 |
| Dichloromethane | = −0.85 T + 432.53 | 0.85 | 432.53 | 508.32 | 0.997 |
| 5% 5-Fluouracil/S-DVB Copolymer | |||||
| Solvents | R2 | ||||
| n-hexane | = −0.91 T + 438.27 | 0.91 | 438.27 | 479.61 | 0.9983 |
| n-heptane | = −0.60 T + 309.29 | 0.60 | 309.29 | 512.15 | 0.9978 |
| n-octane | = −0.55 T + 293.5 | 0.55 | 293.5 | 530.26 | 0.9956 |
| n-nonane | = −0.54 T + 292.32 | 0.54 | 292.32 | 541.53 | 0.9941 |
| Benzene | = −0.6554 T + 347.96 | 0.6554 | 347.96 | 530.91 | 0.9961 |
| Toluene | = −0.6949 T + 415.71 | 0.6949 | 415.71 | 598.23 | 0.9927 |
| Ethyl acetate | = −1.2143 T + 693.27 | 1.2143 | 693.27 | 570.92 | 0.9986 |
| Ethanol | = −1.7361 T + 880.53 | 1.7361 | 880.53 | 507.19 | 0.9993 |
| i-Propanol | = −1.7287 T + 963.71 | 1.7287 | 963.71 | 557.48 | 0.9991 |
| Dichloromethane | = −0.9861 T + 507.27 | 0.9861 | 507.27 | 514.42 | 0.9991 |
| 10% 5-Fluouracil/S-DVB Copolymer | |||||
| Solvents | R2 | ||||
| n-hexane | = −0.94 T + 451.85 | 0.94 | 451.85 | 479.67 | 0.9976 |
| n-heptane | = −0.64 T + 327.09 | 0.64 | 327.09 | 510.76 | 0.9992 |
| n-octane | = −0.59 T + 313.4 | 0.59 | 313.4 | 527.52 | 0.9986 |
| n-nonane | = −0.58 T + 313.9 | 0.58 | 313.9 | 537.68 | 0.9981 |
| Benzene | = −0.70 T + 369.84 | 0.70 | 369.84 | 528.04 | 0.9987 |
| Toluene | = −0.77 T + 484.8 | 0.77 | 484.8 | 627.41 | 0.9978 |
| Ethyl acetate | = −1.28 T + 744.91 | 1.28 | 744.91 | 581.55 | 0.9996 |
| Ethanol | = −1.77 T + 912.74 | 1.77 | 912.74 | 515.38 | 0.9998 |
| i-Propanol | = −1.80 T + 1031.2 | 1.80 | 1031.2 | 572.89 | 0.9997 |
| Dichloromethane | = −0.93 T + 478.52 | 0.93 | 478.52 | 514.04 | 0.9993 |
| S-DVB Copolymer | ||||
|---|---|---|---|---|
| Solvents | (in mJ m−2 K−1) | R2 | (in mJ m−2) | R2 |
| n-hexane | = 0.076 q (Mela) + 0.65 | 0.9757 | = 46.92 q (Mela) + 277.19 | 0.9948 |
| n-heptane | = 0.033 q (Mela) + 0.615 | 0.9945 | = 33.70 q (Mela) + 196.20 | 0.9699 |
| n-octane | = 0.024 q (Mela) + 0.485 | 0.9931 | = 24.44 q (Mela) + 215.01 | 0.9701 |
| n-nonane | = 0.016 q (Mela) + 0.51 | 0.9143 | = 22.05 q (Mela) + 223.96 | 0.9647 |
| Benzene | = 0.065 q (Mela) + 0.46 | 0.9837 | = 34.78 q (Mela) + 242.54 | 0.9821 |
| Toluene | = 0.031 q (Mela) + 0.545 | 0.9468 | = 30.83 q (Mela) + 270.14 | 0.9852 |
| Ethyl acetate | = 0.055 q (Mela) + 0.51 | 0.9181 | = 32.15 q (Mela) + 283.00 | 0.9313 |
| Ethanol | = 0.235 q (Mela) + 0.97 | 0.9612 | = 193.26 q (Mela) + 225.28 | 0.9515 |
| i-Propanol | = 0.146 q (Mela) + 1.04 | 0.9769 | = 101.67 q (Mela) + 517.19 | 0.9238 |
| Dichloromethane | = −0.09 q (Mela) + 1.41 | 0.962 | = 60.23 q (Mela) + 394.56 | 0.9885 |
| S-DVB/5-HMU | ||||
| Solvents | Equation (in mJ m−2 K−1) | R2 | Equation (in mJ m−2) | R2 |
| n-hexane | = −0.003 q (5-HMU) + 0.793 | 0.9963 | = 1.15 q (5-HMU) + 376.06 | 0.9992 |
| n-heptane | = 0.011 q (5-HMU) + 0.592 | 0.9106 | = 3.98 q (5-HMU) + 306.11 | 0.9177 |
| n-octane | = 0.018 q (5-HMU) + 0.582 | 0.9209 | = 7.58 q (5-HMU) + 299.23 | 0.9137 |
| n-nonane | = 0.022 q (5-HMU) + 0.589 | 0.9508 | = 9.35 q (5-HMU) + 306.71 | 0.9276 |
| Benzene | = 0.019 q (5-HMU) + 0.689 | 0.9382 | = 8.66 q (5-HMU) + 355.24 | 0.9383 |
| Toluene | = 0.02 q (5-HMU) + 0.88 | 0.9999 | = 3.55 q (5-HMU) + 527.96 | 0.9914 |
| Ethyl acetate | = −0.006 q (5-HMU) + 1.080 | 0.9382 | = 3.43 q (5-HMU) + 551.78 | 0.9606 |
| Ethanol | = 0.050 q (5-HMU) + 1.233 | 0.9261 | = 33.10 q (5-HMU) + 610.84 | 0.9582 |
| i-Propanol | = 0.033 q (5-HMU) + 1.205 | 0.9999 | = 39.70 q (5-HMU) + 497.81 | 0.9249 |
| Dichloromethane | = −0.026 q (5-HMU) + 1.254 | 0.9008 | = −12.08 q (5-HMU) + 620.49 | 0.9479 |
| S-DVB/5-FU | ||||
| Solvents | Equation (in mJ m−2 K−1) | R2 | Equation (in mJ m−2) | R2 |
| n-hexane | = 0.010 q (5-FU) + 0.848 | 0.9368 | = 4.65 q (5-FU) + 408.29 | 0.9286 |
| n-heptane | = 0.012 q (5-FU) + 0.526 | 0.9523 | = 5.55 q (5-FU) + 274.69 | 0.9462 |
| n-octane | = 0.013 q (5-FU) + 0.467 | 0.9368 | = 6.56 q (5-FU) + 251.75 | 0.9357 |
| n-nonane | = 0.015 q (5-FU) + 0.439 | 0.9089 | = 7.30 q (5-FU) + 245.52 | 0.9311 |
| Benzene | = 0.015 q (5-FU) + 0.557 | 0.9286 | = 7.46 q (5-FU) + 300.03 | 0.9296 |
| Toluene | = 0.032 q (5-FU) + 0.478 | 0.9026 | = 20.74 q (5-FU) + 288.02 | 0.9529 |
| Ethyl acetate | = 0.026 q (5-FU) + 1.037 | 0.9126 | = 25.73 q (5-FU) + 511.32 | 0.8628 |
| Ethanol | = 0.049 q (5-FU) + 1.312 | 0.9243 | = 11.00 q (5-FU) + 809.76 | 0.9292 |
| i-Propanol | = 0.056 q (5-FU) + 1.284 | 0.9141 | = 23.48 q (5-FU) + 811.75 | 0.9257 |
| Dichloromethane | = 0.019 q (5-FU) + 0.892 | 0.9999 | = 5.08 q (5-FU) + 428.94 | 0.9898 |
| Copolymer | R2 | ||
|---|---|---|---|
| S-DVB Copolymer | = 527.12 − 23.502 | 527.12 | 0.9923 |
| 1% Melamine/S-DVB Copolymer | = 476.71 + 42.251 | 476.71 | 0.9672 |
| 2% Melamine/S-DVB Copolymer | = 543.47 − 1.841 | 543.47 | 0.9596 |
| 3% Melamine/S-DVB Copolymer | = 500.3 + 18.342 | 500.3 | 0.9957 |
| 4% Melamine/S-DVB Copolymer | = 532.74 + 1.972 | 532.74 | 0.9882 |
| 1% 5-HMU/S-DVB Copolymer | = 494.38 + 9.860 | 494.38 | 0.9917 |
| 3.5% 5-HMU/S-DVB Copolymer | = 546.19 − 25.452 | 546.19 | 0.9838 |
| 10% 5-HMU/S-DVB Copolymer | = 609.06 − 86.224 | 609.06 | 0.9884 |
| 1% 5-Fluouracil/S-DVB Copolymer | = 558.33 − 11.407 | 558.33 | 0.9793 |
| 5% 5-Fluouracil/S-DVB Copolymer | = 534.46 − 0.318 | 534.46 | 0.9803 |
| 10% 5-Fluouracil/S-DVB Copolymer | = 556.11 − 14.185 | 556.11 | 0.973 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamieh, T.; Gus’kov, V.Y. Effect of Temperature on Adhesion Work of Model Organic Molecules on Modified Styrene–Divinylbenzene Copolymer Using Inverse Gas Chromatography. Crystals 2025, 15, 490. https://doi.org/10.3390/cryst15060490
Hamieh T, Gus’kov VY. Effect of Temperature on Adhesion Work of Model Organic Molecules on Modified Styrene–Divinylbenzene Copolymer Using Inverse Gas Chromatography. Crystals. 2025; 15(6):490. https://doi.org/10.3390/cryst15060490
Chicago/Turabian StyleHamieh, Tayssir, and Vladimir Yu Gus’kov. 2025. "Effect of Temperature on Adhesion Work of Model Organic Molecules on Modified Styrene–Divinylbenzene Copolymer Using Inverse Gas Chromatography" Crystals 15, no. 6: 490. https://doi.org/10.3390/cryst15060490
APA StyleHamieh, T., & Gus’kov, V. Y. (2025). Effect of Temperature on Adhesion Work of Model Organic Molecules on Modified Styrene–Divinylbenzene Copolymer Using Inverse Gas Chromatography. Crystals, 15(6), 490. https://doi.org/10.3390/cryst15060490








