Abstract
Chromium (Cr) is a vital metal utilized in materials physics, healthcare, and various other domains. In this study, we propose an eco-friendly method for separating Cr from potassium chromate (K2CrO4) based on photon–phonon resonance absorption theory. Using first-principles density functional theory calculations, we obtained the Raman and infrared spectra of K2CrO4 and assigned the vibrational modes to the peaks observed in the experimental spectra. We confirmed that the strongest infrared absorption peak corresponds to the Cr-O bond stretching vibration theoretically located at 931 cm−1. We propose employing a high-power terahertz laser at this resonant frequency for photothermal energy transfer. This approach is expected to enhance the efficiency of separating Cr from K2CrO4. Experimental investigations are expected in the future.
1. Introduction
Chromium (Cr) is a hard, lustrous, and corrosion-resistant metal with a body-centered structure [1]. It is widely used in nanotechnology, biomedicine, and electronics [2,3,4,5]. In materials science, Cr can be used to produce luminescent and ferroelectric materials [6,7]. In chemistry, Cr forms the basis of various catalysts [8,9]. Moreover, Cr has industrial uses in lithography and chromized iron manufacturing [10,11]. In recent years, Cr has also been the focus of research on cutting-edge topics in condensed matter physics. In 2023, Chi et al. investigated the anomalous Hall effect in Cr2Te3 films [12]. In 2024, Liu et al. reported superconductivity in a Cr-based kagome metal [13].
Cr can be prepared by numerous methods, including electrolysis and hydrogen reduction [14,15,16,17]. In the traditional production process, the preparation of chromium involves various intermediate compounds, including chromates [18]. At present, the primary method of converting chromates to Cr is via reduction to chromium oxide [19,20], followed by further reduction to Cr [17]. The most commonly used reducing agents for the reduction of chromates include carbon, hydrogen, and carbon monoxide. This approach is energy-intensive, owing to the requisite high-temperature conditions. Furthermore, the process of reduction may produce greenhouse gases, which can have an impact on the environment. Alternatively, chromates can be electrolytically converted to chromium oxide, then reduced to Cr [17,21]. However, the electrolytic method for producing elemental Cr is also energy-consuming and not environmentally friendly. Therefore, there is an urgent need for a novel, environmentally friendly technology for the large-scale extraction of Cr from chromates with minimal pollution, high efficiency, and suitability for industrial production.
Potassium chromate (K2CrO4) is a familiar and widely studied chromate [22,23]. The Raman and infrared (IR) vibrational spectra of K2CrO4 have been extensively investigated in recent decades [24,25,26,27,28,29,30]. In 1992, Etxebarria et al. analyzed its lattice dynamics theoretically [23]. In 2020, Yuriy et al. calculated the interactions between the surfaces of K2CrO4 crystals and carbon nanotubes using density functional theory (DFT) [31].
Conventional applications using photothermal effects, such as IR therapy apparatus, emit thermal radiation with a frequency covering a large region of the IR spectrum [32]. In this work, we introduce a laser-targeted photothermal conversion method named photon–phonon resonant absorption (PPRA), which transfers energy from photons to phonons to promote bond breaking [33,34,35]. We simulated the IR and Raman spectra of K2CrO4 and compared them with the experimental data. Based on the IR-active peaks related to Cr-O bonds, we selected the ideal terahertz laser frequency for enhancing the separation of Cr from oxides.
2. Methods
A primitive cell of the K2CrO4 crystal contains 4 molecules [27]. Using the Cambridge Serial Total Energy Package (CASTEP 6.0), we performed geometric optimization and phonon calculations based on first-principles DFT simulations [36]. Tests of parameter settings showed that generalized gradient approximation (GGA) in the form of the Perdew–Burke–Ernzerhof (PBE, Material Studio 6.0) exchange–correlation functional was the best-matched functional for our purpose [37,38]. The convergence tolerances of both the self-consistent field and energy were set to 1 × 10−9 eV/atom. The k-point mesh was 2 × 2 × 1, and the energy cutoff was set to 830 eV. The linear response approach was used to calculate IR and Raman intensities using norm-conserving pseudopotentials [39,40].
Based on the IR calculations, we analyzed the dynamic processes of the vibrational modes at the gamma point. Through this analysis, the peaks in the simulated IR and Raman spectra were assigned to special vibrational modes. This enabled us to verify the reported experimental peaks and identify the effective Cr-related IR absorption peaks.
3. Results
The K2CrO4 we chose crystallizes in the Pnma space group with a spinel structure, which is same as the crystal structure tested in an experiment on anions on Cs sites [27]. The optimized lattice parameters of the primitive cell were a = 7.771 Å, b = 6.048 Å, c = 10.593 Å, and . Under harmonic approximation, the optical normal modes of K2CrO4 were calculated together with the IR and Raman spectra. As illustrated in Figure 1, the simulated IR and Raman spectra demonstrate the distribution and intensities of the IR and Raman active modes.
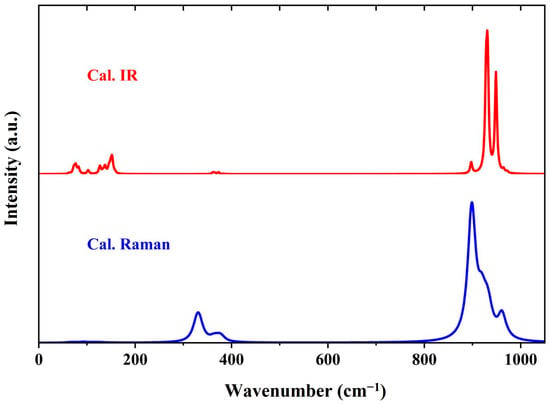
Figure 1.
Simulated Raman scattering and IR absorption spectra of K2CrO4, illustrating principal vibrational modes. The main peaks in the Raman spectrum are complementary to those in the IR spectrum. The two prominent peaks in the IR spectrum are located at 931 and 948 cm−1.
Based on the dynamic process of each vibrational mode, we assigned the IR-active and Raman-active modes as listed in Table 1. We identified 42 Raman-active and 32 IR-active modes. The remaining seven modes are neither IR- nor Raman-active. Among the vibrational modes, 41 modes represent skeletal deformations, which are inter-molecular relative motions and belong to the lowest frequency band. The modes located at 103, 125, and 138 cm−1 exhibit double degeneracy. The intra-molecular bond angle vibrations (referred to as bending vibrations) all exhibit higher vibrational energy. In the band from 324 to 384 cm−1, there are 18 modes representing Cr-O bond bending vibrations. Another 15 vibrations located in the highest frequency band from 897 to 972 cm−1 are intra-molecular stretching vibrations. The stretching vibration of atoms can be simply treated as a harmonic oscillator, where the vibrational angular frequency is given by

Table 1.
Raman- and IR-active vibrational modes. The wavenumbers are displayed in the first column (unit cm−1). The second column indicates whether the mode is Raman- or IR-active, followed by the experimental wavenumber data in the next two columns. The last column presents the assignments of the corresponding vibrational modes.
Thus, lower atomic masses and greater bond strengths result in higher frequencies.
Figure 2 illustrate four vibrational modes in the vibrational band below 200 cm−1. In the vibrational band below 200 cm−1, most of the vibrational modes involve relative motion of the anions. Two vibrational modes correspond to the relative motion of K+ in the crystal lattice (76 and 157 cm−1). Carter reported experimental Raman and IR spectra and identified Raman peaks located at 37, 54, 67, 85, 91, 93, 99, 114, 119, 138, and 157 cm−1 [25]. As shown in Table 1, these peaks correspond to the simulated wavenumbers at 39, 62, 67, 92, 95, 100, 103, 114, 119, 138, and 159 cm−1. As the intensities of these Raman peaks are much lower than the intensities of the Raman peaks at around 900 cm−1, they cannot be observed in Figure 1.
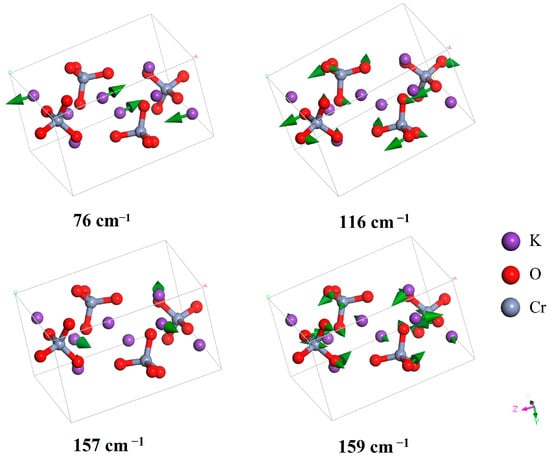
Figure 2.
Four vibrational modes located at 76, 116, 157, and 159 cm−1 in the IR and Raman spectra. The modes at 76 and 157 cm−1 represent two translational motions of K+, and the modes at 115 and 159 cm−1 represent two relative motions of CrO42−. The green arrows indicate the vibrational direction, with the arrow size in proportion to the amplitude.
For the middle band between 300 and 800 cm−1, the vibrational modes are intra-molecular bond angle vibrations. Carter found two peaks in the IR spectrum at 342 and 382 cm−1, corresponding to our simulated modes at 373 and 384 cm−1 [25]. Adams et al. only observed one peak at 343 cm−1 in this band [27]. Davies and Long also confirmed the IR peak at 343 cm−1 [28]. Carter further reported three peaks (345, 346, and 350 cm−1) in the Raman spectrum [25], which correspond to the simulated modes at 374, 378, and 382 cm−1. Adams et al. observed these three peaks at 348, 351, and 352 cm−1, respectively [27]. Davies and Long observed two Raman peaks at 347 and 351 cm−1 in this area [28]. The simulated vibrational modes were consistent with the experimental data, and the dynamic analysis enabled scientific assignment of these peaks. Figure 3 depicts four bending modes located at 373, 378, 382, and 384 cm−1.
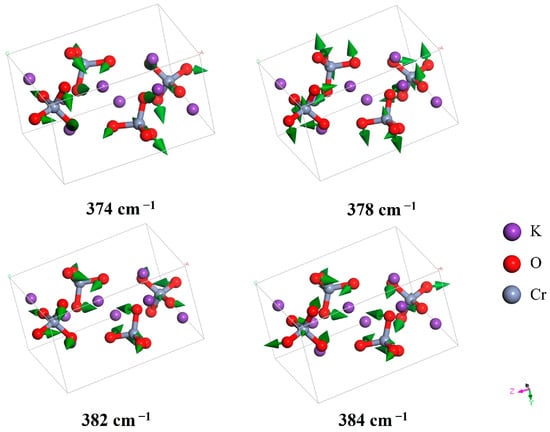
Figure 3.
Four vibrational modes observed in the IR and Raman spectra, representing different bending vibrations of CrO42−. The middle band from 300 to 800 cm−1 corresponds to bending vibrational energy.
The stretching vibrations of CrO42− are located in the high-energy band. Venkateswaran identified four Raman peaks at 486, 513, 859, and 877 cm−1 [24]. However, none of our simulated modes match the two peaks at 486 and 513 cm−1. The peaks at 859 and 877 cm−1 correspond to the Raman-active modes at 898 cm−1 (doubly degenerate) and 918 cm−1 obtained from our simulations. These are different stretching vibrational combinations of the four Cr-O bonds. Carter observed these two Raman peaks at 881 and 918 cm−1 [25], Adams et al. reported them at 884 and 905 cm−1, and Davies and Long reported them at 885 and 905 cm−1 [27,28]. As no other experimental studies support the two peaks at 486 and 513 cm−1 reported by Venkateswaran, we suspect that they are artefacts observed in error. In fact, there are eight Raman-active modes (the mode at 898 cm−1 is doubly degenerate) in this band. The peaks missing from previous experiments were overlooked due to their low intensities.
In this band, there are seven IR-active vibrational modes (the mode at 897 cm−1 is doubly degenerate), of which three peaks have been experimentally reported [24,25,27,28]. Carter observed peaks located at 883, 910, and 936 cm−1. These correspond to the simulated vibrational modes at 897, 928/931, and 948 cm−1, respectively [25]. Note that the IR-active mode at 928 cm−1 is strong with high intensity, and hence may have merged with the mode at 931 cm−1 to produce a single large peak in the experimental observations. Adams et al. observed these three peaks at 876, 890, and 920 cm−1, while Davies and Long reported them at 850, 880, and 918 cm−1 [28]. Figure 4 shows the two doubly degenerate modes at 897 cm−1 (IR-active) and 898 cm−1 (Raman-active). Figure 5 shows another four stretching modes.
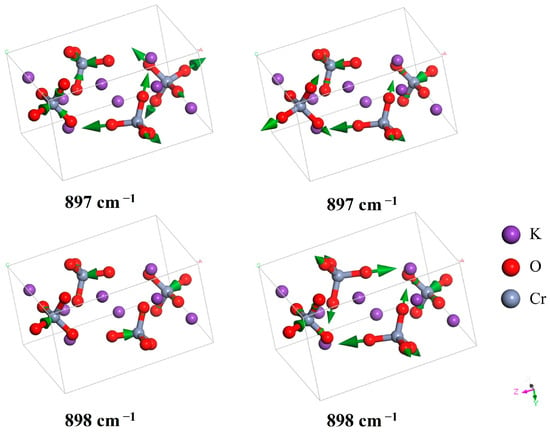
Figure 4.
Two IR-active (897 cm−1) and two Raman-active (898 cm−1) stretching modes of CrO42−. Both exhibit double degeneracy.
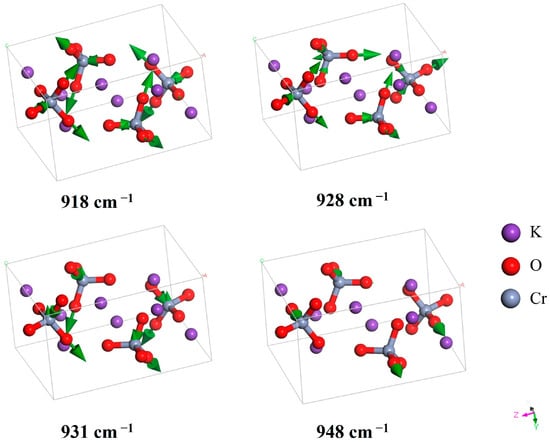
Figure 5.
Four stretching modes of the Cr-O bond in CrO42−. The modes at 928 and 931 cm−1 merge into the highest IR peak depicted in Figure 1, while the mode at 948 cm−1 corresponds to the large IR peak on the right-hand side of the highest peak.
According to the simulations, the highest-intensity Raman-active mode is located at 898 cm−1, while the highest-intensity IR-active mode is located at 931 cm−1. These represent different stretching vibrational combinations of Cr-O bonds. As the absorption peaks in the IR spectrum result from photon–phonon coupling, the IR-active vibrational mode at 931 cm−1 corresponds to the mode with the strongest photon–phonon coupling intensity, meaning that the Cr-O bond exhibits the highest PPRA efficiency at this frequency (56 THz). Treating this vibrational mode as a harmonic oscillator, the phonon energy is equal to
If a photon with a frequency of is absorbed by a phonon during the PPRA process, the phonon will transition to a higher-energy state. Irradiating crystalline K2CrO4 with high-power laser light at this frequency may promote the energy level transition of the Cr-O bond, which in turn may facilitate the breaking of the Cr-O bond; the exact frequency should be accurately measured in real environments. This physical approach to Cr-O bond breaking potentially provides a pollution-free and environmentally friendly method for the separation of Cr.
In chromates, the anionic group CrO42− is independent of the cation in terms of the appearance of its vibrational spectra. As a result, the vibrational modes of the Cr-O bond are similar, irrespective of the cation, in both infrared and Raman spectra. Therefore, this study on potassium chromate provides valuable insights for research on other chromates.
Compared with other PPRA works to induce the separation of rare metals, we found that this method shows broad application prospects. Ren et al. studied the vibrational spectra of sodium molybdate and pointed out that a laser at 25 THz can be used for Mo-O bond breaking [34]. Li et al. investigated the potassium heptafluorotantalate mineral and proposed three laser candidates for tantalum separation from the K2TaF7 compound [36].
4. Conclusions
Based on first-principles DFT, we simulated the IR and Raman spectra of K2CrO4. The experimentally measured peaks were assigned to the simulated vibrational modes. The results indicate that in the low-frequency band, the vibrational modes correspond to the relative motion between the ions in the crystal. In the energy band between 300 and 800 cm−1, the vibrational modes can be attributed to bending vibrations of the Cr-O bonds within the anionic group CrO42−. In the high-energy band, there are 15 vibrational modes corresponding to stretching vibrations of Cr-O bonds. These represent different combinations of Cr-O bond stretching vibrations. In the experimental data, only three IR-active and two Raman-active peaks can be observed.
We focused on the stretching vibrational modes of the Cr-O bond in the high-frequency band. As shown in Figure 1, the strongest IR absorption peak was located at 931 cm−1, implying that this is the most efficient PPRA frequency (56 THz). Thus, we propose the use of high-power terahertz laser radiation at this frequency for photothermal conversion to facilitate the separation of Cr from chromates. The exact frequency needs to be tested in laboratory experiments. The proposed PPRA method has potential applications in ice melting and natural gas hydrate extraction [34,35,41]. However, realizing its full potential remains highly challenging, as this technology requires high-power, frequency-selectable laser equipment. Nowadays, only free-electron laser facilities can conduct high-power frequency-selective laser experiments. However, conducting in situ tests simultaneously with the chemical preparation of chromium is challenging. Experimental validation will be undertaken in subsequent studies.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst15050437/s1: Data S1: The origin simulation files.
Author Contributions
M.X. is mainly responsible for model construction and article writing; H.R. assisted in structural modeling and data processing; Y.H. helped to analyze the data; P.L., Y.L. (Yining Li), Y.L. (Yawen Li) and Y.X. participated in the results and discussion sections; P.Z. conducted simulations and data analysis, and edited the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
We are grateful to the project ZR2022MA017, supported by Shandong Provincial Natural Science, for financial support.
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
Acknowledgments
The numerical calculations were performed on the supercomputing system at the Supercomputing Center, Shandong University, Weihai.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Patterson, R.A. Crystal structure of titanium and chromium. Phys. Rev. 1925, 26, 56–59. [Google Scholar] [CrossRef]
- Chou, S.Y.; Xia, Q.F. Improved nanofabrication through guided transient liquefaction. Nat. Nanotechnol. 2008, 3, 295–300. [Google Scholar] [CrossRef] [PubMed]
- Mena-Gutiérrez, S.; Maiza-Razkin, E.; Pascual-Colino, J.; Araúzo-Bravo, M.J.; Beobide, G.; Castillo, O.; Castellanos-Rubio, A.; Gerovska, D.; Luque, A.; Pérez-Yáñez, S. Drug-delivery and biological activity in colorectal cancer of a supramolecular porous material assembled from heptameric chromium-copper-adenine entities. J. Mat. Chem. B 2024, 12, 11156–11164. [Google Scholar] [CrossRef] [PubMed]
- Karimi, M.; Homayoonfal, M.; Zahedifar, M.; Ostadian, A.; Adibi, R.; Mohammadzadeh, B.; Raisi, A.; Ravaei, F.; Rashki, S.; Khakbraghi, M.; et al. Development of a novel nanoformulation based on aloe vera-derived carbon quantum dot and chromium-doped alumina nanoparticle (Al2O3:Cr@Cdot NPs): Evaluating the anticancer and antimicrobial activities of nanoparticles in photodynamic therapy. Cancer Nanotechnol. 2024, 15, 19. [Google Scholar] [CrossRef]
- Roberts, B.K.; Pakhomov, A.B.; Shutthanandan, V.S.; Krishnan, K.M. Ferromagnetic Cr-doped ZnO for spin electronics via magnetron sputtering. J. Appl. Phys. 2005, 97, 3. [Google Scholar] [CrossRef]
- Dang, P.P.; Wei, Y.; Liu, D.J.; Li, G.G.; Lin, J. Recent Advances in Chromium-Doped Near-Infrared Luminescent Materials: Fundamentals, Optimization Strategies, and Applications. Adv. Opt. Mater. 2023, 11, 27. [Google Scholar] [CrossRef]
- Song, L.Y.; Zhao, Y.; Xu, B.Q.; Du, R.F.; Li, H.; Feng, W.; Yang, J.B.; Li, X.H.; Liu, Z.J.; Wen, X.; et al. Robust multiferroic in interfacial modulation synthesized wafer-scale one-unit-cell of chromium sulfide. Nat. Commun. 2024, 15, 11. [Google Scholar] [CrossRef]
- Yin, Z.B.; Wang, G.X.; Yan, X.C.; Wei, J.N.; Xi, Z.F. Construction of N-E bonds via Lewis acid-promoted functionalization of chromium-dinitrogen complexes. Nat. Commun. 2025, 16, 8. [Google Scholar] [CrossRef]
- Noor, A.; Glatz, G.; Müller, R.; Kaupp, M.; Demeshko, S.; Kempe, R. Carboalumination of a chromium-chromium quintuple bond. Nat. Chem. 2009, 1, 322–325. [Google Scholar] [CrossRef]
- Hild, R.; David, C.; Muller, H.U.; Volkel, B.; Kayser, D.R.; Grunze, M. Formation and characterization of self-assembled monolayers of octadecyltrimethoxysilane on chromium: Application in low-energy electron lithography. Langmuir 1998, 14, 342–346. [Google Scholar] [CrossRef]
- Menzies, I.A.; Davies, G.A.; Ponter, A.B. Nature and Mechanism of Formation of Oxide Films in the Chromium–Iron–Carbon System. Nature 1966, 212, 915–916. [Google Scholar] [CrossRef]
- Chi, H.; Ou, Y.B.; Eldred, T.B.; Gao, W.P.; Kwon, S.; Murray, J.; Dreyer, M.; Butera, R.E.; Foucher, A.C.; Ambaye, H.; et al. Strain-tunable Berry curvature in quasi-two-dimensional chromium telluride. Nat. Commun. 2023, 14, 8. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Liu, Z.Y.; Bao, J.K.; Yang, P.T.; Ji, L.W.; Wu, S.Q.; Shen, Q.X.; Luo, J.; Yang, J.; Liu, J.Y.; et al. Superconductivity under pressure in a chromium-based kagome metal. Nature 2024, 632, 18. [Google Scholar] [CrossRef]
- Chen, G.Z.; Gordo, E.; Fray, D.J. Direct electrolytic preparation of chromium powder. Metall. Mater. Trans. B-Proc. Metall. Mater. Proc. Sci. 2004, 35, 223–233. [Google Scholar] [CrossRef]
- Lei, K.P.V.; Sullivan, T.A.; Hiegel, J.M. Electrolytic preparation of high-purity chromium. J. Less-Common Met. 1972, 27, 353–365. [Google Scholar] [CrossRef]
- Suri, A.K.; Gupta, C.K. Production of chromium by molten salt electrolysis. Surf. Technol. 1977, 5, 271–276. [Google Scholar] [CrossRef]
- Chu, W.F.; Rahmel, A. The kinetics of the reduction of chromium oxide by hydrogen. Metall. Trans. B 1979, 10, 401–407. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, Y.; Zheng, S.L.; Zhang, Y. A New Method of Potassium Chromate Production from Chromite and KOH-KNO3-H2O Binary Submolten Salt System. AIChE J. 2009, 55, 2646–2656. [Google Scholar] [CrossRef]
- Li, P.; Xu, H.B.; Zheng, S.L.; Zhang, Y.; Li, Z.H.; Bai, Y.L. A green process to prepare chromic oxide green pigment. Environ. Sci. Technol. 2008, 42, 7231–7235. [Google Scholar] [CrossRef]
- Xu, H.B.; Zhang, Y.; Li, Z.H.; Zheng, S.L.; Wang, Z.K.; Tao, Q.; Li, H.Q. Development of a new cleaner production process for producing chromic oxide from chromite ore. J. Clean. Prod. 2006, 14, 211–219. [Google Scholar] [CrossRef]
- Feng, B.Y.; Jia, Y.Z.; An, J.L.; Jia, Y.D.; Wang, M.G. Clean preparation of Cr2O3 by direct molten salt electrolysis of sodium chromate. J. Clean. Prod. 2024, 467, 10. [Google Scholar] [CrossRef]
- Fernández-Rodríguez, J.; Lovesey, S.W.; Blanco, J.A. Polarization analysis in resonant x-ray Bragg diffraction by K2CrO4 at the Cr K-edge. Phys. Rev. B 2008, 77, 9. [Google Scholar] [CrossRef]
- Etxebarria, I.; Perezmato, J.M.; Madariaga, G. Lattice dynamics, structural stability, and phase transitions in incommensurate and commensurate A2BX4 materials. Phys. Rev. B 1992, 46, 2764–2774. [Google Scholar] [CrossRef] [PubMed]
- Venkateswaran, C.S. The raman spectra of some inorganic compounds. Proc. Indian Acad. Sci. (Math. Sci.) 1938, 7, 144–155. [Google Scholar] [CrossRef]
- Carter, R.L. Vibrational selection rules in solids. J. Chem. Educ. 1971, 48, 297. [Google Scholar] [CrossRef]
- Engert, C.; Kiefer, W. Raman spectra of the permanganate ion in the solid state with excitation in the near infrared. J. Raman Spectrosc. 2010, 22, 715–719. [Google Scholar] [CrossRef]
- Adams, D.M.; Hooper, M.A.; Lloyd, M.H. Single-crystal vibrational spectrum of potassium chromate. J. Chem. Soc. A 1971, 946–947. [Google Scholar] [CrossRef]
- Davies, J.E.D.; Long, D.A. Solid-state vibrational spectroscopy. Part II. The vibrational spectra of some chromates and dichromates. J. Chem. Soc. A 1971, 1275–1280. [Google Scholar] [CrossRef]
- Serghiou, G.; Guillaume, C. Stability of K2CrO4 to 50 GPa using Raman spectroscopy measurements. J. Solid State Chem. 2004, 177, 4672–4679. [Google Scholar] [CrossRef]
- Huang, Y.; Butler, I.S. High-Pressure Micro-Raman Spectra of Potassium Chromate(VI) and Potassium Tungstate(VI). Appl. Spectrosc. 1990, 44, 1326–1328. [Google Scholar] [CrossRef]
- Hizhnyi, Y.; Nedilko, S.; Borysiuk, V.; Zhydachevskyy, Y. Interaction of K2CrO4 Oxide Nanoparticles with Carbon Nanostructures. In Proceedings of the 2020 IEEE 40th International Conference on Electronics and Nanotechnology (ELNANO), Kyiv, Ukraine, 22–24 April 2020; pp. 263–267. [Google Scholar]
- Li, Y.; Wang, D.; Ping, X.; Zhang, Y.; Zhang, T.; Wang, L.; Jin, L.; Zhao, W.; Guo, M.; Shen, F.; et al. Local hyperthermia therapy induces of white fat and treats. Cell 2022, 185, 949–966. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.X.; Li, Y.N.; Yin, Y.; Liu, S.C.; Zhang, J.Q.; Zhang, J.Y.; Li, P.L.; Wang, Z.; Zhang, P. Theoretical Study of Molybdenum Separation from Molybdate Assisted by a Terahertz Laser. Molecules 2024, 29, 3348. [Google Scholar] [CrossRef]
- Yin, Y.; Li, Y.N.; Liu, S.C.; Jiang, Y.; Liu, X.Y.; Zhang, P. Theoretical Study of Efficient Photon-Phonon Resonance Absorption in the Tungsten-Related Vibrational Mode of Scheelite. ACS Omega 2024, 9, 10517–10521. [Google Scholar] [CrossRef]
- Li, Y.N.; Guo, Q.; Liu, S.C.; Liu, X.Y.; Jiang, Y.; Yin, Y.; Zhang, P. Computational Assignment of Tantalum-related Strong Absorption Peaks in the Infrared Spectrum of Potassium Heptafluorotantalate. ACS Omega 2023, 9, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Kristall. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Hammer, B.; Hansen, L.B.; Norskov, J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 1999, 59, 7413–7421. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Cococcioni, M.; de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B 2005, 71, 16. [Google Scholar] [CrossRef]
- Schluter, M.; Hamann, D.R.; Chiang, C. Norm-Conserving Pseudopotentials. Phys. Rev. Lett. 1980, 25, 394. [Google Scholar]
- Zhu, X.L.; Cao, J.W.; Qin, X.L.; Jiang, L.; Gu, Y.; Wang, H.C.; Liu, Y.; Kolesnikov, A.I.; Zhang, P. Origin of Two Distinct Peaks of Ice in the THz Region and Its Application for Natural Gas Hydrate Dissociation. J. Phys. Chem. C 2020, 124, 1165–1170. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).