Modeling Fatigue Crack Growth Under Compressive Loads: The Role of Non-Monotonic Stress and Crack Closure
Abstract
1. Introduction
2. Numerical Analysis
3. Results and Discussion
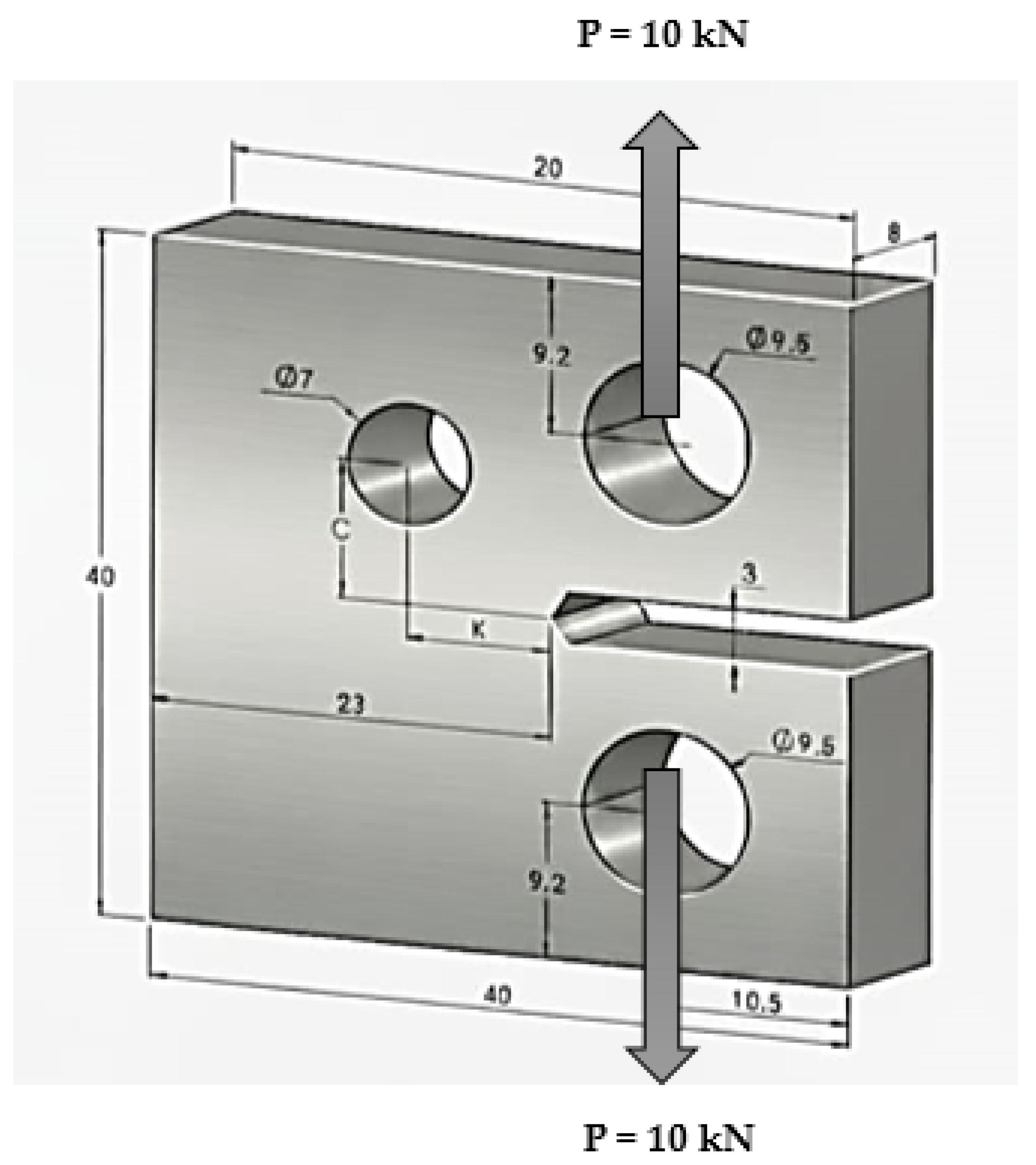
Modified Compact Tension Specimen
- Configuration 1: The hole was positioned with a horizontal distance (K) of 8.3 mm and a vertical distance (C) of 8.1 mm.
- Configuration 2: The distances were adjusted to K = 8.4 mm and C = 6.9 mm.
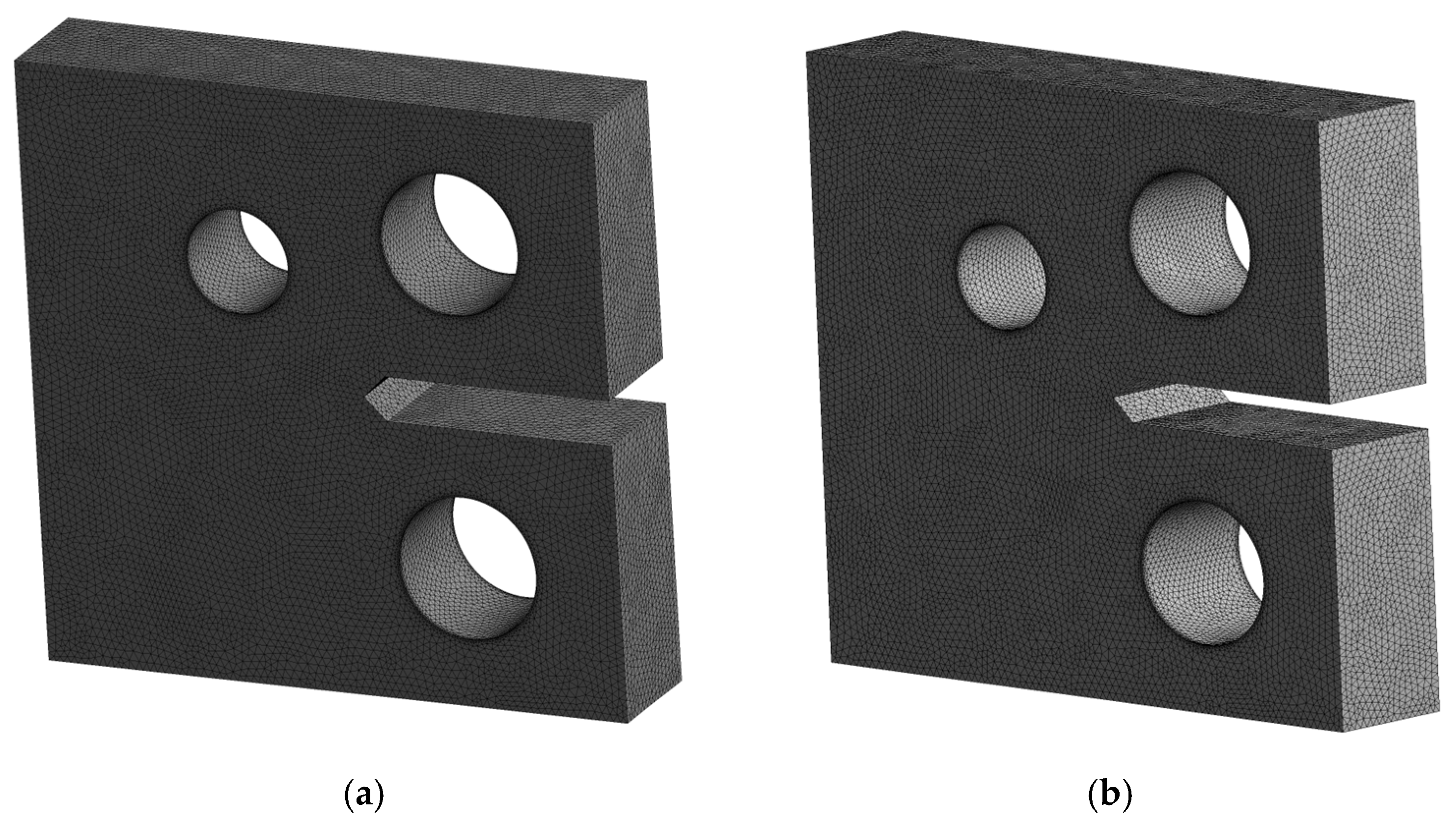
- CT1: 491,691 nodes and 326,808 elements.
- CT2: 503,546 nodes and 334,795 elements.
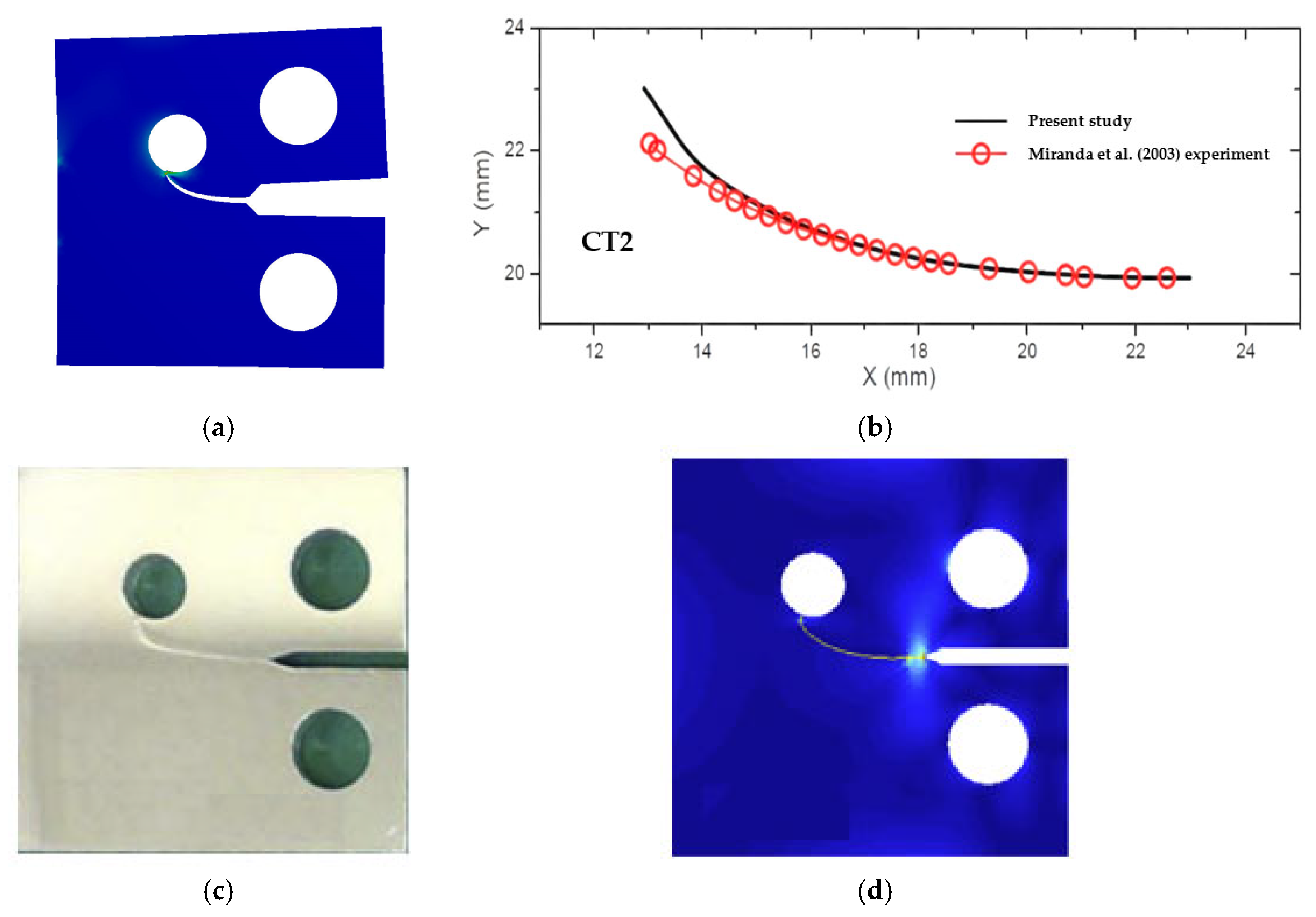
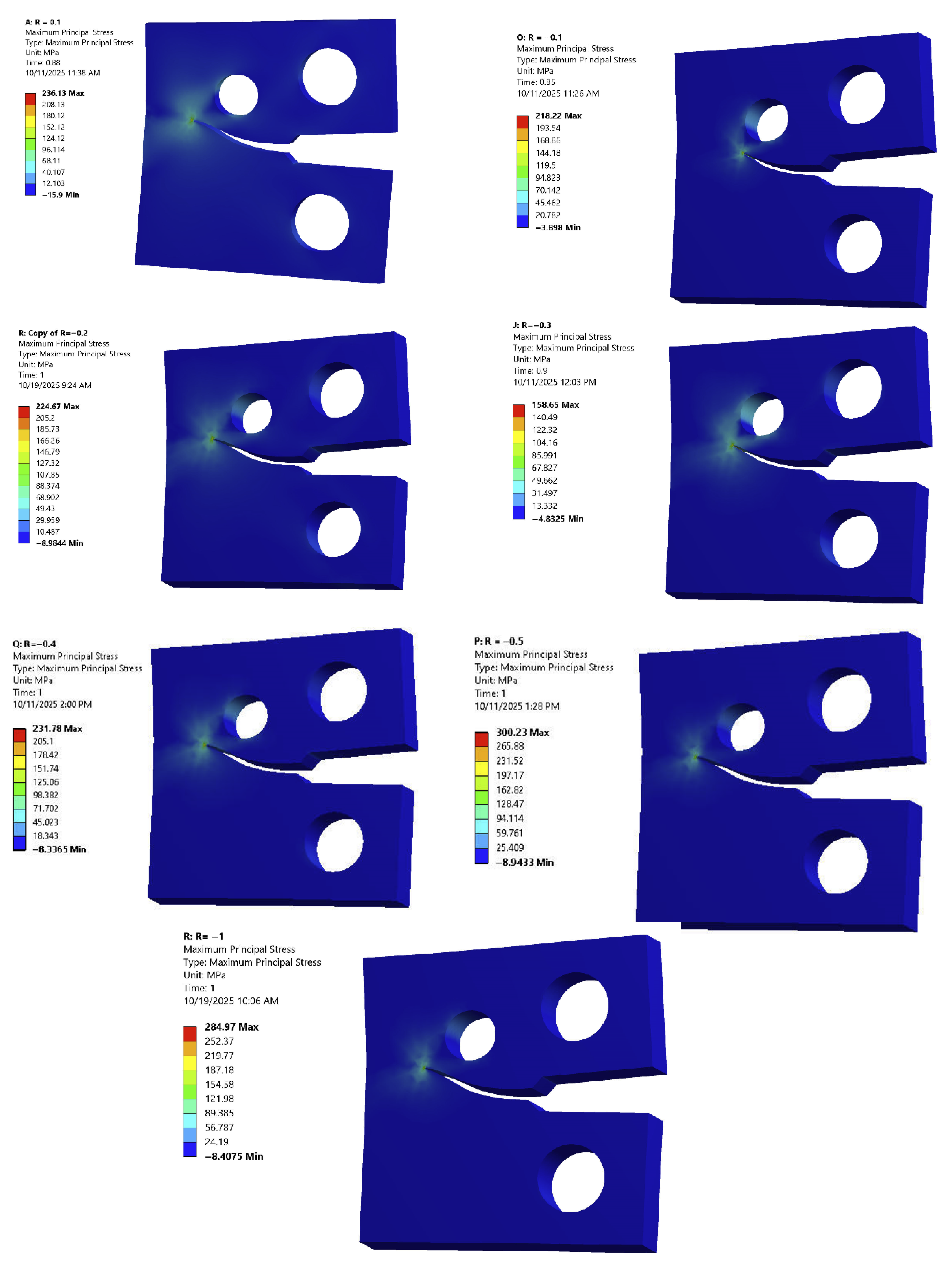
- Maximum Principal Stress () Criterion: The distribution is evaluated based on the Maximum Tangential Stress (MTS) criterion. This criterion is fundamental for predicting the driving force and the propagation path of the crack. The magnitude and orientation of the field at the crack tip directly indicate the local tensile stress responsible for crack opening and growth.
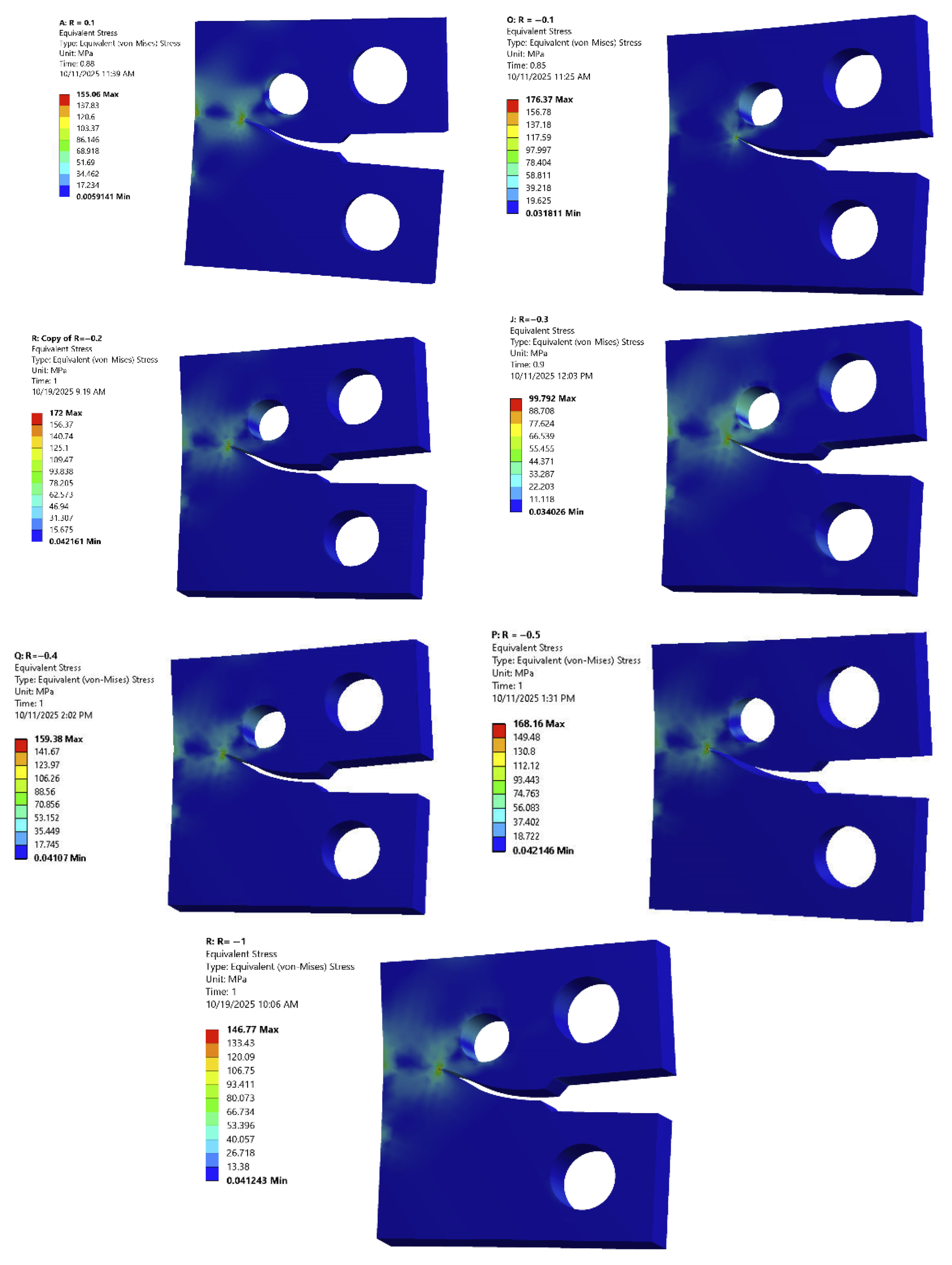
- Equivalent Stress () Criterion: The von Mises equivalent stress () distribution is used as the primary indicator of plastic deformation. The size and shape of the contour define the extent of the plastic zone at the crack tip. This is critical because the plastic zone size dictates the formation of the plastic wake, which is the physical origin of the plasticity-induced crack closure.
- Three-Dimensional Effects: The transition from plane strain (at the specimen core) to plane stress (at the surfaces).
- Material Non-linearity: The complex elastic–plastic material response under cyclic loading.
- Residual Stresses: The residual stresses generated by the plastic zone are intrinsically included in the stress state of the model.
4. Conclusions
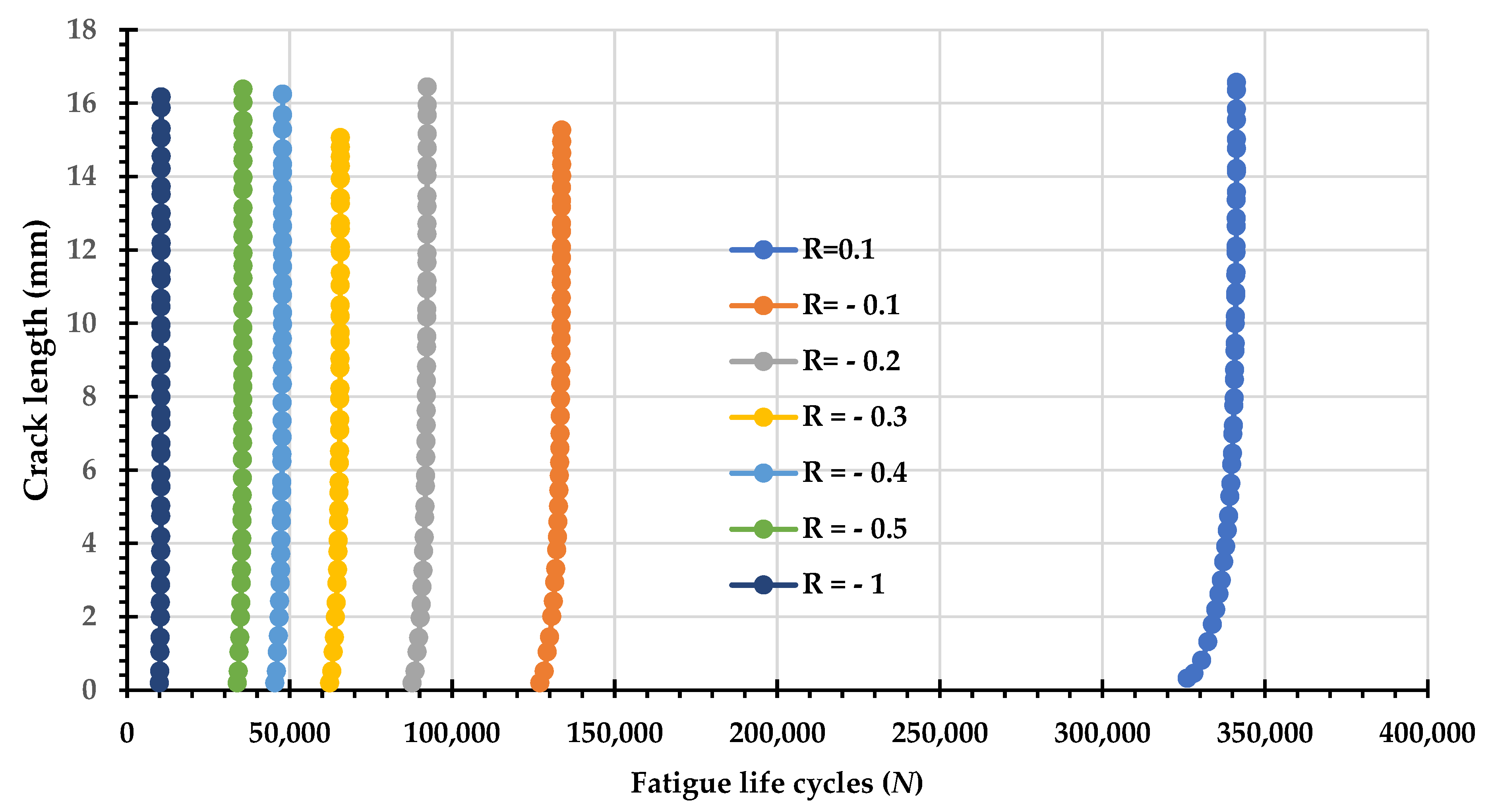
- The results confirm that the presence of a compressive load component fundamentally alters the FCG kinetics. A clear inverse relationship was established between the magnitude of the negative stress ratio and the predicted fatigue life cycles, highlighting the necessity of accounting for the increased tensile mean stress effect associated with these loading condition. The simulation successfully captured the expected inverse correlation between the magnitude of the negative stress ratio and the component’s fatigue life cycles, validating the computational model’s predictive capability under challenging loading conditions.
- The primary mechanism for the observed increase in fatigue life at more negative R-ratios is the enhanced plasticity-induced crack closure resulting from the extensive reversed plastic zone created by the compressive load phase.
- The crack tip stress field exhibits a complex, non-monotonic response to the cyclic loading, which significantly alters the effective stress intensity factor range and necessitates an Elastic–Plastic Fracture Mechanics (EPFM) perspective for accurate analysis.
- The maximum principal stress distribution was confirmed to be the critical parameter governing the crack growth path, aligning with the Maximum Tangential Stress (MTS) criterion.
- The von Mises equivalent stress analysis provided a clear delineation of the plastic zone size, directly correlating the extent of plastic deformation with the magnitude of the crack closure effect.
- This study provides a validated computational methodology for accurately predicting FCG life in engineering components subjected to demanding, fully reversed, and compressive–dominant cyclic loading environments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Manson, S.S.; Halford, G.R. Fatigue and Durability of Structural Materials; ASM International: Novelty, OH, USA, 2006. [Google Scholar]
- Tiwari, S. Fatigue in Structures and Materials; Educohack Press: Delhi, India, 2025. [Google Scholar]
- Krupp, U. Fatigue Crack Propagation in Metals and Alloys: Microstructural Aspects and Modelling Concepts; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Carpinteri, A. Handbook of Fatigue Crack Propagation in Metallic Structures; Newnes: London, UK, 2012. [Google Scholar]
- Sun, C.-T.; Jin, Z. Fracture mechanics; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Gdoutos, E.E. Fracture Mechanics Criteria and Applications; Springer Science & Business Media: Berlin, Germany, 2012; Volume 10. [Google Scholar]
- Fageehi, Y.A.; Alshoaibi, A.M. Investigating the Influence of Holes as Crack Arrestors in Simulating Crack Growth Behavior Using Finite Element Method. Appl. Sci. 2024, 14, 897. [Google Scholar] [CrossRef]
- Fageehi, Y.A.; Alshoaibi, A.M. Comparative Finite Element Analysis of Fatigue Crack Growth in High-Performance Metallic Alloys: Influence of Material Parameters and Paris Law Constants. Crystals 2025, 15, 801. [Google Scholar] [CrossRef]
- Silva, F. Fatigue crack propagation after overloading and underloading at negative stress ratios. Int. J. Fatigue 2007, 29, 1757–1771. [Google Scholar] [CrossRef]
- Xie, L.-Q.; Zhang, P.; He, X.-H.; Zhou, C.-Y. Effect of single tensile overload on fatigue crack growth behavior of CP-Ti at negative load ratio. Int. J. Fatigue 2021, 145, 106129. [Google Scholar] [CrossRef]
- Lu, Z.; Xu, J.; Wang, L.; Zhang, J.; Liu, Y. Curvilinear fatigue crack growth simulation and validation under constant amplitude and overload loadings. J. Aerosp. Eng. 2015, 28, 04014054. [Google Scholar] [CrossRef]
- Oplt, T.; Vojtek, T.; Kubíček, R.; Pokorný, P.; Hutař, P. Numerical modelling of fatigue crack closure and its implication on crack front curvature using ΔCTODp. Int. J. Fatigue 2023, 171, 107570. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, S.; Yang, B.; Xiao, S.; Yang, G.; Zhu, T. Effective stress intensity factor range for fatigue cracks propagating in mixed mode I-II loading. Eng. Fract. Mech. 2024, 312, 110641. [Google Scholar] [CrossRef]
- Benz, C. Fatigue crack growth at negative stress ratios: On the uncertainty of using ΔK and R to define the cyclic crack tip load. Eng. Fract. Mech. 2018, 189, 194–203. [Google Scholar] [CrossRef]
- Benz, C.; Sander, M. Reconsiderations of fatigue crack growth at negative stress ratios: Finite element analyses. Eng. Fract. Mech. 2015, 145, 98–114. [Google Scholar] [CrossRef]
- Zhang, P.; Zhou, C.-Y.; Xie, L.-Q.; He, X.-H. Numerical investigation of mechanical behavior of crack tip under mode I and mixed-mode I-II fatigue loading at negative load ratios. Theor. Appl. Fract. Mech. 2020, 108, 102673. [Google Scholar] [CrossRef]
- Zhang, P.; Zhou, C.-Y.; Li, J.; Miao, X.-T.; He, X.-H. Effect of compressive load and crack closure on fatigue crack growth of commercial pure titanium at negative load ratios. Eng. Fract. Mech. 2019, 219, 106622. [Google Scholar] [CrossRef]
- Zhang, P.; Xie, L.-Q.; Zhou, C.-Y.; He, X.-H. Experimental and numerical investigation on fatigue crack growth behavior of commercial pure titanium under I-II mixed mode loading at negative load ratios. Int. J. Fatigue 2020, 138, 105700. [Google Scholar] [CrossRef]
- Qin, D.; Xiayang, L.; Geng, X. Experimental study on low-cycle fatigue characteristics of marine structural steel. J. Mar. Sci. Eng. 2024, 12, 651. [Google Scholar] [CrossRef]
- Ghafoori Ahangar, R.; Verreman, Y. Assessment of mode I and mode II stress intensity factors obtained by displacement extrapolation and interaction integral methods. J. Fail. Anal. Prev. 2019, 19, 85–97. [Google Scholar] [CrossRef]
- Erdogan, F.; Sih, G. On the crack extension in plates under plane loading and transverse shear. J. Basic Eng. 1963, 85, 519–525. [Google Scholar] [CrossRef]
- Bjørheim, F. Practical Comparison of Crack Meshing in ANSYS Mechanical APDL 19.2. Master’s Thesis, University of Stavanger, Stavanger, Norway, 2019. [Google Scholar]
- Xiangqiao, Y.; Shanyi, D.; Zehua, Z. Mixed-mode fatigue crack growth prediction in biaxially stretched sheets. Eng. Fract. Mech. 1992, 43, 471–475. [Google Scholar] [CrossRef]
- Tanaka, K. Fatigue crack propagation from a crack inclined to the cyclic tensile axis. Eng. Fract. Mech. 1974, 6, 493–507. [Google Scholar] [CrossRef]
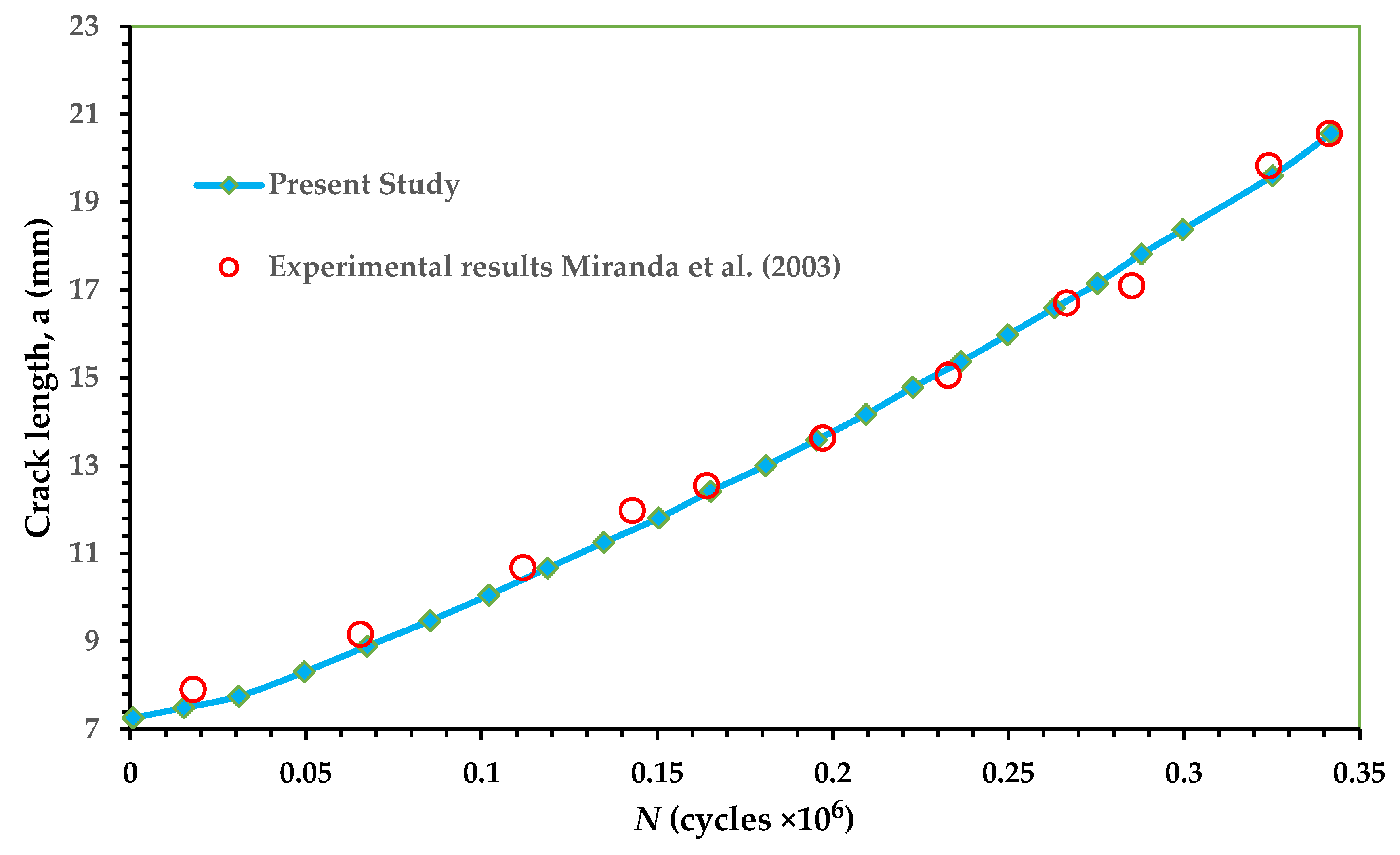
- Miranda, A.; Meggiolaro, M.; Castro, J.; Martha, L.; Bittencourt, T. Fatigue life and crack path predictions in generic 2D structural components. Eng. Fract. Mech. 2003, 70, 1259–1279. [Google Scholar] [CrossRef]
- Pradhan, D.; Mahobia, G.; Chattopadhyay, K.; Fernando, D.; Paulose, N.; Babu, S.; Singh, V. Effect of stress ratio and mean stress on high cycle fatigue behavior of the superalloy IN718 at elevated temperatures. Mater. Res. Express 2019, 6, 0965a6. [Google Scholar] [CrossRef]
- Elber, W. The Significance of Fatigue Crack Closure; American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 1971. [Google Scholar]
- Salvati, E.; Zhang, H.; Fong, K.S.; Song, X.; Korsunsky, A.M. Separating plasticity-induced closure and residual stress contributions to fatigue crack retardation following an overload. J. Mech. Phys. Solids 2017, 98, 222–235. [Google Scholar] [CrossRef]




| Property | Value in Metric Unit |
|---|---|
| Modulus of elasticity, E | 205 GPa |
| Poisson’s ratio, υ | 0.29 |
| Yield strength, σy | 285 MPa |
| Ultimate strength, σu | 491 MPa |
| Paris’ law coefficient, C | 8.59 × 10−14 |
| Paris law exponent, m | 4.26 |
| Stress Ratio (R) | Fatigue Life of CT1 (Cycles to Failure) | Fatigue Life of CT2 (Cycles to Failure) |
|---|---|---|
| 0.1 | 341,250 | 142,092 |
| −0.1 | 133,655 | 56,836 |
| −0.2 | 92,159 | 39,197 |
| −0.3 | 65,622 | 27,998 |
| −0.4 | 47,862 | 20,436 |
| −0.5 | 35,674 | 15,720 |
| −1 | 10,471 | 4623 |
| Stress Ratio (R) | Maximum Principal Stress (MPa), CT1 | Maximum Principal Stress (MPa), CT2 |
|---|---|---|
| 0.1 | 236.13 | 173.71 |
| −0.1 | 218.22 | 159.23 |
| −0.2 | 224.67 | 164.24 |
| −0.3 | 158.65 | 115.85 |
| −0.4 | 231.78 | 169.12 |
| −0.5 | 300.23 | 219.58 |
| −1 | 284.97 | 208.75 |
| Stress Ratio (R) | Max Von Mises Stress (MPa) |
|---|---|
| 0.1 | 153.06 |
| −0.1 | 176.37 |
| −0.2 | 172 |
| −0.3 | 199.76 |
| −0.4 | 198.14 |
| −0.5 | 188.16 |
| −1 | 146.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fageehi, Y.A.; Alshoaibi, A.M. Modeling Fatigue Crack Growth Under Compressive Loads: The Role of Non-Monotonic Stress and Crack Closure. Crystals 2025, 15, 979. https://doi.org/10.3390/cryst15110979
Fageehi YA, Alshoaibi AM. Modeling Fatigue Crack Growth Under Compressive Loads: The Role of Non-Monotonic Stress and Crack Closure. Crystals. 2025; 15(11):979. https://doi.org/10.3390/cryst15110979
Chicago/Turabian StyleFageehi, Yahya Ali, and Abdulnaser M. Alshoaibi. 2025. "Modeling Fatigue Crack Growth Under Compressive Loads: The Role of Non-Monotonic Stress and Crack Closure" Crystals 15, no. 11: 979. https://doi.org/10.3390/cryst15110979
APA StyleFageehi, Y. A., & Alshoaibi, A. M. (2025). Modeling Fatigue Crack Growth Under Compressive Loads: The Role of Non-Monotonic Stress and Crack Closure. Crystals, 15(11), 979. https://doi.org/10.3390/cryst15110979







