Stability of Higher-Order Skyrmion Crystals Under Competing Magnetic Anisotropies in D3d Systems
Abstract
1. Introduction
2. Model and Method
3. Results
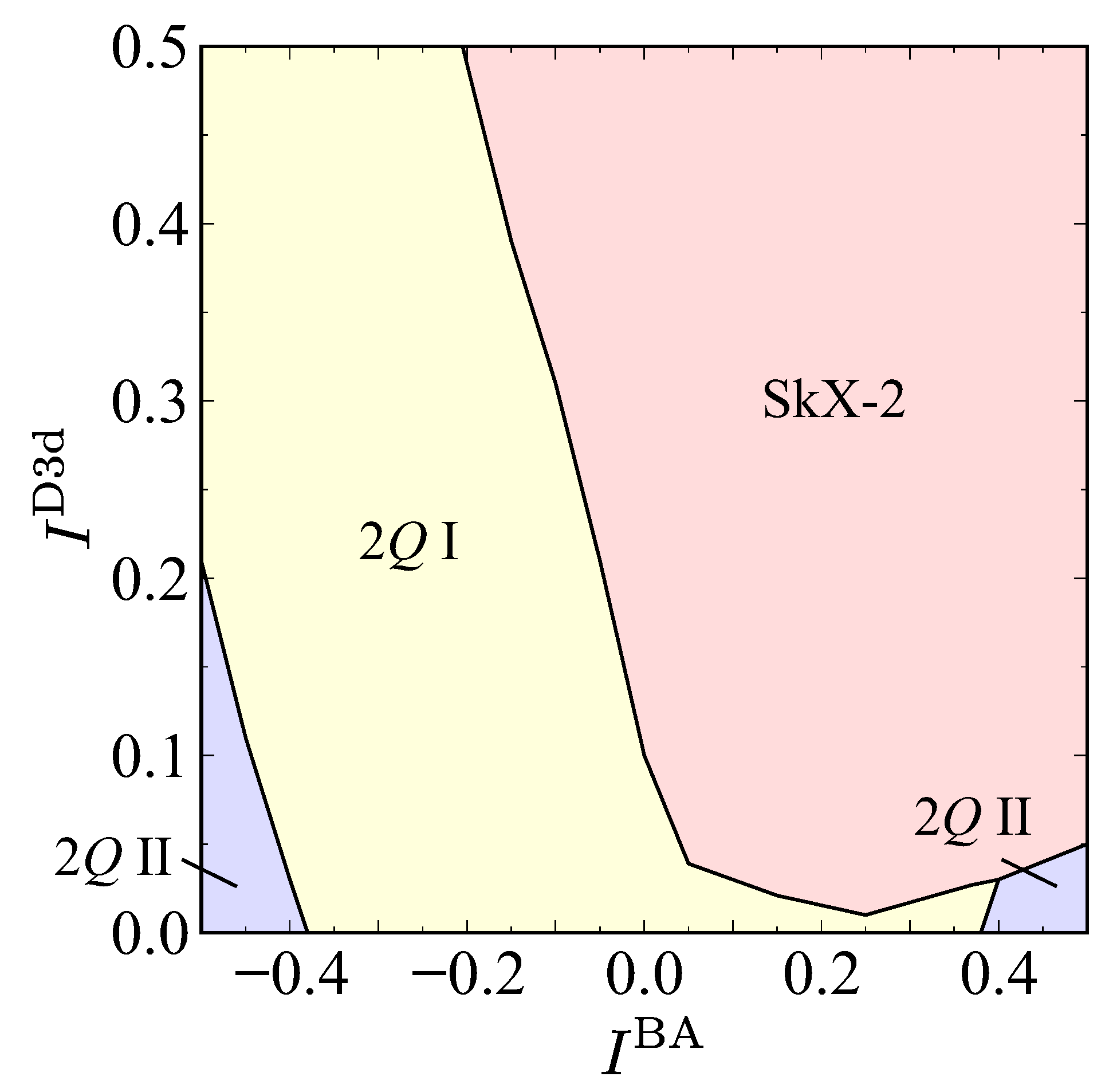
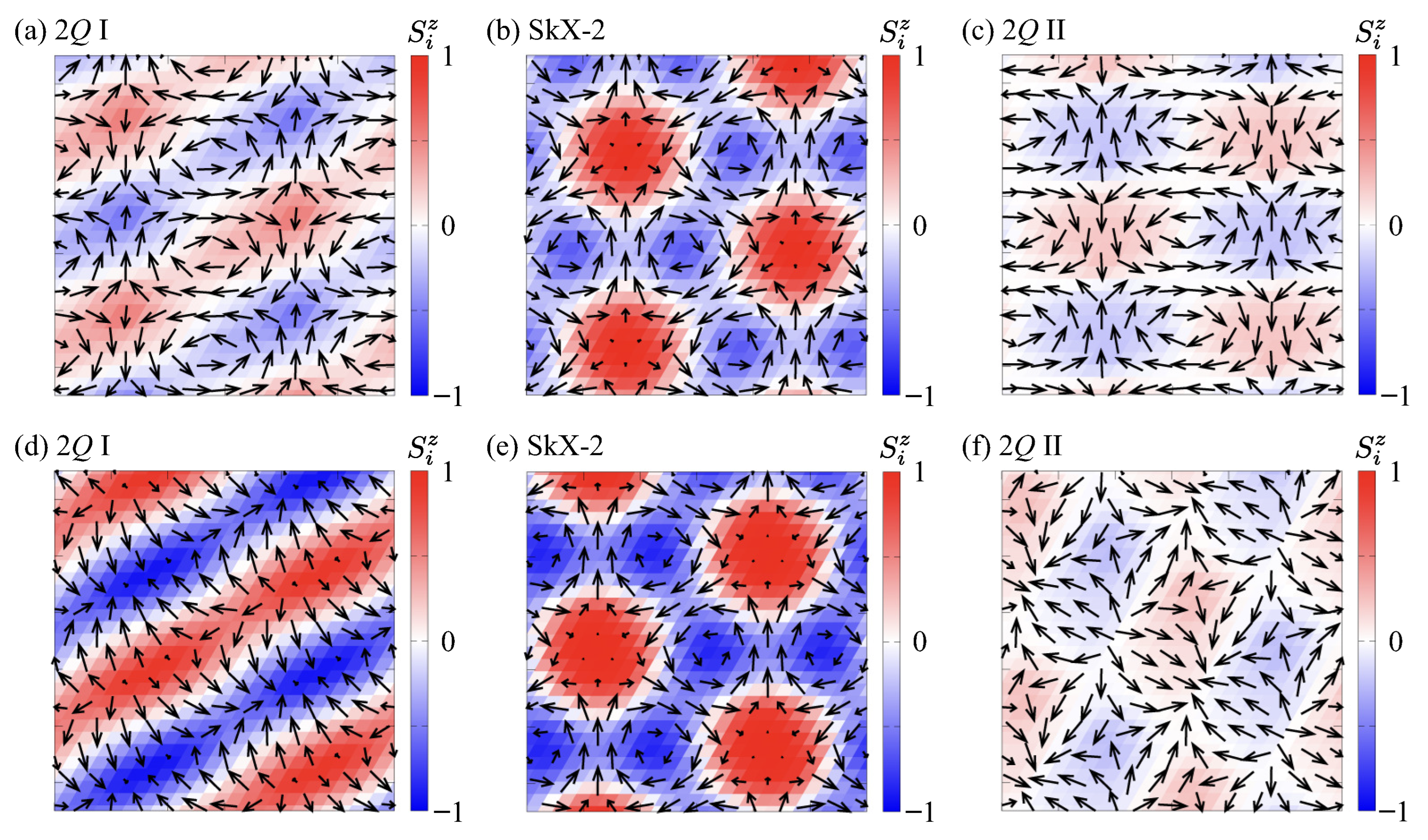
3.1. Zero Magnetic Field
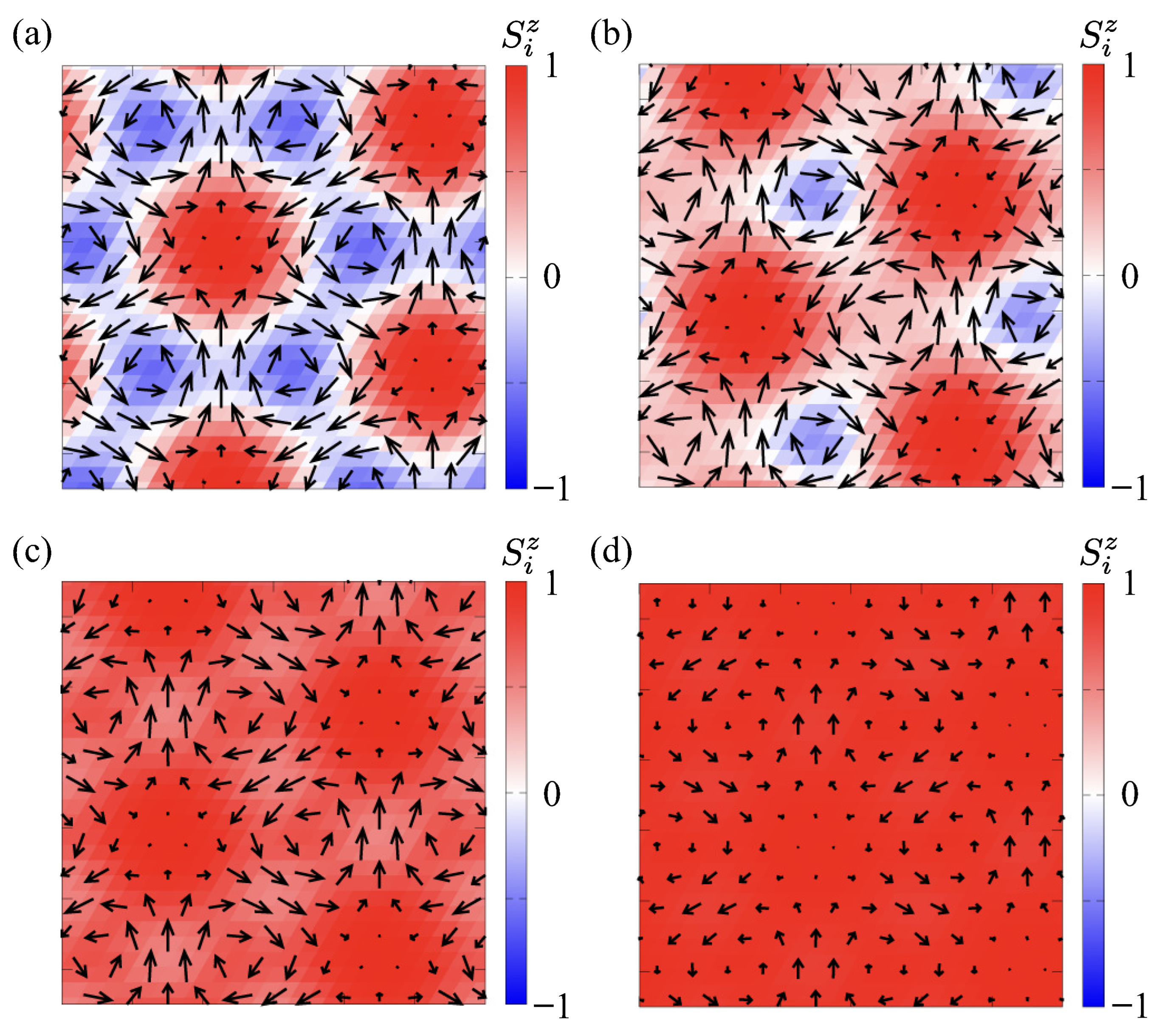
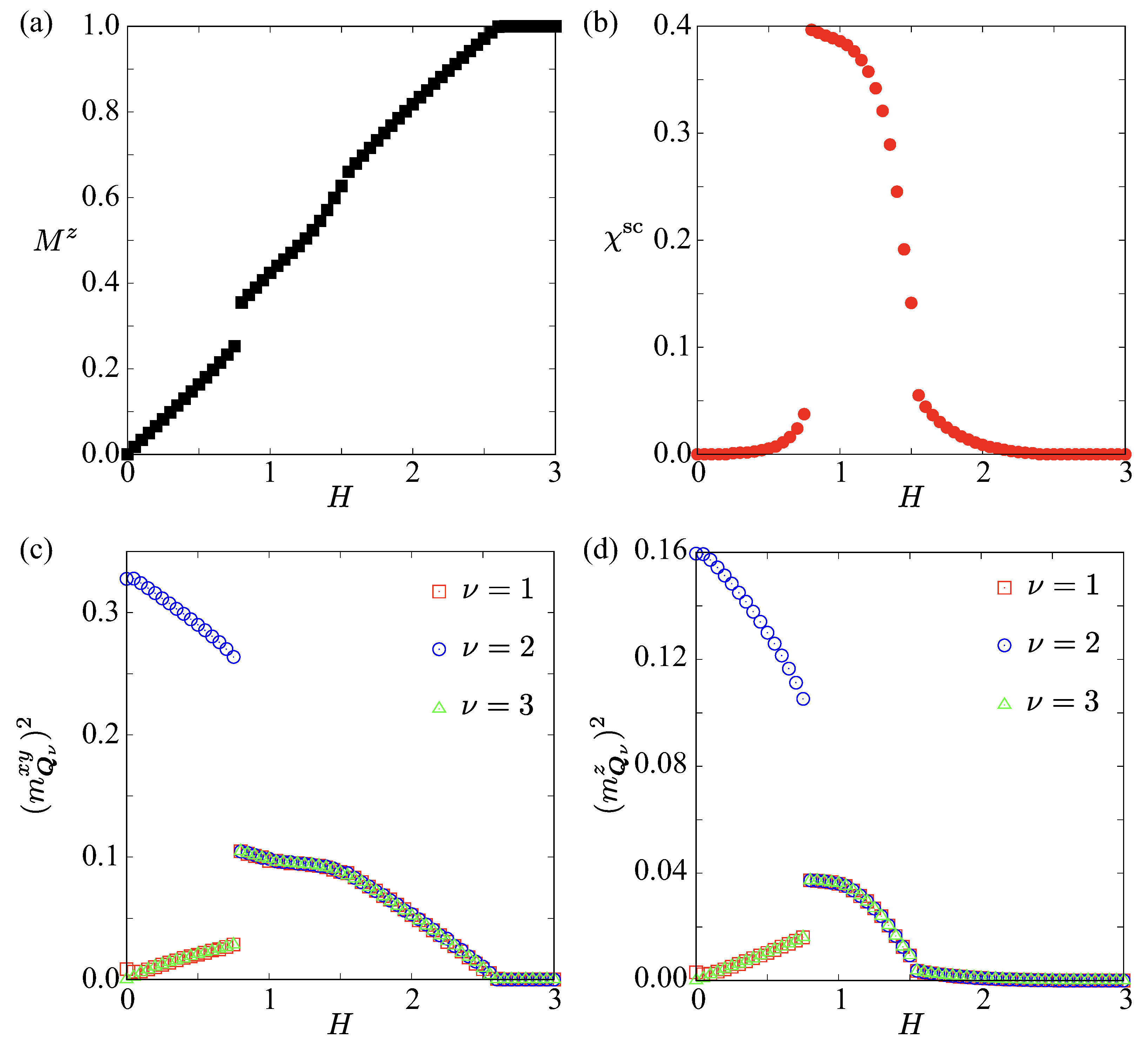
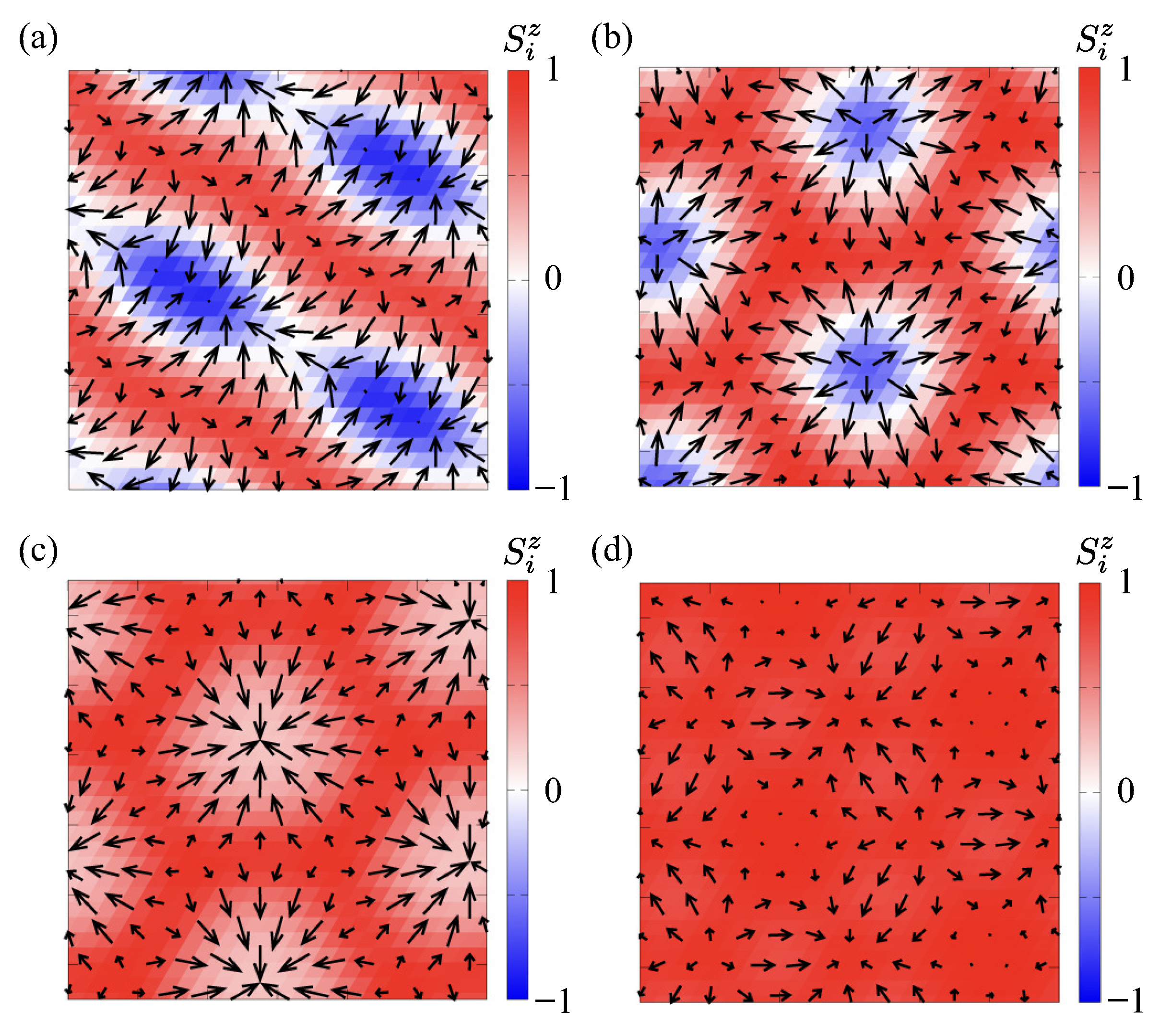
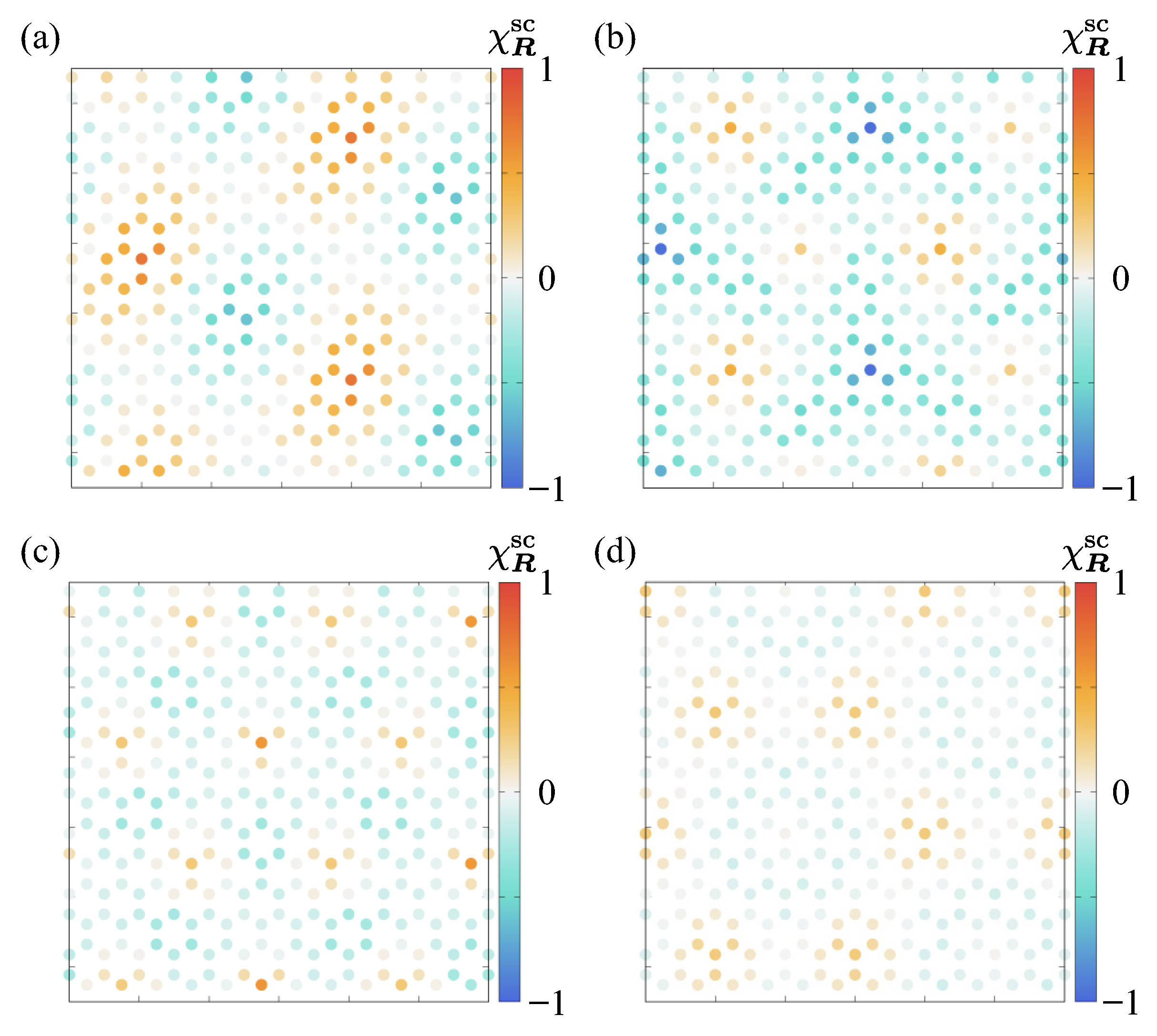
3.2. Effect of Magnetic Field
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Skyrme, T. A non-linear field theory. Proc. R. Soc. 1961, 260, 127. [Google Scholar]
- Skyrme, T.H.R. A unified field theory of mesons and baryons. Nucl. Phys. 1962, 31, 556–569. [Google Scholar] [CrossRef]
- Bogdanov, A.N.; Yablonskii, D.A. Thermodynamically stable “vortices” in magnetically ordered crystals: The mixed state of magnets. Sov. Phys. JETP 1989, 68, 101. [Google Scholar]
- Bogdanov, A.; Hubert, A. Thermodynamically stable magnetic vortex states in magnetic crystals. J. Magn. Magn. Mater. 1994, 138, 255–269. [Google Scholar] [CrossRef]
- Rößler, U.K.; Bogdanov, A.N.; Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 2006, 442, 797–801. [Google Scholar] [CrossRef]
- Loss, D.; Goldbart, P.M. Persistent currents from Berry’s phase in mesoscopic systems. Phys. Rev. B 1992, 45, 13544–13561. [Google Scholar] [CrossRef]
- Ye, J.; Kim, Y.B.; Millis, A.J.; Shraiman, B.I.; Majumdar, P.; Tešanović, Z. Berry Phase Theory of the Anomalous Hall Effect: Application to Colossal Magnetoresistance Manganites. Phys. Rev. Lett. 1999, 83, 3737–3740. [Google Scholar] [CrossRef]
- Ohgushi, K.; Murakami, S.; Nagaosa, N. Spin anisotropy and quantum Hall effect in the Kagomé Lattice: Chiral Spin State Based A Ferromagnet. Phys. Rev. B 2000, 62, R6065–R6068. [Google Scholar] [CrossRef]
- Taguchi, Y.; Oohara, Y.; Yoshizawa, H.; Nagaosa, N.; Tokura, Y. Spin chirality, Berry phase, and anomalous Hall effect in a frustrated ferromagnet. Science 2001, 291, 2573–2576. [Google Scholar] [CrossRef] [PubMed]
- Tatara, G.; Kawamura, H. Chirality-driven anomalous Hall effect in weak coupling regime. J. Phys. Soc. Jpn. 2002, 71, 2613–2616. [Google Scholar] [CrossRef]
- Neubauer, A.; Pfleiderer, C.; Binz, B.; Rosch, A.; Ritz, R.; Niklowitz, P.G.; Böni, P. Topological Hall Effect in the A Phase of MnSi. Phys. Rev. Lett. 2009, 102, 186602. [Google Scholar] [CrossRef]
- Hamamoto, K.; Ezawa, M.; Nagaosa, N. Quantized topological Hall effect in skyrmion crystal. Phys. Rev. B 2015, 92, 115417. [Google Scholar] [CrossRef]
- Nakazawa, K.; Bibes, M.; Kohno, H. Topological Hall effect from strong to weak coupling. J. Phys. Soc. Jpn. 2018, 87, 033705. [Google Scholar] [CrossRef]
- Tai, L.; Dai, B.; Li, J.; Huang, H.; Chong, S.K.; Wong, K.L.; Zhang, H.; Zhang, P.; Deng, P.; Eckberg, C.; et al. Distinguishing the two-component anomalous Hall effect from the topological Hall effect. ACS Nano 2022, 16, 17336–17346. [Google Scholar] [CrossRef]
- Nagaosa, N. Emergent inductor by spiral magnets. Jpn. J. Appl. Phys. 2019, 58, 120909. [Google Scholar] [CrossRef]
- Yokouchi, T.; Kagawa, F.; Hirschberger, M.; Otani, Y.; Nagaosa, N.; Tokura, Y. Emergent electromagnetic induction in a helical-spin magnet. Nature 2020, 586, 232–236. [Google Scholar] [CrossRef] [PubMed]
- Ieda, J.; Yamane, Y. Intrinsic and extrinsic tunability of Rashba spin-orbit coupled emergent inductors. Phys. Rev. B 2021, 103, L100402. [Google Scholar] [CrossRef]
- Kitaori, A.; Kanazawa, N.; Yokouchi, T.; Kagawa, F.; Nagaosa, N.; Tokura, Y. Emergent electromagnetic induction beyond room temperature. Proc. Natl. Acad. Sci. USA 2021, 118. [Google Scholar] [CrossRef]
- Kurebayashi, D.; Nagaosa, N. Electromagnetic response in spiral magnets and emergent inductance. Commun. Phys. 2021, 4, 260. [Google Scholar] [CrossRef]
- Yamane, Y.; Fukami, S.; Ieda, J. Theory of Emergent Inductance with Spin-Orbit Coupling Effects. Phys. Rev. Lett. 2022, 128, 147201. [Google Scholar] [CrossRef] [PubMed]
- Anan, T.; Morimoto, T. Emergent inductors in nonhelical magnets. Phys. Rev. B 2025, 111, 184424. [Google Scholar] [CrossRef]
- Zang, J.; Mostovoy, M.; Han, J.H.; Nagaosa, N. Dynamics of Skyrmion Crystals in Metallic Thin Films. Phys. Rev. Lett. 2011, 107, 136804. [Google Scholar] [CrossRef]
- Lin, S.Z.; Reichhardt, C.; Batista, C.D.; Saxena, A. Particle model for skyrmions in metallic chiral magnets: Dynamics, pinning, and creep. Phys. Rev. B 2013, 87, 214419. [Google Scholar] [CrossRef]
- Reichhardt, C.; Reichhardt, C. Fluctuations and pinning for individually manipulated skyrmions. Front. Phys. 2021, 9, 767491. [Google Scholar] [CrossRef]
- Henderson, M.E.; Bleuel, M.; Beare, J.; Cory, D.G.; Heacock, B.; Huber, M.G.; Luke, G.M.; Pula, M.; Sarenac, D.; Sharma, S.; et al. Skyrmion alignment and pinning effects in the disordered multiphase skyrmion material Co8Zn8Mn4. Phys. Rev. B 2022, 106, 094435. [Google Scholar] [CrossRef]
- Reichhardt, C.; Reichhardt, C.J.O.; Milošević, M.V. Statics and dynamics of skyrmions interacting with disorder and nanostructures. Rev. Mod. Phys. 2022, 94, 035005. [Google Scholar] [CrossRef]
- Gruber, R.; Zázvorka, J.; Brems, M.A.; Rodrigues, D.R.; Dohi, T.; Kerber, N.; Seng, B.; Vafaee, M.; Everschor-Sitte, K.; Virnau, P.; et al. Skyrmion pinning energetics in thin film systems. Nat. Commun. 2022, 13, 3144. [Google Scholar] [CrossRef]
- Jonietz, F.; Mühlbauer, S.; Pfleiderer, C.; Neubauer, A.; Münzer, W.; Bauer, A.; Adams, T.; Georgii, R.; Böni, P.; Duine, R.A.; et al. Spin Transfer Torques in MnSi at Ultralow Current Densities. Science 2010, 330, 1648. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.Z.; Kanazawa, N.; Zhang, W.; Nagai, T.; Hara, T.; Kimoto, K.; Matsui, Y.; Onose, Y.; Tokura, Y. Skyrmion flow near room temperature in an ultralow current density. Nat. Commun. 2012, 3, 988. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, X.; Yu, G.; Zhang, W.; Wang, X.; Benjamin Jungfleisch, M.; Pearson, J.E.; Cheng, X.; Heinonen, O.; Wang, K.L.; et al. Direct observation of the skyrmion Hall effect. Nat. Phys. 2017, 13, 162–169. [Google Scholar] [CrossRef]
- Yu, X.; Morikawa, D.; Nakajima, K.; Shibata, K.; Kanazawa, N.; Arima, T.H.; Nagaosa, N.; Tokura, Y. Motion tracking of 80-nm-size skyrmions upon directional current injections. Sci. Adv. 2020, 6, eaaz9744. [Google Scholar] [CrossRef]
- Pham, V.T.; Sisodia, N.; Di Manici, I.; Urrestarazu-Larrañaga, J.; Bairagi, K.; Pelloux-Prayer, J.; Guedas, R.; Buda-Prejbeanu, L.D.; Auffret, S.; Locatelli, A.; et al. Fast current-induced skyrmion motion in synthetic antiferromagnets. Science 2024, 384, 307–312. [Google Scholar] [CrossRef] [PubMed]
- Song, D.; Wang, W.; Zhang, S.; Liu, Y.; Wang, N.; Zheng, F.; Tian, M.; Dunin-Borkowski, R.E.; Zang, J.; Du, H. Steady motion of 80-nm-size skyrmions in a 100-nm-wide track. Nat. Commun. 2024, 15, 5614. [Google Scholar] [CrossRef]
- Ji, Y.; Yang, S.; Ahn, H.B.; Moon, K.W.; Ju, T.S.; Im, M.Y.; Han, H.S.; Lee, J.; Park, S.y.; Lee, C.; et al. Direct Observation of Room-Temperature Magnetic Skyrmion Motion Driven by Ultra-Low Current Density in Van Der Waals Ferromagnets. Adv. Mater. 2024, 36, 2312013. [Google Scholar] [CrossRef]
- Birch, M.T.; Belopolski, I.; Fujishiro, Y.; Kawamura, M.; Kikkawa, A.; Taguchi, Y.; Hirschberger, M.; Nagaosa, N.; Tokura, Y. Dynamic transition and Galilean relativity of current-driven skyrmions. Nature 2024, 633, 554–559. [Google Scholar] [CrossRef] [PubMed]
- Nagaosa, N.; Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 2013, 8, 899–911. [Google Scholar] [CrossRef]
- Tokura, Y.; Kanazawa, N. Magnetic Skyrmion Materials. Chem. Rev. 2021, 121, 2857. [Google Scholar] [CrossRef]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral magnet. Science 2009, 323, 915–919. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.Z.; Onose, Y.; Kanazawa, N.; Park, J.H.; Han, J.H.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904. [Google Scholar] [CrossRef]
- Adams, T.; Mühlbauer, S.; Neubauer, A.; Münzer, W.; Jonietz, F.; Georgii, R.; Pedersen, B.; Böni, P.; Rosch, A.; Pfleiderer, C. Skyrmion lattice domains in Fe1−xCoxSi. J. Phys. Conf. Ser. 2010, 200, 032001. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 1960, 120, 91. [Google Scholar] [CrossRef]
- Yi, S.D.; Onoda, S.; Nagaosa, N.; Han, J.H. Skyrmions and anomalous Hall effect in a Dzyaloshinskii-Moriya spiral magnet. Phys. Rev. B 2009, 80, 054416. [Google Scholar] [CrossRef]
- Binz, B.; Vishwanath, A.; Aji, V. Theory of the Helical Spin Crystal: A Candidate for the Partially Ordered State of MnSi. Phys. Rev. Lett. 2006, 96, 207202. [Google Scholar] [CrossRef]
- Binz, B.; Vishwanath, A. Theory of helical spin crystals: Phases, textures, and properties. Phys. Rev. B 2006, 74, 214408. [Google Scholar] [CrossRef]
- Heinze, S.; von Bergmann, K.; Menzel, M.; Brede, J.; Kubetzka, A.; Wiesendanger, R.; Bihlmayer, G.; Blügel, S. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 2011, 7, 713–718. [Google Scholar] [CrossRef]
- Okubo, T.; Chung, S.; Kawamura, H. Multiple-q States and the Skyrmion Lattice of the Triangular-Lattice Heisenberg Antiferromagnet under Magnetic Fields. Phys. Rev. Lett. 2012, 108, 017206. [Google Scholar] [CrossRef] [PubMed]
- Leonov, A.O.; Mostovoy, M. Multiply periodic states and isolated skyrmions in an anisotropic frustrated magnet. Nat. Commun. 2015, 6, 8275. [Google Scholar] [CrossRef]
- Hayami, S. Skyrmion crystal and spiral phases in centrosymmetric bilayer magnets with staggered Dzyaloshinskii-Moriya interaction. Phys. Rev. B 2022, 105, 014408. [Google Scholar] [CrossRef]
- Lin, S.Z. Skyrmion lattice in centrosymmetric magnets with local Dzyaloshinsky-Moriya interaction. Mater. Today Quantum 2024, 2, 100006. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Stabilization mechanisms of magnetic skyrmion crystal and multiple-Q states based on momentum-resolved spin interactions. Mater. Today Quantum 2024, 3, 100010. [Google Scholar] [CrossRef]
- Butenko, A.B.; Leonov, A.A.; Rößler, U.K.; Bogdanov, A.N. Stabilization of skyrmion textures by uniaxial distortions in noncentrosymmetric cubic helimagnets. Phys. Rev. B 2010, 82, 052403. [Google Scholar] [CrossRef]
- Wilson, M.N.; Butenko, A.B.; Bogdanov, A.N.; Monchesky, T.L. Chiral skyrmions in cubic helimagnet films: The role of uniaxial anisotropy. Phys. Rev. B 2014, 89, 094411. [Google Scholar] [CrossRef]
- Lin, S.Z.; Saxena, A.; Batista, C.D. Skyrmion fractionalization and merons in chiral magnets with easy-plane anisotropy. Phys. Rev. B 2015, 91, 224407. [Google Scholar] [CrossRef]
- Leonov, A.O.; Monchesky, T.L.; Romming, N.; Kubetzka, A.; Bogdanov, A.N.; Wiesendanger, R. The properties of isolated chiral skyrmions in thin magnetic films. New. J. Phys. 2016, 18, 065003. [Google Scholar] [CrossRef]
- Ehlers, D.; Stasinopoulos, I.; Tsurkan, V.; Krug von Nidda, H.A.; Fehér, T.; Leonov, A.; Kézsmárki, I.; Grundler, D.; Loidl, A. Skyrmion dynamics under uniaxial anisotropy. Phys. Rev. B 2016, 94, 014406. [Google Scholar] [CrossRef]
- Hayami, S. In-plane magnetic field-induced skyrmion crystal in frustrated magnets with easy-plane anisotropy. Phys. Rev. B 2021, 103, 224418. [Google Scholar] [CrossRef]
- Hoffmann, M.; Zimmermann, B.; Müller, G.P.; Schürhoff, D.; Kiselev, N.S.; Melcher, C.; Blügel, S. Antiskyrmions stabilized at interfaces by anisotropic Dzyaloshinskii-Moriya interactions. Nat. Commun. 2017, 8, 308. [Google Scholar] [CrossRef] [PubMed]
- Bogdanov, A.N.; Panagopoulos, C. Physical foundations and basic properties of magnetic skyrmions. Nat. Rev. Phys. 2020, 2, 492–498. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Degeneracy Lifting of Néel, Bloch, and Anti-Skyrmion Crystals in Centrosymmetric Tetragonal Systems. J. Phys. Soc. Jpn. 2020, 89, 103702. [Google Scholar] [CrossRef]
- Fert, A.; Reyren, N.; Cros, V. Magnetic skyrmions: Advances in physics and potential applications. Nat. Rev. Mater. 2017, 2, 17031. [Google Scholar] [CrossRef]
- Amoroso, D.; Barone, P.; Picozzi, S. Spontaneous skyrmionic lattice from anisotropic symmetric exchange in a Ni-halide monolayer. Nat. Commun. 2020, 11, 5784. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Noncoplanar multiple-Q spin textures by itinerant frustration: Effects of single-ion anisotropy and bond-dependent anisotropy. Phys. Rev. B 2021, 103, 054422. [Google Scholar] [CrossRef]
- Amoroso, D.; Barone, P.; Picozzi, S. Interplay between Single-Ion and Two-Ion Anisotropies in Frustrated 2D Semiconductors and Tuning of Magnetic Structures Topology. Nanomaterials 2021, 11, 1873. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Helicity locking of a square skyrmion crystal in a centrosymmetric lattice system without vertical mirror symmetry. Phys. Rev. B 2022, 105, 104428. [Google Scholar] [CrossRef]
- Yambe, R.; Hayami, S. Effective spin model in momentum space: Toward a systematic understanding of multiple-Q instability by momentum-resolved anisotropic exchange interactions. Phys. Rev. B 2022, 106, 174437. [Google Scholar] [CrossRef]
- Hayami, S.; Motome, Y. Effect of magnetic anisotropy on skyrmions with a high topological number in itinerant magnets. Phys. Rev. B 2019, 99, 094420. [Google Scholar] [CrossRef]
- Hayami, S. Multiple-Q magnetism by anisotropic bilinear-biquadratic interactions in momentum space. J. Magn. Magn. Mater. 2020, 513, 167181. [Google Scholar] [CrossRef]
- Day, P.; Moore, M.W.; Wilkinson, C.; Ziebeck, K.R.A. Neutron diffraction study of the incommensurate magnetic phase of Ni0.92Zn0.08Br2. J. Phys. C Solid State Phys. 1981, 14, 3423. [Google Scholar] [CrossRef]
- Regnault, L.; Rossat-Mignod, J.; Adam, A.; Billerey, D.; Terrier, C. Inelastic neutron scattering investigation of the magnetic excitations in the helimagnetic state of NiBr2. J. Phys. 1982, 43, 1283–1290. [Google Scholar] [CrossRef]
- Nakatsuji, S.; Nambu, Y.; Tonomura, H.; Sakai, O.; Jonas, S.; Broholm, C.; Tsunetsugu, H.; Qiu, Y.; Maeno, Y. Spin disorder on a triangular lattice. Science 2005, 309, 1697–1700. [Google Scholar] [CrossRef]
- Ghimire, N.; Ronning, F.; Williams, D.; Scott, B.; Luo, Y.; Thompson, J.; Bauer, E. Investigation of the physical properties of the tetragonal CeMAl4Si2 (M = Rh, Ir, Pt) compounds. J. Phys. Condens. Matter 2014, 27, 025601. [Google Scholar] [CrossRef]
- Ruderman, M.A.; Kittel, C. Indirect Exchange Coupling of Nuclear Magnetic Moments by Conduction Electrons. Phys. Rev. 1954, 96, 99–102. [Google Scholar] [CrossRef]
- Kasuya, T. A Theory of Metallic Ferro- and Antiferromagnetism on Zener’s Model. Prog. Theor. Phys. 1956, 16, 45–57. [Google Scholar] [CrossRef]
- Yosida, K. Magnetic Properties of Cu-Mn Alloys. Phys. Rev. 1957, 106, 893–898. [Google Scholar] [CrossRef]
- Utesov, O.I. Thermodynamically stable skyrmion lattice in a tetragonal frustrated antiferromagnet with dipolar interaction. Phys. Rev. B 2021, 103, 064414. [Google Scholar] [CrossRef]
- Wang, Z.; Su, Y.; Lin, S.Z.; Batista, C.D. Meron, skyrmion, and vortex crystals in centrosymmetric tetragonal magnets. Phys. Rev. B 2021, 103, 104408. [Google Scholar] [CrossRef]
- Utesov, O.I. Mean-field description of skyrmion lattice in hexagonal frustrated antiferromagnets. Phys. Rev. B 2022, 105, 054435. [Google Scholar] [CrossRef]
- Kurumaji, T.; Nakajima, T.; Hirschberger, M.; Kikkawa, A.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Taguchi, Y.; Arima, T.H.; Tokura, Y. Skyrmion lattice with a giant topological Hall effect in a frustrated triangular-lattice magnet. Science 2019, 365, 914–918. [Google Scholar] [CrossRef]
- Hirschberger, M.; Spitz, L.; Nomoto, T.; Kurumaji, T.; Gao, S.; Masell, J.; Nakajima, T.; Kikkawa, A.; Yamasaki, Y.; Sagayama, H.; et al. Topological Nernst Effect of the Two-Dimensional Skyrmion Lattice. Phys. Rev. Lett. 2020, 125, 076602. [Google Scholar] [CrossRef]
- Sampathkumaran, E.V. A report of (topological) Hall anomaly two decades ago in Gd2PdSi3, and its relevance to the history of the field of Topological Hall Effect due to magnetic skyrmions. arXiv 2019, arXiv:1910.09194. [Google Scholar]
- Kumar, R.; Iyer, K.K.; Paulose, P.L.; Sampathkumaran, E.V. Magnetic and transport anomalies in R2RhSi3 (R = Gd, Tb, and Dy) resembling those of the exotic magnetic material Gd2PdSi3. Phys. Rev. B 2020, 101, 144440. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, Q.; Hao, L.; Yang, J.; Noordhoek, K.; Pandey, S.; Zhou, H.; Liu, J. Anomalous magnetoresistance in centrosymmetric skyrmion-lattice magnet Gd2PdSi3. New J. Phys. 2020, 22, 083056. [Google Scholar] [CrossRef]
- Spachmann, S.; Elghandour, A.; Frontzek, M.; Löser, W.; Klingeler, R. Magnetoelastic coupling and phases in the skyrmion lattice magnet Gd2PdSi3 discovered by high-resolution dilatometry. Phys. Rev. B 2021, 103, 184424. [Google Scholar] [CrossRef]
- Paddison, J.A.M.; Rai, B.K.; May, A.F.; Calder, S.; Stone, M.B.; Frontzek, M.D.; Christianson, A.D. Magnetic Interactions of the Centrosymmetric Skyrmion Material Gd2PdSi3. Phys. Rev. Lett. 2022, 129, 137202. [Google Scholar] [CrossRef]
- Bouaziz, J.; Mendive-Tapia, E.; Blügel, S.; Staunton, J.B. Fermi-Surface Origin of Skyrmion Lattices in Centrosymmetric Rare-Earth Intermetallics. Phys. Rev. Lett. 2022, 128, 157206. [Google Scholar] [CrossRef]
- Ju, J.; Saito, H.; Kurumaji, T.; Hirschberger, M.; Kikkawa, A.; Taguchi, Y.; Arima, T.H.; Tokura, Y.; Nakajima, T. Polarized neutron scattering study of the centrosymmetric skyrmion host material Gd2PdSi3. Phys. Rev. B 2023, 107, 024405. [Google Scholar] [CrossRef]
- Nomoto, T.; Arita, R. Ab initio exploration of short-pitch skyrmion materials: Role of orbital frustration. J. Appl. Phys. 2023, 133, 150901. [Google Scholar] [CrossRef]
- Hirschberger, M.; Nakajima, T.; Gao, S.; Peng, L.; Kikkawa, A.; Kurumaji, T.; Kriener, M.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; et al. Skyrmion phase and competing magnetic orders on a breathing kagome lattice. Nat. Commun. 2019, 10, 5831. [Google Scholar] [CrossRef]
- Hirschberger, M.; Hayami, S.; Tokura, Y. Nanometric skyrmion lattice from anisotropic exchange interactions in a centrosymmetric host. New J. Phys. 2021, 23, 023039. [Google Scholar] [CrossRef]
- Nakamura, S.; Kabeya, N.; Kobayashi, M.; Araki, K.; Katoh, K.; Ochiai, A. Magnetic phases of the frustrated ferromagnetic spin-trimer system Gd3Ru4Al12 with a distorted kagome lattice structure. Phys. Rev. B 2023, 107, 014422. [Google Scholar] [CrossRef]
- Ogunbunmi, M.O.; Nair, H.S.; Strydom, A.M. Magnetic frustration-driven ground state properties of rare-earth magnetic ions on a breathing kagome lattice: A review of the Gd3Ru4 Al12 structure type magnets. Crit. Rev. Solid State Mater. Sci. 2023, 48, 480–501. [Google Scholar] [CrossRef]
- Khanh, N.D.; Nakajima, T.; Yu, X.; Gao, S.; Shibata, K.; Hirschberger, M.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Peng, L.; et al. Nanometric square skyrmion lattice in a centrosymmetric tetragonal magnet. Nat. Nanotechnol. 2020, 15, 444. [Google Scholar] [CrossRef]
- Matsuyama, N.; Nomura, T.; Imajo, S.; Nomoto, T.; Arita, R.; Sudo, K.; Kimata, M.; Khanh, N.D.; Takagi, R.; Tokura, Y.; et al. Quantum oscillations in the centrosymmetric skyrmion-hosting magnet GdRu2Si2. Phys. Rev. B 2023, 107, 104421. [Google Scholar] [CrossRef]
- Wood, G.D.A.; Khalyavin, D.D.; Mayoh, D.A.; Bouaziz, J.; Hall, A.E.; Holt, S.J.R.; Orlandi, F.; Manuel, P.; Blügel, S.; Staunton, J.B.; et al. Double-Q ground state with topological charge stripes in the centrosymmetric skyrmion candidate GdRu2Si2. Phys. Rev. B 2023, 107, L180402. [Google Scholar] [CrossRef]
- Eremeev, S.; Glazkova, D.; Poelchen, G.; Kraiker, A.; Ali, K.; Tarasov, A.V.; Schulz, S.; Kliemt, K.; Chulkov, E.V.; Stolyarov, V.; et al. Insight into the electronic structure of the centrosymmetric skyrmion magnet GdRu2Si2. Nanoscale Adv. 2023, 5, 6678–6687. [Google Scholar] [CrossRef]
- Yambe, R.; Hayami, S. Skyrmion crystals in centrosymmetric itinerant magnets without horizontal mirror plane. Sci. Rep. 2021, 11, 11184. [Google Scholar] [CrossRef]
- Hayami, S.; Kato, Y. Widely-sweeping magnetic field–temperature phase diagrams for skyrmion-hosting centrosymmetric tetragonal magnets. J. Magn. Magn. Mater. 2023, 571, 170547. [Google Scholar] [CrossRef]
- Shekhtman, L.; Aharony, A.; Entin-Wohlman, O. Bond-dependent symmetric and antisymmetric superexchange interactions in La2CuO4. Phys. Rev. B 1993, 47, 174–182. [Google Scholar] [CrossRef]
- Khomskii, D.; Mostovoy, M. Orbital ordering and frustrations. J. Phys. A 2003, 36, 9197. [Google Scholar] [CrossRef]
- Jackeli, G.; Khaliullin, G. Mott insulators in the strong spin-orbit coupling limit: From Heisenberg to a quantum compass and Kitaev models. Phys. Rev. Lett. 2009, 102, 017205. [Google Scholar] [CrossRef]
- Li, Y.D.; Wang, X.; Chen, G. Anisotropic spin model of strong spin-orbit-coupled triangular antiferromagnets. Phys. Rev. B 2016, 94, 035107. [Google Scholar] [CrossRef]
- Maksimov, P.A.; Zhu, Z.; White, S.R.; Chernyshev, A.L. Anisotropic-Exchange Magnets on a Triangular Lattice: Spin Waves, Accidental Degeneracies, and Dual Spin Liquids. Phys. Rev. X 2019, 9, 021017. [Google Scholar] [CrossRef]
- Becker, M.; Hermanns, M.; Bauer, B.; Garst, M.; Trebst, S. Spin-orbit physics of j = Mott insulators on the triangular lattice. Phys. Rev. B 2015, 91, 155135. [Google Scholar] [CrossRef]
- Rousochatzakis, I.; Rössler, U.K.; van den Brink, J.; Daghofer, M. Kitaev anisotropy induces mesoscopic Z2 vortex crystals in frustrated hexagonal antiferromagnets. Phys. Rev. B 2016, 93, 104417. [Google Scholar] [CrossRef]
- Liu, C.; Yu, R.; Wang, X. Semiclassical ground-state phase diagram and multi-Q phase of a spin-orbit-coupled model on triangular lattice. Phys. Rev. B 2016, 94, 174424. [Google Scholar] [CrossRef]
- Chern, G.W.; Sizyuk, Y.; Price, C.; Perkins, N.B. Kitaev-Heisenberg model in a magnetic field: Order-by-disorder and commensurate-incommensurate transitions. Phys. Rev. B 2017, 95, 144427. [Google Scholar] [CrossRef]
- Hayami, S. Multiple skyrmion crystal phases by itinerant frustration in centrosymmetric tetragonal magnets. J. Phys. Soc. Jpn. 2022, 91, 023705. [Google Scholar] [CrossRef]
- Matsumoto, T.; Hayami, S. Nonreciprocal magnons due to symmetric anisotropic exchange interaction in honeycomb antiferromagnets. Phys. Rev. B 2020, 101, 224419. [Google Scholar] [CrossRef]
- Takagi, R.; White, J.; Hayami, S.; Arita, R.; Honecker, D.; Rønnow, H.; Tokura, Y.; Seki, S. Multiple-q noncollinear magnetism in an itinerant hexagonal magnet. Sci. Adv. 2018, 4, eaau3402. [Google Scholar] [CrossRef] [PubMed]
- Singh, D.; Fujishiro, Y.; Hayami, S.; Moody, S.H.; Nomoto, T.; Baral, P.R.; Ukleev, V.; Cubitt, R.; Steinke, N.J.; Gawryluk, D.J.; et al. Transition between distinct hybrid skyrmion textures through their hexagonal-to-square crystal transformation in a polar magnet. Nat. Commun. 2023, 14, 8050. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Yambe, R. Field-Direction Sensitive Skyrmion Crystals in Cubic Chiral Systems: Implication to 4f-Electron Compound EuPtSi. J. Phys. Soc. Jpn. 2021, 90, 073705. [Google Scholar] [CrossRef]
- Berg, B.; Lüscher, M. Definition and statistical distributions of a topological number in the lattice O(3) σ-model. Nucl. Phys. B 1981, 190, 412–424. [Google Scholar] [CrossRef]
- Ozawa, R.; Hayami, S.; Motome, Y. Zero-Field Skyrmions with a High Topological Number in Itinerant Magnets. Phys. Rev. Lett. 2017, 118, 147205. [Google Scholar] [CrossRef]
- Hayami, S.; Okubo, T.; Motome, Y. Phase shift in skyrmion crystals. Nat. Commun. 2021, 12, 6927. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Yambe, R. Meron-antimeron crystals in noncentrosymmetric itinerant magnets on a triangular lattice. Phys. Rev. B 2021, 104, 094425. [Google Scholar] [CrossRef]
- Yu, X.Z.; Koshibae, W.; Tokunaga, Y.; Shibata, K.; Taguchi, Y.; Nagaosa, N.; Tokura, Y. Transformation between meron and skyrmion topological spin textures in a chiral magnet. Nature 2018, 564, 95–98. [Google Scholar] [CrossRef]
- Mohylna, M.; Gómez Albarracín, F.A.; Žukovič, M.; Rosales, H.D. Frustration-driven topological textures on the honeycomb lattice: Antiferromagnetic meron-antimeron and skyrmion crystals emerging from spiral spin liquids. Phys. Rev. B 2025, 111, 174435. [Google Scholar] [CrossRef]
- Kamiya, Y.; Batista, C.D. Magnetic Vortex Crystals in Frustrated Mott Insulator. Phys. Rev. X 2014, 4, 011023. [Google Scholar] [CrossRef]
- Hayami, S.; Lin, S.Z.; Kamiya, Y.; Batista, C.D. Vortices, skyrmions, and chirality waves in frustrated Mott insulators with a quenched periodic array of impurities. Phys. Rev. B 2016, 94, 174420. [Google Scholar] [CrossRef]


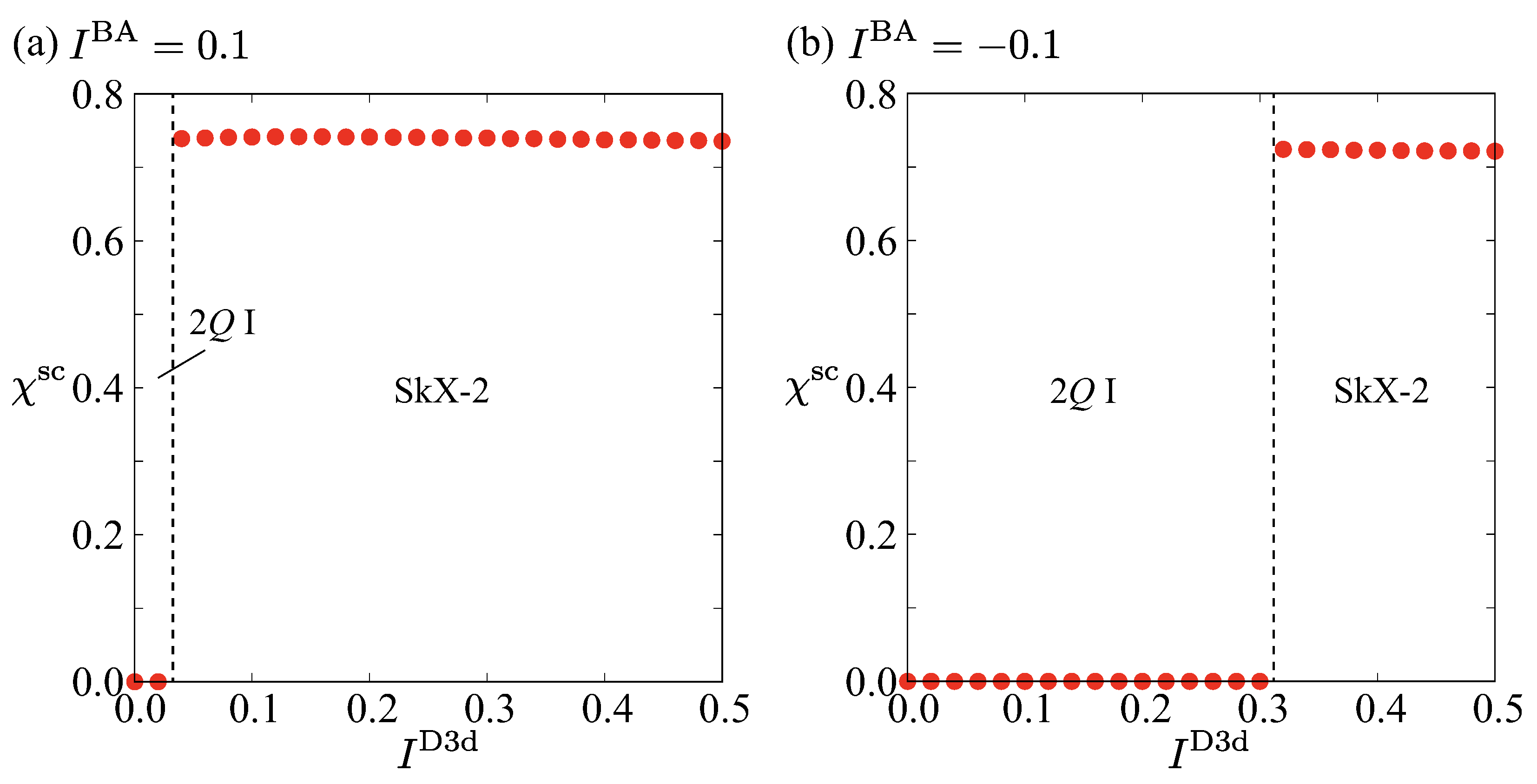


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayami, S. Stability of Higher-Order Skyrmion Crystals Under Competing Magnetic Anisotropies in D3d Systems. Crystals 2025, 15, 978. https://doi.org/10.3390/cryst15110978
Hayami S. Stability of Higher-Order Skyrmion Crystals Under Competing Magnetic Anisotropies in D3d Systems. Crystals. 2025; 15(11):978. https://doi.org/10.3390/cryst15110978
Chicago/Turabian StyleHayami, Satoru. 2025. "Stability of Higher-Order Skyrmion Crystals Under Competing Magnetic Anisotropies in D3d Systems" Crystals 15, no. 11: 978. https://doi.org/10.3390/cryst15110978
APA StyleHayami, S. (2025). Stability of Higher-Order Skyrmion Crystals Under Competing Magnetic Anisotropies in D3d Systems. Crystals, 15(11), 978. https://doi.org/10.3390/cryst15110978





