Explicit Crystal Plasticity Modeling of Texture Evolution in Nonlinear Twist Extrusion
Abstract
1. Introduction
2. Finite Element Model Definition
3. Explicit CPFEM Formulation
3.1. Kinematics
3.2. Power Law Type Flow Model
3.3. Hardening Model
3.4. Plastic Component of Deformation Gradient
3.5. Elastic Component of Deformation Gradient
3.6. Corotational Stress Rate
3.7. Calibration of Crystal Plasticity Model
4. Experimental Procedure
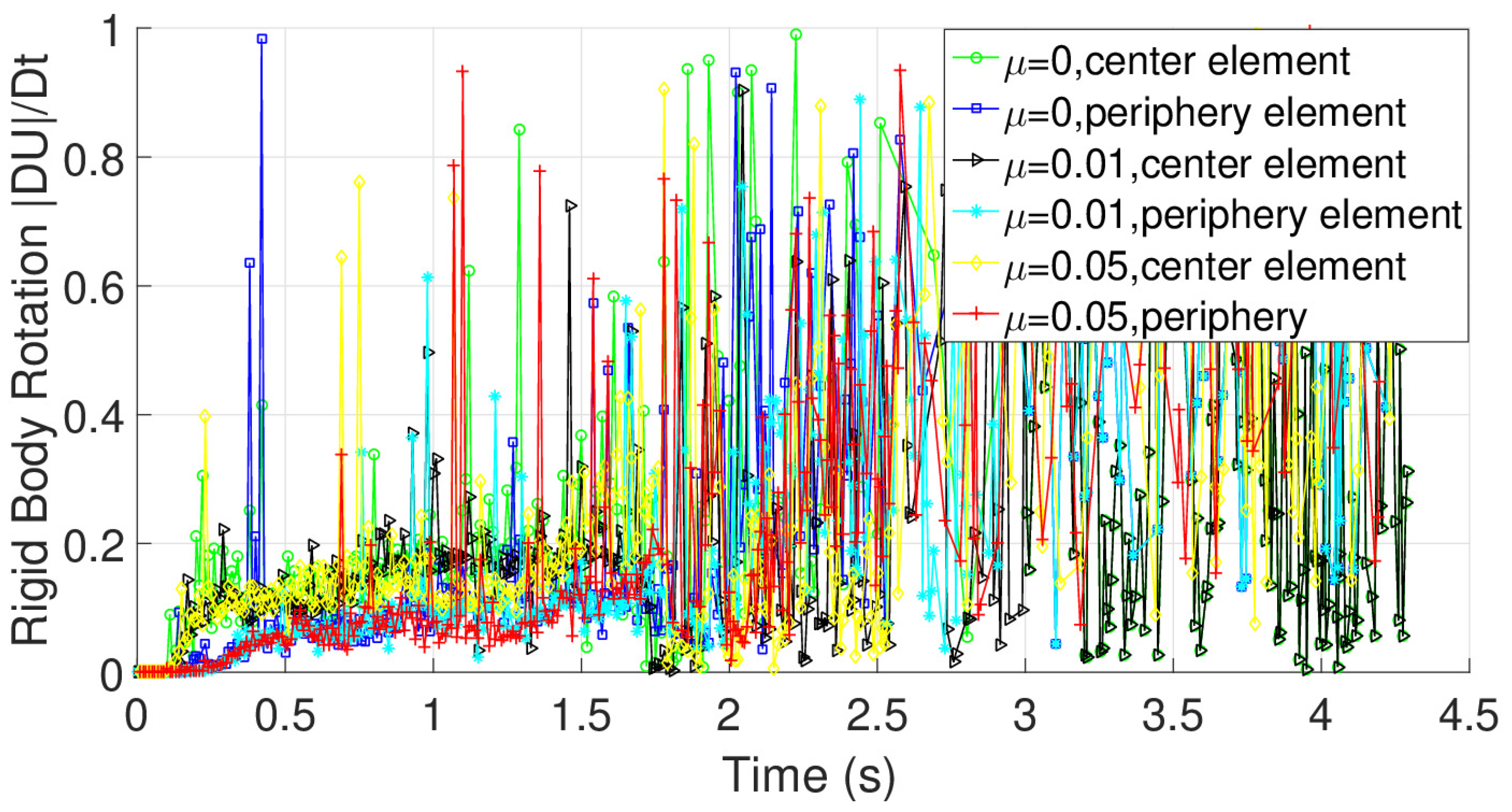
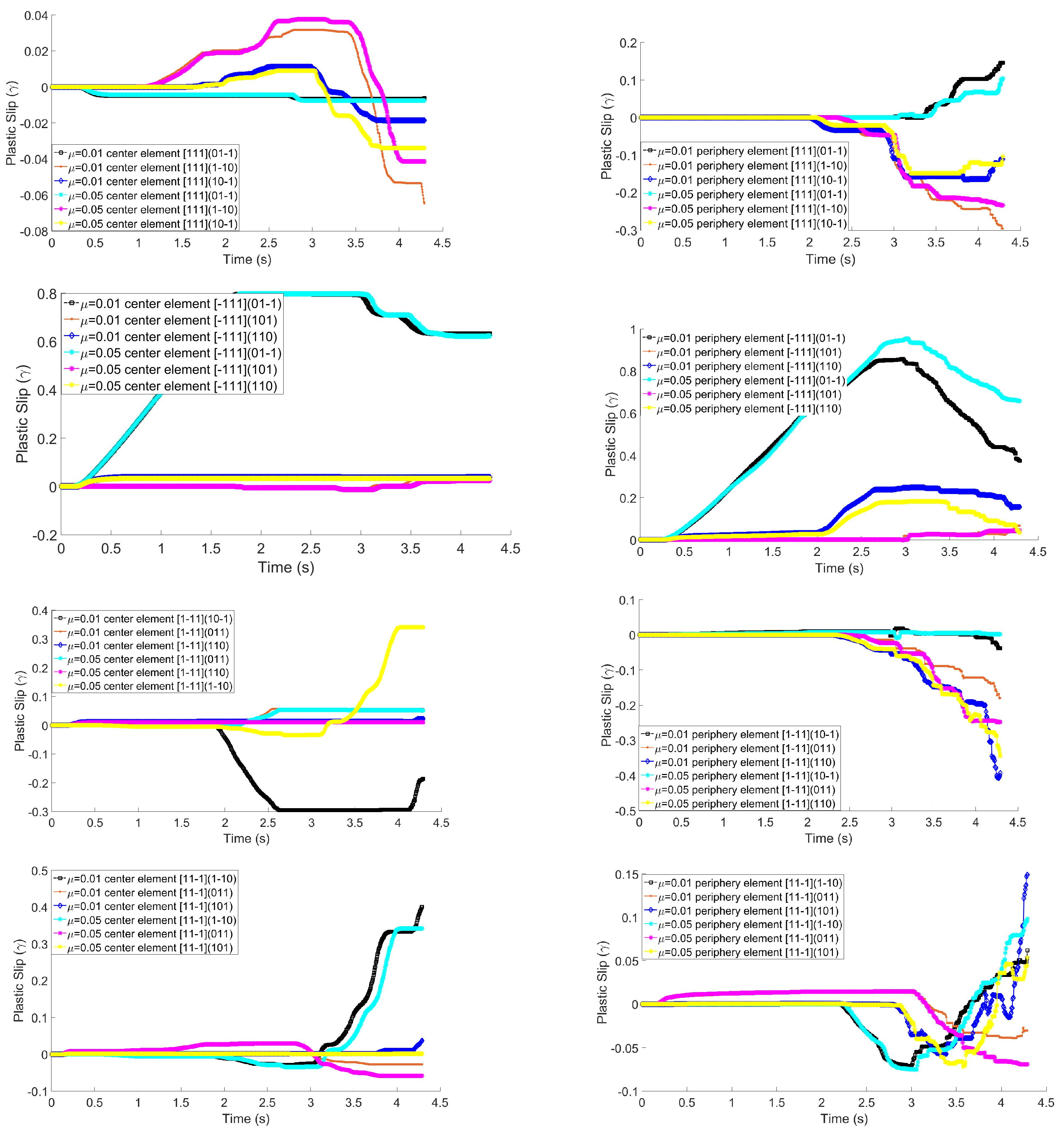
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Burton, M.-T.S.; Hornbuckle, B.C.; Hammond, V.H.; Darling, K.A.; Chan, H.M.; Marvel, C.J.; Harmer, M.P. Enhanced Microstructural Stability and Hardness of Multi-layered Nanocrystalline Nickel Alloys. Met. Mater. Int. 2024, 55, 1338–1350. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Li, J.; Chen, S. On the strain delocalization mechanism of Cu/Nb nanolayered composites with amorphous interfacial layers. Int. J. Plast. 2024, 172, 103856. [Google Scholar] [CrossRef]
- Al-Abboodi, H.; Al-Bahrani, M.; Al-Tameemi, A.; Al-Baghdadi, S.; Al-Maamori, M. Prediction of Crack Propagation of Nano-Crystalline Coating Made from Fe-Based Amorphous Material. Crystals 2023, 13, 365. [Google Scholar] [CrossRef]
- Velilla-Díaz, W.; Zambrano, H.R. Crack Length Effect on the Fracture Behavior of Single-Crystals and Bi-Crystals of Aluminum. Nanomaterials 2021, 11, 2783. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Huang, Q.; Zhou, H. High-entropy alloy nanocrystals with low-angle grain boundary for superb plastic deformability and recoverability. Int. J. Plast. 2023, 167, 103679. [Google Scholar] [CrossRef]
- Segal, V.M. Plastic working of metals by simple shear. Russ. Metall. 1981, 2, 99–105. [Google Scholar]
- Li, J.; Wang, X.; Zhang, Y.; Liu, Q.; Chen, X. Effect of Multi-Pass Equal-Channel Angular Pressing on the Mechanical and Corrosion Properties of TC4-0.55Fe Alloy. Crystals 2025, 15, 815. [Google Scholar] [CrossRef]
- Bridgman, P.W. On torsion combined with compression. J. Appl. Phys. 1943, 14, 274–283. [Google Scholar] [CrossRef]
- Kadirov, P.; Zhukova, Y.; Gunderov, D.; Antipina, M.; Teplyakova, T.; Tabachkova, N.; Baranova, A.; Gunderova, S.; Pustov, Y.; Prokoshkin, S. Effect of Accumulative High-Pressure Torsion on Structure and Electrochemical Behavior of Biodegradable Fe-30Mn-5Si (wt.%) Alloy. Crystals 2025, 15, 351. [Google Scholar] [CrossRef]
- Tsuji, N.; Saito, Y.; Utsunomiya, H.; Tanigawa, S. Ultra-fine grained bulk steel produced by accumulative roll-bonding (ARB) process. Scr. Mater. 1999, 40, 795–800. [Google Scholar] [CrossRef]
- Saito, Y.; Utsunomiya, H.; Tsuji, N.; Sakai, T. Novel ultra-high straining process for bulk materials—development of the accumulative roll-bonding (ARB) process. Scr. Mater. 1999, 47, 579–583. [Google Scholar] [CrossRef]
- Obara, C.; Mwema, F.M.; Keraita, J.N.; Shagwira, H.; Obiko, J.O. A multi-response optimization of the multi-directional forging process for aluminium 7075 alloy using grey-based taguchi method. Sn Appl. Sci. 2021, 3, 596. [Google Scholar] [CrossRef]
- Djavanroodi, F.; Ebrahimi, M.; Nayfeh, J.F. Tribological and mechanical investigation of multi-directional forged nickel. Sci. Rep. 2019, 9, 241. [Google Scholar] [CrossRef]
- Tian, P.; Wang, C.; Nie, K.; Li, Y.; Deng, K. Effect of Multi-Directional Forging on Microstructure and Mechanical Properties of Dual-Phase Mg-8Li-3Al-0.3Si Alloy. Materials 2025, 18, 1829. [Google Scholar] [CrossRef]
- Varyukhin, V.; Beygelzimer, Y.; Kulagin, R.; Prokofeva, O.; Reshetov, A. Twist Extrusion: Fundamentals and Applications. Mater. Sci. Forum 2011, 667-669, 31–37. [Google Scholar] [CrossRef]
- Beygelzimer, Y.; Prilepo, D.; Kulagin, R.; Grishaev, V.; Abramova, O.; Varyukhin, V.; Kulakov, M. Planar Twist Extrusion versus Twist Extrusion. J. Mater. Process. Technol. 2011, 211, 522–529. [Google Scholar] [CrossRef]
- Guan, B.; Xin, Y.; Huang, X.; Liu, C.; Wu, P.; Liu, Q. The mechanism for an orientation dependence of grain boundary strengthening in pure titanium. Int. J. Plast. 2022, 153, 103276. [Google Scholar] [CrossRef]
- Chen, T.; Yao, Y.G.; Cai, W.S.; Kang, L.M.; Ke, H.B.; Wen, H.M.; Wang, W.H.; Yang, C. Designing shell-layer-core architecture in Ti-based composites to achieve enhanced strength and plasticity. Int. J. Plast. 2023, 169, 103723. [Google Scholar] [CrossRef]
- Duan, Y.; Tang, L.; Xu, G.; Deng, Y.; Yin, Z. Microstructure and mechanical properties of 7005 aluminum alloy processed by room temperature ECAP and subsequent annealing. J. Alloys Compd. 2016, 664, 518–529. [Google Scholar] [CrossRef]
- Shen, J.; Gartnerova, V.; Kecskes, L.J.; Kondoh, K.; Jager, A.; Wei, Q. Residual stress and its effect on the mechanical properties of Y-doped Mg alloy fabricated via back-pressure assisted equal channel angular pressing (ECAP-BP). Mater. Sci. Eng. A 2016, 336, 110–117. [Google Scholar] [CrossRef]
- Latypov, M.I.; Beygelzimer, Y.; Kim, H.S. Comparative analysis of two twist-based SPD processes: Elliptical cross-section spiral equal-channel extrusion vs. twist Extrusion. Mater. Trans. 2013, 54, 1587–1591. [Google Scholar] [CrossRef]
- Valiev, R.; Langdon, T.G. Principles of equal-channel angular pressing as a processing tool for grain refinement. Prog. Mater. Sci. 2006, 51, 881–981. [Google Scholar] [CrossRef]
- Maulidi, M.; Miyamoto, H.; Yuasa, M. Grain Refinement of Pure Magnesium Using Nonlinear Twist Extrusion. Mater. Sci. Forum 2018, 939, 54–62. [Google Scholar] [CrossRef]
- Choi, H.-H.; Hwang, S.-M.; Kang, Y.; Kim, J.; Kang, B. Comparison of implicit and explicit finite-element methods for the hydroforming process of an automobile lower arm. Int. J. Adv. Manuf. Technol. 2002, 20, 407–413. [Google Scholar] [CrossRef]
- Yang, D.; Jung, D.; Song, I.; Yoo, D.; Lee, J. Comparative investigation into implicit, explicit, and iterative implicit/explicit schemes for the simulation of sheet-metal forming processes. J. Mater. Process. Technol. 1995, 50, 39–53. [Google Scholar] [CrossRef]
- Noels, L.; Stainier, L.; Ponthot, J.P. Combined implicit/explicit time-integration algorithms for the numerical simulation of sheet metal forming. J. Comput. Appl. Math. 2004, 168, 331–339. [Google Scholar] [CrossRef]
- Kutt, L.M.; Pifko, A.B.; Nardiello, J.A.; Papazian, J.M. Slow-dynamic finite element simulation of manufacturing processes. Comput. Struct. 1998, 66, 1–17. [Google Scholar] [CrossRef]
- Hu, X.; Wagoner, R.H.; Daehn, G.S.; Ghosh, S. Comparison of explicit and implicit finite element methods in the quasistatic simulation of uniaxial tension. Commun. Numer. Methods Eng. 1994, 10, 993–1003. [Google Scholar] [CrossRef]
- Prior, A.M. Applications of implicit and explicit finite element techniques to metal forming. J. Mater. Process. Technol. 1994, 45, 649–656. [Google Scholar] [CrossRef]
- Rust, W.; Schweizerhof, K. Finite element limit load analysis of thin-walled structures by ANSYS (implicit), LS-DYNA (explicit) and in combination. Thin-Walled Struct. 2003, 41, 227–244. [Google Scholar] [CrossRef]
- Gelin, J.; Boulmane, L.; Boisse, P. Quasi-static implicit and transient explicit analyses of sheet-metal forming using a C0 three-node shell element. J. Mater. Process. Technol. 1995, 50, 54–69. [Google Scholar] [CrossRef]
- Soltani, B.; Mattiasson, K.; Samuelsson, A. Implicit and dynamic explicit solutions of blade forging using the finite element method. J. Mater. Process. Technol. 1994, 45, 69–74. [Google Scholar] [CrossRef]
- Lindgren, L.; Edberg, J. Explicit versus implicit finite element formulation in simulation of rolling. J. Mater. Process. Technol. 1990, 24, 85–94. [Google Scholar] [CrossRef]
- Gavalas, E.E.; Pressas, I.S.; Papaefthymiou, S. Mesh sensitivity analysis on implicit and explicit method for rolling simulation. Int. J. Struct. Integr. 2018, 9, 465–474. [Google Scholar] [CrossRef]
- Hardie, C.; Long, D.J.; Demir, E.; Tarleton, E.; Dunne, F.P. A robust and efficient hybrid solver for crystal plasticity. Int. J. Plast. 2023, 170, 103773. [Google Scholar] [CrossRef]
- Rihaček, J.; Mrna, L. Comparison of implicit and explicit algorithms of finite element method for the numerical simulation of hydroforming process. MM Sci. J. 2016, 1, 1326–1331. [Google Scholar] [CrossRef]
- Taylor, L.; Cao, J.; Karafillis, A.P.; Boyce, M.C. Numerical simulations of sheet-metal forming. J. Mater. Process. Technol. 1995, 50, 168–179. [Google Scholar] [CrossRef]
- Sun, J.; Lee, K.; Lee, H. Comparison of implicit and explicit finite element methods for dynamic problems. J. Mater. Process. Technol. 2000, 105, 110–118. [Google Scholar] [CrossRef]
- Şimşek, Ü.; Çoğun, C.; Esen, Z. Effects of Electrolytic Copper and Copper Alloy Electrodes on Machining Performance in Electrical Discharge Machining (EDM). Mach. Sci. Technol. 2022, 26, 229–244. [Google Scholar] [CrossRef]
- Pantalé, O.; Mahendren, S.R.R.; Dalverny, O. Comparative Analysis of Finite Element Formulations for Simulating Hot Forming of Ti-6Al-4V Aerospace Components. Eng 2024, 5, 881–894. [Google Scholar] [CrossRef]
- Turk, T.; Liu, T.; Hung, C.H.; Billo, R.; Park, J.; Leu, M.C. In-situ thermographic monitoring and numerical simulations of laser-foil-printing additive manufacturing. Virtual Phys. Prototyp. 2024, 20, e2440609. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, S.; Sheng, M.; Shao, B.; He, Y.; Liu, Z.; Zhou, G. Bridgman Method for Growing Metal Halide Single Crystals: A Review. Inorganics 2025, 13, 53. [Google Scholar] [CrossRef]
- Turk, T.; Dominguez, C.E.; Sutton, A.T.; Bernardin, J.D.; Park, J.; Leu, M.C. Spot pattern welding scanning strategy for sensor embedding and residual stress reduction in laser-foil-printing additive manufacturing. Rapid Prototyp. J. 2024, 31, 83–99. [Google Scholar] [CrossRef]
- Deng, G.Y.; Lu, C.; Tieu, A.K.; Su, L.H.; Huynh, N.N.; Liu, X.H. Crystal plasticity investigation of friction effect on texture evolution of Al single crystal during ECAP. J. Mater. Sci. 2010, 45, 4711–4717. [Google Scholar] [CrossRef]
- Yalçınkaya, T.; Şimşek, Ü.; Miyamoto, H.; Yuasa, M. Numerical Analysis of a New Nonlinear Twist Extrusion Process. Metals 2019, 9, 513. [Google Scholar] [CrossRef]
- Fang, N. A new quantitative sensitivity analysis of the flow stress of 18 engineering materials in machining. J. Eng. Mater. Technol. 2005, 127, 192–196. [Google Scholar] [CrossRef]
- Hill, R.; Rice, J.R. Constitutive analysis of elastic-plastic crystals at arbitrary strain. J. Mech. Phys. Solids 1972, 20, 401–413. [Google Scholar] [CrossRef]
- Asaro, R.J.; Rice, J.R. Strain localization in ductile single crystals. J. Mech. Phys. Solids 1977, 25, 309–338. [Google Scholar] [CrossRef]
- Lee, E.H. Elastic-Plastic Deformation at Finite Strains. J. Appl. Mech. 1969, 36, 1–6. [Google Scholar] [CrossRef]
- Abaqus Documentation. Solid (continuum) elements. In Theory Manual; Section 14.1.1; Abaqus: Johnston, RI, USA, 2023; pp. 1–2.
- Mandel, J. Plasticite Classique et Viscoplasticite; CISM International Centre for Mechanical Sciences; Springer: Berlin/Heidelberg, Germany, 1972. [Google Scholar]
- Bennett, K.; Regueiro, R.; Borja, R. Finite strain elastoplasticity considering the Eshelby stress for materials undergoing plastic volume change. Int. J. Plast. 2016, 77, 214–245. [Google Scholar] [CrossRef]
- Marin, E. On the Formulation of a Crystal Plasticity Model; Sanda National Laboratories: Albuquerque, NM, USA, 2006; Volume 16, pp. 1–62. [Google Scholar]
- Brannon, R.M. A Review of Useful Theorems Involving Proper Orthogonal Matrices Referenced to Three Dimensional Physical Space; Sandia National Laboratories: Albuquerque, NM, USA, 2002; Volume 1, pp. 1–190. [Google Scholar]
- Zhang, J.; Liu, Y.; Cheng, Y.; Wang, H.; Sha, A.; Duan, H. Modeling of creep in nickel-based superalloy based on microtwinning mechanism. Int. J. Plast. 2024, 174, 103916. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Bounds and self-consistent estimates for creep of polycrystalline materials. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1976, 348, 101–127. [Google Scholar] [CrossRef]
- Şimşek, Ü.; Çoğun, C. An Investigation of the Performance of Equal Channel Angular Pressed Copper Electrodes in Electric Discharge Machining. Crystals 2025, 15, 849. [Google Scholar] [CrossRef]
- Kalidindi, S.; Bronkhorst, C.; Anand, L. Crystallographic texture evolution in bulk deformation processing of fcc metals. J. Mech. Phys. Solids 1992, 40, 537–569. [Google Scholar] [CrossRef]
- Balasubramanian, S.; Anand, L. Elasto-viscoplastic constitutive equations for polycrystalline fcc materials at low homologous temperatures. J. Mech. Phys. Solids 2002, 50, 101–126. [Google Scholar] [CrossRef]
- Bond, W.L. The mathematics of the physical properties of crystals. Bell Syst. Tech. J. 1943, 22, 1–72. [Google Scholar] [CrossRef]
- Cowin, S.C. Continuum Mechanics of Anisotropic Materials; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Zienkiewicz, O.; Taylor, R.; Fox, D. Chapter 5-Geometrically Nonlinear Problems: Finite Deformation. In The Finite Element Method for Solid and Structural Mechanics, 7th ed.; Zienkiewicz, O., Taylor, R., Fox, D., Eds.; Butterworth-Heinemann: Oxford, UK, 2014; pp. 147–177. [Google Scholar]
- Simo, J.C.; Marsden, J.E. On the rotated stress tensor and the material version of the Doyle-Ericksen formula. Arch. Ration. Mech. Anal. 1984, 86, 213–231. [Google Scholar] [CrossRef]
- Dunne, F.; Petrinic, N. Introduction to Computational Plasticity, 2nd ed.; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Takeuchi, T. Work hardening of copper single crystals with multiple glide orientations. Jpn. Inst. Met. Mater. 1975, 16, 629–640. [Google Scholar] [CrossRef]
- Kiener, D.; Grosinger, W.; Dehm, G.; Pippan, R. A Further Step towards an Understanding of Size-Dependent Crystal Plasticity: In Situ Tension Experiments of Miniaturized Single-Crystal Copper Samples. Acta Mater. 2008, 56, 580–592. [Google Scholar] [CrossRef]
- Şimşek, Ü.; Miyamoto, H.; Yalçınkaya, T. Crystal Plasticity Finite Element Analysis of Linear and Non-Linear Extrusion Processes. Mater. Res. Proc. 2023, 28, 553–562. [Google Scholar] [CrossRef]
- Tekoglu, C. Representative volume element calculations under constant stress triaxiality, lode parameter, and shear ratio. Int. J. Solids Struct. 2014, 51, 4544–4553. [Google Scholar] [CrossRef]
- Bharani, R.H. Single Crystal Growth of Constantan by Vertical Bridgman Method; Laboratory for Quantum Magnetism: Lausanne, Switzerland, 2011; Volume 1, pp. 1–30. [Google Scholar]
- Scheel, H.J.; Capper, P.; Rudolph, P. Crystal Growth Technology: Semiconductors and Dielectrics; John Wiley & Sons: Hoboken, NJ, USA, 2010; Volume 1, pp. 177–178. [Google Scholar]
- Şimşek, Ü. Crystal Plasticity Analysis of Severe Plastic Deformation Processes. Ph.D. Thesis, Middle East Technical University, Ankara, Turkey, 2024. [Google Scholar]
- Güler, B.; Şimşek, Ü.; Yalçınkaya, T.; Efe, M. Grain-scale investigations of deformation heterogeneities in aluminum alloys. Aip Conf. Proc. 2018, 1960, 170005. [Google Scholar] [CrossRef]
- Li, S.; Chen, W.; Kosimov, N.; Bhandari, K.S.; Jung, D. Reduction of Explicit Incremental Forming Simulation Time by Mass Scaling Parameters Adjusting and Symmetrical Setting. Int. J. Technol. Eng. Stud. 2021, 7, 27–34. [Google Scholar] [CrossRef]
- Şimşek, Ü.; Davut, K.; Miyamoto, H.; Yalçınkaya, T. Comparison of Linear and Nonlinear Twist Extrusion Processes with Crystal Plasticity Finite Element Analysis. Materials 2024, 17, 1139. [Google Scholar] [CrossRef] [PubMed]
- Guan, Y.; Chen, B.; Zou, J.; Britton, T.B.; Jiang, J.; Dunne, F.P.E. Crystal plasticity modelling and HR-DIC measurement of slip activation and strain localization in single and oligo-crystal Ni alloys under fatigue. Int. J. Plast. 2017, 88, 70–88. [Google Scholar] [CrossRef]
- Raabe, D.; Roters, F. Using texture components in crystal plasticity finite element simulations. Int. J. Plast. 2004, 20, 339–361. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, Z.; Huang, T.; Xia, P.; Li, F. Enhanced fracture toughness in an annealed Al-Cu-Mg alloy by increasing Goss/Brass texture ratio. Mater. Charact. 2016, 119, 47–54. [Google Scholar] [CrossRef]
- Brown, T.L.; Saldana, C.; Murthy, T.G.; Mann, J.B.; Guo, Y.; Allard, L.F.; King, A.H.; Compton, W.D.; Trumble, K.P.; Chandrasekar, S. A study of the interactive effects of strain, strain rate and temperature in severe plastic deformation of copper. Acta Mater. 2009, 57, 5491–5500. [Google Scholar] [CrossRef]
- Engler, O. Recrystallisation textures in copper-manganese alloys. Acta Mater. 2001, 49, 1237–1247. [Google Scholar] [CrossRef]
- Gurao, N.P.; Sethuraman, S.; Suwas, S. Effect of strain path change on the evolution of texture and microstructure during rolling of copper and nickel. Mater. Sci. Eng. A 2011, 528, 7739–7750. [Google Scholar] [CrossRef]
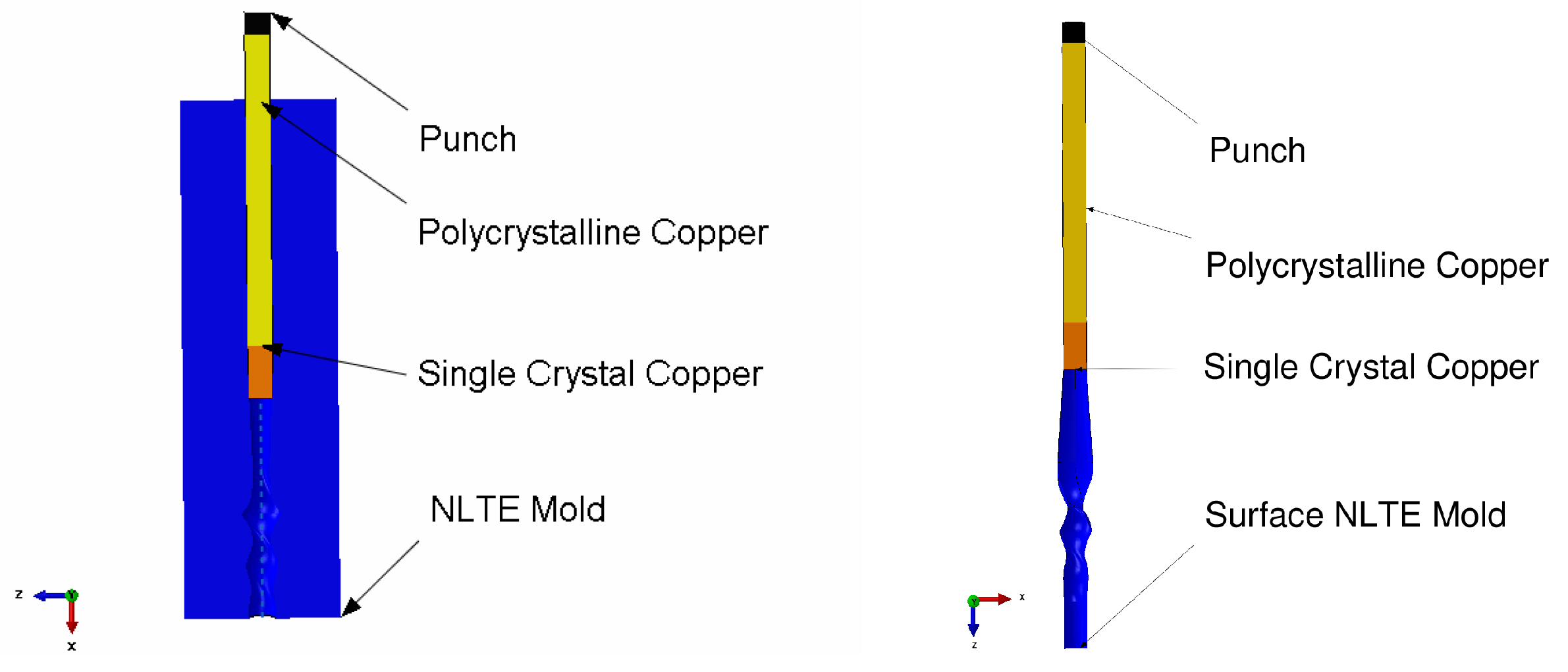



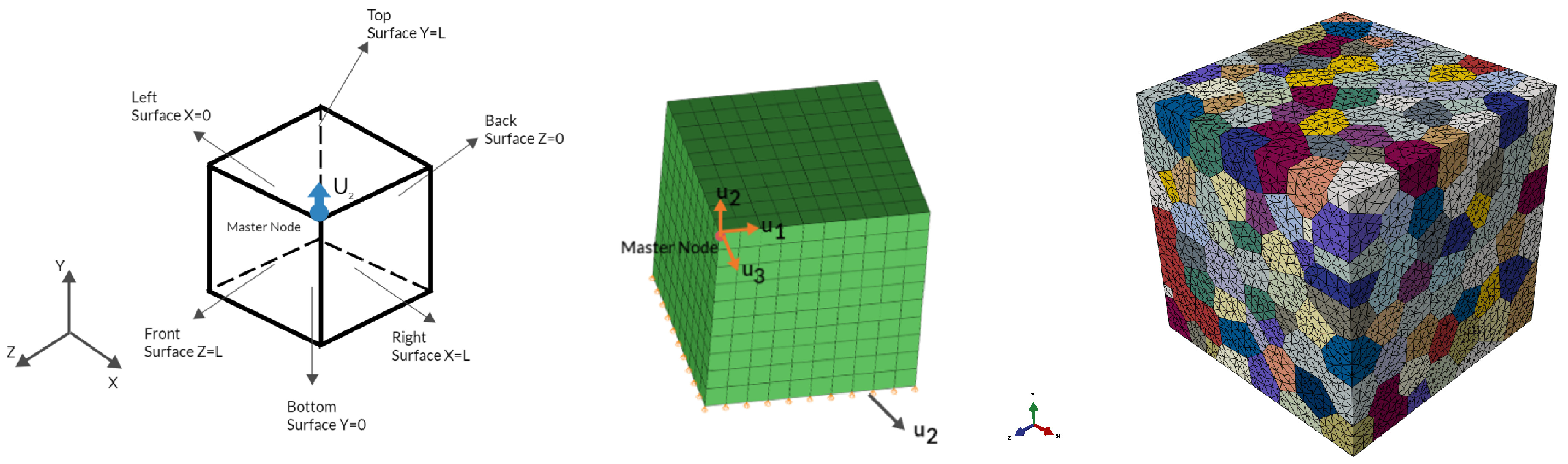
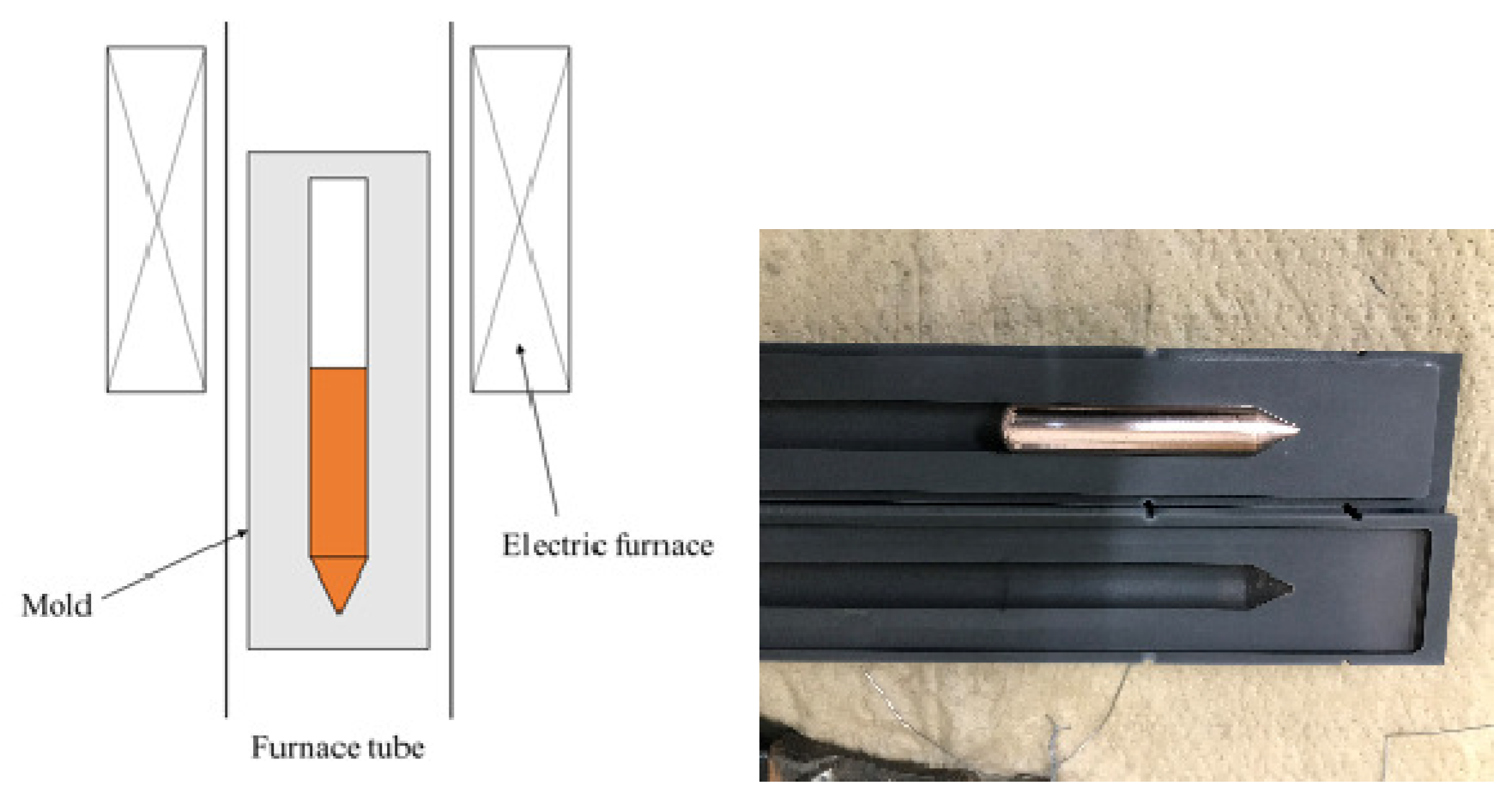
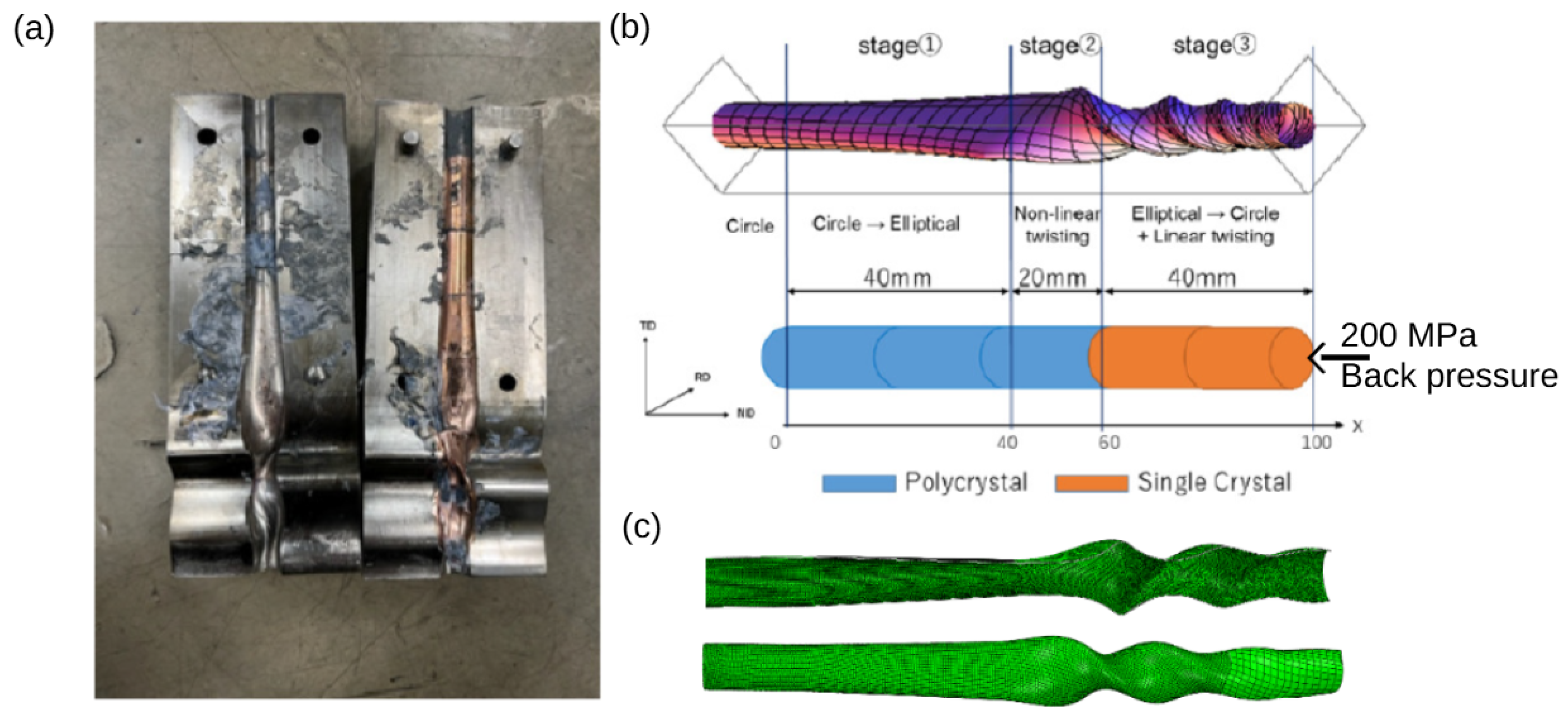

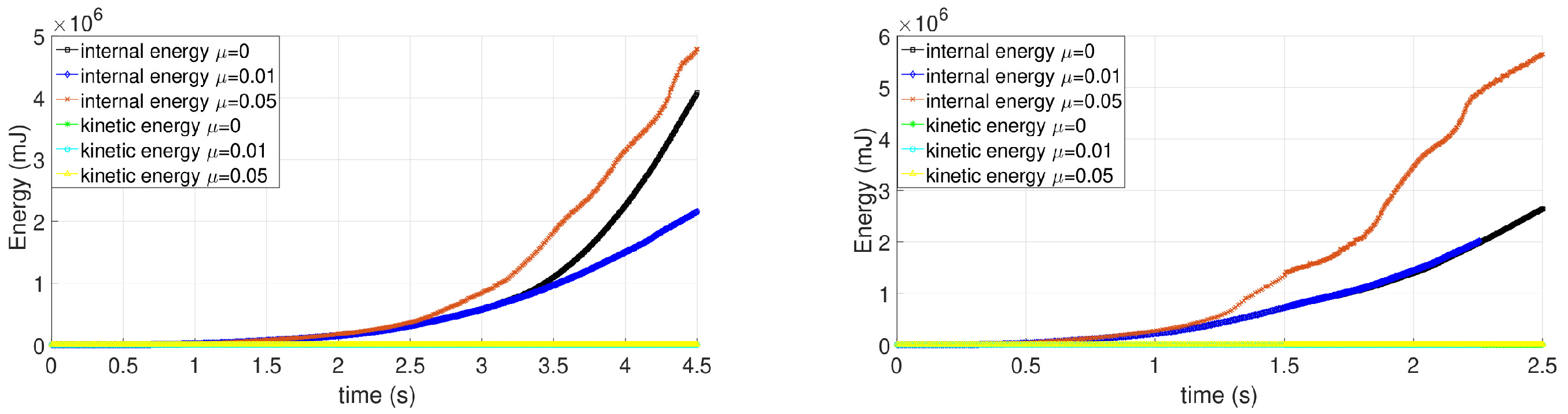
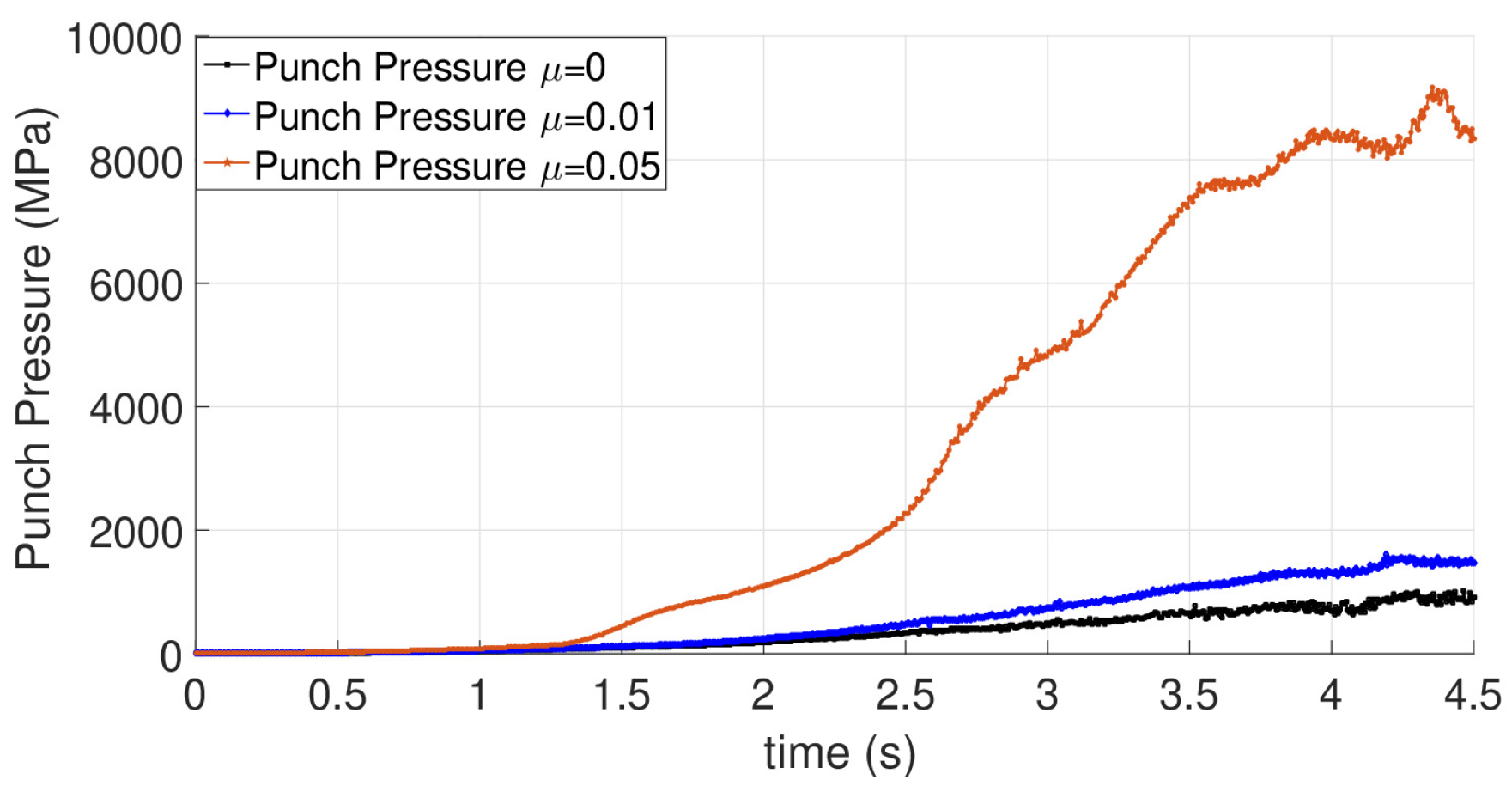


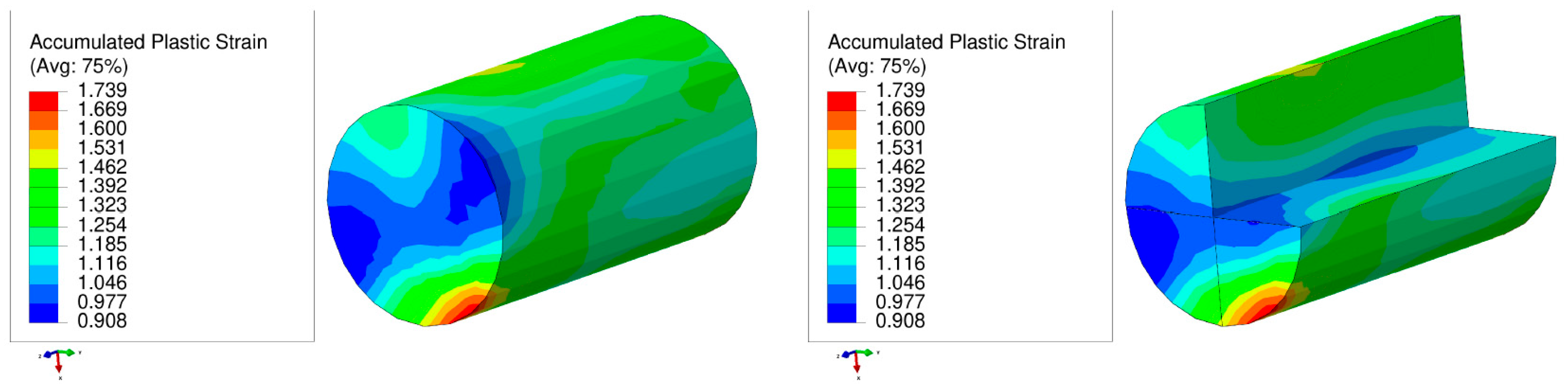
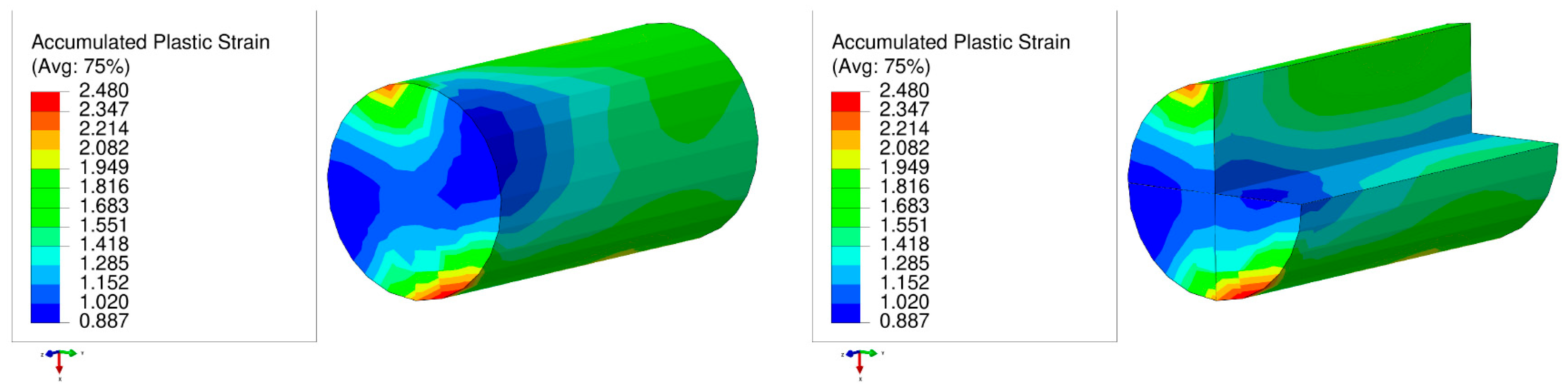
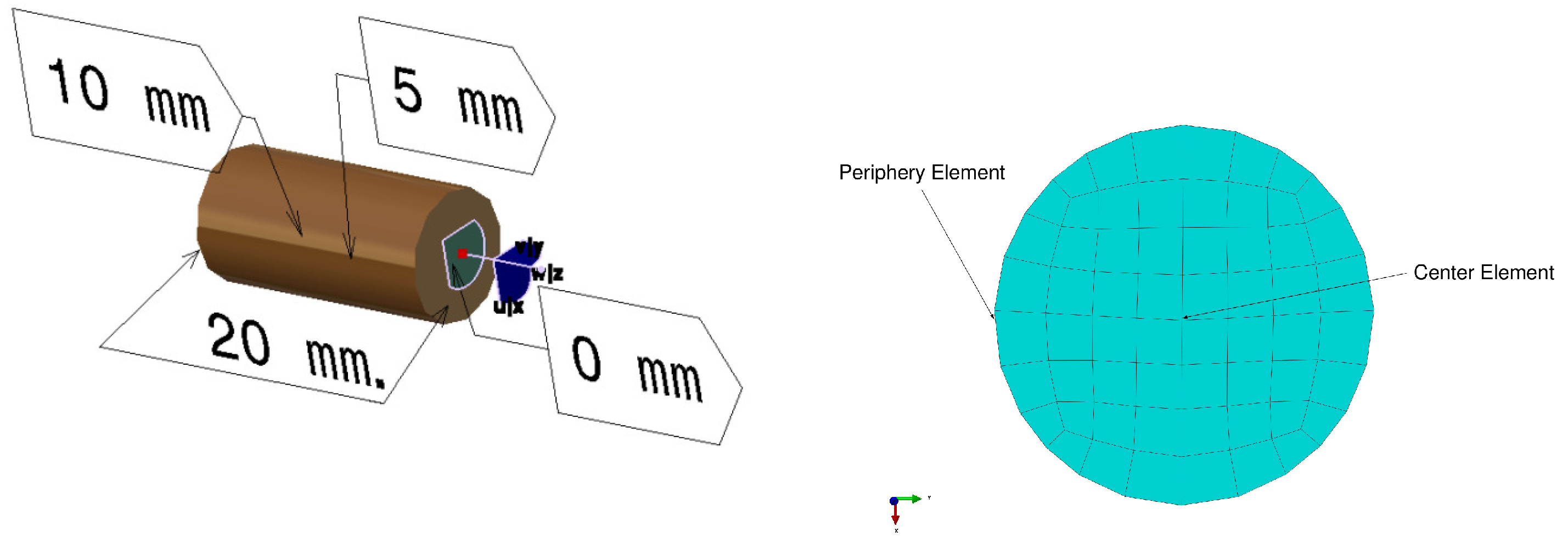

| Model | Element Type | Element Family | Element Number | Model Type |
|---|---|---|---|---|
| NLTE Mold | Linear Tri.-S3R | 2D Stress | 60,707 | Rigid |
| NLTE Punch | Explicit-Hexa-C3D8R | 3D Stress | 864 | Rigid |
| NLTE Specimen | Explicit-Hexa-C3D8R | 3D Stress | 900 | Deformable (CP) |
| Sample Name | Initial Orientation Bunge Euler Angles ( ) and Pole Figures of Initial Orientation | Distribution of [111] Symmetry Planes on 111 Pole Figures |
|---|---|---|
| Single copper crystal | (110.2) (67.3) (203.5) | |
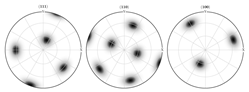 |  |
| C11 | C12 | C44 | τcr | h0 |
|---|---|---|---|---|
| 168,000 MPa | 121,400 MPa | 75,400 MPa | 25 MPa | 147 MPa |
| gsat | m | q | a | |
| 143 MPa | 0.001 s−1 | 17 | 1.4 | 1.75 |
| Framework | Process Speed | CPU Time | Estimated Completion Time (Days) |
|---|---|---|---|
| VUMAT CP | 25 mm/s | 400 h:13 min:50 s | 17 days |
| VUMAT CP | 50 mm/s | 186 h:48 min:00 s | 8 days |
| VUMAT CP | 300 mm/s | 33 h:30 min:26 s | 2 days |
| Component | Direction | Pole Figures of Components | |
|---|---|---|---|
| Cube | [001]<100> | (0) (0) (0) | 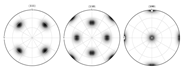 |
| Goss | [011]<100> | (0) (45) (0) | 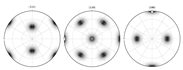 |
| Brass | [01]<211> | (35) (45) (0) |  |
| Copper | [11]<111> | (90) (35) (45) | 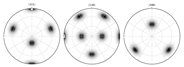 |
| S | [12]<634> | (60) (32) (65) | 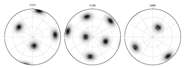 |
| Shear Texture | [111]<110> | (0) (54.74) (45) | 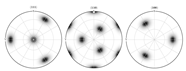 |
| Sample Name | Final Orientation Represented by Bunge Euler Angles ( ) and (111) (110) and (100) Pole Figures | Distribution of [111] Symmetry Planes on 111 Pole Figures |
|---|---|---|
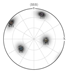
| Center section experimental Pole Figure | (145.183) (85.9) (232.031) | |
 |  | |
| Periphery section experimental Pole Figure | (153.033) (82.3) (229.212) | |
 |  | |
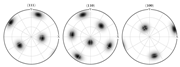
| Center section FEM-based pole figure predictions = 0.01 | (103.849, 74.0036, 199.886) | |
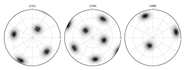 |  | |
| Periphery section FEM-based pole figure predictions = 0.01 | (106.725, 80.8892, 196.131) | |
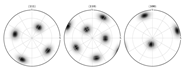 |  | |
| Center section FEM-based pole figure predictions = 0.05 | (101.811, 75.6, 239.707) | |
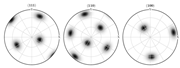 |  | |
| periphery section FEM-based pole figure predictions = 0.05 | (107.428, 84.0542, 240.637) | |
 |  |
| Sample Name | ODF Figures of FCC Components () |
|---|---|
| Brass ODF |  |
| Copper ODF |  |
| Goss ODF |  |
| Cube ODF |  |
| S ODF |  |
| Shear ODF |  |
| Sample Name | ODF Sections of = , and Comparing Experiments and Final Orientations |
|---|---|
| initial ODF |  |
| After NLTE process center section experimental ODF |  |
| After NLTE process periphery section experimental ODF |  |
| Center = 0.01 FEM-based ODF predictions |  |
| Periphery = 0.01 FEM-based ODF predictions |  |
| Center = 0.05 FEM-based ODF predictions |  |
| Periphery = 0.05 FEM-based ODF predictions |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Şimşek, Ü.; Miyamoto, H.; Yalçınkaya, T. Explicit Crystal Plasticity Modeling of Texture Evolution in Nonlinear Twist Extrusion. Crystals 2025, 15, 950. https://doi.org/10.3390/cryst15110950
Şimşek Ü, Miyamoto H, Yalçınkaya T. Explicit Crystal Plasticity Modeling of Texture Evolution in Nonlinear Twist Extrusion. Crystals. 2025; 15(11):950. https://doi.org/10.3390/cryst15110950
Chicago/Turabian StyleŞimşek, Ülke, Hiroyuki Miyamoto, and Tuncay Yalçınkaya. 2025. "Explicit Crystal Plasticity Modeling of Texture Evolution in Nonlinear Twist Extrusion" Crystals 15, no. 11: 950. https://doi.org/10.3390/cryst15110950
APA StyleŞimşek, Ü., Miyamoto, H., & Yalçınkaya, T. (2025). Explicit Crystal Plasticity Modeling of Texture Evolution in Nonlinear Twist Extrusion. Crystals, 15(11), 950. https://doi.org/10.3390/cryst15110950







