Abstract
Liquid crystals, which have both liquid and solid properties, inevitably exhibit fluctuations. Some frustrated liquid-crystalline phases with a hierarchical structure, such as cybotactic nematic, modulated smectic, and bicontinuous cubic phases, are fascinating fluctuation-induced phases. In addition to these equilibrium phases, a pattern formation that is a nonequilibrium order through fluctuation is one of the most attractive research areas in soft matter. In this review, the studies on producing these fluctuation-induced orders in liquid crystals are described. Liquid-crystalline supermolecules in which several mesogens are connected via a flexible spacer have been designed. They have not only a characteristic shape but also an intra-molecular dynamic order. The supermolecules induce the fluctuations in layer structures at a molecular level, producing from the frustrated hierarchical to dynamic dissipative structures. In addition to reviewing molecular design for the hierarchical structures, the pattern propagation in a smectic phase is discussed based on the rotation of smectic blocks through Rayleigh–Bénard convection.
1. Introduction
Liquid crystals contain both anisotropic properties in solids and fluidity in liquids. Therefore, fluctuations are characteristic phenomena of liquid crystals and their phase transitions. The orientational fluctuation exists in a nematic phase. The layers in a smectic A (SmA) phase undergo large fluctuations. Molecular orientational fluctuations increase as a phase transition is approached [1,2]. For an example of the pre-transitional behavior, smectic-like layered clusters are repeatedly generated and annihilated in a nematic phase near the nematic–smectic phase transition. Some frustrated liquid-crystalline phases with a hierarchical structure are induced through fluctuations. Let me introduce several interesting phases. A cybotactic nematic phase (Ncyb) is a nematic phase with a smectic-like ordering, which is ascribed a transient, local, and positional order in the nematic phase [3,4,5,6]. Smectic fluctuations, in which the smectic-like layer is either normal or tilted, related to the nematic director n, exist (Figure 1) [7,8]. The layer fluctuations in smectic A phases produce various frustrated smectic phases. Among them, modulated smectic phases are interesting [9,10,11,12]. Figure 2 shows the sketch of the modulated SmA phase [13]. Interactions between molecules in adjacent layers can form a bilayer structure. If the monolayer and bilayer structures coexist, the layer deformation can appear in the crossover region. [14]. Fluctuations in lamellar phases can produce bicontinuous cubic phases (Figure 3). The bicontinuous cubic liquid-crystalline phases have three-dimensional interpenetrating networks [15,16]. They have attracted much attention due to the intriguing nanoscale structure [16,17,18,19], but for use in applications such as 3D electronic or ionic conductors [20,21]. In addition to these equilibrium hierarchical phases, dissipative structures named as order through fluctuation [22,23] have been investigated. Some research on the pattern formation in both thermotropic and lyotropic systems is described. Figure 4 shows the polarized optical texture of a striped pattern propagation observed for a smectic phase.
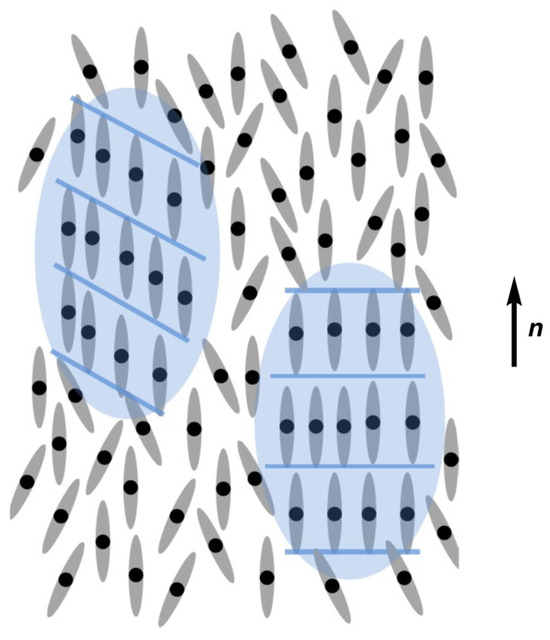
Figure 1.
Sketch of a nematic phase exhibiting skewed (left) and normal (right) smectic fluctuations. The picture was taken from [8]. Copyright (2014) Royal Society of Chemistry.
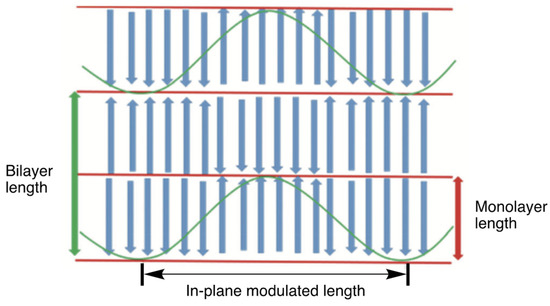
Figure 2.
Sketch of a modulated smectic A phase. The picture was taken from [13]. Copyright (2017) Royal Society of Chemistry.
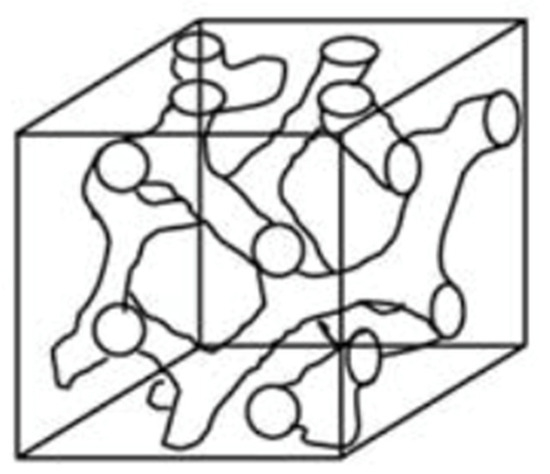
Figure 3.
Sketch of a bicontinuous cubic phase.

Figure 4.
Photomicrograph of the striped pattern propagation in a smectic phase. The picture was taken from [24]. Copyright (2008) Royal Society of Chemistry.
Molecular design for the fluctuations producing these hierarchical and/or dissipative structures is very attractive. However, there are only few reports of such a molecular design [24]. The excluded volume effect determined by hard-core repulsion requires a rod-like molecular shape with a length-to-diameter ratio of larger than 3 for the stabilization of nematic and smectic phases. Super-molecules in which several mesogenic units are connected via a flexible spacer have been investigated (Figure 5) [12,25,26,27]. At the first stage, such molecules classified as unconventional liquid crystals were interesting because they exhibit mesophases despite being significantly different from a rod-like shape. Later, they are recognized as designed molecules for producing characteristic self-organizing structures.
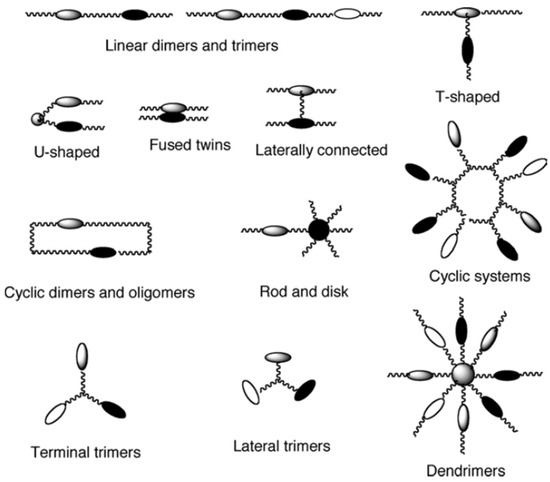
Figure 5.
Types of liquid-crystalline super-molecules. The picture was taken from [24]. Copyright (2008) Royal Society of Chemistry.
Liquid crystal dimers and trimers are simple but attractive supermolecules [12,26]. The transition properties of linear dimeric liquid crystals depend on the length and parity of the flexible spacer. Linear liquid-crystalline dimers show pronounced odd–even effects of the spacer on the Iso–N phase transition temperatures. Non-symmetric dimers in which two different cores are connected via the spacer can exist in two kinds of smectic layer structures depending on the lengths of the spacer and the terminal alkyl chain (Figure 6). When the spacer is longer than the terminal alkyl chains, an “intercalated” SmA phase is observed with the ratio of the smectic layer spacing (d) over the molecular length (l) is about 0.5. On the other hand, the dimers possessing alkyl groups and shorter spacers show an “interdigitated” SmA phase. In the interdigitated SmA phase, the d/l ratio is >1.5 times longer than the molecular length (l). Recently, the twist-bend nematic phase (NTB) showing chiral conglomerates was observed for some achiral liquid crystal dimers with flexible odd-numbered methylene spacers [28,29].
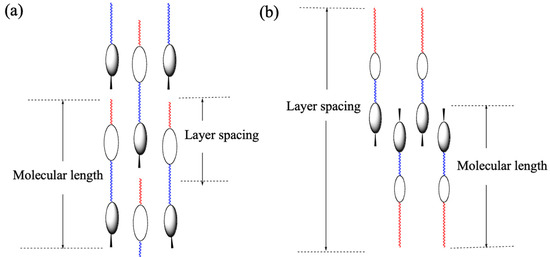
Figure 6.
Schematic representations for (a) intercalated SmA and (b) interdigitated SmA structures. The picture was taken from [24]. Copyright (2008) Royal Society of Chemistry.
The structure–property relationships in the supermolecular systems have been discussed in terms of their static molecular images. Yoshizawa et al. reported the molecular design of liquid-crystalline supermolecules based on the NMR studies of dynamics of molecules in smectic phases (Figure 7) [30]. The NMR studies reveal that intra- and inter-layer correlations of molecular motion tune a long-range order in the smectic phases [31]. The configuration of mesogenic units within a supermolecule plays an important role in producing the macroscopic behavior of their molecular assemblies due to the characteristic molecular shape and the intra-molecular dynamic order. Some liquid crystal oligomers producing a dynamic chiral origin were prepared. For example, a binaphthyl derivative, as shown in Figure 7, exhibited a wide blue phase temperature range on cooling [32]. The U-shaped supermolecule has two twist origins stabilizing the blue phase: the inherent asymmetric axis in the binaphthyl unit and the two mesogens forming a twisted conformation. Then, a linear trimer can enhance the inter-layer correlation. The achiral linear trimer with a nematic phase showed chiral conglomerates in the soft-crystalline layered phase (Figure 7) [33]. It adopts a metastable twisted conformer via intermolecular core–core interactions and exhibits spontaneous mirror symmetry breaking in the low-temperature phase.
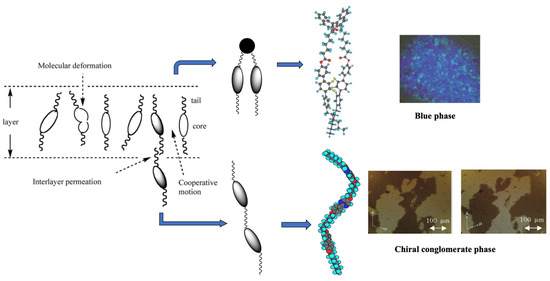
Figure 7.
Molecular design of the liquid crystal oligomers producing a dynamic chirality.
The research on fluctuation-induced orders in liquid crystals, such as the cybotactic nematic, modulated smectic, and bicontinuous cubic phases, is described in this review. This paper shows how the designed supermolecules induce layer fluctuations to produce the frustrated hierarchical structures. Furthermore, the pattern propagation observed for a mixture of unsymmetric liquid crystal dimers in the smectic phase will be shown and explained in terms of the layer fluctuation (Figure 4).
2. Equilibrium Hierarchical Structures
2.1. Cybotactic Nematic Phases
The molecules in nematic phases are spontaneously arranged with their long axes parallel to each other. Although the nematic phases are fluid like the isotropic liquid, they have several viscosity coefficients [34,35]. In addition to the conventional nematic phase, nematic liquid crystals with different types, such as biaxial nematic (Nb) [36,37,38,39], cybotactic nematic (Ncyb), twist bend nematic (Ntb) [28,40], and ferroelectric nematic phases [41,42,43,44,45], have been reported. With respect to the discovery of Ncyb phases, the observation of the short-range order in nematics was performed by De Vries based on X-ray scattering measurements [3,4]. Chystakov and Chaikowsky independently observed the extra four-spot scattering [5]. Ncyb phases appear as the following two types [6,46]. Type I: They appear as a pre-transitional order in the low-temperature range of the nematic phase. They are observed for rod-shaped liquid crystals and considered as fluctuation-induced Ncyb phases. Type II: They appear as structural features in the entirety of the nematic range and do not necessarily have a low-temperature smectic phase. They are observed for bent-core LCs [47,48]. The fluctuation of cybotactic clusters was detected by dielectric spectroscopy in the Ncyb phase of bent-core LCs [49,50]. Although lots of molecules that have been investigated have had a bent-shaped structure, some liquid crystal dimers have been reported to have Ncyb phases [51]. The molecular structures with phase transition properties are shown in Figure 8. Both dimers form the Ncyb phase independent of the parity of the methylene number of the spacer, indicating that the appearance of the Ncyb phase is attributed not to the rigid bent-shape but to the flexible supermolecular dimeric system. Not only low-molecular-mass LCs but also a main-chain LC polymer with a bent-core repeat unit exhibits a cybotactic order in the nematic phase [52]. Structure–property relationships in Ncyb phases are summarized in a recent review [46]. Ncyb phases are attractive not only in terms of structural interests but for their electro-optical properties. Local biaxiality was proposed to be able to arise in Ncyb phases [38,53,54]. The relationship between the cluster formation and the biaxiality has been investigated [6,55]. Some bent-core molecules exhibiting the Ncyb phase stabilize blue phases [56]. Furthermore, ferroelectric-like polar switching has been observed in some Ncyb phases [52,57,58]. Recently, Nishikawa et al. reported the nano-cluster formation in a diastereomerically stabilized ferroelectric nematic system [59].
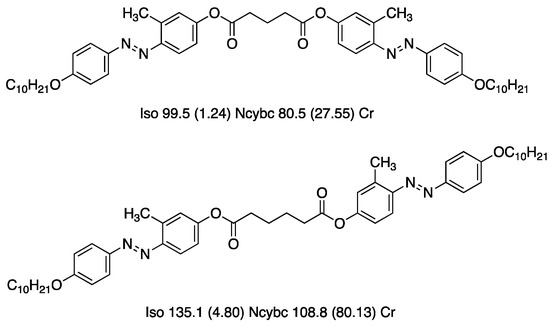
Figure 8.
The molecular structures, transition temperatures (°C), and enthalpies (kJ mol–1, in parentheses) of transition on the first cooling for the liquid crystal dimers [51]. Ncybc: Cybotactic nematic phase composed of smectic C-like nanoclusters.
The Ncyb (Type I) appears in the N phase near the nematic–smectic phase transition, and their temperature ranges are usually narrow. Let me introduce two approaches for stabilizing the fluctuation-induced Ncyb phases, i.e., U-shaped and hydrogen-bonding systems [8]. Their molecular structures and phase transition temperatures are shown in Figure 9.
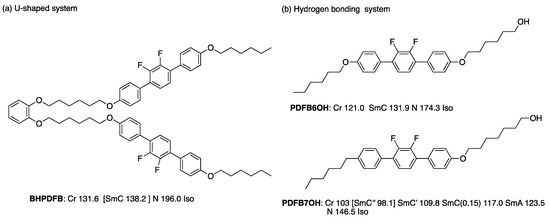
Figure 9.
The molecular structures and transition temperatures (°C) for BHPDFB, PDFB6OH, and PDFB7OH [8,60]. Square brackets denote a monotropic transition.
The first is the U-shaped system using the compound BHPDFB, in which cooperativity between the two mesogenic units exists within the molecule (Figure 9a). The U-shaped compound has an intra-molecular lateral order, which is expected to induce the smectic fluctuation in a nematic phase. BHPDFB exhibited N and SmC phases. Figure 10 shows the X-ray diffraction patterns of BHPDFB in the N and SmC phases. The Ncyb phase appeared at T − TNC = +20 K. Diffuse scattering appeared beside the meridian in the nematic phase (Figure 10b), indicating that molecules are organized in a cybotactic cluster that has an SmC-like skewed structure. The layer spacing decreases continuously in the Ncyb phase and the SmC phase with decreasing temperatures (Figure 11a); on the other hand, the correlation length increases discontinuously at the Ncyb–SmC transition (Figure 11b). The molecular length of BHPDFB using MOPAC-6/PM3 is estimated as 33 Å. Both the Ncyb and SmC phases have a monolayer structure. The lateral cooperative motion enhanced by BHPDFB might produce a smectic-like layer order in the N phase, as shown in Figure 12.

Figure 10.
X-ray diffraction patterns in the small-angle region of BHPDFB: (a) N phase at T − TNC = +24.2 K; (b) N phase at T − TNC = +4.2 K; (c) SmC phase at T − TNC = −0.8 K. The pictures were taken from [8]. Copyright (2014) Royal Society of Chemistry.
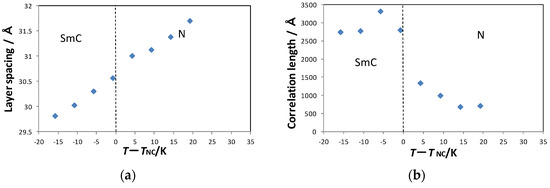
Figure 11.
Temperature dependence of (a) the layer spacing and (b) the correlation length of BHPDFB in the N and SmC phases. The pictures were taken from [8]. Copyright (2014) Royal Society of Chemistry.
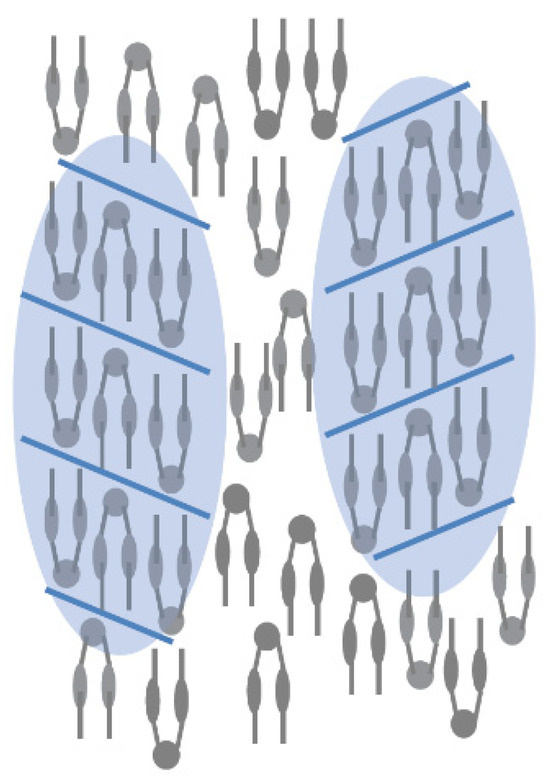
Figure 12.
Model for the Ncyb phase of BHPDFB. The picture was taken from [8]. Copyright (2014) Royal Society of Chemistry.
The second approach is the regulation of interlayer interactions by using the hydrogen bonding system (Figure 9b) [8,60]. Figure 13 shows the temperature dependence of the Figure 13a layer spacing and Figure 13b correlation length for PDFB6OH in the N and SmC phases. The Ncyb phase appeared over 25 K above the N–SmC transition. The molecular length is estimated to be 29 Å. Therefore, both the Ncyb and SmC phases have a monolayer structure. The layer spacing shows a discontinuous decrease at the Ncyb–SmC transition, as observed for a typical SmA–SmC transition. The polarized optical texture of a homeotropic alignment sample of PDFB6OH in the N was completely dark. The smectic fluctuation in the Ncyb phase has a SmA-like normal layer order.
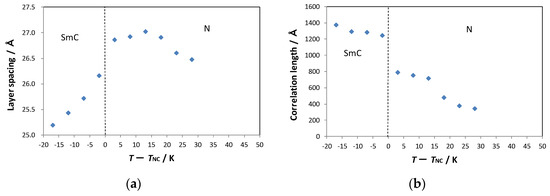
Figure 13.
Temperature dependence of (a) the layer spacing and (b) the correlation length of PDFB6OF in the N and SmC phases. The pictures were taken from [8]. Copyright (2014) Royal Society of Chemistry.
Compound PDFB7OH exhibited N, SmC, SmC′, and SmC″ phases [60]. Smectic-like clusters appeared in the low-temperature region of the N phase [60]. High-resolution and microbeam X-ray diffraction studies reveal the phase structures of the three SmC phases as follows [61]: (1) The SmC phase has a conventional monolayer structure. (2) The SmC′ has an in-plane modulated structure. (3) The SmC″ phase has a uniformly bilayer structure. The appearance of the modulated SmC phase indicates that the competition between the monolayer ordering and the bilayer ordering occurs in the N phase. On the other hand, the difluoroterphenyl derivative possessing two terminal hydroxyl groups shown in Figure 14 showed no diffraction peak corresponding the smectic-like layer structure in the N phase [8]. The inter-layer interactions are uniformly strong due to the hydrogen bonding so that the smectic-like layer order with a short correlation length cannot exist in the N phase.
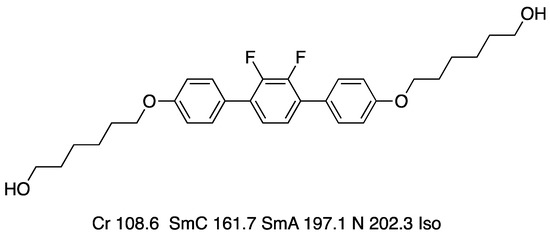
Figure 14.
The molecular structure and transition temperatures (°C) for the terphenylderivatve [8].
Figure 15 shows a possible model for the appearance of the Ncyb phase of the hydrogen bonding system. Micro-segregation prefers a bilayer structure in which the molecules are aligned in parallel. On the other hand, packing entropy prefers a monolayer structure in which the molecules are aligned in an anti-parallel manner. In the case of the bilayer structure, the weaker inter-layer interaction between adjacent alkyl chains compared to the intra-layer hydrogen-bonding interaction might destabilize a smectic-like structure (right side of Figure 15). With respect to the monolayer structure, no difference in the inter-layer interactions might form a layer structure with a relatively long periodicity in the N phase (left side of Figure 15). Competition between the monolayer and bilayer characteristics can induce the smectic fluctuation in the N phase.
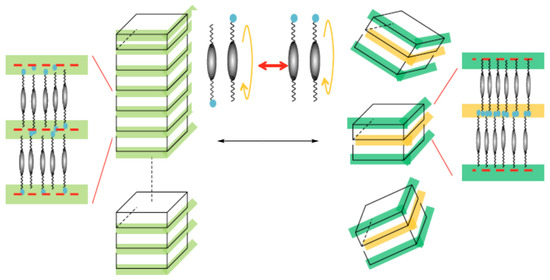
Figure 15.
Possible model for the formation of the Ncyb phase of PDFB6OH. The picture was taken from [8]. Copyright (2014) Royal Society of Chemistry.
2.2. Modulated Smectic Phases
Frustrated smectic phases, such as modulated phases and incommensurate phases, have competitive phase structures different from classical smectic A and C phases [62]. The modulated smectic phases give rise to additional small-angle Brag peaks away from the meridian [11]. They arise as a result of the competition between different characteristic length scales and have a transverse modulation of the structure, as shown in Figure 2. The competing lengths are usually the molecular length and the length of the bilayer structure composed of antiparallel molecular pairs. The dimerization is driven by a strong interaction between molecules in adjacent layers. In the incommensurate phases, several small-angle Brag peaks are observed to align along the meridian. The competing periodicities coexist along the normal layer; in other words, layer structures with different layer spacings coexist. Modulated structures are thought to occur as an escape from incommensurability [63]. The modulated smectic phases have been observed in biforked mesogens [64], dimers [65,66,67], liquid crystals with a terminal hydroxyl group [61], bent-shaped molecules [68], mesogens with terminal fluorinated chains [69], and polymeric mesogens [70,71,72].
Kashima et al. prepared a taper-shaped liquid-crystalline trimer BPYDFB (Figure 16) [73]. The trimer exhibited a phase sequence of isotropic liquid–smectic A–anticlinic smectic C (SmCanti)–modulated smectic C (Sm).
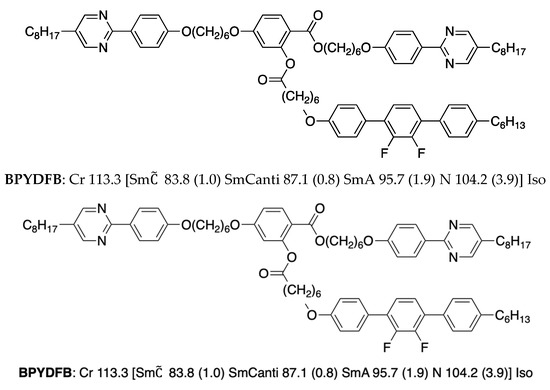
Figure 16.
The molecular structure, transition temperatures (°C), and enthalpies (kJ mol–1, in parentheses) of transition for BPYDFB [73]. Square brackets denote a monotropic transition.
The layer spacing in the SmA phase was 28.4 Å. The molecular length is estimated as 61 Å. The SmA phase is thought to have an intercalated structure. Figure 17 shows two-dimensional X-ray diffraction patterns in the small-angle region of BPYDFB in the SmCanti and Sm phases. In the SmCanti phase, the scattering corresponding to a layer spacing of 27.8 Å indicates that it has an intercalated layer structure. On the other hand, in the Sm phase, additional small-angle diffraction spots appear symmetrically away from the meridian, which are characteristic of a modulated smectic phase possessing an in-plane modulation of a molecular arrangement. The Sm phase has three periodicities: the intercalated layer spacing of 27.2 Å, the monolayer spacing of 54.4 Å, and the in-plane modulated length of 115 Å.

Figure 17.
X-ray diffraction patterns in the small-angle region of BPYDFB in (a) the SmCanti phase at T − TNA = −9.5 K and (b) the Sm phase at T − TNA = −13.5 K. Reprinted with permission from [73]. Copyright (2014) Taylor & Francis Ltd.
How does the supermolecule stabilize those frustrated smectic phases? Figure 18 shows MOPAC models for (a) T-shaped and (b) taper-shaped conformers of BPYDFB. The MOPAC calculations reveal that the taper-shaped conformer is stabler than the T-shaped one by 17 kJ mol–1 [74]. BPYDFB is assumed to form a taper shape in the liquid-crystalline phases. Figure 19 shows molecular organization models of BPYDFB in the SmA and SmCanti phases. Head-to-tail dipole–dipole interactions between phenylpyrimidine units may induce their conformational change from straight to bent, producing the SmA–SmCanti phase transition.
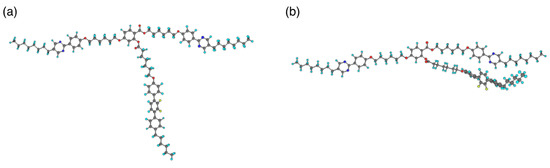
Figure 18.
MOPAC models for (a) T-shaped and (b) taper-shaped conformers of BPYDFB [74].
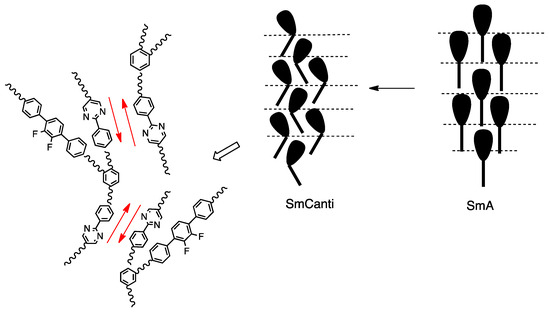
Figure 19.
Molecular organization models for the intercalated SmA and SmCanti phases of BPYDFB. Red arrows indicate the dipole moment of each phenylpyrimidine unit. Reprinted with permission from [73]. Copyright (2014) Taylor & Francis Ltd.
Figure 20 depicts a model for the Sm phase. The conformational change from bent to straight and the molecular packing in an antiparallel manner are thought to drive the synclinic monolayer structure. Therefore, the Sm phase is induced by competition between the intercalated layer structure with a spacing of 27.2 Å and the monolayer structure with a spacing of 54.4 Å. The flexible intra-molecular order of the supermolecule plays an important role in producing the fluctuation between the layer structures.
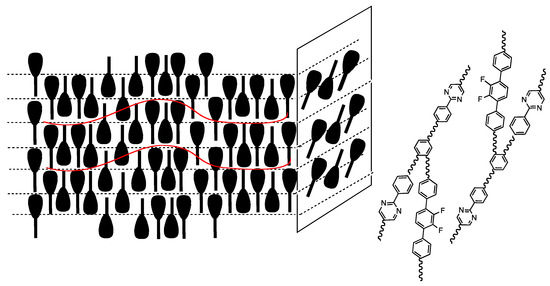
Figure 20.
Molecular organization model for the Sm phase of BPYDFB. The red curves show the layer modulation. Reprinted with permission from [73]. Copyright (2014) Taylor & Francis Ltd.
Sasaki et al. designed a ternary system in which the fluctuation between a monolayer structure (Type I) and bilayer structure (Type II) of an amphiphilic smectic liquid crystal is coupled with the fluctuation between nematic and smectic structures for a mixture of conventional nematic liquid crystals (Type III) (Figure 21) [13]. Figure 22 shows the compounds under investigation.
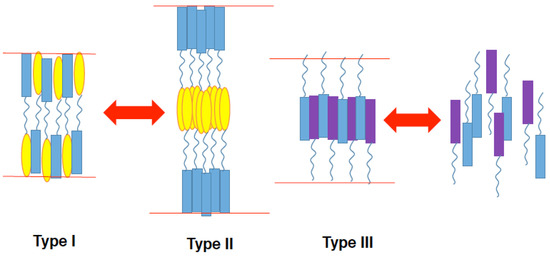
Figure 21.
Design concept of the ternary system. Amphiphilic smectic liquid crystals form a monolayer structure (Type I) or an interdigitated bilayer structure (Type II). Nematic liquid crystals with different cores can induce a smectic phase via interactions between unlike cores (Type III). The picture was taken from [13]. Copyright (2017) Royal Society of Chemistry.
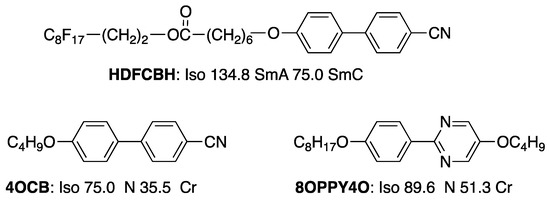
Figure 22.
The molecular structures and transition temperatures on cooling (°C) for compounds HDFCBH, 4OCB, and 8OPPY4O [13].
The semiperfluorinated smectic liquid crystal HDFCBH, designed for the formation of Type I or Type II, exhibited interdigitated SmA and SmC phases. The model for the SmA phase is shown in Figure 23. The layer structures are formed by F-aggregation [75] and dipole–dipole interactions between cyanobiphenyl units. HDFCBH forms Type II rather than Type I. Two nematic liquid crystals 4OCB and 8OPPY4O were used for the formation of Type III. The SmA phase was induced in their binary mixtures. An equimolecular mixture of them (Mixture A) showed a phase sequence of Iso 98.0 °C SmA 24.2 °C Sm E. The SmA phase has a monolayer structure, as shown in Figure 24. The SmA phase is stabilized by core–core interactions between unlike cores. Expectedly, Mixture A formed Type III.
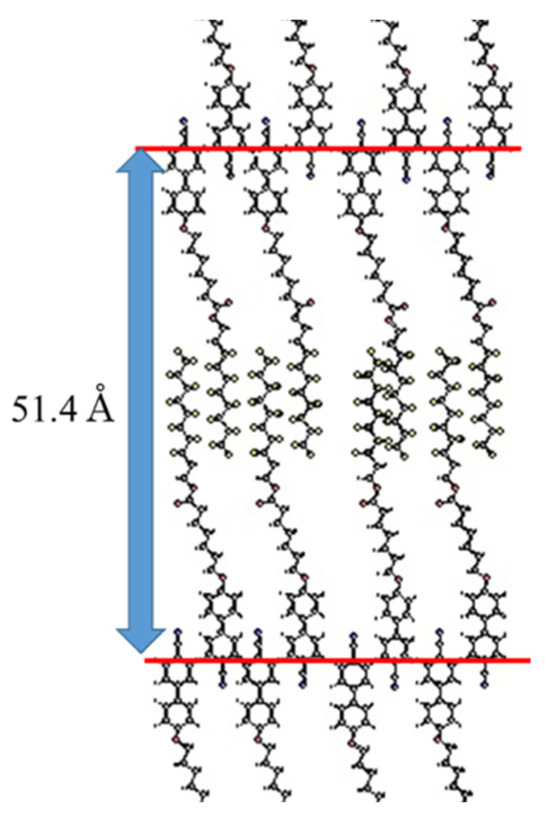
Figure 23.
Model for the SmA phase of HDFCBH. The layer spacing obtained by XRD studies is indicated. The molecular length is estimated as 34.5 Å. The picture was taken from [13]. Copyright (2017) Royal Society of Chemistry.
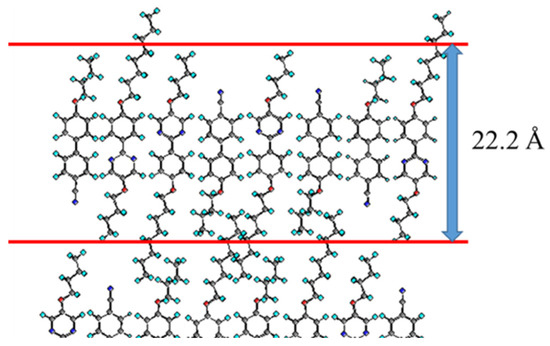
Figure 24.
Model for the SmA phase of Mixture A. The layer spacing obtained by XRD studies is indicated. The molecular lengths of 4OCB and 8OPPY4O are estimated as 16.3 Å and 25.8 Å, respectively. The picture was taken from [13]. Copyright (2017) Royal Society of Chemistry.
Figure 25A presents the phase diagram of HDFCBH and Mixture A. Two modulated smectic phases (Y and Z) were induced in wide regions. A mixture containing 20 mol% of HDFCBH exhibited phase transitions as follows: Iso 102.3 °C Iso + SmA 97.5 °C N 95.6 °C~92.2 °C X 72.8 °C Y 60.7 °C Z. The X, Y, and Z phases are not identified. Their optical textures are shown in Figure 25B. The N–X, X–Y, and Y–Z transitions did not accompany enthalpy change, as shown in Figure 25C. The SmA phase in the Iso + SmA coexistence range has a monolayer structure with a layer spacing of 34.2 Å. 4OCB and 8OPPY4O molecules might enter each layer to stabilize the monolayer structure, as shown in Figure 26. Therefore, the SmA phase of the ternary mixture forms the monolayer structure (Type I) instead of the interdigitated structure (Type II) of the compound HDFCBH itself. The nematic phase existed below the layer-ordered SmA phase. The X phase appeared between the nematic phase and the modulated Y phase. It showed a fan-shaped texture (Figure 25B(c)), indicating that it has a smectic-like layer structure. A homeotropically aligned sample in the X phase showed a completely dark texture, revealing that it is a uniaxial phase. On the other hand, no periodicity corresponding to the layer spacing in the X phase was detected. Furthermore, the fluidity in the X phase was the same as that in the N phase. The X–Y transition was detected by POM and accompanied a discontinuous increase in shear stress. The Y phase has three periodicities: the intercalated monolayer spacing of 29 Å, the interdigitated bilayer spacing of 57 Å, and the in-plane modulated length of 150 Å (Figure 27a).
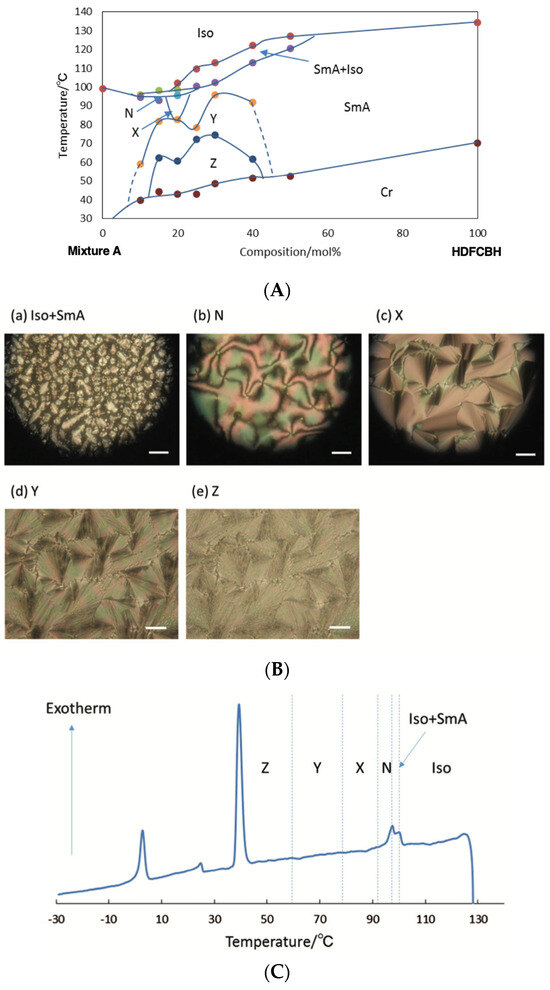
Figure 25.
(A) Phase diagram between Mixture A and HDFCBH. (B) Polarized optical textures of a mixture containing 20 mol% of HDFCBH. White bars represent 100 μm. (C) DSC thermogram of the mixture. The picture was taken from [13]. Copyright (2017) Royal Society of Chemistry.
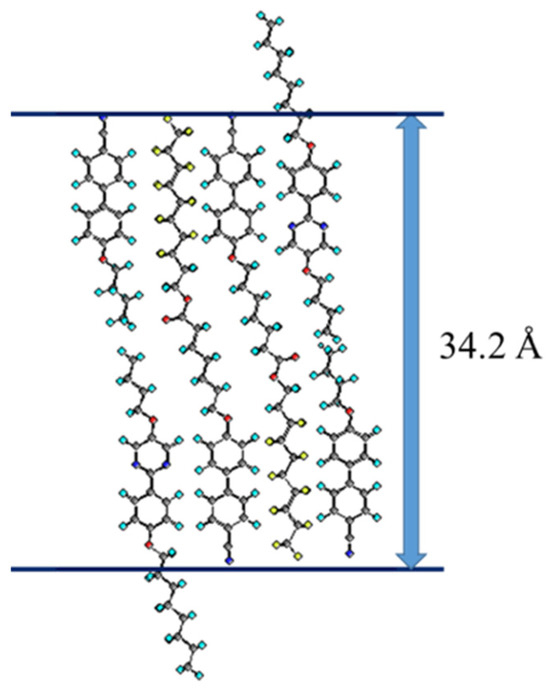
Figure 26.
Molecular model for the SmA phase in the Iso + SmA coexistence region of the mixture containing HDFCBH (20 mol%), 4OCB (40 mol%), and 8OPPY4O (40 mol%). The layer spacing is indicated. The picture was taken from [13]. Copyright (2017) Royal Society of Chemistry.
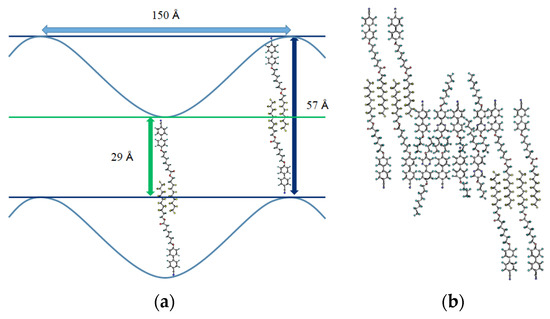
Figure 27.
(a) Molecular arrangements for the periodicities in the Y phase. Monolayer length, interdigitated bilayer length, and in-plane modulated length are indicated. (b) Modulated bilayer molecular organization consisting of the interdigitated packing of the semifluorinated molecules with the nematic liquid-crystalline molecules. The picture was taken from [13]. Copyright (2017) Royal Society of Chemistry.
The N and X phases might appear as the reorganization processes from the high-temperature SmA phase to the modulated Y phase. The reorganization mechanism is explainable as follows. The competition of layer formation among the interdigitated layer structure of HDFCBH (Figure 23), the monolayer structure of Mixture A (Figure 24), and the monolayer structure of the SmA phase (Figure 26) reorganizes the molecular arrangements, inducing the N phase. After further cooling, the three different layer structures (Type I, Tye II, and Type III) with short-range orders are repeatedly generated and annihilated. Therefore, the molecules in the low-temperature X phase cannot organize a certain layered structure. In the Y phase, the layer modulation appears. Both Type I and Type II structures can coexist in the Y phase due to the layer modulation that is stabilized by 4OCB and 8OPPY4O (Figure 27b). The fluctuation between the monolayer and the interdigitated bilayer structures for the amphiphilic molecules HDFCBH is coupled with the fluctuation between the nematic and smectic structures for the nematic molecules 4OCB and 8OPPY4O, producing the frustrated X phase with spatiotemporal fluctuations of the constituted molecules.
2.3. Bicontinuous Cubic Phases
Liquid crystals show birefringence due to the optical anisotropy. However, some liquid crystals, such as cubic phases [15] and blue phases [76], exhibit optical isotropy. The cubic mesophases are commonly observed in surfactant–solvent systems [77]. The typical phase sequence of these systems is lamellar–bicontinuous cubic (CubV)–hexagonal columnar (Colh)–micellar cubic (CubI) (Figure 28) as the volume fraction of one component is increased. There are three types of bicontinuous cubic phases in lyotropic liquid crystals. They are Ia3d double gyroid phases, Im3m triple-network phases, and Pn3m double diamond phases, which are also observed in thermotropic cubic phases [15]. The first thermotropic cubic phase was observed in nitro-substituted carboxylic acids by Gray et al. [78]. Various thermotropic cubic liquid crystals have been reported [15,79]. Some amphiphilic compounds exhibit the same phase sequence as observed in the lamellar–solvent systems. In the case of tetracatenar mesogens (Figure 29a), as the terminal chains increase, the phase changes from SmC to CubV and then to Col [80]. In the case of polyhydroxy derivatives (Figure 29b), they exhibit a phase sequence of SmA–CubV–Colh–CubI as the lipophilic regions increase [81]. Both cases support that the interface curvature between the two incompatible regions is the key factor determining the mesophase morphologies. The structure–property relationships in thermotropic bicontinuous cubic phases are described in some reviews [15,16]. Recently, Dressel and Tschierske et al. reported chiral conglomerates in the bicontinuous cubic phase with Im3m symmetry formed by achiral multichain-terminated diphenyl-2,2′-bithiophes [18]. The aggregation structure of chiral cubic liquid crystals formed by achiral molecules has been reported. The spontaneous mirror symmetry breaking in cubic phases has attracted much attention [82,83,84,85].
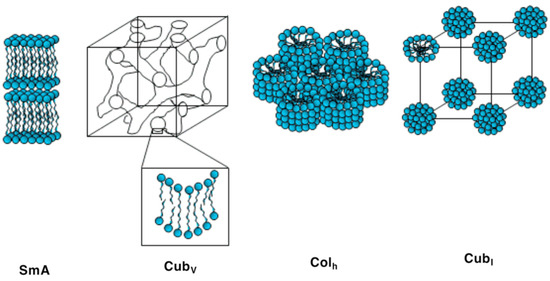
Figure 28.
Schematic sketches for morphologies of lamellar (SmA), bicontinuous cubic (CubV), hexagonal columnar (Colh), and micellar cubic (CubI) phases.
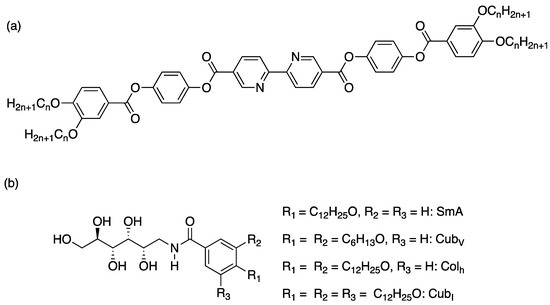
Figure 29.
Chemical structures of thermortropic liquid-crystalline compounds: (a) tetracatenar molecule [80] and (b) polyhydroxy derivatives [81].
Rancon and Charvolin observed the structural fluctuations in the vicinity of the lamellar-to-cubic phase transition in the lyotropic system of hexaethylene glycol mono-n-dodecyl ether and water [86]. X-ray scattering and NMR studies reveal that fluctuations exist in the lamellar phase as the cubic phase appears. They appear to correspond to local fragmentations of the bilayers into cylinders with short-range hexagonal organizations.
The microscopic fluctuation within a layer can induce a lamellar-to-cubic phase transition. Yamaguchi et al. prepared amphiphilic oligomers composed of a semiperfluorinated alkyl chain and cyanobiphenyl units [87]. Figure 30 shows their molecular structures and phase transition properties. These amphiphilic oligomers showed a phase sequence of SmC–Colh–CubV when the numbers of cyanobiphenyl moieties were increased. The sequence of Colh–CubV is opposite to that for an ordinary sequence reported for the tetracatenar compounds and polyhydroxy derivatives, suggesting that the formation mechanisms of the Cubv phase of HDFCBP-3 differ from those of typical low-molecular-mass thermotropic liquid-crystalline cubic systems.
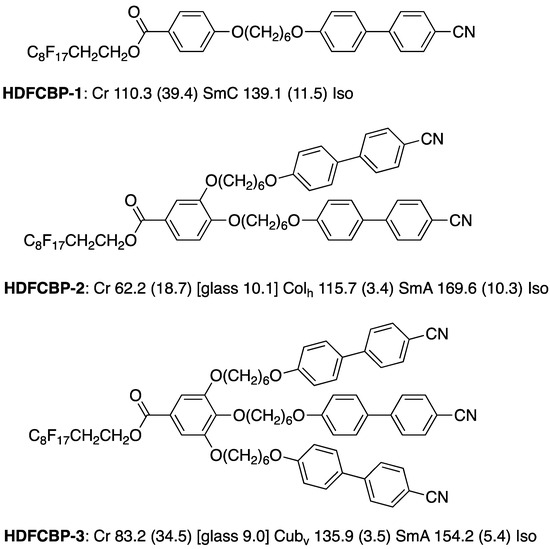
Figure 30.
The molecular structures, transition temperatures (°C), and enthalpies (kJ mol–1, in parentheses) of transition for HDFCBP-1, HDFCBP-2, and HDFCBP-3 [87]. Square brackets denote a monotropic transition.
Figure 31 shows the polarized optical texture of the SmA-to-Cubv transition of HDFCBP-3. Highly viscous optically isotropic domains grew rapidly in the fan texture of the SmA phase. Figure 32 presents X-ray diffraction profiles in the small-angle region of HDFCBP-3. Two peaks, corresponding to the periodicities of 55.8 Å and 45.0 Å, were observed in the SmA phase (Figure 32a). The periodicity lengths are longer than the molecular length estimated as 36.6 Å. The several weak reflections appearing between the two reflections can result from perfluorinated lamellae. A diffuse asymmetric tail around the Bragg peaks originates form the undulation of lamellae [88]. These results indicate the fluctuation of the interdigitated lamellar structure. With respect to the CubV phase (Figure 32b), the observed reflections reveal that the Cubv phase belongs to a space group Ia3d, which represents a bicontinuous cubic phase constructed from two interpenetrating networks of branched cylinders.
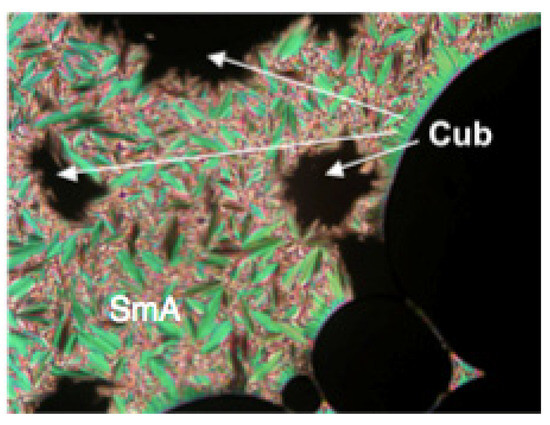
Figure 31.
Polarized optical texture of the SmA–Cubv transition for HDFCBP-3. Reprinted with permission from [87]. Copyright (2006) American Chemical Society.
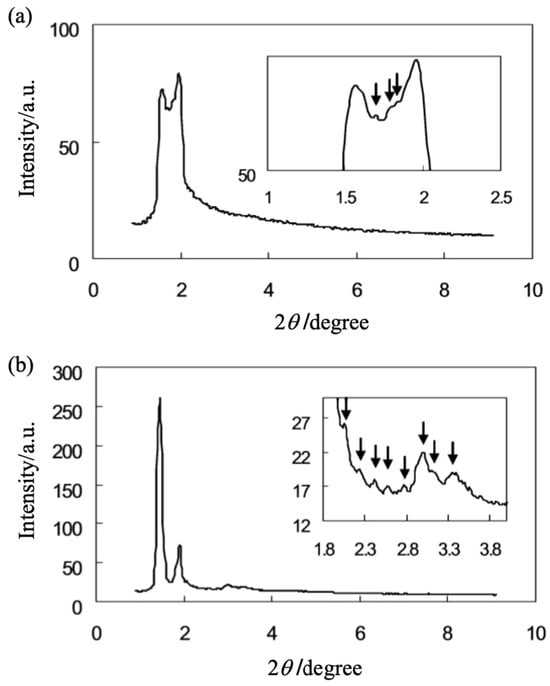
Figure 32.
X-ray diffraction profiles in the small-angle region of HDFCBP-3 in (a) the SmA phase at 150 °C and (b) the CubV phase at 100 °C; expansions are included for clarity. Reprinted with permission from [87]. Copyright (2006) American Chemical Society.
An undulatory lamellar deformation was reported to exist as the unstable transition state between the lamellar and the Gyroid in some block copolymers [89,90,91]. Imai et al. reported fluctuations of the lamellar phase prior to a lamellar-to-gyroid phase transition in a nonionic surfactant-water system and noted that the amplitude-modulation fluctuations develop to a perforation layer [92]. Figure 33 portrays the driving force for the formation of the CubV phase of HDFCBP-3 [93]. The competition of the steric effect attributable to the pronounced taper shape and the segregation effect due to the incompatibility between the semiperfluorinated chain and the cyanobiphenyl units of HDFCBP-3 induces the fluctuation of the lamellar structure. The fluctuation of the interdigitated lamellar structure is likely amplified by antiparallel dipole–dipole interactions between cyanobiphenyl units in adjacent layers, which perforates the lamellar to form the bicontinous cubic phase.
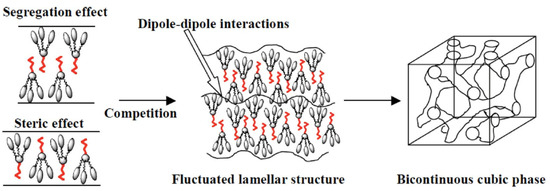
Figure 33.
Schematic illustration of the SmA-to-Cubv transformation of HDFCBP-3. Reprinted with permission from [93]. Copyright (2010) Taylor & Francis Ltd.
3. Dissipative Structures: Order through Fluctuation
3.1. Pattern Formation and Propagation
The fluctuations in a layer structure induce not only the hierarchical structures but also sometimes dissipative structures. Prigogine describes the dissipative structures as follows: “An open system out of equilibrium may be associated with dissipative structures when specific constrains are satisfied. Dissipative structures are associated with an entirely different ordering principle, which may be called order through fluctuation. They arise from the amplification of fluctuations resulting from an instability of the thermodynamic branch” [23]. The behavior and nature of a dissipative structure that can appear beyond a certain critical distance from equilibrium may be multiple, such as Rayleigh–Bénard convection [94,95,96] and Belousov–Zhabotinsky reactions [97,98,99].
The study of pattern-forming phenomena is one of the very attractive areas in liquid crystal science [100,101]. The pattern formation has been observed in some nematic liquid-crystalline systems under electric or magnetic fields [102,103]. Andrade-Sliva et al. reported spontaneous light-induced Turing patterns in a dye-doped twisted nematic layer [104]. Recently, Tang et al. found that solitary waves in nematic liquid crystals exhibit “butterfly”-like or “bullet”-like structures that travel in the direction perpendicular to the applied electric field [105]. Front propagation in smectic liquid crystals has also been extensively investigated. Clerc et al. observed that finger fronts emerge in the SmA phase near the SmA to chiral nematic transition under an electric field [106]. If the layer fluctuations described in Section 2 produce the breaking-down and recombination of a smectic-layer ordering, a dissipative structure is expected to be observed under a nonequilibrium state.
Yoshizawa at al. reported the pattern propagation in the interdigitate anticlinic smectic C (SmCanti) phase of some binary mixtures of the unsymmetric dimers with different odd-numbered spacers in 2006 [107]; however, they have not yet explained this phenomenon. The discussion on the fluctuation-induced hierarchical structures has just given a new interpretation of the pattern propagation. Figure 34 shows the striped pattern of an equivalent-weight mixture of 12PY7OCB and 12PY9OCB contained in a homeotropically aligned cell. Figure 35 shows the molecular structures and transition temperatures. The mixture exhibited phase transitions as follows: Iso 120 °C N 109 °C interdigitated SmA 86 °C interdigitated SmCanti [107].

Figure 34.
Photomicrograph of the striped pattern of an equivalent-weight mixture of 12PY7OCB and 12PY9OCB contained in a homeotropically aligned cell with a cell gap of 5 µm in the induced SmCanti phase at 80 °C under crossed polarizers. The center was pressed to make it thinner.
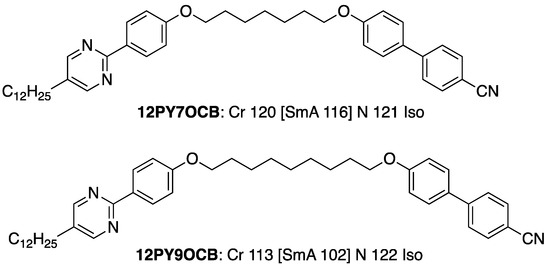
Figure 35.
The molecular structures and transition temperatures (°C) of 12PY7OCB and 12PY9OCB [107].
The pattern propagation was observed when the temperature of the sample was varied. It can be seen in Video S1 (see Supplementary Materials). A certain position of the sample was slightly pressed to induce a gradient in the thickness of the sample. It thickens from that pressed position towards the periphery. The waves were produced repeatedly at that thinner position of the sample in the SmCanti phase near the SmA-to-SmCanti transition when the sample was cooled. They spread out in concentric circles to form the periodic pattern (see Video S2a). On heating in the SmCanti phase, the waves converged from the periphery of the pattern towards the center, where they disappeared (see Video S2b). Figure 36 shows the pattern propagation in the periphery region on cooling. The pattern of dark stripes moved forward while rotating over the bright background (see Video S3). When the sample was rotated about 45° clockwise, the dark stripes barely changed to be bright, while the background became partially dark (Figure 37). These indicate that the black region is close to optically isotropic and the background is the anisotropic texture of the SmCanti phase. Textures similar to the striped pattern have been observed in a biaxial SmA phase of a binary system between a metallomesogen and 2,4,7-trinitrofluorenone [108], in that of a bent-core molecule [109], and in that of a nonsymmetric dimer [110]. For the formation of the dissipative structure, Rayleigh–Bénard convection is thought to occur near the center of the pattern on cooling (Figure 38a). Figure 38b shows a model for the pattern formation and propagation on cooling. The thickness of the sample decreases toward the center of the pattern. The temperature gradient between the top and bottom of the sample increases with its thickness. At the boundary where the bright strip changes to the dark strip in the pattern progressing areas, the smectic layers break to disorderly arranged smectic blocks. These blocks rotate clockwise, moving towards the larger temperature gradient. At the opposite boundary where the dark strip changes to the bright strip in the pattern’s passing areas, the smectic blocks reorganize to form the smectic layers. Therefore, when cooling, the black strip propagates from the center to the periphery, increasing in depth. When heated, the smectic blocks rotate in the opposite direction, moving towards the lower-temperature gradient. The mixture of 12PY7OCB and 12PY9OCB forms the interdigitated layer structure. It is organized by two different interactions, i.e., the strong intra-layer dipole–dipole interaction between cyanobiphenyl units in an antiparallel alignment and the weak inter-layer permeation of the tails of molecules in adjacent layers. The heterogeneous interactions of the layer structure may have fluctuations along the layer normal. Therefore, the smectic layers might break with the thermal convection.

Figure 36.
Pattern propagation of the mixture in the periphery region on cooling under crossed polarizers. The cooling rate was 5 °C min–1. Reprinted with permission from [107]. Copyright (2006) Taylor & Francis Ltd.

Figure 37.
(a) Optical texture of the pattern of the mixture in the periphery region and (b) that for which the sample was rotated about 45° clockwise.
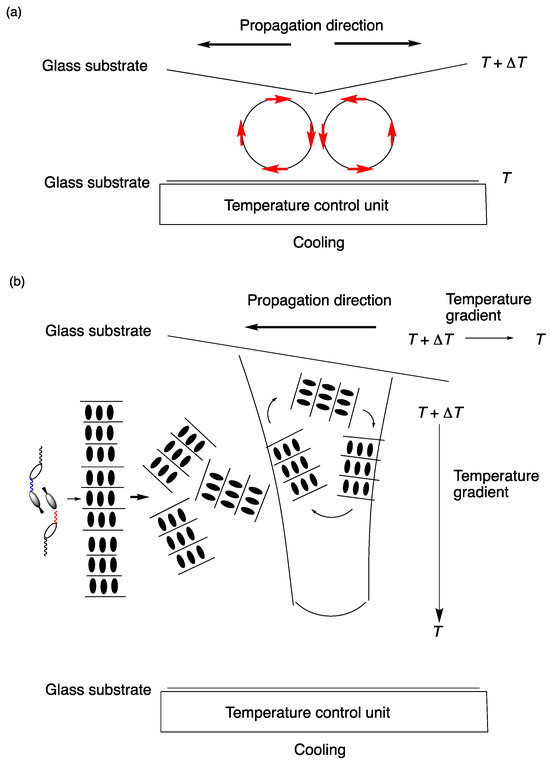
Figure 38.
(a) Rayleigh–Bénard convection (red arrows) near the center of the pattern on cooling. (b) Model for the pattern formation and propagation on cooling in the area of the left side of (a).
3.2. Periodic Formation/Breakdown of Lamellar Aggregates in Water
Hybrid surfactants have attracted considerable interest due to not only them forming self-assembled super-structures but also the applications for new carriers capable of the controlled release of the encapsulated materials [111,112,113,114,115,116]. Sagisaka et al. synthesized a anionic hybrid surfactant CB-B2ES possessing a 4-hexyloxy-4′-cyanobiphenyl (6OCB) unit and a butoxyethoxyethyl tail and found it exhibiting the periodic formation/breakdown of lamellar aggregates in water [117].
CB-B2ES is a mixture of the two isomers, as shown in Figure 39. Figure 40 shows the phase diagram of the 1–30 wt% surfactant/water mixtures as a function of the temperature. An optically isotropic micellar phase appeared in the 1 wt% of the CB-B2ES/water mixture. Then, CB-B2ES exhibited a stable lamellar liquid crystal from 5 wt% for the surfactant. The stability is attributed to the intermolecular interactions between cyanobiphenyl units in an antiparallel arrangement.

Figure 39.
The molecular structure of CB-B2ES. The surfactant has two isomers with different C-S locations [117].
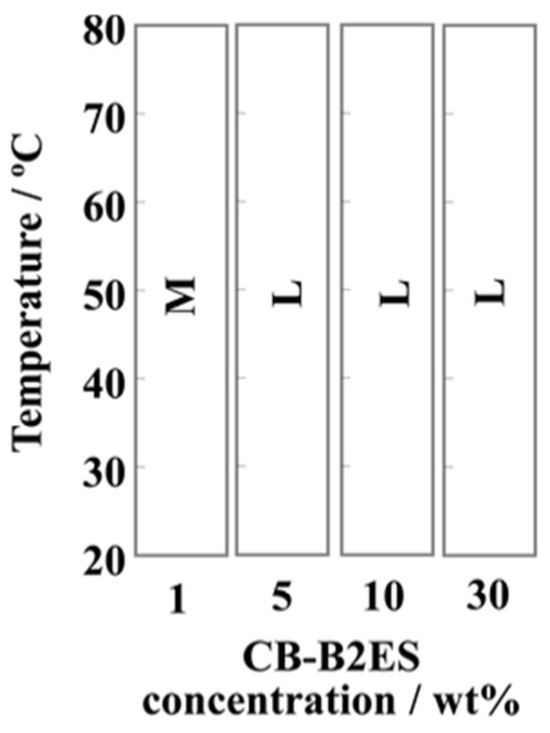
Figure 40.
Phase diagram of 1, 5, 10, and 30 wt% of CB-B2ES/water mixtures as a function of the temperature. The symbols M and L mean the optically isotropic micellar phase and lamellar phase, respectively. Reprinted with permission from [117]. Copyright (2015) American Chemical Society.
The CB-B2ES lamellar LCs exhibited spontaneous formation/breakdown behavior in water. It should be noted that typical lyotropic lamellar LCs are stable, over at least several hours, without external stimuli [118,119,120,121]. Figure 41 shows the time-dependent textures of the lamellar LCs in the 30 wt% of the CB-B2ES/water mixture at 30 °C under crossed polarizers. The maltase cross textures repeatedly disappear and reappear. For example, the maltase cross texture (see white arrow) appeared about 1 s after commencing observations but disappeared at around 14 s. The disappearance of the texture corresponds to the structural change from the lamellar aggregation to the optically isotropic micellar aggregation. A lifetime for the lamellar domains is estimated as ~10 s.

Figure 41.
Spontaneous appearance/disappearance of the maltase cross-texture for 30 wt% of the CB-B2ES/water mixture at 30 °C under crossed polarizers. Reprinted with permission from [117]. Copyright (2015) American Chemical Society.
The self-organization of molecules in a lyotropic liquid-crystalline system is governed by two factors, i.e., the hydrophilic/lipophilic balance (HLB) and critical packing parameter (CPR) of the constituting molecule [120]. Sagisaka et al. explain the periodic formation/breakdown behavior of CB-B2ES lamellar aggregates as follows [117]: “The HBL of the ethoxylated tails and the degree of hydration can be tuned by the temperature. At a low temperature, enhanced oxyethylene hydration is likely to favor the ethoxylated tail orienting toward water (trans form), away from the bilayer center (gauche form), as shown in Figure 42. CB-B2ES will have CPP~1, and this change in hydration should give a rise to a lower CPP, favoring micelle formation more than lamellar LCs. The temperature of 30 °C could be critical temperature to promote reversible gauche/trans conformational changes”. If this is the case, another question arises: “Why does the dominant conformational change happen periodically over micrometer scales?”. One possibility is that cooperative conformational change may occur reversibly. Further investigation is necessary to solve the problem.
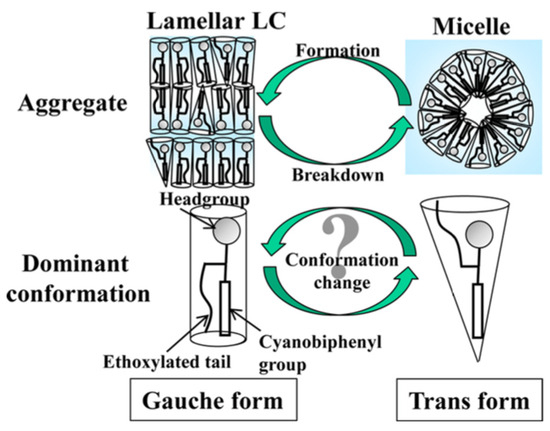
Figure 42.
Gauche–trans conformational changes for the CB-B2ES molecule inducing the periodical formation/breakdown of lamellar aggregates. Reprinted with permission from [117]. Copyright (2015) American Chemical Society.
4. Concluding Remarks
I have demonstrated how liquid-crystalline supermolecules exhibit fluctuation-induced phenomena, i.e., hierarchical phases and dissipative structures. Several mesogenic units connected via a flexible spacer within a molecule are associated with each other. Therefore, liquid-crystalline supermolecules have an intra-molecular assembly order, inducing heterogeneity in their supramolecular assemblies to produce fluctuations. Particularly, the fluctuations in lamellar structures give rise to cybotactic nematic, modulated smectic, and bicontinuous cubic phases. Furthermore, the striped pattern similar to those found in nature is formed in the smectic phase composed of supermolecular LC dimers. The pattern propagation is explainable in terms of a layer fluctuation. The design of fluctuation at a molecular level is a fascinating concept, which contributes to the understanding of fluctuation phenomena.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst14080681/s1, Video S1: The pattern propagation on cooling from 80 °C to 75.5 °C; Video S2: Pattern propagation of the central part on (a) cooling and (b) heating; Video S3: Pattern propagation in the periphery region on cooling from 76.1 °C to 70.5 °C.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The author would like to thank his collaborators named in the reference list.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Cladis, P.E. Fluctuations and liquid crystal phase transitions. In Handbook of Liquid Crystals, 1st ed.; Demus, D., Goodby, J.W., Gray, G.W., Spiess, H.W., Vill, V., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 1998; Volume 1, pp. 379–390. [Google Scholar]
- Moses, T.; Reeves, J.; Pirondi, P. Fluctuations near a phase transition in liquid crystals. Am. J. Phys. 2007, 75, 220–225. [Google Scholar] [CrossRef]
- De Vries, A. Evidence for the existence of more than one type of nematic phase. Mol. Cryst. Liq. Cryst. 1970, 10, 31–35. [Google Scholar] [CrossRef]
- De Vries, A. X-ray photographic studies of liquid crystals I. A cybotactic nematic phase. Mol. Cryst. Liq. Cryst. 1970, 10, 219–236. [Google Scholar] [CrossRef]
- Chistyakov, I.G.; Chaikowsky, W.M. The structure of p-azoxybenzenes in magnetic fields. Mol. Cryst. Liq. Cryst. 1969, 7, 269–277. [Google Scholar] [CrossRef]
- Samulski, E.T. meta-Cybotaxis and nematic biaxiality. Liq. Cryst. 2010, 37, 669–678. [Google Scholar] [CrossRef]
- Leadbetter, A.J. Structural classification of liquid crystals. In Thermotropic Liquid Crystals; Critical Reports on Applied Chemistry; Gray, G.W., Ed.; John Wiley & Sons: Chichester, UK, 1987; Volume 22, pp. 1–27. [Google Scholar]
- Nishiya, W.; Takanishi, Y.; Yamamoto, J.; Yoshizawa, A. Molecular design foe a cybotactic nematic phase. J. Mater. Chem. C 2014, 2, 3677–3685. [Google Scholar] [CrossRef]
- Sigaud, G.; Hardoin, F.; Achard, M.F.; Levelut, A.M. A new type of smectic A phase with long range modulation in the layers. J. Phys. 1981, 42, 107–111. [Google Scholar] [CrossRef]
- Prost, J.; Barois, P. Polymorphism in polar mesogens. II—Theoretical aspects. J. Chim. Phys. 1983, 80, 65–80. [Google Scholar] [CrossRef]
- Seddon, J.M. Structural studies of liquid crystals by X-ray diffraction. In Handbook of Liquid Crystals, 1st ed.; Demus, D., Goodby, J.W., Gray, G.W., Spiess, H.W., Vill, V., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 1998; Volume 1, pp. 635–679. [Google Scholar]
- Imrie, C.T.; Luckhurst, G.R. Liquid crystal dimers and oligomers. In Handbook of Liquid Crystals, 2nd ed.; Goodby, J.W., Collings, P.J., Kato, T., Tschierske, C., Gleeson, H.F., Raynes, P., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2014; Volume 7, pp. 137–210. [Google Scholar]
- Sasaki, T.; Takanishi, Y.; Yamamoto, J.; Yoshizawa, A. A frustrated phase driven by competition among layer structures. Soft Matter 2017, 13, 5194–5203. [Google Scholar] [CrossRef]
- Pociecha, D.; Kardas, D.; Gorecka, E.; Szydlowska, J.; Mieczkowski, J.; Guillon, D. Modulated and intercalated smectic phases formed by dimeric molecules. J. Mater. Chem. 2003, 13, 34–37. [Google Scholar] [CrossRef]
- Ungar, G.; Liu, F.; Zeng, X. Cubic and other 3D thermotropic liquid crystal phases and quasicrystals. In Handbook of Liquid Crystals, 2nd ed.; Goodby, J.W., Collings, P.J., Kato, T., Tschierske, C., Gleeson, H.F., Raynes, P., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2014; Volume 5, pp. 363–436. [Google Scholar]
- Kutsumizu, S. Recent progress in the synthesis and structural clarification of thermotropic cubic phases. Isr. J. Chem. 2012, 52, 844–853. [Google Scholar] [CrossRef]
- Levelut, A.-M.; Clerc, M. Structural investigation on ‘smectic D’ and related mesophases. Liq. Cryst. 1998, 24, 105–115. [Google Scholar] [CrossRef]
- Dressel, C.; Liu, F.; Prehm, M.; Zeng, X.; Ungar, G.; Tschierske, C. Dynamic mirror-symmetry breaking in bicontinuous cubic phases. Angew. Chem. Int. Ed. 2014, 53, 13115–13120. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yang, S.-G.; Li, Y.-X.; Cao, Y.; Zeng, X.-B.; Cseh, L.; Ungar, G. Supertwisted chiral gyroid mesophase in chiral rod-like compounds. Angew. Chem. Int. Ed. 2024, 63, 202403156. [Google Scholar] [CrossRef] [PubMed]
- Ichikawa, T.; Yoshio, M.; Hamasaki, A.; Taguchi, S.; Liu, F.; Zeng, X.-B.; Ungar, G.; Ohno, H.; Kato, T. Induction of thermotropic bicontinuous cubic phases in liquid-crystalline ammonium and phosphonium salts. J. Am. Chem. Soc. 2012, 134, 2634–2643. [Google Scholar] [CrossRef]
- Kato, T.; Yoshio, M.; Ichikawa, T.; Soberats, B.; Ohno, H.; Funahashi, M. Transport of ions and electrons in nanostructured liquid crystals. Nat. Rev. Mater. 2017, 2, 17001. [Google Scholar] [CrossRef]
- Prigogine, I. Time, structure, and fluctuations. Science 1978, 201, 777–785. [Google Scholar] [CrossRef] [PubMed]
- Prigogine, I. Evolution and Consciousness: Human Systems in Transition; Jantsch, E., Ed.; Addison-Wesley: Boulder, CO, USA, 1976; pp. 93–130. [Google Scholar]
- Yoshizawa, A. Uncoventional liquid crystal oligomers with a hierarchical structure. J. Mater. Chem. 2008, 18, 2877–2889. [Google Scholar] [CrossRef]
- Saez, I.M.; Goodby, J.W. Supermolecular liquid crystals. Struct. Bond. 2008, 128, 1–62. [Google Scholar]
- Imrie, C.; Henderson, P.A. Liquid crystal dimers and higher oligomers: Between monomers and polymers. Chem. Soc. Rev. 2007, 36, 2096–2124. [Google Scholar] [CrossRef]
- Saez, I.M. Supermolecular liquid crystals. In Handbook of Liquid Crystals, 2nd ed.; Goodby, J.W., Collings, P.J., Kato, T., Tschierske, C., Gleeson, H.F., Raynes, P., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2014; Volume 7, pp. 211–258. [Google Scholar]
- Cestari, M.; Diez-Berart, S.; Dunmur, D.A.; Ferrarini, M.R.; Jackson, D.J.B.; Lopez, D.O.; Luckhurst, G.R.; Perez-Jubindo, M.A.; Richardson, R.M.; Salud, J. Phase behavior and properties of the liquid-crystal dimer 1″,7″-bis(4-cyanobiphenyl-4′-yl) heptane: A twist-bend nematic liquid crystal. Phys. Rev. E 2011, 84, 031704. [Google Scholar] [CrossRef]
- Paterson, D.A.; Abberley, J.P.; Harrison, W.T.A.; Storey, J.M.D.; Imrie, C.T. Cyanobiphenyl-based liquid crystal dimers and the twist-bend nematic phase. Liq. Cryst. 2017, 44, 127–146. [Google Scholar] [CrossRef]
- Yoshizawa, A. Nanostructured assemblies of liquid-crystalline supermolecules: From display to medicine. Liq. Cryst. 2019, 46, 1950–1972. [Google Scholar] [CrossRef]
- Yoshizawa, A.; Kikuzaki, H.; Fukumasa, M. Microscopic organization of the molecules in smectic A and chiral (racemic) smectic C phases: Dynamic molecular deformation effect on the SA to SC* (SC) transition. Liq. Cryst. 1995, 18, 351–366. [Google Scholar] [CrossRef]
- Yoshizawa, A.; Kogawa, Y.; Kobayashi, K.; Takanishi, Y.; Yamamoto, J. A binaphthyl derivative with a wide temperature range of a blue phase. J. Mater. Chem. 2009, 19, 5759–5764. [Google Scholar] [CrossRef]
- Sasaki, H.; Takanishi, Y.; Yamamoto, J.; Yoshizawa, A. Achiral flexible liquid crystal trimers exhibiting chiral conglomerates. Soft Matter 2016, 12, 3331–3339. [Google Scholar] [CrossRef] [PubMed]
- Mandle, R.J.; Bevis, E.; Goodby, J.W. Phase structures of nematic liquid crystals. In Handbook of Liquid Crystals, 2nd ed.; Goodby, J.W., Collings, P.J., Kato, T., Tschierske, C., Gleeson, H.F., Raynes, P., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2014; Volume 3, pp. 3–29. [Google Scholar]
- Kumar, M.P.; Sai, D.V.; Dhara, S. Effect of Sm-A short-range order on the activation energies of translational and rotational viscosities of nematic liquid crystals with highly polar molecules. Phys. Rev. E 2018, 98, 062701. [Google Scholar] [CrossRef]
- Freiser, M.J. Ordered states of a nematic liquid. Phys. Rev. Lett. 1970, 24, 1041–1043. [Google Scholar] [CrossRef]
- Lehmann, M.; Görtz, V. Design of biaxial nematic mesogens. In Handbook of Liquid Crystals, 2nd ed.; Goodby, J.W., Collings, P.J., Kato, T., Tschierske, C., Gleeson, H.F., Raynes, P., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2014; Volume 3, pp. 335–373. [Google Scholar]
- Tschierske, C.; Photinos, D.J. Biaxial nematic phases. J. Mater. Chem. 2010, 20, 4263–4294. [Google Scholar] [CrossRef]
- Bruce, D.W. Towards the biaxial nematic phase through molecular design. Chem. Rec. 2004, 4, 10–22. [Google Scholar] [CrossRef]
- Mandle, R.J. A ten-year perspective on twist-bend nematic materials. Molecules 2022, 27, 2689. [Google Scholar] [CrossRef] [PubMed]
- Mandle, R.J.; Cowling, S.J.; Goodby, J.W. A nematic to nematic transformation exhibited by a rod-like liquid crystal. Phys. Chem. Chem. Phys. 2017, 19, 11429–11435. [Google Scholar] [CrossRef]
- Mandle, R.J.; Cowling, S.J.; Goodby, J.W. Rational design of rod-like liquid crystals exhibiting two nematic phases. Chem.—A Eur. J. 2017, 23, 14554–14562. [Google Scholar] [CrossRef] [PubMed]
- Nishikawa, H.; Shiroshita, K.; Higuchi, H.; Okumura, Y.; Haseba, Y.; Yamamoto, S.; Sago, K.; Kikuchi, H. A fluid liquid-crystal material with highly polar order. Adv. Mater. 2017, 29, 1702354. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Korblova, E.; Glaser, M.A.; Maclennan, J.E.; Walba, D.M.; Clark, N.A. Polar in-plane surface orientation of a ferroelectric nematic liquid crystal: Polar monodomains and twisted state electro-optics. Proc. Natl. Acad. Sci. USA 2021, 118, e2104092118. [Google Scholar] [CrossRef] [PubMed]
- Karcz, J.; Herman, J.; Rychłowicz, N.; Kula, P.; Górecka, E.; Szydlowska, J.; Majewski, P.; Pociecha, D. Spontaneous chiral symmetry breaking in polar fluid-heliconical ferroelectric nematic phase. Science 2024, 384, 1096–1099. [Google Scholar] [CrossRef]
- Nasir, A.K.; Rahman, M. Cybotactic nematic liquid crystal—An overview. Liq. Cryst. 2024, 51, 503–535. [Google Scholar] [CrossRef]
- Keith, C.; Lehmann, A.; Baumeister, U.; Prehm, M.; Tschierske, C. Nematic phases of bent-core mesogens. Soft Matter 2010, 6, 1703–1721. [Google Scholar] [CrossRef]
- Deb, R.; Nath, R.K.; Sarkar, D.D.; Araoka, F.; Ishikawa, K.; Takezoe, H.; Takanishi, Y. Synthesis of four-ring unsymmetrical bent-core mesogens and cybotactic cluster formation in their nematic phase. J. Mol. Struct. 2024, 1317, 139055. [Google Scholar] [CrossRef]
- Tadapartri, P.; Hiremath, U.S.; Yelamaggad, C.V.; Krishnamurthy, K.S. Permittivity, conductivity, elasticity, and viscosity measurements in the nematic phase of a bent-core liquid crystal. J. Phys. Chem. B 2010, 114, 1745–1750. [Google Scholar] [CrossRef]
- Panarin, Y.P.; Sreenilayam, S.P.; Vij, J.K.; Lehnmann, A.; Tschierske, C. Formation and development of nanometer-sized cybotactic clusters in bent-core nematic liquid crystalline compounds. Beilstein J. Nanotechnol. 2018, 9, 1288–1296. [Google Scholar] [CrossRef] [PubMed]
- Monika, M.; Roy, A.; Prasad, V. Smectic nanoclusters in the nematic mesophases of dimeric compounds composed of rod-like azo moieties with lateral substituents. New J. Chem. 2017, 41, 11576–11583. [Google Scholar]
- Vita, F.; Sparnacci, K.; Panzarasa, G.; Placentino, I.F.; Marino, S.; Scaramuzza, N.; Portale, G.; Cola, E.D.; Ferrero, C.; Torgova, S.I.; et al. Evidence of cybotactic order in the nematic phase of a main-chain liquid crystal polymer with bent-core repeat unit. ACS Macro Lett. 2014, 3, 91–95. [Google Scholar] [CrossRef]
- Yoshizawa, A.; Yamaguchi, A. Kinetically induced intermolecular association: Unusual enthalpy changes in the nematic phase of a novel dimeric liquid-crystalline molecule. Chem. Commun. 2002, 2060–2061. [Google Scholar] [CrossRef] [PubMed]
- Vanakaras, A.G.; Photinos, D.J. Thermotropic biaxial nematic liquid crystals: Spontaneous or field stabilized? J. Chem. Phys. 2008, 128, 154512. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, M. Biaxial nematics from their prediction to the materials and the vicious circle of molecular design. Liq. Cryst. 2011, 38, 1389–1405. [Google Scholar] [CrossRef]
- Taushanoff, S.; Le, K.V.; Williams, J.; Twieg, R.J.; Sadashiva, B.K.; Takezoe, H.; Jakli, A. Stable amorphous blue phase of bent-core nematic liquid crystals doped with a chiral material. J. Mater. Chem. 2010, 20, 5893–5898. [Google Scholar] [CrossRef]
- Francescangeli, O.; Stanic, V.; Torgova, S.I.; Strigazzi, A.; Scaramuzza, N.; Ferrero, C.; Dolbnya, I.P.; Weiss, T.M.; Beradi, R.; Muccioli, L.; et al. ferroelectric response and induced biaxiality in the nematic phase of bent-core mesogens. Adv. Funct. Mater. 2009, 19, 2592–2600. [Google Scholar] [CrossRef]
- Vita, F.; Adamo, F.C.; Francescangeli, O. Polar order in bent-core nematics: An overview. J. Mol. Liq. 2018, 267, 564–573. [Google Scholar] [CrossRef]
- Nishikawa, H.; Sano, K.; Kurihara, S.; Watanabe, G.; Nisjonyanagi, A.; Dhara, B.; Araoka, F. Nano-clustering mediates phase transitions in a diastereomerically-stabilized ferroelectric nematic system. Commun. Mater. 2022, 3, 89. [Google Scholar] [CrossRef]
- Yoshizawa, A.; Nishizawa, A.; Takeuchi, K.; Takanishi, Y.; Yamamoto, J. Interlayer interactions induced by amphiphilicities of a rod-like molecule produce frustrated structures in conventional calamitic phases. J. Phys. Chem. B 2010, 114, 13304–13311. [Google Scholar] [CrossRef] [PubMed]
- Kimoto, Y.; Nishizawa, A.; Takanishi, Y.; Yoshizawa, A.; Yamamoto, J. Layer modulated smectic-C phase in liquid crystals. Phys. Rev. E 2014, 89, 042503. [Google Scholar] [CrossRef] [PubMed]
- Barois, P. Phase transition theories. In Handbook of Liquid Crystals, 1st ed.; Demus, D., Goodby, J.W., Gray, G.W., Spiess, H.W., Vill, V., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 1998; Volume 1, pp. 281–309. [Google Scholar]
- Lobko, T.A.; Ostrovskii, B.I.; Hasse, W. X-ray studies of the smectic phase and transitions between reentrant nematic, smectic A1, Ad and phases in binary mixtures of polar mesogens. J. Phys. II 1992, 2, 1195–1213. [Google Scholar] [CrossRef]
- Tinh, N.H.; Destrade, A.M.; Levelut, A.M.; Malthete, J. Biforked mesognes: A new type of thermotropic liquid crystals. J. Phys. 1986, 47, 553–557. [Google Scholar] [CrossRef]
- Date, R.W.; Luckhurst, G.R.; Shuman, M.; Seddon, J.M. Novel modulated hexatic phases in symmetric liquid crystal dimers. J. Phys. II 1995, 5, 587–605. [Google Scholar] [CrossRef]
- Faye, V.; Babeau, A.; Placin, F.; Nguyen, H.T.; Barois, P.; Laux, V.; Isaert, N. SC*A and S[Ctilde]* phases in chiral non-symmetric dimesogens. Liq. Cryst. 1996, 21, 485–503. [Google Scholar] [CrossRef]
- Walker, R.; Pociecha, D.; Storey, J.M.; Gorecka, E.; Imrie, C.T. Remarkable smectic phase behaviour in odd-membered liquid crystal dimers: The CT6O.m series. J. Mater. Chem. C 2021, 9, 5167–5173. [Google Scholar] [CrossRef]
- Pociecha, D.; Vaupotic, N.; Gorecka, E.; Mieczkowski, J.; Gomola, K. 2-D Density-modulated structures in asymmetric bent-core liquid crystals. J. Mater. Chem. 2008, 18, 881–885. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Sigaud, G.; Achard, M.F.; Hardouin, F. Rod-like mesogens with antipathetic fluorocarbon and hydrocarbon tails. Liq. Cryst. 1991, 10, 389–396. [Google Scholar] [CrossRef]
- Davidson, P.; Keller, P.; Levelut, A.M. Molecular organization in side chain liquid crystalline polymers. J. Phys. 1985, 46, 939–946. [Google Scholar] [CrossRef]
- Watanabe, J.; Nakata, Y.; Shimizu, K. Frustrated bilayer smectic phase in main-chain polymers with two different spacers. J. Phys. II 1994, 4, 581–588. [Google Scholar] [CrossRef]
- Endres, B.W.; Ebert, M.; Wendorff, J.H.; Reck, B.; Ringsdorf, H. Combined main chain/side chain polymers: A new class of liquid crystalline polymers with unusual structural thermotropic and dynamic properties. Liq. Cryst. 1990, 7, 217–239. [Google Scholar] [CrossRef]
- Kashima, S.; Takanishi, Y.; Yamamoto, J.; Yoshizawa, A. Flexible taper-shaped liquid crystal trimer exhibiting a modulated smectic phase. Liq. Cryst. 2014, 41, 1752–1761. [Google Scholar] [CrossRef]
- Kashima, S. Supermolecular liquid crystals exhibiting frustrated phases. Master’s Thesis, Hirosaki University, Hirosaki, Japan, 18 February 2014. [Google Scholar]
- Rybalova, T.V.; Bagryanskaya, I.Y. C–F…π, F…H, and F…F intermolecular interactions and F-aggregation: Role in crystal engineering of fluoroorganic compounds. J. Struct. Chem. 2009, 50, 741–753. [Google Scholar] [CrossRef]
- Collings, P.J. The structures of the blue phases. In Handbook of Liquid Crystals, 2nd ed.; Goodby, J.W., Collings, P.J., Kato, T., Tschierske, C., Gleeson, H.F., Raynes, P., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2014; Volume 3, pp. 587–609. [Google Scholar]
- Alfutimie, A.; Curtis, R.; Tiddy, G.J.T. Lyotropic surfactant liquid crystals: Micellar systems. In Handbook of Liquid Crystals, 2nd ed.; Goodby, J.W., Collings, P.J., Kato, T., Tschierske, C., Gleeson, H.F., Raynes, P., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2014; Volume 6, pp. 377–420. [Google Scholar]
- Gray, G.W.; Jones, B.; Marson, F. 71. Mesomorphism and chemical constitution. Part VIII. The effect of 3′-substituents on the mesomorphism of the 4′-n-alkoxydiphenyl-4-carboxylic acid and their alkyl esters. J. Chem. Soc. 1957, 393–401. [Google Scholar] [CrossRef]
- Diel, S.; Göring, P. Thermotropic cubic phases. In Handbook of Liquid Crystals, 1st ed.; Demus, D., Goodby, J.W., Gray, G.W., Spiess, H.W., Vill, V., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 1998; Volume 2B, pp. 887–900. [Google Scholar]
- Rowe, K.E.; Bruce, D.W. The synthesis and mesomorphism of di-, tetra- and hexa-catenar liquid crystals based on 2,2′-bipyridine. J. Mater. Chem. 1998, 8, 331–341. [Google Scholar] [CrossRef]
- Borisch, K.; Diel, S.; Göring, P.; Müller, H.; Tschierske, C. Amphiphilic N-benzoyl-1-amino-1-deoxy-D-glucitol derivatives forming thermotropic lamellar, columnar and different types of cubic mesophases. Liq. Cryst. 1997, 22, 427–443. [Google Scholar] [CrossRef]
- Tschierske, C.; Ungar, G. Mirror symmetry braking by chirality synchronization in liquids and liquid crystals of achiral molecules. ChemPhysChem 2016, 17, 9–26. [Google Scholar] [CrossRef]
- Vaupotič, N.; Salamończyk, M.; Matraszek, J.; Vogrin, M.; Pociecha, D.; Górecka, E. New structural model of a chiral cubic liquid crystalline phase. Phys. Chem. Chem. Phys. 2020, 22, 12814–12820. [Google Scholar] [CrossRef]
- Reppe, T.; Poppe, S.; Tschierske, C. Controlling mirror symmetry breaking and network formation in liquid crystalline cubic, isotropic liquid and crystalline phases of benzil-based polycatenars. Chem. Eur. J. 2020, 26, 16066–16079. [Google Scholar] [CrossRef] [PubMed]
- Oka, T.; Yamamura, Y.; Kutsumizu, S.; Saito, K. Aggregation structure of chiral cubic liquid crystals revealed by X-ray diffraction utilizing a new algorithm. Soft Matter 2023, 19, 1194–1201. [Google Scholar] [CrossRef] [PubMed]
- Rancon, Y.; Charvolin, J. Fluctuations and phase transformations in a lyotropic liquid crystal. J. Phys. Chem. 1988, 92, 6339–6344. [Google Scholar] [CrossRef]
- Yamaguchi, A.; Maeda, Y.; Yokoyama, H.; Yoshizawa, A. Self-assembly of amphiphilic liquid-crystalline oligomers possessing a semiperfluorinated alkyl chain. Chem. Mater. 2006, 18, 5704–5710. [Google Scholar] [CrossRef]
- Safinya, C.R.; Roux, D.; Smith, G.S.; Sinha, S.K.; Dimon, P.; Clark, N.A.; Bellocq, A.M. Steric interactions in a model multimembrane system: A synchrotron X-ray study. Phys. Rev. Lett. 1986, 57, 2718–2721. [Google Scholar] [CrossRef]
- Hjduk, D.A.; Takenouchi, H.; Hilmyer, M.A.; Bates, F.S.; Vigild, M.E.; Almdal, K. Stability of the perforated layer (PL) phase in deblock copolymer melts. Macromolecules 1997, 30, 3788–3795. [Google Scholar] [CrossRef]
- Qi, S.; Wang, Z.-G. Kinetics of phase transitions in weakly segregated block copolymers: Pseudostable and transient states. Phys. Rev. E 1997, 55, 1682–1697. [Google Scholar] [CrossRef]
- Laradji, M.; Shi, A.-C.; Noolandi, J.; Desai, R.C. Stability of ordered phases in deblock copolymer melts. Macromolecules 1997, 30, 3242–3255. [Google Scholar] [CrossRef]
- Imai, M.; Kawaguchi, A.; Saeki, A.; Nakaya, K.; Kato, T.; Ito, K.; Amemiya, Y. Fluctuations of a lamella r gyroid transition in a nonionic surfactant system. Phys. Rev. E 2000, 62, 6865–6874. [Google Scholar] [CrossRef]
- Takeuchi, K.; Takanishi, Y.; Yamamoto, J.; Yoshizawa, A. Amplification taper-shaped oligomer exhibiting a monolayer smectic A to columnar phase transition. Liq. Cryst. 2010, 37, 507–515. [Google Scholar] [CrossRef]
- Boussinesq, M.J. Theorie de I’intumescene liquid appellee onde solitaire ou de translation, se propagent dans un canal rectangulaire. Comptes Rendus Acad. Sci. 1871, 72, 755–759. [Google Scholar]
- Oberbeck, A. Über die wärmeletiung der flüssigkeiten bei berücksichtigung der strömungen infolge von temperaturdifferenzen. Ann. Phys. Chem. 1879, 7, 271–292. [Google Scholar] [CrossRef]
- Getling, A.V. Rayleigh-Bénard Convection: Structures and Dynamics; World Scientific: Singapore, 1998. [Google Scholar] [CrossRef]
- Belousov, B.P. A periodic reaction and its mechanism. In Collection of Short Papers on Radiation Medicine for 1958; Meditsina Publishers: Moscow, Russia, 1959. [Google Scholar]
- Zhabotinsky, A.M. Periodical oxidation of malonic acid in solution (a study of the Belousov reaction kinetics). Biofizika 1964, 9, 306–311. [Google Scholar]
- Cassani, A.; Monteverde, A.; Piumetti, M. Belousov-Zhabotinsky type reactions: The non-linear behavior of chemical systems. J. Math. Chem. 2021, 59, 792–826. [Google Scholar] [CrossRef]
- Buka, A.; Kramer, L. (Eds.) Pattern Formation in Liquid Crystals; Springer: New York, NY, USA, 1996. [Google Scholar]
- Wang, Z.; Servio, P.; Rey, A.D. Structure and pattern formation in biological liquid crystals: Insights from theory and simulation of self-assembly and self-organization. Front. Soft Matter 2022, 2, 904069. [Google Scholar] [CrossRef]
- Morris, S.W.; De Bruyn, J.R.; May, A.D. Electroconvection and pattern formation in a suspended smectic film. Phys. Rev. Lett. 1990, 65, 2378–2381. [Google Scholar] [CrossRef] [PubMed]
- Migler, K.B.; Meyer, R.B. Solitons and pattern formation in liquid crystals in a rotating magnetic field. Phys. Rev. Lett. 1991, 66, 1485–1488. [Google Scholar] [CrossRef] [PubMed]
- Andrade-Sliva, I.; Bortolozzo, U.; Clerc, M.G.; González-Cortés, G.; Residori, S.; Wilson, M. Spontaneous light-induced turning patterns in a dye-doped twisted nematic layer. Sci. Rep. 2018, 8, 12867. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Atzin, N.; Mozaffari, A.; Das, S.; Abbott, N.L.; De Pablo, J.J. Generation and propagation of flexoelectricity-induced solitons in nematic liquid crystals. ACS Nano 2024, 18, 10768–10775. [Google Scholar] [CrossRef] [PubMed]
- Clerc, M.G.; Gonzalez-Cortes, G.; Morel, M.J.; Hidalgo, P.I.; Vergara, J. Finger front propagation in smectic-A Fréedericksz transition. Phys. Rev. E 2022, 105, 054701. [Google Scholar] [CrossRef]
- Yoshizawa, A.; Kurauchi, M.; Kohama, Y.; Dewa, H.; Yamamoto, K.; Nishiyama, I.; Yamamoto, T.; Yamamoto, J.; Yokoyama, H. Synthesis and physical properties of α-(4-cyanobiphenyl-4′-yloxy)-ω-[4-(5-alkylpyrimidine-2-yl)phenyloxy]alkanes. Liq. Cryst. 2006, 33, 611–619. [Google Scholar] [CrossRef]
- Hegmann, T.; Kain, J.; Diel, S.; Pelzl, G.; Tschierske, C. Evidence for the existence of the McMillan phase in a binary system of a metallomesogen and 2,4,7-trinitrofluorenone. Angew. Chem. Int. Ed. 2001, 40, 887–890. [Google Scholar] [CrossRef]
- Sadashiva, B.K.; Reddy, R.A.; Pratibha, R.; Madhusudana, N.V. Biaxial smectic A phase in homologous series of compounds composed of highly polar unsymmetric substituted core molecules. J. Mater. Chem. 2002, 12, 943–950. [Google Scholar] [CrossRef]
- Yelamaggad, C.V.; Shashikala, I.S.; Rao, D.S.S.; Nair, G.G.; Prasad, S.K. The biaxial smectic (SmAb) phase in nonsymmetric liquid crystal dimers comprising two rodlike anisometric segments: An unusual behavior. J. Mater. Chem. 2006, 16, 4099–4102. [Google Scholar] [CrossRef]
- Guo, V.; Li, Z.; Fung, B.M.; O’Rear, E.A.; Harwell, J.H. Hybrid surfactants containing separate hydrocarbon and fluorocarbon chains. J. Phys. Chem. 1992, 96, 6738–6742. [Google Scholar] [CrossRef]
- Aydogan, N.; Aldis, N.; Guvenir, O. Interfacial and bulk properties of the new fluorocarbon−hydrocarbon hybrid unsymmetrical bolaform surfactant. Langmuir 2003, 19, 10726–10731. [Google Scholar] [CrossRef]
- Ito, A.; Sakai, H.; Kondo, Y.; Yoshino, N.; Abe, M. Micellar solution properties of fluorocarbon−hydrocarbon surfactants. Langmuir 1996, 12, 5768–5772. [Google Scholar] [CrossRef]
- Kondo, Y.; Yoshino, N. Hybrid fluorocarbon/hydrocarbon surfactants. Curr. Opin. Colloid Interface Sci. 2005, 10, 88–93. [Google Scholar] [CrossRef]
- Miyazawa, H.; Igawa, K.; Kondo, Y.; Yoshino, N. Synthesis and solution properties of sulfate-type hybrid surfactants with a benzene ring. J. Fluor. Chem. 2003, 124, 189–196. [Google Scholar] [CrossRef]
- Kondo, Y.; Miyazawa, H.; Sakai, H.; Abe, M.; Yoshino, N. First anionic micelle with unusually long lifetime: Self-assembly of fluorocarbon−hydrocarbon hybrid surfactant. J. Am. Chem. Soc. 2002, 124, 6516–6517. [Google Scholar] [CrossRef]
- Sagisaka, M.; Fujita, Y.; Nakanishi, Y.; Takahashi, H.; Tsuyoshi, N.; James, C.; Yoshizawa, A.; Mohamed, A.; Guittard, F.; Eastoe, J. Periodic formation/breakdown of lamellar aggregates with anionic cyanobiphenyl surfactants. Langmuir 2015, 31, 13040–13047. [Google Scholar] [CrossRef]
- Kunitake, T.; Okahata, Y. A Totally synthetic bilayer membrane. J. Am. Chem. Soc. 1977, 99, 3860–3861. [Google Scholar] [CrossRef]
- Okahata, Y.; Kunitake, T. Formation of stable monolayer membranes and related structures in dilute aqueous solution from two-headed ammonium amphiphiles. J. Am. Chem. Soc. 1979, 101, 5231–5234. [Google Scholar] [CrossRef]
- Fendler, J.H. Surfactant vesicles as membrane mimetic agents: Characterization and utilization. Acc. Chem. Res. 1980, 13, 7–13. [Google Scholar] [CrossRef]
- Zana, R. Dynamics of Surfactant Self-Assemblies: Micelles, Microemulsions, Vesicles and Lyotropic Phases; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).